平行线等分线段定理和平行截割定理

合集下载

平行线等分线段定理及证实[精华]

平行线等分线段定理及证明
附图
定理内容
如果一组等距的平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等
经过三角形一边中点且与另一边平行的直线必平分第三边
经过梯形一腰的中点且与底边平行的直线必平分另一腰
第二条定理也做：三角形过一边中点的直线平行第二边平分第三边。

也称“一二三定理”。

第二第三条即常说的“中位线定理”。

定理证明过程
证明如下：
已知：AB∥CD∥EF,GI,JL交AB,CD,EF于点G,J,H,K,I,L.（如右图)
求证：GH:HI=JK:KL
证明：
过点K作G'I'∥GI交AB ,CD ,EF于点G',H' I'.
∵ AB∥CD∥EF,G'I'∥GI
∴ 四边形GHKG',HII'H‘,GII'G是平行四边形（平行四边形判定定理），∠BJK=∠KLI,∠JG'I'=∠G'I'F（内错角相等）
∴△JG'K∽△I'LK,（相似三角形判定），GH=G'H',HI=H'I'（平行四边形对边相等）
∵G'H':H'I'=JK:KL(相似三角形性质）
∴GH:HI=JK:KL（等量代换）
推论1：过三角形一边中点与另一边平行的直线必平分第三边
推论2：过梯形一腰中点且平行于底边的直线必过另一腰中点。

平行线等分线段定理

A
B
B1
C
C1
推论2：
A
B
B1
C
C1
推论2：
A A1
l1
B
B1
l2
C
C1
l3
推论2：
A
B
B1
C
C1
推论2：
A B1
B
C
C1
推论2：
A B C
B1 C1
推论2：经过三角形一边的中点与另一边平行的直线
必平分第三边.
A
在△ACC1中， AB=BC， BB1∥CC1，
∴AB1=B1C.
B C
B1 C1
求证：AG=2GD. 分析：需要证明GH=2GD=2DH.
证明：
∵AD、BE是中线，
∴AE=EC，BD=DC，
∵CH∥EB， B
∴AG=GH，
GD=DH，
∴AG=2GD.
本题说明三角形的两中线的交点把中线分成2：1的两部分. 这个结论叫做重心定理.（现行课本已把它略去.）
A
E G
D
C
H
6、已知：梯形ABCD中，AD∥BC，
这里给出动画显示，证明的语句略去。证法1：
. . D B
A .
. H
C E
F
7、已知：△ABC中，AB=AC， D在AB上，F在AC的延长线上，且BD=CF，DF交BC于E，
求证：DE=EF. 证法2：
(以下略去。）
A
D B H
C E
F
8、已知：AC⊥AB，DB⊥AB，求证：OA=OB. 分析：需证明点O在AB的垂直平分线上.
M为AD的中点，
直线CM交AB于点P，

2021年高中数学4.1.1第一讲平行线等分线段定理和平行截割定理教案新人教版选修4

2021年高中数学4.1.1第一讲平行线等分线段定理和平行截割定理教案新人教版选修42021年高中数学4.1.1第一讲平行线等分线段定理和平行截割定理教案新人教版选修4教学目标知识与技能：复习相似三角形的定义与性质，了解平行截割定理.过程与方法：以“平行线分线段成比例定理”为起点，给出相似三角形定义后，逐步讨论相似三角形的判定定理、性质定理等等。

情感态度价值观：基本数学思想是比例及其性质的应用，通过观察、探索、发现的创造性过程，培养创新意识。

教学重点平行线分线段成比例定理. 教学难点相似三角形的判定定理、性质定理等等。

课时 3课时一．基础知识回顾1、如图15-1，l 1∥l 2∥l 3，AM=3，BM=5，CM=4.5，EF=16，则DM= ， EK= ，FK= ．答案:DM=7.5，EK=6，FK=10；2、如图，ΔABC 中，点D 为BC 中点，点E 在CA 上，且CE=EA ，AD ，BE 交于点F ，则AF:FD= ．答案:AF:FD=4:1；3、一个等腰梯形的周长是80cm ，如果它的中位线长与腰长相等，它的高是12cm ，则这个梯形的面积为 cm 2．答案:240；4、如图15-3，AB 是斜靠在墙壁上的长梯，梯脚B 距墙80cm ，梯上点D 距墙70cm ，BD 长55cm ，则梯子的长为 cm ．A MCE KFBDl 1 l 2l 3图15-1ABCD FE 图15-2AD B┐ ┐图15-3答案:440．二．典型例题讲解例1．如图15-4，在梯形ABCD 中，AD ∥BC ，∠ADC=90°，E 是AB 边的中点，连结ED 、EC ，求证：ED=EC ．分析：要证明ED=EC ，只要设法证明E 在线段CD 的垂直平分线上．证明：过E 点作EF∥BC 交DC 于F 点．∵在梯形ABCD 中，AD∥BC，∴AD∥EF∥BC ．∵E 是AB 的中点，∴F 是DC 的中点．∵∠ADC=90°，∴∠DFE=90°．∴EF⊥DC，∴EF 是DC 的垂直平分线．∴ED=EC．评析：根据平行线等分线段定理可以得到，在梯形中，若已知一腰的中点，那么过这点作底边的平行线即可得到另一腰的中点，本题正是利用这一结论再结合线段垂直平分线的性质得证的．平行截割定理的应用很广泛，它体现了从简单到复杂、从特殊到一般的数学思想，是研究相似形最重要、最基本的理论．例2．如图15-5，在ΔABC 中，作直线DN 平行于中线AM ，设这条直线交边AB 与点D ，交边CA 的延长线于点E ，交边BC 于点N ．求证：AD ∶AB=AE ∶AC ．分析：要证明AD∶AB=AE∶AC，必须找到与AD∶AB 和AE∶AC 都相等的第三个量．证明：∵AM∥EN，∴AD∶AB=NM∶MB，NM∶MC=AE∶AC．∵MB=MC，∴AD∶AB=AE∶AC．评析：本题的理论依据是平行于三角形一边的直线截其他两边，截得的三角形与原三角形的对应边成比例．由于直接证明相对较困难，所以利用了中间比进行等量代换，这种方法在有关比例式的证明中经常使用．例3．在梯形ABCD 中，点E 、F 分别在腰AB 、CD 上，EF ∥AD ，AE ∶EB=m ∶n ．求证：（m ＋n ）EF=mBC ＋nAD ．你能由此推导出梯形的中位线公式吗？分析：要证明（m ＋n ）EF=mBC ＋nAD ，只要证明EF=，又EF 与AD 、BC 都平行，因此比较容易联想到平行截割定理．证明：【方法一】如图（1），连结AC ，交EF 于点G ．∵AD∥EF∥BC，∴．∴，．∵EG∥BC，FG∥AD，A B E D C图15-4 F AB C DM E 图15-5N C B E FG∴，．∴EG=，GF=，∴EF=EG＋GF=＋，∴（m ＋n ）EF=mBC ＋nAD ．当EF 为中位线时，AE∶EB=1∶1，即m=n=1，得2EF=BC ＋AD ，即EF=（BC ＋AD ）．【方法二】如图（2），过点B 作BG∥CD，交EF 于点H ，交AD 于G ．∵AD∥EF∥BC，BG∥CD，∴BC=HF=GD．∵EH∥AG，，∴，EH=．∴EF=EH＋HF=＋HF ．∴（m ＋n ）EF=nAG ＋（m ＋n ）HF=nAG ＋mBC ＋nGD=mBC ＋nAD ．评析：这个结果称为线性插值公式．当点E 、F 在AB 、DC 的延长线上（或BA 、CD 延长线上）时，由于AE 与EB 的方向相反，可以把m∶n 理解为负值，在此理解下，此公式仍然成立．证明可仿上面的证明给出．三．精选试题演练1、如图15-6，已知：AC ⊥AB ，BD ⊥AB ，AO=78cm ，BO=42cm ，CD=159cm ，则CO= cm ， DO= cm ．答案:103.35，55.65；2、已知，如图15-7，AA ′∥EE ′，AB=BC=CD=DE ，A′B′=B′C′=C′D′=D′E′，若AA′=28mm ，EE ′=36mm ，则BB ′= ，CC ′= ，DD ′= ．答案:30mm ，32mm ，34mm ；3、如图15-8，BC ∥B′C′，AC ∥A ′C′．求证：AB ∥A ′B ′．如果BC=2B′C′，那么AB 是A ′B ′的多少倍？提示：∵BC ∥B′C′，∴．∵AC ∥A ′C′，∴．∴，∴AB ∥A ′B ′，AB=2 A ′B ′．4、如图15-9，EF ∥BC ，FD∥AB ，AE=1.8cm,BE=1.2cm,CD=1.4cm ．求BD ．答案:2.1cm ．提示：∵EF ∥BC ，∴．∵DF ∥AB ，∴，即BD==2.1cm ．5、如图15-10，过梯形ABCD 的对角线交点O 作直线EF 平行于底，分别交两腰AD 、BC 于点E 、F ，求证：．A D CB E F（2） H G AOCB D ┐ └ 图15-6A B C DEE ′D ′C ′B ′A ′图15-7ABCO A ′B ′C ′图15-8AB CDFE图15-9 CD EFO提示：∵EF ∥BC ∥AD ，∴，，，将四个等式相加得到，则．6、如图15-11，直线l 分别交ΔABC 的边BC ，CA ，AB 所在直线于点D ，E ，F ，且AF=AB ，BD=BC ，求．提示：作CN ∥AB 交DF 于点N ，由平行割线定理得，，两式相乘得．又由AF=AB 得，由BD=BC 得，则=2×=．7、已知：M ，N 分别为平行四边形ABCD 的边AB ，CD 的中点，CM ，AN 分别交BD 于点E ，F ，求证：E ，F 三等分BD ．提示：∵∥AB ∥CD 且AB=CD ，M ，N 分别为AB ，CD 的中点，∴AM ∥CN ，AM=CN ，∴四边形ABCD 是平行四边形．∴AN∥CM．∵DN=NC ，由平行截割定理知DF=FE ，同理FE=EB ．则E ，F 三等分BD ．8、如图15-12，在梯形ABCD 中，AD ∥BC ，E ，F 分别是AB ，CD 的中点．求证：GH=（BC －AD ）．提示：由条件得EF 是梯形ABCD 的中位线，则有EF ∥AD ∥BC ，由平行线等分线段定理得AH=HC ，BG=GD ，∴FH=AD ，FG=BC ，∴GH=FG －FH=（BC －AD ）．9、如图15-13，BD=CE ，求证：AC·EF=AB·DF．提示：过点D 作DG ∥AC ，交BC 于点G ，得．或过点E 作EM ∥AB ，可得．四．教学反思本讲的知识重点是平行线等分线段定理、平行截割定理及其推论，是研究相似形最重要和最基本的理论，它一方面可以直接判断线段成比例，另一方面，当不能直接证明要证的比例成立时，常用定理把两条线段的比“转移”成另两条线段的比。

一-平行线等分线段定理

2
作DE//BC
E与E重合
A
作DF//AC
BF=FC =DE D B
E
E′
F
C
如图：有块直角三角形菜地,分配给张,王,李三
家农民耕种,已知张,王,李三家人口分别为2人,4
人,6人,菜地分配方法按人口比例,并要求每户土
地均有一部分紧靠水渠AB,P处是三家合用的肥
料仓库,所以点P必须是三家地的交界地 P
要求：用尺规在图中作出
各家菜地的分界线
张王李
A
E
F
B
小结
1、平行线等分线段定理和两个推论
2、定理和推论的应用
(1)把线段n等分
(2)证明在同一直线上的线段相等
A AD
？
EF
？
E
F
？
B B
CB
？ C
作业
课本第5页习题1.1 题2,3
判断题
1、如图△ABC中点D、E三等分AB，
D
DF∥EG∥BC，DF、EG分别交AC于点 E
F、G，则点F、G三等分AC ( ) B
2、四边形ABCD中，点M、N分别在AB、
CD上若AM=BM、DN=CN 则
A
AD∥MN∥BC ( )
M
F G C D
N
3、一组平行线，任意相邻的两平行线间 B
的距离都相等，则这组平行线能等分线
段。 ( )
A
4、如图l1∥l2∥l3且AB=BC，那么
B
AB=BC=DE=EF ( )
C
C
D l1
E l2 F l3
例如图,要在一块钢板上的A、B两个小孔间再钻三个小孔，使这些小孔都在直线AB上，并且每两个小孔中心的距离相等.如果只有圆规和无刻度直尺,应当怎样确定小孔的中心位置?

平行线等分线段定理课件

求证：AG＝2DE.
图 1－1－4
【思路探究】
【自主解答】在△AEC 中， ∵AF＝FC，GF∥EC， ∴AG＝GE. ∵CE∥FB， ∴∠GBD＝∠ECD，∠BGD＝∠E. 又 BD＝DC， ∴△BDG≌△CDE. 故 DG＝DE，即 GE＝2DE，因此 AG＝2DE.
1．如果已知条件中出现中点，往往运用三角形的中位线定理来解决问题．
图 1－1－3
【证明】 ∵▱ABCD 的对角线 AC、BD 交于点 O， ∴OA＝OC，OB＝OD. ∵AA′⊥a，OO′⊥a，CC′⊥a， ∴AA′∥OO′∥CC′. ∴O′A′＝O′C′，同理：O′D′＝O′B′， ∴A′D′＝B′C′.
如图 1－1－4，在△ABC 中，AD，BF 为中线， AD，BF 交于 G，CE∥FB 交 AD 的延长线于 E.
2．有梯形且存在线段中点时，常过该点作平行线，构造平行线等分线段定理的推论 2 的基本图形，进而进行几何证明或计算．
如图 1－1－7，在梯形 ABCD 中，AD∥BC，BC＝2AD， E，F 分别是 AB，CD 的中点，EF 交 BD 于 G，交 AC 于 H. 求证：EG＝GH＝HF.
图 1－1－7
平行线等分线段定理
1．平行线等分线段定理 (1)文字语言：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．
(2)图形语言
图 1－1－1 如图 1－1－1，l1∥l2∥l3，l 分别交 l1，l2，l3 于 A， B，C，l′分别交 l1，l2，l3 于 A1，B1，C1，若 AB＝BC，则 A1B1＝B1C1 .
1．本题中由 AC⊥AB，DB⊥AB 知 AC∥DB，联想到作 OE⊥AB，再根据平行线等分线段定理证明点 E 是 AB 的中点．

5.平行线等分线段定理及推论

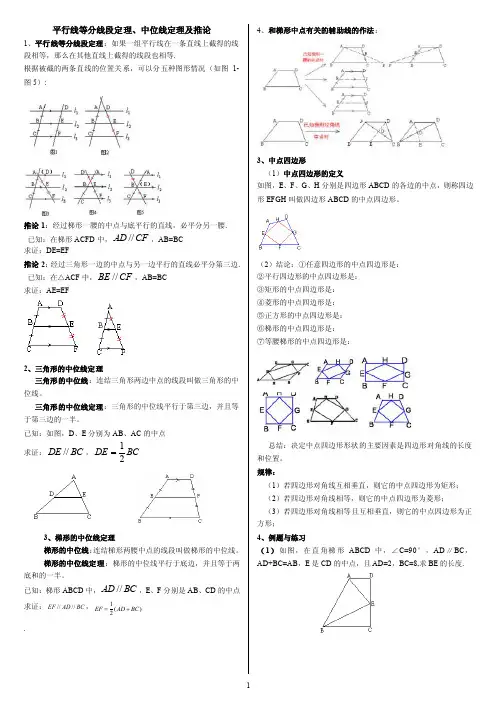
平行线等分线段定理、中位线定理及推论1、平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等.根据被截的两条直线的位置关系，可以分五种图形情况（如图1-图5）:推论1：经过梯形一腰的中点与底平行的直线，必平分另一腰. 已知：在梯形ACFD 中，CF AD //，AB=BC 求证：DE=EF推论2：经过三角形一边的中点与另一边平行的直线必平分第三边. 已知：在△ACF 中，CF BE //，AB=BC求证：AE=EF2、三角形的中位线定理三角形的中位线：连结三角形两边中点的线段叫做三角形的中位线。

三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半。

已知：如图，D 、E 分别为AB 、AC 的中点求证：BC DE //，BC DE21=3、梯形的中位线定理梯形的中位线：连结梯形两腰中点的线段叫做梯形的中位线。

梯形的中位线定理：梯形的中位线平行于底边，并且等于两底和的一半。

已知：梯形ABCD 中，BC AD //，E 、F 分别是AB 、CD 的中点求证：////EF AD BC ，1()2EF AD BC =+. 4、和梯形中点有关的辅助线的作法：3、中点四边形（1）中点四边形的定义如图，E 、F 、G 、H 分别是四边形ABCD 的各边的中点，则称四边形EFGH 叫做四边形ABCD 的中点四边形。

（2）结论：①任意四边形的中点四边形是： ②平行四边形的中点四边形是： ③矩形的中点四边形是： ④菱形的中点四边形是： ⑤正方形的中点四边形是： ⑥梯形的中点四边形是： ⑦等腰梯形的中点四边形是：总结：决定中点四边形形状的主要因素是四边形对角线的长度和位置。

规律：（1）若四边形对角线互相垂直，则它的中点四边形为矩形；（2）若四边形对角线相等，则它的中点四边形为菱形；（3）若四边形对角线相等且互相垂直，则它的中点四边形为正方形； 4、例题与练习（1）如图，在直角梯形ABCD 中，∠C=90°，AD ∥BC ，AD+BC=AB ，E 是CD 的中点，且AD=2，BC=8,求BE 的长度.（2）如图，梯形ABCD 中，AB ∥DC ，M 是腰BC 的中点，MN ⊥AD 于N 。

平行截割(平行线分线段成比例定理运用)

平行截割一、知识纵横：平行线是初中平面几何中基本而重要的图形，平行线能改变角的位置并传递角，可“送”线段到恰当处，完成等积变形，当一组平行线截两条直线时就得到比例线段，平行线分线段成比例定理是研究比例线段、相似形的重要理论．利用、挖掘、创造平行线，是运用平行线分线段成比例定理解题的关键，另一方面，需要熟悉并善于从复杂图形中分解或构造如下形如“E ”、“A ”型或“X ”型的基本图形：二、典型例题：例1.如图，已知在平行四边形ABCD 中，M 、N 为AB 的三等分点，DM 、DN 分别交AC 于P 、Q 两点，则AP ：PQ ：QC= ．思路点拨图中有形如“X ”型的基本图形，建立含AP ，PQ ，QC 的比例式，并把AP ，PQ ，QC 用同一条线段的代数式表示．例2.如图，已知在△ABC 中，AE ：EB=1：3，BD ：DC=2：1，AD 与CE 相交于F ，则FDAF FC EF +的值为( ) A ．21 B ．1 C ．23 D ．2 思路点拨已知条件没有平行线，需恰当作平行线，构造基本图形，产生含FCEF ，FD AF 的比例线段，并设法沟通已知比例式与未知比例式的联系．例3.如图，BD 、BE ，分别是∠ABC 与它的邻补角∠ABP 的平分线，AE ⊥BE ，AD ⊥BD ，E 、D 为垂足．(1)求证：四边形AEBD 为矩形；(2)若AD AE =3，F 、G 分别为AE 、AD 上的点，FG 交AB 于点H ，且3=AGAF ，求证：△AHG是等腰三角形．例4.如图，梯形AB CD 中，AD ∥BC ，AB ＝DC ．(1)如果P 、E 、F 分别是BC 、AC 、BD 的中点，求证：AB=PE+PF ；(2)如果P 是BC 上的任意一点(中点除外)，PE ∥AB ，PF ∥DC ，那么AB=PE+PF 这个结论还成立吗?如果成立，请证明；如果不成立，说明理由．思路点拨对于(2)，先假设结论成立，从平行线出发证明AB=PE+PF ，即需证明1=+ABPF AB PE ，将线段和差问题的证明转化为与比例线段有关问题的证明．注若题设条件无平行线，需作平行线．而作平行线要考虑好过哪一点作平行线，一般是由比的两条线段启发而得的，其目的是构造基本图形．平行线分线段成比例定理是证明比例线段的常用依据之一，比例线段丰富了我们研究几何问题的方法，主要体现在：(1)利用比例线段求线段的长度；(2)运用比例线段证明线段相等，线段和差倍分关系、两直线平行等问题．例5.如图，在四边形ABCD 中，AC 与BD 相交于点O ，直线l 平行于BD ，且与AB 、DC 、BC 、AD 及AC 的延长线分别相交于点M 、N 、R 、S 和P ，求证：PM ×PN=PR ×PS思路点拨由于PM 、PN 、PR 、PS 在同一条直线上，所以不能直接应用平行线分线段成比例推得结论，需观察分解图形，利用中间比沟通不同比例式的联系三、巩固提高：1．如图，△ABC 中有菱形AMPN ，如果21=MB AM ，则=BCBP ． 2．如图，AD 是BC 边上的中线，F 是AD 上一点，CF 的延长线交AB 于点E ，若31=FD AF ，则=BE AE ；若nFD AF 1=，则=BE AE ． 3．如图，已知点D 为△ABC 中AC 边的中点，AE ∥BC ，ED 交AB 于点G ，交BC 的延长线于点F ，若3=GABG ， BC=8，则AE 的长为．4．如图，在平行四边形ABCD 中，AB=4cm ，BC=lcm ，E 是CD 边上一动点，AE 、BC 的延长线交于点F ，设DE=x (㎝)，BF=y(cm)，用x 的代数式表示y 得．5．如图，已知DE ∥BC ，EF ∥AB ，现得到下列结论：①FC BF EC AE =；②BC AB BF AD =；③BC DE AB EF =；④BFEA CF CE = ．其中正确比例式的个数有( )A ．4个B ．3个C ．2个D ．1个6．如图，BD 、CE 是△ABC 的中线，P 、Q 是BD 、CE 的中点，则BCPQ 等于( ) A ．31 B ．41 C ．51 D ．617．如图，已知在平行四边形ABCD 中，O 1、O 2，O 3为对角线BD 上三点，且BO 1=O l Q 2=O 2O 3=O 3D ，连结AO l 并延长交BC 于点C ，连结EO 3延长交AD 于点F ，则AD ：FD 等于( )A ．19：2B ．9：1C ．8：1D ．7：18．如图，在△ABC 中，AB ＝AC ，D 在AB 上，E 在AC 的延长线上，BD=3CE ，DE 交BC 于F ，则DF ：FE等于( )A ．5：2B ．2：lC ．3：1D ．4：19．如图，在梯形ABCD 中，AB ∥CD ，AB=31CD ，E 是AB 上一点，AE=2BE ，M 是腰BC 的中点，连结EM 并延长交DC 的延长线于点F ，连结BD 交EF 于点N 求证：BN ：ND=l ：10．10．如图，梯形ABCD 中，AD ∥BC ，EF 经过梯形对角线的交点O ，且EF ∥AD ．(1)求证：OE=OF ，(2)求BCOE AD OE +的值；（3）求证：EFBC AD 211=+．11．已知如图1，AB ⊥BD ，CD ⊥BD ，垂足分别为B 、D ，AD 和BC 相交于点E ，EF ⊥BD 于F ，我们可以证明EFCD AB 111=+成立．若将图1中的垂直改为斜交，如图2，AB ∥CD ，AD 、BC 相交于点E ，过点E 作EF ∥AB ，交BD 于点F ，则： (1) EFCD AB 111=+还成立吗?如成立，请给出证明；如不成立，请说明理由； (2)请找出S △ABD ，S △BED ，S △BDC 间的关系式，并给出证明．12．如图，在梯形ABCD 中．AB ∥CD ，AB ＝3CD ，E 是对角线AC 的中点，BE 延长后交AD 于F ，那么FDAF = ． 13．如图，平行四边形ABCD 的对角线交于O 点，过O 任作一直线与CD 、BC 的延长线分别交于F 、E 点，设BC=a ，CD=b ，CE=c ，则CF= ．14．如图，在梯形ABCD 中，AD ∥BC ，AD= a ，BC= b ，E 、F 分别是AD 、BC 的中点，且AF 交BE 于P ，CE 交DF 于Q ，则PQ 的长为．15．如图，工地上竖立着两根电线杆AB 、CD ，它们相距15m ，分别自两杆上高出地面4m 、6m 的A 、C 处，向两侧地面上的E 、D 、B 、F 点处，用钢丝绳拉紧，以固定电线杆，那么钢丝绳AD 与BC 的交点P 离地面的高度为 m ．16．如图，在△ABC 中，D 是AC 的中点，E ，F 是BC 的三等分点．AE 、AF 分别交BD 于M 、N 两点，则BM ：MN ：ND=( )A ．3：2；1B ．4：2：lC ．5：2：1D ．5：3：217．如图，在梯形ABCD 中，AD ∥BC ，AD=3，BC=9，AB=6，CD ＝4，若EF ∥BC ，且梯形AEFD 与梯形EBCF 的周长相等，则EF 的长为( )A ．745B ．533C ．539 D ．21518．如图，平行四边形ABCD 中，F 、F 分别是边AD 、BC 的中点，AC 分别交BE 、DF 于G 、H ，试判断下列结论：①BE=DF ；②AG=GH=HC ；③EG=21BG ； ④S △ABE =3S △AGE ，其中正确的结论有( )A ．1个B ．2个C ．3个D ．4个19．如图，已知△ABC ，32=DC BD ，43=EC AE ，AD 、BE 交于F ，则FE BF FD AF ⋅的值( ) A ．37 B ．914 C ．1235 D ．1356 20．如图，已知AB ∥EF ∥CD ，AC+BD=240，BC=100，EC+ED=192，求CF ．21．如图，已知在平行四边形ABCD 中，E 为AB 边的中点，AF=21FD ，FE 与AC 相交于G ，求证：AG=51AC ．22．如图，已知M 、N 为△ABC 的边BC 上的两点，且满足BM=MN=NC ，一条平行于AC 的直线分别交AB 、AM 和AN 的延长线于点D 、E 和F ，求证：EF=3DE ．23．在△ABC 中，D 为BC 边的中点，E 为AC 边上的任意一点，BE 交AD 于点O ．某学生在研究这一问题时，发现了如下的事实：(1)当11121+==AC AE 时，有12232+==AD AO (如图甲)；（2）当21131+==AC AE 时，有22242+==AD AO (如图乙)； (3)当31141+==AC AE 时，有32252+==AD AO (如图丙)；在图丁中，当nAC AE +=11时，参照上述研究结论，请你猜想用n 表示AD AO 的一般结论，并给出证明(其中n 是正整数)24．如图，在平行四边形ABCD 中，P 1，P 2，…，P n 是BD 的n 等分点，连结AP 2并延长交BC 于点E ，连结AP n-2并延长交CD 于点F ．(1)求证：EF ∥BD ；(2)设平行四边形ABCD 的面积是S ，若S △AEF =83S ，求n 的值．。

平行截割定理-高中数学知识点讲解

平行截割定理1．平行截割定理【知识点的知识】1、平行线等分线段定理定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．推论 1：经过三角形一边的中点与另一边平行的直线必平分第三边．推论 2：经过梯形一腰的中点，且与底边平行的直线平分另一腰．2、平行线分线段成比例定理定理：三条平行线截两条直线，所得的对应线段成比例．推论：平行于三角形一边的直线截其他两边（或两边的延长线）所得的对应线段成比例．3、相似三角形的判定定义：对应角相等，对应边成比例的两个三角形叫做相似三角形．相似三角形对应边的比值叫做相似比（或相似系数）．预备定理：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似．判定定理 1：对于任意两个三角形，如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．简述为：两角对应相等，两三角形相似．判定定理 2：对于任意两个三角形，如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．简述为：两边对应成比例且夹角相等，两三角形相似．判定定理 3：对于任意两个三角形，如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似．简述为：三边对应成比例，两三角形相似．4、两个直角三角形相似的判定定理：①如果两个直角三角形的一个锐角对应相等，那么它们相似．②如果两个直角三角形的两条直角边对应成比例，那么它们相似．③如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．5、相似三角形的性质性质定理：①相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比；②相似三角形周长的比等于相似比；③相似三角形面积的比等于相似比的平方；④相似三角形外接圆（或内切圆）的直径比、周长比等于相似比，外接圆（或内切圆）的面积比等于相似比的平方．6、直角三角形的射影定理直角三角形的斜边上的高是两直角边在斜边上的射影的比例中项；两条直角边分别是他们在斜边上射影与斜边的比例中项．。

3平行线等分线段定理

D
C O
F
（二）延长EC交AB于H
四边形ACED是平行四边形 AD=CE AD//CH AB//DC
B
H
CE=CH EF=BF
AD=CH
AB//DC
证明：四边形ABCD是平行四边形 AD//BC AD=BC DF=1/2AD BE=1/2BC 四边形FDEB是平行四边形 BF//DE AF=DF
AH=HG 同理CG=HG
AH=HG=CG
练习题
1) 如图：AD是三角形ABC的中线， E为AD的中点， BE的延长线交 AC于F，求证：AF=1/3AC （1题）证明：（一）过D做DH//BF交AC于H
Ｄ D
Ｆ F
Ａ A
Ｄ D B ＢＥ E ＣC
Ｂ B
Ｃ C
推论１：
经过梯形一腰中点与底平行的直线，必平分另一腰。
推论２：经过三角形一边的中点与另一边平行的直线必平分第三边。
判断题
1、如图△ABC中点D、E三等分AB， DF∥EG∥BC，DF、EG分别交AC于点 F、G，则点F、G三等分AC ( )
练习
已知：如图，梯形ABCD中，AD∥BC，。 ∠ABC=90 M是CD的中点求证：AM=BM
D M C
分析：过M点作ME∥AD交AB A 于点E B E 又∵在梯形ABCD中，MD= MC 有线段中点时，常过该点作平行线，构造 ∴AE=EB 平行线等分线段定理易证ME是AB的垂直平分线及推论的基本图形。
C B
D
N
C
A B
D E
l1 l2 F l 3
例题讲解：
已知：线段ＡＢ求作：线段ＡＢ的五等分点。作法：１）作射线ＡＣ。ＭＤＡＮＥ

第1讲平行截割定理与相似三角形

第1讲平行截割定理与相似三角形【2013年高考会这样考】考查相似三角形的判定和性质定理的应用及直角三角形的射影定理的应用．【复习指导】复习本讲时，只要掌握好教材上的内容，熟练教材上的习题即可达到高考的要求，该部分的复习以基础知识、基本方法为主，掌握好解决问题的基本技能即可.基础梳理1．平行截割定理(1)平行线等分线段定理及其推论①定理：如果一组平行线在一条直线上截得的线段相等，那么在任一条(与这组平行线相交的)直线上截得的线段也相等．②推论：经过梯形一腰的中点而且平行于底边的直线平分另一腰．(2)平行截割定理及其推论①定理：两条直线与一组平行线相交，它们被这组平行线截得的对应线段成比例．②推论：平行于三角形一边的直线截其他两边(或两边的延长线)，截得的三角形与原三角形的对应边成比例．(3)三角形角平分线的性质三角形的内角平分线分对边成两段的长度比等于夹角两边长度的比．(4)梯形的中位线定理梯形的中位线平行于两底，并且等于两底和的一半．2．相似三角形(1)相似三角形的判定①判定定理a．两角对应相等的两个三角形相似．b．两边对应成比例且夹角相等的两个三角形相似．c．三边对应成比例的两个三角形相似．②推论：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似．③直角三角形相似的特殊判定斜边与一条直角边对应成比例的两个直角三角形相似．(2)相似三角形的性质相似三角形的对应线段的比等于相似比，面积比等于相似比的平方．(3)直角三角形射影定理直角三角形一条直角边的平方等于该直角边在斜边上射影与斜边的乘积，斜边上的高的平方等于两条直角边在斜边上射影的乘积．双基自测1．如图所示，已知a ∥b ∥c ，直线m 、n 分别与a 、b 、c 交于点A ，B ，C 和A ′，B ′，C ′，如果AB ＝BC ＝1，A ′B ′＝32，则B ′C ′＝________.解析由平行线等分线段定理可直接得到答案．答案 322．如图所示，BD 、CE 是△ABC 的高，BD 、CE 交于F ，写出图中所有与△ACE 相似的三角形________．解析由Rt △ACE 与Rt △FCD 和Rt △ABD 各共一个锐角，因而它们均相似，又易知∠BFE ＝∠A ，故Rt △ACE ∽Rt △FBE .答案 △FCD 、△FBE 、△ABD3．(2011·西安模拟)如图，在△ABC 中，M 、N 分别是AB 、BC 的中点，AN 、CM 交于点O ，那么△MON 与△AOC 面积的比是________．解析 ∵M 、N 分别是AB 、BC 中点，故MN 綉12AC ，∴△MON ∽△COA ，∴S △MON S △AOC ＝MN 2AC 2＝14.答案 1∶44．如图所示，已知DE ∥BC ，BF ∶EF ＝3∶2，则AC ∶AE ＝______，AD ∶DB ＝________.解析 ∵DE ∥BC ，∴AE AC ＝DE BC ＝EFBF .∵BF ∶EF ＝3∶2，∴AE AC ＝EF BF ＝23.∴AC ∶AE ＝3∶2.同理DE ∥BC ，得AB ∶AD ＝3∶2，即AB AD ＝32.∴AD AB ＝23，即AD AB －AD ＝23－2＝2. 即ADBD＝2.∴AD ∶BD ＝2∶1. 答案 3∶2 2∶15．(2010·广东)如图，在直角梯形ABCD 中，DC ∥AB ，CB ⊥AB ，AB ＝AD ＝a ，CD ＝a2，点E 、F 分别为线段AB 、AD 的中点，则EF ＝________.解析连接DE 和BD ，依题知，EB ∥DC ，EB ＝DC ＝a2，∴EBCD 为平行四边形，∵CB ⊥AB ，∴DE ⊥AB ，又E 是AB 的中点，故AD ＝DB ＝a ，∵E ，F 分别是AD 、AB 的中点，∴EF ＝12DB ＝12a .答案 a 2考向一平行截割定理的应用【例1】►(2011·广州测试(二))在梯形ABCD 中，AD ∥BC ，AD ＝2，BC ＝5，点E 、F 分别在AB 、CD 上，且EF ∥AD ，若AE EB ＝34，则EF 的长为________．[审题视点] 把梯形的两腰BA 、CD 分别延长交于一点，利用平行截割定理可求解．解析如图所示，延长BA 、CD 交于点P ，∵AD ∥BC ，∴P A PB ＝AD BC ＝25，∴P A AB ＝23，又∵AE EB ＝34，∴AE AB ＝37，∴P A AE ＝149，∴P A PE ＝1423.∵AD ∥EF ，∴AD EF ＝P A PE ＝1423，又AD ＝2，∴EF ＝237.答案 237在解题时要注意添加辅助线．【训练1】如图，在△ABC 中，DE ∥BC ，EF ∥CD ，若BC ＝3，DE ＝2，DF ＝1，则AB 的长为________．解析由⎩⎪⎨⎪⎧DE ∥BC ，EF ∥CD ，BC ＝3，DE ＝2⇒AE AC ＝AF AD ＝DE BC ＝23，又DF ＝1，故可解得AF ＝2，∴AD ＝3，又AD AB ＝23，∴AB ＝92. 答案 92考向二相似三角形的判定和性质的应用【例2】►已知，如图，在△ABC 中，AB ＝AC ，BD ⊥AC ，点D 是垂足．求证：BC 2＝2CD ·AC .[审题视点] 作AE ⊥BC ，证明△AEC 和△BDC 相似即可．证明过点A 作AE ⊥BC ，垂足为E ，∴CE ＝BE ＝12BC ，由BD ⊥AC ，AE ⊥BC .又∴∠C ＝∠C ，∴△AEC ∽△BDC .∴EC DC ＝AC BC ，∴12BC CD ＝ACBC，即BC 2＝2CD ·AC.判定两个三角形相似要注意结合图形的性质特点灵活选择判定定理．在一个题目中，相似三角形的判定定理和性质定理可能多次用到．【训练2】 (2011·惠州调研)如图，在△ABC 中，DE ∥BC ，DF ∥AC ，AE ∶AC ＝3∶5，DE ＝6，则BF ＝________.解析因为DE ∥BC ，所以△ADE ∽△ABC ，所以AE AC ＝DE BC ，即35＝6BC，所以BC ＝10.又DF ∥AC ，所以四边形DECF 是平行四边形，故BF ＝BC －FC ＝BC －DE ＝10－6＝4.答案 4考向三直角三角形射影定理的应用【例3】►已知圆的直径AB ＝13，C 为圆上一点，过C 作CD ⊥AB 于D (AD ＞BD )，若CD ＝6，则AD ＝________.[审题视点] △ACB为直角三角形，可直接利用射影定理求解．解析如图，连接AC ，CB ，∵AB 是⊙O 的直径，∴∠ACB ＝90° 设AD ＝x ，∵CD ⊥AB 于D ， ∴由射影定理得CD 2＝AD ·DB ，即62＝x (13－x )，∴x 2－13x ＋36＝0，解得x 1＝4，x 2＝9. ∵AD ＞BD ，∴AD ＝9. 答案9注意射影定理的应用条件．【训练3】在△ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，AD ∶BD ＝2∶3.则△ACD 与△CBD 的相似比为________．解析如图所示，在Rt△ACB中，CD⊥AB，由射影定理得：CD2＝AD·BD，又∵AD∶BD＝2∶3，令AD＝2x，BD＝3x(x＞0)，∴CD2＝6x2，∴CD＝6x.又∵∠ADC＝∠BDC＝90°，∴△ACD∽△CBD.易知△ACD与△CBD的相似比为ADCD＝2x6x＝63.即相似比为6∶3.答案6∶3高考中几何证明选讲问题(一)从近两年新课标高考试题可以看出，高考主要以填空题的形式考查平行截割定理和相似三角形判定定理的应用，难度不大．【示例1】►(2011·陕西)如图，∠B＝∠D，AE⊥BC，∠ACD＝90°，且AB＝6，AC＝4，AD＝12，则AE＝________.【示例2】►(2011·广东)如图，在梯形ABCD中，AB∥CD，AB＝4，CD＝2，E，F分别为AD，BC上的点，且EF＝3，EF∥AB，则梯形ABFE与梯形EFCD的面积比为________．。

平行线等分线段定理课件

[证明] 过点 M 作 ME∥BC 交 AB 于点 E.
∵AD∥BC，∴AD∥EM∥BC. 又∵M 是 CD 的中点， ∴E 是 AB 的中点． ∵∠ABC＝90°， ∴ME 垂直平分 AB. ∴AM＝BM.
Hale Waihona Puke 有梯形且存在线段中点时，常过该点作平行线，构造平行线等分线段定理推论2的基本图形，进而进行几何证明或计算．
[思路点拨] AF＝FC，GF∥EC → AG＝GE → △BDG≌△CDE → AG＝2DE
[证明] 在△AEC 中， ∵AF＝FC，GF∥EC， ∴AG＝GE. ∵CE∥FB， ∴∠GBD＝∠ECD，∠BGD＝∠E. 又 BD＝DC， ∴△BDG≌△CDE. 故 DG＝DE，即 GE＝2DE， ∴AG＝2DE.
[说明] (1)定理中的平行线组是指每相邻的两条距离都相等的一组特殊的平行线，它是由三条或三条以上的平行线组成的． (2)“相等线段”是指在“同一条直线”上截得的线段相等． 2．平行线等分线段定理的推论 (1)推论1：经过三角形一边的中点与另一边平行的直线必 _平__分__第三边． (2)推论2：经过梯形一腰的中点，且与底边平行的直线平分 _另__一__腰__． [说明] 推论既可用来平分已知线段，也可用来证明线段的倍数问题．
平行线等分线段定理
[例1] 如图，已知直线l1∥l2∥l3∥l4，l， l′分别交l1，l2，l3，l4于A，B，C，D和A1， B1，C1，D1，AB＝BC＝CD.
求证：A1B1＝B1C1＝C1D1.
[思路点拨] 直接利用平行线等分线段定理即可． [证明] ∵直线l1∥l2∥l3，且AB＝BC，∴A1B1＝B1C1. ∵直线l2∥l3∥l4，且BC＝CD，∴B1C1＝C1D1， ∴A1B1＝B1C1＝C1D1.

高考数学一轮复习第一节平行线截割定理与直角三角形的射影定理课件文

第一节平行线截割定理与直角三角形的射影定理
1．平行线等分线段定理 (1)定理：如果一组平行线在一条直线上截得的线段_______，
那么在其他直线上截得的线段也________． (相2)等推论1：经过三角形一边的中点与另一边平相行等的直线必
________第三边． (3)推论2：经过梯形一腰的中点，且与底边平行的直线
∴△ADB为直角三角形，
又∵DE⊥AB，由射影定理知，AD2＝AE·AB. 同理在Rt△ADC中，AD2＝AF·AC，又AE·AB＝5， ∴AF·AC＝AE·AB＝5. 【答案】 5
1．应用射影定理有两个前提条件：(1)是直角三角形； (2)是斜边上的高线．
2．直角三角形的射影定理是相似三角形性质在直角三角形中的应用，在直角三角形中，灵活利用射影定理，可简化某些命题的证明和线段的计算，研究相关的相似与比例式问题．
由AF∥BC知，
EF BE
＝
AF BC
＝2，∴BE＝
1 2
EF
＝8.
【答案，DE∥BC，且
AD DB
＝
2，那么△ADE与四边形DBCE的面积比
是________．
【解析】 ∵ADDB＝2，∴AADB＝23，
故S△ADE＝4， S△ABC 9
因此△DBF∽△ADF， ∴ADDB＝DAFF＝34.
【答案】
3 4
射影定理及应用
如图9，在△ABC中，AD⊥BC
于D，DE⊥AB于E，DF⊥AC
于F.若AE·AB＝5，则AF·
AC＝________．
【思路点拨】由垂直条件，联想射影定理，进行线段的
计算与证明．
图9
【尝试解答】 ∵AD⊥BC，
【解析】 ∵DE∥BC，∴AADB＝AACE， ∵EF∥CD，∴AADF ＝AACE ， ∴AADB＝AADF，∴AF＝AADB2＝（ 22）2＝1.

高考数学(苏教,理)配套课件：第十三章第一节平行截割定理与相似三角形

(2)从边角的关系判定两个三角形相似的条件是_____________
_____________.
(3)从边的关系判定两个三角形相似的条件是___________两__角__对. 应相等推论：如果一条直线与三角形的一条边平行，且与三角形的另
两条边相交，那么截得的三角形与原三角形相似.
两边对应成比
例且夹角相等
射影斜边
两条直角边
射影
判断下面结论是否正确(请在括号中打“√”或“×”). (1)三角形相似不具有传递性.( ) (2)相似多边形的面积比等于相似比的平方.( ) (3)所有的等腰三角形都相似.( ) (4)所有的直角三角形都相似.( )
【解析】(1)错误.根据三角形相似的判定方法可证明具有传递性. (2)正确.可以通过作辅助线将多边形化为三角形加以证明. (3)错误.虽然两边对应成比例，但所夹顶角不一定相等，故无法判断其相似. (4)错误.只满足一直角对应相等，故无法判断其相似. 答案：(1)× (2)√ (3)× (4)×
BF
FC
【规范解答】(1)过D点作DG∥BC，并交AF于G点， ∵E是BD的中点， ∴BE=DE. 又∵∠EBF=∠EDG， ∠BEF=∠DEG， ∴△BEF≌△DEG，则BF=DG， ∴BF∶FC=DG∶FC，又∵D是AC的中点，则DG∶FC=1∶2，则BF∶FC=1∶2.
(2)若△BEF以BF为底，△BDC以BC为底，则由(1)知BF∶BC=1∶3，又由BE∶BD=1∶2可知h1∶h2=1∶2，其中h1,h2分别为△BEF的边BF上的高和△BDC的边BC上的高，则
SVBEF SVBDC
11 32
16，则S∶1 S2
1∶5．
【拓展提升】 1.作辅助线的技巧见到中点，想到作中位线. 2.三角形的两类面积转化关系 (1)当两个三角形相似时，用相似三角形的面积比等于相似比的平方来转化三角形的面积. (2)当两个三角形同(等)高或同(等)底时，用三角形的面积之比为底边之比或对应高之比来转化三角形的面积.

高中数学第十一章几何证明选讲(选修4-1)

第十一章⎪⎪⎪几何证明选讲(选修4－1)第一节相似三角形的判定及有关性质1．平行线的截割定理 (1)平行线等分线段定理定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．推论1：经过三角形一边的中点与另一边平行的直线必平分第三边．推论2：经过梯形一腰的中点，且与底边平行的直线平分另一腰． (2)平行线分线段成比例定理定理：三条平行线截两条直线，所得的对应线段成比例．推论：平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例． 2．相似三角形的判定定理(1)判定定理1：两角对应相等，两三角形相似．(2)判定定理2：两边对应成比例且夹角相等，两三角形相似． (3)判定定理3：三边对应成比例，两三角形相似． 3．相似三角形的性质定理(1)性质定理：相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．(2)推论：相似三角形外接圆的直径比、周长比等于相似比，外接圆的面积比等于相似比的平方．4．直角三角形相似的判定定理(1)判定定理1：如果两个直角三角形有一个锐角对应相等，那么它们相似． (2)判定定理2：如果两个直角三角形的两条直角边对应成比例，那么它们相似． (3)判定定理3：如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．5．直角三角形射影定理直角三角形斜边上的高是两直角边在斜边上射影的比例中项；两直角边分别是它们在斜边上射影与斜边的比例中项．[小题体验]1.(教材习题改编)如图，AB ∥EM ∥DC ，AE ＝ED ，EF ∥BC ，EF＝12 cm ，则BC 的长为________ cm.解析：由⎭⎪⎬⎪⎫AB ∥EM ∥DC AE ＝ED ⇒E 为AD 中点，M 为BC 的中点，又EF ∥BC ⇒EF ＝MC ＝12 cm. ∴BC ＝2MC ＝24 cm. 答案：242.(教材习题改编)如图，D ，E 分别是△ABC 的边AB ，AC 上的点，DE ∥BC 且ADDB＝2，那么△ADE 与四边形DBCE 的面积比是________．解析：∵DE ∥BC ，∴△ADE ∽△ABC ， ∴S △ADE S △ABC ＝AD 2AB 2. ∵AD DB ＝2，∴AD AB ＝23，∴S △ADE S △ABC ＝49，故S △ADE S 四边形DBCE ＝45. 答案：451．在使用平行线截割定理时易出现对应边的对应顺序混乱，导致错误． 2．在解决相似三角形的判定或应用时易出现对应边和对应角的对应失误．3．射影定理是直角三角形中的一个重要结论，其实质就是三角形的相似．但要注意满足直角三角形射影定理结论的三角形不一定是直角三角形，所以要搞清楚定理中的条件和结论之间的关系，不能乱用．[小题纠偏]1.(2016·鞍山模拟)如图，在▱ABCD 中，E 是BC 上一点，BE ∶EC ＝2∶3，AE 交BD 于点F ，则BF ∶FD 的值为________．解析：因为AD ＝BC ，BE ∶EC ＝2∶3，所以BE ∶AD ＝2∶5，因为AD ∥BC ，所以BF ∶FD ＝BE ∶AD ＝2∶5，所以BF ∶FD 的值为25.答案：252.如图，在Rt △ABC 中，∠BAC ＝90°，AD 是斜边BC 上的高，若AB ∶AC ＝2∶1，则AD ∶BC 为________．解析：设AC ＝k ，则AB ＝2k ，BC ＝5k ， ∵∠BAC ＝90°，AD ⊥BC ， ∴AC 2＝CD ·BC ， ∴k 2＝CD ·5k ，∴CD ＝55k ，又BD ＝BC －CD ＝455k ， ∴AD 2＝CD ·BD ＝55k ·455k ＝45k 2， ∴AD ＝255k ，∴AD ∶BC ＝2∶5. 答案：2∶5考点一平行线分线段成比例定理的应用(基础送分型考点——自主练透)[题组练透]1．如图，在梯形ABCD 中，AD ∥BC ，BD 与AC 相交于点O ，过点O 的直线分别交AB ，CD 于E ，F ，且EF ∥BC ，若AD ＝12，BC ＝20，求EF 的值．解：∵AD ∥BC ， ∴OB OD ＝BC AD ＝2012＝53， ∴OB BD ＝58.∵OE ∥AD ，∴OE AD ＝OB BD ＝58.∴OE ＝58AD ＝58×12＝152，同理可求得OF ＝38BC ＝38×20＝152，∴EF ＝OE ＋OF ＝15.2．如图，在△ABC 中，点D 是AC 的中点，点E 是BD 的中点，AE 交BC 于点F ，求BFFC 的值．解：如图，过点D 作DM ∥AF 交BC 于点M . ∵点E 是BD 的中点，∴在△BDM 中，BF ＝FM . 又点D 是AC 的中点， ∴在△CAF 中，CM ＝MF ， ∴BF FC ＝BF FM ＋MC ＝12.[谨记通法]平行线分线段成比例定理及推论的应用的一个注意点及一种转化(1)一个注意点：利用平行线分线段成比例定理来计算或证明，首先要观察平行线组，再确定所截直线，进而确定比例线段及比例式，同时注意合比性质、等比性质的运用．(2)一种转化：解决此类问题往往需要作辅助的平行线，要结合条件构造平行线组，再应用平行线分线段成比例定理及其推论转化比例式解题．考点二相似三角形的判定及性质 (重点保分型考点——师生共研)[典例引领]如图，在△ABC 中，AB ＝AC ，∠BAC ＝90°，D ，E ，F 分别在AB ，AC ，BC 上，AE ＝13AC ，BD ＝13AB ，且CF ＝13BC .求证：(1)EF ⊥BC ； (2)∠ADE ＝∠EBC . 证明：设AB ＝AC ＝3a ，则AE ＝BD ＝a ，CF ＝2a . (1)CE CB ＝2a 32a ＝23，CF CA ＝2a 3a ＝23. 又∠C 为公共角，故△BAC ∽△EFC ，由∠BAC ＝90°，得∠EFC ＝90°，故EF ⊥BC .(2)由(1)得EF ＝FC AC ·AB ＝2a ，故AE EF ＝a 2a ＝22，AD BF ＝2a 22a ＝22，∴AE EF ＝AD BF， ∴△ADE ∽△FBE ，所以∠ADE ＝∠EBC .[由题悟法]证明相似三角形的一般思路(1)先找两对内角对应相等．(2)若只有一个角对应相等，再判定这个角的两邻边是否对应成比例． (3)若无角对应相等，就要证明三边对应成比例．[即时应用]如图，已知在△ABC 中，D 是BC 边的中点，且AD ＝AC ，DE ⊥BC ，DE 与AB 相交于点E ，EC 与AD 相交于点F .(1)求证：△ABC ∽△FCD ；(2)若S △FCD ＝5，BC ＝10，求DE 的长．解：(1)证明：因为DE ⊥BC ，D 是BC 的中点，所以EB ＝EC ，所以∠B ＝∠BCE .又因为AD ＝AC ，所以∠ADC ＝∠ACB.所以△ABC ∽△FCD.(2)如图，过点A 作AM ⊥BC ，垂足为点M .因为△ABC ∽△FCD ，BC ＝2CD ，所以S △ABC S △FCD ＝⎝⎛⎭⎫BC CD 2＝4.又因为S △FCD ＝5，所以S △ABC ＝20. 因为S △ABC ＝12BC ·AM ，BC ＝10，所以20＝12×10×AM ，所以AM ＝4.因为DE ∥AM ，所以DE AM ＝BDBM . 因为DM ＝12DC ＝52，BM ＝BD ＋DM ，所以DE 4＝55＋52，解得DE ＝83.考点三直角三角形中的射影定理 (重点保分型考点——师生共研)[典例引领]如图所示，CD 垂直平分AB ，点E 在CD 上，DF ⊥AC ，DG ⊥BE ，F ，G 分别为垂足．求证：AF ·AC ＝BG ·BE . 证明：因为CD 垂直平分AB ，所以∠ADC ＝∠BDC ＝90°，AD ＝D B.在Rt △ADC 中，因为DF ⊥AC ，所以AD 2＝AF ·AC . 同理BD 2＝BG ·BE . 所以AF ·AC ＝BG ·BE .[由题悟法]对射影定理的理解和应用(1)利用直角三角形的射影定理解决问题首先确定直角边与其射影．(2)要善于将有关比例式进行适当的变形转化，有时还要将等积式转化为比例式或将比例式转化为等积式，并且注意射影定理的其他变式．(3)注意射影定理与勾股定理的结合应用．[即时应用]在Rt △ACB 中，∠C ＝90°，CD ⊥AB 于D ，若BD ∶AD ＝1∶9，求tan ∠BCD 的值．解：由射影定理得CD 2＝AD ·BD ，又BD ∶AD ＝1∶9，令BD ＝x ，则AD ＝9x (x >0)． ∴CD 2＝9x 2， ∴CD ＝3x .Rt △CDB 中，tan ∠BCD ＝BD CD ＝x 3x ＝13.1.如图，在四边形ABCD 中，EF ∥BC ，FG ∥AD ，求EF BC ＋FGAD 的值．解：由平行线分线段成比例定理得 EF BC ＝AF AC ，FG AD ＝FC AC ，故EF BC ＋FG AD ＝AF AC ＋FC AC ＝AC AC ＝1.2.如图，等边三角形DEF 内接于△ABC ，且DE ∥BC ，已知AH ⊥BC 于点H ，BC ＝4，AH ＝3，求△DEF 的边长．解：设DE ＝x ，AH 交DE 于点M ，显然MH 的长度与等边三角形DEF 的高相等，又DE ∥BC ，则DE BC ＝AM AH ＝AH －MH AH ，所以x4＝3－32x 3＝2－x 2，解得x ＝43.故△DEF 的边长为43.3.如图，M 是平行四边形ABCD 的边AB 的中点，直线l 过点M 分别交AD ，AC 于点E ，F ，交CB 的延长线于点N .若AE ＝2，AD ＝6，求AFAC的值．解：∵AD ∥BC ， ∴△AEF ∽△CNF ， ∴AF CF ＝AE CN ， ∴AF AF ＋CF ＝AEAE ＋CN.∵M 为AB 的中点，∴AE BN ＝AMBM ＝1，∴AE ＝BN ， ∴AF AC ＝AF AF ＋CF ＝AE AE ＋BN ＋BC ＝AE 2AE ＋BC. ∵AE ＝2，BC ＝AD ＝6， ∴AF AC ＝22×2＋6＝15.4.如图，AD ，BE 是△ABC 的两条高，DF ⊥AB ，垂足为F ，交BE 于点G ，交AC 的延长线于H ，求证：DF 2＝GF ·HF .证明：在△AFH 与△GFB 中，因为∠H ＋∠BAC ＝90°， ∠GBF ＋∠BAC ＝90°，所以∠H ＝∠GBF .因为∠AFH ＝∠BFG ＝90°，所以△AFH ∽△GFB ，所以HF BF ＝AF GF ，所以AF ·BF ＝GF ·HF .因为在Rt △ABD 中，FD ⊥AB ，所以DF 2＝AF ·BF . 所以DF 2＝GF ·HF .5.(2016·大连模拟)如图，已知D 为△ABC 中AC 边的中点，AE ∥BC ，ED 交AB 于G ，交BC 延长线于F ，若BG ∶GA ＝3∶1，BC ＝8，求AE 的长．解：因为AE ∥BC ，D 为AC 的中点，所以AE ＝CF ，AE BF ＝AG BG ＝13.设AE ＝x ，又BC ＝8，所以x x ＋8＝13，所以x ＝4. 所以AE ＝4.6.(2016·大连模拟)如图，在△ABC 中，D 是AC 的中点，E 是BD 的中点，AE 的延长线交BC 于F .(1)求BFFC 的值；(2)若△BEF 的面积为S 1，四边形CDEF 的面积为S 2，求S 1∶S 2的值．解：(1)过点D 作DG ∥BC ，并交AF 于点G ，因为E 是BD 的中点，所以BE ＝DE . 又因为∠EBF ＝∠EDG ，∠BEF ＝∠DEG ，所以△BEF ≌△DEG ，则BF ＝DG ，所以BF ∶FC ＝DG ∶FC .又因为D 是AC 的中点，则DG ∶FC ＝1∶2，则BF ∶FC ＝1∶2，即BF FC ＝12.(2)若△BEF 以BF 为底，△BDC 以BC 为底，则由(1)知BF ∶BC ＝1∶3，又由BE ∶BD ＝1∶2，可知h 1∶h 2＝1∶2，其中h 1，h 2分别为△BEF 和△BDC 的高，则S △BEF S △BDC ＝13×12＝16，则S 1∶S 2＝1∶5. 故S 1∶S 2的值为15.7.如图，在△ABC 中，AB ＝AC ，过点A 的直线与其外接圆交于点P ，交BC 的延长线于点D.(1)求证：PC AC ＝PDBD ；(2)若AC ＝3，求AP ·AD 的值．解：(1)证明：因为∠CPD ＝∠ABC ，∠PDC ＝∠PDC ，所以△DPC ∽△DBA ，所以PC AB ＝PD BD . 又AB ＝AC ，所以PC AC ＝PD BD. (2)因为∠ABC ＋∠APC ＝180°，∠ACB ＋∠ACD ＝180°， ∠ABC ＝∠ACB ，所以∠ACD ＝∠APC .又∠CAP ＝∠DAC ，所以△APC ∽△ACD ，所以AP AC ＝AC AD. 所以AP ·AD ＝AC 2＝9.8.△ABC 中，D ，E ，F 分别是BC ，AB ，AC 上的点，AD ，EF 交于点P ，若BD ＝DC ，AE ＝AF .求证：AB AC ＝PF PE .证明：过F 作MN ∥AD 交BA 的延长线及DC 于M ，N .对△MEF ，有PF PE ＝AMAE ，因为AE ＝AF ，所以PF PE ＝AM AF. 对△MBN ，有AB AM ＝BDDN ，因为BD ＝DC ，所以AB AM ＝DCDN . 对△ADC ，有AC AF ＝DC DN ，所以AB AM ＝ACAF . 所以AB AC ＝AM AF ，所以AB AC ＝PF PE .第二节直线与圆的位置关系1．圆周角(1)定理：圆上一条弧所对的圆周角等于它所对的圆心角的一半． (2)推论1：①同弧或等弧所对的圆周角相等； ②同圆或等圆中，相等的圆周角所对的弧也相等． (3)推论2：①半圆(或直径)所对的圆周角是直角； ②90°的圆周角所对的弦是直径． 2．圆的切线(1)判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线． (2)性质定理：圆的切线垂直于经过切点的半径．(3)切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．3．弦切角定理及其推论(1)定理：弦切角等于它所夹的弧所对的圆周角． (2)推论：弦切角的度数等于它所夹的弧的度数的一半． 4．圆中的比例线段(1)相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等．(2)割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等．(3)切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．[小题体验]1.(教材习题改编)如图，已知AB ，BC 是⊙O 的两条弦，AO ⊥BC ，AB ＝3，BC ＝22，则⊙O 的半径等于________．解析：设垂足为D ，⊙O 的半径等于R ， ∵AB ，BC 是⊙O 的两条弦， AO ⊥BC ，AB ＝3，BC ＝22， ∴AD ＝1，∴R 2＝2＋(R －1)2， ∴R ＝1.5.故⊙O 的半径为1.5. 答案：1.52.如图，AC 为⊙O 的直径，OB ⊥AC ，弦BN 交AC 于点M .若OC ＝3，OM ＝1，则MN 的长为________．解析：由题意得： CM ＝CO ＋OM ＝3＋1， AM ＝AO －OM ＝3－1， BM 2＝OB 2＋OM 2＝4，BM ＝2，根据相交弦定理有CM ·AM ＝BM ·MN ，代入数值可解得MN ＝CM ·AM BM ＝(3＋1)(3－1)2＝1.答案：13.如图，⊙O 的直径AB ＝6 cm ，P 是AB 延长线上的一点，过P 点作⊙O 的切线，切点为C ，连接AC ，若∠CPA ＝30°，PC ＝________ cm.解析：连接OC ，则OC ⊥PC .又OC ＝3，∠CPA ＝30°， ∴CP ＝OCtan 30°＝3 3.答案：3 31．解决圆周角、圆心角及弦切角问题时，角之间关系易于混淆导致错误．2．使用相交弦定理与切割线定理时，注意对应线段成比例及相似三角形知识的应用．[小题纠偏]1.如图所示，CD 是圆O 的切线，切点为C ，点B 在圆O 上，BC ＝2，∠BCD ＝30°，则圆O 的面积为________．解析：设圆O的半径为r，过B作⊙O的直径BA，连接AC，则∠ACB＝90°.又由弦切角定理得∠CAB＝∠BCD＝30°，∴AB＝2BC＝4.∴r＝2，∴S＝πr2＝4π.答案：4π2.如图所示，已知⊙O的割线PAB交⊙O于A，B两点，割线PCD经过圆心，若PA＝3，AB＝4，PO＝5，则⊙O的半径为________．解析：设⊙O的半径为r.由割线定理得PA·PB＝PC·PD,3×7＝(PO－r)(PO＋r)，即21＝25－r2，∴r2＝4，∴r＝2.答案：2考点一圆周角、弦切角和圆的切线问题(基础送分型考点——自主练透)[题组练透]1.(2016·黄冈模拟)已知点C在圆O的直径BE的延长线上，直线CA与圆O相切于A，∠ACB的平分线分别交AB，AE于D，F两点，求∠AFD的大小．解：因为AC为圆O的切线，由弦切角定理，得∠B＝∠EAC.又因为CD平分∠ACB，则∠ACD＝∠BCD，所以∠B＋∠BCD＝∠EAC＋∠ACD.根据三角形外角定理，∠ADF＝∠AFD.因为BE是圆O的直径，则∠BAE＝90°，所以△ADF是等腰直角三角形．所以∠ADF＝∠AFD＝45°.2．(2015·广东高考改编)如图，已知AB是圆O的直径，AB＝4，EC是圆O的切线，切点为C，BC＝1.过圆心O作BC的平行线，分别交EC和AC于点D和点P，求OD的长．解：由题意得OP ＝12BC ＝12，OA ＝2，于是PA ＝CP ＝22－⎝⎛⎭⎫122＝152. 因为∠DCP ＝∠B ＝∠POA ，又∠DPC ＝∠APO ，所以△DCP ∽△AOP ，故PD PA ＝PCPO，即PD ＝15212×152＝152，所以OD ＝152＋12＝8.[谨记通法]1．圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系，从而证明三角形全等或相似，可求线段或角的大小．2．涉及圆的切线问题时要注意弦切角的转化；关于圆周上的点，常作直径(或半径)或向弦(弧)两端作圆周角或弦切角．考点二圆内接四边形的性质及判定 (重点保分型考点——师生共研)[典例引领](2016·昆明模拟)如图所示，已知D 为△ABC 的BC 边上一点，⊙O 1经过点B ，D ，交AB 于另一点E ，⊙O 2经过点C ，D ，交AC 于另一点F ，⊙O 1与⊙O 2的另一交点为G .(1)求证：A ，E ，G ，F 四点共圆；(2)若AG 切⊙O 2于G ，求证：∠AEF ＝∠ACG . 证明：(1)如图，连接GD ，四边形BDGE ，四边形CDGF 分别内接于⊙O 1，⊙O 2， ∴∠AEG ＝∠BDG ， ∠AFG ＝∠CDG ，又∠BDG ＋∠CDG ＝180°， ∴∠AEG ＋∠AFG ＝180°，∴A，E，G，F四点共圆．(2)∵A，E，G，F四点共圆，∴∠AEF＝∠AGF，∵AG与⊙O2相切于点G，∴∠AGF＝∠ACG，∴∠AEF＝∠ACG.[由题悟法]证明四点共圆的常用方法(1)若四个点到一定点等距离，则这四个点共圆．(2)若一个四边形的一组对角的和等于180°，则这个四边形的四个顶点共圆．(3)若一个四边形的一个外角等于它的内对角，则这个四边形的四个顶点共圆．(4)若两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线段的两个端点共圆．[即时应用](2016·吉林实验中学)如图，圆周角∠BAC的平分线与圆交于点D，过点D的切线与弦AC的延长线交于点E，AD交BC于点F.(1)求证：BC∥DE；(2)若D，E，C，F四点共圆，且AC＝BC，求∠BAC.解：(1)证明：因为DE为圆的切线，所以∠EDC＝∠DAC.又因为∠DAC＝∠DAB，∠DAB＝∠DCB，所以∠EDC＝∠DCB，所以BC∥DE.(2)因为D，E，C，F四点共圆，所以∠CFA＝∠CED，由(1)知∠ACF＝∠CED，所以∠CFA＝∠ACF.设∠DAC＝∠DAB＝x，因为AC＝BC，所以∠CBA＝∠BAC＝2x，所以∠CFA＝∠FBA＋∠FAB＝3x，在等腰△ACF中，180°＝∠CFA＋∠ACF＋∠CAF＝7x，则x≈25.7°，所以∠BAC＝2x≈51.4°.考点三与圆有关的比例线段 (重点保分型考点——师生共研)[典例引领](2015·陕西高考)如图，AB 切⊙O 于点B ，直线AO 交⊙O 于D ，E 两点，BC ⊥DE ，垂足为C .(1)证明：∠CBD ＝∠DBA;(2)若AD ＝3DC ，BC ＝2，求⊙O 的直径．解：(1)证明：因为DE 为⊙O 的直径，所以∠BED ＋∠EDB ＝90°.又BC ⊥DE ，所以∠CBD ＋∠EDB ＝90°，从而∠CBD ＝∠BED.又AB 切⊙O 于点B ，得∠DBA ＝∠BED ，所以∠CBD ＝∠DBA . (2)由(1)知BD 平分∠CBA ，则BA BC ＝ADCD＝3. 又BC ＝2，从而AB ＝3 2. 所以AC ＝AB 2－BC 2＝4，所以AD ＝3.由切割线定理得AB 2＝AD ·AE ，即AE ＝AB 2AD ＝6，故DE ＝AE －AD ＝3，即⊙O 的直径为3.[由题悟法]与圆有关的比例线段解题思路(1)见到圆的两条相交弦就要想到相交弦定理． (2)见到圆的两条割线就要想到割线定理． (3)见到圆的切线和割线就要想到切割线定理．[即时应用]1．(2015·天津高考改编)如图，在圆O 中，M ，N 是弦AB 的三等分点，弦CD ，CE 分别经过点M ，N ，若CM ＝2，MD ＝4，CN ＝3，求线段NE 的长．解：由题意可得CM ·MD ＝AM ·MB ，则2×4＝2AM 2，AM ＝2. 又CN ·NE ＝AN ·NB ，即3NE ＝4×2，解得NE ＝83.2．(2015·湖北高考改编)如图，PA 是圆的切线，A 为切点，PBC 是圆的割线，且BC ＝3PB ，求ABAC的值．解：因为PA 是圆的切线， A 为切点，PBC 是圆的割线，由切割线定理，知PA 2＝PB ·PC ＝PB (PB ＋BC )，因为BC ＝3PB ，所以PA 2＝4PB 2，即PA ＝2PB. 由弦切角定理，得∠PAB ＝∠PCA ，又∠APB ＝∠CPA ，故△PAB ∽△PCA ，所以AB AC ＝PB PA ＝12.1．(2015·重庆高考改编)如图，圆O 的弦AB ，CD 相交于点E ，过点A 作圆O 的切线与DC 的延长线交于点P ，若PA ＝6，AE ＝9，PC ＝3，CE ∶ED ＝2∶1，求BE 的长．解：由切割线定理，知PA 2＝PC ·PD ，即62＝3PD ，解得PD ＝12，所以CD ＝PD －PC ＝9，所以CE ＝6，ED ＝3.由相交弦定理，知AE ·EB ＝CE ·ED ，即9BE ＝6×3，解得BE ＝2.2．(2016·兰州双基测试)如图，在正△ABC 中，点D ，E 分别在BC ，AC 上，且BD ＝13BC ，CE ＝13CA ，AD ，BE 相交于点P .求证：(1)P ，D ，C ，E 四点共圆； (2)AP ⊥CP .证明：(1)在正△ABC 中，由BD ＝13BC ，CE ＝13CA ，知：△ABD ≌△BCE ，∴∠ADB ＝∠BEC ，即∠ADC ＋∠BEC ＝180°， ∴P ，D ，C ，E 四点共圆．(2)连接DE ，在△CDE 中，CD ＝2CE ，∠ACD ＝60°，由正弦定理知∠CED ＝90°，由P ，D ，C ，E 四点共圆知，∠DPC ＝∠DEC ， ∴AP ⊥CP .3．(2016·陕西一检)如图，设AB 为⊙O 的任一条不与直线l 垂直的直径，P 是⊙O 与l 的公共点，AC ⊥l ，BD ⊥l ，垂足分别为C ，D ，且PC ＝PD.(1)求证：l 是⊙O 的切线；(2)若⊙O 的半径OA ＝5，AC ＝4，求CD 的长．解：(1)证明：连接OP ， ∵AC ⊥l ，BD ⊥l ， ∴AC ∥BD.又OA ＝OB ，PC ＝PD ， ∴OP ∥BD ，从而OP ⊥l .∵点P 在⊙O 上，∴l 是⊙O 的切线． (2)由(1)可得OP ＝12(AC ＋BD )，∴BD ＝2OP －AC ＝10－4＝6. 过点A 作AE ⊥BD ，垂足为E ，则BE ＝BD －AC ＝6－4＝2. ∴在Rt △ABE 中，AE ＝AB 2－BE 2＝102－22＝4 6. ∴CD ＝4 6.4.(2015·全国卷Ⅰ)如图，AB 是⊙O 的直径，AC 是⊙O 的切线，BC交⊙O 于点E .(1)若D 为AC 的中点，证明：DE 是⊙O 的切线； (2)若OA ＝3CE ，求∠ACB 的大小．解：(1)证明：如图，连接AE ，由已知得AE ⊥BC ，AC ⊥AB. 在Rt △AEC 中，由已知得DE ＝DC ，故∠DEC ＝∠DCE . 连接OE ，则∠OBE ＝∠OEB. 又∠ACB ＋∠ABC ＝90°，所以∠DEC ＋∠OEB ＝90°，故∠OED ＝90°，即DE 是⊙O 的切线． (2)设CE ＝1，AE ＝x .由已知得AB ＝23，BE ＝12－x 2. 由射影定理可得AE 2＝CE ·BE ，所以x 2＝12－x 2，即x 4＋x 2－12＝0. 解得x ＝3，所以∠ACB ＝60°.5．(2015·沈阳一模)如图所示，已知AB 为圆O 的直径，C ，D 是圆O 上的两个点，CE ⊥AB 于E ，BD 交AC 于G ，交CE 于F ，CF ＝FG .(1)求证：C 是劣弧BD 的中点； (2)求证：BF ＝FG .证明：(1)∵CF ＝FG ，∴∠CGF ＝∠FCG . ∵AB 是圆O 的直径，∴∠ACB ＝∠ADB ＝π2.∵CE ⊥AB ，∴∠CEA ＝π2.∵∠CBA ＝π2－∠CAB ，∠ACE ＝π2－∠CAB ，∴∠CBA ＝∠ACE .∵∠CGF ＝∠DGA ，∠DGA ＝∠ABC ， ∴π2－∠DGA ＝π2－∠ABC ， ∴∠CAB ＝∠DAC ， ∴C 为劣弧BD 的中点．(2)∵∠GBC ＝π2－∠CGB ，∠FCB ＝π2－∠GCF ，∴∠GBC ＝∠FCB ，∴CF ＝FB ，∴BF ＝FG .6．(2016·贵州七校联考)如图，⊙O 1和⊙O 2的公切线AD 和BC 相交于点D ，A ，B ，C 为切点，直线DO 1交⊙O 1于E ，G 两点，直线DO 2交⊙O 2于F ，H 两点．(1)求证：△DEF ∽△DHG ；(2)若⊙O 1和⊙O 2的半径之比为9∶16，求DEDF 的值．解：(1)证明：∵AD 是两圆的公切线， ∴AD 2＝DE ·DG ，AD 2＝DF ·DH ， ∴DE ·DG ＝DF ·DH ，∴DE DH ＝DF DG ，又∵∠EDF ＝∠HDG ， ∴△DEF ∽△DHG .(2)连接O 1A ，O 2A ， ∵AD 是两圆的公切线， ∴O 1A ⊥AD ，O 2A ⊥AD ， ∴O 1，A ，O 2共线，∵AD 和BC 是⊙O 1和⊙O 2的公切线， DG 平分∠ADB ，DH 平分∠ADC ， ∴DG ⊥DH ，∴AD 2＝O 1A ·O 2A .设⊙O 1和⊙O 2的半径分别为9x 和16x ，则AD ＝12x ， ∵AD 2＝DE ·DG ，AD 2＝DF ·DH ，∴144x 2＝DE (DE ＋18x )，144x 2＝DF (DF ＋32x )， ∴DE ＝6x ，DF ＝4x ， ∴DE DF ＝32.7．(2016·沈阳模拟)如图，已知圆O 1与圆O 2外切于点P ，直线AB 是两圆的外公切线，分别与两圆相切于A ，B 两点，AC 是圆O 1的直径，过C 作圆O 2的切线，切点为D.(1)求证：C ，P ，B 三点共线； (2)求证：CD ＝CA .证明：(1)连接PC ，PA ，PB ，BO 2，∵AC是圆O1的直径，∴∠APC＝90°.连接O1O2必过点P，∵AB是两圆的外公切线，A，B为切点，∴设∠BAP＝∠ACP＝α，∴∠AO1P＝2α.由于O1A⊥AB，O2B⊥AB，∴∠BO2P＝π－2α，∴∠O2BP＝α.又∠ABP＋∠O2BP＝90°，∴∠ABP＋∠BAP＝90°，∴C，P，B三点共线．(2)∵CD切圆O2于点D，∴CD2＝CP·CB.在△ABC中，∠CAB＝90°，又∵AP⊥BC，∴CA2＝CP·CB，故CD＝CA.8．(2015·全国卷Ⅱ)如图，O为等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．(1)证明：EF∥BC；(2)若AG等于⊙O的半径，且AE＝MN＝23，求四边形EBCF的面积．解：(1)证明：由于△ABC是等腰三角形，AD⊥BC，所以AD是∠CAB的平分线．又因为⊙O分别与AB，AC相切于点E，F，所以AE＝AF，故AD⊥EF，从而EF∥BC.(2)由(1)知，AE＝AF，AD⊥EF，故AD是EF的垂直平分线．又EF为⊙O的弦，所以O在AD上．连接OE，OM，则OE⊥AE.由AG等于⊙O的半径得AO＝2OE，所以∠OAE ＝30°.因此△ABC 和△AEF 都是等边三角形．因为AE ＝23，所以AO ＝4，OE ＝2.因为OM ＝OE ＝2，DM ＝12MN ＝3，所以OD ＝1.于是AD ＝5，AB ＝1033. 所以四边形EBCF 的面积为12×⎝⎛⎭⎫10332×32－12×(23)2×32＝1633.。

2-平行线分割线段相关定理

一、基础知识点1．平行线分线段成比例定理：两条直线被三条平行的直线所截，截得的对应线段成比例.2．平行线等分线段定理：两条直线被三条平行的直线所截，如果在一直线上所截得的线段相等，那么在另一直线上所截得的线段也相等.3. 熟悉定理的几种变形井字型 A字型 X字型倒A字型畸形4．定理的两个推论推论1 经过梯形一腰的中点与底平行的直线，必平分另一腰。

推论2 经过三角形一般的中点与另一边平行直线必平分第三边。

5．应用平行线等分线段定理，可以等分任意一条直线。

通过中点的证明，从而转换为梯形或三角形的中位线进行解题，同时作为三角形、梯形中位线定理证明的根据.二、例题解析1．如图，直线l1∥l2∥l3，AB=5cm，BC=8cm，EG=2cm，GF=3cm.求线段DE与GC的长。

2. 如图，已知：在梯形ABCD中，AD∥BC，两腰AB、DC分别与两对角线AC、BD垂直，M、N分别是梯形两底AD、BC的中点，求证：MN⊥BC.D C B A Q M PH GF E A C B D 3. 如图，M 、N 分别为□ABCD 中AB 、CD 的中点，求证：BE ＝EF ＝FD.4. 如图，在四边形ABCD 中，90B D ∠=∠=︒，点M 在AC 上，MP BC ⊥，MQ AD ⊥，P 、Q 为垂足，求MP MQAB CD+的值。

5. 如图，梯形ABCD 中，AD BC ，2AD =，6BC =，点E F 分别是AD 、BC 的中点，BE 交AF 于点G ，DF 交CE 于点H ，那么GH 的值为多少？6. 如图，在△ABC 中，AD 是BC 边上的中线，M 是AD 的中点，BM 的延长线交AC 于N ，求证：AN=21CN 。

7. 如图，梯形ABCD 中，AD//BC ，∠B=60°,AB=BC,E 为AB 的中点，求证:△ECD 为等边三角形。

三、练习(一)填空题1.在△ABC 中，AB ＝AC ，AD ⊥BC 于D ，若DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ，则四边形AEDF 是.2.在梯形ABCD 中，AD ∥BC ，E 为DC 中点，EF ∥AD 交AB 于F ，则S △AEF ∶S △BEF ＝ .3.已知三条直线AB ∥CD ∥EF ，它们之间的距离分别为2cm ，作一条直线MN 分别与三条平行线交于30°角，且与AB 、CD 、EF 分别交于M 、N 、P ，则MN ＝ cm ，NP ＝ cm.4.如图1所示，F 为AB 的中点，FG ∥BC ，EG ∥CD ，则AG ＝，AE ＝ .5.如图2，直线l 过梯形ABCD 一腰AB 的中点E ，且平行于BC ，l 与BD ，AC 、CD 分别交于F 、G 、H ，那么，BF ＝，CG ＝，DH ＝ .图 1 图26.直角梯形ABCD 中，AD ∥BC ，∠A ＝90°，EF 是AB 的垂直平分线，EF 交AB 于E ，交CD 于F ，则DF ＝ .7.如图，已知CE 是△ABC 的中线，CD=21AD,EF ∥BD ，EG ∥AC ，若EF=10cm ，则BG = cm ，若CD=5cm ，则AF= cm.(二)选择题1.如图5，在□ABCD 中，对角线AC 、BD 相交于O ，OE ∥AB 交BC 于E ，则S △BOE ∶S □ABCD 等于( )A.1∶4B.1∶8C.1∶16D.1∶12 图52.如图6，AB ∥CD ∥EF ，AO ＝OD ＝DF ，OE ＝6，则BE ＝( )图6A.9B.10C.11D.123.AD 是△ABC 的高，DC ＝21BD ，M 、N 在AB 上，且AM ＝MN ＝NB ，ME ⊥BC 于E ，NF ⊥BC 于F ，则FC ＝( ) A.32BCB. 32BD C. 97BC D. 76BD4.在梯形ABCD 中，AB ∥DC ，DC ∶AB ＝1∶2，E 是AD 的中点，EF ∥AB 交BC 于F ，则EF ∶AB ＝( )A.31B.21 C.43 D.1(三)解答题1. 如图9，AD 是△ABC 的角平分线，E 为BC 的中点，EF ∥AB 交AD 于F ，CF 的延长线交AB 于G. 求证：AG ＝AC图9 2.△ABC 中，AB=AC ，AD ⊥BC ，P 是AD 的中点，延长BP 交AC 于点N ，求证：AN=31AC3.如图12，△ABC 中，CH 是∠ACB 的的角平分线，AD ⊥CH 于D ，DE//BC 交AB 于E ，求证：AE=EB .图124.如图13，△ABC 中，AD 、BF 为中线，AD 、BF 交于G ，CE//FB 交AD 延长线于E ，求证：AG=2DE .图13 签字确认学员教师班主任。

一平行线等分线段定理

)
A
B
C
D
E
F
填空题：
已知AD∥EF∥BC， E是AB的中点，
则DG= BG
H是 AC 的中点，
F是 CD 的中点
A
.
D
E G HF
B
C
填空题：
已知AD∥EF∥BC，
且AE=BE，那么DF= CF .
A
D
EF
CB
已知AB∥CD∥EF，
AF交BE于O，且AO=OD=DF，
若BE=60厘米，那么BO= 20 厘米.
∴A1B1=B1C1
A1
E
3
B1 1
2 4
F C1
平行线等分线段定理: 如果一组平行线在一条直线上截得
的线段相等，那么在其他直线上截得
l1
的线段也相等
l2
符号语言
l3
∵直线l1∥l2∥l3 ，AB=BC ∴ A1B1=B1C1
A B C
A1 ？B1 ？C1
推论1: 经过三角形一边的中点与另一边平行的直线，必平分第三边。
A
E
F
B
C
符号语言 ∵△ABC中，EF∥BC，AE=EB ∴AF=FC
推论2: 经过梯形一腰的中点与底平行的直线，必平分另一腰。
AD
E ？F
？
B
C
符号语言： ∵在梯形ABCD，AD∥EF∥BC，AE=EB ∴DF=FC
例题讲解：
已知：线段ＡＢ
ＨＣ
Ｇ
Ｆ
Ｍ
Ｅ
Ｄ
求作：线段ＡＢ的五等分点。作法：１）作射线ＡＣ。
上截得的线段相等，那么在其他直线上截得的线段也相等
AD

北师大版九上数学4.2平行线分线段成比例知识点精讲

平行线分线段成比例定理指的是两条直线被一组平行线（不少于3条）所截，截得的对应线段的长度成比例。

推论：平行于三角形一边的直线，截其他两边（或两边延长线）所得的对应线段成比例。

1简介编辑平行线分线段成比例亦称平行截割定理，平面几何术语，指三条平行线截两条直线，所得的四条线段对应成比例，如图1，，则平行截割定理是研究相似形最常用的一个性质，它的重要特例：在一直线上截得相等线段的一组平行线，也把其他直线截成相等的线段，称其为平行线等分线段。

[1]图12定理证明编辑设三条平行线与直线 m 交于 A、B、C 三点，与直线 n 交于 D、E、F 三点。

连结AE、BD、BF、CE根据平行线的性质可得 S△ABE=S△DBE， S△BCE=S△BEF，∴S△ABE/S△CBE=S△DBE/S△BFE根据不同底等高三角形面积比等于底的比可得：AB/BC=DE/EF。

由更比性质、等比性质得：AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF。

3定理推论编辑过一点的一线束被平行线截得的对应线段成比例。

平行于三角形一边的直线截其它两边（或两边的延长线）所得对应线段成比例。

平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例。

平行线分线段成比例定理：三条平行线截两条直线，所得对应线段成比例。

推广：过一点的一线束被平行线截得的对应线段成比例。

定理推论：①平行于三角形一边的直线截其它两边（或两边的延长线）所得对应线段成比例。

②平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例。

01平行线分线段成比例的基本事实1.基本事实：两条直线被一组平行线所截，所得的对应线段成比例。

2.符号表示：如图02平行线分线段成比例的基本事实的推论1.推论：平行于三角形一边的直线与其他两边相交，截得的对应线段成比例。

2.符号表示：如图【知识梳理】1. 平行线分线段成比例定理：两条直线被一组平行线所截，所得的对应线段成比例。

备战高考数学(精讲+精练+精析)专题13.1几何证明选讲试题文(含解析)

专题1 几何证明选讲（文科）【三年高考】1. 【2016高考天津】如图，AB是圆的直径，弦CD与AB相交于点E，BE=2AE=2，BD=ED，则线段CE的长为__________.【答案】2.【2016高考新课标1卷】如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,OA为半径作圆.(I)证明：直线AB与O相切；(II)点C,D在⊙O上,且A,B,C,D四点共圆,证明：AB∥CD.【解析】（Ⅰ）设是的中点,连结,因为,所以,．在中,,即到直线的距离等于圆的半径,所以直线与⊙相切．（Ⅱ）因为,所以不是四点所在圆的圆心,设是四点所在圆的圆心,作直线．由已知得在线段的垂直平分线上,又在线段的垂直平分线上,所以．同理可证,．所以．3．【2016高考新课标2】如图，在正方形中，分别在边上（不与端点重合），且，过点作，垂足为．(Ⅰ) 证明：四点共圆；(Ⅱ)若，为的中点，求四边形的面积．4．【2016高考新课标3】如图，中的中点为，弦分别交于两点．（I）若，求的大小；（II）若的垂直平分线与的垂直平分线交于点，证明．【解析】（Ⅰ）连结，则.因为，所以，又，所以.又，所以，因此.（Ⅱ）因为，所以，由此知四点共圆，其圆心既在的垂直平分线上，又在的垂直平分线上，故就是过四点的圆的圆心，所以在的垂直平分线上，又也在的垂直平分线上，因此．5.【2015高考新课标2，】如图，为等腰三角形内一点，圆与的底边交于、两点与底边上的高交于点，与、分别相切于、两点．（Ⅰ）证明：；（Ⅱ）若等于的半径，且，求四边形的面积．【解析】（Ⅰ）由于是等腰三角形，，所以是的平分线．又因为分别与、相切于、两点，所以，故．从而．（Ⅱ）由（Ⅰ）知，,，故是的垂直平分线，又是的弦，所以在上．连接，，则．由等于的半径得，所以．所以和都是等边三角形．因为，所以，．因为，，所以．于是，．所以四边形的面积．6．【2015高考陕西，】如图，切于点，直线交于，两点，，垂足为．（I ）证明：；（II ）若，，求的直径．7.【2015高考新课标1】如图，AB是O的直径，AC是O的切线，BC交O于E.（Ⅰ）若D为AC的中点，证明：DE是O的切线；（Ⅱ）若，求∠ACB的大小.【解析】（Ⅰ）连结AE，由已知得，AE⊥BC，AC⊥AB，在Rt△AEC中，由已知得DE=DC，∴∠DEC=∠DCE，连结OE，∠OBE=∠OEB，∵∠ACB+∠ABC=90°，∴∠DEC+∠OEB=90°，∴∠OED=90°，∴DE是圆O的切线. （Ⅱ）设CE=1，AE=,由已知得AB=，，由射影定理可得，，∴，解得=，∴∠ACB=60°.8.【2015高考湖南】如图，在圆中，相交于点的两弦，的中点分别是，，直线与直线相交于点，证明：（1）；（2）【解析】（1）如图所示，∵，分别是弦，的中点，∴，，即，，，又四边形的内角和等于，故；（2）由（I）知，，，，四点共圆，故由割线定理即得9. 【2014高考辽宁第22题】如图，EP交圆于E、C两点，PD切圆于D，G为CE上一点且，连接DG并延长交圆于点A，作弦AB垂直EP，垂足为F.（Ⅰ）求证：AB为圆的直径；（Ⅱ）若AC=BD，求证：AB=ED.【解析】（Ⅰ）因为PD=PG,所以∠PDG=∠PGD. 由于PD为切线，故∠PDA=∠DBA, 又由于∠PGD=∠EGA,故∠DBA=∠EGA,所以∠DBA+∠BAD=∠EGA+∠BAD,从而∠BDA=∠PFA.由于AF垂直EP，所以∠PFA=90°，于是∠BDA=90°，故AB是直径.(Ⅱ)连接BC，DC.由于AB是直径，故∠BDA=∠ACB=90°，在Rt△BDA与Rt△ACB中，AB=BA,AC=BD，从而Rt△BDA≌Rt△ACB，于是Rt△BDA与∠DAB=∠CBA.又因为∠DCB=∠DAB,所以∠DCB=∠CBA，故DC∥AB. 由于ED是直径，由（Ⅰ）得ED=AB.10. 【2014高考全国2第22题】如图，P是O外一点，PA是切线，A为切点，割线PBC与O相交于点B，C，PC=2PA，D为PC的中点，AD的延长线交O于点E.证明：（Ⅰ）BE=EC；（Ⅱ）AD DE=2【解析】（Ⅰ）连结AB，AC，由题意知PA=PD，故，因为，，，所以，从而，因此BE=EC. （Ⅱ）由切割线定理得：，因为，所以，，由相交弦定理得：===，所以等式成立.11. 【2014高考全国1第22题】如图，四边形是的内接四边形，的延长线与的延长线交于点，且.（Ⅰ）证明：；（Ⅱ）设不是的直径，的中点为，且，证明：为等边三角形.【三年高考命题回顾】纵观前三年各地高考试题, 高考对几何证明的考查，主要考查有关三角形相似、全等、面积、线段长度及角相等的求解及证明，以平行线等分线段定理，平行线截割定理，相似三角形的判定与性质定理，直角三角形射影定理，圆心角、圆周角定理，圆内接四边形的性质定理及判定定理，圆的割线定理，切割线定理，弦切角定理，相交弦定理等为主要考查内容，题目难度一般为中、低档，备考中应严格控制训练题的难度．【2017年高考复习建议与高考命题预测】由前三年的高考命题形式可以看出, 高考对这部分要求不是太高，要求会以圆为几何背景，利用直角三角形射影定理，圆周角定理、圆的切线的判定定理及性质定理，相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理证明三角形相似，全等，求线段长等，预测2017年高考还会以圆为几何背景，考查相交线定理，切割线定理，以及圆内接四边形的性质定理与判定定理，考查学生的数形结合的能力.“几何证明选讲”是选修系列4的一个专题,该专题在高考中只考查“相似三角形”和“圆”这两部分平面几何内容,且与另三个选修4的专题一起命题,供考生选择作答.其核心内容为:线段成比例与相似三角形,圆的切线及其性质,与圆有关的相似三角形等.对同学们来说,“几何证明选讲”是初中所学知识的深化,因而倍感亲切.试题题型为解答题,且难度不大.题型以比例问题为主，平行线分线段成比例定理、相似形、角平分线定理、直角三角形中的射影定理、圆中的割线定理、切割线定理和相交弦定理等,都涉及线段成比例,因此比例问题是本专题中所占比重最大的题型.解决这类问题,主要方法就是设法利用上述定理,并灵活变形.复习建议：圆内接四边形的重要结论：内接于圆的平行四边形是矩形；内接于圆的菱形是正方形；内接于圆的梯形是等腰梯形.应用这些性质可以大大简化证明有关几何题的推证过程.与圆有关的比例线段的证明要诀：相交弦、切割线定理是法宝，相似三角形中找诀窍，联想射影定理分角线，辅助线来搭桥，第三比作介绍，代数方法不可少，分析综合要记牢，十有八九能见效.【2017年高考考点定位】几何证明选讲的内容涉及的考点可归纳为:①相似三角形的定义与性质;②平行线截割定理;③直角三角形射影定理;④圆周角与圆心角定理;⑤圆的切线的判定定理及性质定理;⑥弦切角的性质;⑦相交弦定理;⑧圆内接四边形的性质定理和判定定理;⑨切割线定理.【考点1】相似三角形的判定与性质【备考知识梳理】1．平行线等分线段定理如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．推论1：经过三角形一边的中点与另一边平行的直线必平分第三边．推论2：经过梯形一腰的中点，且与底边平行的直线平分另一腰．2．平行线分线段成比例定理三条平行线截两条直线，所得的对应线段成比例．推论：平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例．3．相似三角形的判定与性质(1)判定定理：结论相似三角形外接圆的直径比、周长比等于相似比，外接圆的面积比等于相似比的平方射影定理直角三角形中，每一条直角边是这条直角边在斜边上的射影和斜边的比例中项；斜边上的高是两条直角边在斜边上的射影的比例中项【规律方法技巧】1．判定两个三角形相似的常规思路(1)先找两对对应角相等；(2)若只能找到一对对应角相等，则判断相等的角的两夹边是否对应成比例；(3)若找不到角相等，就判断三边是否对应成比例，否则考虑平行线分线段成比例定理及相似三角形的“传递性”．2．借助图形判断三角形相似的方法(1)有平行线的可围绕平行线找相似；(2)有公共角或相等角的可围绕角做文章，再找其他相等的角或对应边成比例；(3)有公共边的可将图形旋转，观察其特征，找出相等的角或成比例的对应边．3.比例线段常用平行线产生，利用平行线转移比例是常用的证题技巧，当题中没有平行线条件而有必要转移比例时，也常添加辅助平行线，从而达到转移比例的目的.4.判定两个三角形相似要注意结合图形特征灵活选择判定定理，特别要注意对应角和对应边．在一个题目中，相似三角形的判定定理和性质定理可能多次用到．相似三角形的性质可用来证明线段成比例、角相等；也可间接证明线段相等．5.．在使用直角三角形射影定理时，要学会将“乘积式”转化为相似三角形中的“比例式”．证题时，要注意作垂线构造直角三角形是解直角三角形时常用的方法．6.相似关系的证明中，经常要应用比例的性质：若，则①；②；③；④；⑤；⑥.7.辅助线作法：几何证明题的一个重要问题就是作出恰当的辅助线，相似关系的基础就是平行截割定理，故作辅助线的主要方法就是作平行线，见中点取中点连线利用中位线定理，见比例点取等比的分点构造平行关系，截取等长线段构造全等关系，立体几何中通过作平行线或连结异面直线上的点化异为共等等都是常用的作辅助线方法．【考点针对训练】1.【2016届河南省郑州一中高三考前冲刺四】如图所示，已知圆O外有一点P，作圆O的切线PM，M为切点，过PM的中点N作割线NAB，交圆O于A，B两点，连接PA并延长，交圆O于点C，连接PB交圆O于点D，若MC=BC.（1）求证：△APM△ABP；（2）求证：四边形PMCD是平行四边形.2.【2016年山西省右玉一中高考冲刺压轴卷三】如图，已知⊙和⊙相交于两点，为⊙的直径，直线交⊙于点，点为弧中点，连结分别交⊙、于点，连结.（Ⅰ）求证：；（Ⅱ）求证：.【解析】（Ⅰ）连结，∵为⊙的直径，∴，∵为⊙的直径，∴，∵，∴，∵为弧中点，∴，∵，∴，∴，∴，∴.（Ⅱ）由（Ⅰ）知，，∴，∴，由（Ⅰ）知，∴.【考点2】圆的有关问题【备考知识梳理】1．圆周角定理(1)圆周角：顶点在圆周上且两边都与圆相交的角．(2)圆周角定理：圆上一条弧所对的圆周角等于它所对的圆心角的一半．(3)圆心角定理：圆心角的度数等于它所对弧的度数．推论1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等．推论2：半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径．2．圆内接四边形的性质与判定定理(1)性质：定理1：圆内接四边形的对角互补．定理2：圆内接四边形的外角等于它的内角的对角．(2)判定：判定定理：如果一个四边形的对角互补，那么这个四边形的四个顶点共圆．推论：如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点共圆．另外：若两点在一条线段同侧且对该线段张角相等，则此两点与线段两个端点共圆，特别的，对定线段张角为直角的点共圆．3.圆的切线(1)直线与圆的位置关系直线与圆交点的个数直线到圆心的距离d与圆的半径r的关系相交两个d＜r相切一个d＝r相离无d＞r性质定理：圆的切线垂直于经过切点的半径．推论1：经过圆心且垂直于切线的直线必经过切点．推论2：经过切点且垂直于切线的直线必经过圆心．判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．(3)切线长定理：从圆外一点引圆的两条切线长相等．3．弦切角(1)弦切角：顶点在圆上，一边与圆相切，另一边与圆相交的角．(2)弦切角定理及推论①定理：弦切角的度数等于所夹弧的度数的一半．②推论：同弧(或等弧)上的弦切角相等，同弧(或等弧)上的弦切角等于它所夹的弧所对的圆周角． 4．与圆有关的比例线段定理名称基本图形条件结论应用相交弦定理弦AB、CD相交于圆内点P(1)PA·PB＝PC·PD；(2)△ACP∽△DBP(1)在PA、PB、PC、PD四线段中知三求一；(2)求弦长及角切割线定理PA切⊙O于A，PBC是⊙O的割线(1)PA2＝PB·PC；(2)△PAB∽△PCA(1)已知PA、PB、PC知二可求一；(2)求解AB、AC割线定理PAB、PCD是⊙O的割线(1)PA·PB＝PC·PD；(2)△PAC∽△PDB(1)求线段PA、PB、PC、PD及AB、CD；(2)应用相似求AC、BD(1)(2)割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等．(3)切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．(4)切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．【规律方法技巧】1. 与圆有关的比例线段： (1)应用相交弦定理、切割线定理要抓住几个关键内容：如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等．(2)相交弦定理、切割线定理主要是用于与圆有关的比例线段的计算与证明．解决问题时要注意相似三角形知识及圆周角、弦切角、圆的切线等相关知识的综合应用．(3)相交弦定理、切割线定理、割线定理、切线长定理统称为圆幂定理：圆的两条弦或其延长线若相交，各弦被交点分成的两条线段长的积相等.当两交点在圆内时为相交弦定理，当两交点在圆外时为割线定理，两交点重合时为切线，一条上两点重合时为切割线定理，两条都重合时为切线长定理，应用此定理一定要分清两条线段是指哪两条．2. 弦切角定理及推论的应用(1)圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系，从而证明三角形全等或相似，可求线段或角的大小．(2)涉及圆的切线问题时要注意弦切角的转化；关于圆周上的点，常作直线(或半径)或向弦(弧)两端画圆周角或作弦切角．3. 证明多点共圆，当两点在一条线段同侧时，可证它们对此线段张角相等，也可以证明它们与某一定点距离相等；如两点在一条线段异侧，则证明它们与线段两端点连成的凸四边形对角互补．4.涉及圆的切线问题时要注意弦切角的转化；关于圆周上的点，常作直径(或半径)或向弦(弧)两端画圆周角或作弦切角．5.一般地，涉及圆内两条相交弦时首先要考虑相交弦定理，涉及两条割线时要想到割线定理，涉及切线和割线时要注意应用切割线定理，要注意相交弦定理中线段之间的关系与切割线定理线段关系之间的区别．6.在平面几何的有关计算中往往要使用比例线段，产生比例线段的一个主要根据是两三角形相似．在涉及两圆的公共弦时，通常是作出两圆的公共弦．如果有过公共点的切线就可以使用弦切角定理．在两个圆内实现角的等量代换，这是解决两个圆相交且在交点处有圆的切线问题的基本思考方向．【考点针对训练】1.【2016届湖北七市教研协作体高三4月联考】已知中，，是外接圆劣弧上的点（不与点重合），延长至，延长至.（1）求证：；（2）若，中边上的高为，求外接圆的面积.2.【2016届陕西省高三下学期教学质检二】如图，已知圆与相交于两点，过点作圆的切线交圆于点，过点作两圆的割线，分别交圆、圆于点、，与相交于点. （Ⅰ）求证：；（Ⅱ）若是圆的切线，且，求的长.【解析】（Ⅰ）连接．∵是圆的切线，∴.又∵，∴，∴.（Ⅱ）证明：设，∵，∴.又∵，∴，∴.又∵，联立上述方程得到，∴.∵是圆的切线，∴.∴.【应试技巧点拨】1．辅助线作法：几何证明题的一个重要问题就是作出恰当的辅助线，相似关系的基础就是平行截割定理，故作辅助线的主要方法就是作平行线，见中点取中点连线利用中位线定理，见比例点取等比的分点构造平行关系，截取等长线段构造全等关系，立体几何中通过作平行线或连结异面直线上的点化异为共等等都是常用的作辅助线方法．2．比例的性质的应用相似关系的证明中，经常要应用比例的性质：若，则①；②；③；④；⑤；⑥.3．同一法：先作出一个满足命题结论的图形，然后证明图形符合命题已知条件，确定所作图形与题设条件所指的图形相同，从而证明命题成立．4.证明多点共圆，当两点在一条线段同侧时，可证它们对此线段张角相等，也可以证明它们与某一定点距离相等；如两点在一条线段异侧，则证明它们与线段两端点连成的凸四边形对角互补．5.与圆有关的比例线段(1)应用相交弦定理、切割线定理要抓住几个关键内容：如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等．(2)相交弦定理、切割线定理主要是用于与圆有关的比例线段的计算与证明．解决问题时要注意相似三角形知识及圆周角、弦切角、圆的切线等相关知识的综合应用．二年模拟1. 【2016年山西榆林高三二次模考】如图所示，在中，是的平分线，的外接圆交于点，.（1）求证：；（2）当时，求的长.2. 【2016年湖北八校高三四次联考】如图，在锐角三角形中，，以为直径的圆与边另外的交点分别为，且于．（Ⅰ）求证：是的切线；（Ⅱ）若，，求的长．【解析】（Ⅰ）连结则又，∴为的中点，而为中点，∴，又，∴，而是半径，∴是的切线.（Ⅱ）连，则，则，∴，设，则，由切割线定理得：，即，解得：（舍），∴EFDOC BA3. 【2016年安徽安庆二模】如图,以的边为直径作圆,圆与边的交点恰为边的中点,过点作于点．（I ）求证：是圆的切线；（II ）若,求的值．【解析】（Ⅰ）如图,连接.因为是的中点,是的中点,所以//.因为,所以,所以是⊙的切线. （Ⅱ）因为是⊙的直径,点在⊙上,所以. 又是的中点,所以. 故.因为,所以. 在直角三角形中,；在直角三角形中,. 于是.4.【2016年江西高三九校联考】如图所示，为的直径，为的中点，为的中点．（1）求证：；（2）求证：．5. 【2016年安徽淮北一中高三模考】如图，是圆上的两点，为圆外一点，连结分别交圆于点，且，连结并延长至，使．（1）求证：；（2）若，且，求．【解析】（1）连结，因为，又因为，所以，所以，由已知，所以，且，所以，所以．（2）因为，所以，则，所以，又因为，所以，所以，所以．6. 【2016年江西南昌高三一模】如图，圆M与圆N交于A， B两点，以A为切点作两圆的切线分别交圆M和圆N于C、D两点，延长DB交圆M于点E，延长CB交圆N于点F．已知BC=5， DB=10. (I)求AB的长；（II）求.【解析】（Ⅰ）根据弦切角定理，知，，∴△∽△，则，故.（Ⅱ）根据切割线定理，知，，两式相除，得（*）.由△∽△，得，，又，由（*）得．7. 【2016年河南八市高三三模】已知，内接于圆，延长到点，使得交圆于点.（1）求证：；（2）若，求证：.【解析】(1）如图，连结．．又（2）8.【2016届河北省石家庄市高三二模】如图，内接于⊙，，弦交线段于，为的中点，在点处作圆的切线与线段的延长线交于，连接.（I）求证：；（II）若，⊙的半径为，求切线的长.【解析】（I）证明：在中，弦相交于E，，又E为AC的中点，所以，又因为,，根据射影定理可得,;（II）因为为直径，所以，又因为，所以为等腰直角三角形．，根据勾股定理得，解得，所以，由（I）得所以，所以．9.【2016届陕西省高三高考全真模拟四】如下图,是圆的两条互相垂直的直径,是圆上的点,过点作圆的切线交的延长线于.连结交于点.（1）求证：；（2）若圆的半径为,求的长.【解析】（1）证明：连接,由弦切角定理知，又,即.由切割线定理得,所以.（2）由知，.在中，由得，.在中，由得，于是.10.【2016届山西右玉一中高三下学期模拟】已知如图，四边形是圆的内接四边形，对角线交于点，直线是圆的切线，切点为，.（1）若，求的长；（2）在上取一点，若，求的大小.11. 【2015届陕西西安西北工大附中高三下学期5月模拟】如图，和相交于A，B两点，过A 作两圆的切线分别交两圆于两点，连结并延长交于点．证明：（Ⅰ）；（Ⅱ）．【解析】（1）由与相切于，得，同理，所以从而，即（2）由与相切于，得，又，得从而，即，综合（1）的结论，12.【2015届陕西省西工大附中高三下学期模拟考试一】如图,⊙的直径的延长线与弦的延长线相交于点,为⊙上一点,AE＝AC ,交于点,且,（Ⅰ）求的长度．（Ⅱ）若圆F 与圆内切，直线PT与圆F切于点T，求线段PT的长度【解析】（Ⅰ）连结,由同弧对应的圆周角与圆心角之间的关系结合题中条件弧长等于弧长可得,又,,从而,故∽,∴, 由割线定理知,故．（Ⅱ）若圆F 与圆内切，设圆的半径为，因为即，所以是圆的直径，且过点圆的切线为，则，即.13.【2015届吉林省吉林市高三第三次模拟考试】如图，在△ABC 中，，以为直径的⊙O 交于，过点作⊙O 的切线交于，交⊙O 于点．（Ⅰ）证明：是的中点；（Ⅱ）证明：.【解析】（Ⅰ）证明：连接，因为为⊙O 的直径，所以，又，所以CB切⊙O于点B ，且ED 切于⊙O 于点E ，因此，，所以，得，因此，即是的中点（Ⅱ）证明：连接BF ，可知BF 是△ABE 斜边上的高，可得△ABE ∽△AFB ，于是有，即，同理可证，所以.14.【2015届辽宁省师大附中高三模拟考试】如图，圆周角的平分线与圆交于点，过点的切线与弦的延长线交于点，交于点．（1）求证：;（2）若四点共圆，且弧与弧相等，求【解析】（1）因为与圆相切，，平方，所以，，所以（2）弧与弧相等，设，，，.15.【2015届陕西省西安市第一中学高三下学期自主命题二】如图，在中，是的角平分线，的外接圆交于点，．EDCA B（Ⅰ）求证：；（Ⅱ）当，时，求的长．【解析】（Ⅰ）连接，因为是圆内接四边形，所以又∽，即有，又因为，可得因为是的平分线，所以，从而（Ⅱ）由条件知，设，则，根据割线定理得，即即，解得或（舍去），则．EDCA B拓展试题以及解析 1. 如图，内接于⊙，弦AE 交BC 于点D ，已知，，OD =1,. （Ⅰ）求；（Ⅱ）求中BC 边上的高．【入选理由】本题主要考查平面几何的相关知识，同时考查考生的逻辑推理能力.高考对平面几何的考查主要是通过三角形全等或三角形相似进行边角转化，并综合运用圆的切割线定理、相交弦定理等进行证明计算．以圆为背景是基本不变的，因而灵活应用圆的几何性质，找准有关的对应三角形、对应边和对应角是解题的关键.本题构思巧妙，难度不大，故选此题.2．如图，过圆外一点作圆的切线，切点为，割线、割线分别交圆于与、与．已知的垂直平分线与圆相切．（1）求证：；（2）若，，求的长．【解析】（1）证明：连结，∵与圆相切，∴．又为的垂直平分线，∴，∴，∴．（2）由（1）知且为的中点，∴为的中点，且，∴．∵为圆的切线，∴，∴，∴，∴．【入选理由】本题考查圆的切割线定理，弦切角定理等基础知识，意在考查逻辑思维能力和推理论证能力. 切割线定理、三角形相似、四点共圆的性质，是高考重点考查知识点，本题难度不大，故选此题.3.如图，直线AB过圆心O，交圆O于A、B，直线AF交圆O于F（不与B重合），直线与圆O相切于C，交AB于E，且与AF垂直，垂足为G，连接AC．求证：（Ⅰ）；（Ⅱ）．【证明】（Ⅰ）连接，是直径，，．切圆于，．．（Ⅱ）连接，切圆于，．又∽．．【入选理由】本题考查圆的弦切角定理、三角形相似等基础知识，意在考查逻辑思维能力和推理论证能力.本题由弦切角定理入手，得出三角形相似，从而可证，本题难度不大，故选此题.4.如图，是⊙的直径，是圆上两点，交于点，若，．（Ⅰ）求证：；（Ⅱ）求线段的长度．【入选理由】本题考查平面几何的证明，具体涉及圆的性质，四点共圆，割线定理等基础知识，意在考察学生推理证明和逻辑思维能力.本题考查知识基础，综合性强，是高考出题方向，故选此题.5.如图，圆内接四边形满足∥，在的延长线上，且. 若，.（Ⅰ）证明：；（Ⅱ）求的长.【解析】（Ⅰ）由知是圆的切线. ∴由弦切线角定理得，又，∴，∴；（Ⅱ）由（Ⅰ）知，又，∴∽，∴，又，，∴，∵，∴. 【入选理由】本题考查圆的切线的性质，圆內接四边形的性质，三角形相似等基础知识，意在考察学生推理证明和逻辑思维能力.本题考查知识基础，难度不大，故选此题.6.如图，点P是△ABC的外接圆O在C点的切线与直线AB的交点．（Ⅰ）若∠ACB＝∠APC，证明：BC⊥PC；（Ⅱ）若D是圆O上一点，∠BPC=∠DAC，AC=，AB=，PC＝4，求CD的长．【证明】（Ⅰ）由弦切角定理知，∠ABC=∠ACP，∵∠ACB＝∠APC，∴△ACB∽△APC，∴∠BAC=∠CAP，∵∠BAC+∠CAP=，∴∠BAC=∠CAP=90°，∴BC是圆O的直径，又PC是圆O的切线，∴BC⊥PC. （Ⅱ）由切割线定理知，，即，即，解得（负值舍去），由弦切角定理及同弧所对的圆周角相等知，∠ACP=∠ABC=∠CDA，∵∠BPC=∠DAC，∴△CAD∽△APC，∴，∴=.【入选理由】本题考查三角形相似的判定与性质、弦切角定理、切割线定理等基础知识，意在考查学生推理证明和逻辑思维能力.本题第一问由弦切角入手，得三角形相似，从而得结论，第二问由切割线定理入手，结合弦切角定理及同弧所对的圆周角相等，得三角形相似，像这种题型考查知识基础，综合性强，是高考出题方向，故选此题.7.如图所示，在四边形中，交于点，.（Ⅰ）求证：、、、四点共圆;（Ⅱ）过作四边形外接圆的切线交的延长线于，,求证：平分.【证明】（Ⅰ）∵,∴,,∵,, ∴,,∴=,=,=,=,∴=+++=+++==,∴、、、四点共圆；（Ⅱ）由弦切角定理可知：∠=∠，∵,∴∽,∴=，∵，∴=,∴=,∴=,∴=,∴=∠,∴平分.。

(3)平行线等分线段定理

E
.
M B C
.F
∵四边形ABCD是平行四边形， ∴AB=DC，AB∥DC； ∵E、F分别是AB、DC的中点，∴AE=FC， ∴四边形AECF是平行四边形，∴EC∥AF, ∴BM=MN, MN=ND, 即BM=MN=ND.
例题讲解：
2.已知：梯形ABCD中，AD∥BC， E是AB边的中点， E EF∥DC，交BC于F，求证：DC=2EF. 证明：作EM∥BC交DC于M， B ∵E是梯形ABCD的腰AB的中点，
符号语言：
边平行的直线，必平分第三边。
符号语言 ∵△ABC中，EF∥BC，AE=EB ∴AF=FC
∵在梯形ABCD，AD∥EF∥BC，AE=EB
∴DF=FC
判断题：
小试牛刀
(
AC=CE， 1.若AB∥CD∥EF，则 BD=DF=AC=CE. A
×)
B D F
C E
填空题：
小试牛刀
E是AB的中点， 2.已知AD∥EF∥BC，则DG= BG H是的中点 AC 的中点，
平行线等分线段定理:
如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等.
已知：如图，直线 l1∥l2∥l3， AB=BC
求证： A1B1=B1C1 证明：过B1作EF∥AC，分别交l1、l3于点E、F
l1 l2 l3
A B
A1 B1
3 1 2 4
E
C
∵ l1∥l2∥l3 ∴得到□ ABB1E和□ BCFB1 ∴EB1 =AB ，B1F=BC ∵AB=BC ∴EB1=B1F 又∠1=∠2，∠3=∠4 ∴△A1B1E≌△C1B1F ∴A1B1=B1C1
A
.
F

平行线等分线段定理

平行线等分线段定理平行线等分线段定理平行线等分线段定理教学建议1．定理：如果一组平行线在一条直线上截得的线段相等，那么在其他需直线上截得的线段也相等．注意事项：定理中的平行线组是指每相邻的两条距离都相等的特殊的平行线组；它是由三条或三条以上的平行线组成．定理的作用：可以用来证明同一直线上的线段相等；可以等分线段．2．的推论推论1：经过梯形一腰的中点与底平行的直线，必平分另一腰．推论2：经过三角形一边的中点与另一边平行的直线，必平分第三边。

记忆方法：“中点”＋“平行”得“中点”．推论的用途：（1）平分已知线段；（2）证明线段的倍分．重难点分析本节的重点是.因为它不仅是推证三角形、梯形中位线定理的基础，而且是第五章中“平行线分线段成比例定理”的基础. 本节的难点也是.由于学生初次接触到，在认识和理解上有一定的难度，在加上的两个推论以及各种变式，学生难免会有应接不暇的感觉，往往会有感觉新鲜有趣但掌握不深的情况发生，教师在教学中要加以注意. 教法建议的引入生活中有许多的例子，并不陌生，的引入可从下面几个角度考虑：①从生活实例引入，如刻度尺、作业本、栅栏、等等；②可用问题式引入，开始时设计一系列与概念相关的问题由学生进行思考、研究，然后给出和推论.示例一、教学目标1. 使学生掌握及推论. 2. 能够利用任意等分一条已知线段，进一步培养学生的作图能力．3. 通过定理的变式图形，进一步提高学生分析问题和解决问题的能力．4. 通过本节学习，体会图形语言和符号语言的和谐美二、教法设计学生观察发现、讨论研究，教师引导分析三、重点、难点1．教学重点：2．教学难点：四、课时安排l课时五、教具学具计算机、投影仪、胶片、常用画图工具六、师生互动活动设计教师复习引入，学生画图探索；师生共同归纳结论；教师示范作图，学生板演练习七、教学步骤【复习提问】1．什么叫平行线？平行线有什么性质．2．什么叫平行四边形？平行四边形有什么性质？【引入新课】由学生动手做一实验：每个同学拿一张横格纸，首先观察横线之间有什么关系？（横线是互相平等的，并且它们之间的距离是相等的），然后在横格纸上画一条垂直于横线的直线，看看这条直线被相邻横线截成的各线段有什么关系？（相等，为什么？）这时在横格纸上再任画一条与横线相交的直线，测量它被相邻横线截得的线段是否也相等？（引导学生把做实验的条件和得到的结论写成一个命题，教师总结，由此得到）：如果一组平行线在一条直线上挂得的线段相等，那么在其他直线上截得的线段也相等．注意：定理中的“一组平行线”指的是一组具有特殊条件的平行线，即每相邻两条平行线间的距离都相等的特殊平行线组，这一点必须使学生明确．下面我们以三条平行线为例来证明这个定理（由学生口述已知，求证）．已知：如图，直线，．求证：．分析1：如图把已知相等的线段平移，与要求证的两条线段组成三角形（也可应用平行线间的平行线段相等得），通过全等三角形性质，即可得到要证的结论．（引导学生找出另一种证法）分析2：要证的两条线段分别是梯形的腰，我们借助于前面常用的辅助线，把梯形转化为平行四边形和三角形，然后再利用这些熟悉的知识即可证得．证明：过点作分别交、于点、，得和，如图．∴∵，∴又∵，，∴∴为使学生对定理加深理解和掌握，把知识学活，可让学生认识几种定理的变式图形，如图（用计算机动态演示）．引导学生观察下图，在梯形中，，，则可得到，由此得出推论1．推论1：经过梯形一腰的中点与底平行的直线，必平分另一腰．再引导学生观察下图，在中，，，则可得到，由此得出推论2．推论2：经过三角形一边的中点与另一边平行的直线必平分第三边．注意：推论1和推论2也都是很重要的定理，在今后的论证和计算中经常用到，因此，要求学生必须掌握好．接下来讲如何利用来任意等分一条线段．例已知：如图，线段．求作：线段的五等分点．作法：①作射线．②在射线上以任意长顺次截取．③连结．④过点．、、分别作的平行线、、、，分别交于点、、、．、、、就是所求的五等分点．（说明略，由学生口述即可）【总结、扩展】小结：（l）及推论．（2）定理的证明只取三条平行线，是在较简单的情况下证明的，对于多于三条的平行线的情况，也可用同样方法证明．（3）定理中的“平行线组”，是指每相邻两条平行线间的距离都相等的特殊平行线组．（4）应用定理任意等分一条线段．八、布置作业教材P188中A组2、9 九、板书设计十、随堂练习教材P182中1、2。

平行线等分线段定理和平行截割定理

平行线等分线段定理及证实[精华]

平行线等分线段定理

2021年高中数学4.1.1第一讲平行线等分线段定理和平行截割定理教案新人教版选修4

一-平行线等分线段定理

平行线等分线段定理 课件

5.平行线等分线段定理及推论

平行截割(平行线分线段成比例定理运用)

平行截割定理-高中数学知识点讲解

3平行线等分线段定理

第1讲平行截割定理与相似三角形

平行线等分线段定理 课件

高考数学一轮复习 第一节平行线截割定理与直角三角形的射影定理课件 文

高考数学(苏教,理)配套课件：第十三章 第一节平行截割定理与相似三角形

高中数学第十一章 几何证明选讲(选修4-1)

2-平行线分割线段相关定理

一平行线等分线段定理

北师大版九上数学4.2平行线分线段成比例知识点精讲

备战高考数学(精讲+精练+精析)专题13.1几何证明选讲试题文(含解析)

(3)平行线等分线段定理

平行线等分线段定理

平行线等分线段定理课件

平行线等分线段定理课件

高考数学一轮复习第一节平行线截割定理与直角三角形的射影定理课件文

高考数学(苏教,理)配套课件：第十三章第一节平行截割定理与相似三角形

高中数学第十一章几何证明选讲(选修4-1)