含参一元一次方程解法doc资料
6.3一元一次方程及其解法3

求方程的整数解
2x 1 2x 2 3
x 1或x 0
小结
1、含参数的一元一次方程的解法
2、绝对值方程的解法
绝对值方程
2 x 1 x 2 3、解方程 (1ห้องสมุดไป่ตู้
1 ( 2 ) x 1 2 0.5 x 1 0 2
4、解方程
(1) x 1 x 2 5
(2) 2 x 1 x 2 5
说明:去掉绝对值符号的关键是确定绝对 值记号内式子的值是正还是负.为此先要求 出使它们的值为0的x值;并把求出的值在 数轴上表示出来,将所有的有理数分类; 然后分别加以讨论,即可求出绝对值方程 的解.
6.3 一元一次方程及其解法3 ---含参方程&绝对值方程
含参数的一元一次方程
解关于x的方程
解关于x的方程 (a-1)x=b
已知关于x的方程k(x-1)=6-k (1)若方程有解,求有理数k的范围 (2)若方程有正整数解,求k的值.
(3)若方程有负数解,求有理数k的 范围
1、解关于x的方程 2ax-4=(a+1)x
2、若上述方程的解是整数,求正整数a 的值 3、解关于x的方程:ax-b=cx+d
绝对值方程
1、解方程 (1) 2 3x 1 5
(2) 2x 1 0
5 ( 3 ) 3x 2 - 3
绝对值方程
2、已知方程 ax b c ,a 0 当a、b、c满足什么条件有: (1)方程有两个解; (2)方程只有一个解; (3)无解.
含参数的一元一次方程
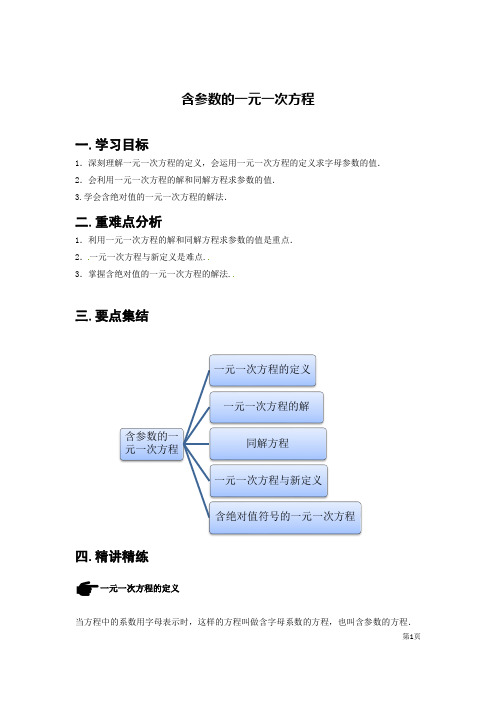
含参数的一元一次方程一.学习目标1.深刻理解一元一次方程的定义,会运用一元一次方程的定义求字母参数的值. 2.会利用一元一次方程的解和同解方程求参数的值. 3.学会含绝对值的一元一次方程的解法.二.重难点分析1.利用一元一次方程的解和同解方程求参数的值是重点. 2.一元一次方程与新定义是难点. 3.掌握含绝对值的一元一次方程的解法.三.要点集结四.精讲精练一元一次方程的定义当方程中的系数用字母表示时,这样的方程叫做含字母系数的方程,也叫含参数的方程.含参数的一元一次方程一元一次方程的定义一元一次方程的解同解方程一元一次方程与新定义含绝对值符号的一元一次方程只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,它的一般形式是ax+b=0(a,b是常数且a≠0),高于一次的项系数是0.注意:(1)含字母参数的一元一次方程中未知数是x,且x的指数是1,(2)x的系数不等于0,(3)x的指数高于一次的项系数是0.例1.已知关于x的方程(m+5)x|m|﹣4+18=0是一元一次方程.试求:(1)m的值;(2)代数式的值.【答案】解:(1)由题意得,|m|﹣4=1,m+5≠0,解得,m=5;(2)当m=5时,原方程化为10x+18=0,解得,x=﹣,∴==﹣.练习1.已知关于x的方程(k﹣1)x|k|﹣1=0是一元一次方程,则k的值为.【答案】-1【解析】根据一元一次方程定义可得:|k|=1,且k﹣1≠0,再解即可.练习2.已知方程(a﹣1)x|a|+2=﹣6是关于x的一元一次方程,则a=【答案】﹣1【解析】根据一元一次方程的定义,得到|a|=1和a﹣1≠0,结合绝对值的定义,解之即可.练习3.已知ax2+2x+14=2x2﹣2x+3a是关于x的一元一次方程,则其解是().A、x=﹣2B、x=12C、x=﹣12D、x=2【答案】A【解析】根据一元一次方程的定义,2次方的项的系数必为零,才能满足题意要求,故解:方程整理得:(a-2)x+4x+14-3 a=0,由方程为一元一次方程,得到a-2=0,即a=2,方程为4x+14-6=0,解得:x=-2.小结根据定义判断含字母参数的一元一次方程,一般先将方程化为标准型,x的指数高于一次的项系数是0,x的指数为1的项的系数不等于0。
一元一次方程含参问题

例5、若a,b为定值,关于x的一元一次方 2kx a x bk 1 程 ,无论k为何值 3 6 时,它的解总是x=1,求a,b的值。 解:将x=1代入 2kx a x bk
3 2k a 1 bk 1 3 6 6 1
化简得:(4+b)k=7-2a ① ∵无论ห้องสมุดไป่ตู้为何值时,原方程的解总是x=1 ∴无论k为何值时,①总成立 ∴4+b=0且7-2a=0,解得a=-4,b=3.5
4、整数解问题
例6、已知关于x的方程9x+3=kx+14有整数解, 求整数k。
解:由题意知:(9-k)x=11
11 x 9k
∵x,k均为整数 ∴9-k= ±1, ±11 ∴k=-2,8,10,20
练习: 2 (1)关于x的方程 (n 1) x (m 1) x 3 0 是一元一次方程 ①则m,n应满足的条件为:m ≠1 ,n =1 ; ②若此方程的根为整数,求整数m=-2,0,2,4 。
练习: (1)已知关于x的方程2a(x-1)=(5-a)x+3b有无 数个解,则a= 5 ,b= 10 。
3
2
(2)已知关于x的方程a(2x-1)=3x-2无解,则 a= 3 。 (3)(3a 2b) x ax b 0 是关于x的一元 一次方程,且x有唯一值,则x= 3 。
2
9
2
2
一、含有参数的一元一次方程
2、同解方程
ax 2 0 例2、关于x的方程4x-1=-5与 3
的解相同,求a的值;若解互为倒数,互 为相反数时,求a的值 练习:当m= 4x-2m=3x-1的解是x=2x-3m的解的2倍。
1 4 时,关于x的方程
含参数的一元一次方程、含绝对值的一元一次方程

含参数的一元一次方程、含绝对值的一元一次方程一. 含有参数的一元一次方程1. 整数解问题2. 两个一元一次方程同解问题3. 已知方程解的情况求参数4. 一元一次方程解的情况(分类讨论)二: 解含有绝对值的一元一次方程一. 含有参数的一元一次方程1. 整数解问题(常数分离法)例题1:⑴ 【中】 已知关于x 的方程9314x kx +=+有整数解,求整数_____k = 答案:(9)11k x -=119x k=- ∵,x k 均为整数∴91,11k -=±±∴2,8,10,20k =-⑵ 【中】 关于x 的方程()2(1)130n x m x -+--=是一元一次方程 (1)则,m n 应满足的条件为:___m ,____n ;(2)若此方程的根为整数,求整数=____m答案:(1)1,1≠=;(2)由(1)可知方程为(1)3m x -=, 则31x m =- ∵此方程的根为整数.∴31m -为整数 又∵m 为整数,则13,1,1,3m -=--∴2,0,2,4m =-测一测1: 【中】 关于x 的方程143+=+x ax 的解为正整数,则整数a 的值为( )A.2B.3C.1或2D.2或3答案:D方程143+=+x ax 可化简为:()24-=-x a 解得42--=a x 解为正整数,()214--=-或a 32或=a测一测2: 【中】 关于x 的方程917x kx -=的解为正整数,则k 的值为___________ 答案:917x kx -=可以转化为(9)17k x -=即:179x k =-,x 为正整数,则88k =或-测一测3: 【中】m 为整数,关于x 的方程 6x mx =- 的解为正整数,求_____m = 答案: 由原方程得:61x m =+ ,x 是正整数,所以1m + 只能为6的正约数, 11,2,3,6m += 所以0,1,2,5m =2. 两个一元一次方程同解问题例题2:⑴ 【易】若方程29ax x -=与方程215x -=的解相同,则a 的值为_________【答案】第二个方程的解为3x =,将3x =代入到第一个方程中,得到369a -= 解得 5a =⑵ 【中】若关于x 的方程:k (x +3)(2)10354k x x --=-与方程1252(1)3x x --+=的解相同,求___k = 【答案】由方程k(x+3)(2)10354k x x --=-解得x=2, 代入方程1252(1)3x x --+=中解得k=4测一测1:【易】方程213x +=与202a x --=的解相同,则a 的值是( ) A 、7 B 、0 C 、3 D 、5【答案】D第一个方程的解为1x =,将1x =代入到第二个方程中得:12=02a --,解得5a = 例题3: 【中】 若关于x 的方程231x -=和32x k k x -=-解互为相反数,则k 的值为() A. 143- B. 143 C. 113k =- D. 113k = 【答案】 A首先解方程231x -=得:2x =;把2x =-代入方程32x k k x -=-,得到:232k k x --=-; 得到:143k =- 测一测1:【中】当m=_______时,关于x 的方程4231x m x -=-的解是23x x m =-的解的2倍【答案】由4231x m x -=-可知21x m =-,由23x x m =-可知3x m =∵ 关于x 的方程4231x m x -=-的解是23x x m =-的2倍∴2123m m -=⨯解得14m =- 3. 已知方程解的情况求参数例题4:⑴ 【易】已知方程()2412x a x +=-的解为3x =,则____a = 【答案】根据方程的意义,把3x =代入原方程,得()234312a ⨯+=-,解这个关于a 的方程,得10a =测一测1:【易】 若3x =是方程123x b -=的一个解,则b=________。
含参一元一次方程

含参数的一元一次方程
一元一次方程:
(一)定义:在一个方程中,只含有一个未知数,且未知数的次数都是1, 这样的方程叫做一元一次方程.
(二)任何一个一元一次方程,通过变形后,可化为:
关于x的方程 ax=b(a≠0)
参数是用字 母表示的
字母x是未知数
字母a,b是参数
即3b﹣6a+2=﹣4
含参数的一元一次方程
与定义相关:
y=9
方法一:代入法 方法二:
先求得m的值 再求得y的值 已知方程的解,可 以使用代入法,求 参数的值.
(y-2)看作整体x 还可使用整体思 ∴y-2=x=7 想,求参数.
含参数的一元一次方程
( 2 ) 解 第 二 方 程 2x ﹣ 2a = x+6a , 解得:x=8a,
∵m≠3, ∴ m-3 ≠0, 原方程为一元一次方程.
含参数的一元一次方程
解:3(mx+1)=2(x-n) (3m-2)x= ﹣2n﹣3
(1)当3m-2 ≠0, 原方程为一元一次方程,
(2)当3m-2 =0,且﹣2n﹣3=0
∴原方程有无数个解. (3)当3m-2=0,且﹣2n﹣3≠0
∴原方程有唯一解.
3a-5 =0
2a+3b ≠0
含参数的一元一次方程
(4k-10)x= 0 4k-10= 0
含参数的一元一次方程
∴原方程无解.
含参数的一元一次方程
a,b
ห้องสมุดไป่ตู้
a≠0
a=0
b=0
a=0
b≠0
无数个
含参数的一元一次方程
解: mx-x=-2018 (m-1)x=-2018
专题3.2 一元一次方程中含参数问题(六大类型)(原卷版)

专题3.2 一元一次方程中含参数问题(六大类型)【题型1:一元一次方程的定义】【题型2:一元一次方程的解】【题型3:一元一次方程-整体法】【题型4:一元一次方程-同解】【题型5:一元一次方程-错解】【题型6:根据特殊关系列一元一次方程并解答】【题型1:一元一次方程的定义】【典例1】当a=时,关于x的方程3x a﹣2﹣6a=0是一元一次方程.【变式1-1】已知关于x的方程(m+2)x|m+3|+12=﹣3是一元一次方程,则m的值是.【变式1-2】若(2﹣a)x|a﹣1|﹣5=0是关于x的一元一次方程,则a=.【变式1-3】若关于x的方程x m+1﹣2=1是一元一次方程,则m的值是.【变式1-4】如果(k﹣1)x2+kx+8=0是关于x的一元一次方程,则k=.【题型2:一元一次方程的解】【典例2】若x=1是关于x的方程2x+a=0的解,则a的值为()A.﹣1B.﹣2C.1D.2【变式2-1】若x=2是方程4x+2m﹣14=0的解,则m的值为()A.10B.4C.3D.﹣3【变式2-2】如果x=3是关于x的方程3m﹣2x=6的解,则m的值是()A.0B.C.﹣4D.4【变式2-3】关于x的方程3a+x=18的解为x=﹣3,则a的值为()A.4B.5C.6D.7【变式2-4】已知方程﹣3(a﹣9)=5x﹣1的解是x=5,则a的值为()A.1B.2C.3D.4【变式2-5】关于x的方程(k﹣3)x﹣1=0的解是x=﹣1,那么k的值是()A.k≠3B.k=﹣2C.k=﹣4D.k=2【题型3:一元一次方程-整体法】【典例3】(2022秋•绥德县期末)若x=2是关于x的一元一次方程mx﹣n=3的解,则1+4m﹣2n的值为()A.3B.5C.7D.9【变式3-1】(2022秋•金华期末)若x=﹣2是关于x的方程2x﹣a+2b=0的解,则代数式2a﹣4b+1的值为()A.﹣7B.7C.﹣9D.9【变式3-2】(2023春•德宏州期末)若x=2是关于x的一元一次方程mx+n=3的解,则代数式6m+3n﹣2的值是()A.2B.3C.7D.9【变式3-3】(2022秋•海兴县期末)若x=﹣1是方程ax﹣(2a+x)=4的解,则a的值为()A.﹣1B.1C.D.【变式3-4】(2023春•淮阳区期末)已知x=﹣1是方程ax+1=bx﹣4的解,则﹣3a+5b﹣2(b﹣5)的值是()A.5B.﹣5C.﹣10D.10【题型4:一元一次方程-同解】【典例4】(惠山区校级月考)关于x的方程=﹣x与方程4(3x﹣7)=19﹣35x有相同的解,求m的值.【变式4-1】(2022秋•依安县期末)若方程3x﹣5=1与方程1﹣=0有相同的解,则a的值等于.【变式4-2】(罗湖区校级期末)已知关于x的方程3[x﹣2(x﹣)]=4x和有相同的解,求a的值和这个解.【变式4-3】(房山区校级月考)若关于x的方程2x﹣3=1和=k﹣3x有相同的解,求k的值.【变式4-4】(江都市校级期中)已知关于x的方程:2(x﹣1)+1=x与3(x+m)=m﹣1有相同的解,求以y为未知数的方程的解.【题型5:一元一次方程-错解】【典例5】小明是七年级(2)班的学生,他在对方程=﹣1去分母时由于粗心,方程右边的﹣1没有乘6而得到错解x=4,你能由此判断出a的值吗?如果能,请求出方程正确的解.【变式5-1】某同学解方程5x﹣1=□x+3时,把□处数字看错得x=﹣4,他把□处看成了()A.3B.﹣6C.6D.﹣4【变式5-2】某同学解方程5x﹣1=□x+3时,把□处数字看错得x=﹣,他把□处看成了()A.3B.﹣9C.8D.﹣8【变式5-3】某同学解方程5x﹣1=□x+3时,把□处数字看错得x=﹣,他把□处看成了()A.3B.﹣9C.8D.﹣8【变式5-4】小华同学在解方程3x﹣1=□x+2时,把“□”里的数字看错了,解得x=2,则该同学把“□”里的数字看成了.【变式5-5】某同学在解方程5x﹣5=△x时,把△处的数字看错了,解得x=﹣4,该同学把△看成了.【题型6:根据特殊关系列一元一次方程并解答】【典例7】(2022秋•新泰市期末)(1)x取何值时,代数式4x﹣5与3x﹣6的值互为相反数?(2)k取何值时,代数式的值比的值小1?【变式7-1】(2022秋•咸阳期末)已知关于x的方程3x+2a﹣1=0的解与方程x ﹣2a=0的解互为相反数,求a的值.【变式7-2】(2022秋•汉台区期末)若4(x﹣1)与﹣2(x﹣3)互为相反数,求x的值.【变式7-3】(2022秋•惠东县期末)如果关于x的方程的解与关于x 的方程4x﹣(3a+1)=6x+a+1的解互为相反数,求a的值.【变式7-4】(2022秋•长寿区期末)设y1=1﹣,y2=(1)当x为何值时,y1,、y2互为相反数;(2)当x为何值时,y1、y2相等.【变式7-5】(2022秋•南岗区校级月考)已知代数式与代数式,当x为何值时,代数式与代数式的值相等.【变式7-6】(2022秋•昭平县期中)x取何值时,2x﹣3与﹣5x+4的值满足下列条件:(1)相等;(2)2x﹣3比﹣5x+4多7.。
第03讲 含参数一元一次不等式(组)(教师版)A4

含参数一元一次不等式(组)含参数一元一次不等式(组)一.含参一元一次不等式(组)含字母系数的一次不等式(组):未知数的系数含有字母或常数项含有字母一次不等式(组). 任何一个含有字母系数的一元一次不等式都可以化为ax b >的一般形式,在这个形式中:若0a >,那么ax b >的解为b x a >;若0a <,那么ax b >的解为b x a<;若0a =,则当0b ≥时,ax b >无解,当0b <时,ax b >的解为任何实数.一.考点:含参的一元一次方程(组).二.重难点:参数与解集之间的关系,整数解问题,不等式与方程综合.三.易错点:注意参数取值范围导致的变号问题.知识图谱知识精讲三点剖析题模精讲题模一:解含参一元一次不等式(组)例1.1.1 已知23a ≠,解关于x 的不等式()()14321a x a x ++<-- 【答案】 当23a >时,不等式的解为523x a <-;当23a <时,不等式的解为523x a >- 【解析】 原不等式化为:()()13214a x a x +--<-- ()325a x -<-,因为23a ≠,所以320a -≠,即32a -为正数或负数.(1)当320a ->时,即23a >时,不等式的解为523x a <-;(2)当320a -<,即23a <时,不等式的解为523x a >- 例1.1.2 解下列关于x 的不等式组:()23262111x a x x x +⎧->⎪⎨⎪+>-⎩;【答案】 13a >时,32x a >+;13a ≤时,3x > 【解析】 原不等式组可化为323x a x >+⎧⎨>⎩. 当323a +>,即13a >时,不等式组的解集为32x a >+. 当323a +≤,即13a ≤时,不等式组的解集为3x > 题模二:参数与解集之间的关系例1.2.1 例若关于x 的不等式组3(2)224x x a x x --<⎧⎪⎨+>⎪⎩有解,则实数a 的取值范围是__________. 【答案】 4a >【解析】 由3(2)2x x --<得2x >,由24a x x +>得12x a <,因为不等式组有解,所以122a >,解得4a >.题模三:整数解问题例1.3.1 已知关于x 的不等式40x a -≤只有四个正整数解1、2、3、4,求正数a 的取值范围.【答案】 1620a ≤<【解析】 解不等式得4a x ≥又因为有且只有4个正整数解,故45a <⨯且44a ≥⨯1620a ∴≤<例1.3.2 已知不等式组221x a x b ->⎧⎨+<⎩的整数解只有5、6,求a 和b 的范围 【答案】 23a ≤<,1315b <≤【解析】 解不等式组得212x a b x >+⎧⎪⎨-<⎪⎩,因为整数解只有5、6,所以425a ≤+<,1672b -<≤,故23a ≤<,1315b <≤.题模四:不等式与方程的综合例1.4.1 已知2310a x -+=,32160b x --=,且4a b ≤≤,求x 的取值范围.【答案】 23x -≤≤【解析】 由2310a x -+=可得312x a -=,由32160b x --=可得2163x b +=,又因为4a b ≤≤,所以31216423x x -+≤≤,解得23x -≤≤.例1.4.2 求使方程组24563x y m x y m +=+⎧⎨+=+⎩的解x 、y 都是正数的m 的取值范围. 【答案】 572m << 【解析】 解原方程组得725x m y m =-+⎧⎨=-⎩,由x 、y 都是正数可得70250m m -+>⎧⎨->⎩,解得572m <<例 1.4.3 已知非负数x 、y 、z 满足123234x y z ---==,设345w x y z =++,求w 的最大值与最小值.【答案】 最大值1063,最小值19 【解析】 设123234x y z k ---===,则21x k =+,23y k =-,43z k =+,所以1426w k =+,又因为x 、y 、z 都是非负数,所以210230430k k k +≥⎧⎪-≥⎨⎪+≥⎩,解得1223k -≤≤,当23k =时,w 取最大值1063,当12k =-时,w 取最小值19随堂练习随练1.1 已知不等式424233x x a +<-(x 是未知数)的解也是不等式12162x -<的解,求a 的取值范围.【答案】 7a ≥-【解析】 由12162x -<得1x >-,由424233x x a +<-得6x a >+,由题意得61a +≥-,故7a ≥- 随练1.2 若关于x 的不等式0mx n ->的解集是15x <,则关于x 的不等式()m n x n m +>-的解集是( ) A . 23x <- B . 23x >- C . 23x < D . 23x > 【答案】A 【解析】 该题考查的是含参的不等式.∵关于x 的不等式0mx >的解集是15x <,, ∴0m <,15n m =, ∴解关于x 的不等式()m n x n m +>-得,n m x n m -<+, ∴55253n x n n -<=-+, 故答案是A .随练1.3 已知a 、b 为常数,解关于x 的不等式22ax x b ->+ 【答案】2a >时,()212b x a +>- 2a <时,()212b x a +<-2a =时,①如果10b +≥,不等式无解;②如果10b +<,则不等式的解为任何实数【解析】 原不等式可化为()()221a x b ->+,(1)当20a ->,即2a >时,不等式的解为()212b x a +>-; (2)当20a -<,即2a <时,不等式的解为()212b x a +<-;(3)当20a -=,即2a =时,有①:如果10b +≥,不等式无解;②如果10b +<,则不等式的解为任何实数.随练1.4 当k 满足___________时,方程组24x y k x y +=⎧⎨-=⎩中x 大于1,y 小于1 【答案】 13k -<<【解析】 由24x y k x y +=⎧⎨-=⎩可得22x k y k =+⎧⎨=-⎩,所以2121k k +>⎧⎨-<⎩,解得13k -<<. 随练1.5 若关于x 的不等式423202x x x a ++⎧>⎪⎪⎨+⎪<⎪⎩的解集为x <2,则a 的取值范围是____. 【答案】 a≤-2【解析】 本题考查了不等式的性质、解一元一次不等式(组)的应用,关键是能根据不等式的解集得出关于a 的不等式,题目比较好,难度不大.根据不等式的性质求出每个不等式的解集,根据找不等式组解集的规律得出-a≥2,求出即可. 423202x x x a ++⎧>⎪⎪⎨+⎪<⎪⎩①②, 解不等式①得:x <2,解不等式①得:x <-a ,①不等式组的解集是x <2,①-a≥2,①a≤-2,故答案为:a≤-2随练1.6 已知方程组3951x y a x y a +=+⎧⎨-=+⎩的解都为正数 (1)求a 的取值范围(2)化简454a a +--【答案】 (1)544a -<<(2)51a + 【解析】 先把a 看作常数,解方程组得454x a y a =+⎧⎨=-+⎩,由方程组的解都为正数可得45040a a +>⎧⎨-+>⎩,解得544a -<<,由45040a a +>⎧⎨-+>⎩可得4545a a +=+,44a a -=-,故45451a a a +--=+随练1.7 若关于x 的不等式0721x m x ⎧-<⎨-≤⎩的整数解共有4个,则m 的取值范围是( )A . 6<m <7B . 6≤m <7C . 6≤m ≤7D . 6<m ≤7【答案】D 【解析】 本题是一道较为抽象的中考题,利用数轴就能直观的理解题意,列出关于m 的不等式组,再借助数轴做出正确的取舍.首先确定不等式组的解集,先利用含m 的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于m 的不等式,从而求出m 的范围.由(1)得,x <m ,由(2)得,x≥3,故原不等式组的解集为:3≤x <m ,①不等式的正整数解有4个,①其整数解应为:3、4、5、6,①m 的取值范围是6<m≤7.故选D .随练1.8 已知关于x 的不等式组4(1)23617x x x a x -+>⎧⎪-⎨-<⎪⎩有且只有三个整数解,求a 的取值范围.【答案】 1≤a <2【解析】解不等式4(x -1)+2>3x ,得:x >2,解不等式x -1<67x a -,得:x <7-a , ①此不等式组有且只有三个整数解,①这三个整数解为3,4,5,①5<7-a≤6,解得1≤a <2.①实数a 的取值范围是1≤a <2.随练1.9 已知2310a x -+=,32160b x --=,且4a b ≤<,求x 的取值范围.【答案】 23x -<≤【解析】 由2310a x -+=可得312x a -=,由32160b x --=可得2163x b +=,又因为4a b ≤<,所以31216423x x -+≤<,解得23x -<≤自我总结拓展1 若关于x 的不等式21a x ->的解集是1x <,则a 的值是( )A . 1a =B . 1a >C . 1a <D . 1a =-【答案】A【解析】 该题考查的是含参数的不等式.∵21a x ->,∴21x a <-,∵1x <,∴211a -=,解得1a =.故答案是A .拓展2 10.(3分)(2016•江西校级模拟)已知关于x 的不等式组1x a x ⎧>⎨>⎩的解集为x >1,则a 的取值范围是_____________.【答案】 a ≤1【解析】 由关于x 的不等式组1x a x ⎧>⎨>⎩的解集为x >1,得 a ≤1,拓展3 若关于x 的不等式组232x a x a >+⎧⎨<-⎩无解,则a 的取值范围是__________.能力拓展【答案】 2a ≤【解析】 由题意可知232a a +≥-,解得2a ≤拓展4 若不等式组200x b x a -≥⎧⎨+≤⎩的解集为3≤x ≤4,则不等式ax+b <0的解集为____. 【答案】 x >32【解析】200x b x a -≥⎧⎨+≤⎩①② ①解不等式①得:x≥2b , 解不等式①得:x≤-a ,①不等式组的解集为:2b ≤x≤-a , ①不等式组200x b x a -≥⎧⎨+≤⎩的解集为3≤x≤4, ①2b =3,-a=4, b=6,a=-4, ①-4x+6<0,x >32, 故答案为:x >32拓展5 如果方程组32335x y k x y +=+⎧⎨+=⎩的解为x 、y ,且9k ≤时,求x y -的取值范围 【答案】 8x y -≤【解析】 由原方程组可得()222x y k -=-,所以1x y k -=-,由9k ≤得8x y -≤拓展6 若关于x 的不等式组430x x m -≥⎧⎨≥⎩有2个整数解,则m 的取值范围是( ) A . 1m >- B . 0m ≥ C . 10m -<≤ D . 10m -≤≤【答案】C【解析】 该题考察的是一元一次不等式组的整数解.解不等式430x -≥得43x ≤,故不等式组的解集为:43m x ≤≤, 因为不等式组只有2个整数解, 所以这两个整数解为:0,1,因此实数m 的取值范围是10m -<≤. 故选答案是C .拓展7 关于x 的不等式组232x a x a <+⎧⎨≥-⎩只有非负数解,求a 的取值范围. 【答案】 223a ≤< 【解析】 232320a a a +>-⎧⎨-≥⎩. 223a ∴≤<拓展8 适当选择a 的取值范围,使1.7x a <<的整数解:(1)x 只有一个整数解(2)x 一个整数解也没有【答案】 (1)23a <≤(2)1.72a <≤【解析】 (1)由1.7x a <<,x 只有一个整数解,即2x =,得到23a <≤;(2)由1.7x a <<,x 一个整数解也没有得到1.72a <≤.拓展9 已知关于x ,y ,z 的方程组212325x y z x y z -+=⎧⎨+-=⎩满足524x y ≥⎧⎨≤<⎩,求3S x y z =+-的取值范围. 【答案】 41115S ≤< 【解析】 解方程组得到417527z x z y -⎧=⎪⎪⎨-⎪=⎪⎩,根据题意415752247z z -⎧≥⎪⎪⎨-⎪≤<⎪⎩,解得1665z ≤<,而5S z =+.。
一元一次方程含参问题

一元一次方程含参问题
基本概念
一元一次方程含参问题是指在形如ax + b = c的一元一次方程中,将系数a、b和c中的某个或某些项用参数表示,并研究方程解随参数的变化而变化的问题。
解法
解一元一次方程含参问题的基本思路是:
1. 将含参数的方程表示为一元一次方程形式;
2. 根据方程的系数和常数项的变化情况,讨论方程解的取值范围;
3. 根据参数的取值范围,确定方程在不同条件下的解。
例题
1. 已知一元一次方程8x + a = 10,其中参数a的取值范围为[1, 5],求方程的解。
- 当a = 1时,方程化简为8x + 1 = 10,解得x = 1。
- 当a = 5时,方程化简为8x + 5 = 10,解得x = 1/2。
因此,当a取值范围为[1, 5]时,方程的解为x = 1或x = 1/2。
2. 已知一元一次方程2x + 3y = m,其中参数m的取值范围为[1, 10],求方程的解。
- 当m = 1时,方程化简为2x + 3y = 1,解的取值范围较广。
- 当m = 10时,方程化简为2x + 3y = 10,解的取值范围较窄。
因此,当m取值范围为[1, 10]时,方程的解的取值范围也会相
应变化。
总结
一元一次方程含参问题是通过引入参数,使一元一次方程的解与参数的取值相联系的问题。
解决这类问题需要将含参数的方程化简为一元一次方程,然后根据参数的取值范围讨论方程的解的取值范围。
通过掌握一元一次方程含参问题的解法和应用,可以进一步提高数学问题的分析解决能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
含参一元一次方程的解
法
1.一元一次方程:只含有一个未知数,并且未知数的最高次数是1,系数不等于0的整式方程叫做一元一次方程,这里的“元”是指未知数,“次”是指含未知数的项的最高次数.2.解一元一次方程的一般步骤:⑴去分母;⑵去括号;⑶移项;⑷合并同类项;⑸未知数的系数化为1.
这五个步骤在解一元一次方程中,有时可能用不到,有时可能重复用,也不一定按顺序进行,要根据方程的特点灵活运用.
3.易错点1:去括号:括号前是负号时,括号里各项均要变号.
易错点2:去分母:漏乘不含分母的项.
易错点3:移项忘记变号.
【巩固1
是关于x的一元一次方程,则.
【巩固2
】方程去分母正确的是()
A
B
.
C
D
.
【巩固3
1.1一元一次方程的巧解
求解一元一次方程的一般步骤是:⑴去分母;⑵去括号;⑶移项;⑷合并同类项;⑸未知数的系数化为1.在求解的过程中要要根据方程的特点灵活运用.
对于复杂的一元一次方程,在求解过程中通常会采用一些特殊的求解方法,需要同学们掌握,
的应用.
具体归纳起来,巧解的方法主要有以下三种:⑴提取公因式;⑵对系数为分数的一元一次方程的系数进行裂项;⑶进行拆项和添项,从而化简原方程.
知识回顾
基础巩固
知识导航
【例1】
⑴
【例
2】 解方程:
⑴
⑵
()()1123233211191313
x x x -+-+= 1.2同解方程
若两个一元一次方程的解相同,则称它们是同解方程.同解方程一般有两种解法: ⑴只有一个方程含有参数,另外一个方程可以直接求解.此时,直接求得两个方程的公共解,然后代入需要求参数的方程,能够最快的得到答案.
⑵两个方程都含有参数,无法直接求解.此时,由于两个方程的解之间有等量关系,因此,可以先分别用参数来表示这两个方程的解,再通过数量关系列等式从而求得参数,这是求解同解方程的最一般方法.
注意:⑴两个解的数量关系有很多种,比如相等、互为相反数、多1、2倍等.
(2)一元一次方程的公共根看似简单,其实却是一元二次方程公共根问题的前铺和基础.
【例3】
与有相同的解,求a
得值.;
⑵若
是关于x
的同解方程,求
的值.
【例4】
x 的一元一次方
程,且它们的解互为相反数,求m,n
分别是多少?关于x 的方程
的
解是多少? ⑵当
时,
关于x 的解是关于y 的方程
的
解得2倍.
1.3含参方程
当方程的系数用字母表示时,这样的方程称为含字母系数的方程,含字母系数的方程总能化成
的解根据
的取值范围分类讨论.
1. 当时,方程有唯一解
.
2. 当
时,方程有无数个解,解是任意数.
经典例题
知识导航
经典例题
知识导航
3.
当
时,方程无解.
【例5】 解关于x
的方程
【例6】
⑴若方程没有解,则a 的值为.
⑵若方程有无数解,则的值是.
x
是一元一次方程.若该方程的唯一解是
,求p 得值. ⑷已知:关于
的方程
的值.
1.4绝对值方程
解绝对值方程的一般步骤:⑴分类讨论去绝对值;⑵分别求解两个方程;⑶综合两个方程的解;⑷验证.
【例7】 解绝对值方程:
⑴
1.5课后习题
【演练1】
【演练2】
【演练3】
与方程
的解相同,则a 的值为.
⑵若关于x
的解互为相反数,则=.
⑶若关于x
和
a 得值.
【演练4】 解关于x
【演练5】 ⑴已知关于x
无解,那么
,
.
⑵若关于x
的方程
.
经典例题
知识导航
经典例题。
