一元一次方程含参问题
专题3.2 一元一次方程中含参数问题(六大类型)(解析版)

专题3.2 一元一次方程中含参数问题(六大类型)【题型1:一元一次方程的定义】【题型2:一元一次方程的解】【题型3:一元一次方程-整体法】【题型4:一元一次方程-同解】【题型5:一元一次方程-错解】【题型6:根据特殊关系列一元一次方程并解答】【题型1:一元一次方程的定义】【典例1】当a= 3 时,关于x的方程3x a﹣2﹣6a=0是一元一次方程.【答案】3.【解答】解:∵关于x的方程3x a﹣2﹣6a=0是一元一次方程,∴a﹣2=1,解得:a=3.故答案为:3.【变式1-1】已知关于x的方程(m+2)x|m+3|+12=﹣3是一元一次方程,则m的值是 ﹣4 .【答案】﹣4.【解答】解:由题意可知:|m+3|=1,∴m=﹣4或﹣2,∵m+2≠0,∴m≠﹣2,∴m=﹣4,故答案为:﹣4.【变式1-2】若(2﹣a)x|a﹣1|﹣5=0是关于x的一元一次方程,则a= 0 .【答案】0.【解答】解:(2﹣a)x|a﹣1|﹣5=0是关于x的一元一次方程,∴2﹣a≠0且|a﹣1|=1,解得:a=0.故答案为:0.【变式1-3】若关于x的方程x m+1﹣2=1是一元一次方程,则m的值是 0 .【答案】0.【解答】解:由一元一次方程的特点得m+1=1,解得:m=0.故答案为:0.【变式1-4】如果(k﹣1)x2+kx+8=0是关于x的一元一次方程,则k= 1 .【答案】见试题解答内容【解答】解:由(k﹣1)x2+kx+8=0是关于x的一元一次方程,得k﹣1=0,解得k=1,故答案为:1.【题型2:一元一次方程的解】【典例2】若x=1是关于x的方程2x+a=0的解,则a的值为( )A.﹣1B.﹣2C.1D.2【答案】B【解答】解:由题意得:当x=1时,2+a=0.∴a=﹣2.故选:B.【变式2-1】若x=2是方程4x+2m﹣14=0的解,则m的值为( )A.10B.4C.3D.﹣3【答案】C【解答】解:把x=2代入4x+2m﹣14=0,得4×2+2m﹣14=0,解得m=3.故选:C.【变式2-2】如果x=3是关于x的方程3m﹣2x=6的解,则m的值是( )A.0B.C.﹣4D.4【答案】D【解答】解:把x=3代入方程得:3m﹣6=6,解得:m=4,故选:D.【变式2-3】关于x的方程3a+x=18的解为x=﹣3,则a的值为( )A.4B.5C.6D.7【答案】D【解答】解:把为x=﹣3代入方程3a+x=18,得3a﹣3=18,解得a=7.故选:D.【变式2-4】已知方程﹣3(a﹣9)=5x﹣1的解是x=5,则a的值为( )A.1B.2C.3D.4【答案】A【解答】解:根据题意得,﹣3(a﹣9)=5x﹣1,把x=5代入得,﹣3(a﹣9)=5×5﹣1,﹣3(a﹣9)=24,方程两边同时除以﹣3,a﹣9=﹣8,移项得,a=﹣8+9,∴a=1,故选:A.【变式2-5】关于x的方程(k﹣3)x﹣1=0的解是x=﹣1,那么k的值是( )A.k≠3B.k=﹣2C.k=﹣4D.k=2【答案】D【解答】解:把x=﹣1代入(k﹣3)x﹣1=0,﹣k+3﹣1=0,k=2,故选:D.【题型3:一元一次方程-整体法】【典例3】(2022秋•绥德县期末)若x=2是关于x的一元一次方程mx﹣n=3的解,则1+4m﹣2n的值为( )A.3B.5C.7D.9【答案】C【解答】解:∵x=2是关于x的一元一次方程mx﹣n=3的解,∴2m﹣n=3,∴1+4m﹣2n=1+2(2m﹣n)=1+2×3=7.故选:C.【变式3-1】(2022秋•金华期末)若x=﹣2是关于x的方程2x﹣a+2b=0的解,则代数式2a﹣4b+1的值为( )A.﹣7B.7C.﹣9D.9【答案】A【解答】解:将x=﹣2代入方程可得:﹣4﹣a+2b=0,整理得:a﹣2b=﹣4,则原式=2(a﹣2b)+1=﹣8+1=﹣7.故选:A.【变式3-2】(2023春•德宏州期末)若x=2是关于x的一元一次方程mx+n=3的解,则代数式6m+3n﹣2的值是( )A.2B.3C.7D.9【答案】C【解答】解:把x=2代入方程可得2m+n=3,∴6m+3n﹣2=3(2m+n)﹣2=3×3﹣2=7.故选:C.【变式3-3】(2022秋•海兴县期末)若x=﹣1是方程ax﹣(2a+x)=4的解,则a的值为( )A.﹣1B.1C.D.【答案】A【解答】解:将x=﹣1代入方程ax﹣(2a+x)=4得:﹣a﹣2a+1=4,解得a=﹣1.故选:A.【变式3-4】(2023春•淮阳区期末)已知x=﹣1是方程ax+1=bx﹣4的解,则﹣3a+5b﹣2(b﹣5)的值是( )A.5B.﹣5C.﹣10D.10【答案】B【解答】解:∵x=﹣1是方程ax+1=bx﹣4的解,∴﹣a+1=﹣b﹣4,整理,得a﹣b=5.∴﹣3a+5b﹣2(b﹣5)=﹣3a+5b﹣2b+10=﹣3(a﹣b)+10=﹣3×5+10=﹣5.故选:B.【题型4:一元一次方程-同解】【典例4】(惠山区校级月考)关于x的方程=﹣x与方程4(3x﹣7)=19﹣35x有相同的解,求m的值.【答案】见试题解答内容【解答】解:解方程4(3x﹣7)=19﹣35x得:x=1,将x=1代入得:=﹣,解得:m=﹣.【变式4-1】(2022秋•依安县期末)若方程3x﹣5=1与方程1﹣=0有相同的解,则a的值等于 2 .【答案】见试题解答内容【解答】解:由方程3x﹣5=1得:x=2把x=2代入方程1﹣=0中得:1﹣=0∴a=2故答案为:2.【变式4-2】(罗湖区校级期末)已知关于x的方程3[x﹣2(x﹣)]=4x和有相同的解,求a的值和这个解.【答案】见试题解答内容【解答】解:由3[x﹣2(x﹣)]=4x,得x=.由,得x=.因为它们的解相同,所以=.所以a=.所以x=×=.【变式4-3】(房山区校级月考)若关于x的方程2x﹣3=1和=k﹣3x有相同的解,求k的值.【答案】见试题解答内容【解答】解:解方程2x﹣3=1得,x=2,解方程=k﹣3x得,x=k,∵两方成有相同的解,∴k=2,解得k=.【变式4-4】(江都市校级期中)已知关于x的方程:2(x﹣1)+1=x与3(x+m)=m﹣1有相同的解,求以y为未知数的方程的解.【答案】见试题解答内容【解答】解:解方程2(x﹣1)+1=x得:x=1将x=1代入3(x+m)=m﹣1得:3(1+m)=m﹣1解得:m=﹣2将x=1,m=﹣2代入得:,解得:.【题型5:一元一次方程-错解】【典例5】小明是七年级(2)班的学生,他在对方程=﹣1去分母时由于粗心,方程右边的﹣1没有乘6而得到错解x=4,你能由此判断出a的值吗?如果能,请求出方程正确的解.【答案】见试题解答内容【解答】解:∵方程右边的﹣1忘记乘6,求出的解为x=4,∴2(2×4﹣1)=3(4+a)﹣1,解得a=1,则原方程为:=﹣1,去分母,得4x﹣2=3x+3﹣6,移项、合并同类项,得x=﹣1.【变式5-1】某同学解方程5x﹣1=□x+3时,把□处数字看错得x=﹣4,他把□处看成了( )A.3B.﹣6C.6D.﹣4【答案】C【解答】解:□用a表示,把x=﹣4代入方程,得:﹣20﹣1=﹣4a+3,解得:a=6.故选:C.【变式5-2】某同学解方程5x﹣1=□x+3时,把□处数字看错得x=﹣,他把□处看成了( )A.3B.﹣9C.8D.﹣8【答案】C【解答】解:把x=代入5x﹣1=□x+3,得:﹣﹣1=﹣□+3,解得:□=8.故选:C.【变式5-3】某同学解方程5x﹣1=□x+3时,把□处数字看错得x=﹣,他把□处看成了( )A.3B.﹣9C.8D.﹣8【答案】C【解答】解:把x=﹣代入5x﹣1=□x+3,得5×(﹣)﹣1=﹣□+3,解得□=8.故选:C.【变式5-4】小华同学在解方程3x﹣1=□x+2时,把“□”里的数字看错了,解得x=2,则该同学把“□”里的数字看成了 .【答案】见试题解答内容【解答】解:把x=2代入方程3x﹣1=□x+2,得3×2﹣1=2□+2,即5=2□+2,解得□=.故答案为:.【变式5-5】某同学在解方程5x﹣5=△x时,把△处的数字看错了,解得x=﹣4,该同学把△看成了 .【答案】见试题解答内容【解答】解:将x=﹣4代入方程,得﹣20﹣5=﹣4△,△=,故答案为:.【题型6:根据特殊关系列一元一次方程并解答】【典例7】(2022秋•新泰市期末)(1)x取何值时,代数式4x﹣5与3x﹣6的值互为相反数?(2)k取何值时,代数式的值比的值小1?【答案】见试题解答内容【解答】解:(1)根据题意得:4x﹣5+3x﹣6=0,解得:x=;(2)根据题意得:+1=,去分母得:2k+2+6=9k+3,解得:k=.【变式7-1】(2022秋•咸阳期末)已知关于x的方程3x+2a﹣1=0的解与方程x ﹣2a=0的解互为相反数,求a的值.【答案】见试题解答内容【解答】解:解方程x﹣2a=0得:x=2a,∵方程3x+2a﹣1=0的解与方程x﹣2a=0的解互为相反数,∴3(﹣2a)+2a﹣1=0,解得:a=﹣.【变式7-2】(2022秋•汉台区期末)若4(x﹣1)与﹣2(x﹣3)互为相反数,求x的值.【答案】﹣1.【解答】解:∵4(x﹣1)与﹣2(x﹣3)互为相反数,∴4(x﹣1)+[﹣2(x﹣3)]=0,去括号,可得:4x﹣4﹣2x+6=0,移项,可得:4x﹣2x=4﹣6,合并同类项,可得:2x=﹣2,系数化为1,可得:x=﹣1.【变式7-3】(2022秋•惠东县期末)如果关于x的方程的解与关于x 的方程4x﹣(3a+1)=6x+a+1的解互为相反数,求a的值.【答案】1.【解答】解:,去分母得:x﹣1﹣4=﹣2a,移项得:x=﹣2a+1+4,合并同类项得,系数化为1得:x=﹣2a+5,4x﹣(3a+1)=6x+a+1,移项得:4x﹣6x=a+1+3a+1,合并同类项得:﹣2x=4a+2,系数化为1得:x=﹣2a﹣1,∵关于x的方程的解与关于x的方程4x﹣(3a+1)=6x+a+1的解互为相反数,∴﹣2a+5+(﹣2a﹣1)=0,解得a=1.【变式7-4】(2022秋•长寿区期末)设y1=1﹣,y2=(1)当x为何值时,y1,、y2互为相反数;(2)当x为何值时,y1、y2相等.【答案】见试题解答内容【解答】解:(1)根据题意得:1﹣+=0,去分母得:6﹣3(x﹣1)+2x=0,移项合并得:x=9;(2)根据题意得:1﹣=,去分母得:6﹣3x+3=2x,移项合并得:5x=9,解得:x=1.8.【变式7-5】(2022秋•南岗区校级月考)已知代数式与代数式,当x为何值时,代数式与代数式的值相等.【答案】当x=时,代数式与代数式的值相等.【解答】解:由题意可得:=,∴3x=4(2﹣x),∴3x=8﹣4x,∴7x=8,∴x=.当x=时,代数式与代数式的值相等.【变式7-6】(2022秋•昭平县期中)x取何值时,2x﹣3与﹣5x+4的值满足下列条件:(1)相等;(2)2x﹣3比﹣5x+4多7.【答案】(1)x=1;(2)x=2.【解答】解:(1)根据题意得:2x﹣3=﹣5x+4,移项得:2x+5x=4+3,合并得:7x=7,系数化为1得:x=1;(2)根据题意得:(2x﹣3)﹣(﹣5x+4)=7,移项合并得:7x=14,系数化为1得:x=2.。
初一数学一元一次方程专题,详解五类含参题型
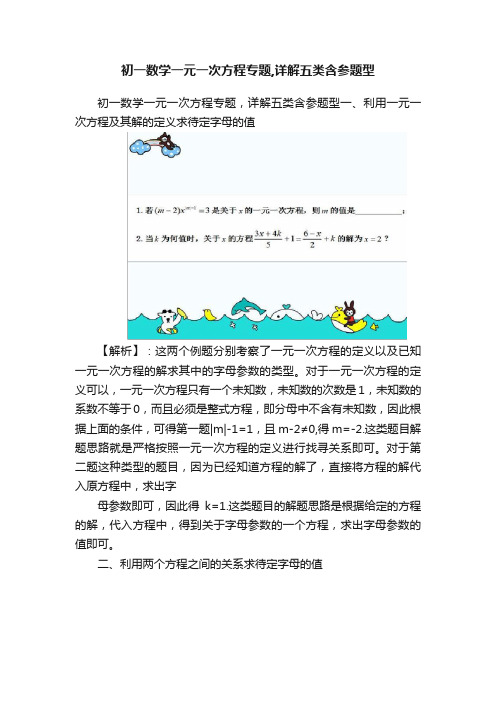
初一数学一元一次方程专题,详解五类含参题型初一数学一元一次方程专题,详解五类含参题型一、利用一元一次方程及其解的定义求待定字母的值【解析】:这两个例题分别考察了一元一次方程的定义以及已知一元一次方程的解求其中的字母参数的类型。
对于一元一次方程的定义可以,一元一次方程只有一个未知数,未知数的次数是1,未知数的系数不等于0,而且必须是整式方程,即分母中不含有未知数,因此根据上面的条件,可得第一题|m|-1=1,且m-2≠0,得m=-2.这类题目解题思路就是严格按照一元一次方程的定义进行找寻关系即可。
对于第二题这种类型的题目,因为已经知道方程的解了,直接将方程的解代入原方程中,求出字母参数即可,因此得k=1.这类题目的解题思路是根据给定的方程的解,代入方程中,得到关于字母参数的一个方程,求出字母参数的值即可。
二、利用两个方程之间的关系求待定字母的值【解析】:这两个题目的类型时,给定两个一元一次方程,根据给定的方程的解的情况,进行字母参数的求值。
第三题属于同解问题,这类题目的解题思路是,首先根据给定的不含字母参数的方程,求出方程的解,然后因为两个方程的解相同,将解出来的值代入到另一个方程中,从而求出字母参数,本题中首先得x=-1,将x=-1代入第一个方程中,得a=-11。
第四题中,两个方程都有字母参数,而且两个方程的解是相反数,这类题目的解题思路是,分别求出两个方程的解,这时的解带有字母参数,然后根据题目中的条件,列出相应的关系式,本题中,第一个方程的解是x=(3m+1)/2,第二个方程的解是x=-(2m+4)/3,因为两个方程的解互为相反数,因此相加等于0.从而得m=1.三、利用方程的错解确定待定字母的值【解析】:这两个题目属于错解问题,告诉你求解过程中,什么地方做错了,然后让你求出字母参数和正确的解。
这类题目的解题思路是,首先根据题目中告诉的错误答案是怎么求解出来的,然后按照错误的解题过程求解出字母参数,之后按照正确的解题过程求解出正确的方程的解即可。
2024-2025学年度北师版七上数学-专题5-一元一次方程中的含参问题【课件】

(2)若关于 x 的一元一次方程5 x - m =1是差解方程,求 m
的值.
+1
解:(2)解5 x - m =1,得 x =
.
5
因为关于 x 的一元一次方程5 x - m =1是“差解方程”.
+1
21
所以 m +1-5=
,解得 m = .
5
4
返回目录
数学 七年级上册 BS版
类型三 与一元一次方程解有关的含参问题
返回目录
数学 七年级上册 BS版
0 2
典例讲练
数学 七年级上册 BS版
类型一 与一元一次方程定义有关的含参问题
已知( a +2 b ) y2-
1
1
−
3
3
=3是关于 y 的一元一次方程,求
a + b 的值.
【思路导航】从“一次”和“一元”两个条件列出关于 a , b 的
两个方程,求出 a , b 的值,再代入计算.
2−1
+
-
=2的解相同,求 a 的值.
5
3
解:解4( x -1)-3( x +1)=-4,得 x =3.
2−1
+
把 x =3代入
-
=2,得
5
3
2×3−1
3+
-
=2,解得 a =-6.
5
3
返回目录
数学 七年级上册 BS版
2. 当 k 为何值时,关于 x 的方程2( x -3)=3 k -1与3 x +2=-
数学 七年级上册 BS版
第五章
专题5
一元一次方程
一元一次方程中的含参问题
数学 七年级上册 BS版
目录
CONTENTS
含参的一元一次方程专题

含参的一元一次方程专题步入初中,在初一数学解一元一次方程以及一元一次方程的应用,有一类考点是经常考到的,就是含有参数的一元一次方程求解问题,有以下五类含参的题型。
一、利用一元一次方程的定义求待定参数的值例、若(a+3)x^|a+2|=4是一元一次方程,求a的值。
分析:本题考察的主要知识点是一元一次方程的定义,也即利用其定义来求出参数的值。
一元一次方程,指的是在整式方程中,只有一个未知数,未知数的最高次数为1,在本题中则是丨a+2丨=1,解得a=-1或a=-3;又一元一次方程的一次项系数不能为0,在本题中则是a+3≠0,即a≠-3。
综上可知a=-1。
二、利用一元一次方程解的定义求待定参数的值。
例、当m取何值时,关于x的一元一次方程(2m+1)x-(m-3)/2=4的解为x=-1?分析:本题已经知道该方程的解x=-1,那么把x=-1代入方程,得到一个关于m的一元一次方程,解之即可。
将x=-1代入得:-(2m+1)-(m-3)/2=4。
-4m-2-m+3=8。
-5m=7。
解得m=-7/5。
三、利用两个方程之间的关系(同解或互为相反数等)来求待定参数的值例、已知关于x的一元一次方程2x/3+n/2=x/2+1与2x-n=-2是同解方程,求n的值。
分析:分别用含有字母n的代数式把两个方程的解表达出来,再根据题意令他们相等,解关于n的一元一次方程即可。
解:2x/3+n/2=x/2+1。
4x+3n=3x+6。
x=6-3n;2x-n=-2。
x=(n-2)/2。
由题意得:6-3n=(n-2)/2。
12-6n=n-2。
7n=14。
解得n=2。
四、利用一元一次方程的错解来确定字母参数的值例、马虎同学在解一元一次方程2(x+p)=3x-4时,在计算时忘记-4了,解得x=-1,求p的值并求出该方程正确的解。
分析:首先根据题目中告诉的错误答案将错就错,按照错误的解题过程求解出字母参数,之后按照正确的解题过程求解出正确的方程的解即可。
一元一次方程含参问题

1 2
(x
1)]
2 3
(x
1)
x
11
5
1、已知方程解的情况求参数
例1、已知方程 3ax ax3 的解是x=4,
求a的值。
2
练习:
①已知关于x的方程mx+2=2(m-x)的解满足方
程|x-0.5 |=0,则m= 2 。
②若方程2(x+1)-3(x-1)=0的解为a+2,求方程:
2[2(x+3)-3(x-a)]=3a的解。 21
(3)当m-3=0且-n-4≠0时,即m=3且n≠-4时, 方程无解
练习:
(1)已知关于x的方程2a(x-1)=(5-a)x+3b有无
数个解,则a= 5 ,b= 10 。
3
9
(2)已知关于x的方程a(2x-1)=3x-2无b)x2a xb0是关于x的一元
一次方程,且x有唯一值,则x= 3 。
练习:已知a,b为定值,关于x的方程 kx3a12x6bk,无论k为何值,它
的解总是1,求a+b的值。
解:把x=1代入方程得 ka12bk
3
6
化简得:(2+b)k=4-2a ∵ 无论k为何值,它的值总是1 ∴2+b=0且4-2a=0 解得b=-2,a=2
∴a+b=0
4、整数解问题
例6、已知关于x的方程9x+3=kx+14有整数 解,求整数k。
2
一、含有参数的一元一次方程
2、同解方程
例2、关于x的方程4x-1=-5与
2 a x 3
的0
解相同,求a的值;若解互为倒数,互为
相反数时,求a的值
练习:当m=
一元一次方程含参问题知识点

一元一次方程含参问题知识点
嘿,朋友们!今天咱就来好好唠唠一元一次方程含参问题的知识点。
比如说方程 ax+b=c 这样的,这里面的 a 就是参数啦!哎呀呀,就好
比你要去一个地方,a 就像是你选择走的路,不同的 a 就会让你走不同的路线呢!咱来看个例子哈,3x+5=14,这时候参数就是 3 呀。
那在一元一次方程含参问题里,咱得搞清楚参数对整个方程的影响嘞!这就好像搭积木,每一块积木的位置都很重要,参数就是那关键的一块呀!比如给你个方程 mx+2=7,这里的 m 就是关键参数咧,如果 m 不同,那
整个方程的解可就不一样咯!你想想,是不是很神奇?
有时候呢,我们得根据条件求出参数的值,就像寻找宝藏一样刺激呢!比如说知道方程 ax-3=0 的解是 x=2,那你就得赶快算出 a 是多少呀!
哎呀,一元一次方程含参问题可真是有趣又充满挑战呢!总之呢,咱只要认真去研究,肯定能把它搞明白!
我的观点结论就是:一元一次方程含参问题虽然有点难搞,但只要用心,就一定能掌握好它!。
一元一次方程含参问题含答案(教师版)

一元一次方程含参问题含答案(教师版) 精锐教育学科教师辅导教案学员编号。
年级:初一。
课时数:3学员姓名。
辅导科目:数学。
学科教师:授课时间。
课程主题:含参数的一元一次方程研究目标:研究一元一次方程的定义、解及解的讨论教学内容:知识点1:一元一次方程的定义一元一次方程是只含有一个未知数(元)x,未知数x的指数都是1(次),这样的方程叫做一元一次方程。
其一般形式是ax+b=(a,b为常数,且a≠0)。
经典题型:1、已知方程(m+1)xm+3=0是关于x的一元一次方程,则m的值是___。
解答:根据一元一次方程的特点可得|m|=1且m+1≠0,解得m=1.故填1.2、方程5m-4+5=0是关于x的一元一次方程,求m的值。
解答:方程5m-4+5=0是关于x的一元一次方程,所以5m-4=1,解得:m=1.3、方程x3m-4+5=0是关于x的一元一次方程,求m的值。
4、已知(m-1)x+(m+1)x-5=0是关于x的一元一次方程,求m的值。
知识点2:一元一次方程的解1、已知关于x方程1/(2x-1)=x-1/x,解互为倒数,求m的值。
2、已知y=3是6+(m-y)=2y的解,试求-m+m^2的值。
3、某书中有一方程2+口x3-x=-1,其中△处的数字是多少?4、已知方程2kx^2+2kx+3k=4x^2+x+1是关于x的一元一次方程,求k值,并求出这个方程的根。
知识点3:一元一次方程解的情况关于方程ax=b1)当a≠0时,方程有唯一解,x=b/a;2)当a=0,b≠0时,方程无解;3)当a=0,b=0时,方程有无数解。
经典题型:1、关于x的方程kx+2=4x+5有正整数解,求满足条件的k的正整数值。
解答:kx+2=4x+5,(k-4)x=3,由于x,k都是正整数,所以(k-4),x都是正整数,因此k-4=1,k=5,满足条件的k的正整数值为5.3k-4=1,x=3;或k-4=3,x=1;因此,k=5或7.因此答案为5或7.已知方程a(2x-1)=3x-2无解,求a的值。
一元一次方程含参问题

第⼗讲⼀元⼀次⽅程含参问题⼀解的关系求参数1⼀含参不含参⽅法先解出不含参⽅程的解根据解的关系求出含参⽅程的解再代⼊求参e gl关于x的⽅程2x31和YR k3X有相同的解求k由2x31解得x2代⼊X k3X得2k3X2解得k i92关于x的⽅程恐x in与X122x1的解互为倒数求m由x122X1解得x j则X x⼗号的解为x3代⼊得33in解得m f2两含参⽅法解出两个⽅程的解根据解的关系到等式g关于X的⽅程2x1m-2m2的解⽐⽅程5x11m4X1t m的解⼤2求m的值⽅程2x1m-2m2解得x2⽅程5X11m4X1t m解得x2m9由两⽅程解的关系得2-mz2m9216解得⼏⼆5⼆解的个数求参关于x的⽅程⽐功解的个数①at01为任意实数时x有唯⼀解②a0b0时x有⽆数解③a0bt0时x⽆解e gl关我的⽅程ax1⼆0它的解的个数是多少ax-1①a0时X⽆解②at0时x有唯⼀解eg2关于x的⽅程axt53X1它的解的个数是多少a x3X-1-5a3x-6D a30即a3时X⽆解②a3to即at3时x有唯⼀解eg3关于⼒的⽅程mxt43X n分别求出mn为何值时⽅程有①唯解20元数解30⽆解mx3X n4m3X n4①当m3to即m3⼏为任意实数时ㄨ有唯⼀解②当m30即m3n40即n-4x有⽆数解③当m30即m3n4to即⼏⼗-4x⽆解三整体法求解⽅程的数学形式⼀样则解⼀样egl关于x的⽅程2x12的解是ㄨ2则关刊的⽅程24-12的解是⽕2关于X的⽅程x b C的解是ㄨ2则关刊的⽅程a y b C的解是y25 egz已知关于X的⽅程a X tb C的解是ㄨ5则关于ㄨ的⽅程a2b的解是ㄨ22X5x2593已知关我的⽅程acxtb C的解是x5则关于⼒的⽅程a2ㄨt b1C 的解是X22X153X2994已知关于x的⽅程Ījxt32九⼗⼝的解是ㄨ5则关刊的⽅程i y t332y3t b的解是y2y t35y2四整数解问题⽅法把含参⽅程解出来找分⼦的约数不要漏了负的91关于⼒的⽅程ax7的解是整数求整数ax da-7-1 1.7egz关我的⽅程x7tax的解是整数求整数aX a1-a-7-1.1.7a8 2.0-6eg了已知关我的⽅程2ax13⼗九的解是整数求整数a13X z a12a1-13-1113a-6.0 1.794已知关我的⽅程a x_x4的解是正整数求整魏的值x4a1G1124a23595已知关于ㄨ的⽅程a1x6的解是正整数求正整数a6X a1at1 1.2.3.6a0舍去 1.2.5五错解问题将错就错egl语⽂⽼师在解关于ㄨ的⽅程2a2x5ㄨ时误将等号前⼆2x看作x解出解为⼒-1则a的值是-3原⽅程的解为X⼆千错解⽅程为2a x_x将x-1代⼊得2a-15ㄨ-1解得a-3原⽅程为-6-2x5解得x-67egz英语⽼师在解⽅程i那么去分⺟时⽅程右边-1漏乘了3因⽽求得⽅程的解为X-2请你帮这位⽼师求出的值并且求出原⽅程正确的解错解⽅程为2x1x a1将x-2代⼊得2ㄨ-2-1-2t a1解得a-2原⽅程为i今2-1解得ㄨ-4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例5、若a,b为定值,关于x的一元一次方 2kx a x bk 1 程 ,无论k为何值 3 6 时,它的解总是x=1,求a,b的值。 解:将x=1代入 2kx a x bk
3 2k a 1 bk 1 3 6 6 1
化简得:(4+b)k=7-2a ① ∵无论ห้องสมุดไป่ตู้为何值时,原方程的解总是x=1 ∴无论k为何值时,①总成立 ∴4+b=0且7-2a=0,解得a=-4,b=3.5
4、整数解问题
例6、已知关于x的方程9x+3=kx+14有整数解, 求整数k。
解:由题意知:(9-k)x=11
11 x 9k
∵x,k均为整数 ∴9-k= ±1, ±11 ∴k=-2,8,10,20
练习: 2 (1)关于x的方程 (n 1) x (m 1) x 3 0 是一元一次方程 ①则m,n应满足的条件为:m ≠1 ,n =1 ; ②若此方程的根为整数,求整数m=-2,0,2,4 。
练习: (1)已知关于x的方程2a(x-1)=(5-a)x+3b有无 数个解,则a= 5 ,b= 10 。
3
2
(2)已知关于x的方程a(2x-1)=3x-2无解,则 a= 3 。 (3)(3a 2b) x ax b 0 是关于x的一元 一次方程,且x有唯一值,则x= 3 。
2
9
2
2
一、含有参数的一元一次方程
2、同解方程
ax 2 0 例2、关于x的方程4x-1=-5与 3
的解相同,求a的值;若解互为倒数,互 为相反数时,求a的值 练习:当m= 4x-2m=3x-1的解是x=2x-3m的解的2倍。
1 4 时,关于x的方程
3、含字母系数的一元一次方程 例3、讨论关于x的方程ax=b的解的情况
一元一次方程的含参问题
1、已知方程解的情况求参数 2、两个一元一次方程同解问题 3、一元一次方程解的情况(分类讨论) 4、整数解问题
基础巩固:
1、若 (m 2) x (k 1) x 11 0 是关于x的一 元一次方程,则m= -2 ,k= -1 。
2
k
2、解方程:
2x 1 x 1 X=3 (1)3 17 5 2 x 11 0.2 x 0.1 0.5 x 0.1 ( 2) 1 0.6 0.4 1 1 2 (3) [ x ( x 1)] ( x 1) 11 2 2 3 x
(2)关于x的方程4x-5=kx+4的解为正整数, 则k的值为 3或1或-5 。
(3)关于x的方程4x-5=kx+4有整数解,则k的 所有值为 3,1,-5,5,7,13 。
练习:已知a,b为定值,关于x的方程 kx a 2 x bk 1 3 6 ,无论k为何值,它 的解总是1,求a+b的值。
k a 2 bk 解:把x=1代入方程得 1 3 6
化简得:(2+b)k=4-2a ∵ 无论k为何值,它的值总是1 ∴2+b=0且4-2a=0 解得b=-2,a=2 ∴a+b=0
5
1、已知方程解的情况求参数
ax 例1、已知方程 3a x 3 的解是x=4, 2 求a的值。
练习: ①已知关于x的方程mx+2=2(m-x)的解满足方 程|x-0.5 |=0,则m= 2 。
②若方程2(x+1)-3(x-1)=0的解为a+2,求方程: 2[2(x+3)-3(x-a)]=3a的解。 21
b x 1、当a≠0时,方程有唯一解 a 2、当a=0且b=0时,方程有无数个解, 解是任意数 3、当a=0且b≠0时,方程无解。
例4、关于x的方程mx+4=3x-n,分别求m, n为何值时,原方程: (1)有唯一解; (2)有无数个解; (3)无解 解:由题意知:(m-3)x=-n-4 (1)当m-3≠0时,即m≠3,n为任意数时,方 程有唯一解。 (2)当m-3=0且-n-4=0时,即m=3且n=-4时, 方程有无数个解。 (3)当m-3=0且-n-4≠0时,即m=3且n≠-4时, 方程无解
