第四章 一阶逻辑基本概念分析
合集下载
谓词逻辑的基本概念

三、4.4.6 三例不等
(x)(A(x) B(x)) (x)A(x) (x)B(x)
(x)(A(x) B(x)) (x)A(x) (x)B(x)
(x)(A(x) B(x)) (x)A(x) (x)B(x)
四、三个有趣的例子 4.4.7 积木世界的形式描述
若以P(x)表示x是有理数,Q(x)表示x是实数, 这句话的形式描述应为
(x)(P(x)Q(x))
“所有的……都是……”,这类语句的形式描述 只能使用而不能使用∧. 当P(x)与Q(x)为此例 中的谓词常项时,上式真值与论域无关。
4.4.2 “有的实数是有理数”的形式化
以P(x)表x是有理数,Q(x)表示x是实数,这句 话的形式描述应为 (x)(P(x)∧Q(x))
辑的个体域除明确指明外,都认为是包括一切事 物的一个最广的集合.以D表示. 谓词的变化范围:不做特别声明时,指一切关系或 一切性质的集合. 同一谓词在不同论域下的描述形式可能不同,所 取的真假值也可能不同.
4.1.3 谓词的抽象定义
将谓词视作为一个个体的性质或多个个体间的 关系.还可进一步抽象地定义: 谓词是给定的个体域到集合{T,F}上的一个 映射.
设P(x,y)是二元谓词,对两个变元的量化可得4 种形式.
(1) (x)(y)P(x, y) (x)((y)P(x, y))
注意x和y可交换
(2) (x)(y)P(x, y) (x)((y)P(x, y))
注意x和y不可交换,且y是x的函数
(3) (x)(y)P(x, y) (x)((y)P(x, y))
非合式公式: (x)F(x)∧G(x),违反第三条 (x)((x)F(x)),违反第四条 (x)P(y)违反第四条
一阶逻辑基本概念

问:(司能否将Q)符号化为
Vx(M(x) AF(x)) ?
常项或变项之间数量关系的词。称表示个体常项或变项之间数量关系的词为 量词。量词可分两种:
(1)全称*i司 日常生活和数学中所用的〃一切的〃,〃所有的〃,〃每一个〃,"任意 的",〃凡〃,〃都〃等词可统称为全称量词,将它们符号化为7'。并用 Vx , Vy等表示个体域里斤有个依,而用VxF(x) , VyG(y)等分别表示个体 域里所有 个体都有性质F和都有性质G。
S P
H
用d
KI
3 、 茹
7 a1 3回 A国 m今
Tt
R鄂
由例4.2可知,命题(1) , (2)在不同的个体域D]和D2中符号化的形式不
I 一样。主要区别在于,在使用个体域D2时,要将人与其他事物区分开来。
\ 为此引进了谓词M(x),像这样的谓词称为特性谓词。在命题符号化时一定 荽
正确使用特性谓词。
域可以是有穷集合,例如,{:1,2,3}, {a , b , c , d}, {a , b , c,…,x , y ,
z};也可以是无穷集合,例如,自然数 集合N={0,1,2 ,…},实数集合R={x|x是实数}。有一个特殊的个体域, 它是由宇宙间一切事物组成的,称它为全总个
体域。本书在论述或推理中如没有指明 所采用的个体域,都是使用全总个体域。
( ()
赣 炀
m
s e
S 般
m 畏、、
、 ^ 任、
w 1Mx
m §、
、、 q
葛屈 倒蟹
c
I H 腐、
5 -孵I
C @暇 l
妇犯色 6
屈 型 、 挝 |
挝 , € 眠
F4一阶逻辑基本概念

(a)非空个体域 DI . (b) DI 中一些特定元素的集合{a1,a2 , …,ai , …}. (c) DI 上特定函数的集合{fin|i, n 1}. (d) DI 上特定谓词的集合{Fin|i, n 1}. †其实质是明确公式中各个变项, 繁琐之处毋庸细究.
第四章一阶逻辑基本概念
§4.1 一阶逻辑命题的符号化 §4.2 一阶逻辑公式及解释
091离散数学(60). W&M. §4.2 一阶逻辑公式及解释
命题逻辑形式系统 I = A, E, AX, R, 其中A, E是语言系统. 谓词逻辑形式系统的语言 , 它便于翻译自然语言. (下一章
Dx2Dx1A(x1, x2, …, xn) 可记为 A2(x3, x4, …, xn), …… ,
Dxn…Dx1A(x1, x2, …, xn) 中没有自由出现的个体变项, 可z) = x(F(x, y) G(x, z)) B(z) = yA(y, z) = yx(F(x, y) G(x, z)) C =zyA(y, z) = zyx(F(x, y) G(x, z))
(3) H(a, b), 其中 H: “…与…同岁”, a: 小王, b: 小 李.
(4) L(x, y), 其中L: “…与…具有关系L”.
091离散数学(60). W&M. §4.1 一阶逻辑命题的符号化
一元谓词 F(x) 表示 x 具有性质 F.
二元谓词 F(x, y) 表示个体变项 x, y 具有关系 F.
xy(x + y = 0) 与 yx(x + y = 0) 含义不同. ‡†句子的符号化形式不止一种. 设 H(x): x 是人, P(x): x 是完美的, 则 “人无完人”可 符号化为
第四章一阶逻辑基本概念
§4.1 一阶逻辑命题的符号化 §4.2 一阶逻辑公式及解释
091离散数学(60). W&M. §4.2 一阶逻辑公式及解释
命题逻辑形式系统 I = A, E, AX, R, 其中A, E是语言系统. 谓词逻辑形式系统的语言 , 它便于翻译自然语言. (下一章
Dx2Dx1A(x1, x2, …, xn) 可记为 A2(x3, x4, …, xn), …… ,
Dxn…Dx1A(x1, x2, …, xn) 中没有自由出现的个体变项, 可z) = x(F(x, y) G(x, z)) B(z) = yA(y, z) = yx(F(x, y) G(x, z)) C =zyA(y, z) = zyx(F(x, y) G(x, z))
(3) H(a, b), 其中 H: “…与…同岁”, a: 小王, b: 小 李.
(4) L(x, y), 其中L: “…与…具有关系L”.
091离散数学(60). W&M. §4.1 一阶逻辑命题的符号化
一元谓词 F(x) 表示 x 具有性质 F.
二元谓词 F(x, y) 表示个体变项 x, y 具有关系 F.
xy(x + y = 0) 与 yx(x + y = 0) 含义不同. ‡†句子的符号化形式不止一种. 设 H(x): x 是人, P(x): x 是完美的, 则 “人无完人”可 符号化为
第四章 一阶逻辑基本概念

在一阶逻辑中将下列命题符号化1大熊猫都可爱2有人爱发脾气3说所有人都爱吃面包是不对的4没有不爱吃糖的人5一切人都不一样高6并不是所有的汽车都比火车快由于没指出个体域故用全总个体域其中fx
第四章 一阶逻辑基本概念
本章的主要内容 一阶逻辑基本概念、命题符号化 一阶逻辑公式、解释及分类
4.1 一阶逻辑命题符号化
2 (1)所有的狮子都是凶猛的。 (2)有些狮子不喝咖啡。 (3)有些凶猛的动物不喝咖啡。 论域为动物的集合:
3、 如果某人是女性而且有子女,那么此人 一定是某人的母亲。论域为人的集合。
2、解:令P(x): x是狮子;Q(x): x是凶猛的; R(x): x喝咖啡;则有: (1) x(P(x)Q(x)) (2) x(P(x)R(x)) (3) x(Q(x)R(x)) 3、解:令F(x):x是女性;P(x):x有子女; M(x,y):x是y的母亲;则有: x(( F(x)P(x) )yM(x,y))
(1) (2)
x x((F F((x x)) G G (x (x )))) 两个基本公式
例 在一阶逻辑中将下面命题符号化
(1)正数都大于负数 (2)有的无理数大于有的有理数
解: 注意:题目中没给个体域,一律用全总个体域
(1)令F(x):x为正数,G(y):y为负数 L(x,y):x>y
x(F(x)y(G(y)L(x,y))) xy(F(x)G(y)L(x,y)) (以后讨论)
3.闭式的性质. 定理4.1 闭式在任何解释下都是命题. 注意:不是闭式的公式在某些解释下也可能是命题. 4.公式的类型 定义4.8 (1)永真式(逻辑有效式) (2)矛盾式(永假式)(3)可满足式 说明: 永真式为可满足式,但反之不真; 判断公式是否为永真式不是易事; 通过某些代换实例可判断公式类型.
第四章 一阶逻辑基本概念
本章的主要内容 一阶逻辑基本概念、命题符号化 一阶逻辑公式、解释及分类
4.1 一阶逻辑命题符号化
2 (1)所有的狮子都是凶猛的。 (2)有些狮子不喝咖啡。 (3)有些凶猛的动物不喝咖啡。 论域为动物的集合:
3、 如果某人是女性而且有子女,那么此人 一定是某人的母亲。论域为人的集合。
2、解:令P(x): x是狮子;Q(x): x是凶猛的; R(x): x喝咖啡;则有: (1) x(P(x)Q(x)) (2) x(P(x)R(x)) (3) x(Q(x)R(x)) 3、解:令F(x):x是女性;P(x):x有子女; M(x,y):x是y的母亲;则有: x(( F(x)P(x) )yM(x,y))
(1) (2)
x x((F F((x x)) G G (x (x )))) 两个基本公式
例 在一阶逻辑中将下面命题符号化
(1)正数都大于负数 (2)有的无理数大于有的有理数
解: 注意:题目中没给个体域,一律用全总个体域
(1)令F(x):x为正数,G(y):y为负数 L(x,y):x>y
x(F(x)y(G(y)L(x,y))) xy(F(x)G(y)L(x,y)) (以后讨论)
3.闭式的性质. 定理4.1 闭式在任何解释下都是命题. 注意:不是闭式的公式在某些解释下也可能是命题. 4.公式的类型 定义4.8 (1)永真式(逻辑有效式) (2)矛盾式(永假式)(3)可满足式 说明: 永真式为可满足式,但反之不真; 判断公式是否为永真式不是易事; 通过某些代换实例可判断公式类型.
4.1一阶谓词逻辑基本概念

(1) (2) (3)
(1) (2) (3) (4) (5) (6)
(7)
(8) (9) (10) (11) (12)
x(J(x)→L(x)) (4) x(L(x)∧S(x)) (5) x(J(x)∧O(x)∧V(x)) (6) (7) J(j)∧O(j)∧V(j) (8) x(L(x)→J(x)) (9) x(S(x)∧L(x)∧C(x)) (10) x(C(x)∧V(x)) (11) x((C(x)∧O(x))→L(x)) (12) x(W(x)∧C(x)∧H(x)) x(W(x)∧J(x)∧C(x)) x(L(x)→y(J(y)∧A(x,y))) x(S(x)∧y(L(y)→A(x,y)))
◦ 由一个谓词和若干个个体变元组成的命题形式称为简单命 题函数,表示为P(x1,x2,…,xn)。由一个或若干个简单命题函 数以及逻辑联结词组成的命题形式称为复合命题函数
◦ 命题函数不是命题,没有确定真值,但其中谓词是谓词常量时,可 通过个体指派使其成为命题。如:若简单命题函数P(X)表示“x是 质数”,则P(1)为F,P(2)为T。
(1) 5是质数 (2) 张明生于北京 (3) 7=3×2
P(5)
G(a,b)
H(7,3,2)
P(x):x是质数
G(x, y): x生于y ,a:张明,b:北京
H(x, y, z) :x=y×z
谓词 个体词 谓词函数
例 将下列命题在一阶逻辑中用0元谓词符号化,并讨论真值。 (1)只有2是素数,4才是素数。 (2)如果5大于4,则4大于6.
除个体指派外,还常用“量”作出判断,如:“所有的人都是要死 的”、“有的数是质数”。这种表述在数理逻辑目标语言中需要引 入量词,当然量化与个体指派之间是有联系的,数理逻辑中常用量 词有两个——全称量词和存在量词。
一阶谓词逻辑的基本概念与原理

一阶谓词逻辑的基本概念与原理一阶谓词逻辑是数学逻辑的一个重要分支,它是对自然语言中的命题进行形式化描述和推理的工具。
在数理逻辑中,一阶谓词逻辑也被称为一阶逻辑或一阶谓词演算。
本文将介绍一阶谓词逻辑的基本概念与原理。
一、命题逻辑与谓词逻辑的区别在介绍一阶谓词逻辑之前,我们先来了解一下命题逻辑与谓词逻辑的区别。
命题逻辑是研究命题之间的关系和推理规则的逻辑系统,它只关注命题的真值(真或假)以及命题之间的逻辑连接词(如与、或、非等)。
而谓词逻辑则引入了谓词和量词的概念,可以描述对象之间的关系和属性,以及量化的概念。
二、一阶谓词逻辑的基本概念1. 语言一阶谓词逻辑的语言包括常量、变量、函数和谓词。
常量是指代具体对象的符号,如"1"、"2"等;变量是占位符号,可以代表任意对象,如"x"、"y"等;函数是将一组对象映射到另一组对象的符号,如"f(x)"、"g(x, y)"等;谓词是描述对象之间关系或属性的符号,如"P(x)"、"Q(x, y)"等。
2. 公式一阶谓词逻辑的公式由谓词、变量、常量、函数和逻辑连接词构成。
常见的逻辑连接词有否定、合取、析取、蕴含和等价等。
例如,"¬P(x)"表示谓词P对于变量x的否定,"P(x)∧Q(x)"表示谓词P和Q对于变量x的合取。
3. 全称量词和存在量词一阶谓词逻辑引入了全称量词和存在量词,用于对变量进行量化。
全称量词∀表示对所有对象都成立,存在量词∃表示存在至少一个对象成立。
例如,∀xP(x)表示谓词P对于所有的x都成立,∃xP(x)表示谓词P至少存在一个x成立。
三、一阶谓词逻辑的推理原理一阶谓词逻辑的推理基于一些基本规则和推理规则。
1. 基本规则一阶谓词逻辑的基本规则包括等词规则、全称推广规则、全称特化规则、存在引入规则和存在消去规则等。
第四章一阶逻辑的基本概念
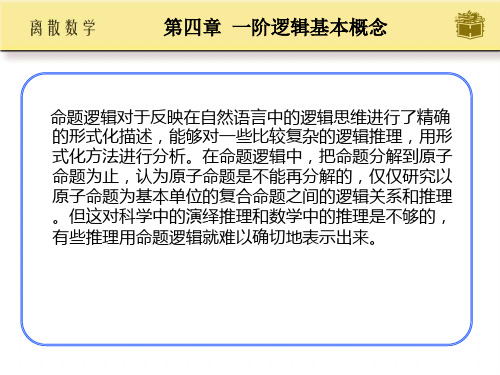
xy(F(x)G(y)L(x,y))
(2) 令F(x):x是无理数,G(y):y是有理数,L(x,y):x>y x(F(x)y(G(y)L(x,y) ) )
或者 xy(F(x)G(y)L(x,y))
14
实例4
例4 在一阶逻辑中将下面命题符号化 (1) 没有不呼吸的人 (2) 不是所有的人都喜欢吃糖 解 (1) M(x): x是人, G(x): x呼吸
合式公式 (4) 若A是合式公式,则xA, xA也是合式公式 (5) 只有有限次地应用(1)—(4)形成的符号串才是合式公式. 合式公式简称公式
如, F(x), F(x)G(x,y), x(F(x)G(x)) xy(F(x)G(y)L(x,y))等都是合式公式
19
量词的辖域
定义4.5 在公式 xA 和 xA 中,称x为指导变元,A为相应 量词的辖域. 在x和 x的辖域中,x的所有出现都称为约束 出现,A中不是约束出现的其他变项均称为是自由出现的.
9
(3)存在唯一量词!,用来表达“恰有一个”、“存在唯一”等词语。
“(!x)R(x)”表示命题:“在个体域中恰好有一个个体使谓词R(x)为
真”。(了解)
全称量词、存在量词统称量词。量词是由逻辑学家Fray引入的,有了量 词之后,用逻辑符号表示命题的能力大大增强。
实例1
例1 用0元谓词将命题符号化 (1) 墨西哥位于南美洲
(2) 2 是无理数仅当 3 是有理数
(3) 如果2>3,则3<4
解:在命题逻辑中: (1) p, p为墨西哥位于南美洲(真命题)
(2) p→q, 其中, p:2 是无理数, q: 3 是有理数. 是假命题
(3) pq, 其中, p:2>3, q:3<4. 是真命题
(2) 令F(x):x是无理数,G(y):y是有理数,L(x,y):x>y x(F(x)y(G(y)L(x,y) ) )
或者 xy(F(x)G(y)L(x,y))
14
实例4
例4 在一阶逻辑中将下面命题符号化 (1) 没有不呼吸的人 (2) 不是所有的人都喜欢吃糖 解 (1) M(x): x是人, G(x): x呼吸
合式公式 (4) 若A是合式公式,则xA, xA也是合式公式 (5) 只有有限次地应用(1)—(4)形成的符号串才是合式公式. 合式公式简称公式
如, F(x), F(x)G(x,y), x(F(x)G(x)) xy(F(x)G(y)L(x,y))等都是合式公式
19
量词的辖域
定义4.5 在公式 xA 和 xA 中,称x为指导变元,A为相应 量词的辖域. 在x和 x的辖域中,x的所有出现都称为约束 出现,A中不是约束出现的其他变项均称为是自由出现的.
9
(3)存在唯一量词!,用来表达“恰有一个”、“存在唯一”等词语。
“(!x)R(x)”表示命题:“在个体域中恰好有一个个体使谓词R(x)为
真”。(了解)
全称量词、存在量词统称量词。量词是由逻辑学家Fray引入的,有了量 词之后,用逻辑符号表示命题的能力大大增强。
实例1
例1 用0元谓词将命题符号化 (1) 墨西哥位于南美洲
(2) 2 是无理数仅当 3 是有理数
(3) 如果2>3,则3<4
解:在命题逻辑中: (1) p, p为墨西哥位于南美洲(真命题)
(2) p→q, 其中, p:2 是无理数, q: 3 是有理数. 是假命题
(3) pq, 其中, p:2>3, q:3<4. 是真命题
一阶谓词原理

14:08
14
D.举例
1.设个体域为D={0,1,2,……,10},将下列命题符号化: (1)D中所有元素都是整数;
∀xF(x), 其中F(x):x是整数 (2)D中有的元素是偶数; ∃xG(x), 其中G(x):x是偶数 (3)D中所有的偶数都能被2整除;
∀x(G(x) H(x)), 其中G(x):x是偶数; H(x):x能被2整除 (4)D中有的偶数是4的倍数。
(5)数量词:表示全体概念的数量词,如“每个”、“任何”、“所 有”等译为全称量词,表示部分概念的数量词,如“有”、“存 在”、“若干”、“有些”等,译为存在量词;
(6)副词和前置词与其它词类合并,不再进行单独分析;
(7)连词一般译为逻辑联结词。
14:08
19
2.谓词合式公式
A.原子公式 定义:不出现命题联结词和量词的谓词命名式
(1)非空个体域D;
(2)D中一些特定元素的集合 {a1, a2 ,..., ai ,...}
个体变项的取值范围为个 体域,个体域可以是有穷 集合,也可以是无穷集合。
全总个体域:由宇宙间一切事物组成的域为全总个体域。
14:08
4
一、谓词和个体
B. 谓词
a.小陈是大学生 b.小张生于苏州 c. 8=3*2
x是大学生
小陈-----个体;是大学生-----谓词: 是大学生刻划了x 的性质
x生于y x=y*z
14:08
7
•例如
S(x):表示x是大学生。
一元谓词
G(x,y):表示 x>y。
二元谓词
B(x,y,z):表示x在y与z之间。三元谓词
一般地
P(x1,x2,…,xn)
是n元谓词。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018/10/11
13
4.2 一阶逻辑公式及解释
定义4.1 设L是一个非逻辑符号集合, 由L生成的一阶语言L 的 字母表包括下述符号: 非逻辑符号 (1) 个体常项符号:a, b, c, …, ai, bi, ci, …, i 1 (2) 函数符号:f, g, h, …, fi, gi, hi, …, i 1 (3) 谓词符号:F, G, H, …, Fi, Gi, Hi, …, i 1 逻辑符号 (4) 个体变项符号:x, y, z, …, xi, yi, zi, …, i 1 (5) 量词符号:, (6) 联结词符号:, , , , (7) 括号与逗号:(, ), ,
2018/10/11 14
一阶语言L 的项与原子公式
定义4.2 L 的项的定义如下: (1) 个体常项和个体变项是项. (2) 若(x1, x2, …, xn)是任意的n元函数,t1, t2, …, tn是任意的 n个项,则(t1, t2, …, tn) 是项. (3) 所有的项都是有限次使用(1),(2)得到的 如, a, x, x+y, f(x), g(x,y)等都是项 定义4.3 设R(x1, x2, …, xn)是L 的任意n元谓词,t1, t2, …, tn 是L 的任意n个项,则称R(t1, t2, …, tn)是L 的原子公式. 如,F(x, y), F(f(x1, x2), g(x3, x4))等均为原子公式
2018/10/11
假
3 3 如: 3 3 ,但 2 2
20
x(xy=0)
真值不定, 不是命题
公式的类型
定理4.1 闭式在任何解释下都是命题 注意: 不是闭式的公式在解释下可能是命题, 也可能不是命题 . 定义4.8 若公式A在任何解释下均为真, 则称A为永真式(逻辑 有效式). 若A在任何解释下均为假, 则称A为矛盾式(永假式). 若至少有一个解释使A为真, 则称A为可满足式.
2018/10/11 10
实例5
例5 设个体域为实数域, 将下面命题符号化 (1) 对每一个数x都存在一个数y使得x<y (2) 存在一个数x使得对每一个数y都有x<y 解 L(x,y):x<y
(1) xyL(x,y) (2) xyL(x,y) 注意: 与不能随意交换
显然(1)是真命题, (2)是假命题
8
实例3
例3 在一阶逻辑中将下面命题符号化 (1) 正数都大于负数 (2) 有的无理数大于有的有理数 解 (注意:题目中没给个体域,一律用全总个体域) (1) 令F(x):x为正数,G(y):y为负数, L(x,y):x>y x(F(x)y(G(y)L(x,y))) 或者 xy(F(x)G(y)L(x,y)) (2) 令F(x):x是无理数,G(y):y是有理数,L(x,y):x>y x(F(x)y(G(y)L(x,y))) 或者 xy(F(x)G(y)L(x,y))
2018/10/11
4
量词
量词——表示数量的词 全称量词: 表示所有的. x : 对个体域中所有的x 如, xF(x)表示个体域中所有的x具有性质F xyG(x,y)表示个体域中所有的x和y有关系G 存在量词: 表示存在, 有一个. x : 个体域中有一个x 如, xF(x)表示个体域中有一个x具有性质F xyG(x,y)表示个体域中存在x和y有关系G xyG(x,y)表示对个体域中每一个x都存在一个y使得 x和y有关系G xyG(x,y)表示个体域中存在一个x使得对每一个y, x和y有关系G
2018/10/11 17
封闭的公式
定义4.6 若公式A中不含自由出现的个体变项,则称A为封闭 的公式,简称闭式. 例如,xy(F(x)G(y)H(x,y)) 为闭式, 而 x(F(x)G(x,y)) 不是闭式
2018/10/11
18
公式的解释
定义4.7 设L 是L生成的一阶语言, L 的解释I由4部分组成: (a) 非空个体域 DI . (b) 对每一个个体常项符号aL, 有一个 a DI, 称 a 为a在I 中的解释. (c) 对每一个n元函数符号fL, 有一个DI上的n元函数 f : DIn DI , 称 f 为f在I中的解释. (d) 对每一个n元谓词符号FL, 有一个DI上的n元谓词常项F , 称 F 为F在I中的解释. 设公式A, 取个体域DI , 把A中的个体常项符号a、函数符 号f、谓词符号F分别替换成它们在I中的解释 a 、 f 、F , 称 所得到的公式A为A在I下的解释, 或A在I下被解释成A.
2018/10/11
12
(1) xy(F(x)G(y)H(x,y)) (2) x(F(x) y(G(y)H(x,y))) (3) xy(F(x)G(y)H(x,y)) 或 xy(F(x) G(y) H(x,y)) (4) xy(F(x) F(y) L(x,y)) 或 xy(F(x)F(y) L(x,y))
2018/10/11
6
实例1解答
在一阶逻辑中: (1) F(a),其中,a:墨西哥,F(x):x位于南美洲. (2) F( 2 )G( 3 ), 其中,F(x):x是无理数,G(x):x是有理数 (3) F(2, 3)G(3, 4),其中,F(x, y):x>y,G(x, y):x<y
2018/10/11
定理4.2 重言式的代换实例都是永真式,矛盾式的代换实例 都是矛盾式.
2018/10/11
22
实例
例7 判断下列公式中,哪些是永真式,哪些是矛盾式? (1) xF(x)(xyG(x,y)xF(x)) 重言式 p(qp) 的代换实例,故为永真式. (2) (xF(x)yG(y))yG(y) 矛盾式 (pq)q 的代换实例,故为永假式. (3) x(F(x)G(x)) 解释I1: 个体域N, F(x):x>5, G(x): x>4, 解释I2: 个体域N, F(x):x<5, G(x):x<4, 结论: 非永真式的可满足式
7
实例2
例 2 在一阶逻辑中将下面命题符号化 (1) 人都爱美 (2) 有人用左手写字 个体域分别为 (a) D为人类集合 (b) D为全总个体域 解 (a) (1) xF(x), F(x):x爱美 (2) xG(x), G(x):x用左手写字 (b) M(x):x为人,F(x):x爱美 (1) x(M(x)F(x)) (2) x(M(x)G(x)) 1. 引入特性谓词M(x) 2018/10/11 式 2. (1),(2)是一阶逻辑中两个“基本”公
几点说明: 永真式为可满足式,但反之不真 判断公式是否是可满足的(永真式, 矛盾式)是不可判定的
2018/10/11 21
代换实例
定义4.9 设A0是含命题变项 p1, p2, …, pn的命题公式,A1, A2, …, An是n个谓词公式,用Ai (1in) 处处代替A0中的pi,所得 公式A称为A0的代换实例. 例如, F(x)G(x), xF(x)yG(y)等都是pq的代换实例.
例如,x(F(x,y)G(x,z)), x为指导变元,(F(x,y)G(x,z))为 x 的辖域,x的两次出现均为约束出现,y与 z 均为自由出现. 又如, x(F(x,y,z)y(G(x,y)H(x,y,z))), x中的x是指导变元, 辖域为(F(x,y,z)y(G(x,y)H(x,y,z))). y中的y是指导变元, 辖 域为(G(x,y)H(x,y,z)). x的3次出现都是约束出现, y的第一次出 现是自由出现, 后2次是约束出现, z的2次出现都是自由出现.
第四章 一阶逻辑基本概念
为什么要研究一阶逻辑 命题逻辑的局限性 在命题逻辑中,命题是最基本的单位,对简单命题不再分解, 并且不考虑命题间的内在联系和数量关系,具有局限性. 考虑下面的推理: 凡偶数都能被2整除.6是偶数.所以,6能被2整除. 在数学中这是真命题,但在命题逻辑中却无法判断它的正确性 . 因将以上三个简单命题依次符号化为p,q,r,则将推理的形式 结构化为: (p q )r (非重言式,推理错误) 克服命题逻辑的局限性:一阶逻辑(谓词逻辑)
2018/10/11 5
实例1
例1 用0元谓词将命题符号化 (1) 墨西哥位于南美洲 (2) 2 是无理数仅当 3 是有理数 (3) 如果2>3,则3<4 解:在命题逻辑中: (1) p, p为墨西哥位于南美洲(真命题) (2) p→q, 其中, p: 2是无理数,q: 3 是有理数. 是假命题 (3) pq, 其中,p:2>3,q:3<4. 是真命题
2018/10/11 19
实例
例6 给定解释 I 如下: (a) 个体域 D=R (b) a 0 (c) f ( x, y) x y, g( x, y) x y (d) F ( x, y) : x y 写出下列公式在I下的解释, 并指出它的真值. (1) xF(f(x,a),g(x,a)) x(x+0=x0) 真 (2) xy(F(f(x,y),g(x,y))F(x,y)) xy(x+y=xyx=y) (3) xF(g(x,y),a)
如, F(x), F(x)G(x,y), x(F(x)G(x)) xy(F(x)G(y)L(x,y))等都是合式公式
2018/10/11 16
封闭的公式
定义4.5 在公式 xA 和 xA 中,称x为指导变元,A为相应 量词的辖域. 在x和 x的辖域中,x的所有出现都称为约束 出现,A中不是约束出现的其他变项均称为是自由出现的.
2018/10/11
3
谓词
谓词——表示个体词性质或相互之间关系的词 谓词常项 如, F(a):a是人 谓词变项 如, F(x):x具有性质F n(n1)元谓词 一元谓词(n=1)——表示性质 多元谓词(n2)——表示事物之间的关系 如, L(x,y):x与 y 有关系 L,L(x,y):xy,… 0元谓词——不含个体变项的谓词, 即命题常项 或命题变项 如 P56 例4.1
