08第八章：附有限制条件的间接平差
第八章 附有限制条件的间接平差
⎡ w1 ⎤
⎢⎢v
2
⎥ ⎥
⎢ ⎢
0
0
1
⎢⎢⎢vv43
⎥ ⎥ ⎥
=
⎢−1 ⎢⎢− 1
1 0
0 1
⎢ ⎢
v5
⎥ ⎥
⎢ 0 −1 1 ⎢
⎢v6 ⎥ ⎢ 0 −1 0
0 0 0 0 1
⎥
⎥ ⎥ ⎥ ⎥ ⎥ ⎥
⎡ ⎢ ⎢ ⎢ ⎢ ⎣
xˆ1 xˆ 2 xˆ3 xˆ 4
⎤ ⎥ ⎥ ⎥ ⎥ ⎦
⎥
−
⎢ ⎢
w2
⎢ ⎢ ⎢
⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦
∧
σ0 = ±
V T PV = ± r
19.75 = 2.2mm 4
⎢⎢⎢⎡σσXX∧∧12
⎤ ⎥ ⎥ ⎥
=
⎡ ⎢ ⎢ ⎢
∧
σ0
∧
σ0
∧
0.5320= ±1.6mm⎥⎤ 0.7739= ±1.9m⎥ ⎦
⎢⎢⎣σ0 1.1432= ±2.35mm⎥⎥⎦
+ W
CT x=
K 0
s
−
BT
Pl
=0
矩阵表示：
⎡ ⎢ ⎣
N bb C
CT 0
⎤ ⎡ xˆ ⎤
⎥ ⎦
⎢ ⎣
K
s
⎥ ⎦
−
⎡ B T Pl
⎢ ⎣
Wx
⎤ ⎥ ⎦
=
0
⎡ ⎢
∧
x
⎢⎣ K s
⎤ ⎥ ⎥⎦
=
⎡ ⎢ ⎣
N bb C
C T ⎤ − 1 ⎡ B T Pl ⎤
0
⎥ ⎦
⎢
⎥
⎣ Wx ⎦
N cc
第八章 附有限制条件的间接平差
第八章 附有限制条件的间接平差知识点1、附有限制条件的间接平差法的概念依据几何模型，针对具体的平差问题，确定观测值个数n ，必要观测数t ，则多余观测数r=n-t 。
如果又选了u 个量为参数（而u>t 且包含t 个独立量）参加平差计算，则u 中存在s 个限制条件式，则根据几何模型中的几何关系，将n 个观测值的平差值利用所选u 个参数表示出来，列出s 个函数式，共可列出n+s 个函数式，即为附有参数的条件平差的函数模型。
然后转换为误差方程的形式⎭⎬⎫=+-=0ˆˆx W x C l xB V ，然后按求自由极值的方法，解出使V T PV=min 的V 、xˆ，最后计算出X ˆ，L ˆ； 2、公式汇编函数模型和随机模型⎪⎭⎪⎬⎫=Φ+=0)ˆ(ˆˆX d X B L ，转化后⎭⎬⎫=+-=0ˆˆx W xC l x B V ，12020-==P Q D σσ其中 )(0X F L l -=，)(0X W x Φ= 。
法方程⎭⎬⎫=+=-+0ˆ0ˆx s T BB W x C W K C xN式中PB B N T BB =，Pl B W T= 。
其解x CC T BB X X x CC T BB BB CC T BB BB W N C N W Q W N C N W CN N C N N x 11ˆˆ111111)(ˆ---------=--=)(11x BB CC s W W CN N K +=--式中TBB CC C CN N 1-= 。
观测值和参数的平差值x X Xˆˆ0+=，V L L +=ˆ单位权方差的估值su n PVV T +-=20ˆσPV V T 的计算：（1）PV l PV B x PV V T T T -=ˆ；（2）x PB l Pl l PV V TT T ˆ-=；参数平差值函数)ˆ(ˆX Φ=ϕ平差值函数的权函数式 x F X d F d T T ˆˆˆ==ϕ协因数： F Q F Q X XT ˆˆˆˆ=ϕϕ；方差：ϕϕϕϕσˆˆ20ˆˆQ D =； 3、按附有限制条件按的间接平差求平差值的计算步骤：（1）确定n 、t ，选u （u>t 且包含t 个独立量）个量为参数参与平差；得出s 个参数是相关的（2）列出n+s 个方程，即先将n 个观测值的平差值利用所选参数表示出来，再列出s 个函数式：即先列出平差值形式，再转化为误差方程形式，最后矩阵形式⎭⎬⎫=+-=0ˆˆx W xC l xB V ；（3）确定权阵P ；（4）依据以下公式计算，PB B N T BB =，Pl B W T=，TBB CC C CN N 1-=，x CC T BB BB CC T BB BB W N C N W CN N C N N x 111111)(ˆ--------=，x X Xˆˆ0+=，V L L +=ˆ；（5）检核；（6）精度评定。
测量平差第八章
• 令:
V T PV 2K T ( AV Bx转 W置) 后2K得ST (Cx WX )
x
2K
T
B
2K
T S
C
0
V QAT K
2V T P 2K T A 0 V
BT K CT KS 0
§8.2 基础方程和它的解
• 于是统一平差模型的基础方程为
(1) A V B xW 0
• 令:
V T
PV
2K T
( AV
B转x置 W后) 得2K
T S
(Cx
WX
)
x
2K
T
B
2K
T S
C
0
V QAT K
2V T P 2K T A 0 V
BT K CT KS 0
§8.2 基础方程和它的解
• 或者
N aa
cc
BT
uc
0
sc
B
cu
0
uu
C
su
0
cs
CT
us
0
ss
K
cn n1 cu u1 c1 c1
(2)
C
su
x
u1
WX
s1
0 s1
(3) V Q AT K n,1 n,n n,c c,1
(4) BT u,c
K CT
c,1 u,s
Ks
s1
0
u ,1
§8.2 基础方程和它的解
• （3）、若选u<t，且未知数参数独立，条件方程中含
未知参数x ，线性形式为A V B x。W 这0时基础方程（2）
多只能列出t个函数独立的参数。在不选择参数时，
一般条件方程数c等于多余观测数 ，r 若n又t选用了
08第八章 概括平差函数模型
第八章 概括平差函数模型§8.1概述在已经介绍过的条件平差，间接平差，附有参数的条件平差以及附有限制条件的间接平差等四种基本平差方法，其差别就在于函数模型不同。
若将误差方程也视为参数形式的条件方程，以未知参数为纽带，可以对4种平差方法概括如下：（1）、条件平差：0)ˆ(=L F ，不选择未知参数，方程数等于多余观测数：c=t n r -= （2）、间接平差：)ˆ(ˆX F L=，选函数独立未知数t u =，方程数n t r u r c =+=+= （3）、附有参数的条件平差：0)ˆ,ˆ(=X LF ，选择t u <个函数独立参数，除应列出r 个条件方程外，还要附加u 个对未知参数的约束条件方程，所以必须列出u r c +=个条件方程。
（4）、附有限制条件的间接平差：)ˆ(ˆX F L =，0)ˆ(=ΦX 。
选择t u >个参数，参数间存在t u s -=个函数关系。
所以除列出n 个误差方程)ˆ(ˆX F L=（也可视为特殊形式的条件方程－参数方程形式的条件方程），还要列出s 个限制条件方程0)ˆ(=ΦX。
方程数c=n ＋s 。
由此可见，是否选择参数及如何选择参数决定着平差方法，即参数是联系各种平差方法的纽带。
另外可以看到，前三种函数模型中都含有观测量，或者同时包含观测量和未知参数，而后一种只含有未知参数而无观测量。
为了便于区别，将前三种统称为一般条件方程，而后者称为限制条件方程，并统称为条件方程。
在任何几何模型中，函数独立参数个数总是介于下列范围之内： t u ≤≤0。
也就是说，在任一平差问题中，最多只能列出t u =个函数独立的参数。
在不选择参数时，一般条件方程数c 等于多余观测数t n r -=，若又选用了u 个函数独立参数，则总共应当列出u r c +=个一般条件方程。
由于t u ≤，因此一般条件方程的个数总是介于n c r ≤≤范围，即一般条件方程总数不超过n 个。
附有条件的间接平差)ppt课件
平差对象
地理数据，如经纬度、高程等
案例描述
在GIS中，为了确保地图的准确性，需要使用附有 条件的间接平差对地理数据进行处理，如对全球定 位系统（GPS）数据进行平差处理，以提高其定位 精度。
案例二：气象数据平差
• 应用领域：气象预报
• 平差对象：气象观测数据，如温度、湿度、风速、气压等 • 平差方法：利用已知的气象数据和气象站的位置信息，通过平差计算，对未知的气象数据进行修正，提高其准确性 • 案例描述：在气象预报中，需要对大量的气象观测数据进行平差处理，以获取更准确的气象信息。例如，通过附有条件的间接平差方法，可以修正气象观测数据的误差，提高气象预报的准确率。
附有条件的间接平差的应用场景
附有条件的间接平差广泛应用于大地 测量、工程测量、航空摄影测量等领 域。
在工程测量中，附有条件的间接平差 可以用于桥梁、隧道、建筑物等工程 的施工测量和监测，提高工程质量和 安全性。
在大地测量中，附有条件的间接平差 可以用于处理地球重力场模型的数据， 提高模型精度和可靠性。
解算参数
通过计算或软件解算，得 出未知点的坐标和其它相 关参数的估计值。
参数精度评估
对解算出的参数进行精度 评估，了解其可靠性和误 差范围。
结果检验
残差分析
对解算出的结果进行残差 分析，检查是否符合预期 的误差分布。
精度验证
通过实地测量或其它方式， 验证解算结果的精度和可 靠性。
模型适用性评估
评估所建立的数学模型是 否适用于实际测量情况， 并根据评估结果进行必要 的调整或改进。
常用的计算方法包括最小二乘法、梯度下降法等，选择合 适的计算方法可以提高求解效率和结果的准确性。
03
附有条件的间接平差的 实现步骤
误差理论与测量平差基础习题集4
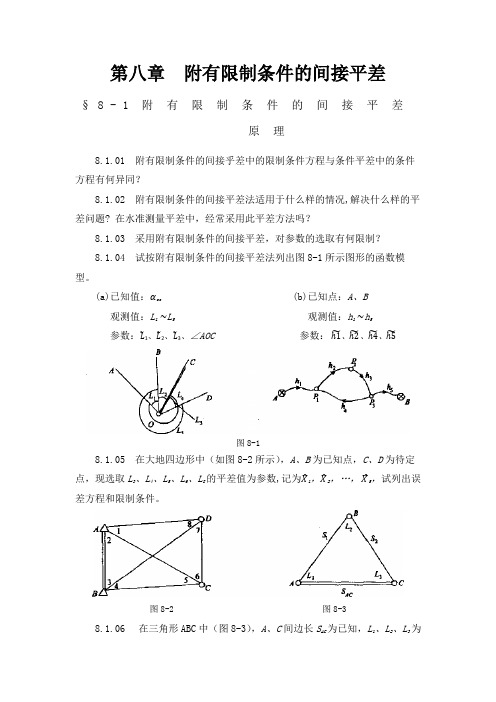
若设参
数
X=[X1X2X3 ]T=[HBh3h4]T，定权时 C=2km。试列出 （1）误差方程式及限制条件； （2）法方程式。 8.1.09 在图 8-6 中，A、B 为已知三角点，C、D 为待定点，观测了 9 个内
角 L1~L9。现选取参数X=[X1X2X3X4X5 ]T =[L1L2L3L4L5 ]T，试列出误差方程 式和限制条件。 8.1.10 在图 8-7 所示的测边网中，A、B 为已知点，1,2 为待定点，观
角度观测精度均为������
= 1″。
������
观测了边长 S1、S2，观测精度均为������ ������
2
= 10mm，
0 ������
������
1
= 148.283m，
= 107.967m。 设 P 点的坐标为未知参数，其近似坐标为������ = 882.270m，
������
0 ������
9.2.04 附有限制条件的条件平差模型在解决实际平差问题中有什么意 义？ 9.2.05 某平差问题有 15 个同精度观测值，必要观测数等于 8，现选取 8 个参数，且参数之间有 2 个限制条件。若按附有限制条件的条件平差法进行 平差，应列出多少个条件方程和限制条件方程？由其组成的法方程有几个？ 9.2.06 在测站 O 上观测 A、B、C、D 四个方向（如图 9-1 所示） ，得等精 度观测值为： L1=44°03′14.5″， L2=43°14′20.0″， L3=53°33′32.0″, L4=87°17′31.5″,
(a)已知值：矩形的对角边 S 观测值：L1~L4 参数：������1、������2、������3
图 8-4
8.1.08
误差理论与测量平差基础第八章 附有限制条件的间接平差
Q XX Q XL B T ˆˆ ˆ QLL BQXX B T ( B E ) ˆˆ Q ˆ Q E LX LL
（1）根据具体问题，按（1）式列出误差方程和条件方 程。
（2）由误差方程和条件方程列出法方程（3）式。
（3）按（4）式计算参数的改正数 x 。 ˆ
（4）按（5）式计算观测值的平差值和参数的平差值。
教材：8－1
第八章——附有限制条件的间接平差
4、举例
水准网如图所示，同 精度观测值为： L1 0.008m
观测值的平差值（略）
习题：8.1.10，8.1.11
第八章——附有限制条件的间接平差 §8-2 精度评定
(1)、单位权中误差 在附有条件的间接平差中，单位权中误差的估值仍为
V T PV ˆ2 0 r
(2)、基本向量的协因数矩阵 在附有条件的间接平差中，基本向量为：
ˆ ˆ L, W , X , K s , V , L
求解法方程，得
ˆ xC 1.8505 , yC 0.6653 cm ˆ cm ˆ x D 0.1399 , y D 2.4593 cm ˆ cm k S 28.9655
第八章——附有限制条件的间接平差
改正数为：
V 2.4 5.7 5.7 8.0 0.0 0.0
第八章——附有限制条件的间接平差
误差方程和条件方程如下：
1.786 1.031 1.786 1.031 2.24 ˆ 0 2.063 xC 4.62 1.786 1.032 0 y 6.62 2.063 1.786 1.032 ˆ C V x 0.38 0 2.063 ˆ D 1.786 1.032 0 y 1.38 2.063 1.786 1.032 ˆ D 1.786 1.032 1.786 1.032 6.24 ˆ ˆ 0.500x D 0.866y D 2.20 0
误差理论与测量平差(山东联盟)智慧树知到答案章节测试2023年山东建筑大学
第一章测试1.误差是不可避免的。
A:对B:错答案:A2.构成观测条件的要素有哪些A:外界条件B:计算工具C:观测者D:测量仪器答案:ACD3.对中误差属于那种误差A:系统误差B:偶然误差C:不是误差D:粗差答案:B第二章测试1.两随机变量的协方差等于0时，说明这两个随机变量A:相关B:互不相关C:相互独立答案:B2.观测量的数学期望就是它的真值A:错B:对答案:A3.衡量系统误差大小的指标为A:精确度B:准确度C:不确定度D:精度答案:B4.精度是指误差分布的密集或离散程度，即离散度的大小。
A:错B:对答案:B5.若两观测值的中误差相同，则它们的A:测量仪器相同B:真误差相同C:观测值相同D:精度相同答案:D第三章测试1.设L的权为1，则乘积4L的权P=（）。
A:1/4B:4C:1/16D:16答案:C2.有一角度测20测回，得中误差±0.42秒，如果要使其中误差为±0.28秒，则还需增加的测回数N=（）。
A:25B:45C:20D:5答案:A3.在水准测量中，设每站观测高差的中误差均为1cm，今要求从已知点推算待定点的高程中误差不大于5cm，问可以设25站。
A:对B:错答案:A4.已知距离AB=100m，丈量一次的权为2，丈量4次平均值的中误差为2cm，若以同样的精度丈量CD的距离16次，CD=400m，则两距离丈量结果的相对中误差分别为（ 1/5000 ）、（1/20000 ）。
A:错B:对答案:B5.A:29B:35C:5D:25答案:D第四章测试1.当观测值为正态随机变量时，最小二乘估计可由最大似然估计导出。
A:对B:错答案:A2.多余观测产生的平差数学模型，都不可能直接获得唯一解。
A:对B:错答案:A3.在平差函数模型中，n、t、r、u、s、c等字母各代表什么量？它们之间有何关系？( n观测值的个数 )(t必要观测数 )(r多余观测数,r=n-t )(u所选参数的个数 )( s非独立参数的个数,s=u-t )( c所列方程的个数,c=r+u )A:对B:错答案:A4.A:对B:错答案:A5.A:错B:对答案:B第五章测试1.关于条件平差中条件方程的说法正确的是：A: 这r个条件方程应彼此线性无关B: 应列出r个条件方程C: r个线性无关的条件方程必定是唯一确定的，不可能有其它组合。
间接平差
§4-1 间接平差原理2学时间接平差法（参数平差法）是通过选定t 个与观测值有一定关系的独立未知量作为参数，将每个观测值都分别表达成这t 个参数的函数，建立函数模型，按最小二乘原理，用求自由极值的方法解出参数的最或然值，从而求得各观测值的平差值。
例如，在一个三角形中，等精度独立观测了三个角，观测值分别为L 1、L 2和L 3。
求此三角形各内角的最或然值。
若能选取两个内角的最或然值作为参数 1ˆX 、 2ˆX ，则可以建立参数与观测值之间的函数关系式⎪⎪⎭⎪⎪⎬⎫--=+=+=+2133222111ˆˆ180ˆˆX X v L Xv L X v L（4-1-1）可得⎪⎪⎭⎪⎪⎬⎫---=-=-=3213222111ˆˆ180ˆˆL X X v L Xv L Xv （4-1-2）为了计算方便和计算数值的稳定性，通常引入未知参数的近似值，这一点在实际计算中是非常重要的，令 x X X ˆˆ0+=，则（4-1-2）式可写成如下形式：⎪⎭⎪⎬⎫-++---=--=--=)180(ˆˆ)(ˆ)(ˆ020132130222201111X X L x x v X L x v X L xv （4-1-3）式（4-1-2）叫做误差方程，也可以称为某种意义上的条件方程（包含改正数、观测值和参数，“条件个数=观测值个数”），每个条件方程中仅只含有一个观测值，且系数为1。
单纯为消除矛盾， 1v 、 2v 、 3v 可有多组解，为此引入最小二乘原则： min =PV V T可求得唯一解。
因此，间接平差是选取与观测值有一定关系的独立未知量作为参数，建立参数与观测值之间的函数关系，按最小二乘原则，求解未知参数的最或然值，再根据观测值与参数间的函数关系，求出观测值的最或然值，故又称为参数平差。
对上述三角形，引入最小二乘原则，要求：min =PV V T ，设观测值为等精度独立观测，则有：[]min )180ˆˆ()ˆ()ˆ(2321222211=-+--+-+-=L X X L X L X vv按数学上求自由极值的方法对上式分别求偏导数并令等于零，可得60313132ˆ60313231ˆ02180ˆ3)1(2)2()2()1(0180ˆ2ˆ0180ˆˆ20)ˆˆ180(2)ˆ(2ˆ][0)ˆˆ180(2)ˆ(2ˆ][32113212321232213121321222321111+--+=⇒+-+-=⇒=+-+-⇒-⨯⎭⎬⎫=+--+=+--+⇒⎪⎪⎭⎪⎪⎬⎫=-----=∂∂=-----=∂∂L L L X L L L X L L L X L L X X L L X X L X X L X X vv L X X L X X vv代入误差方程式，得到观测值的最或然值603231316031323160313132321332123211++--=+-+-=+--+=∧∧∧L L L L L L L L L L L L此结果显然与采用条件平差方法解算的结果一致，说明只要遵循相同的平差原则、定权方法相同，平差结果与具体平差方法无关。
6.5 第二十讲 附有条件的间接平差资料
QWW BT PQPB BT PB N bb ,
1 1 T 1 1 1 1 T 1 1 T QX ( N N C N CN ) Q ( N N C N CN ˆX ˆ bb bb cc bb WW bb bb cc bb )
1 1 T 1 1 1 1 T 1 1 ( N bb N bb C N cc CN bb ) N bb ( N bb N bb C N cc CN bb )
T
Av W 0 W ( AL A0 )
2018/11/1
v B~ x l l L ( BX 0 d )
2
第二十讲
附有限制条件的间接平差
附有限制条件的间接平差： 看成是特殊的间接平差； 特殊在所选参数个数要比 间接平差时个数多； 参数个数ｕ：ｕ＞t 函数模型的个数： ｃ=ｎ+（ｕ-t）=ｎ+ｓ 函数模型的类型： 1.按间接平差的观测方程、 2.未知数之间的条件方程（限 ~ ~ 制条件式）。 L F(X ) ~ 函数模型可表示为： ( X )0
u ,1 u ,s s ,1
ˆ Wx 0. C x
s ,u u ,1 s ,1
2018/11/1 12
第二十讲
附有限制条件的间接平差
u ,u
法方程解法一（显性形式）： 用
1 CN bb
ˆ CT Ks W 0 N bb x
u ,1 u ,s s ,1 u ,1
左乘（1）-（2）得：
s ,u u ,1 s ,1
B PB x C T K s B T Pl 0,
T
u,n
B
T
n , n n ,1
P V C Ks O.
《误差理论与测量平差基础》第八章
dΦ ˆ ˆ ˆ d F T dX ˆ dX dX 0
—— 权函数式！
Φ FT ˆ X 1 Φ Φ ˆ ˆ X X 2 u 0
其中：
1 1 T 1 1 QX ˆX ˆ N BB N BBC NCC CN BB
u ,u u ,1 u ,s s ,1 u ,1
代入 ④ 得：
u ,1 1 1 T 1 1 1 T 1 ˆ ( N BB x N BB C N CC CN BB )Wl N BB C N CC Wx
④ ⑤
ˆ l B x 代入 ① 得：V n ,u u ,1 n ,1 n ,1
二、示例
n = 18 t = 2 × 5 – 2 = 8 u = 2×5 = 10 限制条件方程个数： s = u – t = 2
方程总数 C = r + u = n + s = 20
误差方程数：n = 18 = c – s 详见课本 P165-169
1
1 1
§8.3 公式汇编和示例
一、公式汇编 1.函数模型：
ˆl VB x
n ,1 n ,u u ,1 n ,1
3.参数的解：
u ,1 1 1 T 1 1 1 T 1 ˆ ( N BB x N BB C N CC CN BB )Wl N BB C N CC Wx
1 T 1 QX ˆLeabharlann ˆ Wl N BBC NCCWx
§8.3 公式汇编和示例
ˆ) ˆ Φ( X
ˆ ˆ F T dX d
Φ Φ Φ FT ˆ X ˆ ˆ 1,u X X 2 u 0 1
T Q ˆ ˆ F QX ˆX ˆF
《误差理论与数据处理》课程教学大纲
《误差理论与数据处理》课程教学大纲【课程代码】：13319608【英文译名】：Error Theory and Surveying Adjustment 【适用专业】：地理信息系统【学分数】：4 【总学时数】：64一、本课程教学目的和课程性质误差理论与数据处理是地理信息系统专业的工程技术基础必修课之一、通过学习本门课程，使学生能够应用概率和数理统计方法来分析观测数据，采用最小二乘法作为处理观测数据的基本原则，合理计算处理，以得到更接近真值的结果。
在内容上，主要讲解测量平差的基本原理、方法和技能；论述近代测量平差的基本理论与方法，介绍测量数据处理的最新研究成果。
二、本课程的基本要求通过本门课程的学习,掌握平差课程的任务和研究对象,并很好的掌握几种主要的平差方法.在了解了近代平差基本理论和最新的研究成果基础上，在后续的课程中灵活应用对数据的处理和误差分析，为以后的工作和进一步深造打下良好的基础。
三、本课程与其他课程的关系前修课程:测量学、高等数学、线性代数、概率论与数理统计；后续课程:GPS原理、摄影测量学、遥感原理与应用。
四、课程内容《误差理论与数据处理》是研究误差的一门学科，通过学习本门课程，使学生能正确处理测量数据，合理计算处理，以得到理想的结果。
本课程要求：基本知识的掌握，掌握误差的基本概念，不同性质误差的变化规律及处理方法。
权的概念及不等精度测量的数据处理方法，误差的合成及分配，回归、相关等。
本课程内容安排如下：第一章绪论基本内容：主要介绍有关误差的一些基本概念，观测误差及测量平差理论研究的对象。
属于了解内容。
第二章误差分布及精度指标环境与资源学院基本内容：本章节主要介绍有关平差的含义、观测条件、系统误差、偶然误差的概念。
及偶然误差的统计规律性及精度、方差、中误差的概念。
重点：掌握概念：观测条件、系统误差、偶然误差；难点：偶然误差的规律性以及所服从的分布；第三章协方差传播律及权基本内容：本章节主要介绍有关协因数传播率的概念及应用领域，使学生掌握协因数、协因数阵、权阵的概念；掌握协因数传播律的一般形式与特殊形式权倒数传播律。
第八章-具有约束条件的间接平差2008
133第八章 具有约束条件的间接平差在一个平差问题中，观测数为n ，多余观测数为t n r -=，t 为必要观测次数。
如果在平差问题中，不是选t 个而是选择t u >个参数，其中包含t 个独立参数，则多选择的t u s -=个参数必然是t 个独立参数的函数，亦即在u 个参数之间存在着t u s -=个函数关系，它们用来约束参数之间应该满足的关系。
因此在选定t u >个参数进行间接平差时，除了n 个观测方程外，还要增加t u s -=个约束参数的条件方程，故称此平差方法为具有约束条件的间接平差法。
在第四章中已给出了具有约束条件的间接平差的函数模型为：⎪⎩⎪⎨⎧=++=⨯⨯⨯⨯⨯⨯⨯⨯1111110~~~s s u u s n u u n n U X d X L C B 且t s u +==)(R B ，s =)(R C ；n u s <<另外，d 和U 分别是n 行1列、和s 行1列的常数向量。
以估值代替真值，即 V L L L +=→ˆ~，x X XX ˆˆ~0+=→ 这样模型化为00ˆ()ˆ⎧=-=-+-⎨+==+⎩X X B B C 0C 其中：其中：V xl l X d L x W W X U该平差问题的自由度是)(s u n r --=。
观测值向量L 的随机模型为nn nn nn ⨯-⨯⨯==12020P Q D σσ平差的准则为min T =V V P具有约束条件的间接平差就是要求在满足n 个误差方程和s 个参数条件方程下，利用最小二乘原理求V 值，在数学中就是求函数的条件极值问题。
§8.1 平差原理在具有约束条件的间接平差的函数模型中，有n u r c <+=个条件方程，即111111ˆˆn u n u n s u u s s ⨯⨯⨯⨯⨯⨯⨯⨯=-⎧⎪⎨+=⎪⎩X B C 0V x l x W (8.1.1) 其中134)(0L d X l -+-=B ，U X W +=0C X由于未知数⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n v v v 21V ，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=u x xxˆˆˆˆ21 x (8.1.2) 为u n +个。
08附有条件的间接平差
n1
s1
ˆ C x Wx 0
2 2 D 0 Q 0 p 1 nn
s1
随机模型为： 平差原则：
V PV min
T
组成新函数
ˆ V T PV 2 K sT (Cx Wx ) ˆ
对取偏导数并令其为零
解联系数和参数：
1 1 K s NCC (CN BBW Wx ) 1 1 1 1 1 1 ˆ x ( N BB N BB C T NCC CN BB )W N BBC T N CCWx 1 ( N BB BT PB,W BT Pl , N CC CN BBC T )
求参数和观测值的平差值：
ˆ L L V ˆ ˆ X X0 x
平差计算步骤：
1)选个数大于必要观测数的参数（包含t个独 立）； 2)列出误差方程和限制条件方程；
3)组法方程，解
ˆ x
、
Ks
；
、
4)求改正数V，最后求
ˆ L
ˆ X
；
8-2 精度评定
一、单位权方差的估值公式
T T
V PV V PV ˆ r n (u s)
得到的法方程以及基本向量的自（互）协因 数阵公式有所不同！
8-1 附有限制条件的间接平差原理
若选P1，P2点高程以及第四段高差的平差值为参数 进行最小二乘平差，该如何作？
在作间接平差时多选了未知数（例1）、或者有 时为了列立误差方程方便而多选了未知数（例 2）；
这样，未知数之间会存在条件式，这种情况下所 作的平差方法就是附有限制条件的间接平差。
T V 2VP 2 K sT C 2V T PB 2 K sT C 0 ˆ ˆ x x
第8章 附有限制条件的间接平差
ˆ l PV x ˆ TB T PV l T PV 2. V T PV Bx
T
ˆ TCTK S l T PBx ˆ l x
顾及 B PV ＝ C K
T T S
ˆ TCTK S l T PB x ˆ l T Pl x
ˆ l T Pl WxT K S W T x
10
转置得
B T PV C T K S 0
上式与误差方程和限制条件方程联立得附有限制条件 的间接平差法的基础方程：
u ,n
B P V C KS 0
n , n n ,1 u ,s s ,1
T
T
u ,1
ˆ l VBx
n ,1 n ,u u ,1
n ,1
ˆ Wx 0 Cx
s ,u u ,1 s ,1
s ,1
8 /17
方程的个数与未知数的个数相同，方程有唯一解。
主页
附有限制条件的间接平差
三、基础方程的解
误差理论与测量平差
1 2 3 4 5 6 7 8 9
10
将基础方程的第二式代入第一式与第三式联立，得 ˆ CT KS W 0 N BB x －法方程 ˆ Cx Wx 0 1 将法方程第一式左乘 CN BB 与第二式相减，得
S
Q LX ˆ QWX ˆ QK
SX
QLV QW V Q K SV QX ˆV QVV QL ˆV
ˆ
QX ˆX ˆ QVX ˆ QL ˆX ˆ
13 /17
QVK S
S
Q LL ˆ QWL ˆ QK L ˆ S QX ˆL ˆ QVL ˆ QL ˆL ˆ
主页
附有限制条件的间接平差
测量平差 答案
南京师范大学模拟试卷课程误差理论与测量平差基础一、填空题（20分）1. 某平差问题有以下函数模型(Q=I)（11分） 1L ∧=1x ∧2L ∧=1x ∧-2x ∧3L ∧=-1x ∧+3x ∧4L ∧=-3x ∧+A 5L ∧=-2x ∧-B 1x ∧+3x ∧+C=0试问：（1）以上函数模型为何种平差方法的模型？（3分）答：附有限制条件的间接平差。
（2）本题中，n= ，t= ，c= ，u= ，s= 。
（5分） 答：n=5，t=2，c=5，u=3，s=1 （3）将上述方程写成矩阵形式。
（3分）答：5,1L ∧=100110101001010⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥-⎣⎦3,1x ∧+000A B ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦()1013,1x ∧+C=02. 衡量精度的指标有方差和中误差、平均误差、或然误差、 、 。
（4分）答：极限误差 相对中误差3. 测定A 、B 两点间高差，共布设了16个测站，各测站观测高差是同精度独立观测值，其方差均值为2σ站=1m 2m ，则AB 两点间高差的中误差为ABh σ= 。
（5分） 答：ABh σ=4mm 。
二、证明题在间接平差中，参数1n X ∧与1n V 改正数是否相关？试证明之。
（10分）证明：X ∧=0x +x ∧BB N x ∧-TB Pl=0x ∧=1BBN -T B Pl又l=L-oLx ∧=1BBN -T B Pl -1BB N -T B P o L V=B x ∧-l=B 1BBN -TB Pl -B 1BB N -TB P oL -L+oL = (B 1BBN -TB P-E)L- B 1BB N -TB P oL +oL 令 LL Q =Qx vQ ∧=1BB N -TB PQ 1(-E)T T BB BN B P -=1BBN -T B ( P 1BB N -TB P -E) =1BBN -TB P 1BB N -TB P-E 1BB N -TB =1BBN -TB -1BB N -TB =0 ∴1n X ∧与1n V 不相关。