附有限制条件的间接平差
第八章 附有限制条件的间接平差

⎡ w1 ⎤
⎢⎢v
2
⎥ ⎥
⎢ ⎢
0
0
1
⎢⎢⎢vv43
⎥ ⎥ ⎥
=
⎢−1 ⎢⎢− 1
1 0
0 1
⎢ ⎢
v5
⎥ ⎥
⎢ 0 −1 1 ⎢
⎢v6 ⎥ ⎢ 0 −1 0
0 0 0 0 1
⎥
⎥ ⎥ ⎥ ⎥ ⎥ ⎥
⎡ ⎢ ⎢ ⎢ ⎢ ⎣
xˆ1 xˆ 2 xˆ3 xˆ 4
⎤ ⎥ ⎥ ⎥ ⎥ ⎦
⎥
−
⎢ ⎢
w2
⎢ ⎢ ⎢
⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦
∧
σ0 = ±
V T PV = ± r
19.75 = 2.2mm 4
⎢⎢⎢⎡σσXX∧∧12
⎤ ⎥ ⎥ ⎥
=
⎡ ⎢ ⎢ ⎢
∧
σ0
∧
σ0
∧
0.5320= ±1.6mm⎥⎤ 0.7739= ±1.9m⎥ ⎦
⎢⎢⎣σ0 1.1432= ±2.35mm⎥⎥⎦
+ W
CT x=
K 0
s
−
BT
Pl
=0
矩阵表示:
⎡ ⎢ ⎣
N bb C
CT 0
⎤ ⎡ xˆ ⎤
⎥ ⎦
⎢ ⎣
K
s
⎥ ⎦
−
⎡ B T Pl
⎢ ⎣
Wx
⎤ ⎥ ⎦
=
0
⎡ ⎢
∧
x
⎢⎣ K s
⎤ ⎥ ⎥⎦
=
⎡ ⎢ ⎣
N bb C
C T ⎤ − 1 ⎡ B T Pl ⎤
0
⎥ ⎦
⎢
⎥
⎣ Wx ⎦
N cc
第四章 间接平差

参数的选取
在水准网中,常选取待定点高程作为参数,也 可选取点间的高差作为参数,但要注意参数的 独立性。当选取待定点高程作为参数时可以保 证参数的独立性。 在平面控制网、GPS网中选取未知点的二维坐标 或三维坐标作为未知参数,可以保证参数之间 的独立性,也可以选取观测值的平差值作为未 知数。 因此如上所述,采用间接平差,应该选定刚好t 个而又函数独立的一组量作为参数。至于应选 择其中哪些量作为参数,则应按实际需要和是 否便于计算而定。
测量平差
太原理工大学测绘科学与技术系
第四章
间接平差
第四章 间接平差
§4-1
§4-2 §4-3 §4-4 §4-5 §4-6
间接平差原理
误差方程 精度评定 间接平差公式汇编 附有限制条件的间接平差 间接平差估值的统计性质
§4-1
间接平差原理
间接平差法(参数平差法)是通过选定t个 与观测值有一定关系的独立未知量作为参 数,将每个观测值都分别表达成这t个参数 的函数,建立函数模型,按最小二乘原理, 用求自由极值的方法解出参数的最或然值, 从而求得各观测值的平差值。
0 xt Li f i X 10 , X 2 ,, X t0 ˆ 0
f f a i i bi i X X ˆ ˆ 2 0 1 0
f i ti X ˆ t
0
T
T
1
2
t
ˆˆ XX
1 bb
1 Q F T QXX F F T Nbb F ˆˆ ˆˆ
参数函数中的误差
一般,设有函数向量
ˆ ˆ FT x
m ,1 m ,t t ,1
ˆ
附有限制条件的间接平差

Ks
s1
0
(2)
(2)基础方程的解
以上基础方程中,方程的个数为n+u+s个,而 未知数为n个改正数、u个参数、s个联系数,也是 n+u+s个,故有唯一解。将基础方程的第一式代 入第三式,得
BT PBxˆ CT Ks BT Pl 0 Cxˆ Wx 0
或 Nbb xˆ CT K s W 0
V T PV min的一组解,组成新函数
V
T
PV
2
K
T s
(Cxˆ
Wx )
上式对参数求偏导数,并令其为零,得
即
xˆ
2V
T
PB
2K
T s
C
0
BT PV C T K s 0
于是,可得附有条件的间接平差的基础方程:
V B xˆ l
n1 nu u1 n1
C
su
xˆ
s1
Wx
s1
0
BT
un
P V CT
1 0 0 1 x1 0
0
0 1
1 0 1
0 1 1
1 x2
1 0
x3 kS
0 0 6
0
解之得: x1 2 1 1 1 0 2
x2
x3 kS
1 1
3
1 1
2 1 1
1 2 1
1 0
11
0 6
2
22
代入误差方程,得:
v1 2mm
v2 2mm
于是:
v3 2mm
4)按式(5)计算观测值的平差值和参数的平差值。
2.精度评定 (1)单位权中误差
在附有条件的间接平差中,单位权中误差的 估值仍为
8附有限制条件的间接平差

aik xˆ i + bik ˆyi aik xˆ k bik ˆyk w2 0
w1
X
0 k
X
0 i
2
+
Yk0 Yi0
2
Sik
w2
arctan
Yk0
X
0 k
Yi0
X
0 i
aik
§8-1 附有限制条件的间接平差原理
二、基础方程
已知附有限制条件的间接平差法的函数模型
K
s ,1
k1
k2
ks T
称为联系数向量。组成极值函数
V T PV
2K
T s
Cxˆ Wx
将对 求xˆ 一阶导数,并令其为零,得:
xˆ
2V T P V xˆ
2
K
T s
C
2V
T
PB
2
K
T s
CLeabharlann 0转置得 BT PV C T K s 0
§8-1 附有限制条件的间接平差原理
§8-2 精度评定
三、平差值的精度评定
DLˆ Lˆ
ˆ
Q 2
0 Lˆ Lˆ
DXˆ Xˆ
ˆ
Q 2
0 Xˆ Xˆ
§8-2 精度评定
四、参数平差值函数的精度评定
设参数平差值函数为:
ˆ
G(
Xˆ )
G(
Xˆ
1,Xˆ
,
2
Xˆ
)
u
线性化得权函数式为:
dˆ
G Xˆ 1
X0
误差理论与测量平差基础习题集4
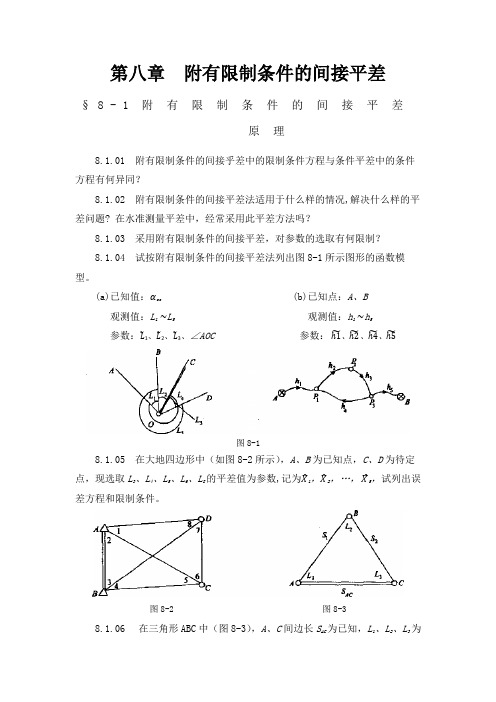
若设参
数
X=[X1X2X3 ]T=[HBh3h4]T,定权时 C=2km。试列出 (1)误差方程式及限制条件; (2)法方程式。 8.1.09 在图 8-6 中,A、B 为已知三角点,C、D 为待定点,观测了 9 个内
角 L1~L9。现选取参数X=[X1X2X3X4X5 ]T =[L1L2L3L4L5 ]T,试列出误差方程 式和限制条件。 8.1.10 在图 8-7 所示的测边网中,A、B 为已知点,1,2 为待定点,观
角度观测精度均为������
= 1″。
������
观测了边长 S1、S2,观测精度均为������ ������
2
= 10mm,
0 ������
������
1
= 148.283m,
= 107.967m。 设 P 点的坐标为未知参数,其近似坐标为������ = 882.270m,
������
0 ������
9.2.04 附有限制条件的条件平差模型在解决实际平差问题中有什么意 义? 9.2.05 某平差问题有 15 个同精度观测值,必要观测数等于 8,现选取 8 个参数,且参数之间有 2 个限制条件。若按附有限制条件的条件平差法进行 平差,应列出多少个条件方程和限制条件方程?由其组成的法方程有几个? 9.2.06 在测站 O 上观测 A、B、C、D 四个方向(如图 9-1 所示) ,得等精 度观测值为: L1=44°03′14.5″, L2=43°14′20.0″, L3=53°33′32.0″, L4=87°17′31.5″,
(a)已知值:矩形的对角边 S 观测值:L1~L4 参数:������1、������2、������3
图 8-4
8.1.08
第五章 附有限制条件的条件平差

§5-2 精度评定
任何一种平差方法,其精度评定的内容都包括 以下三方面内容:单位权方差估值的计算、各向 量的协因数阵及向量间的互协因数阵的推导、平 差值函数协因数及其中误差的计算,本节也将对 这三方面内容作介绍。
一、单位权方差估值的计算公式
如果在u个参数中有s个是不独立的或者说在这u个参数中存在着s个函数关系式则建立平差模型时应列出s个限制条件方程除此之外再列出crus个一般条件方程因此方程总数也可以认为是cs个形成如下的函数模型若为线性形式则为无论线性模型还是非线性模型按照第二章介绍的线性化方法和结论并考虑到则可写出其线性化后的函数模型为以上式作为函数模型而进行的平差称为附有限制条件的条件平差有的文献也称其为概括平差函数模型
CN C K s CN We W x 0
N cc CN bb1C T
1 bb
于是前式可写成
N cc K s CN W e W x 0 由此式可得
1 bb
K s N (Wx CN We )
1 cc
1 bb
(5-1-25)
将上式代入(5-1-24)式,整理可得
Qww AQll A N aa
T
(5-2-4)
We B T N aa1W
QW eW e B N N aa N B B N B N bb (5-2-5)
T T
Q XˆX ( N bb1 N bb1C T N cc1CN bb1 ) N bb ( N bb1 N bb1C T N cc1CN bb1 ) T ˆ
u 1
1 aa
1 aa
1 aa
( E N bb1C T N cc1C )( N bb1 N bb1C T N cc1CN bb1 )
条件平差与间接平差探讨
观测数 必要观测数 多余观测数 所设参数数 方程数 待求量数 t
n
n t r=n-t 0<u<t 且独立 c= r+u n+u
n t r=n-t u=t 且独立 r+u=n n+u
n t r=n-t u>t 且包含 t 个独立 r+u=n+s n+u
r=n-t 0 r n
方程形式
ΑΔ+W=0
ΑΔ+Β X +W=0
β3
1 2 180。 0
β1 A P( X P , YP ) β2 B
~
~
~
sab s1 ~ ~ 0 sin sin s1 s2 ~ ~ 0 sin 1 sin 2
~
~
S1
S2
已知点:A、B、C 观测值:S1-S3 S3 参数;P 点坐标 X P、YP C 求平差方程?(间接平差)
~
~
A B
~ S1 (~ xp ~ xA )2 ( ~ yp ~ y A )2 ~ S 2 (~ xp ~ xB ) 2 ( ~ yp ~ yB )2 ~ S3 (~ xp ~ xC ) 2 ( ~ yp ~ yC ) 2
如何区别附有参数的条件平差、间接平差、附有限制条件的间接平差? 解: (1)看参数的个数(u)与必要观测值的个数(t)的关系。u>t,附有限制条件的间 接平差。u=t,间接平差。 u<t,附有参数的条件平差。 例三:在右图水准网中,A 为已知点,B、C、D、E 为待定点,观测 9 条线路的高差 h1-h9 (1)试问该模型可列出多少个条件方程? A 1 (2)选取 B、C、D 三点高程平差值为参数 5 (3)选取 h1-h5 的高差平差值为参数 B (4)选取 h5-h8 的平差值为参数 6 (5)选取 B、E 两点间的高差为参数 E 7 8 解: (1)n=9,t=4,r=n-t=5 (2)附有参数的条件平差; n=8,t=4,r=5,u=3,c=u+r=8 (3)附有限条件的间接平差; c=r+u=10 (4)间接平差(c=9) (5)附有参数的条件平差; c=r+u=5+1=6(两点的高差为参数 u) 9 4 D 3 C 2
误差理论与测量平差(山东联盟)智慧树知到答案章节测试2023年山东建筑大学
第一章测试1.误差是不可避免的。
A:对B:错答案:A2.构成观测条件的要素有哪些A:外界条件B:计算工具C:观测者D:测量仪器答案:ACD3.对中误差属于那种误差A:系统误差B:偶然误差C:不是误差D:粗差答案:B第二章测试1.两随机变量的协方差等于0时,说明这两个随机变量A:相关B:互不相关C:相互独立答案:B2.观测量的数学期望就是它的真值A:错B:对答案:A3.衡量系统误差大小的指标为A:精确度B:准确度C:不确定度D:精度答案:B4.精度是指误差分布的密集或离散程度,即离散度的大小。
A:错B:对答案:B5.若两观测值的中误差相同,则它们的A:测量仪器相同B:真误差相同C:观测值相同D:精度相同答案:D第三章测试1.设L的权为1,则乘积4L的权P=()。
A:1/4B:4C:1/16D:16答案:C2.有一角度测20测回,得中误差±0.42秒,如果要使其中误差为±0.28秒,则还需增加的测回数N=()。
A:25B:45C:20D:5答案:A3.在水准测量中,设每站观测高差的中误差均为1cm,今要求从已知点推算待定点的高程中误差不大于5cm,问可以设25站。
A:对B:错答案:A4.已知距离AB=100m,丈量一次的权为2,丈量4次平均值的中误差为2cm,若以同样的精度丈量CD的距离16次,CD=400m,则两距离丈量结果的相对中误差分别为( 1/5000 )、(1/20000 )。
A:错B:对答案:B5.A:29B:35C:5D:25答案:D第四章测试1.当观测值为正态随机变量时,最小二乘估计可由最大似然估计导出。
A:对B:错答案:A2.多余观测产生的平差数学模型,都不可能直接获得唯一解。
A:对B:错答案:A3.在平差函数模型中,n、t、r、u、s、c等字母各代表什么量?它们之间有何关系?( n观测值的个数 )(t必要观测数 )(r多余观测数,r=n-t )(u所选参数的个数 )( s非独立参数的个数,s=u-t )( c所列方程的个数,c=r+u )A:对B:错答案:A4.A:对B:错答案:A5.A:错B:对答案:B第五章测试1.关于条件平差中条件方程的说法正确的是:A: 这r个条件方程应彼此线性无关B: 应列出r个条件方程C: r个线性无关的条件方程必定是唯一确定的,不可能有其它组合。
第2讲附有条的间接平差
5.2 附有限制条件的间接平差
如果在某平差问题中,选取 u>t 个参数, 其中包含t个独立参数 ,则多选的 s=u-t 个参 数必定是 t个独立参数的函数,即在 u个参数 之间存在着 s 个函数关系式。
方程的总数 r+u=r+t+s=n+s 个,建立模 型时,除了列立 n个观测方程 外,还要增加 参 数之间满足的s个条件方程 。
x?T C T ? (Cx?)T
二、精度评定
2. 协因数阵
基本思想是把其它变量表示为已知协因数阵的量的线性函数。
L ? L,
W ? BT Pl ? BT PL ? W 0 ,
X?
?
X0
?
x? ?
X0
?
(
N
?1 bb
?
N
C ?1
bb
T
N
c?c1CN
?1 bb
)W
?
N
C ? 1
bb
T
N
W ?1
cc x
,
Ks
?
N
c?c1CN
W ? 1
bb
?
N
W ? 1
cc
x
,
V ? Bx? ? l,
L? ? L ? V .
QLL ? Q QWW ? BT PQPB ? BT PB ? N bb
二、精度评定
2. 协因数阵
X?
?
X0
?
x? ?
X0
?
(
N
?1 bb
?
N
C ? 1
bb
T
N
c?c1CN
?1 bb
)W
间接平差
§4-1 间接平差原理2学时间接平差法(参数平差法)是通过选定t 个与观测值有一定关系的独立未知量作为参数,将每个观测值都分别表达成这t 个参数的函数,建立函数模型,按最小二乘原理,用求自由极值的方法解出参数的最或然值,从而求得各观测值的平差值。
例如,在一个三角形中,等精度独立观测了三个角,观测值分别为L 1、L 2和L 3。
求此三角形各内角的最或然值。
若能选取两个内角的最或然值作为参数 1ˆX 、 2ˆX ,则可以建立参数与观测值之间的函数关系式⎪⎪⎭⎪⎪⎬⎫--=+=+=+2133222111ˆˆ180ˆˆX X v L Xv L X v L(4-1-1)可得⎪⎪⎭⎪⎪⎬⎫---=-=-=3213222111ˆˆ180ˆˆL X X v L Xv L Xv (4-1-2)为了计算方便和计算数值的稳定性,通常引入未知参数的近似值,这一点在实际计算中是非常重要的,令 x X X ˆˆ0+=,则(4-1-2)式可写成如下形式:⎪⎭⎪⎬⎫-++---=--=--=)180(ˆˆ)(ˆ)(ˆ020132130222201111X X L x x v X L x v X L xv (4-1-3)式(4-1-2)叫做误差方程,也可以称为某种意义上的条件方程(包含改正数、观测值和参数,“条件个数=观测值个数”),每个条件方程中仅只含有一个观测值,且系数为1。
单纯为消除矛盾, 1v 、 2v 、 3v 可有多组解,为此引入最小二乘原则: min =PV V T可求得唯一解。
因此,间接平差是选取与观测值有一定关系的独立未知量作为参数,建立参数与观测值之间的函数关系,按最小二乘原则,求解未知参数的最或然值,再根据观测值与参数间的函数关系,求出观测值的最或然值,故又称为参数平差。
对上述三角形,引入最小二乘原则,要求:min =PV V T ,设观测值为等精度独立观测,则有:[]min )180ˆˆ()ˆ()ˆ(2321222211=-+--+-+-=L X X L X L X vv按数学上求自由极值的方法对上式分别求偏导数并令等于零,可得60313132ˆ60313231ˆ02180ˆ3)1(2)2()2()1(0180ˆ2ˆ0180ˆˆ20)ˆˆ180(2)ˆ(2ˆ][0)ˆˆ180(2)ˆ(2ˆ][32113212321232213121321222321111+--+=⇒+-+-=⇒=+-+-⇒-⨯⎭⎬⎫=+--+=+--+⇒⎪⎪⎭⎪⎪⎬⎫=-----=∂∂=-----=∂∂L L L X L L L X L L L X L L X X L L X X L X X L X X vv L X X L X X vv代入误差方程式,得到观测值的最或然值603231316031323160313132321332123211++--=+-+-=+--+=∧∧∧L L L L L L L L L L L L此结果显然与采用条件平差方法解算的结果一致,说明只要遵循相同的平差原则、定权方法相同,平差结果与具体平差方法无关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N BB C
T ˆ C x W K W 0 s x
1
— 法方程
将法方程第一式左乘
1 T
CN BB 与第二式相减,得
CN BB C K s CN BBW W x
1
0
令 则有
N CC CN BB C
1
1
1 1 T 1 1 1 T 1 ˆ x N BB N BB C N CC CN BB W N BB C N CCW x
代入误差方程可解出改正数V,从而可解出:
ˆ V Bx l B N BB N BBC N CC CN BB W BN BBC N CCW x l
0 ˆ ˆ X X x
为此,可用观测值平差值和参数平差值表示附有限制 条件的间接平差法的函数模型,即
ˆ ˆ L F X
n,1 u,1
—— 平差值方程(观测方程) —— 限制条件方程
ˆ X 0
s ,1
§8-1 附有限制条件的间接平差原理
二、基础方程
或用观测值改正数和参数改正数表示附有限制条件的
ˆ C x Wx 0
s ,u u ,1 s ,1
s ,1
方程的个数与未知数的个数相同,方程有唯一解。
8-1 附有限制条件的间接平差原理
三、基础方程的解
将基础方程的第二式代入第一式与第三式联立,得
T ˆ N BB x C K s W 0 ˆ Cx Wx 0
1
T
N CC K s CN BBW W x 0
1
§8-1 附有限制条件的间接平差原理
三、基础方程的解
N CC K s CN BBW W x 0
1 式中, N CC 的秩 R ( N CC )=R ( CN BB C T )=R (C )=s, T T 1 1 且 N CC CN BB C T CN BB C T ,故 N CC 为 s 阶满秩对
S
QLX ˆ QWX ˆ QK
ˆ SX
QLV QWV QK
SV
S
S KS
Q XW ˆ QVW QLW ˆ
Q XK ˆ QVK QLK ˆ
S
Q XX ˆ ˆ QVX ˆ QLX ˆ ˆ
Q XV ˆ QVV QLV ˆ
S
S
QLL ˆ QWL ˆ QK L ˆ S Q XL ˆˆ QVL ˆ QLL ˆˆ
各量的协因数阵和各量之间的互协因数阵的结果列表如下:
Q L W
1
L
W B
KS
BN BBC N CC
C N CC
1 CC
T 1
ˆ X
T 1
V
QVV
ˆ L
Q QVV
T T
T
Q
B
T
1
BQ XX ˆˆ
N BB Q XX ˆ ˆ
T
N BB
T
Q
ˆˆ XX
N BB I B
1 1 T
T T T
1 1 1
0
1 1 1
K s N CC CN BBW N CCW x N CC CN BBW N CC X
0
0 1 1 T 1 1 1 T 1 0 ˆ ˆ X X x N BB N BB C N CC CN BB W N BB C N CCW x X
T T
1
1
1
1
1
1
ˆ L L V ,
0 ˆ ˆ X X x
8-2 精度评定
一、单位权方差估值计算 二、协因数阵与互协因数阵 三、参数的精度评定
四、参数函数的精度评定
8-2 精度评定
一、单位权方差估值计算
ˆ 0
2 T T
V PV r
V PV nu s
T V PV 的计算:
Wx = X
0
0
8-1 附有限制条件的间接平差原理
二、基础方程
不能求得 和 的唯一解,只 x 能按最小二乘原理求 和 的最佳估值V 和 x ,从 ˆ x 由于n + s < n+ u,
ˆ ˆ 而求得观测量 和 X 的最佳估值 L 和 X ,即 L
ˆ L L V
8-2 精度评定
四、参数平差值函数的精度评定
其中
F f1 fu
T
f2
G ˆ X 1
X
0
G ˆ X
X
0
2
G ˆ X
u
X
0
T
由协因数传播律得:
Q F QX F ˆ
T
ˆ D 0 Q ˆ
2
1. V PV p1v1 p2 v2 pnvn
T 2 2
2
权阵为对角阵时
T ˆ ˆT T 2. V PV Bx l PV x B PV l PV T T
T ˆT T ˆ x C K s l P Bx l
顾及 BT PV C T K s
ˆ ˆ G X) G X 1, 2, X u) ( ˆ ( ˆ X ˆ
线性化得权函数式为:
G ˆ X G ˆ dX 1 ˆ X 2 G ˆ dX 2 ˆ X u ˆ dX u
X
0
ˆ d
1 X0
X
0
T ˆ ˆ ˆ ˆ f 1dX 1 f 2 dX 2 f t dX u F dX
握求平差值的方法、步骤。
重点、难点:
求平差值的方法、步骤。
8-1 附有限制条件的间接平差原理
一、概述
如图平面测边控制网,A、B为 已知点,i、k为待定点, 而i、k 的边长 S ik 和方位角 ik 为已 知的固定值。
S1
i
ik , S ik
S3
k
S4
S2
A
B
t=2p-2=2×2-2=2 ;r=n-t=4-2=2 选取 i、k 两点的坐标为未知数, 可列出4个平差值方 程。由于选定的未知数个数u 多于必要观测数t ,所以在 所选定的未知数之间存在 s = u – t 个限制条件。
0
BQ XX ˆˆ
Q BQ XX B ˆˆ
T
0
Q QVV
ˆ L
Q QVV
0
BQ XX N BB ˆˆ
0
8-2 精度评定
三、平差值的精度评定
ˆ 2 ˆˆ DLL 0 QLL ˆˆ ˆ2 ˆˆ DXX 0 QXX ˆˆ
8-2 精度评定
四、参数平差值函数的精度评定
设参数平差值函数为:
8-1 附有限制条件的间接平差原理
一、概述
即
ˆ X
k
i
ˆ Xi ˆ + Y
2 k
ik , Sik
k
ˆ Yi
2
Sik 0
ˆ ˆ Yk Yi arctan aik 0 ˆ X ˆ Xk i
把上列两式线性化得
0 0 0
A
0
B
Hale Waihona Puke ˆ ˆ cosaik xi sinaik ˆ i + cosaik xk + sinaik ˆ k w1 = 0 y y
ˆ ˆ l Pl x C K s l PBx
T T T T
T T T ˆ l Pl W x K s W x
3、在线性方程组解算表中计算
8-2 精度评定
二、协因数阵与互协因数阵
令:
Z L
T
T
W
T
Ks
T
ˆT X
V
T
ˆT L
已知 L IL 0
W B Pl B PL B PF X
N BBQXX B ˆˆ
KS
ˆ X
V
N CC C N BB B Q N ˆˆ BB XX
1
N
0
1 BB 1 BB 1 CC
N CC CN BB B
T 1 BB
0
QXX B ˆˆ
T
QXX B ˆˆ
QVV
T
N
1 CC
C
0
N
N C N
CN
0
1 1 BQXX N BB I BN BBC T N CC ˆˆ
F X L
n,1
0
u,1
线性化:
L F X
0
F X X
n ,u
X
0
X
s,1
X
X
0
X X
s ,u
X
0
X 0
其线性形式为
B l x
C + W x 0 x
其中
l LF X
二、基础方程
按求函数极值的拉格朗日乘数法,设其乘数为:
K k1
s ,1
k2
ks
T
称为联系数向量。组成极值函数
ˆ V PV 2K s Cx Wx
T T
ˆ 将 对 x 求一阶导数,并令其为零,得:
ˆ x 2V P
T
T
V ˆ x
2K s C 2V PB 2K s C 0
T T T
T
