现代控制理论：控制系统的状态空间表达式
现代控制理论课件2
38
二、从系统的机理出发建立状态空间表达式
例1、求图示机械系统的状态空间表达式
外力 u(t)
K ---弹性系数 m
牛顿力学定律 my u by ky
阻 尼 系 数
y(t) b
位移 令
b u(t ) ky m y y
x1 y
x2 y
39
动态方程如下
x1 x2
x1 y 1 0 x2
41
例：设有如图所示的机 械系统。它由两个彼 此耦合的平台构成。 并借助于弹簧和阻尼 到达地基。试选择合 适的状态变量，写出 该系统的状态空间模 型。
42
解答：依题意，进行受力分析，可得如下的微分方程：
M1y1 = u -k1 (y1 - y 2 )-f1 (y1 - y 2 ) M2y 2 = k1 (y1 - y 2 ) + f1 (y1 - y 2 )-k 2y 2 -f 2y 2
其中： a11 a12 a1n a a22 a2 n 21 A — 系统内部状态的联系， an1 an 2 ann
18
称为系统矩阵 , 为n n方阵；
多输入——多输出定常系统： 用向量矩阵表示时的状态空间表达式为：
Ax Bu x y Cx Du
其状态变量为： x1 , x2 ,, xn , 则状态方程的一般形式 为：
1 a11x1 a12 x2 a1n xn b11u1 b12u2 b1r ur x 2 a21x1 a22 x2 a2 n xn b21u1 b22u2 b2 r ur x n an1 x1 an 2 x2 ann xn bn1u1 bn 2u2 bnr ur x
第1章 控制系统的状态空间表达式
§1－1 状态空间变量及状态空间表达式
三. 状态空间 以状态变量为坐标轴所构成的空间为状态空间。
x2
x
x1
x3
●系统任一时刻的状态均可表示为状态空间中的一个点。 ●系统状态随时间变化的过程，在状态空间中描绘出一条轨迹，称为
. 状态轨迹。
§1－1 状态空间变量及状态空间表达式
四. 状态方程 由系统状态变量构成的描述系统动态过程的一阶微分方程组称为 系统的状态方程 。 ●状态方程用于描述系统输入引起系统状态变化的动态过程 。
K1 Kp
u
K1 Kp
＋
K1
Kp
x6
x6
＋
x5
x5
1 x4 J1
x3
x3
Kn
＋
x4
§1－3 状态空间表达式的建立（一）
由以上方框图可知：x1 x 2 x2 x3
状态方程：
x4 x5 x6
J2 x4 Kb K n x4 Kp Kp 1 1 x3 x4 x5 x6 J1 J1 J1 J1 K1 x4 K1 x6 K1 K1 K1 x1 x6 u Kp Kp Kp
ቤተ መጻሕፍቲ ባይዱ
1 K p K1 s
＋
故：
K p s K1 s
K1
Kp
＋
§1－3 状态空间表达式的建立（一）
一.从系统方框图出发建立状态空间表达式
1 J1
J2 Kb
J 2S 2
Kn s
Kn
Kb
1 J1s
§1－3 状态空间表达式的建立（一）
现代控制理论习题解答(第一章)
Ra
La
i f = 常数
ua
f ia D J
ω
ML
【解】： 设状态变量为：
题 1-2 图
⎡ x1
⎢ ⎣
x
2
⎤ ⎥ ⎦
=
⎡ia ⎢⎣ω
⎤ ⎥ ⎦
其中 ia 为流过电感上的电流， ω 电动机轴上的角速度。 电动机电枢回路的电压方程为：
eb 为电动机反电势。 电动机力矩平衡方程为
•
ua = La ia + Ra ⋅ ia + eb
(4) y (4) + 3y + 2y = −3u + u
【解】：
5
在零初始条件下，方程两边拉氏变换，得到传递函数，再根据传递函数求状态空间 表达式。 此题多解，一般写成能控标准型、能观标准型或对角标准型，以下解法供参考。 （1）传递函数为：
状态空间表达式为：
G(s) =
2
s3 + 2s2 + 4s + 6
1⎤
R 2 C1 −1
R2C2
⎥ ⎥ ⎥
⎡ ⎢ ⎣
x1 x2
⎥⎦
⎤ ⎥ ⎦
+
⎡ ⎢ ⎢ ⎣
1
R1C1 0
⎤ ⎥⎥u i ⎦
y = u0 = [0
1]⎢⎡
⎣
x1 x2
⎤ ⎥ ⎦
(2)
设状态变量： x1 = iL 、 x2 = uc 而
1
根据基尔霍夫定律得： 整理得
•
iL = C uc
•
ui = R ⋅ iL + LiL + uc
•
M D = J ω + fω + M L
现代控制理论课后题及答案
第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示，设输入为1u ，输出为2u ，试自选状态变量并列写出其状态空间表达式。
图P2.1解 此题可采样机理分析法，首先根据电路定律列写微分方程，再选择状态变量，求得相应的系统状态空间表达式。
也可以先由电路图求得系统传递函数，再由传递函数求得系统状态空间表达式。
这里采样机理分析法。
设1C 两端电压为1c u ，2C 两端的电压为2c u ，则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =，22c x u =，由式(1)和(2)得：1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为：12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。
1图P2.2解 这是一个物理系统，采用机理分析法求状态空间表达式会更为方便。
令()f t 为输入量，即u f =，1M ，2M 的位移量1y ，2y 为输出量， 选择状态变量1x =1y ，2x = 2y ，3x =1dy dt，24dyx dt =。
现代控制理论：控制系统的状态空间模型
y(tk ) g[x(tk ), u(tk ), tk ]
2020/8/8
14
1.1 状态空间模型 1.1.1 状态空间模型表达式
线性定常系 统
x Ax Bu
y
Cx
Du
线性离散系 统
x(k 1) Gx(k) Hu(k)
y(k) Cx(k) Du(k)
u
di(t) R i(t) uC (t) u(t)
dt L
LL
duC (t) 1 i(t) dt C
2020/8/8
图 R-L-C网络
i
di dt
R L
i
1 L
uc
1 L
u
uc
duc dt
1i c
9
1.1 状态空间模型 1.1.1 状态空间模型表达式
向量矩阵表示形式： di(t) R i(t) uC (t) u(t)
Modern Control Theory
第一章 控制系统的状态空间模型
2020/8/8
1
本章内容提纲
1.1 状态空间模型 1.2 传递函数和状态空间模型间的转换 1.3 状态空间模型的性质
2020/8/8
2
1.1 状态空间模型
➢是描述系统的另外一种数学模型,是现代控制 理论的基础. ➢不仅可以描述系统的输入输出之间的关系,而 且还可以描述系统的内部特性.
如果将电容上的电压作为电路的输出量，则 该方程是联系输出量和状态变量关系的方程， 称为该电路的输出方程或观测方程。这是一 个矩阵代数方程。
2020/8/8
10
1.1 状态空间模型 1.1.1 状态空间模型表达式
第二章现代控制理论状态空间表达式
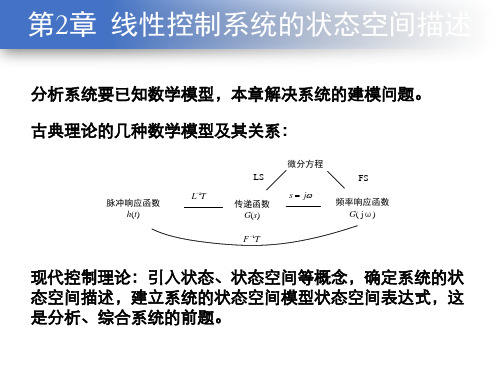
即
(2-11)
(3) 列出状态空间描述iL 1 − ( R + R )C 1 2 R1 L( R1 + R2 ) − R1 1 ( R1 + R2 )C uC ( R1 + R2 )C (2-12) + e(t ) R1 R2 iL R2 − L( R + R ) L( R1 + R2 ) 1 2
§2.1 状态空间描述的概念 2.1.2 控制系统的状态空间描述举例
例2-1 R-L-C系统，求其状态空间描述
R
u
L i
C
uC
解 (1) 确定状态变量 选择电容两端电压 uC (t )、电感通过的电流 i (t ) (2) 列写微分方程并化为一阶微分方程组 基尔霍夫（Kirchhoff）电压定律，
(2-13)
令
1 − ( R + R )C 1 2 A= R1 L( R + R ) 1 2
1 ( R + R )C 2 b= 1 R2 L( R + R ) 1 2
−
R1 ( R1 + R2 )C R1 R2 − L( R1 + R2 )
n 维列向量，状态向量
a12 a1n a22 a2 n an 2 ann
n×n方阵，系统矩阵(或状态矩阵)， 反映系统状态的内在联系
§2.1 状态空间描述的概念
现代控制理论知识点汇总
１．状态空间表达式n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯:r n B ⨯:n m C ⨯:rm D ⨯:A 称为系统矩阵，描述系统内部状态之间的联系；Ｂ为输入（或控制）矩阵，表示输入对每个状态变量的作用情况；C 输出矩阵，表示输出与每个状态变量间的组成关系，Ｄ直接传递矩阵，表示输入对输出的直接传递关系。
２．状态空间描述的特点①考虑了“输入－状态－输出”这一过程，它揭示了问题的本质，即输入引起了状态的变化，而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数，n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说，把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤：a 选择状态变量；b 列写微分方程并化为状态变量的一阶微分方程组；c 将一阶微分方程组化为向量矩阵形式，即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法，特别适合于用计算机计算。
３．模拟结构图（积分器加法器比例器）已知状态空间描述，绘制模拟结构图的步骤：积分器的数目应等于状态变量数，将他们画在适当的位置，每个积分器的输出表示相应的某个状态变量，然后根据状态空间表达式画出相应的加法器和比例器，最后用箭头将这些元件连接起来。
４．状态空间表达式的建立1由系统框图建立状态空间表达式：a 将各个环节（放大、积分、惯性等）变成相应的模拟结构图；b 每个积分器的输出选作i x ，输入则为i x；c 由模拟图写出状态方程和输出方程。
2由系统的机理出发建立状态空间表达式：如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程，整理。
③由描述系统的输入输出动态方程式（微分方程）或传递函数，建立系统的状态空间表达式，即实现问题。
实现是非唯一的。
方法：微分方程→系统函数→模拟结构图→状态空间表达式。
现代控制理论-第二章 控制系统的状态空间描述
DgXu
2.2.1.由物理机理直接建立状态空间表达式： 例2.2.1 系统如图所示
L
R2
u
iL
R1
uc
选择状态变量：
x1 iL , x2 uC ,
13 中南大C diL 1 iL (u L ) C dt R1 dt duC diL L uC C R2 u dt dt
y(s) [C(sI A) B D]U (s)
1
1
得
9
G(s) C (sI A) B D
命题得证
中南大学信息学院自动化系
1
DgXu
例2.1.3
已知系统的状态空间描述为
x1 0 1 0 x1 0 x 0 1 1 x 1 u 2 2 x3 0 0 3 x3 1
28 中南大学信息学院自动化系
DgXu
故有(n-1) 个状态方程：
对xl求导数且考虑式 (2.3.12)，经整理有：
则式 (2.3.12) bn=0 时的动态方程为：
(2.3.16)
式中：
29 中南大学信息学院自动化系
DgXu
30 中南大学信息学院自动化系
DgXu
3)
化输入-输出描述为状态空间描述
11 中南大学信息学院自动化系
DgXu
2.3. 线性定常连续系统状态空间表达式的建立
建立状态空间表达式的方法主要有两种： 一是直接根据系统的机理建立相应的微分方程或差分方 程，继而选择有关的物理量作为状态变量，从而导出其状态 空间表达式； 二是由已知的系统其它数学模型经过转化而得到状态达 式。由于微分方程和传递函数是描述线性定常连续系统常用 的数学模型，故我们将介绍已知 n 阶系统微分方程或传递函 数时导出状态空间表达式的一般方法，以便建立统一的研究 理论，揭示系统内部固有的重要结构特性。
第2章(2) 控制系统的状态空间表达式
2-3 由控制系统的方块图求系统状态空间表达式系统方块图是经典控制中常用的一种用来表示控制系统中各环节、各信号相互关系的图形化的模型，具有形象、直观的优点，常为人们采用。
要将系统方块图模型转化为状态空间表达式，一般可以由下列三个步骤组成：第一步：在系统方块图的基础上，将各环节通过等效变换分解，使得整个系统只有标准积分器（1/s ）、比例器（k ）及其综合器（加法器）组成，这三种基本器件通过串联、并联和反馈三种形式组成整个控制系统。
第二步：将上述调整过的方块图中的每个标准积分器（1/s ）的输出作为一个独立的状态变量i x ，积分器的输入端就是状态变量的一阶导数dtdx i。
第三步：根据调整过的方块图中各信号的关系，可以写出每个状态变量的一阶微分方程，从而写出系统的状态方程。
根据需要指定输出变量，即可以从方块图写出系统的输出方程。
例2-5 某控制系统的方块图如图2-6所示，试求出其状态空间表达式。
解：该系统主要有一个一阶惯性环节和一个积分器组成。
对于一阶惯性环节，我们可以通过等效变换，转化为一个前向通道为一标准积分器的反馈系统。
图2-6所示方块图经等效变换后如下图所示。
我们取每个积分器的输出端信号为状态变量1x 和2x ，积分器的输入端即1x和2x 。
图2-6 系统方块图从图可得系统状态方程： ()⎪⎪⎩⎪⎪⎨⎧+--=-+-==uT K x T x T K K x K u T K x T x x T K x 112111311311212222111 取y 为系统输出，输出方程为：1x y =写成矢量形式，我们得到系统的状态空间表达式：[]⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎦⎤⎢⎢⎣⎡=x y u T K x K K T K x 010********例2-6 求如图2-7（a ）所示系统的动态方程。
解：图2-7(a)中第一个环节21++s s 可以分解为⎪⎭⎫ ⎝⎛+-211s ，即分解为两个通道。
现代控制理论 第1章 状态空间描述
得动态方程组 1 x2 x k b 1 x 2 y y u y m m m k b 1 x1 x2 u m m m y x 1
问题：到底有 何区别？
13
状态空间表达式为
1 0 x k x 2 m
如果将储能元件的物理变量选为系统的状态变量，则状态变量的个数 等于系统中独立储能元件的个数
5
基本概念
状态方程：系统状态方程描述的结构图如下图所示
假设：causal system ——现在的输出只取决 于现在和过去的输入， 而与将来的输入无关。
输入引起状态的变化是一个动态过程，每个状态变量的一阶导数与所有 状态变量和输入变量的数学表达(常微分方程ODE)称为状态方程，一般形式 为：
1896192019872006状态变量和状态空间表达式状态变量和状态空间表达式化输入化输入输出方程为状态空间表达式输出方程为状态空间表达式系统的线性变换对角线标准型和约当标准型系统的线性变换对角线标准型和约当标准型由状态空间表达式导出传递函数阵由状态空间表达式导出传递函数阵离散时间系统的状态空间表达式离散时间系统的状态空间表达式时变系统的状态空间表达式时变系统的状态空间表达式从系统黑箱的输入输出因果关系中获悉系统特性传递函数描述属系统的外部描述系统的内部描述白箱系统完整地表征了系统的动力学特征状态空间表达式属系统的内部描述状态变量
x1 f1 ( x1 , x2 f 2 ( x1 , xn f n ( x1 , , xn , u1 , , xn , u1 , , xn , u1 , , um , t ) , um , t ) , um , t )
标量形式，繁琐!
6
矢量形式
现代控制理论试题与答案
现代控制理论1.经典-现代控制区别:经典控制理论中,对一个线性定常系统,可用常微分方程或传递函数加以描述,可将某个单变量作为输出,直接和输入联系起来;现代控制理论用状态空间法分析系统,系统的动态特性用状态变量构成的一阶微分方程组描述,不再局限于输入量,输出量,误差量,为提高系统性能提供了有力的工具.可以应用于非线性,时变系统,多输入-多输出系统以及随机过程.2.实现-描述由描述系统输入-输出动态关系的运动方程式或传递函数,建立系统的状态空间表达式,这样问题叫实现问题.实现是非唯一的.3.对偶原理系统=∑1A1,B1,C1和=∑2A2,B2,C2是互为对偶的两个系统,则∑1的能控性等价于∑2的能观性, ∑1的能观性等价于∑2的能控性.或者说,若∑1是状态完全能控的完全能观的,则∑2是状态完全能观的完全能控的.对偶系统的传递函数矩阵互为转置4.对线性定常系统∑0=A,B,C,状态观测器存在的充要条件是的不能观子系统为渐近稳定第一章控制系统的状态空间表达式1.状态方程:由系统状态变量构成的一阶微分方程组2.输出方程:在指定系统输出的情况下,该输出与状态变量间的函数关系式3.状态空间表达式:状态方程和输出方程总合,构成对一个系统完整动态描述4.友矩阵:主对角线上方元素均为1:最后一行元素可取任意值;其余元素均为05.非奇异变换:x=Tz,z=T-1x;z=T-1ATz+T-1Bu,y=CTz+为任意非奇异阵变换矩阵,空间表达式非唯一6.同一系统,经非奇异变换后,特征值不变;特征多项式的系数为系统的不变量第二章控制系统状态空间表达式的解1.状态转移矩阵:eAt,记作Φt2.线性定常非齐次方程的解:xt=Φtx0+∫t0Φt-τBuτdτ第三章线性控制系统的能控能观性1.能控:使系统由某一初始状态xt0,转移到指定的任一终端状态xtf,称此状态是能控的.若系统的所有状态都是能控的,称系统是状态完全能控2.系统的能控性,取决于状态方程中系统矩阵A和控制矩阵b3.一般系统能控性充要条件:1在T-1B中对应于相同特征值的部分,它与每个约旦块最后一行相对应的一行元素没有全为0.2T-1B中对于互异特征值部分,它的各行元素没有全为0的4.在系统矩阵为约旦标准型的情况下,系统能观的充要条件是C中对应每个约旦块开头的一列的元素不全为05.约旦标准型对于状态转移矩阵的计算,可控可观性分析方便;状态反馈则化为能控标准型;状态观测器则化为能观标准型6.最小实现问题:根据给定传递函数阵求对应的状态空间表达式,其解无穷多,但其中维数最小的那个状态空间表达式是最常用的.第五章线性定常系统综合1.状态反馈:将系统的每一个状态变量乘以相应的反馈系数,然后反馈到输入端与参考输入相加形成控制律,作为受控系统的控制输入.K为rn维状态反馈系数阵或状态反馈增益阵2.输出反馈:采用输出矢量y构成线性反馈律H为输出反馈增益阵3.从输出到状态矢量导数x的反馈:A+GC4.线性反馈:不增加新状态变量,系统开环与闭环同维,反馈增益阵都是常矩阵动态补偿器:引入一个动态子系统来改善系统性能5.1状态反馈不改变受控系统的能控性2输出反馈不改变受控系统的能控性和能观性6.极点配置问题:通过选择反馈增益阵,将闭环系统的极点恰好配置在根平面上所期望的位置,以获得所希望的动态性能1采用状态反馈对系统任意配置极点的充要条件是∑0完全能控2对完全能控的单输入-单输出系统,通过带动态补偿器的输出反馈实现极点任意配置的充要条件1∑0完全能控2动态补偿器的阶数为n-13对系统用从输出到x线性反馈实现闭环极点任意配置充要条件是完全能观7.传递函数没有零极点对消现象,能控能观8.对完全能控的单输入-单输出系统,不能采用输出线性反馈来实现闭环系统极点的任意配置9.系统镇定:保证稳定是控制系统正常工作的必要前提,对受控系统通过反馈使其极点均具有负实部,保证系统渐近稳定1对系统采用状态反馈能镇定的充要条件是其不能控子系统渐近稳定2对系统通过输出反馈能镇定的充要条件是其结构分解中的能控且能观子系统是输出反馈能镇定的,其余子系统是渐近稳定的3对系统采用输出到x反馈实现镇定充要条件是其不能观子系统为渐近稳定10.解耦问题:寻求适当的控制规律,使输入输出相互关联的多变量系统的实现每个输出仅受相应的一个输入所控制,每个输入也仅能控制相应的一个输出 11.系统解耦方法:前馈补偿器解耦和状态反馈解耦 12.全维观测器:维数和受控系统维数相同的观测器现代控制理论试题1 ①已知系统u u uy y 222++=+ ,试求其状态空间最小实现;5分 ②设系统的状态方程及输出方程为11000101;0111x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦[]001y x =试判定系统的能控性;5分2 已知系统的状态空间表达式为00001⎛⎫⎡⎤=+ ⎪⎢⎥⎝⎭⎣⎦x x u t ；[]x y 01=； ⎥⎦⎤⎢⎣⎡=11)0(x 试求当0;≥=t t u 时,系统的输出)(t y ;10分 3给定系统的状态空间表达式为u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=100100110100013 ,211021y x -⎡⎤=⎢⎥⎣⎦ 试确定该系统能否状态反馈解耦,若能,则将其解耦10分 4 给定系统的状态空间表达式为设计一个具有特征值为 1 1 1---，，的全维状态观测器10分 5 ①已知非线性系统 ⎩⎨⎧--=+-=2112211sin 2x a x xx x x试求系统的平衡点,并确定出可以保证系统大范围渐近稳定的1a 的范围;5分② 判定系统11221223x x x x x x =-+⎧⎨=--⎩在原点的稳定性;5分6 已知系统 u x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=110011 试将其化为能控标准型;10分 7 已知子系统1∑ 111121011x x u -⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦,[]1110y x = 求出串联后系统现代控制理论试题1 ① 取拉氏变换知 )()2()()22(33s u s s s y s ++=+21121)1(21)(2213++-=+++=s s s s s g 3分其状态空间最小实现为u x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=101110 ； 21021+⎥⎦⎤⎢⎣⎡=x y 2分② 1n c u B ABA B -⎡⎤=⎣⎦012111101⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,秩为2,系统状态不完全能控; 2 解 02210(,)0.50.51⎛⎫Φ= ⎪-⎝⎭t t t t , 0()(,0)(0)(,)()tx t t x t B d τττ=Φ+Φ⎰ 1y = 3解 [][]100211101101c B ⎡⎤⎢⎥=-=-⎢⎥⎢⎥⎣⎦, [][]200021102101c B ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦所以120d d ==,121121E E E -⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦; 1111213--⎡⎤=⎢⎥⎣⎦E 又因为E 非奇异,所以能用实现解耦控制; 2分12630011c A F c A ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦1分 求出u kx Lv =-+4 解 令122E E E E ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦, 代入系统得()123120()011100101sE sI A EC sE s E --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--=---⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭理想特征多项式为*332()(1)331f x s s s s =-=+++ 列方程,比较系数求得 001E ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 全维状态观测器为[]ˆˆx A EC x Bu Ey =-++ 12020ˆ01100,00111x u y --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦5 解 ①显然原点为一个平衡点,根据克拉索夫斯基方法,可知 因为 02<-；所以,当0)cos 21(42cos 21cos 212211111>--=----x a a x x时,该系统在原点大范围渐近稳定;解上述不等式知,491>a 时,不等式恒成立; 即491>a 时,系统在原点大范围渐近稳定; ② 解 2114523I A λλλλλ+--==+++,两个特征根均具有负实部,系统大范围一致渐近稳定;2分6 解 1210c u ⎡⎤=⎢⎥⎣⎦,1112201c u -⎡⎤=⎢⎥-⎣⎦ [][][]1111221122010101c p u -⎡⎤===-⎢⎥-⎣⎦[][]11112122221100p p A ⎡⎤==-=⎢⎥⎣⎦11221112211,11P P --⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦能控标准型为u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=101010 7 解 组合系统状态空间表达式为[]1200101001,00010011010010x x u y x -⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=+=⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦⎣⎦5分组合系统传递函数为21()()()G s G s G s = 2分21331(1)(1)(1)(1)s s s s s s s ++=⨯=+-+-+ 3分。
现代控制理论总结
现代控制理论总结第一章：控制系统的状态空间表达式1、状态变量，状态空间与状态轨迹的概念：在描述系统运动的所有变量中，必定可以找到数目最少的一组变量，他们足以描述系统的全部运动，这组变量就称为系统的状态变量。
以状态变量X1,，X2，X3，……X n为坐标轴所构成的n维欧式空间（实数域上的向量空间）称为状态空间。
随着时间的推移，x（t）在状态空间中描绘出一条轨迹，称为状态轨迹。
2、状态空间表达式：状态方程和输出方程合起来构成对一个系统完整的动态描述，称为系统的状态空间表达式。
3、实现问题：由描述系统输入输出关系的运动方程或传递函数建立系统的状态空间表达式，这样的问题称为实现问题单入单出系统传函：W(s)=，实现存在的条件是系统必须满足m<=n，否则是物理不可实现系统最小实现是在所有的实现形式中，其维数最低的实现。
即无零，极点对消的传函的实现。
三种常用最小实现：能控标准型实现，能观标准型实现，并联型实现（约旦型）4、能控标准型实现，能观标准型实现，并联型实现（约旦型）传函无零点系统矩阵A的主对角线上方元素为1，最后一行元素是传函特征多项式系数的负值，其余元素为0，A为友矩阵。
控制矩阵b除最后一个元素是1，其他为0，矩阵A，b具有上述特点的状态空间表达式称为能控标准型。
将b与c矩阵元素互换，另输出矩阵c除第一个元素为1外其他为0，矩阵A，c具有上述特点的状态空间表达式称为能观标准型。
传函有零点见书p17页……..5、建立空间状态表达式的方法：①由结构图建立②有系统分析基里建立③由系统外部描述建立（传函）6、子系统在各种连接时的传函矩阵：设子系统1为子系统2为1）并联：另u1=u2=u，y=y1+y2的系统的状态空间表达式所以系统的传递函数矩阵为：2）串联：由u1=u，u2=y1，y=y2得系统的状态空间表达式为：W(S)=W2(S)W1(S)注意不能写反，应为矩阵乘法不满足交换律3）反馈：系统状态空间表达式：第二章：状态空间表达式的解：1、状态方程解的结构特征：线性系统的一个基本属性是满足叠加原理，把系统同时在初始状态和输入u作用下的状态运动x（t）分解为由初始状态和输入u分别单独作用所产生的运动和的叠加。
现代控制理论--2控制系统的状态空间模型
4. 非线性定常系统:
X (t ) f X (t ) u(t ) Y (t ) g X (t ) u(t )
5.非线性时变系统：
x(t) f x(t), u(t), t y(t) g x(t), u(t), t
6.线性系统状态空间表达式的简便写法：
x1
y
x2 y
令
xn
1
yn2
xn
y n 1
x1 x2
x2
x3
xn1
xn
xn
yn
a1 yn1
=-an x1 an1x2
an1 y a1xn bu
an y
bu
0
K F(t)
y(t)
f
弹簧-质量-阻尼器系统
解：列基本方程：
d2y
dy
m dt 2 f dt ky u t
选择状态变量：取：
x1 (t) y(t)
故得：
x2(t) y(t)
x1(t) x2 (t)
x2 (t)
k m
x1
f m
x2
1 m
u
y(t) x1
将以上方程组写矩阵形式
u(t) 1
La
Ra
+++
x1 L
dt
x1
Ca
L
x2
dt
x2 1 Y(t)
1
Cm
J
+ x3 +
现代控制理论_制系统的状态空间表达式
i
uc 1
1 C
i
0
0 1
C
uc
i
1 0
P 0
1 C
P：非奇异矩阵
单输入单输出定常线性系统
其状态变量为[x1, x2 , , xn ]，则一般形式的状态 空间描述写作：
x1 a11x1 a12 x2 a1n xn b1u x2 a21x1 a22 x2 a2n xn b2u xn an1x1 an2 x2 ann xn bnu
电机
从传递函数的零点、极点分布得出系统定性特征，并已建 立起一整套图解分析设计法，至今仍得到广泛成功地应用。
➢现代控制理论描述系统数学模型的方法： 内部描述：一阶微分方程（时域）
利用状态分析法，对系统进 行一系列特性分析，来设计状态 反馈和输出反馈。
经典控制理论的传递函数描述方法的不足之处： ➢ 系统模型为单输入单输出系统； ➢ 忽略初始条件的影响； ➢ 不包含系统的所有内部信息； ➢ 无法利用系统的内部信息来改变系统的性能。
A, B, C
大写细体字母——拉氏变换符号、系统符号
U (s), R(s), Y (s), S1, S2
作业 预习
常用符号：
积分器
比例器 ki
加法器
注：有几个状态变量，就建几个积分器
注:负反馈时为－
D
u
x x
y
B
C
A
状态空间描述的模拟结构图绘制步骤：
⑴画出所有积分器； • 积分器的个数等于状态变量数，每个积分器的 输出表示相应的某个状态变量。
⑵根据状态方程和输出方程，画出相应的加法器和 比例器；
现代控制理论第一章-控制系统数学模型
y b0
b1
bn1
xn
注：如果输入项的导数阶次和输出项导数阶次相同，则有d。
Y (s) R(s)
bn s n an s n
b1s b0 a1s a0
d
bn1sn1 b1s b0 ansn a1s a0
例1-4 已知描述系统的微分方程为 y18y 192y 640y 160u 640u
y bn1z(n1) b1z b0 z b0 x1 b1x2 bn1xn
写成矩阵形式
x1
x2
xn
0
0
0
a0
1 0 0 a1
0 1 0 a2
0 0 0 a3
0
0
0 1 an1
x1 x2
xn
0 u 0
1
x1
第1章 控制系统数学模型
本课程的任务是系统分析和系统设计。而不论是系统分析还是系 统设计，本课程所研究的内容是基于系统的数学模型来进行的。因 此，本章首先介绍控制系统的数学模型。
本章内容为： 1、状态空间表达式 2、由微分方程求出系统状态空间表达式 3、传递函数矩阵 4、离散系统的数学模型 5、线性变换(状态变量选取非唯一）
写成矩阵形式
x1 0 1 0 x1 0
x2
0
0
1
x2
0
u
x3 a0 a1 a2 x3 b0
x1
y 1
0
0
x2
x3
状态图如下：
一般情况下，n 阶微分方程为： y(n) an1 y(n1) a1 y a0 y b0u
选择状态变量如下：
x1 y x1 x2 y x2 x3 y
0
x2
1 M
《现代控制理论》第3版(刘豹_唐万生)课后习题答案
（本题思路：使用教材 P41 方法，专门用来把传递函数转化为约旦标准型）
6
7
10(−1)
解：(1)由 () = (+1)(+3)可得到系统表达式为
6(+1)
−4
−
10
3
3
(2)() = (+2)(+3)2 = (+3)2 + +3 + +2 +
2
则状态空间表达式为：
.
1
0
1
0 1
0
.
[2 ] = [ 0
0
1 ] [2 ] + [0]
.
−3 −7 −5 3
1
3
1
= [2 3 1] [ 2 ]
3
相应的模拟结构图如下：
1
3
+
u
-
-
2
+
+
y
5
x3
x2
x1
7
3
1-6
(−)
(+)
已知系统传递函数(1)() = (+)(+) (2)() = (+)(+)
11
0
1
0 11
当1 = −1时，[ 3
0
2 ] [21 ] = − [21 ]
31
−12 −7 −6 31
10
解得： 21 = 31 = −11
（或令11
令11 = 1
11
1
1 = [21 ] = [−1]
31
天津大学 现代控制理论课件 第1章 控制系统的状态空间表达式
例题 1.1 【解答】 1 选择状态变量
图1.1-1 R-L-C电路
状态变量个数：独立储能元件个数。所以选择电容C两 端电压，和流经电感L的电流。
状态：x1 (t ) = uC , x2 (t ) = iL = i, 输入：u (t ), 输出：y (t ) = uC = x1
1.1 状态变量及状态空间表达式
& x(t ) = Ax(t ) + Bu (t ) y (t ) = Cx(t ) + Du (t )
（2）MIMO
L a1n b11 b12 L L a2 n , B = b21 b22 L M O M M O L ann bn1 bn 2 L u1 y1 c11 c12 L c1n d11 y u c d c22 L c2 n 2 2 21 , D = 21 u= ,y= ,C = M M M M M O M cm1 cm 2 L cmn d m1 u r ym
1.1 状态变量及状态空间表达式
1 状态
描述一个系统得过去、现在和将来的状况
2 状态变量
足以表征系统运动状态的最小个数的一组变量 为状态变量 例如微分方程：
& & y ( n ) + a1 y ( n−1) + L + an−1 y + an y = bou ( n ) + b1u ( n−1) + L + bn−1u + bnu (1.1 − 1)
注1.1-1：一个用n阶微分方程描述的系统，有n个独立变量，当这n 个独立变量的时间响应都求得时，系统的运动也就被揭示无遗。 注1.1-2：状态变量的个数等于系统独立储能元件的个数。
现代控制理论状态空间表达式
《现代控制理论》MOOC课程第一章控制系统的状态空间表达式第一章控制系统的状态空间表达式状态空间变量及状态空间表达式状态空间表达式的建立状态向量的线性变换从状态空间表达式求传递函数组合系统的状态空间表达式离散系统、时变系统和非线性系统的状态空间表达式经典控制理论：数学模型：传递函数)()()(s U s Y s G =uy∑G(s)传递函数的定义线性定常系统的传递函数是指在初始状态为零的条件下，系统输出变量的拉氏变换与输入变量的拉氏变换之比。
G(s)=Y(s)U(s)经典控制理论：数学模型：传递函数)()()(s U s Y s G =uy∑G(s)现代控制理论：Xuy∑数学模型：状态空间表达式《现代控制理论》MOOC课程1.1 状态空间变量及状态空间表达式一. 状态变量足以完全表征系统运动状态的最少个数的一组变量，称为状态变量。
完全表征) (t u1R1L2R2LC)(1ti)(2ti-)(tu c+)(),(),(210ctutiti)(tu已知：确定系统在任何t≥t0时间的动态行为。
只要给定状态变量的初值x(t0)以及t≥t0时刻的输入u(t)，就能够完全一. 状态变量最小性而增加变量的个数则是完全表征系统动态行为所不需要的。
) (t u1R1L2R2LC)(1ti)(2ti-)(tu c+)(c tidttduti c)(C)(c=体现在减少变量个数就不能够完全表征系统的动态行为，)(),(),(21tutiti c关于状态变量的几点说明状态变量是相互独立的。
对于一个实际的物理系统,状态变量个数等于系统中独立储能元件的个数。
不能多，也不能少。
对同一个动态系统，状态变量的选取不是唯一的，但状态变量的个数是唯一确定的，) (t u1R1L2R2LC)(1ti)(2ti-)(tu c+)(),(),(21tutiti c状态变量1：)(),(),(21tititi c状态变量2：二. 状态向量由系统状态变量构成的向量，称为系统的状态向量。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Y (s) U (s)
sn
bn1sn1 b1s b0 an1sn1 a1s a0
系统动态过程的两类数学描述
• 系统的内部描述
状态空间描述是系统内部描述的基本形式，需要 由两个数学方程表征—— 状态方程
输出方程
u1
y1
u2
x1, x2,, xn
y2
ur
ym
系统动态过程的两类数学描述
• 外部描述和内部描述的比较
u
w2
y
s2+2zws+w2
u
w2 s+2zw
1y s
u
w2
x2
x1 y
2zw
x1 x2
x2 w2 x1 2zw x2 w2u
y x1
1.3 状态空间表达式的建立
已知系统的结构框图，求状态空间表达式
u
K1
K2
K3
y
T1s+1
T2s+1
T3s
K4
1.3 状态空间表达式的建立
系统的状态空间表达式为
x1
K3 T3
x2
x2
1 T2
x2
K2 T2
x3
x3
K1K4 T1
x1
1 T1
x3
K1 T1
u
y x1
0
K3 T3
x 0 1
• 输出：系统的被控量或从外部测量到的
系统信息。 若输出是由传感器测量得到的，又称为
观测。
1.1 状态空间及状态空间表达式
• 状态变量:
一个动力学系统的状态变量组定义为：能完全表 征其时间域行为的一个最小内部变量组
• 状态矢量：
一个动力学系统的状态定义为由其状态变量组
x1(t), x2 (t),, xn (t)
1.1 状态空间及状态空间表达式
几点解释
(1) 状态变量组对系统行为的完全表征性
只要给定初始时刻 t0 的任意初始状态变量组 x1(t0 ), x2 (t0 ), , xn (t0 )
和t ≥ t0 各时刻的任意输入变量组
u1(t), u2 (t),, ur (t)
那么系统的任何一个内部变量在t≥t0各时刻的运动 行为也就随之而完全确定
所组成的一个列向量
x1(t)
x(t)
x2
(t
)
xn
(t
)
1.1 状态空间及状态空间表达式
• 状态空间：
状态空间定义为状态向量的一个集合，状态空间 的维数等同于状态的维数
• 状态轨线：
系统在某个时刻的状态，在状态空间可以看作是 一个点。随着时间的推移，系统状态不断变化， 并在状态空间中描述出一条轨迹，这种轨迹称 为状态轨线或状态轨迹。
写成矩阵形式
x1 x2
0
1
L
1
C R
x1 x2
0 1
L
u
L
y 1
0
x1 x2
以上方程可表为形如
x Ax Bu y Cx Du
1.1 状态空间及状态空间表达式
动态系统的结构
u1
x1
u2
x2
动力学部件
ur
xn
y1
输出部件
y2
ym
连续时间线性系统的状态空间描述
线性时不变系统
x Ax Bu
y
Cx
Du
线性时变系统
x A(t)x B(t)u
y
C (t )
x
D(t)u
1.1 状态空间及状态空间表达式
x Ax Bu y Cx Du
状态方程 输出方程
• x n维状态矢量 • u r维输入(或控制)矢量 • y m维输出矢量 • A nxn系统矩阵 • B nxr输入(或控制)矩阵 • C mxn输出矩阵 • D mxr直接传递矩阵
– 一般的说外部描述只是对系统的一种不完全描 述，不能反映黑箱内部结构的不能控或不能观 测的部分。
– 内部描述则是系统的一种完全的描述，能够完 全反映系统的所有动力学特性。
1.1 状态空间及状态空间表达式
• 状态空间描述常用的基本概念
• 输入：外部对系统的作用(激励)，输入
包括控制输入和干扰输入。
• 线性系统的状态空间表达式
描述系统输入、输出和状态变量之间关系的方程 组称为系统的状态空间表达式（动态方程或运 动方程），包括
– 状态方程 描述状态变量与输入之间的关系 – 输出方程 描述输出与状态变量之间的关系
1.1 状态空间及状态空间表达式
如图所示RLC的电路
RL
根据回路电压定律
u(t)
i(t) C uc(t)
1.2 状态空间表达式的模拟结构图
• 状态空间方程
1.2 状态空间表达式的模拟结构图
• 多输入多输出系统
x1
x2
a11 a21
a12 a22
x1
x2
b11 b21
y1 y2
c11 c21
c12 x1
c22
x2
b12 u1
b22
u2
1.2 状态空间表达式的模拟结构图
Ri(t)
L
di(t) dt
uc
(t)
u(t)
C duC (t) i(t) dt
duC (t) 1 i(t) dt C
di(t) dt
1 L
uc (t)
R L
i(t)
1 L
u(t)
1.1 状态空间及状态空间表达式
uC
(t)
1 C
i(t)
i(t)
1 L
uc (t)
R L
i(t)
1 L
u(t)
令状态变量 x1=uc，x2=i，系统输出 y=uc=x1
1.1 状态空间及状态空间表达式
(2) 状态变量组最小性的物理特征 (3) 状态变量组最小性的数学特征 (4) 状态变量组的不唯一性 (5) 系统任意两个状态变量组之间的关系 (6) 有穷维系统和无穷维系统 (7) 状态空间的属性
状态空间为建立在实数域R上的一个向量空间Rn
1.1 状态空间及状态空间表达式
控制系统的状态空间表达式
系统动态过程的两类数学描述
• 系统的外部描述
外部描述常被称作输出—输入描述
例如，对SISO线性定常系统 u
y
时间域的外部描述：
y(n) an1 y(n1) a1 y(1) a0 y bn1u(n1) b1u (1) b0u
复频率域描述即传递函数描述：
W (s)
1.3 状态空间表达式的建立
• 1.3.2 从系统结构图建立状态空间表达式
u
1
x
s
u
x
x u
u
K
x
u
K/T
x
u
x
Ts+1
s+1/T
x 1 x K u TT
1.3 状态空间表达式的建立
u
s+z
y
s+p
u
zp
s+p
y
u zp
xy
p
x px (z p)u
y
x
u
1.3 状态空间表达式的建立
1.1 状态空间及状态空间表达式
பைடு நூலகம்
• 连续时间线性系统的方框图
x Ax Bu y Cx Du
D
u
x
x
B
C
y
A
1.2 状态空间表达式的模拟结构图
• 一阶标量微分方程
x ax bu
y cx
u
x
x
y
b
c
a
1.2 状态空间表达式的模拟结构图
• 三阶系统微分方程
x a2x a1x a0x bu x a2x a1x a0x bu