关于检校张拉千斤顶的回归方程式
张拉计算书

张拉计算书一、钢绞线的张拉预应力混凝土达到一定强度后拆除模板,砼强度达到100%后,穿钢绞线,用两端张拉法进行张拉,用标定好的千斤顶进行张拉,张拉两端同时进行,确保张拉时两端操作要一致。
①、张拉前的准备工作1)、梁体验收,混凝土强度达到100%后张拉。
穿束张拉前,对构件的质量,几何尺寸等进行检查,预留孔道用通孔器或压气、压水等方法进行检查。
构件端部预埋铁板与锚具和垫板接触处的焊渣,毛刺、混凝土残渣等清理干净。
2)、标定千斤顶油表读数,施工过程中定期检校,依据标定的曲线计算各张拉力对应的油表读数。
3)、穿入钢绞线:对加工好的钢绞线进行编号,钢绞线穿束时,将一端打齐套上穿束器,将穿束器的引线穿过孔道,然后向前拉动,直至两端均露出60cm 的工作长度,穿束后检查两端编号,防止钢绞线在孔道内交叉扭结。
②、预应力的张拉程序预应力钢绞线张拉顺序严格按照图纸要求进行张拉,千斤顶张拉作用线与预应力钢绞线的轴线重合一致。
钢绞线的张拉程序如下:0→15%σk →30%σk →50%σk →100σk →103σk (持荷2分钟) →锚固。
在张拉过程中15%、30%、50%、100%时必须有技术停留,其中15%停留目的是保证钢绞线均匀受力,同时量测其伸长;30%停留并量测其伸长的目的是推测30%已下的伸长量;50%停留是为了保证两端张拉同步进行;100%停留并量测其伸长量;103%时持荷2分钟能有效消除张拉过程中的各种应力损失;钢绞线的实际伸长量与理论伸长值的差值应控制在±6%以内,否则应暂停张拉,分析原因提出解决方案,待监理工程师审批后方可继续张拉。
实际伸长值按以下公式计算:△L=△L1+△L2(mm)△L1=100%的伸长值-15%的伸长值(mm)△L2=30%的伸长值-15%的伸长值(mm)③、张拉的操作步骤四人配备一套张拉顶,一人负责油泵,两人负责千斤顶,一人观测并记录读数,张拉按设计要求的顺序进行,并保证对称张拉。
应用线性回归模型校准液压千斤顶

应用线性回归模型校准液压千斤顶【摘要】本文先介绍了最小二乘法的定义和最小二乘法在线性回归模型中的表示方法。
然后再介绍了最小二乘法的相关公式。
最后利用已经校准的液压千斤顶来检测井盖的破坏荷载是否满足规范要求。
一、最小二乘法与线性回归模型1、最小二乘法的定义在实际工作中,常常会遇到这样的问题:给出两个变量x,y的n组试验数据,怎么才能从中找出变量x、y的函数关系式呢?然后利用这个函数关系式对x与y之间的除了试验数据之外的其它对应情况作出某种判断。
这样的问题一般可以分为两类:一类是对x与y之间所存在的对应规律一无所知,这时要从试验数据中找出符合实际情况的函数关系式是很困难的,这类问题为黑箱问题;另一类是通过问题作出分析,然后再建立数学模型或者通过整理归纳试验数据,得出x与y之间符合某种类型的函数关系式,其中有m个待定参数,这些参数的值可以通过n组试验数据来确定,这类问题称为灰箱问题。
解决灰箱问题的方法通常会利用到“最小二乘法”。
2、最小二乘法在线性回归模型中的表示方法上面我们已经说明了最小二乘法的数据全部来自于试验取得。
在建立一元线性回归方程中,虽然有很多种不同的方法来求样本回归函数,但是在回归分析中最常用的方法就是最小二乘法。
如果变量x与y有精确的线性关系比如说y=kx+b,那么观测值与回归值是相等的。
然而在实际工作中诸多变量的关系不一定都是如此,由于受到许多随机因素的干扰使得物与物之间没有那么明确的一一对应关系。
那么我们就需要通过数学的方法来来使之对应。
首先通过试验取得数据,其次把数据描绘出来。
然后拟合一条跟已知的函数图像最为接近的曲线,这样就可以相对地将他们之间的关系表示出来了。
在处理诸如此类的事件中常常应用到最小二乘法。
3、最小二乘法的适用范围(1)本文所讨论的最小二乘法仅且只适用于一元线性函数,比如y=bx+a。
(2)不适用于非线性函数和多元线性函数。
二、最小二乘法的公式为了定量地给出y=bx+a与实验数据之间线性关系的符合程度,可以用Pearson(皮尔逊)相关系数R来衡量。
张拉设备回归公式
20% 30% 50% 100% 15%
17束
3296.4
30% 50% 100%
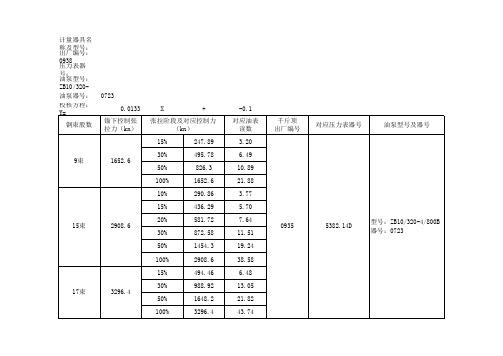
计量器具名称及型号:液压千斤顶,400t 出厂编号:0937 压力表器号:5203.14D 油泵型号:ZB10/320-4/800B 油泵器号: 校核方程:Y= 钢束股数 0723 0.0134 锚下控制张 拉力(kn) X + -0.38 对应油表 读数 2.94 6.26 10.69 21.76 3.52 5.47 7.42 11.31 19.11 38.60 6.25 12.87 21.71 43.79 0936 5203.14D 型号:ZB10/320-4/800B 器号:0723 千斤顶 出厂编号 对应压力表器号 油泵型号及器号
计量器具名称及型号:液压千斤顶,400t 出厂编号:0938 压力表器号:5382.14D 油泵型号:ZB10/320-4/800B 油泵器号: 校核方程:Y= 钢束股数 0723 0.0133 锚下控制张 拉力(kn) X + -0.1 对应油表 读数 3.20 6.49 10.89 21.88 3.77 5.70 7.64 11.51 19.24 38.58 6.48 13.05 21.82 43.74 0935 5382.14D 型号:ZB10/320-4/800B 器号:0723 千斤顶 出厂编号 对应压力表器号 油泵型号及器号
张拉阶段及对应控制力 (kn) 15% 247.89 495.78 826.3 1652.6 290.86 436.29 581.72 872.58 1454.3 2908.6 494.46 988.92 1648.2 3296.4
9束
1652.6
30% 50% 100% 10% 15%
15束
2019年关于检校张拉千斤顶的回归方程式.doc
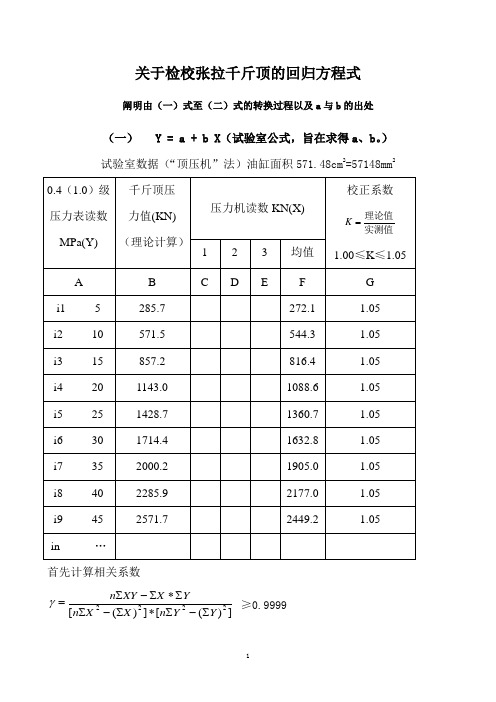
关于检校张拉千斤顶的回归方程式阐明由(一)式至(二)式的转换过程以及a 与b 的出处(一) Y = a + b X (试验室公式,旨在求得a 、b 。
) 试验室数据(“顶压机”法)油缸面积571.48cm 2=57148mm 2首先计算相关系数])([])([2222Y Y n X X n YX XY n ∑-∑*∑-∑∑*∑-∑=γ ≥0.9999计算公式:截距 222)(X n X X Y X XY a ∑-∑∑*∑-∑*∑=斜率 22)(Xn X XYn Y X b ∑-∑∑-∑*∑= 说明:①“Σ”读“西格玛”是“∑=ni 11”的简化。
表示与a 、b 相关的数据(即“回归因素”)Y 或X 由 i 1=5MPa(或272.1KN)……至i 9=45MPa(或2449.2KN)……i n =……之总和。
② n 表示数据量即因数发生的次数,此处n=9。
例如:22229124515105+++=∑= i y 。
()22914515105+++=⎪⎭⎫ ⎝⎛∑= i y 。
()2.2449454.816153.544101.2725991⨯+⨯+⨯+⨯=∑= i YX n 。
③ i 表示因素发生的次序,如i 1=5 , i 2=10 ……i 9=45等等(因素:原因要素)。
④按公式计算求得Y = a + b X = 0 + 0.018373 X = 0.018373X回归方程(即经验方程、经验公式)之意义(使用价值)在于将各个处于离散分布状态的相关数据(因素)通过统计手段(如a 、b 计算公式)使它们趋于(回归于)统一稳定(如ρ = a + b F 方程式)。
因此,这种回归分析所得数据永远是一个近似数。
其近似于理想值(或理想状态、要求精度)的程度由相关系数γ表达,此处要求γ=0.9999,同时要求校正系数K等于1小于1.05,就是说当γ和K的条件满足后,a、b的运算结果可信(可以在实际生产、工作中应用)。
SF第二联千斤顶线性回归方程

15-17
设计张拉力(MN) 3.261 19.304 39.358 总监办:
SF匝道桥第二联13束钢绞线液压千斤顶线性回归方程 千斤顶编号 线性回归方程 400T 钢束规格 初应力(10%)Mpa 初应力(50%)Mpa 设计应力(100%)Mpa 15-17 401 油表编号 P=12.6256F+0.43 设计张拉力(MN) 3.636 16.458 32.485
201110531
15-17
设计张拉力(MN) 3.261 19.304 39.358 总监办:
3.1248
驻地监理:
SF匝道桥第二联16束钢绞线液压千斤顶线性回归方程 千斤顶编号 线性回归方程 400T 钢束规格 初应力(10%)Mpa 初应力(50%)Mpa 设计应力(100%)Mpa 15-17 401 油表编号 P=12.6256F+0.43 设计张拉力(MN) 4.375 20.156 39.882施工单位:Fra bibliotek驻地监理:
总监办:
顶线性回归方程 201110631
P=12.6256F+0.43 3.1248 4.375 20.156 39.882
201110626
P=12.7439F+0.34 3.1248 4.322 20.251 40.162
201110544
P=12.7342F-0.48 3.1248 3.499 19.416 39.312
千斤顶编号 线性回归方程 400T 钢束规格 初应力(10%)Mpa 初应力(50%)Mpa 设计应力(100%)Mpa
401
油表编号 P=12.7439F+0.34
201110626
15-17
张拉千斤顶工作原理及校验 (1)

a)构造与工作原理; b)加撑脚后的外貌 1一张拉油缸;2—顶压油缸(即张拉活塞);3—顶压活塞;4—弹簧; 5—预应力筋;6—工具锚;7—螺帽;8—锚环;9—构件;10—撑脚; 11一张拉杆;12—连接器;13—张拉工作油室;14—顶压工作油室; 15—张拉回程油室;16—张拉缸油嘴;17一顶压缸油嘴;18—油孔
1-张拉油缸;2-顶压油缸(张拉活塞);3-顶压活塞;4-弹簧; 5-预应力筋;6-楔块;7-对中套;8-锚塞;9-锚环;10-构件
(三)拉杆式千斤顶
• 拉杆式千斤顶用于螺母锚具、锥形螺杆锚具、钢丝镦 头锚具等。它由主油缸、主缸活塞、回油缸、回油活 塞、连接器、传力架、活塞拉杆等组成。 • 目前常用的一种千斤顶是YL60型拉杆式千斤顶。另外, 还生产YL400型和YL500型千斤顶,其张拉力分别为4 000 kN和5 000 kN,主要用于张拉力较大的钢筋张拉。 • 下图是用拉杆式千斤顶张拉时的工作示意图。
图4-29 YC-60型千斤顶具和JM型锚的安装 1—工作锚;2—YC-60型千斤顶;3—工具锚;4—预应力筋束
• 其工作原理是:张拉预应力筋时,张拉缸油嘴进 油、顶压缸油嘴回油,顶压油缸、连接套和撑套 连成一体右移顶住锚环;张拉油缸、端盖螺母及 堵头和穿心套连成一体带动工具锚左移张拉预应 力筋;顶压锚固时,在保持张拉力稳定的条件下, 顶压缸油嘴进油,顶压活塞、保护套和顶压头连 成一体右移将夹片强力顶入锚环内;此时张拉缸 油嘴回油、顶压缸油嘴进油、张拉缸液压回程。 最后,张拉缸、顶压缸油嘴同时回油,顶压活塞 在弹簧力作用下回程复位。 • 大跨度结构、长钢丝束等引伸量大者,用穿心式 千斤顶为宜。
张拉千斤顶工作原理 及校验 一、张拉千斤顶的工作 原理
•
桥梁工程中施加预应力所用的机具设备通常称为 张拉设备。常用的张拉设备由油压千斤顶和配套的高压 油泵、压力表及外接油管组成。液压千斤顶按其构造可 分为台式(普通油压千斤顶)、穿心式、锥锚式和拉杆 式。工地上比较常见的张拉千斤顶一般为穿心结构,其 主要结构包括张拉外套、活塞、油室,纵剖面结构示意 如图所示。 • 千斤顶在张拉时,将其抵住工作锚具,将工作锚具安装 在活塞前端,并安装工作、工具夹片,通过张拉油泵向 进油嘴进油,在高压油的推动作用下,使活塞向前运动, 在工具锚作用下,带动钢束向前运动,实现钢束的张拉。 • 油室内油压的大小通过张拉油泵上的油表读出。
张拉千斤顶工作原理及校验 (1)

• 3.千斤顶校验的方法 • 校验应在经主管部门授权的法定计量技术机构进行。 • (1)校验用的标准仪器的精度不得低于1%,压力表 的精度不宜低于1.5级,最大量程不宜小于设备额定张 拉力的1.3倍,校验时,千斤顶活塞运行方向应与实际 张拉工作状态一致。 • (2)千斤顶的校验可以根据现场实际情况,采用压力 机、已经标定的传感器进行标定; • (3) 标定时应将油压表、千斤顶等配套标定; • (4)在标定千斤顶时,应注意千斤顶的工作状态和实 际相同,即让千斤顶顶压力机,不能让压力机压千斤 顶的活塞;
千斤顶构造原理图
• 1)用长柱压力试验机校验 • 校验时,应采取被动校验法,即在校验时用千斤顶顶试 验机,这样活塞运行方向、摩阻力的方向与实际工作时 相同,校验比较准确。 • 在进行被动校验时,压力机本身也有摩阻力,并且与正 常使用时相反,所以,试验机表盘读书反映的也不是千 斤顶的实际作用力。因此用被动法校验千斤顶时,必须 事先用具有足够吨位的标准测力计对试验机进行被动标 定,以确定试验机的表盘读数值。标定后在校验千斤顶 时,就可以从试验机表盘上直接读出千斤顶的实际作用 力以及油压表的准确读数。用压力试验机校验的步骤如 下:
三、检验结果的回归计算
• 千斤顶的作用力T和油缸的油压P的关系是线性关 系,考虑活塞和油缸之间的摩阻力后,它们的关 系可以表示为:
T AP B
•
•
可以利用千斤顶检验测得的作用力和油压
( ( 、T 2 , P2 ) 、T 3 , P3 )、……(T , P ) , 对上式 式进行线性回归,利用最小二乘法原理求上式的回 归值: ˆ ˆ ˆ T AP B
•
• •
如张拉油缸的面积为A,有活塞力的平衡:
A f N
千斤顶线性方程计算公式

顶号 0257 表号 548434(7) 张拉力(KN) 油表读数 319.3 10
60
y = 0.035x - 1.564
50
603.9 906.1 1198.2 1432.6
20 30 40 50
40
30
系列1 线性 (系列1)
Y
20
10
0 0 1000 X 2000
顶号 / 表号 548435(8) 张拉力(KN) 油表读数 302.5 10 617.2 20 906.9 30 1194.1 40 1461.4 50
40
30
系列1 线性 (系列1)
Y
20
10
0 0 1000 X 2000
顶号 0255 表号 6A2834(4) 张拉力(KN) 油表读数 293.6 10 592.7 20 894.1 30 1195.2 40 1488.6 50
60
y = 0.033x + 0.164
50
40
30
20
系列1 线性 (系列1)
Y
10
0 0 1000 X 2000
顶号 0250 表号 548432(6) 张拉力(KN) 油表读数 317.9 10 584.8 20 880.8 30 1196.7 40 1431.2 50
60
50
y = 0.035x - 1.025
40
30
系列1 线性 (系列1)
Y
20
10
0 0 1000 X 2000
线性方程:y=aF+b a 0.0358 0.0356 0.035 0.0334 0.0343 0.0352 0.0354 0.0345 b -1.6714 -1.3433 -1.2601 0.1647 -0.859 -1.0254 -1.5645 -0.9417
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于检校张拉千斤顶的回归方程式
关于检校张拉千斤顶的回归方程式
阐明由(一)式至(二)式的转换过程以及a 与b 的出处
(一) Y = a + b X (试验室公式,旨在求得a 、b 。
) 试验室数据(“顶压机”法)油缸面积571.48cm 2=57148mm 2
0.4(1.0)级压力表读数MPa(Y) 千斤顶压 力值(KN) (理论计算)
压力机读数KN(X)
校正系数
实测值理论值
=
K
1.00≤K ≤1.05
1 2 3 均值 A B C D E F G i1 5 285.7 272.1 1.05 i2 10 571.5 544.3 1.05 i3 15 857.2 816.4 1.05 i4 20 1143.0 1088.6 1.05 i5 25 1428.7 1360.7 1.05 i6 30 1714.4 1632.8 1.05 i7 35 2000.2 1905.0 1.05 i8 40 2285.9 2177.0 1.05 i9 45 2571.7 2449.2 1.05 in …
首先计算相关系数
]
)([])([2222Y Y n X X n Y
X XY n ∑-∑*∑-∑∑*∑-∑=γ ≥0.9999
计算公式:
截距 2
22
)(X n X X Y X XY a ∑-∑∑*∑-∑*∑=
斜率 2
2)(X
n X XY
n Y X b ∑-∑∑-∑*∑= 说明:
①“Σ”读“西格玛”是“∑=n
i 11”的简化。
表示与a 、b 相关的数据(即“回归因素”)
Y 或X 由 i 1=5MPa(或272.1KN)……至i 9=45MPa(或2449.2KN)……i n =……之总和。
② n 表示数据量即因数发生的次数,此处n=9。
例如:2
2229
124515105+++=∑= i y 。
()2
2
9
14515105+++=⎪⎭
⎫
⎝⎛
∑= i y 。
()2.2449454.816153.544101.272599
1
⨯+⨯+⨯+⨯=∑= i YX n 。
③ i 表示因素发生的次序,如i 1=5 , i 2=10 ……i 9=45等等(因素:原因要素)。
④按公式计算求得
Y = a + b X = 0 + 0.018373 X = 0.018373X
回归方程(即经验方程、经验公式)之意义(使用价值)在于将各个处于离散分布状态的相关数据(因素)通过统计手段(如a 、b 计算公式)使它们趋于(回归于)统一稳定(如ρ = a + b F 方程式)。
因此,这种回归分析所得数据永远是一个近似数。
其近似于理想值(或理想状态、要求精度)的程度由相关系数γ表达,此处要求γ=0.9999,
同时要求校正系数K等于1小于1.05,就是说当γ和K的条件满足后,a、b的运算结果可信(可以在实际生产、工作中应用)。
关于回归运算公式的根源,涉及应用数学如概率论、最小二乘法……等等,须作深入复杂的学习研究。
随着X、Y这两个关系密切的因素的细分即“n”值增加,将相应提高回归分析的质量,即γ将愈加趋于“1”!这就是数学的辩证法。
(二)ρ= a + b F (现场实用公式,旨在求ρ)
ρ——油泵0.4级压力表的现场张拉读数(MPa)。
[注意:ρ×油缸面积即每一预应力钢束的实际张拉
力值KN/束]。
F——每一预应力钢束的设计张拉力值(KN/束)。
a与b是线性回归方程式中的两个常数(参数),a相当于截距,b
是F变量的系数,也是斜率[b =(ρ- a)/ F]。
a、b乃回归运算
之核心,其运算依据由试验室提供,即校顶时油泵0.4级压力表
的分档读值设为Y(自5MPa……至50MPa,共10档;今又改为按
4MPa的倍数分档,自4MPa……至48MPa,共12档。
)和相应的压
力机读数(KN)设为X,或测力计(压力环)百分表读数(mm)经
换算后的相应压力值(KN)。
(一)与(二)两式中Y与ρ的影响因素(人、泵、表、顶)及F(设计值)与X(实测值)具备可代换的逻辑性【先有(一)后有(二)】。
已知 Y = 0.018373X, 所以ρ= a + b F = 0 + 0.018373F。
值得提醒的是,计算表明,校顶系数与b(斜率)正相关,即与预施应
力值正相关,这也是要求K ≥1.00的内在原因;但千斤顶油缸面积的
大小却与b(斜率)反相关。
