求函数f(x)周期的几种常见方法解读
高中数学解题方法系列:三角函数周期问题的3种方法

=(sin2 x+ cos2 x)(sin4 x-sin2 x·cos2 x+ cos4 x) =( sin2 x+ cos2 x)2-3 sin2 x·cos2 x =1-3 sin2 x·cos2 x =1- 3 sin22 x
cos x cos 3x
2.公式法: (1)如果所求周期函数可化为 y=Asin(x )、y=Acos(x )、
y=tg(x )形成(其中 A、 、 为常数,且 A 0、 >0、 R), 则可知道它们的周期分别是: 2 、 2 、 。
例 4:求函数 y=1-sinx+ 3 cosx 的周期
2
例 12:求函数 y=sin2x+sin3x 的周期
解:∵sin2x
的周期为
T1=
,sin3x
的周期为
T2=
2 3
而 T1
T2
=
3 2
,即是
T=2T1=3T2,
∴y=sin2x+sin3x 的周期为 T=2T1=2
例 13:求函数 y=cos x +sin x 的周期
3
4
解:∵cos x 的周期为 T1=6 ,sin x 的周期为 T2=8
的周期为 T=P2T1=P1T2,其中 P1、P2N,且(P1、P2)=1
事实上,由 T1
T2
P1 (既约分数),得 T=
P2
P2T1=P1T2
∵f(x+ P1T2)=f1(x+ P1T2)+f2(x+ P1T2) =f1(x+ P2T1)+ f2(x+ P1T2) = f1(x)+ f2(x) =f(x)
高中数学周期函数、公式总结、推导、证明过程
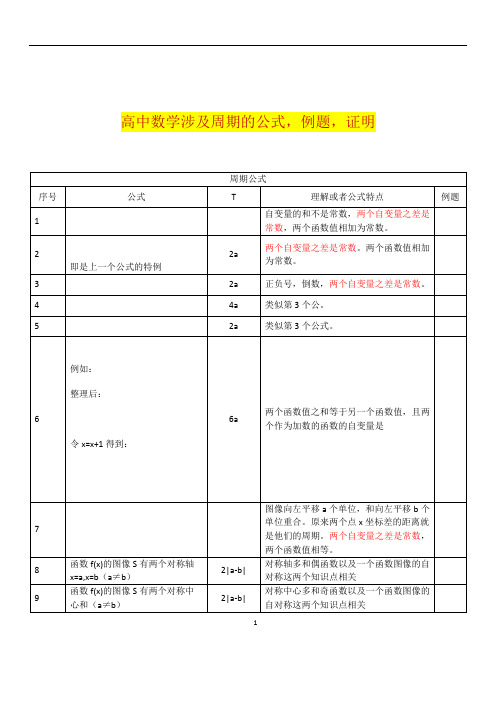
高中数学涉及周期的公式,例题,证明12以上基本是高中阶段遇到的各种周期公式及其变形的总结。
解周期问题,两种方法:1.列举多个数据,找寻规律和周期;2.通过抽象函数直接得到周期。
1. 已知f(X)是R 上不恒为零的偶函数,且对任意实数x 都有xf (x +1)=(x +1)f(x),则f [f (52)]= 解:令x=0,f(0)=0; 令x =−12,f (−12)=0; 令x =12,f (32)=0; 令x =32,f (52)=0; ∴ f [f (52)]=f (0)=02. 定义在R 上的函数f(x)满足f (x )={log 2(1−x ),x ≤0f (x −1)−f (x −2),x >0,则f(2009)=解:整理f (x )=f (x −1)−f (x −2), 得到f (x −1)=f (x )+f (x −2)令x=x+1得到,f (x )=f (x +1)+f (x −1)由公式6知道周期为6,即f (x +6)=f(x),x>0 f(2009)=f (334×6+5)=f(5)。
由公式f (x )=f (x −1)−f (x −2)得f(5)=f(4)−f(3)=(f(3)−f(2))−f(3)=−f(2)=−(f(1)−f(0))=−((f(0)−f(−1))−f(0))=f(−1)=0,4f(x)f(y)=f(x+y)+f(x−y),x,y∈R,则f(2010)=3.已知函数f(x)满足f(1)=14思路:消元和赋值。
令x=x,y=1,则f(x)=f(x+1)+f(x−1),根据公式6知道,f(x+6)=f(x),∴f(2010)=f(335×6)=f(0)。
令y=0,则4f(x)f(0)=2f(x),∵ x不恒为零,∴f(0)=12∴f(2010)=1。
2下面两页是周期函数公式的周期推导证明过程,并总结了推导周期过程的一般思路。
寻找函数的规律高中数学函数问题的解题方法

寻找函数的规律高中数学函数问题的解题方法寻找函数的规律—高中数学函数问题的解题方法在高中数学中,函数问题是一个重要的学习内容。
寻找函数的规律是解决函数问题的关键,下面将介绍一些解题方法,帮助同学们更好地理解和解决函数问题。
1. 列表法列表法是寻找函数规律的常见方法之一。
通过将自变量和函数值列成表格,观察函数值与自变量之间的关系,推断出函数的规律。
举个例子,考虑一个函数f(x) = 2x + 1,要求列出x从1到5的函数值。
我们可以使用列表法解决这个问题:x | 1 | 2 | 3 | 4 | 5 |f(x)| 3 | 5 | 7 | 9 | 11 |通过观察列表中的数字,我们可以发现f(x)的值始终比x的值大2,并且函数值与自变量之间存在线性关系。
因此,可以总结出函数f(x)的规律为:f(x) = 2x + 1。
2. 图像法图像法是寻找函数规律的另一种常用方法。
通过绘制函数的图像,观察图像的形状和趋势,推断出函数的规律。
以函数f(x) = x^2为例,我们可以绘制出其图像。
通过观察图像,我们可以看到函数图像为一个开口朝上的抛物线,顶点位于原点,曲线向右开口。
这个图像可以帮助我们理解函数f(x)的规律:随着x值的增加,f(x)的值也在增加,增加的速度越来越快。
3. 代数法代数法通常适用于一些具体的函数问题,通过代数表达式推导出函数的规律。
考虑函数f(x) = 3x + 2和g(x) = 2x + 4,现在需要比较f(x)和g(x)的大小。
我们可以通过代数法解决这个问题。
将f(x)和g(x)相减得到一个新的函数h(x) = f(x) - g(x),化简后得到h(x) = x - 2。
这个代数表达式告诉我们,当x大于2时,h(x)的值为正数,也就是f(x)大于g(x);当x小于2时,h(x)的值为负数,也就是f(x)小于g(x);而当x等于2时,h(x)的值为0,也就是f(x)等于g(x)。
通过代数法,我们可以比较两个函数的大小,并得到函数规律:当x大于2时,f(x)大于g(x);当x小于2时,f(x)小于g(x);当x等于2时,f(x)等于g(x)。
求函数f(x)周期的几种常见方法解读

求函数f(x)周期的几种常见方法函数的周期性是函数的一个重要性质.对一般函数f(x)的周期,不少中学生往往不知从何入手去求.为了加深对函数f(x)周期概念的理解,本文以实例来说明求函数f(x)周期的几种常见方法,供读者参考.1 定义法根据周期函数的定义以及题设中f(x)本身的性质推导出函数的周期的方法称为定义法.(1)∴f(x)为周期函数,且2a是它的一个周期.注:如果题设函数方程中只有一边含有不为零的常数a,另一边与a无关,这时周期T应取决于a,假设T能被a整除,就分别试算f(x+2a),f(x+3a),f(x+4a),…,当出现f(x+T)=f(x)(T≠0)的形式时,就可知T是f(x)的周期.周期函数,若是,求出它的周期;若不是,说明理由.(1)∴f(x+2a)=f[(x+a)+a](2)∴f(x)为周期函数,3a是它的周期.2 特殊值法当题设条件中有f(m)=n(m,n为常数)时,常常以此条件为突破口,采用特殊值法解即可奏效.f(x)是不是周期函数.若是,求出它的一个周期;若不是,说明理由.∴f(x)为周期函数,2π是它的一个周期.3 变量代换法例4设函数f(x)在R上有定义,且对于任意x都有f(x+1995)=f(x+1994)+f(x+1996),试判断f(x)是否周期函数.若是,求出它的一个周期;若不是,说明理由.解在f(x+1995)=f(x+1994)+f(x+1996) (x∈R)中,以x代x +1995,得f(x)=f(x-1)+f(x+1);(1)在(1)中以x+1代x,得f(x+1)=f(x)+f(x+2).(2)(1)+(2),得f(x-1)+f(x+2)=0,∴f(x-1)=-f(x+2).(3)在(3)中以x+1代x,得f(x)=-f(x+3);(4)在(4)中以x+3代x,得f(x+3)=-f(x+6).(5)将(5)代入(4),得f(x+6)=f(x).∴f(x)为周期函数,6是它的一个周期.4 递推法f(x)是不是周期函数.若是,求出它的一个周期;若不是,说明理由.(1)在(1)中以x+2代x,得f(x+4)=f(x+6)+f(x+2).(2)(1)+(2),得f(x)+f(x+6)=0,∴f(x)=-f(x+6).(3)在(3)中以x+6代x,得f(x+6)=-f(x+12).(4)(4)代入(3),得f(x+12)=f(x).∴f(x)为周期函数,12是它的一个周期.5 消去法例6若函数f(x)定义在R上,且对一切实数x,都有f (5+x)=f (5-x),f (7+x)=f (7-x),试判断f(x)是不是周期函数.若是,求出它的一个周期;若不是,说明理由.解在f(5+x)=f(5-x)中以5-x代x,得f(x)=f(10-x);(1)在f(7+x)=f(7-x)中以7-x代x,得f(x)=f(14-x).(2)由(1)和(2),得f(10-x)=f(14-x).(3)在(3)中以10-x代x,得f(x+4)=f(x).∴f(x)是周期函数,4为它的一个周期.6 结构类比法f(x)是不是周期函数.若是,求出它的一个周期;若不是,说明理由.解:可视sinx为本题中f(x)的一个实例,由此可设想f(x)为周期函数,且2π是它的一个周期.下面进行证明:于是f(x+2π)=f[(x+π)+π]=-f(x+π)=f(x).∴f(x)为周期函数,2π是它的一个周期.7 公式法例8已知y=f(x)(x∈R)的图象是连续的曲线,且f(x)不为常数,f(x)的图象关于直线x=a和直线x=b对称(a<b).(1)求证:f(x)=f(2a-x),f(x)=f(2b-x);(2)求证f(x)是周期函数,并求出它的一个正周期.证明(1)∵ f(x)的图象关于直线x=a对称,且图象连续,不是平行于x轴的直线,∴设P(x,y)为曲线上任一点,点P关于x=a的对称点P'的坐标为P'(x',y'),同理可证 f(x)=f(2b-x).解(2)由(1)可知,f(x)=f(2a-x)=f(2b-x),∴f(2a-x)=f(2b-x),以x代2a-x,得f[x+(2b-2a)]=f(x).∵a<b,2b-2a>0且为常数,∴f(x)是周期函数,2b-2a为它的周期.由例8可得到如下的定理若函数y=f(x)(x∈R)的图象关于直线x=a和直线x=b(a<b)对称,且在这两条直线之间再无对称轴,那么f(x)是周期函数,2b -2a为它的周期.此定理可当作一个公式用,如例6中函数f(x)的周期为-=4.。
函数的奇偶性与周期性专题题型讲解与例题突破

考纲解读 1.根据函数奇偶性定义和图象判断简单函数的奇偶性;2.根据函数奇偶性求函数值、求参数、解与函数有关的不等式;3.综合应用函数的周期性、奇偶性、单调性、求解抽象函数问题.[基础梳理]1.函数的奇偶性2.(1)周期函数:对于函数y =f (x ),如果存在一个非零常数T ,使得当x 取定义域内的任何值时,都有f (x +T )=f (x ),那么就称函数y =f (x )为周期函数,称T 为这个函数的周期.(2)最小正周期:如果在周期函数f (x )的所有周期中存在一个最小的正数,那么这个最小正数就叫作f (x )的最小正周期.[三基自测]1.已知函数f (x )是定义在R 上的奇函数,且当x >0时,f (x )=x 2+1x ,则f (-1)等于( )A .-2B .0C .1D .2答案:A2.函数f (x )=1-x1+x 是( )A .奇函数B .偶函数C .既是奇函数又是偶函数D .非奇非偶函数 答案:D3.下列函数中,既是奇函数又是增函数的为( ) A .y =x +1 B .y =-x 3 C .y =1xD .y =x |x | 答案:D4.(2017·高考全国卷Ⅱ改编)已知函数f (x )是定义在R 上的奇函数,则f (0)=__________. 答案:05.(必修1·第一章复习参考题改编)函数f (x )=4x 2-kx -8为偶函数,则k 为________.[考点例题]考点一 函数奇偶性的判断|易错突破[例1] (1)(2018·肇庆模拟)在函数y =x cos x ,y =e x +x 2,y =lg x 2-2,y =x sin x 中,偶函数的个数是( )A .3B .2C .1D .0(2)定义两种运算:a ⊕b =a 2-b 2,a ⊗b =(a -b )2,则f (x )=2⊕x2-(x ⊗2)是( )A .奇函数B .偶函数C .既奇又偶函数D .非奇非偶函数[解析] (1)y =x cos x 是奇函数,y =lg x 2-2和y =x sin x 是偶函数,y =e x +x 2是非奇非偶函数,故选B.(2)因为2⊕x =4-x 2,x ⊗2=(x -2)2, 所以f (x )=4-x 22-(x -2)2=4-x 22-|2-x |,该函数的定义域是[-2,0)∪(0,2], ∴f (x )=4-x 2x ,且满足f (-x )=-f (x ).故函数f (x )是奇函数. [答案] (1)B (2)A [易错提醒]1.函数f (x )=lg(x +1)+lg(x -1)的奇偶性是( ) A .奇函数 B .偶函数 C .非奇非偶函数D .既奇又偶函数解析:由⎩⎪⎨⎪⎧x +1>0x -1>0,知x >1,定义域不关于原点对称,故f (x )为非奇非偶函数.答案:C2.函数f (x )=x 2-1+1-x 2,则f (x )为( ) A .奇函数C .既是奇函数,又是偶函数D .非奇非偶函数解析:由⎩⎪⎨⎪⎧x 2-1≥0,1-x 2≥0,得x =±1,∴f (x )的定义域为{-1,1}.又f (1)+f (-1)=0,f (1)-f (-1)=0,即f (x )=±f (-x ).∴f (x )既是奇函数又是偶函数. 答案:C考点二 函数的周期性|方法突破[例2] (1)函数f (x )=lg|sin x |是( ) A .最小正周期为π的奇函数 B .最小正周期为2π的奇函数 C .最小正周期为π的偶函数 D .最小正周期为2π的偶函数(2)已知定义在R 上的奇函数f (x )满足f (x )=-f ⎝⎛⎭⎫x +32,且f (1)=2,则f (2 018)=__________.(3)函数y =f (x )满足对任意x ∈R 都有f (x +2)=f (-x )成立,且函数y =f (x -1)的图象关于点(1,0)对称,f (1)=4,则f (2 016)+f (2 017)+f (2 018)的值为__________.[解析] (1)∵f (-x )=lg|sin(-x )|=lg|sin x |, ∴函数f (x )为偶函数.∵f (x +π)=lg|sin(x +π)|=lg|sin x |, ∴函数f (x )的周期为π.故选C. (2)∵f (x )=-f ⎝⎛⎭⎫x +32, ∴f (x +3)=f ⎣⎡⎦⎤⎝⎛⎭⎫x +32+32=-f ⎝⎛⎭⎫x +32=f (x ). ∴f (x )是以3为周期的周期函数.则f (2 018)=f (672×3+2)=f (2)=f (-1)=-f (1)=-2. (3)∵函数y =f (x -1)的图象关于点(1,0)对称, ∴f (x )是R 上的奇函数,f (x +2)=-f (x ), ∴f (x +4)=-f (x +2)=f (x ), 故f (x )的周期为4,∴f (2 017)=f (504×4+1)=f (1)=4,∴f (2 016)+f (2 018)=f (2 016)+f (2 016+2)=f (2 016)-f (2 016)=0, ∴f (2 016)+f (2 017)+f (2 018)=4. [答案] (1)C (2)-2 (3)4 1.求函数周期的方法 [方法提升](1)函数f (x )满足f (a +x )=-f (x ),则f (x )是周期为2a 的函数; (2)若f (x +a )=±1f (x )(a ≠0)恒成立,则T =2a ;(3)若f (x +a )=f (x -a ),则T =2a ; (4)若f (x +a )=1-f (x )1+f (x ),则T =4a .[母题变式]将本例(3)改为已知f (x )是定义在R 上的偶函数,并且f (x +2)=-1f (x ),当2≤x ≤3时,f (x )=x ,则f (105.5)=________.解析:由已知,可得f (x +4)=f [(x +2)+2] =-1f (x +2)=-1-1f (x )=f (x ).故函数的周期为4.∴f (105.5)=f (4×27-2.5)=f (-2.5)=f (2.5). ∵2<2.5<3,由题意,得f (2.5)=2.5. ∴f (105.5)=2.5. [答案] 2.5考点三 函数奇偶性、周期性应用|模型突破角度1 求函数解析式[例3] (1)函数f (x )在R 上为奇函数,且x >0时,f (x )=x +1,则当x <0时,f (x )=________.[解析] ∵f (x )为奇函数,x >0时,f (x )=x +1, ∴当x <0时,-x >0, f (x )=-f (-x )=-(-x +1), ∴f (x )=--x -1. [答案] --x -1(2)f (x )、g (x )分别为R 上的奇函数和偶函数,且f (x )+g (x )=e x ,求f (x )和g (x )的解析式. [解析] ∵f (x )是R 上的奇函数,g (x )是偶函数, ∴由f (x )+g (x )=e x ,① 得f (-x )+g (-x )=e -x , 即-f (x )+g (x )=e -x .②由①+②得g (x )=e x +e -x 2,①-②得f (x )=e x -e -x 2.[模型解法]角度2 求参数值[例4] 若函数f (x )=k -2x1+k ·2x 在定义域上为奇函数,则实数k =________.[解析] 法一:∵f (-x )=k -2-x 1+k ·2-x =k ·2x -12x +k , ∴f (-x )+f (x )=(k -2x )(2x +k )+(k ·2x -1)·(1+k ·2x )(1+k ·2x )(2x +k )=(k 2-1)(22x +1)(1+k ·2x )(2x +k ). 由f (-x )+f (x )=0可得k 2=1,∴k =±1. 法二:f (x )为奇函数,∴f (-1)+f (1)=0, ∴k -21+2k+k -121+k 2=0,即k 2=1,∴k =±1.[答案] ±1 [模型解法]角度3 求函数值[例5] 已知f (x )=22x+1+sin x ,则f (-4)+f (-3)+f (-2)+f (-1)+f (0)+f (1)+f (2)+f (3)+f (4)的值是__________.[解析] 因为f (x )-1=1-2x1+2x +sin x 是奇函数,所以f (-x )-1=-[f (x )-1]=1-f (x ),故f (-x )+f (x )=2,且f (0)=1,所以f (-4)+f (-3)+f (-2)+f (-1)+f (0)+f (1)+f (2)+f (3)+f (4)=[f (-4)+f (4)]+[f (-3)+f (3)]+[f (-2)+f (2)]+[f (-1)+f (1)]+f (0)=2×4+1=9.[答案] 9[模型解法][高考类题]1.(2017·高考全国卷Ⅱ)已知函数f (x )是定义在R 上的奇函数,当x ∈(-∞,0)时,f (x )=2x 3+x 2,则f (2)=__________.解析:依题意得,f (-2)=2×(-2)3+(-2)2=-12,由函数f (x )是奇函数,得f (2)=-f (-2)=12.答案:122.(2015·高考全国卷Ⅰ)若函数f (x )=x ln(x +a +x 2)为偶函数,则a =__________. 解析:由题意得f (x )=x ln(x +a +x 2)=f (-x )=-x ln(a +x 2-x ),所以a +x 2+x =1a +x 2-x ,解得a =1.答案:1[真题感悟]1.[考点一](2017·高考北京卷)已知函数f (x )=3x -⎝⎛⎭⎫13x,则f (x )( ) A .是偶函数,且在R 上是增函数 B .是奇函数,且在R 上是增函数 C .是偶函数,且在R 上是减函数 D .是奇函数,且在R 上是减函数解析:由f (-x )=⎝⎛⎭⎫13x-3x=-f (x ),知f (x )为奇函数,因为y =⎝⎛⎭⎫13x 在R 上是减函数,所以y =-⎝⎛⎭⎫13x 在R 上是增函数,又y =3x 在R 上是增函数,所以函数f (x )=3x -⎝⎛⎭⎫13x在R 上是增函数,故选B.答案:B2.[考点二、三](2016·高考山东卷)已知函数f (x )的定义域为R .当x <0时,f (x )=x 3-1;当-1≤x ≤1时,f (-x )=-f (x );当x >12时,f ⎝⎛⎭⎫x +12=f ⎝⎛⎭⎫x -12.则f (6)=( ) A .-2 B .-1 C .0D .2解析:由题意可知,当-1≤x ≤1时,f (x )为奇函数,且当x >12时,f (x +1)=f (x ),所以f (6)=f (5×1+1)=f (1).而f (1)=-f (-1)=-[(-1)3-1]=2,所以f (6)=2.故选D.答案:D3.[考点一](2014·高考新课标全国卷Ⅰ)设函数f (x ),g (x )的定义域都为R ,且f (x )是奇函数,g (x )是偶函数,则下列结论中正确的是( )A .f (x )g (x )是偶函数B .|f (x )|g (x )是奇函数C .f (x )|g (x )|是奇函数D .|f (x )g (x )|是奇函数解析:f (x )为奇函数,g (x )为偶函数,故f (x )g (x )为奇函数,f (x )|g (x )|为奇函数,|f (x )|g (x )为偶函数,|f (x )g (x )|为偶函数,故选C.答案:C4.[考点三](2015·高考山东卷)若函数f (x )=2x +12x -a 是奇函数,则使f (x )>3成立的x 的取值范围为( )A .(-∞,-1)B .(-1,0)C .(0,1)D .(1,+∞)解析:f (-x )=2-x +12-x -a =2x +11-a ·2x ,由f (-x )=-f (x )得2x +11-a ·2x =-2x +12x-a ,即1-a ·2x =-2x+a ,化简得a ·(1+2x)=1+2x,所以a =1,f (x )=2x +12x -1.由f (x )>3得0<x <1.故选C.答案:C5.[考点二、三](2017·高考山东卷)已知f (x )是定义在R 上的偶函数,且f (x +4)=f (x -2).若当x ∈[-3,0]时,f (x )=6-x ,则f (919)=__________.解析:∵f (x +4)=f (x -2),∴f (x )的周期为6,∵919=153×6+1,∴f (919)=f (1).又f (x )为偶函数,∴f (919)=f (1)=f (-1)=6.答案:6。
函数的周期性有哪些公式呢?

函数的周期性有哪些公式呢?
一、函数的周期性:
设函数 f(x)在区间 X 上有定义,若存在一个与 x 无关的正数 T , 使对于任一x∈X,恒有 f(x+T)= f(x)
则称f(x)是以T 为周期的周期函数,把满足上式的最小正数T 称为函数 f(x)的周期。
二、周期函数的运算性质:
①若T为f(x)的周期,则f(ax+b)的周期为 T/|a| 。
②若f(x),g(x)均是以T为周期的函数,则f(x)±g(x)也是以T为周期的函数。
③若f(x),g(x)分别是以T1,T2,T1≠T2为周期的函数,则f(x)±g(x)是以T1,T2的最小公倍数为周期的函数。
三、常见的周期函数有:
sinx,cosx,其周期T=2π;
tanx,cotx,|sinx|,|cosx|,其周期T=π。
解题提示:判别给定函数f(x)是否为周期函数,主要是根据周期的定义,有时也用其运算性质。
四、例题:
设对一切实数x,有f(1/2 + x)= 1/2 + √【f(x)- f^2(x)】,则f (x)是周期为多少的周期函数?
解:f【1/2 +(1/2 + x)】= 1/2 + √【f(1/2 + x)- f^2(1/2 + x)】
=1/2 + √【1/4 - f(x) + f^2(x)】= 1/2 + 【 f(x) - 1/2】
= f(x),(由题设f(x)≥1/2)
即 f(1+x) = f(x) ,故可知f(x)的周期为1 。
高中数学函数周期性总结

( 4) y f ( x 3) 与 y f (3 x) 的图象关于直线 x 3 对称。
其中正确命题的序号为
。
11、若 f ( x) 为定义在 R 上的函数, 且 f (10 x) f (10 x) , f (20 x) f (20 x) ,则 f ( x) 为(
)
A. 奇函数且周期函数;
B.
奇函数且非周期函数;
f(x)=C(C 为常数 ) 是周期函数吗?有最小正周期吗? 三、抽象函数的周期总结
1、 f ( x T ) f ( x)
y f (x) 的周期为 T
2、 f ( x a) f (b x) (a b)
y f (x) 的周期为 T b a
3、 f ( x a) f (x)
y f ( x) 的周期为 T 2a
(C)1
(D)2
4、定义在 R 上的函数 f ( x) ,给出下列四个命题:
( 1)若 f ( x) 是偶函数,则 f ( x 3) 的图象关于直线 x 3 对称
( 2)若 f ( x 3) f (3 x), 则 f (x) 的图象关于点 (3,0) 对称
( 3)若 f ( x 3) = f (3 x) ,且 f (x 4) f (4 x) ,则 f ( x) 的一个周期为 2。
11 、 y f (x) 有两个对称中心 (a,0) 和 (b,0)
y f (x) 周期 T 2(b a)
12 、 y f (x) 有一条对称轴 x a 和一个对称中心 (b,0) y f (x) 周期 T 4(b a)
13 、奇函数 y f ( x) 满足 f (a x) f (a x)
y f ( x) 周期 T 4a 。
f (x)
f ( x)
角函数周期的几种求法

三角函数周期的几种求法深圳市福田区皇岗中学 蔡舒敏高中数学第一册第二节中涉及到函数周期的问题,学生们往往对此类的问题感到比较困难。
本文就这个问题谈三角函数周期的几种求法。
1.定义法:定义:一般地y=c ,对于函数,如果存在一个不为零的常数,使得当取定义域内的每一个值时,f(x+T )=f(x)都成立,那么就把函数y=f(x)叫做周期函数;不为零的常数叫做这个函数的周期。
对于一个周期函数来说,如果在所有的周期中存在着一个最小的正数,就把这个最小的正数叫做最小的正周期。
下面我们谈到三角函数的周期时,一般指的是三角函数折最小正周期。
例1.求函数y=3sin (332π+x )的周期解:∵y=f (x )=3sin (332π+x )=3sin (332π+x +2π)=3sin (3232ππ++x )=3sin[3)3(32ππ++x ]= f (x+3π)这就是说,当自变量由x增加到x+3π,且必增加到x+3π时,函数值重复出现。
∴函数y=3sin (332π+x )的周期是T=3π。
例2:求f (x )=sin 6x+cos 6x 的周期解∵f (x+2π)= sin 6(x+2π)+ cos 6(x+2π) = cos 6x +sin 6x= f (x )∴f (x )=sin 6x+cos 6x 的周期为T=2π例3:求f (x )=xx xx 3cos cos 3sin sin ++的周期解:∵f (x+π)=)cos()cos()(3sin )sin(ππππ++++++x x x x=x cox xx 3cos 3sin sin ----=xx x x 3cos cos 3sin sin ++ = f (x )∴求f (x )=xx xx 3cos cos 3sin sin ++的周期:T=π2.公式法:(1)如果所求周期函数可化为y=Asin (ϕω+x )、y=Acos (ϕω+x )、y=tg (ϕω+x )形成(其中A 、ω、ϕ为常数,且A ≠0、ω>0、ϕ∈R ),则可知道它们的周期分别是:ωπ2、ωπ2、ωπ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求函数f(x)周期的几种常见方法
函数的周期性是函数的一个重要性质.对一般函数f(x)的周期,不少中学生往往不知从何入手去求.为了加深对函数f(x)周期概念的理解,本文以实例来说明求函数f(x)周期的几种常见方法,供读者参考.
1 定义法
根据周期函数的定义以及题设中f(x)本身的性质推导出函数的周期的方法称为定义法.
(1)
∴f(x)为周期函数,且2a是它的一个周期.
注:如果题设函数方程中只有一边含有不为零的常数a,另一边与a无关,这时周期T应取决于a,假设T能被a整除,就分别试算f(x+2a),f(x+3a),f(x+4a),…,当出现f(x+T)=f(x)(T≠0)的形式时,就可知T是f(x)的周期.
周期函数,若是,求出它的周期;若不是,说明理由.
(1)
∴f(x+2a)=f[(x+a)+a]
(2)
∴f(x)为周期函数,3a是它的周期.
2 特殊值法
当题设条件中有f(m)=n(m,n为常数)时,常常以此条件为突破口,采用特殊值法解即可奏效.
f(x)是不是周期函数.若是,求出它的一个周期;若不是,说明理由.
∴f(x)为周期函数,2π是它的一个周期.
3 变量代换法
例4设函数f(x)在R上有定义,且对于任意x都有f(x+1995)=f(x+1994)+f(x+1996),试判断f(x)是否周期函数.若是,求出它的一个周期;若不是,说明理由.
解在f(x+1995)=f(x+1994)+f(x+1996) (x∈R)中,以x代x +1995,得
f(x)=f(x-1)+f(x+1);
(1)
在(1)中以x+1代x,得
f(x+1)=f(x)+f(x+2).
(2)
(1)+(2),得f(x-1)+f(x+2)=0,
∴f(x-1)=-f(x+2).
(3)
在(3)中以x+1代x,得
f(x)=-f(x+3);
(4)
在(4)中以x+3代x,得
f(x+3)=-f(x+6).
(5)
将(5)代入(4),得f(x+6)=f(x).
∴f(x)为周期函数,6是它的一个周期.
4 递推法
f(x)是不是周期函数.若是,求出它的一个周期;若不是,说明理由.
(1)
在(1)中以x+2代x,得
f(x+4)=f(x+6)+f(x+2).
(2)
(1)+(2),得f(x)+f(x+6)=0,
∴f(x)=-f(x+6).
(3)
在(3)中以x+6代x,得
f(x+6)=-f(x+12).
(4)
(4)代入(3),得f(x+12)=f(x).
∴f(x)为周期函数,12是它的一个周期.
5 消去法
例6若函数f(x)定义在R上,且对一切实数x,都有f (5+x)=f (5-x),f (7+x)=
f (7-x),试判断f(x)是不是周期函数.若是,求出它的一个周期;若不是,说明理由.
解在f(5+x)=f(5-x)中以5-x代x,得
f(x)=f(10-x);
(1)
在f(7+x)=f(7-x)中以7-x代x,得
f(x)=f(14-x).
(2)
由(1)和(2),得
f(10-x)=f(14-x).
(3)
在(3)中以10-x代x,得f(x+4)=f(x).
∴f(x)是周期函数,4为它的一个周期.
6 结构类比法
f(x)是不是周期函数.若是,求出它的一个周期;若不是,说明理由.
解:
可视sinx为本题中f(x)的一个实例,由此可设想f(x)为周期函数,且2π是它的一个周期.下面进行证明:
于是f(x+2π)=f[(x+π)+π]=-f(x+π)=f(x).
∴f(x)为周期函数,2π是它的一个周期.
7 公式法
例8已知y=f(x)(x∈R)的图象是连续的曲线,且f(x)不为常数,f(x)的图象关于直线x=a和直线x=b对称(a<b).
(1)求证:f(x)=f(2a-x),f(x)=f(2b-x);
(2)求证f(x)是周期函数,并求出它的一个正周期.
证明(1)∵ f(x)的图象关于直线x=a对称,且图象连续,不是平行于x轴的直线,
∴设P(x,y)为曲线上任一点,点P关于x=a的对称点P'的坐标为P'(x',y'),
同理可证 f(x)=f(2b-x).
解(2)由(1)可知,f(x)=f(2a-x)=f(2b-x),
∴f(2a-x)=f(2b-x),以x代2a-x,得f[x+(2b-2a)]=f(x).∵a<b,2b-2a>0且为常数,
∴f(x)是周期函数,2b-2a为它的周期.
由例8可得到如下的
定理若函数y=f(x)(x∈R)的图象关于直线x=a和直线x=b(a
<b)对称,且在这两条直线之间再无对称轴,那么f(x)是周期函数,2b -2a为它的周期.
此定理可当作一个公式用,如例6中函数f(x)的周期为2.7-2.5=4.。
