四舍六入五留双_终极完美版
四舍六入公式
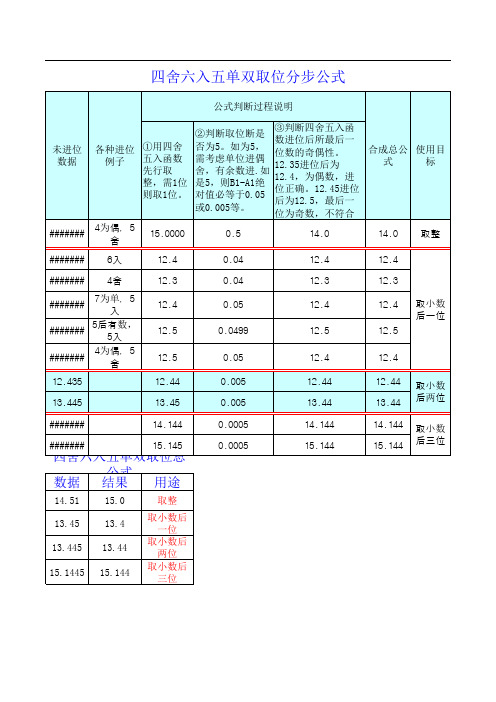
未进位 数据
####### #######,5 入 5后有数, ####### 5入 4为偶,5 ####### 舍 12.435 13.445 ####### #######
四舍六入五单双取位总 公式 数据 结果 用途
14.51 13.45 13.445 15.1445 15.0 13.4 13.44 15.144 取整 取小数后 一位 取小数后 两位 取小数后 三位
四舍六入五单双取位分步公式
公式判断过程说明 ②判断取位断是 各种进位 ①用四舍 否为5。如为5, 五入函数 需考虑单位进偶 例子 先行取 舍,有余数进.如 整,需1位 是5,则B1-A1绝 则取1位。 对值必等于0.05 或0.005等。 4为偶,5 舍 6入 4舍 15.0000 12.4 12.3 12.4 12.5 12.5 12.44 13.45 14.144 15.145 0.5 0.04 0.04 0.05 0.0499 0.05 0.005 0.005 0.0005 0.0005 ③判断四舍五入函 数进位后所最后一 合成总公 使用目 位数的奇偶性。 式 标 12.35进位后为 12.4,为偶数,进 位正确。12.45进位 后为12.5,最后一 位为奇数,不符合 14.0 12.4 12.3 12.4 12.5 12.4 12.44 13.44 14.144 15.144 14.0 12.4 12.3 12.4 12.5 12.4 12.44 13.44 14.144 15.144 取小数 后两位 取小数 后三位 取小数 后一位 取整
数字修约规则-----四舍五入和四舍六入五留双规则之令狐文艳创作

数字修约规则令狐文艳现在被广泛使用的数字修约规则主要有四舍五入规则和四舍六入五留双规则。
[编辑] 四舍五入规则四舍五入规则是人们习惯采用的一种数字修约规则。
四舍五入规则的具体使用方法是:在需要保留有效数字的位次后一位,逢五就进,逢四就舍。
例如:将数字2.1875精确保留到千分位(小数点后第三位),因小数点后第四位数字为5,按照此规则应向前一位进一,所以结果为2.188。
同理,将下列数字全部修约为四位有效数字,结果为:0.53664—0.5366 10.2750—10.28 18.06501—18.070.58346—0.5835 6.4050—16.4127.1850—27.19按照四舍五入规则进行数字修约时,应一次修约到指定的位数,不可以进行数次修约,否则将有可能得到错误的结果。
例如将数字15.4565修约为两位有效数字时,应一步到位:15.4565——15(正确)。
如果分步修约将得到错误的结果:15.4565——15.457——15.46——15.5——16(错误)。
四舍五入修约规则,逢五就进,必然会造成结果的系统偏高,误差偏大,为了避免这样的状况出现,尽量减小因修约而产生的误差,在某些时候需要使用四舍六入五留双的修约规则。
[编辑] 四舍六入五留双规则为了避免四舍五入规则造成的结果偏高,误差偏大的现象出现,一般采用四舍六入五留双规则(Banker's Rounding)。
四舍六入五留双应该改为: 四舍六入逢五无后则留双,这样描述更容易理解和记住。
四舍六入五留双规则的具体方法是:(一)当尾数小于或等于4时,直接将尾数舍去。
例如将下列数字全部修约为四位有效数字,结果为:0.53664—0.53660.58344—0.5834 16.4005—16.40 27.1829—27.1810.2731—10.27 18.5049—18.50(二)当尾数大于或等于6时,将尾数舍去并向前一位进位。
例如将下列数字全部修约为四位有效数字,结果为:0.53666—0.53678.3176—8.31816.7777—16.780.58387—0.5839 10.29501—10.30 21.0191—21.02(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。
四舍六入五单进规则

数值修约规则四舍六入五留双规则四舍六入五留双规则的具体方法是:(一)当尾数小于或等于4时,直接将尾数舍去。
例如将下列数字全部修约为四位有效数字,结果为:0.53664—0.5366 10.2731—10.2718.5049—18.50 0.58344—0.583416.4005—16.40 27.1829—27.18(二)当尾数大于或等于6时,将尾数舍去并向前一位进位。
例如将下列数字全部修约为四位有效数字,结果为:0.53666—0.5367 8.3176—8.31816.7777—16.78 0.58387—0.583910.29501—10.30 21.0191—21.02(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。
数字“0”在此时应被视为偶数。
例如将下列数字全部修约为四位有效数字,结果为:0.153050—0.1530 12.6450—12.6418.2750—18.28 0.153750—0.153812.7350—12.74 21.845000—21.84(四)当尾数为5,而尾数“5”的后面还有任何不是0的数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0的数字在哪一位上,都应向前进一位。
例如将下列数字全部修约为四位有效数字,结果为:0.326552—0.3266 12.73507—12.7421.84502—21.85 12.64501—12.6518.27509—18.28 38.305000001—38.31按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则那样,一次性修约到指定的位数,不可以进行数次修约,否则得到的结果也有可能是错误的。
例如将数字10.2749945001修约为四位有效数字时,应一步到位:10.2749945001—10.27(正确)。
如果按照四舍六入五留双规则分步修约将得到错误结果:10.2749945001—10.274995—10.275—10.28(错误)。
四舍六入五单双法

四舍六入五单双法
四舍六入五单双法
由于“四舍五入”造成“入得多,舍得少”的问题,给实际数据采集造成一定程度的不便。
因此GB/T8170-2000的进舍规则规定为“四舍六入五单双法”。
具体如下:
a)拟舍去的数字的最左边一位数字小于5,则舍去,保留的数字不变;
例:将12.1498修约到个数位,得12;修约到一位小数,得12.1 b)拟舍去的数字的最左边一位数字大于5,则进1,保留的数字最后一位加1;例:将1268修约到“百”数位,得1300 c)拟舍去的数字的最左边一位数字是5,且其后面跟有非0数字时,则进1,保留的数字最后一位加1;
例:将10.5002修约到个数位,得11
d)拟舍去的数字的最左边一位数字是5,且其后无数字或皆为0时,若保留数字的最后一位为奇数(1,3,5,7,9),则进1;保留数字的最后一位为偶数(0,2,4,6,8),则舍去。
例:将1.050修约到一位小数,得1.0;0.35修约到一位小数,得0.4
以上法则的口诀归纳为“四舍六入五考虑,五后非零则进一,五后皆零视奇偶,五前为偶应舍去,五前为奇应进一”。
四舍六入五成双的计算方法

四舍六入五成双的计算方法
宝子,今天咱来唠唠这个“四舍六入五成双”的计算方法。
你看啊,平常咱们老说四舍五入,这个“四舍六入五成双”可有点不一样的小脾气呢。
先说这个“四舍”,就和咱们平常的四舍五入里的四舍差不多啦。
要是一个数要保留到某一位,这一位后面的数字小于等于4呢,那就直接舍掉。
比如说3.42,要保留到整数位,后面的0.42里4是小于5的,那就舍掉,结果就是3啦。
再讲讲“六入”。
要是这一位后面的数字大于等于6呢,就往前进一位。
就像3.61,保留到整数位,0.61里6大于5,那就进一位,结果就是4喽。
最有趣的就是这个“五成双”啦。
如果这一位后面的数字是5,就不是简单的进一位了哦。
如果这个5后面没有其他数字了,或者说5后面的数字都是0,那就要看前面的数字是奇数还是偶数。
要是前面的数字是奇数呢,就进一位让它变成偶数;要是前面的数字是偶数,那就直接舍掉这个5。
比如说2.5,保留到整数位,2是偶数,那就舍掉0.5,结果就是2;要是3.5,3是奇数,那就进一位,结果就是4。
这个计算方法在一些比较精确的统计或者科学计算里可有用了呢。
它能让数据的处理更加合理,减少一些因为简单四舍五入带来的小偏差。
宝子,你可别小瞧它,虽然感觉有点复杂,但是一旦你掌握了,就会觉得还挺好玩的呢。
它就像是一个有点小个性的朋友,有自己独特的规则。
不像普通的四舍五入那么直白,但是却更加细腻地处理数字。
下次你要是遇到需要精确处理数字的时候,不妨试试这个“四舍六入五成双”的方法呀。
四舍六入五留双规则的具体方法之欧阳地创编

时间:2021.03.04
创作:欧阳地
当尾数小于或等于4时,直接将尾数舍去
例如将下列数字全部修约到两位小数,结果为:
10.2731——10.27
18.5049——18.50
16.4005——16.40
27.1829——27.18
当尾数大于或等于6时将尾数舍去向前一位进位
例如将下列数字全部修约到两位小数,结果为:
16.7777——16.78
10.29501——10.30
21.0191——21.02
(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。数字“0”在此时应被视为偶数。
例如将下列数字全部修约到两位小数,结果为:
12.6450——12.64
18.2750——18.28
12.7350——12.74
21.845000——21.84
(四)当尾数为5,而尾数“5”的后面还有任何不是0的数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0的数字在哪一位上,都应向前进一位。
例如将下列数字全部修约到两பைடு நூலகம்小数,结果为:
12.73507——12.74
21.84502——21.85
12.64501——12.65
18.27509——18.28
38.305000001——38.31
按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则那样,一次性修约到指定的位数,不可以进行数次修约,否则得到的结果也有可能是错误的。例如将数字10.2749945001修约到两位小数时,应一步到位:10.2749945001——10.27(正确)。如果按照四舍六入五留双规则分步修约将得到错误结果:10.2749945001——10.274995——10.275——10.28(错误)。
四舍六入五留双规则的具体方法之欧阳德创编

四舍六入五留双规则的具体方当尾数小于或等于4时,直接将尾数舍去例如将下列数字全部修约到两位小数,结果为:10.2731——10.2718.5049——18.5016.4005——16.4027.1829——27.18当尾数大于或等于6时将尾数舍去向前一位进位例如将下列数字全部修约到两位小数,结果为:16.7777——16.7810.29501——10.3021.0191——21.02(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。
数字“0”在此时应被视为偶数。
例如将下列数字全部修约到两位小数,结果为:12.6450——12.6418.2750——18.2812.7350——12.7421.845000——21.84(四)当尾数为5,而尾数“5”的后面还有任何不是0的数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0的数字在哪一位上,都应向前进一位。
例如将下列数字全部修约到两位小数,结果为:12.73507——12.7421.84502——21.8512.64501——12.6518.27509——18.2838.305000001——38.31按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则那样,一次性修约到指定的位数,不可以进行数次修约,否则得到的结果也有可能是错误的。
例如将数字10.2749945001修约到两位小数时,应一步到位:10.2749945001——10.27(正确)。
如果按照四舍六入五留双规则分步修约将得到错误结果:。
四舍六入五留双规则的具体方法之欧阳与创编

四舍六入五留双规则的具体方
当尾数小于或等于4时,直接将尾数舍去
例如将下列数字全部修约到两位小数,结果为:
10.2731——10.27
18.5049——18.50
16.4005——16.40
27.1829——27.18
当尾数大于或等于6时将尾数舍去向前一位进位
例如将下列数字全部修约到两位小数,结果为:
16.7777——16.78
10.29501——10.30
21.0191——21.02
(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇
数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。
数字“0”在此时应被视为偶数。
例如将下列数字全部修约到两位小数,结果为:
12.6450——12.64
18.2750——18.28
12.7350——12.74
21.845000——21.84
(四)当尾数为5,而尾数“5”的后面还有任何不是0的数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0的数字在哪一位上,都应向前进一位。
例如将下列数字全部修约到两位小数,结果为:
12.73507——12.74
21.84502——21.85
12.64501——12.65
18.27509——18.28
38.305000001——38.31
按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则那样,一次性修约到指定的位。
