5-5横隔梁内力计算
作用于横隔梁上的计算荷载

① 作用于横隔梁上的计算荷载横隔梁的计算荷载应采用车辆荷载加载计算,对于跨中横隔梁的最不利布置如图2-23所示,纵向一辆车辆荷载对跨中横隔梁的计算荷载为:kN y P P i i oq 10.128)806.0140000.1140028.0120(2121=⨯+⨯+⨯==∑图2-23 横隔梁荷载纵向加载图② 2.10.2 跨中横隔梁的内力影响线通常横隔梁靠近桥中线的截面处弯矩较大,而靠近桥两侧边梁的截面处剪力较大,故选取a a -、b b -两个截面计算横隔梁的弯矩,选取c c -、d d -两个截面计算横隔梁的剪力。
在表2-4 中已经求得各梁号的横向影响线竖标值。
2.10.2.1 绘制弯矩影响线1)影响系数计算公式在桥梁跨中当单位荷载1=p 作用于j 号梁时,i 号梁所受的作用为竖向力ij R 和抗扭矩Tij M 。
则当1=p 作用于截面a a -左侧时,a a j T j T a a j a a j j a a e M Mb b -----+++=2,1,,22,11,ηηη当1=p 作用于截面a a -右侧时,a a j T j T a a j a a j j a a M Mb b ----+++=2,1,,22,11,ηηη中横梁内力影响线图见图2-24. 2)计算T 梁扭矩Tij MTij M 可按下列公式计算:∑=⋅⋅=ni ii hTi j Tij I aE I l e G M 12212β (2-53)式中:i I 、Ti I ——分别为i 号梁抗弯惯矩和抗扭惯矩,本设计主梁刚度按T 梁跨中截面考虑,抗弯惯矩44031.0m I =、抗扭惯矩40088.0m I T =G ——混凝土的剪切弹性模量MPa E G h 441038.11045.34.04.0⨯=⨯⨯==;j e ——单位荷载1=p 作用位置到横截面中心的距离。
各T 梁扭转力矩计算见表2-45。
表2-45 T 梁扭转力矩计算表梁号 i I Ti I j e βl i ai i I a 2 Tij M1 0.4031 0.0088 4.20 0.901228.90 4.20 7.1107 0.0522 2 0.4031 0.0088 2.10 28.90 2.10 1.7778 0.0261 3 0.4031 0.0088 0.0 28.90 0.0 0.0000 0 4 0.4031 0.0088 -2.10 28.90 -2.10 1.7778 -0.0261 50.4031 0.0088 -4.2028.90-4.207.1107-0.0522ii I a2∑ 17.77803)计算弯矩影响线坐标值 弯矩影响线坐标值计算表2-46.表2-46 弯矩影响线坐标值计算表截面 梁号 j 1η1bj 2η2b j T M 1 j T M 2 S S e -j S S ,-ηa a -1 0.5604 4.2000 0.3802 2.1000 0.0522 0.0522 4.20 -0.9435 2 0.3802 4.2000 0.2901 2.1000 0.0261 0.0261 2.10 0.1583 3 0.2000 4.2000 0.2000 2.1000 0 0 1.26004 0.0198 4.2000 0.1099 2.1000 -0.0261 -0.0261 0.26185 -0.1604 4.2000 0.0198 2.1000 -0.0522 -0.0522 -0.7365 b b -1 0.5604 3.1500 0.3802 1.0500 0.0522 0.0522 3.15 -0.8811 2 0.3802 3.1500 0.2901 1.0500 0.0261 0.0261 1.05 0.50443 — — — — — — — —4 0.0198 3.1500 0.1099 1.0500 -0.0261 -0.0261 0.1256 5-0.16043.1500 0.01981.0500 -0.0522 -0.0522-0.5889截面b b -的3号梁弯矩影响线坐标3,b b -η由影响线图2-24中量出。
主梁内力计算

主梁的内力计算主梁的内力计算包括恒载内力计算和活载内力计算。
根据上述梁跨结构纵、横截面的布置,计算活载作用下的梁桥荷载横向分布系数,求出各主梁控制截面(取跨中、四分点、变化点截面及支点截面)的恒载和最大活载内力,然后再进行主梁内力组合。
一、恒载内力计算1、恒载集度⑴预制梁自重(第一期恒载)①.跨中截面段主梁自重(四分点截面至跨中截面,长7.25m )(1)0.861625.07.25156.165g KN =⨯⨯=②.马蹄抬高与腹板变宽段梁的自重近似计算(长3.7m ) 主梁端部截面面积为A=1.176m 2()(2) 1.17600.8616 3.725.0/294.239g KN =+⨯⨯=③.支点段梁的自重(长3.55m )(3) 1.1760 3.5525.0=104.37g KN =⨯⨯④.横隔梁的自重 中横隔梁体积为:()30.16 1.590.920.240.72/20.120.12/20.219072m ⨯⨯-⨯-⨯= 端横隔梁体积为:()30.25 1.840.80.20.6/20.353m ⨯⨯-⨯=故半跨内横隔梁重量()(4)20.21907210.3532519.7786g KN =⨯+⨯⨯=⑤.主梁永久作用集度()156.16594.239104.3719.7786/14.9825.00/g KN m KN m I =+++= (2)第二期恒载①翼缘板中间湿接缝集度()50.40.1625.0 1.6/g KN m =⨯⨯=②现浇部分横隔梁一片中横隔梁(现浇部分)体积:30.16 1.590.20.05088m ⨯⨯= 一片端横隔梁(现浇部分)体积:30.250.2 1.840.092m ⨯⨯= 故()()630.0508820.09225.0/29.960.2809/g KN m =⨯+⨯⨯=③桥面铺装层6cm 沥青混凝土铺装:0.0612.52317.25/KN m ⨯⨯=将桥面铺装重量均分给五片主梁,则()717.25/5 3.45/g KN m ==④防撞栏:两侧防撞栏均分给五片主梁,则()87.52/53/g KN m =⨯=⑤主梁二期永久作用集度II 1.60.2809 3.4538.3309/g KN m =+++=2、永久作用效用:下面进行永久作用效用计算(参照图1-4),设c 为计算截面至左侧支座的距离,并令/a c l =。
桥梁荷载横向分布系数的各种计算方法综述

桥梁荷载横向分布系数的各种计算方法综述姓名:XXX 学号:50XXXXXXX3摘要:公路桥梁荷载横向分布有多种计算模型,其中比较实用的有:1)杠杆原理法;2)偏心压力法、修正偏心压力法;3)铰接板(梁)法;4)刚接板(梁)法等。
这些理论方法有各自的适用范围,应按具体情况选用适当的方法来运用。
关键词:混凝土简支梁桥;荷载横向分布系数;影响线;影响因素1 引言随着国民经济的发展,对交通的需求日益提高,众多的高速公路及城市快速干道相继修建。
公路桥梁上行驶车辆的轴重加重、速度提高,车流密度也相应提高。
使之在设计过程中如何确保桥梁结构在使用寿命期限内的安全性,准确计算各片梁所需承担的最大活载弯矩就显得尤为重要。
特别是对于中小跨多片梁型的桥梁,当跨数较多时,用测试横向分布状态的方法对桥梁运营状态进行评价,具有简洁、实用、可靠等优点,具有较高的推广价值。
所谓荷载横向分布系数(Lateral Distribution Factor of Live Load)是指公路车辆荷载在桥梁横向各主梁间分配的百分数。
普通简支桥梁中它和各主梁间的联结方式(铰接或刚接),有无内横梁及其数目,断面的抗弯刚度和抗扭刚度,以及车辆荷载在桥上的位置等有关。
它是一个复杂的空间结构问题,在桥梁设计中常简化为平面问题而引用荷载横向分布系数。
[1]目前广泛采用的是利用主梁的纵向影响线和它的荷载横向分布影响线相结合的方法,荷载横向分布系数是在荷载横向分布影响线的基础上按荷载的最不利位置布载,并将荷载位置相应的影响线竖标值求和得到的最后数值结果。
对于混凝土简支梁桥,荷载横向分布系数的影响因素主要有桥粱跨度(Z)、主梁间距(S)、桥面板的厚度(t0)、主梁刚度(K0)、横隔梁(板)的数量及位置、车载类型及布栽位置、车辆间距、栏杆及横跨比等。
[2][3][4][9]2 计算方法及其适用范围荷载横向分布理论在桥梁设计中占有重要地位。
目前桥梁荷载横向分布系数常用的计算方法主要有杠杆原理法、偏心压力法(修正偏心压力法)、铰接板(梁)法、刚接梁法和比拟正交异性板法(G-M法)等。
内力组合及内力调整

7 内力组合及内力调整7.1内力组合各种荷载情况下的框架内力求得后,根据最不利又是可能的原则进行内力组合。
当考虑结构塑性内力重分布的有利影响时,应在内力组合之前对竖向荷载作用下的内力进行增幅。
分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合,并比较两种组合的内力,取最不利者。
由于构件控制截面的内力值应取自支座边缘处,为此,进行组合前,应先计算各控制截面处的(支座边缘处的)内力值。
1)、在恒载和活载作用下,跨间max M 可以近似取跨中的M 代替,在重力荷载代表值和水平地震作用下,跨内最大弯矩max M 采用解析法计算:先确定跨内最大弯矩max M 的位置,再计算该位置处的max M 。
当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时,按公式7-1计算。
计算方式见图7-1、7-2括号内数值,字母C 、D 仅代表公式推导,不代表本设计实际节点标号字母。
2max182M M M ql +≈-右左 且满足2max 116M ql = (7-1) 式中:q ——作用在梁上的恒荷载或活荷载的均布线荷载标准值;M 左、M 右——恒载和活载作用下梁左、右端弯矩标准值;l ——梁的计算跨度。
2)、在重力荷载代表值和地震作用组合时,左震时取梁的隔离体受力图,见图7-1所示, 调幅前后剪力值变化,见图7-2。
图7-1 框架梁内力组合图图7-2 调幅前后剪力值变化图中:GC M 、GD M ——重力荷载作用下梁端的弯矩; EC M 、CD M ——水平地震作用下梁端的弯矩C R 、D R ——竖向荷载与地震荷载共同作用下梁端支座反力。
左端梁支座反力:()C 1=2GD GC EC ED ql R M M M M l--++;由0M ddx=,可求得跨间max M 的位置为:1C /X R q = ; 将1X 代入任一截面x 处的弯矩表达式,可得跨间最大弯矩为: 弯矩最大点位置距左端的距离为1X ,1=/E X R q ;()101X ≤≤; 最大组合弯矩值:2max 1/2GE EF M qX M M =-+;当10X <或11X >时,表示最大弯矩发生在支座处,取1=0X 或1=X l ,最大弯矩组合设计值的计算式为:2max C 11/2GE EF M R X qX M M =--+; 右震作用时,上式中的GE M 、EF M 应该反号。
横隔梁内力计算
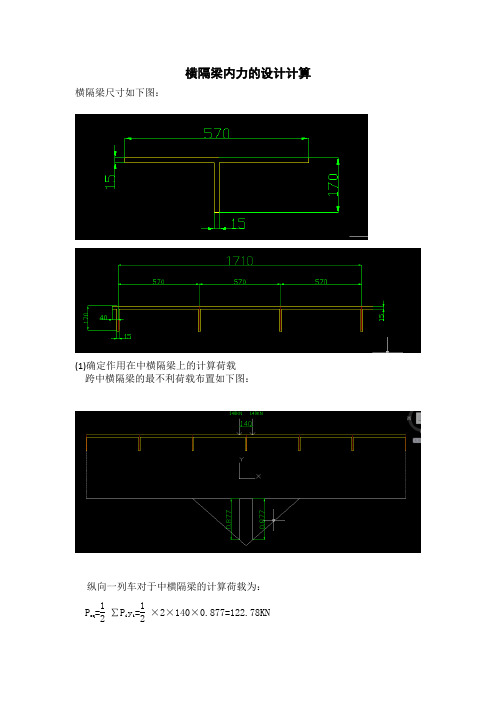
横隔梁内力的设计计算横隔梁尺寸如下图:(1)确定作用在中横隔梁上的计算荷载跨中横隔梁的最不利荷载布置如下图:纵向一列车对于中横隔梁的计算荷载为:Poq =12∑Piyi=12×2×140×0.877=122.78KN车道对于中横隔梁的计算荷载为:Poq =12(Pk+qkΩ)=12(267.1+7.875×5.7)=156KN因此选用Poq=156KN通常横隔梁的弯矩在靠近桥中线的截面处较大,剪力则在靠近桥两侧边缘处的截面较大。
所以以本桥为例,一般可以只求4号梁处和3号与4号梁之间截面的弯矩,以及1号主梁右侧和2号主梁左侧等截面的剪力。
(1)绘制中横隔梁的内力影响线由之前G-M法可得到1号梁的荷载横向分布影响线竖坐标为:η11=0.464 η17=-0.179 η12=0.347 η16=-0.060同理,也可求得2号梁的荷载横向分布影响线竖坐标为:η21=0.354 η27=-0.071 η22=0.282 η26=-0.0013号梁的荷载横向分布影响线竖坐标为:η31=0.238 η37=0.039η32=0.206 η36=0.071①绘制剪力V1右的影响线P=1作用在计算截面以右时:Vr =∑左Ri=0.466P=1作用在计算截面以左时:Vr=∑左Ri-1=-0.534绘成的V1右如下图所示:②绘制弯矩Mr影响线P=1作用在计算截面以左时:Mr =∑左Ribi-eP=1作用在计算截面以右时:Mr =∑左Ribiηr1M=η11×2.5d+η21×1.5d+η31×0.5d-2.5d=-0.685 ηr7M=η17×2.5d+η27×1.5d+η37×0.5d=-0.535ηr2M=η12×2.5d+η22×1.5d+η32×0.5d-1.5d=-0.1065 ηr6M=η16×2.5d+η26×1.5d+η36×0.5d=-0.113ηr3M=η13×2.5d+η23×1.5d+η33×0.5d-0.5d=0.493ηr5M=η15×2.5d+η25×1.5d+η35×0.5d=0.242中横隔梁的Mr影响线如下图:(2)截面内力计算将求得的计算荷载Poq在相应的影响线上按最不利荷载位置加载,并按1+µ=1.3计入冲击影响力,则得弯矩:M3-4=(1+µ)ζPoq∑η=1.3×0.67×156×(0.431+0.741+0.453+0.205)=248.65KN•m剪力: V1右=(1+µ)ζPoq∑η×1.2=1.3×0.67×156×(0.466+0.391+0.337+0.262)×1.2 =237.42KN。
桥梁工程第二篇第6章 主梁内力计算

计算主梁支点或靠近支点截面的剪力时,荷载横向 分布系数在这一区段内是变化的。
当
时 , 为负值,这意味着剪力反而减小了
2 .计算示例 已知:五梁式桥,计算跨径 19.5m 。 荷载:公路 — Ⅱ级,人群: 3.0kN/m2 求:跨中最大弯矩和最大剪力,支点截面最大剪力
解: ( 1 )公路 — Ⅱ级车道荷载标准值计算 ( 2 )冲击系数: 《桥规》:
第六章 简支梁桥的计算
桥梁工程计算的内容
内力计算——桥梁工程、基础工程课解决 截面计算——混凝土结构原理、预应力混凝
土结构课程解决 变形计算
简支梁桥的计算构件
上部结构——主梁、横梁、桥面板 支座 下部结构——桥墩、桥台
计算过程
开始 拟定尺寸 内力计算 截面配筋验算
否
是否通过 是
计算结束
2、作用在横梁上的计算荷载Ps
1)集中荷载 当一个集中荷载P作用在跨中时, Ps=2P/l 2) 均布荷载
全跨布满荷载q时, Ps=4q/
第三节 桥面板计算
行车道板的作用——直接承受车轮荷载、 把荷载传递给主梁
一.行车道板的类型
板支承在纵梁和横梁上,按支承情况和板尺寸,从力学计算 角度分为以下几类:
wa wb Pala3 Pblb3 48EIa 48EIb
如
Ia Ib
Pb Pa
la lb
3
二、车轮荷载在板上分布 轮压一般作为分布荷载处理,以力求精确
车轮着地面积:a2×b2
桥面板荷载压力面:a1×b1 荷载在铺装层内按45°扩散。 沿纵向:a1=a2 +2H 沿横向:b1=b2+2H 桥面板的轮压局部分布荷载
横梁的作用与受力特点
连续梁按弹性理论五跨梁内力系数及弯矩分配法
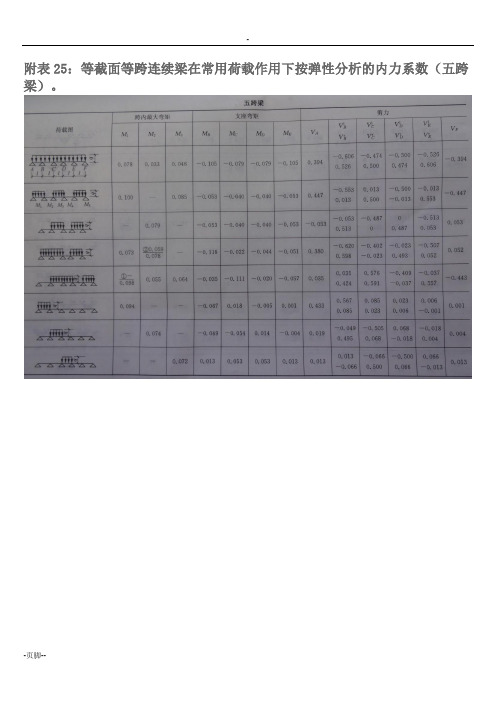
附表25:等截面等跨连续梁在常用荷载作用下按弹性分析的内力系数(五跨梁)。
弯矩分配法(弯矩分配法计算连续梁和刚架及举例)一、名词解释弯矩分配法在数学上属于逐次逼近法,但在力学上属于精确法的范畴,主要适用于连续梁和刚架的计算。
在弯矩分配法中不需要解联立方程,而且是直接得出杆端弯矩。
由于计算简便,弯矩分配法在建筑结构设计计算中应用很广。
(一)线刚度i杆件横截面的抗弯刚度EI 被杆件的长度去除就是杆件的线刚度i :l EI i(a ) 当远端B 为固定支座时,对于A 点处,AB 杆的转动刚度i S AB 4=; (b ) 当远端B 为铰支座时,对于A 点处,AB 杆的转动刚度i S AB 3=;(c ) 当远端B 为滑动支座时,对于A 点处,AB 杆的转动刚度i S AB =;(d ) 当远端B 为自由端时,对于A 点处,AB 杆的转动刚度0=AB S 。
连续梁和刚架的所有中间支座在计算转动刚度时均视为固定支座。
(二)转动刚度S转动刚度表示靠近节点的杆件端部对该节点转动的反抗能力。
杆端的转动刚度以S 表示,等于杆端产生单位转角需要施加的力矩,θ/M S =。
施力端只能发生转角,不能发生线位移。
AB S 中的第一个角标A 是表示A 端,第二个角标B是表示杆的远端是B 端。
AB S 表示AB 杆在A 端的转动刚度。
(三)分配系数μ⎪⎭⎪⎬⎫⋅=⋅=⋅=⋅=⋅=⋅=A AD A AD AD A AC A AC AC A AB A AB AB i S M i S M i S M θθθθθθ34 ⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⋅=⋅=⋅==++=++=++=∑∑∑∑M S S M M S S M M S S M SM S S S M M M M S S S M AD AD AC AC AB AB AD AC AB A ADAC AB A AD A AC A AB θθθθ各杆A 端所承担的弯矩与各杆A 端的转动刚度成正比。
房建横梁的受力计算

房建横梁的受力计算
房建横梁的受力计算通常涉及静力学和结构力学的原理,需要考虑横梁的几何形状、荷载情况以及材料特性等因素。
一般来说,横梁受力计算主要包括以下几个步骤:
一、确定荷载类型:首先需要确定横梁所受的荷载类型,包括自重、活载、雪载、风载等。
这些荷载会对横梁产生不同的作用力和弯矩。
二、荷载分布:根据设计要求和荷载标准,确定各种荷载在横梁上的分布情况,包括集中荷载、均布荷载、集中力矩等。
三、计算受力:根据静力平衡和结构力学的原理,计算横梁在各种荷载作用下的受力情况,包括横梁的受力分布、内力大小、弯矩、剪力等。
四、确定截面尺寸:根据受力计算结果,确定横梁截面的尺寸和形状,以满足受力要求和结构稳定性的要求。
五、验算和优化:对计算得到的横梁受力情况进行验算,确保满足设计要求和结构安全性的要求。
根据需要,可以对横梁的截面尺寸和材料进行优化设计。
六、绘制受力图:根据计算结果,绘制横梁的受力图,显示横梁在不同位置的受力情况,以便后续施工和监测。
需要注意的是,房建横梁的受力计算是一个复杂的工程问题,涉及到多个因素的综合考虑和分析,通常需要由专业的结构工程师进行计算和设计。
