最新5-5横隔梁内力计算汇总
主梁内力计算

主梁的内力计算主梁的内力计算包括恒载内力计算和活载内力计算。
根据上述梁跨结构纵、横截面的布置,计算活载作用下的梁桥荷载横向分布系数,求出各主梁控制截面(取跨中、四分点、变化点截面及支点截面)的恒载和最大活载内力,然后再进行主梁内力组合。
一、恒载内力计算1、恒载集度⑴预制梁自重(第一期恒载)①.跨中截面段主梁自重(四分点截面至跨中截面,长7.25m )(1)0.861625.07.25156.165g KN =⨯⨯=②.马蹄抬高与腹板变宽段梁的自重近似计算(长3.7m ) 主梁端部截面面积为A=1.176m 2()(2) 1.17600.8616 3.725.0/294.239g KN =+⨯⨯=③.支点段梁的自重(长3.55m )(3) 1.1760 3.5525.0=104.37g KN =⨯⨯④.横隔梁的自重 中横隔梁体积为:()30.16 1.590.920.240.72/20.120.12/20.219072m ⨯⨯-⨯-⨯= 端横隔梁体积为:()30.25 1.840.80.20.6/20.353m ⨯⨯-⨯=故半跨内横隔梁重量()(4)20.21907210.3532519.7786g KN =⨯+⨯⨯=⑤.主梁永久作用集度()156.16594.239104.3719.7786/14.9825.00/g KN m KN m I =+++= (2)第二期恒载①翼缘板中间湿接缝集度()50.40.1625.0 1.6/g KN m =⨯⨯=②现浇部分横隔梁一片中横隔梁(现浇部分)体积:30.16 1.590.20.05088m ⨯⨯= 一片端横隔梁(现浇部分)体积:30.250.2 1.840.092m ⨯⨯= 故()()630.0508820.09225.0/29.960.2809/g KN m =⨯+⨯⨯=③桥面铺装层6cm 沥青混凝土铺装:0.0612.52317.25/KN m ⨯⨯=将桥面铺装重量均分给五片主梁,则()717.25/5 3.45/g KN m ==④防撞栏:两侧防撞栏均分给五片主梁,则()87.52/53/g KN m =⨯=⑤主梁二期永久作用集度II 1.60.2809 3.4538.3309/g KN m =+++=2、永久作用效用:下面进行永久作用效用计算(参照图1-4),设c 为计算截面至左侧支座的距离,并令/a c l =。
(完整版)梁的内力计算

(2) 荷载简化一一将荷载简化为集中力、线分布力或力偶等;
(3) 支座简化——主要简化为以下三种典型支座:
(a)活动铰支座(或辊轴支座),其构造图及支座简图如图4—3(a)所示。这
种支座只限制梁在沿垂直于支承平面方向的位移, 其支座反力过铰心且垂直于支
(1)求支座反力
正,如图4-7(c)o
由
Y0
Q2
qa
0
得
Q2qa
由
M20
m2
a小
qa 0
2
得
m2
2
qa
2
(4)求3-3截面(D截面左侧边一点)内力
取右端为脱离体,3-3截面无限靠近D点,线分布力q的分布长度趋于0,则3-3
截面上Q=0,M=0o
2.2截面法直接由外力求截面内力的法则
上例说明了运用截面法求任一截面内力的方法。因脱离体的平衡条件丫0的 含义为:脱离体上所有外力和内力在丫轴方向投影的代数和为零。其中只有剪力Q为未知量,移到方程式右边即得直接由外力求任一截面剪力的法则:
对称平面内,称为弯矩
则得
由Mc0,有YaxM0
则得MYaX
注意此处是对截面形心C取矩,因剪力Q通过截面形心C点,故在力矩方程中为 零。同样可取右脱离体,由平衡方程求出梁截面m-n上的内力Q和M,其结果与 左脱离体求得的Q M大小相等,方向(或转向)相反,互为作用力与反作用力 关系。
为使梁同一截面内力符号一致,必须联系到变形状态规定它们的正负号。 若从梁m-n处取一微段梁dx,由于剪力Q作用会使微段发生下错动的剪切变形。 我们规 定:使微段梁发生左端向上而右端向下相对错动的剪力Q为正(如图4—6(a)),反之为负(如图4—6(b));使微段梁弯曲为向下凸时的弯矩M为正,反之为负
横梁内力计算

1号梁的横向影响线竖标值:11 0.60,15 0.20 2号梁的横向影响线竖标值:21 0.40,25 0 3号梁的横向影响线竖标值:31 0.20,35 0.20
(1)绘制弯矩影响线 M23 :
P=1
作用在1号梁轴上:
M ( 2 3 )1
11
1.5d
21
0.5d
1 1.5d
0.64
✓荷载 P=1 位于截面 r 的右侧
左
Mr R1b1 R2b2 Ribi
左
Vr R1 R2 Ri
R1
R2 M 23R3
R4
R5
b2 b1
图 横隔梁计算图示
b2 :支承反力Ri到计算截面的距离
可以直接利用已经求得的 Ri 的横向影响线绘制横梁的内力影响线。
通常横隔梁的弯矩在靠近桥中线的截面处较大,剪力在靠近桥两侧 边缘处的截面较大。
P=1 作用在计算截面左侧时:V1右 R1,即1Vi右 1i 1
180
180
130
180
图 中横隔梁的内力影响线
求解:3. 计算截面内力
M23 (1 ) P0q
1.254 1144.46 (0.92 0.29) 219.19kN m
V1右 (1 ) P0q
1.254 1144.46 (0.575 0.35 0.188 0.038) 194.74kN
M 31
11 2d
21 d
1 2d
M 32
12
2d
22
d
1 d
M 35
15
2d
25
d
M 36
16
2d
26 d
一、 横隔梁的内力影响线
3-4截面的正弯矩:
《桥梁工程》简支梁桥的计算、横隔梁内力计算

横隔梁的内力影响线
1
②梁处横隔梁截面的 剪力影响线
右 1 21 11 21
Q
①
右 Q 16 26 26
②
③
④
⑤
⑥
1
ηQ21
ηQ26
5.5横隔梁内力计算
Computing the internal force on transverse beam
横隔梁的内力计算
横隔梁的内力
P=1
当荷载P作用于r截面左边时, 截面上的弯矩和剪力:
M r R1 b1 R2 b2 1 e Ri bi e
左
P=1
e
r
Qr R1 R2 1 Ri 1
左
R1
b1
R2
b2
R3
R4
R5
5.5横隔梁内力计算
Computing the internal force on transverse beam 2.偏压法计算横隔梁内力
横隔梁的内力
e
a
P=1
P=1
e
1
a
r截面弯矩影响线
r截面剪力影响线
5.5横隔梁内力计算
Computing the internal force on transverse beam 2.偏压法计算横隔梁内力
Computing the internal force based on the stiffness transverse beam
计算模型
Model 横隔梁相当于弹性支撑上的连续梁 continuous beam on elastic support
P
Ri=?
(完整版)梁的内力计算
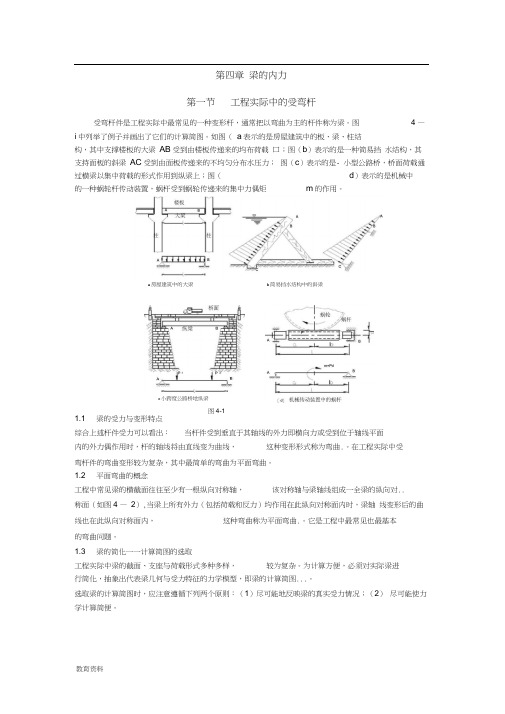
第四章梁的内力第一节工程实际中的受弯杆受弯杆件是工程实际中最常见的一种变形杆,通常把以弯曲为主的杆件称为梁。
图 4 —i中列举了例子并画出了它们的计算简图。
如图(a表示的是房屋建筑中的板、梁、柱结构,其中支撑楼板的大梁AB受到由楼板传递来的均布荷载口;图(b)表示的是一种简易挡水结构,其支持面板的斜梁AC受到由面板传递来的不均匀分布水压力;图(c)表示的是- 小型公路桥,桥面荷载通过横梁以集中荷载的形式作用到纵梁上;图(d)表示的是机械中的一种蜗轮杆传动装置,蜗杆受到蜗轮传递来的集中力偶矩m的作用。
1.1 梁的受力与变形特点综合上述杆件受力可以看出:当杆件受到垂直于其轴线的外力即横向力或受到位于轴线平面内的外力偶作用时,杆的轴线将由直线变为曲线,这种变形形式称为弯曲.。
在工程实际中受弯杆件的弯曲变形较为复杂,其中最简单的弯曲为平面弯曲。
1.2 平面弯曲的概念工程中常见梁的横截面往往至少有一根纵向对称轴,该对称轴与梁轴线组成一全梁的纵向对..称面(如图4 —2),当梁上所有外力(包括荷载和反力)均作用在此纵向对称面内时,梁轴线变形后的曲线也在此纵向对称面内,这种弯曲称为平面弯曲.。
它是工程中最常见也最基本的弯曲问题。
1.3 梁的简化一一计算简图的选取工程实际中梁的截面、支座与荷载形式多种多样,较为复杂。
为计算方便,必须对实际梁进行简化,抽象出代表梁几何与受力特征的力学模型,即梁的计算简图...。
选取梁的计算简图时,应注意遵循下列两个原则:(1)尽可能地反映梁的真实受力情况;(2)尽可能使力学计算简便。
a房屋建筑中的大梁c小跨度公路桥地纵梁图4-1b简易挡水结构中的斜梁图4-2 梁的平面弯曲一般从梁本身、支座及荷载等三方面进行简化:(1) 梁本身简化一一以轴线代替梁,梁的长度称为跨度; (2) 荷载简化一一将荷载简化为集中力、线分布力或力偶等; (3) 支座简化——主要简化为以下三种典型支座:(a ) 活动铰支座(或辊轴支座),其构造图及支座简图如图4— 3 (a )所示。
(完整版)梁的内力计算

第四章 梁的内力 第一节 工程实际中的受弯杆受弯杆件是工程实际中最常见的一种变形杆,通常把以弯曲为主的杆件称为梁。
图4-1中列举了例子并画出了它们的计算简图。
如图(a )表示的是房屋建筑中的板、梁、柱结构,其中支撑楼板的大梁AB 受到由楼板传递来的均布荷载q ;图(b )表示的是一种简易挡水结构,其支持面板的斜梁AC 受到由面板传递来的不均匀分布水压力;图(c )表示的是一小型公路桥,桥面荷载通过横梁以集中荷载的形式作用到纵梁上;图(d )表示的是机械中的一种蜗轮杆传动装置,蜗杆受到蜗轮传递来的集中力偶矩m 的作用。
a房屋建筑中的大梁b简易挡水结构中的斜梁c 小跨度公路桥地纵梁d 机械传动装置中的蜗杆图4-1 工程实际中的受弯杆1.1 梁的受力与变形特点 综合上述杆件受力可以看出:当杆件受到垂直于其轴线的外力即横向力或受到位于轴线平面内的外力偶作用时,杆的轴线将由直线变为曲线,这种变形形式称为弯曲..。
在工程实际中受弯杆件的弯曲变形较为复杂,其中最简单的弯曲为平面弯曲。
1.2 平面弯曲的概念工程中常见梁的横截面往往至少有一根纵向对称轴,该对称轴与梁轴线组成一全梁的纵向对...称面..(如图4-2),当梁上所有外力(包括荷载和反力)均作用在此纵向对称面内时,梁轴线变形后的曲线也在此纵向对称面内,这种弯曲称为平面弯曲....。
它是工程中最常见也最基本的弯曲问题。
1.3 梁的简化——计算简图的选取工程实际中梁的截面、支座与荷载形式多种多样,较为复杂。
为计算方便,必须对实际梁进行简化,抽象出代表梁几何与受力特征的力学模型,即梁的计算简图....。
选取梁的计算简图时,应注意遵循下列两个原则:(1)尽可能地反映梁的真实受力情况;(2)尽可能使力学计算简便。
梁轴线图4-2 梁的平面弯曲一般从梁本身、支座及荷载等三方面进行简化:(1)梁本身简化——以轴线代替梁,梁的长度称为跨度;(2)荷载简化——将荷载简化为集中力、线分布力或力偶等;(3)支座简化——主要简化为以下三种典型支座:(a)活动铰支座(或辊轴支座),其构造图及支座简图如图4-3(a)所示。
桥梁工程简支梁桥的计算横隔梁内力计算 课件

③梁处横隔梁截面的
弯矩影响线
a
? ? ? M ? 31
11 ?2d ?
21 ?d ? 2d
? ? ? M ? 36
16 ?2d ?
26 ?d
① ②③④ ⑤⑥
2d
ηM31
ηM36
5.5横隔梁内力计算
Computing the internal force on transverse beam 2.偏压法计算横隔梁内力
5.5横隔梁内力计算
Computing the internal force on transverse beam 2.偏压法计算横隔梁内力
Computing the internal force based on the stiffness transverse beam
? 横隔梁的内力影响线
a
BRIDGE ENGRG PART II
Part 2 RC & PC beam bridge
第二篇 钢筋混凝土和预应力混凝土梁式桥
第五章
Chapter 5
简支梁桥的计算 Analysis of simple supported
beam bridge
5.5横隔梁内力计算
Computing the internal force on transverse beam
2 ?11.5d ?
3 ?01.5d ? 2.5d
? ? ? ? M ? (3?4 )6
16 ?2.5d ?
26 ?1.5d ?
36 ?0.5d
5.5横隔梁内力计算
Computing the internal force on transverse beam 2.偏压法计算横隔梁内力
2-5-3横隔梁内力计算.

在横隔梁计算截面的内力影响线上按最不利布载,求出该 截面上的荷载效应。
Sq 1 Poq Sr Por
例题
【例题】 计算【例题2-4-5】中所示装配式钢砼简支梁桥跨中横 隔梁在②、③号主梁之间r–r截面上的弯矩和靠近①号边主梁处 截面ro–ro上的剪力(公路-Ⅱ级)。
为计算跨径;对于悬臂体系,悬臂端点的挠度不应超过l’/300 ,l’ 为
悬臂长度。
挠度验算
一、挠度验算 (一)钢筋混凝土构件
挠度验算
挠度验算
挠度验算
(二)预应力混凝土构件
挠度验算
钢筋混凝土、预应力混凝土简支梁的长期挠度:
fc c f
c 长期挠度增长系数 f 按短期效应组合计算的 短期挠度
3)内力组合 分别按承载能力极限状态和正常使用极限状态(不计冲
击)进行组合。 【注】横隔梁自重集度较小,且全跨满布,而内力影响线有正
有负,所以自重内力甚小,计算时可忽略。
5-6 挠度、预拱度的计算
§5-6 挠度、预拱度的计算
桥梁挠度产生的原因:永久作用挠度和可变荷载挠度。
永久作用挠度:恒久存在的,其产生挠度与持续时间相 关,可分为短期挠度和长期挠度。可以通过施工时预设 的反向挠度(又称预拱度)来加以抵消,使竣工后的桥 梁达到理想的线型。
可变荷载挠度:临时出现的,但是随着可变荷载的移动, 挠度大小逐渐变化,在最不利的荷载位置下,挠度达到最 大值,一旦汽车驶离桥梁,挠度就告消失。因此在桥梁设 计中需要验算可变荷载挠度来体现结构的刚度特性。
挠度、预拱度的计算
《桥规》规定:对于钢筋混凝土及预应力混凝土梁式桥,用可变荷 载频遇值计算的上部结构长期的跨中最大竖向挠度,不应超过l/600,l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《桥规》规定: 受弯构件预拱度: (1)钢筋混凝土受弯构件
当由荷载短期效应组合并考虑荷载长期效应影响产 生的长期挠度不超过跨径的1/600时,可不设预拱度;
当不符合上述规定时应设预拱度,且其值应按结构 自重和1/2可变荷载频遇值计算的长期挠度值之和采用。 (2)预应力混凝土受弯构件
当预加应力产生的长期反拱值大于按荷载短期效应 组合计算的长期挠度时,可不设预拱度;
四、 计算举例(用偏压法计算中横隔梁)
已知:荷载:公路—Ⅱ级,人群:3.0kN/m2 求:M2-3,Qi右
步骤: 1、确定计算荷载 2、求各主梁横向分布影响线 (偏心压力法) 3、绘制中横隔梁内力影响线 (1)荷载P=1,在r 的左侧:
(2)荷载P=1,在r 的右侧:
说明: 弯矩:三个竖标值及影响线折点位置; 剪力:落差为1 4、不利荷载布置,求截面内力(组合)
《桥规》6.5.1 钢筋混凝土和预应力混凝土受弯构 件,在正常使用极限状态下的挠度,可根据给定 的构件刚度用结构力学的方法计算。
6.5.2 受弯构件的刚度可按下式计算: 1.钢筋混凝土构件
Ms——按作用(或荷载)短期效应组合计算的弯矩
2.预应力混凝土构件
(1)全预应力混凝土和A类预应力混凝土构件
(2)允许开裂的B类预应力混凝土构件
பைடு நூலகம்
说明:
(1)受弯构件在使用阶段的挠度应考虑荷载长 期效应的影响(长期挠度),即按荷载短期效应 计算的挠度值,乘以挠度长期增长系数。 (2)预应力混凝土受弯构件由预加力引起的反 拱值,可用结构力学方法按刚度进行计算,并乘 以长期增长系数。 (3)预应力混凝土受弯构件在施工阶段的挠度 可按构件自重和预加力产生的初始弹性变形乘以
二、 作用在横隔梁上的计算荷载
按杠杆原理法求得影响线====〉加载求截面内力
汽车: (车辆荷载)
人群:
三、 横隔梁内力计算
说明: (1)汽车荷载计冲击和车道折减。 (2)横隔梁和普通的连续梁一样,在其跨中位 置承受最大正弯矩,支点截面存在负弯矩和较大 的剪力,因此,设计时应计算。 (3)横梁的自重与活载相比较小,一般可忽略。
反之应设预拱度,其值应按该项荷载的挠度值与预 加应力长期反拱值之差采用。
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
第六节 挠度、预拱度计算
1、为什么要进行梁的变形计算?
2、桥梁挠度按产生的原因分为:
(1)永久作用产生的挠度(短期挠度+长期挠 度):恒久存在,与持续时间有关,不表征刚 度特性,设预拱度抵消; (2)可变作用产生的挠度:临时出现,体现刚 度特性,引起梁反复变形,设计中需验算;
《桥规》规定:
对于钢筋混凝土及预应力混凝土受弯构件, 在使用阶段的长期挠度值,在消除结构自重产 生的长期挠度后梁式桥主梁的最大挠度处不应 超过计算跨径的1/600,梁式桥主梁的悬臂端不 应超过悬臂长度的1/300。此挠度为不计冲击力 时的值。
5-5横隔梁内力计算
计算原理:
r
在跨中单位荷载P=1
作用下,各主梁反作
用于横隔梁上的力为
Ri,由平衡条件得横 隔梁任意截面r 的内
力为:
1、荷载P=1,在r 的左侧:
2、荷载P=1,在r 的右侧:
说明:
(1)若r 一定,则bi为已知,Ri随e而变,故 可由Ri的影响线绘制横隔梁内力影响线 (2)通常,可只求典型截面的M、Q,Mmax 靠近桥中线,Qmax桥两侧边缘处 (3)Ri影响线为直线,M、Q影响线为折线 (4)亦可利用修正的偏心压力法,仅Ri影响 线不同,计算原理相同
