41 截面的几何参数
截面的几何性质截面的几何性质

I y1 z1 =
Iz − I y
sin 2α + I yz cos 2α
• 图形对通过一点的任一对相互垂直的轴的惯
性矩之和为一常数。
I y1 + I z 1 = I z + I y
30
截面的几何性质 • 平面图形的静矩和形心 • 平面图形的惯性矩、惯性积和惯性半径 • 惯性矩和惯性积的平行移轴公式 • 惯性矩和惯性积的转轴公式 • 主惯性轴和主惯性矩
组合图形的静矩和形心位置 • 组合图形 — 由几个简单图形(如矩形、圆形
或三角形等规则图形)组成的图形。
• 组合图形的静矩 — 整个图形对某一轴的静矩
等于各组成部分对该轴静矩的代数和。
S z = ∑ Ai yC i S y = ∑ Ai zC i
Ai − 第i 个简单图形的面积;
( yC i , zC i ) − 第i 个简单图形的形心坐标。
I y = ∫A z 2dA
I P = ∫ A r 2 dA
• 惯性矩及极惯性矩与截面面积有关; • 惯性矩及极惯性矩与坐标设置有关; • 惯性矩及极惯性矩恒为正值; • 惯性矩及极惯性矩的单位为m4或mm4。
11
平面图形的惯性半径 • 定义
iz = Iz A iy = Iy A
分别为图形对于z 轴和y 轴的惯性半径。
• 组合图形形心位置的计算式
yC =
∑ Ai yC i ∑ Ai
zC =
8
∑ Ai zC i ∑ Ai
截面的几何性质 • 平面图形的静矩和形心 • 平面图形的惯性矩、惯性积和惯性半径 • 惯性矩和惯性积的平行移轴公式 • 惯性矩和惯性积的转轴公式 惯性矩 • 定义
yzyz2012123232组合图形的惯性矩1121主惯性轴和主惯性矩截面的几何性质22ababs惯性矩和惯性积的平行移轴公式1223ababs惯性矩和惯性积的平行移轴公式24在截面对所有平行轴的惯性矩中以对通过其形心的轴的惯性矩为最小
截面的几何特性---扩展
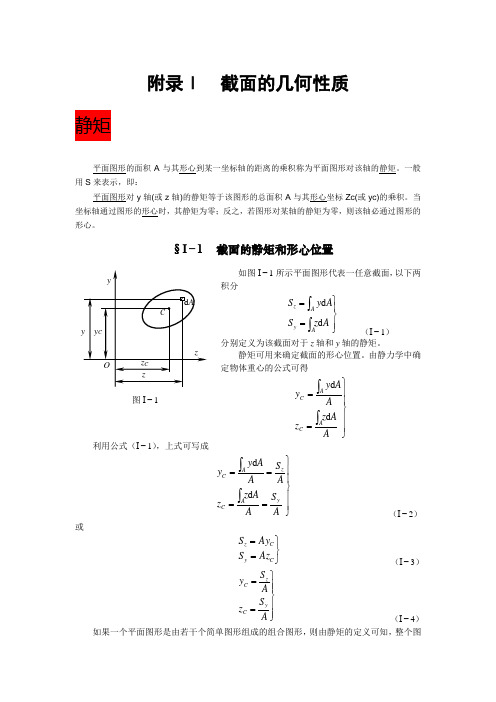
附录Ⅰ 截面的几何性质§I −1 截面的静矩和形心位置如图I −1所示平面图形代表一任意截面,以下两积分⎪⎭⎪⎬⎫==⎰⎰A z S A y S A y Az d d (I −1) 分别定义为该截面对于z 轴和y 轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得⎪⎪⎭⎪⎪⎬⎫==⎰⎰A A z z A A y y AC ACd d利用公式(I −1),上式可写成⎪⎪⎭⎪⎪⎬⎫====⎰⎰A S A A z z A S A Ay y y AC z AC d d (I −2) 或⎭⎬⎫==C y C z Az S Ay S (I −3)⎪⎪⎭⎪⎪⎬⎫==A S z A S y y C z C (I −4)如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图图I −1形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。
即:⎪⎪⎭⎪⎪⎬⎫==∑∑==ni ci i y ni ci i z z A S y A S 11(I −5)式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标的计算公式为⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫==∑∑∑∑====n i i ni ci i c ni i ni ci i c A z A z A y A y 1111 (I −6) 例题I −1 图a 所示为对称T 型截面,求该截面的形心位置。
解:建立直角坐标系zOy ,其中y 为截面的对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则A Ⅰ=0.072m 2,A Ⅱ=0.08m 2 y Ⅰ=0.46m ,y Ⅱ=0.2mm323.008.0072.02.008.046.0072.0III IIII I I 11=+⨯+⨯=++==∑∑==A A y A y A AyA y ni ini cii c§I −2 惯性矩、惯性积和极惯性矩如图I −2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
附录 截面的几何性质(材料力学)

b b( y ) ( h y ) h
b(y )
S x A y d A 0
b bh2 (h y ) y d y h 6
h
dy
材 料 力 学 Ⅰ 电 子 教 案
例 试确定图示截面心 C 的位置。 解:将截面分为 1,2 两个矩形。 取 x 轴和 y 轴分别与截面 的底边和左边缘重合 y
10
1
x1
C( y, x )
y1
o
2
y2
10
x2
80
x
材 料 力 学 Ⅰ 电 子 教 案
思考: 求下图所示截面的形心位置
50
10 A1
z
60
A2
10
y
12
yc1 A1 yc 2 A2 yc A1 A2
材 料 力 学 Ⅰ 电 子 教 案
例 半径为r的半圆:求半圆的形心。 解 在距 z 轴任意高度 y 处取狭长条 作为微面积,即
分别称为截面图形对于z轴和y 轴的惯性矩。 惯性矩的数值恒为正,常用单位为m4 。
14
dA
y x
材 料 力 学 Ⅰ 电 子 教 案
二、极惯性矩
y
I p 2 dA
A
称为截面图形对O点的极惯性矩。
x
dA y x
2 x2 y 2
I p 2dA x 2 y 2 dA x 2dA y 2dA I y I x
A
y
z y A o
A
A
y
dA z
y
ydA S A z A A
求静矩的另一公式:
Sy x A
5
Sx y A
第4章 截面的几何参数[16页]
![第4章 截面的几何参数[16页]](https://img.taocdn.com/s3/m/90c4371bad02de80d4d840df.png)
第4章 截面的几何参数 4.2.2 极惯性矩 微元面积对坐标原点的极惯性矩
截面对坐标原点的极惯性矩
第4章 截面的几何参数 4.2 惯性矩、极惯性矩、惯性积
惯性矩也可以用惯性半径表示
第4章 截面的几何参数 4.2.3惯性积 微元面积对坐标原点的惯性积
截面对坐标轴的惯性积
第4章 截面的几何参数 4.2.4组合截面的惯性矩
截面对于主惯性轴的惯性矩称为主惯性矩
截面对于形心主惯性轴的惯性矩就称 形心主惯性矩 4.4.3形心主惯性平面
截面的形心主惯性轴和杆件轴线所确定 的平面称为杆件的) 4.9
形心主惯性轴的确定
(1)平面图形有一根对称轴,此轴是形心主惯性轴,而 另一根形心主惯性轴通过形心,并与此轴垂直。 (2)如果平面图形有两根对称轴,则此两轴都为形心 主惯性轴 。 (3)如果平面图形有三根或更多根的对称轴
第4章 截面的几何参数
4.4.2形心主惯性矩
惯性积等于零的一对坐标轴就称为该截面的主惯性轴
第4章 截面的几何参数 4.1.2面积矩 组合截面的面积矩为
截面的形心坐标也可表 示为:
面积矩性质:(1) 轴不同,面积矩不同; (2)面积矩可正可负,也可为零
第4章 截面的几何参数 4.2 惯性矩、极惯性矩、惯性积 4.2.1惯性矩 微元面积对z轴和y轴的惯性矩
截面对z轴和y轴的惯性矩
惯性矩性质:正值 惯性矩单位:量纲为长度的四次方
根据积分原理,组合截面的惯性矩可以用代数和求得
第4章 截面的几何参数
4. 3 平行移轴公式 C点是形心,yc轴和zc轴是通过形心的坐标轴
第4章 截面的几何参数
4.4 形心主惯性轴、形心主惯性矩
惯性积等于零的一对坐标轴就称为该截面的主惯性轴
常用型钢截面尺寸
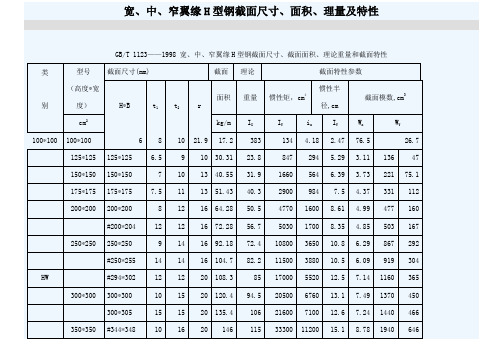
宽、中、窄翼缘H型钢截面尺寸、面积、理量及特性GB/T 1123——1998 宽、中、窄翼缘H型钢截面尺寸、截面面积、理论重量和截面特性类别型号(高度*宽度)截面尺寸(mm) 截面理论截面特性参数H*B t1t2r面积重量惯性矩,cm4惯性半径,cm截面模数,cm3cm2kg/m IXIYixIYWxWY100*100 100*100 6 8 10 21.9 17.2 383 134 4.18 2.47 76.5 26.7 125*125 125*125 6.5 9 10 30.31 23.8 847 294 5.29 3.11 136 47 150*150 150*150 7 10 13 40.55 31.9 1660 564 6.39 3.73 221 75.1 175*175 175*175 7.5 11 13 51.43 40.3 2900 984 7.5 4.37 331 112 200*200 200*200 8 12 16 64.28 50.5 4770 1600 8.61 4.99 477 160 #200*204 12 12 16 72.28 56.7 5030 1700 8.35 4.85 503 167 250*250 250*250 9 14 16 92.18 72.4 10800 3650 10.8 6.29 867 292 #250*255 14 14 16 104.7 82.2 11500 3880 10.5 6.09 919 304 HW #294*302 12 12 20 108.3 85 17000 5520 12.5 7.14 1160 365 300*300 300*300 10 15 20 120.4 94.5 20500 6760 13.1 7.49 1370 450 300*305 15 15 20 135.4 106 21600 7100 12.6 7.24 1440 466 350*350 #344*348 10 16 20 146 115 33300 11200 15.1 8.78 1940 646350*350 12 19 20 173.9 137 40300 13600 15.2 8.84 2300 776#388*402 15 15 24 179.2 141 49200 16300 16.6 9.52 2540 809#394*398 11 18 24 187.6 147 56400 18900 17.3 10 2860 951400*400 13 21 24 219.5 172 66900 22400 17.5 10.1 3340 1120 400*400 #400*408 21 21 24 251.5 197 71100 23800 16.8 9.73 3560 1170 #414*405 18 28 24 296.2 233 93000 31000 17.7 10.2 4490 1530#428*407 20 35 24 361.4 284 119000 39400 18.2 10.4 5580 1930*458*417 30 50 24 529.3 415 187000 60500 18.8 10.7 8180 2900*498*432 45 70 24 770.8 605 298000 94400 19.7 11.1 12000 4370 150*100 148*100 6 9 13 27.25 21.4 1040 151 6.17 2.35 140 30.2 200*150 194*150 6 9 16 39.76 31.2 2740 508 8.3 3.57 283 67.7 250*275 244*175 7 11 16 5.24 44.1 6120 985 10.4 4.18 502 113 300*200 294*200 8 12 20 73.03 57.3 11400 1600 12.5 4.69 779 160 350*250 340*250 9 14 20 101.5 79.7 21700 3650 14.6 6 1280 292 HM 400*300 390*300 10 16 24 136.7 107 38900 7210 16.9 7.26 2000 481 450*300 440*300 11 18 24 157.4 124 56100 8110 18.9 7.18 2550 541 500*300 482*300 11 15 28 146.4 115 60800 6770 20.4 6.8 2520 451 488*300 11 18 28 164.4 129 71400 8120 20.8 7.03 2930 541582*300 12 17 28 174.5 137 103000 7670 24.3 6.63 3530 511 600*300 588*300 12 20 28 192.5 151 118000 9020 24.8 6.85 4020 601#594*302 14 23 28 222.4 175 137000 10600 24.9 6.9 4620 701 100*50 100*50 5 7 10 12.16 9.54 192 14.9 3.98 1.11 38.5 5.96 125*60 125*60 6 8 10 17.01 13.3 417 29.3 4.95 1.31 66.8 9.75 150*75 150*75 5 7 10 18.16 14.3 679 49.6 6.12 1.65 90.6 13.2 175*90 175*90 5 8 10 23.21 18.2 1220 97.6 7.26 2.05 140 21.7 200*100 198*99 4.5 7 13 23.59 18.5 1610 114 8.27 2.2 163 23 200*100 5.5 8 13 27.57 21.7 1880 134 8.25 2.21 188 26.8 250*125 248*124 5 8 13 32.89 25.8 3560 255 10.4 2.78 287 41.1 250*125 6 9 13 37.87 29.7 4080 294 10.4 2.79 326 47 300*150 298*149 5.5 8 16 41.55 32.6 6460 443 12.4 3.26 433 59.4 300*150 6.5 9 16 47.53 37.3 7350 508 12.4 3.27 490 67.7 350*175 346*174 6 9 16 53.19 41.8 11200 792 14.5 3.86 649 91 350*175 7 11 16 63.66 50 13700 985 14.7 3.93 782 113 #400*150 #400*150 8 13 16 71.12 55.8 18800 734 16.3 3.21 942 97.9 400*200 396*199 7 11 16 72.16 56.7 20000 1450 16.7 4.48 1010 145 400*200 8 13 16 84.12 66 23700 1740 16.8 4.54 1190 174 #450*150 #450*150 9 14 20 83.41 65.5 27100 793 18 3.08 1200 106 HN 450*200 446*199 8 12 20 84.95 66.7 29000 1580 18.5 4.31 1300 159 450*200 9 14 20 97.41 76.5 33700 1870 18.6 4.38 1500 187 #500*150 #500*150 10 16 20 98.23 77.1 38500 907 19.8 3.04 1540 121496*199 9 14 20 101.3 79.5 41900 1840 20.3 4.27 1690 185 500*200 500*200 10 16 20 114.2 89.6 47800 2140 20.5 4.33 1910 214 #506*201 11 19 20 131.3 103 56500 2580 20.8 4.43 2230 257596*199 10 15 24 121.2 95.1 69300 1980 23.9 4.04 2330 199 600*200 600*200 11 17 24 135.2 106 78200 2280 24.1 4.11 2610 228 #606*201 12 20 24 153.3 120 91000 2720 24.4 4.21 3000 271 700*300 #692*300 13 20 28 211.5 166 172000 9020 28.6 6.53 4980 602 700*300 13 24 28 235.5 185 201000 10800 29.3 6.78 5760 722 800*300 792*300 14 22 28 243.4 191 254000 9930 32.3 6.39 6400 662 800*300 14 26 28 267.4 210 292000 11700 33 6.62 7290 782*890*299 15 23 28 270.9 213 345000 10300 35.7 6.16 7760 688 *900*300 *900*300 16 28 28 309.8 243 411000 12600 36.4 6.39 9140 843 *912*302 18 34 28 364 286 498000 15700 37 6.56 10900 1040 注:1、“#”表示的规格为非常用规格。
第5章 截面的几何参数

式中 yCi、zCi及Ai分别为各简单图形的形心 坐标和面积; 坐标和面积 n为组成组合图形的简单图形的个数。 为组成组合图形的简单图形的个数。 为组成组合图形的简单图形的个数
∑ Ai z Ci z C = i =1n ∑ Ai i =1 n ∑ Ai yCi i =1 yC = n ∑ Ai i =1
如果坐标轴z或 中有一 如果坐标轴 或y中有一 根是图形的对称轴, 根是图形的对称轴,则该图 形对这一对坐标轴的惯性积 一定等于零。 一定等于零。
I zy = ∫ zydA = 0
A
5.2.4 惯性半径
常将图形的惯性矩表示为图形面积A与某一长度平方 常将图形的惯性矩表示为图形面积 与某一长度平方 的乘积, 的乘积,即
将平面图形看作由矩形Ⅰ 解 将平面图形看作由矩形Ⅰ和Ⅱ组成 2 2 × 矩形Ⅰ 矩形Ⅰ A1=10×120mm =1200mm
y C1 =
C1
y1
10
120 mm = 60mm 2
10 mm = 5mm 2
120
z C1 =
矩形Ⅱ 矩形Ⅱ
10 C2
A2=70×10mm2=700mm2 ×
yC 2 =
5.1
重心和形心
5.1.1 重心的概念 地球上的任何物体都受到地球引力的作用, 地球上的任何物体都受到地球引力的作用, 这个力称为物体的重力。 这个力称为物体的重力。 可将物体看作是由许多微小部分组成, 可将物体看作是由许多微小部分组成,每一 微小部分都受到地球引力的作用, 微小部分都受到地球引力的作用,这些引力汇交 于地球中心。但是, 于地球中心。但是,由于一般物体的尺寸远比地 球的半径小得多,因此, 球的半径小得多,因此,这些引力近似地看成是 空间平行力系。 空间平行力系。 这些平行力系的合力就是物体的重力 合力就是物体的重力。 这些平行力系的合力就是物体的重力。 由实验可知,不论物体在空间的方位如何, 由实验可知,不论物体在空间的方位如何, 物体重力的作用线始终是通过一个确定的点, 物体重力的作用线始终是通过一个确定的点,这 个点就是物体重力的作用点,称为物体的重心 重心。 个点就是物体重力的作用点,称为物体的重心。
截面的几何参数解析

n
S z Ai yci i 1
zc
yc
Ai zci
A (正负面积法公式) Ai yci
A
四. 确定匀质物体重心(形心)的几种方法
1.对称性法 匀质物体的重心一定在其对称面、对称轴或对称中心上
c
c
c
c
c
c
c
c c
2.组合法 (1)分割法 适用于形状较复杂的物体
10cm 20cm 10cm
2、掌握面积矩和形心、惯性矩的计算,惯性矩平行移轴 公式的计算,组合图形惯性矩的计算,有对称轴截面图 形的形心主惯性矩的计算。
重点:面积矩和形心,惯性矩,形心主惯性矩。
难点:惯性矩的移轴公式 学时安排:2学时(44页后的讨论题由学生课后完成)
§ 4.1 截面的形心位置和面积矩
一、静矩的概念
z Iyz 可为正,可为负,亦可为0
如果 z 或 y 是对称轴,则Iyz =0
y
z
dA
y
O
Iy
z2dA
A
>0
Iz
y2dA
A
>0
z
Iyz
yzdA
A
> 0 或 < 0或=0
I
2dA
A
>0
四、惯性半径
y
z
dA
y
O
iy
Iy A
——图形对 y 轴的惯性半径
iz
Iz A
z ——图形对 z 轴的惯性半径
解: 由对称性可知
x 0
A R
B θ dθ
y
αα
dL=Rdθ y=Rcosθ
o
x
例:已知圆弧AB半径R,圆 心角2α。求:AB圆弧段的 重心。
北师大版高中数学选修4-1几何证明选讲截面欣赏

AB与l确定一平面O1ABO2,它与平面α的交线为OP,与⊙O1所在的 平面的交线为O1A, 因此O1A∥OP。 所以O1APO为平行四边形, 所以OP=O1A=r(常数)。 故点P的轨迹为一个圆,即平面α与柱面的交线为一个圆。
2.将两个球放入圆柱内,使它们位于平面γ的两侧,且每一个球 既与圆柱相切,又与平面γ相切,则平面γ与圆柱面的截线是椭 圆。根据上面的结论,你能猜想这个椭圆的两个焦点的位置是 切点F1,F2,长轴为G1G2,由前面可知G1G2=BC=AD,短轴 为球的直径.为了说明假设的正确性,可以对其进行证明,即 截口上任意一点P,PF1+PF2=定值。 若P与G1或G2重合时有PF1+PF2=G1F1+G1F2=AD=G2F1+ G2F2=定值。
A.2 3 3B.4 3 3源自48C.3
D.3
3.半径分别为 1 和 2 两个球的球心相距 12,则这两个球的外公切 线的长为____1_4_3__,内公切线的长为__3__1_5___。
当点P不在端点时,连接PF1、PF2,则PF1、PF2分别是两个球面 的切线,切点为F1、F2.过P作母线,与两球面分别相交于K1、K2, 则PK1、PK2分别是两球面的切线,切点为K1、K2。根据切线长定 理的空间推广,知PF1=PK1,PF2=PK2,所以PF1+PF2=PK1+ PK2=AD。
(2)∵G1G2=G1F2+G2F2, 由切线长定理可知G1F2=G1D,F2G2=G2C, ∴G1G2=G1D+G2C. 连接F1O1,F2O2, 由于O1F1=O2F2,∠O1F1E=∠O2F2F=90°,∠E=∠F, ∴△EF1O1≌△FF2O2. ∴O1E=O2F. ∵O1A=O2C,∴EA=FC. ∴△FCG2≌△EAG1. ∴G1A=G2C. ∴G1G2=G1D+G1A=AD.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
i 1
i
120015 (400) 20 =12.5cm 1200 (400)
3.积分法 适用于形状规则的物体。
y A R
解: 由对称性可知
dL
B
x 0
dL=Rdθ
y
θ α α
o
dθ
y=Rcosθ
R cos Rd y dL Rd
L L
I 2 dA
A
y
——图形对 O 点的极惯性矩
dA
A
O
ρ z
I dA
2 A
>0
量纲[L4]-(m4)
例题4
y dA dρ ρ
C
已知:圆截面直径d,求:
解:取圆环微元面积
dA 2π d
I
d /2 0
z
dA
2
d
d /2
0
2 π d
2 A
IZ I
I
I
ZCI
3 80 20 AI (25) 20 80 625 12 8 4 105.33 10 m
2
80
I C
I I
II
Z
II
ZCII
AII (25)
2
20
ZCⅠ
Z 80
65
20 80 3 20 80 625 12
ZCⅡ
185.33 108 m4
10cm
A
20cm y
10cm
A
30cm
y
A
o
2
y y
10cm
x
A1 A2 10 30 300cm
A3 10 20 200cm2
y1=y2=15cm
y3 5cm
300 15 2 200 5 yc =12.5cm 300 2 200 A i
2
1 c
注意: C点必须为形心
I y z I y z abA
1 1 c c
Iy Iy b A
2
1 c
Iz Iz a A
2
1 c
I y z I y z abA
1 1 c c
因为面积及包含a2、b2的项恒为正,故 自形心轴移至与之平行的任意轴,惯性矩 总是增加的。 a、b为原坐标系原点在新坐标系中的坐 标,要注意二者的正负号;二者同号时abA 为正,异号时为负。所以,移轴后惯性积有 可能增加也可能减少。
x
ydL
例:已知圆弧AB半径R,圆 心角2α。求:AB圆弧段的 重心。
R
sin
例题
2
如图所示将截面任意分为两部分A1与A2,证明这两部分 面积对整个截面形心轴xc的面积矩绝对值相等。
设: A1,A2对xc轴的静矩分别Sxc1和Sxc2
S xc S xc1 S xc2 S xc A y c A 0 0
A
I z1 y dA 2a ydA a dA
2 2 A A A
I y1z1 yzdA b ydA a zdA ab dA
A A A A
2 I z1 I z 2aS z a A I y1z1 I yz aS y bS z abA I y1 I y 2bS y b 2 A
A
I z1 y12 dA
A
y1=y+a
z1=z+b
dA
I y1z1 y1 z1dA
A
O
a O´ b
y
y1
z
I y1 z b dA
2 A
I z1 y a dA
2 A
I y1z1 y a z b dA
A
A A
I y1 z 2 dA 2b zdA b2 dA
重点:面积矩和形心,惯性矩,形心主惯性矩。 难点:惯性矩的移轴公式 学时安排:2学时(44页后的讨论题由学生课后完成)
§ 4.1
一、静矩的概念
截面的形心位置和面积矩
S y zdA
A
y z dA
——图形对于 y 轴的静矩
y
O z
S z ydA
A
——图形对于 z 轴的静矩
可正、可负、也可为零 量纲[L3]-(m3)
2
3
dA h dz
I y z dA z 2 hdz hb
2 b 2 b 2
b 2 b 2
3
12
三、惯性积:面积与其到两轴距离之积。
y
z
I yz yzdA
A
dA
A
O
ρ
——图形对 y z 轴的惯性积 z Iyz 可为正,可为负,亦可为0 如果 z 或 y 是对称轴,则Iyz =0
S z ydA
A
S yc z A
A
ydA A
zc
Sy A
A
zdA A
zc
Sy A
A
zdA A
Sz yc A
A
ydA A
当截面由若干简单图形组成(等厚均质板的重心与形心 重合。) n n
S y Ai z ci
i 1
S z Ai yci
[例7]确定形心轴Z的位置,并求 IZ, Iy
y 80 I
解(1)确定形心轴Z的位置:
取y为对称轴,形心必位于对 称轴上。
Z 80
C
20
Ay y
i c
i
A
yc
Ⅱ
Z1 20
20 80 90 20 80 40 65(mm) 20 80 2
(2)求IZ
I z y dA I zI I ZII
已知: Iy ,Iz , Iyz ,y、z是形心轴。 y z1
z
求: Iy1,Iz1,Iy1z1 A dA
y
I y1 z12 dA
A
I z1 y12 dA
A
O a O´ b
y1
z
I y1z1 y1 z1 dA
A
y1=y+a
z1=z+b
y
z1
z
I y1 z12 dA
2 I z1 I z 2aS z a A I y1z1 I yz aS y bS z abA I y1 I y 2bS y b 2 A
如果y、z轴通过图形形心,上述各式中的Sy=Sz=0
Iy Iy b A
2
1 c
Iz Iz a A
由对称性可知
Iz I y
4
Iz Iy
1 d I 2 64
例题6
y
dA
dy
已知:矩形截面b× h 求:Iy, Iz
解:取平行于x轴和y轴的微元面积 C z dz b h
dA
y
z
dA bdy
I z y dA
2 h 2 h 2
h 2 h 2
bh y bdy 12
2
πd 32
4
二、(轴)惯性矩:(与转动惯量类似) 是面积与它到轴的距离的平方之积。
y
z
I y z 2 dA
A
——图形对 y 轴的惯性矩
dA
A
O
r
I z y 2 dA
A
y
z
——图形对 z轴的惯性矩
大于零 量纲[L4]-(m4)
y
z
I y z 2 dA
A
I z y 2 dA
iபைடு நூலகம்1 3 i ci i 1
Ay
3
(2)负面积法 解:由对称性可知
10cm
20cm y
A
10cm
30cm
A y
y
xc 0
A1 40 30 1200 cm2
A2 20 20 400cm2
yc
10cm
o x
y1=15cm
y2 20cm
Ay
i 1 3 i
3
ci
0
R4 (sin ) 2 d 4
R4 1 1 ( sin 2 ) 4 2 4
2 0
D 4
64
圆对直径的惯性矩求法二:
y
I y z dA
2 A
I z y dA
2 A
z
dA
y
I
dA A
2
A
(y A
2
z ) dA
2
O
2 2 y dA z z dA I z I y A
i 1
Ai zci zc A y Ai yci c A
(正负面积法公式)
四. 确定匀质物体重心(形心)的几种方法 1.对称性法 匀质物体的重心一定在其对称面、对称轴或对称中心上
c
c
c
c
c
c
c c c
2.组合法
(1)分割法
适用于形状较复杂的物体 例1:试求匀质槽形钢板的 形心。 解:由对称性可知 xc 0
A
dA
A
O
ρ
y
I 2 dA
A
z
I I y Iz
例5、求圆对直径的惯性矩
dA dd
I y Z dA
2
D
z sin
( sin ) 2 dA
