高考高中数学正态分布共23页文档
合集下载
2025届高中数学一轮复习课件《正态分布》ppt
高考一轮总复习•数学
A．甲工厂生产的零件尺寸的平均值等于乙工厂生产的零件尺寸的平均值 由正态曲线的对称轴相等可知． B．甲工厂生产的零件尺寸的平均值小于乙工厂生产的零件尺寸的平均值 C．甲工厂生产的零件尺寸的稳定性高于乙 甲的正态曲线瘦高，即稳定性高于乙． 工厂生产的零件尺寸的稳定性 D．甲工厂生产的零件尺寸的稳定性低于乙工厂生产的零件尺寸的稳定性
(2)由已知得 E(ξ)＝3，D(ξ)＝4，故 E(2ξ＋1)＝2E(ξ)＋1＝7，D(2ξ＋1)＝4D(ξ)＝16.故选 D．
解析
高考一轮总复习•数学
第21页
题型
服从正态分布的概率计算
典例 2 (1)(2024·陕西西安模拟)陕西洛川苹果享誉国内外，据统计，陕西洛川苹果(把
苹果近似看成球体)的直径 X(单位：mm)服从正态分布 N(70,52)，则直径在(80,85]内的概率
高考一轮总复习•数学
第27页
135 分的为特别优秀，那么本次数学考试成 μ＋2σ 绩特别优秀的大约有________人．(若 X～N(μ，σ2)，则 P(μ－σ≤X≤μ＋σ)≈0.68，P(μ －2σ≤X≤μ＋2σ)≈0.95) (2)(2024·河北张家口统考)某校举办乒乓球颠球比赛，现从高一年级 1 000 名学生中随机 选出 40 名学生统计成绩(单位：个)，其中 24 名女生的平均成绩 x 女＝70，标准差 s 女＝4；16 名男生的平均成绩 y 男＝80，标准差 s 男＝6.
σ ＝ 9. 因 为
μ
－ 2σ
＝
110
－
2×9
＝ 92
，
P(ξ≥90)>P(ξ≥92) ＝
P(ξ≥μ －
2σ)
＝
1 2
高中数学---正态分布
（5）若 固定, 随 值的变化而沿x轴平移, 故 称为位置参数 （6）当μ一定时，曲线的形状由σ确定 .σ越大，曲线越“矮 胖”，表示总体的分布越分散；σ越小，曲线越“瘦高”，表示 总体的分布越集中.
练习：
一台机床生产一种尺寸为10mm的零件，现从中抽 测10个，它们的尺寸分别如下（单位：mm）：10.2, 10.1, 10, 9.8, 9.9, 10.3, 9.7, 10, 9.9, 10.1.如果机床生产零
正态曲线下的面积规律
• X轴与正态曲线所夹面积恒等于1 。 • 对称区域面积相等。
S(-,-X)
S(X,)＝S(-,-X)
正态曲线下的面积规律
• 对称区域面积相等。
S(-x1, -x2)
S(x1,x2)=S(-x2,-x1)
-x1 -x2
x2 x1
5、特殊区间的概率:
若X~N (, 2 ),则对于任何实数a>0,概率
( 3由当 ,于a这 33些概)时之率正内值态,很其总小他体（区的间一取取般值值不几几超乎乎过总不5取％可值能）于.，区 在通实间常 际称运这用些中情就况只发考生虑为这小个概区率间事,件称。为 3 原则.
例1、在某次数学考试中，考生的成绩 服从一个 正态分布，即 ~N(90,100). （1）试求考试成绩 位于区间(70,110)上的概率是
2、已知X~N (0,1)，则X在区间 (, 2) 内取值的概率
等于（ D ）
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设离散型随机变量X~N(0,1),则P(X 0)= 0.5 ,
P(2 X 2) = 0.9544 .
4、若已知正态总体落在区间 (0.3, ) 的概率为0.5，则
练习：
一台机床生产一种尺寸为10mm的零件，现从中抽 测10个，它们的尺寸分别如下（单位：mm）：10.2, 10.1, 10, 9.8, 9.9, 10.3, 9.7, 10, 9.9, 10.1.如果机床生产零
正态曲线下的面积规律
• X轴与正态曲线所夹面积恒等于1 。 • 对称区域面积相等。
S(-,-X)
S(X,)＝S(-,-X)
正态曲线下的面积规律
• 对称区域面积相等。
S(-x1, -x2)
S(x1,x2)=S(-x2,-x1)
-x1 -x2
x2 x1
5、特殊区间的概率:
若X~N (, 2 ),则对于任何实数a>0,概率
( 3由当 ,于a这 33些概)时之率正内值态,很其总小他体（区的间一取取般值值不几几超乎乎过总不5取％可值能）于.，区 在通实间常 际称运这用些中情就况只发考生虑为这小个概区率间事,件称。为 3 原则.
例1、在某次数学考试中，考生的成绩 服从一个 正态分布，即 ~N(90,100). （1）试求考试成绩 位于区间(70,110)上的概率是
2、已知X~N (0,1)，则X在区间 (, 2) 内取值的概率
等于（ D ）
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设离散型随机变量X~N(0,1),则P(X 0)= 0.5 ,
P(2 X 2) = 0.9544 .
4、若已知正态总体落在区间 (0.3, ) 的概率为0.5，则
高中数学课件正态分布
( x0 )
( x0 ) 1 ( x0 )
( x0 ) P( x x0 ) ( x0 0)
由于两阴影部分的面积相等可知：
( x0 ) 1 ( x0 )
利用这个表，可求出标准正态总体在任一区间 x1 , x2 内取值的概率。
y
( x2 ) ( x1 )
正态分布的实际意义
在实际中遇到的许多随机现象都服从或近似服从正态分布 生产中，在正常生产条件下各种产品的质量指标 在测量中，测量结果的随机误差，
在生物学中，同一群体的某种特征 在气象中，气温、湿度、降雨量、水文中的水位，
正态分布广泛存在于自然现象、生产及科学技术的许多领 域之中．正态分布在概率和统计中占有重要地位． 一般地，当一随机变量是大量微小的独立随机因素共同作 用的结果，而每一种因素都不能起到压倒其他因素的作用 时，这个随机变量就被认为服从正态分布。
标准正态分布表
在标准正态分布表中相应于 x 0 的值 ( x 0 )是指总体取值 小于 x 0 的概率，即
( x0 ) P( x x0 ) ( x0 0)
P( x x0 ) 0
P( x x0 ) 1 P( x x0 ) 1 P( x x0 ) 1 ( x0 )
5 1 0 1 P(0 5) F (5) F (0) ( ) ( ) (2) (0.5) 2 2 (2) (0.5) 1
3 1 F (3) ( ) (1) 0.8413 2
例1、分别求正态总体 N (, 2 )在区间: , 、 内取值的概率. 2 , 2 、 3 , 3 、 解： F
我们从上图看到，正态总体在 2 , 2 以外取值的概率 只有4.6％，在 3 , 3 以外取值的概率只有0.3 ％。 由于这些概率值很小（一般不超过5％），通常称这些情况 发生为小概率事件。
高中数学正态分布
指数分布与正态分布关系
指数分布是一种连续型概率分布 ，用于描述两个连续事件之间的 时间间隔。
在某些情况下，指数分布可以近 似为正态分布。具体来说，当指 数分布的参数 $lambda$ 足够大 时，指数分布 $Exp(lambda)$ 可以用正态分布 $N(frac{1}{lambda}, frac{1}{lambdasqrt{2}})$ 来近似 。然而，这种近似通常不如二项 分布和泊松分布逼近正态分布那 样准确。
多元正态分布的定义
多元正态分布是指多个随机变 量组成的向量服从正态分布的 情况。
多元正态分布的性质
多元正态分布具有一些重要的 性质，如联合分布、边缘分布 、条件分布和独立性等。
多元正态分布在统计学中 的应用
多元正态分布广泛应用于多元 统计分析中，如多元线性回归 、主成分分析、因子分析等。
多元正态分布的参数估计 和假设检验
对于多元正态分布的参数估计 和假设检验，可以使用最大似 然估计、协方差矩阵的估计和 多元t检验等方法进行。
感谢您的观看
THANKS
对两个正态总体均值或方差进行 比较的假设检验，如t检验和F检 验的两样本版本。
置信区间构建
利用样本数据构造总体均值的置 信区间，以估计总体均值可能落 入的范围。
01
02
单样本假设检验
对单个正态总体均值或方差进行 假设检验，如t检验和F检验。
03
04
配对样本假设检验
对配对观测值之差的均值进行假 设检验，如配对t检验。
智商分布
智商测试的结果也符合正态分布，大 部分人的智商处于中等水平，极高和 极低的智商相对较少。
生产过程中质量控制
产品质量分布
在生产线上，产品质量往往呈现 正态分布，大部分产品符合质量 标准，极少数产品存在严重缺陷
《高中数学正态分布》课件
正态分布的实例分析
1 案例一：商品售价的概率分布
探讨商品售价符合正态分布时的概率分布情况，为合理定价提供依据。
2 案例二：身高的概率分布
分析人类身高在不同群体中的分布，理解身高的统计特征和差异。
3 案例三：考试成绩的分布
研究考试成绩的正态分布特征，评估学生的相对表现和优势科目。
总结与思考
正态分布在数学与实践中的重要 性
3
应用示例
通过标准化后的数据，可以进行正态分布的统计估计、抽样与推论，并用于描述 实际情况。
正态分布的应用
统计估计
正态分布在估计总体参数和进行 置信区间估计时非常有用。
抽样与推论
正态分布可用于抽样分布的建立 和统计推断的进行。
实际情况分析
通过近似描述实际情况，例如商 品售价、身高和考试成绩的分布。
《高中数学正态分布》 PPT课件
引言
正态分布的定义
正态分布是一种连续型概率分布，具有钟形曲线，以均值μ和标准差σ来描述。
正态分布的性质
正态分布的均值、中位数和众数相等；左右对称；68%的数据落在一个标准差内；95%的数 据落在两个标准差内。
概率密度函数
密度函数的输入和输出，函数图 像
密度函数接受一个输入值x并给出对应的概率密度 值。函数图像呈现出正态分布的钟形曲线。
正态分布是统计学中最重要的概率分布之一，在自 然科学、社会科学和经济金融等领域有广泛应用。
对于其他分布的启示
正态分布的性质和应用可以启发我们研究和理解其 他概率分布。
参考文献
• 统计学与实际 • 十二年高等数学 • 数学建模及其应用 • 离散数学及其应用
均值和标准差对函数图像的影响
均值决定函数图像的中心位置，标准差影响函数图 像的分散程度。正态分布的Fra bibliotek准化1
人教版高中数学选修正态分布PPT课件(共22张PPT)
缩小，那么频率分布直方图就会无限接近于一条光滑曲线，这条曲线叫做总体密度曲线．
σ越小，曲线越“瘦高”，表示总体的分布越集中.
例2 关于正态曲线性质的叙述：
正态分布密度曲线(正态曲线)
上述叙述中，正确的有
.
（3）曲线在x=μ处达到峰值(最高点)
正态分布密度曲线(正态曲线)
解：由正态曲线的对称性可得，
例3.商场经营的某种包装的大米质量服从正态分布 N（10，2）（单位：kg）任选一袋这种大米质量在kg的 概率是多少？
x
则称X 的分布为正态分布. 正态分布由参数m、s唯一
确定, m、s分别表示总体的平均数与标准差.正态分
布记作N（ m，s2）.其图象称为正态曲线.
如果随机变量X服从正态分布，则记作记为 X~N(m,s2)
例题探究
例1．给出下列两个正态总体的函数表达式，请找出其
均值m和标准差s
(1)
(x)
1
x2
e2,x( ,)
％。 a
由于这些概率值很小（一般不超过5 ％ ），通常 称这些情况发生为小概率事件。
当 a 3s 时正态总体的取值几乎总取值于区间 (m 3s , m 3s ) 之内,其他区间取值几乎不可能. 在实际运用中就只考虑这个区间,称为 3s 原 则.
例4 某厂生产的T型零件的外直径x~ N（10，2），
C
n n
p
n
q
0
复习与思考
1.由函数 y f( x 及)直线 x a ,x b ,y 0 y b
围成的曲边梯形的面积S=_____f _( _x_)d_x； a
2. 在我班同学身高频率分布直方图中 O a ①区间（a,b）对应的图形的面积表示 __身__高__在__区__间___(a_,_b_) _内__取__值__的__频__率___，
高中数学“正态分布”知识点讲解——以2024年全国1卷第9题为例
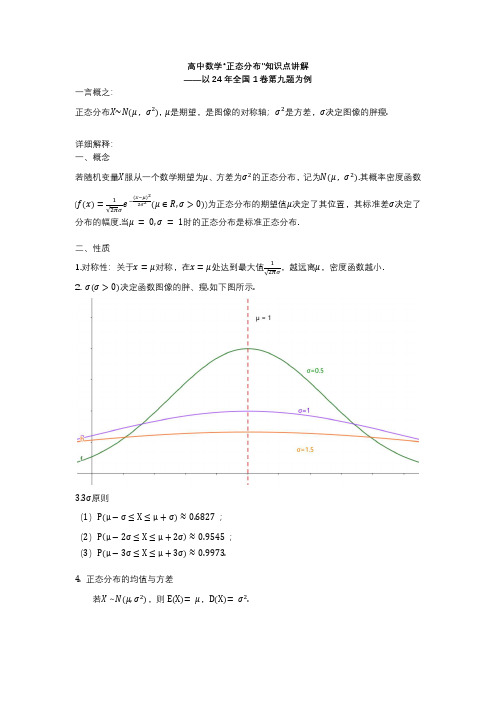
高中数学“正态分布”知识点讲解——以24年全国1卷第九题为例一言概之：正态分布X~N(μ，σ ),μ是期望，是图像的对称轴；σ 是方差，σ决定图像的胖瘦.详细解释：一、概念若随机变量X服从一个数学期望为μ、方差为σ 的正态分布，记为N(μ，σ ).其概率密度函数(f(x)=√ e( )(μ∈R,σ>0))为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度.当μ = 0,σ = 1时的正态分布是标准正态分布.二、性质1.对称性：关于x=μ对称，在x=μ处达到最大值√，越远离μ，密度函数越小.2.σ(σ>0)决定函数图像的胖、瘦.如下图所示.3.3σ原则（1）P(μ−σ≤X≤μ+σ)≈0.6827 ；（2）P(μ−2σ≤X≤μ+2σ)≈0.9545 ；（3）P(μ−3σ≤X≤μ+3σ)≈0.9973.4. 正态分布的均值与方差若X～N(μ,σ )，则E(X)=μ，D(X)=σ .以2024年全国1卷第9题为例2024年全国1卷T9. 为了解推动出口后的亩收入（单位：万元）情况，从该种植区抽取样本，得到推动出口后亩收入的样本均值 2.1x ，样本方差20.01s ，已知该种植区以往的亩收入X 服从正态分布 21.8,0.1N ，假设推动出口后的亩收入Y 服从正态分布 2,N x s ，则（ ）（若随机变量Z 服从正态分布 2,N u ，()0.8413P Z ）A. (2)0.2P XB. (2)0.5P XC. (2)0.5P YD. (2)0.8P Y 解析： 2~ 1.8,0.1X N 的图像：1.80.1 1.9∴ 1.910.84130.1587P X ，显然 2 1.9P X P X ，所以A 错误.B 正确. 2~ 2.1,0.1Y N 的图像：与 2~ 1.8,0.1X N 的图像一致，仅对称轴改变.∵ 2.10.5P X （对称性，对称轴为 2.1x ，故左右各为0.5）2 2.1P Y P Y ，故C 正确；又∵ 2 2.10.10.8413P Y P Y （对称性： 0.8413P Y P Y ） 即：D 错误.解题建议：①画出图像；②标明对称轴；③标明 与 .。
人教A版高中数学选择性必修第三册 正态分布
[微判断] 1．函数
拓展深化 (x∈R)中参数 μ，σ 的意义分别是样本的均值与方差．( )×
提示 函数中σ的意义为标准差．
2．正态曲线是单峰的,其与x轴围成的面积是随参数μ,σ的变化而变化的． 提示 正态曲线与x轴围成的面积为定值1.
3．正态曲线可以关于y轴对称．
( )× (√)
[微训练]
1．若 X～N1，1D
[微思考] 函数 f(x)的解析式．
，x∈R 的图象如图所示．试确定函数
提示
由图可知，该曲线关于直线
x＝72
对称，最大值为 1 ，由函数表达式可知， 10 2π
函数图象的对称轴为 x＝μ，
∴μ＝72，且σ
1＝ 1 ， 2π 10 2π
∴σ＝10.
∴f(x)＝10
1
（x－72）2
2πe－ 200 (x∈R).
故函数的解析式为 φμ，σ(x)＝4 12πe－3x22，x∈(－∞，＋∞)．
题型二 利用正态分布的对称性求概率 【例2】 设X～N(1,22),试求：
(1)P(－1≤X≤3)； (2)P(3≤X≤5)． 解 ∵X～N(1,22),∴μ＝1,σ＝2, (1)P(－1≤X≤3)＝P(1－2≤X≤1＋2) ＝P(μ－σ≤X≤μ＋σ)≈0.682 7. (2)∵P(3≤X≤5)＝P(－3≤X≤－1),
3．正态分布的期望与方差 若X～N(μ,σ2),则E(X)＝ ____,μD(X)＝______．σ2
4．正态变量在三个特殊区间内取值的概率 (1)P(μ－σ≤X≤μ＋σ)≈__0_._6_8_2_7___； (2)P(μ－2σ≤X≤μ＋2σ)≈_0_._9_5_4_5___； (3)P(μ－3σ≤X≤μ＋3σ)≈__0_._9_9_7_3___． 在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取[μ－3σ,μ＋3σ] 中的值,这在统计学中称为3 σ原则.