《结构力学考试样题库》2-静定结构内力
《结构力学考试样题库》2-静定结构内力

《结构力学考试样题库》2-静定结构内力 work Information Technology Company.2020YEAR第二章 静定结构内力计算一、是非题1、 静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图示结构||M C =0。
aa5、图示结构支座A 转动ϕ角,M AB = 0, R C = 0。
BCaaAϕ2a26、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图示静定结构,在竖向荷载作用下, AB 是基本部分,BC 是附属部分。
ABC8、图示结构B 支座反力等于P /2()↑。
9、图示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图示桁架有9根零杆。
12、图示桁架有:N 1=N 2=N 3= 0。
aaaa13、图示桁架DE 杆的内力为零。
a a14、图示对称桁架在对称荷载作用下,其零杆共有三根。
15、图示桁架共有三根零杆。
16、图示结构的零杆有7根。
17、图示结构中,CD 杆的内力N 1=-P 。
a418、图示桁架中,杆1的轴力为0。
4a19、图示为一杆段的M 、Q 图,若Q 图是正确的,则M 图一定是错误的。
图M Q 图二、选择题1、对图示的AB段,采用叠加法作弯矩图是:A.可以;B. 在一定条件下可以;C. 不可以;D. 在一定条件下不可以。
2、图示两结构及其受载状态,它们的内力符合:A. 弯矩相同,剪力不同;B. 弯矩相同,轴力不同;C. 弯矩不同,剪力相同;D. 弯矩不同,轴力不同。
PPP2l ll l3、图示结构MK(设下面受拉为正)为: A. qa22; B. -qa2;C. 3qa22;D. 2qa2。
2a4、图示结构MDC(设下侧受拉为正)为:A. -Pa;B. Pa;C. -Pa;D. Pa2。
结构力学复习题

结构力学复习题
一、选择题
1. 结构力学中,梁的剪力图表示了梁上各截面的()。
A. 弯矩
B. 剪力
C. 轴力
D. 扭矩
2. 在静定结构中,内力可以通过()来确定。
A. 材料力学公式
B. 静力平衡方程
C. 能量守恒定律
D. 弹性力学理论
3. 单跨静定梁在均布荷载作用下,其弯矩图的形状是()。
A. 抛物线
B. 直线
C. 折线
D. 曲线
二、填空题
4. 简支梁在集中荷载作用下,其最大弯矩发生在荷载作用点的()。
5. 悬臂梁在自由端受到向下的集中荷载作用时,其最大弯矩发生在()。
6. 连续梁在支座处的弯矩为(),而在跨中弯矩最大。
三、简答题
7. 简述静定结构和超静定结构的区别。
8. 描述一下在结构力学中,如何通过弯矩图来分析梁的受力情况。
四、计算题
9. 已知一简支梁,跨度为L,梁上作用有均布荷载q和集中荷载P,试求梁的反弯点位置。
10. 有一悬臂梁,长度为L,自由端作用有向下的集中荷载P,求梁端部的弯矩和剪力。
五、分析题
11. 给定一连续梁的支座反力和跨中弯矩,请分析该连续梁的受力特性。
12. 讨论在结构设计中,如何通过优化结构布局来减少梁的内力。
六、论述题
13. 论述在结构力学中,为什么需要考虑荷载的不确定性以及如何进行荷载组合。
14. 论述在结构分析中,静力平衡方程和几何不变性条件的重要性及其应用。
结构力学试题答案

结构力学试题答案结构力学是一门研究结构受力和变形规律的学科,对于工程领域的学生来说,掌握这门学科的知识至关重要。
以下是一套结构力学试题的答案及详细解析。
一、选择题1、关于静定结构的内力,下列说法正确的是()A 内力与杆件的材料性质无关B 内力与杆件的截面形状无关C 内力与结构所受的荷载有关D 以上都对答案:D解析:静定结构的内力只与结构的几何形状、约束条件和所受荷载有关,而与杆件的材料性质和截面形状无关。
2、图示刚架,支座 A 发生竖向位移 a,支座 B 发生水平位移 b,不计杆件的轴向变形,利用单位荷载法求 C 点的竖向位移时,应在 C 点施加的单位力是()A 竖向单位集中力B 水平单位集中力C 顺时针单位集中力偶D 逆时针单位集中力偶答案:A解析:要求 C 点的竖向位移,应在 C 点施加竖向单位集中力。
3、力法的基本未知量是()A 多余约束力B 广义位移C 结点位移D 杆件内力答案:A解析:力法是以多余约束力为基本未知量,将超静定结构转化为静定结构进行分析。
二、填空题1、平面桁架在计算杆件内力时,通常采用__________法。
答案:节点法、截面法解析:节点法是依次取桁架的节点为研究对象,利用平衡条件求出杆件内力;截面法是用一截面截取桁架的一部分作为研究对象,利用平衡条件求出杆件内力。
2、梁在集中力作用处,剪力图发生__________,弯矩图发生__________。
答案:突变、转折解析:集中力会使剪力发生突变,弯矩发生转折。
3、结构的稳定性是指结构在__________作用下,保持其原有平衡状态的能力。
答案:微小干扰解析:稳定性指结构在微小干扰作用下不发生显著的变形或失去平衡。
三、计算题1、图示简支梁,受均布荷载 q 作用,跨度为 l ,求支座 A、B 的反力。
解:对整体进行受力分析,由平衡方程∑Fy = 0 可得:RA + RB ql = 0 (1)对 A 点取矩,由∑MA = 0 可得:RB × l ql × l/2 = 0 (2)联立(1)(2)解得:RA = ql/2 ,RB = ql/22、用力法计算图示超静定梁,EI 为常数。
结构力学静定结构内力计算练习题.
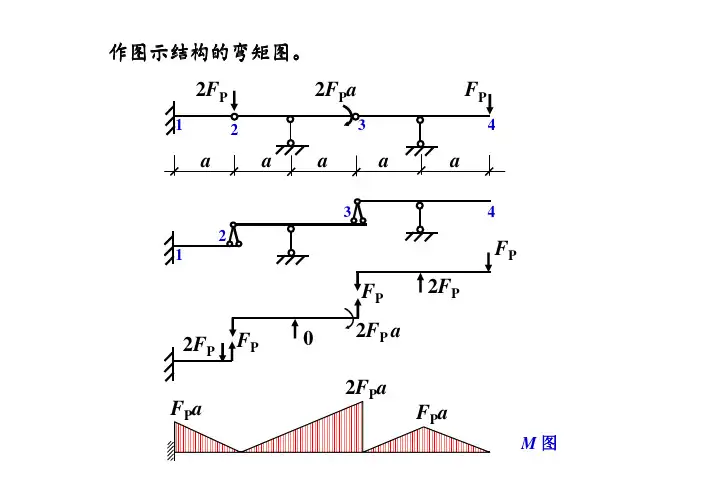
M 图分析分析:EB 杆件无弯矩杆件无弯矩→→杆件无弯矩杆件无弯矩→0kN 2445cos =−oB F 0=AMkN(4↓=I F求图示桁架指定杆件内力。
求图示桁架指定杆件内力。
(分析方法)1 1 F F FF F 1 1例 计算图示组合结构。
计算图示组合结构。
FP A D a 2FP /3 F a Ⅰ a/2 a/2 Ⅰ E G a B解A D 2FP /3 FP /3 F FP CFNCD FSCD FNFGC∑M ∑F ∑FC= 0 FNFG = FP / 2FNFAFNDFFy= 0 FSCD = FP / 3 = 0 FNCD = − FP / 2FP /2x∑Fx= 0 FNFA = 2 FP / 2= 0 FNDF = − FP / 2一般情况下应先计算链杆的轴力 取隔离体时不要截断 取隔离体时不要截断受弯杆件 不要截断受弯杆件∑Fy例:作组合结构的内力图 解 FP E D a A a C B aFP有无零杆?FNECFNDC FNDBFN DB = FPFN EC = −2 FPFN DC = 0FP a 2FP aFP 2FP -2FP FPM图FS图FN图例:计算图示组合结构。
计算图示组合结构。
FP E G FP A 0 a a a 2FPB取隔离体FJBC FNEFF J B C a 2FP 2FP -2FP FP a 2FP 2FP CF J aFNGJa B解:1、求支反力 2、求FNEF、FNGJ∑M = 0 F = 2F (↑) ∑F = 0 F = 2F (↓)Cy PyByP∑M ∑FJ=0FN EF = −2 FP2FP ax=0FN GJ = 2 FP内力图例:计算图示组合结构。
计算图示组合结构。
4m 5kN/m 15kN B C D E解:左边为基本部分, 左边为基本部分, 右边为附属部分。
右边为附属部分。
10kN 20 40A 2m 5 15 10 4mF 4mG 10 30 52m 2m20 (2.5)10 5 1012.52.55M图(kN·m)例:分析图示组合结构。
结构力学在线测试题及答案

《结构力学》第03章在线测试剩余时间:46:42答题须知:1、本卷满分20分。
2、答完题后,请一定要单击下面的“交卷”按钮交卷,否则无法记录本试卷的成绩。
3、在交卷之前,不要刷新本网页,否则你的答题结果将会被清空。
第一题、单项选择题(每题1分,5道题共5分)1、在梁的弯矩图发生突变处作用有什么外力?A、轴向外力B、横向集中力C、集中力偶D、无外力2、静定结构的内力与刚度A、无关B、绝对大小有关C、比值有关D、有关3、温度变化对静定结构会产生A、轴力B、剪力C、弯矩D、位移和变形4、桁架计算的结点法所选分离体包含几个结点A、单个B、最少两个C、任意个D、最多两个5、桁架计算的截面法所选分离体包含几个结点A、单个B、只能有两个C、两个或两个以上D、无穷多个第二题、多项选择题(每题2分,5道题共10分)1、外力作用在基本梁上时,附属梁上的A、内力为零B、变形为零C、位移为零D、反力为零E、位移不为零2、下列哪些因素对静定梁不产生内力A、荷载B、温度改变C、支座移动D、制造误差E、材料收缩3、梁上横向均布荷载作用区段的内力图的特征是A、剪力图平行轴线B、剪力图斜直线C、剪力图二次抛物线D、弯矩图平行轴线E、弯矩图二次抛物线4、如果某简支梁的剪力图是一平行轴线,则梁上荷载可能是A、左支座有集中力偶作用B、右支座有集中力偶作用C、跨间有集中力偶作用D、跨间均布荷载作用E、跨间集中力作用5、静定梁改变截面尺寸,下列哪些因素不会发生改变?位移A、轴力B、剪力C、弯矩D、支座反力E、位移第三题、判断题(每题1分,5道题共5分)1、对于静定结构,改变材料的性质,或改变横截面的形状和尺寸,不会改变其内力分布,也不会改变其变形和位移。
正确错误2、静定结构在支座移动作用下,不产生内力。
正确错误3、刚架内杆件的截面内力有弯矩、轴力和剪力。
正确错误4、静定结构满足平衡方程的内力解答由无穷多种。
正确错误5、零杆不受力,所以它是桁架中不需要的杆,可以撤除。
建筑力学:静定结构的内力分析
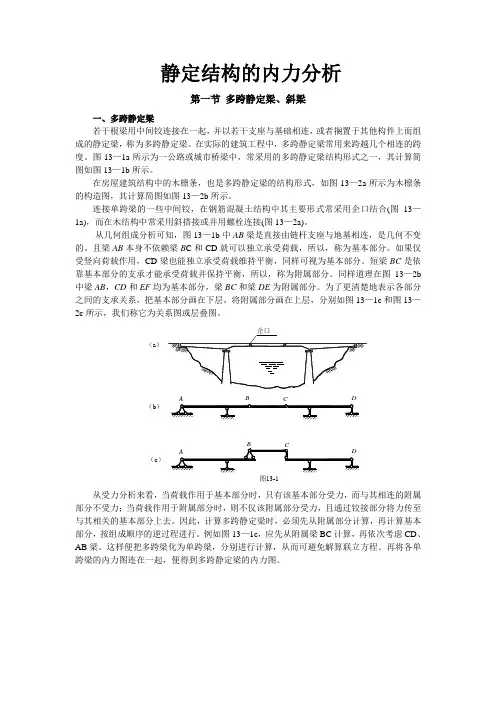
静定结构的内力分析第一节多跨静定梁、斜梁一、多跨静定梁若干根梁用中间铰连接在一起,并以若干支座与基础相连,或者搁置于其他构件上而组成的静定梁,称为多跨静定梁。
在实际的建筑工程中,多跨静定梁常用来跨越几个相连的跨度。
图13—1a所示为一公路或城市桥梁中,常采用的多跨静定梁结构形式之一,其计算简图如图13—1b所示。
在房屋建筑结构中的木檩条,也是多跨静定梁的结构形式,如图13—2a所示为木檩条的构造图,其计算简图如图13—2b所示。
连接单跨梁的一些中间铰,在钢筋混凝土结构中其主要形式常采用企口结合(图13—1a),而在木结构中常采用斜搭接或并用螺栓连接(图13—2a)。
从几何组成分析可知,图13—1b中AB梁是直接由链杆支座与地基相连,是几何不变的。
且梁AB本身不依赖梁B C和CD就可以独立承受荷载,所以,称为基本部分。
如果仅受竖向荷载作用,CD梁也能独立承受荷载维持平衡,同样可视为基本部分。
短梁BC是依靠基本部分的支承才能承受荷载并保持平衡,所以,称为附属部分。
同样道理在图13—2b 中梁AB,CD和EF均为基本部分,梁BC和梁DE为附属部分。
为了更清楚地表示各部分之间的支承关系,把基本部分画在下层,将附属部分画在上层,分别如图13—1c和图13—跨梁的内力图连在一起,便得到多跨静定梁的内力图。
要依靠AC 梁才能保证其几何不变性,所以CE 梁为附属部分。
(2)计算支座反力从层叠图看出,应先从附属部分CE 开始取隔离体,如图13-3c 所示。
∑=0CM 04680=⨯-⨯D V kN V D 120=(↑) ∑=0DM04280=⨯-⨯C V kN V C 40=(↓)将C V 反向,作用于梁AC 上,计算基本部分∑=0X 0=AH∑=0AM -40×10+V B ×8+10×8×4-64=0 ∑=0BM-40×2-10×8×4-64+V A ×8=0V A =58kN (↑) V B =18kN (↓) 校核:由整体平衡条件得∑Y =—80十120—18十58—10×8=0, 无误。
结构力学二3-静定结构的内力计算
(3) 利用微分关系作内力图
梁的荷载集度 q 、剪力 Q 、弯矩 M 三者间存 在如下的微分关系(q 以向下为正): 2 d M dM dQ q ( x ) Q q ( x ) 2 dx dx dx
据此,得直梁内力图的形状特征
q=0
q=常数 q→ q↑
斜直线 抛物线
梁上情况
P 作用处
2.多跨静定梁
概念:若干根梁用铰相联,并用若干支座与基础相联 而组成的结构。
2.多跨静定梁的特点:
(1)几何组成上: 可分为基本部分和附属部分. 。
(2)受力分析方面: 作用在基本部分上的力不传递给附属部分,而作用在 附属部分上的力传递给基本部分,如图示
P1 P2
(a)
B
P2
A
P1
VB
VC
(b)
4m
Y、 =15kN 由∑ Y=0 可得 GE 然后依次取结点 F E 、D、(拉) C计算。 4 YGE XGE=15 由比例关系求得 SFE=+15kN 分析桁架的几何组成:此桁架为简单桁 3 S , 到结点B时,只有一个未知力 XGE E BA 5 SED=+60kN 架,由基本三角形 ABC 按二元体规则依 G SGE=15× =25kN(+20kN 及 拉) SFC=-20kN 3 最后到结点A时,轴力均已求出, SGF XEC=-40kN 次装入新结点构成。由最后装入的结点 F 20kN +15kN 再由∑ X=0 可得 S =-X =-20kN( 压) Y =-30kN EC GF GE 故以此二结点的平衡条件进行校核。 G开始计算。(或由 A结点开始) 29
RB
1.作EF段的弯矩图 用简支梁叠加法
2.剪力等于零截面K 的位置 QK=QE-qx=8-5x=0 x=1.6m 3.K截面弯矩的计算 qx 2 MK=ME+QE x- 2 2 5 1 6 =26+8×1.6-
结构力学-静定结构的内力分析
计算多跨梁的原则:先附属,后基本。
多跨梁
单跨梁
单跨梁内力图
多跨梁内力28 图
[例1] 作多跨静定梁的弯矩图和剪力图
40KN/m
120KN
A
D
B
C
3m
8m
2m
6m
解: (1)作层次图
40KN/m
C
A B
120KN D
29
(2)求反力
40KN/m A
B 8m
C 2m
120KN D
3m 6m
C
120KN D
A
mC 0
FAH
FBH
FAV
l 2 FP1 f
l 2 a1
FA0V
a2
C
FP2
f
B FBH
FBV
l
FP2
C
B
FH
M
0 C
f
FB0V 55
三、 静定拱的内力计算:
1. 静定拱的内力有: M、 FQ 、FN 。
弯矩:使拱内侧受拉为正。
145KN 8m
60KN
60KN
B 235KN
3m
2m
6m
60KN
32
[例2] 作多跨静定梁的弯矩图和剪力图
q
A
B
C
qa
D
E
2qa2 F
a/2 a/2
a
a
a/2 a/2
q
AB
C 7qa/ 8
3qa/8 D
qa D
2qa2
E
F
3qa/8
6qa/8
11qa3/38
作弯矩图: 3qa2
qa2
8
8
结构力学(2.1.2)--静定结构内力分析习题及参考答案
Fp
Fp
4×d
(d)
3-7 试求图示抛物线( y 4 fx(l x) / l 2 ) 三铰拱距左支座 5m 的截面内力。
4m 4m 3d
4m
5 kNF P 1
d
10 kN 1 F3(Pf×)d F2P
2
NN N
习题 3-6 图
2
d
N
15 kN
1
d2/02kN/md d/2
40 kN·m
y
A
B 20 kN
8×1 m
习题 3-5 图
杆件的内力。
80 kN
1 N
2 N
4m 2m
4m
2m
(a)
2m 2m 2×d
20 kN
3.6 试 用 较 简单的 方法求 图示桁 架指定
4
3
1
N 2
NN
Fp
Fp
Fp Fp 8×d
Fp
Fp N
Fp N
(b)
3×2 m d
60 kN
1
N
2
N
4×2 m (c)
Fp 1
2m
6m
6m
2m
(b)
习题 3-16 图
l
3m
4m 4m
3-17 试作图示组合结构的弯矩图和轴力图。
20 kN/m
B
C
A 4m 4m 4m 4m
(a)
习题 3-17 图
20 kNA 20 kN/m
BCD源自4m4m4m(b)
3-1 略
参考答案
3-2 (a) FNAB 25kN (b) FNAB 2.5FP
A
3m
(a) C
东北石油大学结构力学考试题库3章静定结构的内力计算
第三章 静定结构的内力计算内容提要1、静定梁(1) 内力。
静定梁在任意荷载作用下,其截面上一般有三个内力分量,即轴力N F 、剪力s F 和弯矩M 。
内力符号规定如下:轴力以拉力为正,剪力以绕隔离体内部任一点顺时针转动为正,弯矩以使梁的下边纤维受拉力正。
(2) 内力图。
内力图是反映结构中各个截面上内力变化规律的图形。
其绘制方法可归纳如下:1)基本法。
先用理论力学的基本方法求外力;再用结构力学理论列内力方程;最后用数学方法绘图2)微分关系法。
在直梁中荷载集度q 、剪力s F 弯矩M 之间有如下关系(荷载集度向上为正):)()(x q dxx dF s = )()(x F dxx dM s = )()(22x q dx x M d = 以外力不连续点为分段点,如集中力及力偶作用点、分布荷载的两个端点等。
用截面法求得各分段点截面上的内力值,再由上述微分关系式可描绘出内力图的形状。
3)区段叠加法。
当梁段上作用有几个荷载时,则可用叠加原理绘制梁段的内力图。
先求出杆段始端、末端的弯矩竖标,连一虚直线,然后以该连线为基线,叠加相应简支梁在区段荷载作用下的弯矩图。
(3)多跨静定梁是主从结构,由附属部分和基本部分组成。
其受力特点是:外力作用在基本部分时,附属部分不受力;外力作用在附属部分时,附属部分和基本部分都受力。
其计算方法是:先算附属部分,将附属部分上的反方向加在基本部分上,再算基本部分。
所以多跨静定梁可以拆成若干个单跨梁分别进行内力计算,然后将各单跨梁的内力图连在一起即可得多跨静定梁的内力图。
上述多跨静定梁的计算方法,同样适用于其他型式的主从结构。
2.静定刚架静定刚架的内力计算方法,原则上与静定梁相同。
通常先由理论力学的基本方法求出支座反力,然后按静定梁计算内力的方法杆绘制内力图。
在绘制刚架的弯矩图时,不定义弯矩的正负号,只将弯矩图绘在杆件的受拉侧,剪力、轴力的正负号规定与静定梁相同。
3.三铰拱(1)水平推力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 静定结构内力计算一、是非题1、 静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图示结构||M C =0。
aa5、图示结构支座A 转动ϕ角,M AB = 0, R C = 0。
BCaaAϕ2a26、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图示静定结构,在竖向荷载作用下,AB 是基本部分,BC 是附属部分。
AB C8、图示结构B 支座反力等于P /2()↑。
9、图示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图示桁架有9根零杆。
12、图示桁架有:N 1=N 2=N 3= 0。
aaaa13、图示桁架DE 杆的内力为零。
a a14、图示对称桁架在对称荷载作用下,其零杆共有三根。
15、图示桁架共有三根零杆。
16、图示结构的零杆有7根。
17、图示结构中,CD 杆的内力 N 1=-P 。
a418、图示桁架中,杆1的轴力为0。
4a19、图示为一杆段的M 、Q 图,若Q 图是正确的,则M 图一定是错误的。
图M Q 图二、选择题1、对图示的AB 段,采用叠加法作弯矩图是:A. 可以;B. 在一定条件下可以;C. 不可以;D. 在一定条件下不可以。
2、图示两结构及其受载状态,它们的内力符合:A. 弯矩相同,剪力不同;B. 弯矩相同,轴力不同;C. 弯矩不同,剪力相同;D. 弯矩不同,轴力不同。
PPP2 l ll l3、图示结构MK(设下面受拉为正)为: A. qa2; B. -qa22;C. 3qa2;D. 2qa2。
2a4、图示结构MDC(设下侧受拉为正)为:A. -Pa;B. Pa;C. -Pa2;D. Pa2。
a a5、在径向均布荷载作用下,三铰拱的合理轴线为:A.圆弧线;B.抛物线;C.悬链线;D.正弦曲线。
6、图示桁架C杆的内力是:A. P ;B. -P/2 ;C. P/2 ;D. 0 。
7、图示桁架结构杆1的轴力为:A. 2P;B. -2PC. 2P/2;D. -2P/2。
a a a aa a8、图示结构NDE(拉)为:A. 70kN ;B. 80kN ;C. 75kN ;D. 64kN 。
4m4m4m4m三、填充题1、在图示结构中,无论跨度、高度如何变化,MCB永远等于M BC的倍,使刚架侧受拉。
q2、图示结构支座A 转动ϕ角,AB M =______________ ,R C = ______________ 。
BCaaAϕ2a23、对图示结构作内力分析时,应先计算_______部分,再计算_______部分。
4、图示结构DB 杆的剪力Q DB = _______ 。
5、图示梁支座B 处左侧截面的剪力Q B 左=_______。
已知 l = 2m 。
llll 26、图示带拉杆拱中拉杆的轴力N a = 。
6m6m7、图示抛物线三铰拱,矢高为4m ,在D 点作用力偶M = ,M D 左=_______,M D 右=________。
8m4m 4m8、图示半圆三铰拱,α为30°,V A = qa (↑),H A = qa /2 (→), K 截面的ϕK =_______, Q K=________,Q K的计算式为_____________________ 。
qAB Kαaa9、图示结构中,AD杆上 B 截面的内力MB=______ ,____侧受拉。
QB右= ______,NB右= ________。
Pd d210、图示结构CD杆的内力为 ______。
a a a aa11、三铰拱在竖向荷载作用下,其支座反力与三个铰的位置_______ 关 , 与拱轴形状________ 关。
12、图示结构固定支座的竖向反力V A= 。
13、图示结构1杆的轴力和K截面弯矩为:N1=,MK = ( 内侧受拉为正)。
1mmmmmq=11m1m1m14、图示三铰拱的水平推力H = 。
5m15、图示结构中,FEN=,FDN=。
a aa a四、作图题:作出下列结构的弯矩图(组合结构要计算链杆轴力)。
1、2a/a34/a34/2a/2、40kN2m2m3、a a aaa4、4m2m2m5、10kN/m8m4m4m6、4m2m7、q8、qa2aa9、2a2a10、a a11、12、/213、aaa14、am15、ll16、l217、4m4m6m18、19、llq20、ql l ll21、3m3m22、a2a23、24、25、26、l l27、2ql28、3m3m3m29、2m=8m×430、4m2m31、5a32、a a33、3m1m1m 34、35、a2a36、4m2m37、2m2m 38、qa 2a2a a39、40、l ll41、mll l42、a a a43、l/2ql44、P l/2l /2l /245、q46、lll47、aa a a48、23m 1m49、ll ll50、.51、a 3aa52、53、54、55、2kN/m56、3m3m3m2m2m 57、2m2m2m 2m 58、aa259、60、作出下列结构的内力图五、计算题:1、计算图示半圆三铰拱K截面的内力M K,NK。
已知:q =1kN/m,M =18kN·m。
2、计算图示抛物线三铰拱K截面的内力M K,NK ,拱轴方程为:y = 4 f x(l-x)/l2.已知:P= 4kN,q=1kN/m, f=8m,|ϕK|=45°.4m4m4m4m3、图示三铰拱K截面倾角ϕ = 2633'(sinϕ = ,cosϕ = ),计算K截面内力MK,NK。
y=41642fx l x l l f()/,(,)-==m m4m4m 8m4、计算图示半圆拱K 截面弯矩。
5、计算图示桁架中杆1、2、3的内力。
6、计算图示桁架中杆1,2的内力。
P1.5m 1.5m7、计算图示桁架中杆1 ,2的内力。
P a /2a 8、计算图示桁架中杆1,2,3的内力。
40kN4m 4m4m4m9、计算图示桁架杆1、2的内力。
10、计算图示桁架杆1、2、3的内力。
aaaa11、计算图示桁架杆1、2的内力。
/2a /2a /3/3/312、计算图示桁架杆1、2的内力。
a a13、计算图示桁架结构杆1、2的轴力。
d dd2/d2/14、计算图示桁架结构杆1、2的轴力。
15、计算图示桁架杆1、2的轴力。
16、计算图示桁架中a杆的内力N a,d = 3m。
d d d d17、计算图示桁架杆a、b的内力。
4a18、计算图示桁架杆1、2的内力。
4m3m2m19、计算图示桁架杆件a 的内力。
4m4m20、计算图示桁架杆a、b的内力。
4449m60kN3m21、计算图示桁架杆1、2的内力。
aaa22、计算图示桁架各杆轴力及反力。
4m4m23、作图示结构的M 图并求杆1的轴力。
l ll l l l l24、作图示结构的M 图并求链杆的轴力。
d =4m 。
40kN md5kN25、作图示结构弯矩图。
m mm第二章 静定结构内力计算(参考答案)一、是非题:1、(O )2、(X )3、(O )4、(O )5、(O )6、(O )7、(X ) 8、(X )9、(O ) 10、(X ) 11、(O )12、(O ) 13、(O )14、(X ) 15、(X ) 16、(O ) 17、(X )18、(O )19、(O )二、选择题:1、(A )2、(B )3、(C )4、(C ) 5、(A )6、(A )7、(B )8、(B )三、填充题:1、 2 外侧2、 0 , 03、 CB , CD (或 ACD )4、 –8kN5、–30kN6、30kN7、–30kN ·m ,50kN ·m8、–30,–qa /2(()3212-, (–qa /2)cos(–30)–(qa /2)sin(–30)9、 Pd ,下,–P ,010、P11、有 , 无 12、30 kN(↑)13、N 1102=-kN ,M K =⋅20kN m 14、20kN 15、4P , 0四、作图题:1、 2、m 0m 0m0m 021213434Pa +1.5BCD40120图 M ()kN .m A 4080403、 4、2PaPa PaM 图Pa602040M 图5、 6、8082618M 图 M 图7、 8、212qh qh22 M 图122qa M 图9、 10、PaPaM 图PaPaM 图11、 12、211421m 0mm34mm 021M 图PaPaPaPaPa PaM 图13、 14、3Pa1.53.552PaPa PaPaM图图M m CAB15、 16、m/2m /2m M 图图M PlPl2Pl ABC D17、 18、图 M ()kN .m 16040253.3216.6160Pa Pa 3PaPaPaPa Pa2 M 图19、 20、R A ql H 0M B B ql 0.5( )图M Bql0.522______Aql20.5ql2ql20.5图M DCBA21、22、()图M kN .m AB151515151515C D E F 1515Pa 2/3图Pa 2/3Pa 2/3Pa 2/3M AB23、 24、图M 2Pa2Pa 2Pa Pa6Pa 6ABC D E FG图M 2qa 22qa 22qa 22qa 2qa225、 26、图M2ql 2/2ql 2/图M ql /2227、 28、0.50.1250.5M 图(ql 2)3030M 图29、 30、10101010101010M图 mm m /2m /2M 图31、 32、PM 图PaPaPaPa PaPa Pa Pa Pa 2Pa2 M 图33、 34、M 图M 图35、 36、kN-N =28.8363654544M 图37、、().图 M kN m图M qa 22qa 2239、 40、PaPa2图MmmmM 图41、 42、2121mmm 0m 0m 02121M图ABC EDF Pa Pa 1323M 图43、 44、图M ql 28ql223ABDCPlPl/2Pl /2Pl 图M45、 46、qa2M 图PlPl M 图47、 48、kNX M 图49、 50、1Pl 2Pl 4Pl 34M 图Pl 2N 1= -P8812121818M 图51、 52、M 图M 图53、 54、PaPaPaPa2M 图图55、 56、48120120M图图 M ()kN .m57、 58、321611212图 M ()kN .m图M59、 60、12M 图3Pl 3Pl 3Pl 4Q 图(kN)1515().图 M kN m 555512.55157.512.52N 图 (kN)15N P 1223=-/N P 2223=-/五、计算题:1、H = 3Kn ,M K =– kN m ⋅,N K =–2、H = 3kN ()→←,M K = 2kN ·m ,N K =– kN3、M K =⋅15kN m ( 下 拉 ),N k =-4470.kN4、)(289.0),(5.0→←=↑=P H P V ,K A A M V R R H RPR =--⋅=-().2200585、N = 0 ,N = 4P (拉 ),N P 35=- (压)6、N 1= 3 = (拉),N 2=-2P /3 =- (压)7、N 1 =–P /2( 压 ),N 2 =–P ( 压 )8、N 1= 120kN (拉),N 2= 0,N 3= 198kN (拉) 9、 N 10=, N P 22=10、N 10=,N P 2=,N P 322=/11、N P 2=,N P 106=.12、对 称 情 况 : N N 120''==,N N N P 1112=+=-'"反 对 称 情 况 : N N P 122""=-=-,N N N P 2222=+='"13、N P N P 1222236=-=,. 14、N P N P 1205=-=-.,15、N 1 =5P /2,N 2 = P 16、N a =-20kN17、N P a =354,N b =018、 N = 0,N = –4/3P 19、N a =-2P /320、 N 1=P ,N 21414=-.P 21、N a =–100 kN ,b N =022、7Pl/6图M 7Pl/6N P 12=24、 25、)kN m )kN图M。
