用几何画板动态演示正弦曲线
教师资格考试高中数学学科知识与教学能力2024年下半年测试试题及答案解析

2024年下半年教师资格考试高中数学学科知识与教学能力测试试题及答案解析一、单项选择题(本大题有8小题,每小题5分,共40分)1.题目:若函数f(x) = x^3 - 3x^2 + ax + b 在x = 1 处取得极值,则a 的值为( )A. 0B. 1C. 3D. -3答案:C解析:首先求函数 f(x) = x^3 - 3x^2 + ax + b 的导数。
f’(x) = 3x^2 - 6x + a由于函数在 x = 1 处取得极值,根据极值的性质,函数在该点的导数为0。
f’(1) = 3(1)^2 - 6(1) + a = 0即 3 - 6 + a = 0解得 a = 3。
2.题目:已知函数f(x) = sin(2x + φ) (0 < φ < π) 的图象关于直线x = π/6 对称,则φ的值为( )A. π/6B. π/3C. 2π/3D. 5π/6答案:B解析:由于正弦函数f(x) = sin(2x + φ) 的图象关于直线x = π/6 对称,根据正弦函数的对称性,有:2 (π/6) + φ = kπ + π/2,其中k ∈ Z化简得:φ = kπ + π/6但由于0 < φ < π,唯一满足条件的是φ = π/3。
3.题目:若直线y = kx + 1 与圆x^2 + y^2 - 2x - 4y = 0 相交于M, N 两点,且OM⊥ ON (O 为坐标原点),则k 的值为( )A. 1B. -1C. 7 或-1D. 7答案:D解析:首先,将圆的方程 x^2 + y^2 - 2x - 4y = 0 化为标准形式:(x - 1)^2 + (y - 2)^2 = 5圆心为O’(1, 2),半径为√5。
设交点 M(x1, y1), N(x2, y2),联立直线和圆的方程:{ y = kx + 1{ x^2 + y^2 - 2x - 4y = 0消去 y,得到关于 x 的二次方程,并利用韦达定理求出 x1 + x2 和 x1x2。
几何画板在正弦型函数教学中的应用

几何画板在正弦型函数教学中的应用各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢几何画板在正弦型函数教学中的应用文/高杰谢志林摘要:“几何画板”在图像的动态化和“形”和“数”的同步化上具有较大的优势,是一个适合数学教学的辅助教学工具软件。
正弦型函数内容较抽象,运用几何画板进行教学,探索正弦型函数图像随参数变化的规律,以实现数学教学的直观化与动态化。
关键词:几何画板;正弦型函数;应用传统的数学教学是教师用粉笔、直尺、三角板和圆规等工具在黑板作图,不仅图像不精确,而且又浪费大量的课堂时间,降低了课堂教学的效率,画出来的图像被固定化在黑板上,不能动态描述图像的运动、变化规律。
结果往往是教师口干舌燥,学生感到枯燥无味。
而借助于几何画板,我们比较容易地解决了上述问题。
几何画板画图的方便性、准确性、图形的几何关系不变性和强大的度量、计算、解题功能,以及巧妙的图形变换和动画功能,正好可以满足数学教学中数形结合、图形变换、几何建构及教学问题情境的创设等需要。
在实际教学实践中,我们利用结合画板研究函数知识,收到了良好的效果,下面以正弦型函数为例,探讨利用几何画板研究函数的一般方法:一、动态演示正弦型函数y=Asin中A的作用1.绘制函数y=sin的图像;2.创建新参数A并动画参数A;3.绘制新函数y=Asin,动画参数A,学生可以直观地观察到图像随参数A改变而产生的变化,从而顺利总结出规律:A改变函数的振幅;4.学生自己操作参数A,观察函数图像的变化。
二、动态演示ω的作用1.创建新参数ω,并动画参数ω;2.绘制函数y=4sin,并动画参数ω,随着参数ω的变化,图像会像弹簧一样压缩、扩张,能充分展示参数ω的作用:ω改变函数的周期。
三、演示初相φ的作用1.创建参数φ;2.绘制函数y=4sin;3.改变参数φ的值观察图像的变化,并总结规律:φ导致图像平移。
四、总结有了上述动态直观的准备之后,学生可以自己操作参数,通过观察图像随参数的变化,系统总结出函数y=Asin的图像与函数y=sin之间的关系,从而在更高层次上理解运用此规律。
玲珑画板基本教程-3动态函数6. 综合应用(几种不同的办法做动态正弦函数)

如何使用玲珑画板画动态函数(之六)几种不同的办法做动态正弦函数一、学习目标用五种不同的办法做正弦函数的动态演示。
二、<通过计算值生成点轨迹办法>作图步骤2.1 作图思路:先创建一个参数a,范围置为0——2*pi,绑定到变量点。
然后创建一个测量值:sin(a)。
再在坐标系内,创建一个<双参数坐标点>。
最后由这个双参数坐标点生成动画点轨迹。
2.2引入坐标系,单击工具栏,2.3单击菜单:参数/添加参数。
2.4画一条线及线上一点,双击参数a,输入最大值为:2*pi,在画面上只选中那个线上的点,单击按钮[绑定动点]。
确定后,拖动变量点,可以看到参数的变化了。
2.5单击菜单:测量/计算…。
输入sin(a)。
2.6创建双参数坐标点。
单击菜单:参数/添加双参数坐标点。
设置范围:X从0到2*pi。
只选中参数a,单击[X参数]。
只选中测量值sin(a),单击[Y参数]。
单击[添加坐标点]。
则坐标系内新增了一个点,拖动变量点时,这个点在坐标系内随之运动。
2.7单击菜单:动画/动画点线轨迹。
2.8 只选中变量点,单击[轨迹变量点]。
只选中坐标系中的参数坐标点,单击[创建轨迹对象]。
则画面上出现一条正弦轨迹线,双击这条正弦线,修改属性。
三、<通过计算值生成可擦除的点轨迹办法>作图步骤3.1 作图思路:与第二办法思路一样,只是生成的轨迹方法不同,可擦除。
3.2 与前例一样直到2.7。
3.8只选中坐标系中的参数坐标点,单击[添加轨迹点]。
则拖动变量点会有轨迹产生。
如想擦除轨迹,按Esc键。
如要永久删除轨迹,单击[取消所有轨迹]。
四、<通过计算值生成测量值轨迹办法>作图步骤4.1 作图思路:先创建一个参数a,范围置为0——2*pi,绑定到变量点。
然后创建一个测量值:sin(a)。
由测量值及动画点,生成测量值点轨迹。
4.2 与第一例一样直到2.5。
4.6 单击菜单:动画/测量值点轨迹。
正弦函数的图像课件

通过掌握正弦函数的性质和图像, 可以解决许多实际问题,提高解决 实际问题的能力和素养。
未来研究方向和挑战
深入研究和探索
随着科学技术的发展,正弦函数的应用领域也在 不断扩大和深化,需要进一步研究和探索其性质 和应用。
数值分析和计算物理
随着计算机技术的发展,如何利用正弦函数进行 数值分析和计算物理的研究也是未来的一个重要 方向。
数学建模和算法设计
如何利用正弦函数建立数学模型和设计算法,是 未来研究的一个重要方向。
跨学科应用
正弦函数作为数学中的基础函数,可以与其他学 科进行交叉融合,例如与物理学、工程学、经济 学等学科的结合,需要进一步探索其跨学科应用 的价值和可能性。
THANKS
感谢观看
图像形状
正弦函数和对数函数的图像形状也不同。正弦函数的图像呈现波形,而对数函数的图像 呈现向上或向下凸出的趋势。
05
总结与展望
正弦函数的重要性和应用价值
数学基础
正弦函数是数学中的基本函数之 一,是学习三角函数、复数、微
积分等数学领域的基础。
应用广泛
正弦函数在物理学、工程学、经济 学等多个领域都有广泛的应用,例 如振动分析、交流电、信号处理等 。
振幅和相位
通过调整正弦函数中的振幅和相位参 数,可以改变图像的高度和位置。了 解这些参数对理解正弦函数图像的影 响非常重要。
03
正弦函数的应用
在物理中的应用
简谐振动
正弦函数描述了许多物理现象, 如简谐振动。在物理中,简谐振 动是一种基本的振动类型,其位 移与时间的关系通常可以用正弦
函数表示。
交流电
操作步骤
在软件中选择相应的函数图像绘制工具,输入正弦函数公式(例如y=sin(x)), 然后选择x的取值范围(例如-π到π),最后点击“绘制”按钮即可生成正弦函数 的图像。
几何画板描点画线绘制正选函数一个周期图像
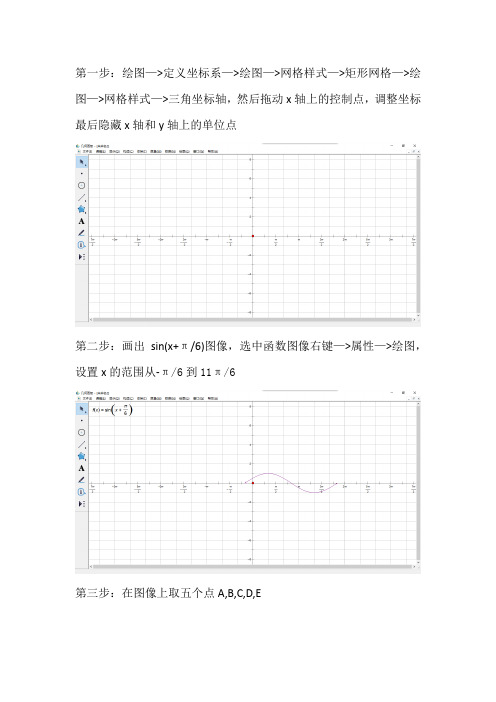
第一步:绘图—>定义坐标系—>绘图—>网格样式—>矩形网格—>绘图—>网格样式—>三角坐标轴,然后拖动x轴上的控制点,调整坐标最后隐藏x轴和y轴上的单位点
第二步:画出sin(x+π/6)图像,选中函数图像右键—>属性—>绘图,设置x的范围从-π/6到11π/6
第三步:在图像上取五个点A,B,C,D,E
第四步:选中点A—>编辑—>操作类按钮—>显示/隐藏,对点BCDE 做同样的操作
第五步:选中所有的五个操作按钮—>编辑—>操作类按钮—>序列,选择依序执行,时间选1s
第六步:在函数图像上任取一个点,编辑—>操作类按钮—>显示/隐藏,然后是:显示—>生成点的动画(把动画暂停),接着是:显示—>操作类按钮—>动画,设置动画方向为向前
第六步:选中刚才的动点,显示—>追踪点。
做好上面的步骤后,选中函数图像—>右键,隐藏函数图像—>点击顺序5个动作—>隐藏点。
最后开始演示:点击顺序5个动作—>点击隐藏点—>点击动画点。
1.4.1正弦、余弦函数的图象

正弦函数的图象
y=sinx ( x∈[0,2] )
2 y
5
6
3
2
31
6
● ●
●
7
6 4
2
●
0
11
3 5 6 -1
632
3 23
●
7 4 3 5 11
●
6 3 2 3 6 2
2 5 ●
(2)用五点作图法画正弦、余弦函数的简图
作业:1.课本P46. 1题,《导学案》1题
2.预习1.4.2
函数y=sinx, x[0,2]
y
1
. 函数y=sinx, x[0,2]的图象
.
.
.
o /2 3/2 2
xห้องสมุดไป่ตู้
-1
.
关键点:
(0,0)、(
2
,1)、(
,
0)、(
3
2
,-1)、(
2
,
0)
y=sinx的图象与y=cosx的图象之间的关系
y=cosx=sin(x + ), xR
2
y y = sin x, x∈R 1
x
0
sinx 0
2
3
2
2
1 0 -1 0
1+sinx 1
21 0 1
y
2
y=1+sinx,x[0, 2]
1
o
2
-1●
● 2
●
y=sinx,x[0, 2]
3
2
x
2
●
用几何画板动态演示正弦曲线

HMR($% 3HNR12+HV(红色)和正弦曲线 ; H8
(黑色) 重合 B ($%&
常生活中发现的一些问题进行研究, 培 养学生的数学学习兴趣和数学应用意识B 课本中介绍了用图解法解决线性规 划最优解问题B 首先根据给定的实际问 题建立数学模型,即先根据实际条件找 出两个自变量的可能取值范围,然后寻 找出可行域(由几个二元一次不等式确 定的平面区域) B 建立要寻找最值的量的
3:; 在 振 幅 线 上 任 取 三 点 < 、 =、 > , 分 离 出 这 三 点 的 纵 坐 标 ?<、 ?=、 ?@, 拖 动 <、 =、 @ 使 ?<8/ 、 ?=80 、 ?@ 8
角 频 率 线 上 任 取 三 点 D、 分 ABC ; E、 F, 离出这三点的纵坐标 ?G、 拖动 HI、 HF, 标出相 G、 I、 F 使 HG8/、 HI80 、 HF8ABC ; 位线和 1 轴的交点 J , 在相位线上任 取一点 K ,分离出这点的纵坐标 HK, 拖动点 K 使 HK8/BCLB 分离 3C; 在振幅线上任取一点 M, 出 这 点 的 纵 坐 标 HM;在 角 频 率 线 上 任 取 一 点 N, 分 离 出 这 点 的 纵 坐 标 在 相 位 线 上 任 取 一 点 P, 分离出 ?O; 这 点 的 纵 坐 标 HP; 计 算 HQR($% 现在若想看振幅变化情况, 只要分别 双击三个振幅按钮就会出现相应的效果; 若想看角频率、 相位变化情况, 只需分别 双击另外两组中的相应按钮即可 B 二、 综合变化 (接着上面) : 在其上分别取五点, 3[; 任 划 五 个 圆 , 分别作出这五点绕各自的圆周双向、 慢速 的动画按钮, 并改标签为 “动 画 Z ” 、 “动 画 、 “ 动 画 9” 、 “ 动 画 :” 、 “ 动 画 C” (这 五 个 0” 按钮添加到下面的 “序列” 按钮时, 有延迟 动作的效果) B 、 3\; 先后选择按钮 “振幅增大 0 倍” “动 画 Z ” 、 “角 频 率 扩 大 0 倍 ” 、 “ 动 画 0” 、 “相 位 增 加 ZBCL ” 、 “ 动 画 9” 、 “还 原 振 幅 ” 、 “动画 : ” 、 “ 还原角频率” 、 “ 动画 C ” 、 “ 还原 相位” , 点 击 5 编 辑 6 U 5 按 钮 6 U 5 序 列 6, 制作出 “序列” 按钮 B
正弦函数、余弦函数的图像及五点法作图

正弦函数、余弦函数的图像及五点法作图
【函数y=sinx的图象】
把角x (x∈R)的正弦线平行移动,使得正弦线的起 点与x轴上相应的点x重合,则正弦线的终点的轨迹 就是正弦函数y=sinx的图象.
y=cosx的图象. 正弦函数y=sinx的图象和余弦函数y=cosx的图象 分别叫做正弦曲线和余弦曲线.
正弦函数、余弦函数的图像及五点法作图
【余弦函数y=cosx的图象】
-6 -5 -6 -5
-4 -3 -4 -3Leabharlann -2 --2-
y y=sinx
1
o
-1
y y=cosx
1
正弦函数、余弦函数的图像及五点法作图
【余弦函数y=cosx的图象】
也可以用“旋转法”把角 的余弦线“竖立”(把
角置诱x=x,导si的n则公x余的式O弦1图cM线o象s1与Ox向1OM左1sM按i平n长(逆移x度时 2相2针)单等方,还位,向可即方旋以得向转把余相2正弦同到弦函.O)函数1M根数1据位
知识点——
正弦函数、余弦函数 的图像及五点法作图
正弦函数、余弦函数的图像及五点法作图
【函数y=sinx的图象】
第一步:在直角坐标系的x轴上任取一点O1 ,以O1 为圆心作单位圆,从这个圆与x轴的交点A起把圆分
成n(这里n=12)等份.把x轴上从0到2π这一段分成n(
这里n=12)等份.(预备:取自变量x值—弧度制下角
(0,1) ( ,0) (,-1) (3 ,0) (2,1)
2
2
只要这五个点描出后,图象的形状就基本
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电脑天地
3HNR1S+HV;B
“序 列 ” 按钮外, 隐藏其它的 3Z]; 除 按钮、 五个圆及图面上所有的点B 现在双击 “序列” 按钮, 就会先看到 增大振幅的效果, 然后再单击 “序列” 按 钮就会看到增大角频率、增大相位、 还 原到正弦曲线的效果 B
用几何画板动态 演示正弦曲线
3W; 分别制作 M 到 <、 M 到 =、 M到@的
本
课件是在 《几何画板》 环境中制 作的,用鼠标点击按钮就可动
态 地 显 示 正 弦 曲 线 !"#$%& 向 正 弦 型 曲线 !"’($%)*&+,- 的变化过程 . 一、 单项变化: (/) 进入 《几何画板》 工作界面, 建 立平面直角坐标系, 调整单位长度. (0) 在 1 轴 上 任 取 一 点 2, 分离 出这点的横坐标 12,然后计算出 ($% 以 (12, 为坐标画 点 4 (设 312-, ($%312-) 点击5构 置为黑色) , 先后选择点 2、 4, 造6 7 5轨迹6, 就作出正弦曲线 !8($%&. (9 ) 画三条与 1 轴垂直的直线, 从左到右依次设标签为 “调节振 幅” 、 “调 节 角 频 率 ” 、 “调 节 相 位 ” .
WA :CA /AA
:A /CA 0AA
/0AA WLCA CAAA
我们设 & 为甲产品生产数量, !为 乙产品生产数量 B 则目标函数为 ^8C]&+
3HNR1S +HP; 的 值 ; 以(1S, HMR($%
为坐标画点 T (设置为红 3HNR1S+HP; ) 色) ; 先 后 选 择 点 S、 点击5构 造6 U T,
表达式, 即目标函数, 目标函数的最优解 可以借助平移目标函数对应直线获得B 例如: 某企业生产两种产品, 甲产 品每台利润 C] 元, 乙 产 品 每 台 利 润 \] 元,有关生产用的资源如下表所示, 求 当企业利润最大时两种产品的产量 B 表: 甲、 乙产品的生产用资源
资源名称 原材料 设备 劳动力 单位产品消耗定额 可利用资源 甲产品 乙产品
\]! ,其中 & 、 ! 应该满足 的 线 性 约 束 条 W]&+:]!!Z0]] , !
# :C]&+ZC]!!WLC]_ 件为" /]]&+0]]! !C]]]‘ #
5 轨迹 6 ,就作出正弦型曲线 !8HMR($%
&"A‘!"AB $
W:
3:; 在 振 幅 线 上 任 取 三 点 < 、 =、 > , 分 离 出 这 三 点 的 纵 坐 标 ?<、 ?=、 ?@, 拖 动 <、 =、 @ 使 ?<8/ 、 ?=80 、 ?@ 8
角 频 率 线 上 任 取 三 点 D、 分 ABC ; E、 F, 离出这三点的纵坐标 ?G、 拖动 HI、 HF, 标出相 G、 I、 F 使 HG8/、 HI80 、 HF8ABC ; 位线和 1 轴的交点 J , 在相位线上任 取一点 K ,分离出这点的纵坐标 HK, 拖动点 K 使 HK8/BCLB 分离 3C; 在振幅线上任取一点 M, 出 这 点 的 纵 坐 标 HM;在 角 频 率 线 上 任 取 一 点 N, 分 离 出 这 点 的 纵 坐 标 在 相 位 线 上 任 取 一 点 P, 分离出 ?O; 这 点 的 纵 坐 标 HP; 计 算 HQR($% 现在若想看振幅变化情况, 只要分别 双击三个振幅按钮就会出现相应的效果; 若想看角频率、 相位变化情况, 只需分别 双击另外两组中的相应按钮即可 B 二、 综合变化 (接着上面) : 在其上分别取五点, 3[; 任 划 五 个 圆 , 分别作出这五点绕各自的圆周双向、 慢速 的动画按钮, 并改标签为 “动 画 Z ” 、 “动 画 、 “ 动 画 9” 、 “ 动 画 :” 、 “ 动 画 C” (这 五 个 0” 按钮添加到下面的 “序列” 按钮时, 有延迟 动作的效果) B 、 3\; 先后选择按钮 “振幅增大 0 倍” “动 画 Z ” 、 “角 频 率 扩 大 0 倍 ” 、 “ 动 画 0” 、 “相 位 增 加 ZBCL ” 、 “ 动 画 9” 、 “还 原 振 幅 ” 、 “动画 : ” 、 “ 还原角频率” 、 “ 动画 C ” 、 “ 还原 相位” , 点 击 5 编 辑 6 U 5 按 钮 6 U 5 序 列 6, 制作出 “序列” 按钮 B
Y 的 运 动 按 钮 ,并 改 标 记 为 “相 位 增 加
、 “还 原 相 位 ” (上 面 运 动ห้องสมุดไป่ตู้按 钮 都 设 置 ZBCL” 为慢速) B 点击 3L; 隐藏图面上测算的所有数据, 三个 “还原” 按钮就可看到正弦型曲线 H8
用几何画板研究 线性规划最优解问题
线
性规划是师范数学教材的新增内 容, 它可以让学生从数学角度对日
HMR($% 3HNR12+HV(红色)和正弦曲线 ; H8
(黑色) 重合 B ($%&
常生活中发现的一些问题进行研究, 培 养学生的数学学习兴趣和数学应用意识B 课本中介绍了用图解法解决线性规 划最优解问题B 首先根据给定的实际问 题建立数学模型,即先根据实际条件找 出两个自变量的可能取值范围,然后寻 找出可行域(由几个二元一次不等式确 定的平面区域) B 建立要寻找最值的量的
