§相对运动
理论力学 第八章

x o ' = x o ' (t ) 牵连运动方程 y o ' = y o ' ( t ) = ( t )
动系与定系之间的坐标变换关系
x = xO′ + x′ cos y′sin y = yO′ + x′ sin + y′ cos
沿半径为r的圆 例8-1 点M相对于动系 Ox′y′ 沿半径为 的圆 相对于动系 周以速度v作匀速圆周运动 圆心为O 作匀速圆周运动(圆心为 周以速度 作匀速圆周运动 圆心为 1 ) ,动系x′y′ O Oxy 以匀角速度ω绕点 作定轴转动, 相对于定系 以匀角速度 绕点O作定轴转动, 绕点 作定轴转动 如图所示。 重合, 重合。 如图所示。初始时x′y′ 与 与 重合 O Oxy 重合,点M与O重合。 的绝对运动方程。 求:点M的绝对运动方程。 的绝对运动方程
. 已知: 已知 ω, OA, = r, OO1 = l, OA水平 求: ω1 = ?
解:
1.动点:滑块A . 动系:摇杆AB 2. 运动分析 绝对运动:绕O点的圆周运动
相对运动:沿O1B的直线运动 牵连运动:绕O1轴定轴转动
√ √ √
3.
ve = va sin = ωr
r
2 2
l +r ve r2ω ∴ω1 = = 2 2 O A l +r 1
4. 绝对运动方程 vt vt x = x′ cos y′ sin = r1 cos r cosωt r sin r sin ωt y = x′ sin + y′ cos = r1 cos vt sin ωt + r sin vt co-3 用车刀切削工件的直径端面,车刀刀尖 M沿水平轴 作往复运动,如图所示。设oxy为定坐 沿水平轴x作往复运动 沿水平轴 作往复运动,如图所示。 为定坐 标系,刀尖的运动方程为 x = bsin (ωt ) 。工件以 标系, 逆时针转向转动。 等角速度 ω逆时针转向转动。 求:车刀在工件圆端面上切出的痕迹。 车刀在工件圆端面上切出的痕迹。
大学物理3相对运动

极坐标系
极坐标系是一种以原点为中心,通过极径和极角来表示物体位置和运动的坐标系。在处理某些相对运动问题时,极坐 标系可能更加方便。
自然坐标系
自然坐标系是一种以物体运动轨迹为轴的坐标系,通过角度和距离来表示物体的位置和运动状态。在处 理曲线运动的相对运动问题时,自然坐标系可能更加直观。
大学物理3相对运动
目录
• 引言 • 相对运动的基本概念 • 相对运动的基本定律 • 相对运动的实例分析 • 相对运动的数学表达 • 相对运动的实验验证 • 结论
01 引言
主题简介
相对运动的概念
相对运动是指两个或多个物体在空间中相对于彼此的 运动,是大学物理中的一个重要概念。
相对运动的分类
根据参照物的不同,相对运动可以分为匀速运动和变 速运动。
牛顿第三定律
总结词
描述了作用力和反作用力的关系。
详细描述
牛顿第三定律指出,对于两个相互作用力,它们的大小相等、方向相反,作用在同一条 直线上。公式表示为F=-F',其中F和F'是一对相互作用力。
04 相对运动的实例分析
两物体间的相对运动
定义
01
两物体间的相对运动是指一个物体相对于另一个物体的位置和
相对运动在科学研究中的应用
相对运动在科学研究中也具有广泛的应用,例如天文学中研究行星运动 规律需要用到相对运动的概念,地球物理学中研究地震波传播也需要用 到相对运动的知识。
02 相对运动的基本概念
相对位置和绝对位置
相对位置
描述一个物体相对于另一个物体 的位置,以另一个物体为参考点 。
相对运动

牛顿定律的几点说明 1. 牛顿定律只适用于惯性系 2.牛顿第二定律只适用于质点或可看作质点的物体 2.牛顿第二定律只适用于质点或可看作质点的物体
v v 中 v 是物体所受合外力 3. F = ma F 是物体所受合外力
v v 体的质量保持不变时才和 F = ma 等价 r r r d(mv ) r dv r r =m F= = ma d p = F dt dt dt
2.电磁力 2.电磁力
N m /kg
2
2
电磁力: 电磁力 : 存在于静止电荷之间的电性力以及存在 于运动电荷之间的磁性力,总称为电磁力。 于运动电荷之间的磁性力,总称为电磁力。 例如: 弹力、 摩擦力, 气体的压力、 浮力、 例如 : 弹力 、 摩擦力 , 气体的压力 、 浮力 、 粘滞 阻力。 阻力。 3.强力 3.强力 4.弱力 4.弱力
三、牛顿第三定律
对于每一个作用力,总有一个对应的反作用力; 对于每一个作用力,总有一个对应的反作用力; 两者大小相等、方向相反、在同一直线上。 两者大小相等、方向相反、在同一直线上。 数学表达式: 数学表达式:
r r F12 = F21
注意:1.作用力与反作用力同生同灭。 注意:1.作用力与反作用力同生同灭。 :1.作用力与反作用力同生同灭 2.作用力与反作用力分别作用于两个不同的 2.作用力与反作用力分别作用于两个不同的 物体上 3.作用力与反作用力性质相同。 3.作用力与反作用力性质相同。 作用力与反作用力性质相同
v
x
二、常见力
1.重力 1.重力(gravity) 重力 重力:在地球表面的物体, 重力 : 在地球表面的物体 , 受到地球的吸引而使物 体受到的力。 体受到的力。
r r G = mg
机械原理 第二章-2相对运动图解、解析
方向:? A B
§3-3 用矢量方程图解法作机构速度和加速度分析 D A B C D A B C
大小: ? ? B 大小: ? B ? 方向: A D 方向: A D
C
C
D A B C
2-3 用相对运动图解法求机构的速度和加速度
一、矢量方程图解法的基本原理和作法
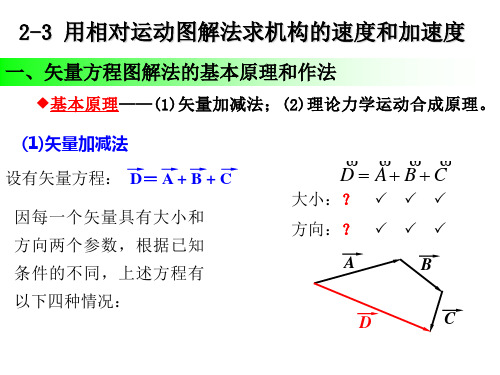
基本原理——(1)矢量加减法;(2)理论力学运动合成原理。
(1)矢量加减法
设有矢量方程: D= A + B + C 因每一个矢量具有大小和 方向两个参数,根据已知 条件的不同,上述方程有 以下四种情况: D C
D A B C
实际尺寸 取长度比例尺 l m / m m, 作机构运动简图。 图示尺寸
(1) 速度关系:
①根据运动合成原理,列出速度矢量方程式:
VC2 VB2 VC2B2
ω1lAB ?
大小: ?
方向: ∥xx ⊥AB ⊥BC ②确定速度图解比例尺μv( (m/s)/mm) ③作图求解未知量: 速度多边形
大小: ?
方向: ? A D
B C
特别注意矢 量箭头方向!
(2) 理论力学运动合成原理
绝对运动 = 牵连运动 + 相对运动 作法:1)根据运动合成原理 —— 列出矢量方程式。
2)根据矢量方程式 —— 作图求解。
构件间的相对运动问题可分为两类:
同一构件上的两点间的运动关系
(4) 求aE6和6
2
A
ω3 a3 5
akE6E5 =
n3
b
25vrE6E5
B ω4
ω2
相对性运动常见力和基本力课件

动量守恒定律适用于封闭系统,即系统不受外界作用力或系统所受的外力矢量 和为零。在碰撞、爆炸等物理过程中,动量守恒定律确保系统内各物体动量的 矢量和保持不变。
动能定理
总结词
动能定理揭示了力对物体运动状态改变的作 用效果,即合外力对物体所做的功等于物体 动能的改变量。
详细描述
动能定理指出,在运动过程中,合外力对物 体所做的功等于物体动能的增加量。这意味 着力对物体的作用会导致物体运动状态的改 变,即速度和方向的改变。动能定理广泛应 用于分析物体的运动轨迹、速度和加速度等 问题。
动能定理
动能定理指出,力对物体 所做的功等于物体动能的 增量。
相对性运动的应用场景
车辆动力学
车辆动力学是研究车辆在行驶过程中 受到的力和运动规律的科学,相对性 运动在车辆动力学中有着广泛的应用 。
航空航天工程
体育运动
在体育运动中,相对性运动原理可以 帮助运动员更好地理解技术动作和提 高运动表现。
航空航天工程中,飞行器的运动涉及 到复杂的力和运动关系,相对性运动 是理解和分析这些关系的重要工具。
潮汐现象
由于地球自转和月球引力作用,海水 周期性的涨落现象。潮汐能对海岸线 地貌和海洋生态系统产生影响。
火箭的发射与推进力
火箭发射
利用推进剂在发动机内燃烧产生高速 气体,通过喷嘴向下喷出,产生反作 用力使火箭升空。
推进力
火箭发动机产生的推力,使火箭克服 重力上升或前进。推进力的大小和方 向影响火箭的运动轨迹。
优化产品设计
在产品设计和制造过程中,相对性运动理论的应用可以帮助工程师更好地预测和控制产品 的运动性能,提高产品的稳定性和可靠性。例如,在机械、航空、船舶等领域,相对性运 动理论的应用可以帮助优化机器部件的配合和整体性能。
相对运动问题解题技巧

相对运动问题解题技巧一、相对运动问题的基本概念1.相对运动的定义相对运动是指两个物体之间的相对运动状态。
当两个物体之间有相对运动时,我们称其中一个物体相对于另一个物体的运动状态为相对运动。
在相对运动中,我们通常会考虑两个物体之间的相对速度、相对加速度等物理量。
2.相对速度的概念相对速度是指一个物体相对于另一个物体的速度。
在相对运动中,我们通常用一个固定参照物体作为参考,通过比较两个物体的速度来确定它们之间的相对速度。
相对速度的方向可以是同向、相反或者垂直等不同情况。
3.相对加速度的概念相对加速度是指一个物体相对于另一个物体的加速度。
在相对运动中,两个物体之间的相对加速度可以反映它们之间的加速度差异。
相对加速度可以是同方向、相反方向或者垂直等不同情况。
二、相对运动问题的解题技巧1.确定参照物体在解决相对运动问题时,首先需要确定一个固定的参照物体作为参考。
这个参照物体可以是地面、某个物体或者某个坐标系,通过确定参照物体可以更清晰地描述两个物体之间的相对运动关系。
2.建立坐标系在确定参照物体之后,我们需要建立一个适当的坐标系来描述两个物体的位置和运动情况。
建立坐标系是解决相对运动问题的关键步骤,可以帮助我们更准确地计算两个物体之间的相对速度、相对加速度等物理量。
3.分析相对运动的方向在解决相对运动问题时,需要分析两个物体之间的相对运动方向。
根据相对运动的方向不同,我们可以将问题转化为同向、相反或者垂直等不同情况,从而更好地理解两个物体之间的相对运动关系。
4.应用运动方程在确定参照物体、建立坐标系和分析相对运动方向之后,我们可以根据运动方程来解决相对运动问题。
通过应用运动方程,我们可以计算出两个物体之间的相对速度、相对加速度等物理量,从而解决相对运动问题。
5.考虑相对速度和相对加速度在解决相对运动问题时,需要考虑两个物体之间的相对速度和相对加速度。
相对速度和相对加速度可以反映两个物体之间的速度差异和加速度差异,通过这些物理量可以更清晰地描述两个物体之间的相对运动状态。
相对运动知识点总结

相对运动知识点总结相对运动的基本概念可以通过以下几个方面来进行总结:1. 参考系的选择在研究相对运动时,我们需要选择一个参考系作为基准。
参考系是一个用来描述物体位置和运动状态的参照物,可以是固定不动的地面、运动的车厢、飞机等等。
在选择参考系时,需要考虑到对问题的便捷性和简化处理,以及使得问题能够得以解决。
同时,在选择参考系时,需要根据具体情况选择合适的参考系以便于解题。
2. 相对位置和相对速度在不同的参考系中,同一物体的位置和速度可能会有不同的描述。
这就涉及到相对位置和相对速度的概念。
相对位置指的是物体在不同参考系中的位置关系,而相对速度则是物体在不同参考系中的速度关系。
由于相对位置和相对速度的存在,同一物体的运动状态可能会出现不同的描述。
3. 相对运动的描述描述相对运动的一种方法是通过参考系之间的转换。
在不同参考系中,同一物体的位置和速度可以用不同的方式来描述,因此需要进行参考系的转换。
当我们改变参考系时,物体的位置和速度也会相应的发生改变。
这就需要我们通过相对运动的转换公式和方法来确定物体在不同参考系中的位置和速度。
4. 相对运动的应用相对运动的理论可以应用到很多不同的领域中。
在物理学中,相对运动的概念是研究力学、动力学和运动学的基础。
在工程学和技术领域中,相对运动理论也被广泛应用到机械运动、车辆运动和航天器运动的研究与设计中。
在日常生活中,相对运动的概念可以帮助我们理解和解释很多日常现象,比如车辆行驶、人体运动等。
总的来说,相对运动是一个涉及到物理学、工程学和日常生活的重要概念。
通过对相对运动的理解,我们可以更好地理解和描述物体的运动状态,从而提高我们对物体运动的认识和理解。
相对运动的知识对于我们解决各种物理问题和工程问题都有很大的帮助,因此深入研究和理解相对运动的概念是非常有意义的。
相对运动

高一物理竞赛培训任何物体的运动都是相对于一定的参照系而言的,相对于不同的参照系,同一物体的运动往往具有不同的特征、不同的运动学量。
通常将相对观察者静止的参照系称为静止参照系;将相对观察者运动的参照系称为运动参照系。
物体相对静止参照系的运动称为绝对运动,相应的速度和加速度分别称为绝对速度和绝对加速度;物体相对运动参照系的运动称为相对运动,相应的速度和加速度分别称为相对速度和相对加速度;而运动参照系相对静止参照系的运动称为牵连运动,相应的速度和加速度分别称为牵连速度和牵连加速度。
绝对运动、相对运动、牵连运动的速度关系是:绝对速度等于相对速度和牵连速度的矢量和。
牵连相对绝对v v v += 这一结论对运动参照系是相对于静止参照系作平动还是转动都成立。
当运动参照系相对静止参照系作平动时,加速度也存在同样的关系:牵连相对绝对a a a+=位移合成定理:S A 对地=S A 对B +S B 对地如果有一辆平板火车正在行驶,速度为火地v (脚标“火地”表示火车相对地面,下同)。
有一个大胆的驾驶员驾驶着一辆小汽车在火车上行驶,相对火车的速度为汽火v ,那么很明显,汽车相对地面的速度为:火地汽火汽地v v v +=(注意:汽火v 和火地v 不一定在一条直线上)如果汽车中有一只小狗,以相对汽车为狗汽v 的速度在奔跑,那么小狗相对地面的速度就是火地汽火狗汽狗地v v v v ++=从以上二式中可看到,上列相对运动的式子要遵守以下几条原则: ①合速度的前脚标与第一个分速度的前脚标相同。
合速度的后脚标和最后一个分速度的后脚标相同。
②前面一个分速度的后脚标和相邻的后面一个分速度的前脚标相同。
③所有分速度都用矢量合成法相加。
④速度的前后脚标对调,改变符号。
以上求相对速度的式子也同样适用于求相对位移和相对加速度。
相对运动有着非常广泛的应用,许多问题通过它的运用可大为简化,以下举两个例子。
例1 如图2-2-1所示,在同一铅垂面上向图示的两个方向以s m v s m v B A /20/10==、的初速度抛出A 、B 两个质点,问1s 后A 、B 相距多远?这道题可以取一个初速度为零,当A 、B 抛出时开始以加速度g 向下运动的参考系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O
x(东)
太原理工大学物理系
y(北) 由图中的几何关系,知:
vx 10(m / s)
v y 5m / s
风速的大小:
O
v
45
10ms-1 15ms-1#39;
太原理工大学物理系
例2:一货车在行驶过程中,遇到5m/s竖直下落的大 雨,车上仅靠挡板平放有长为l=1m的木板。如果木 板上表面距挡板最高端的距离h=1m,问货车以多大 的速度行驶,才能使木板不致淋雨?
相对运动解题 要点: •一个运动物体;
•两个参考系;
•三个运动速度。 步骤: 选定运动质点和两种参考系; 1. 2. 按相对运动公式列出矢量方程;
3. 画出矢量图,利用几何三角知识 求解(或矢量代数运算) 。
太原理工大学物理系
例1:某人骑摩托车向东前进,其速率为10m∙s-1时 觉得有南风,当其速率为15m∙s-1 时,又觉得有东 南风,试求风速度。 解 : 取 风 为 研 究 对 象 , y(北) 骑车人和地面作为两 v 个相对运动的参考系。 45 作图 根据速度变换公式得到:
【教育类精品资 料】
太原理工大学物理系
§1-3 相对运动
本节给出:同一物体在不同参考系中各自测量的
状态量之间的定量关系。 太原理工大学物理系
车 质点—人, 参考系--- , 车相对地作平动,速度 地 位移间的关系:
r r ' ut
速度间的关系: dr dr ' u dt dt
太原理工大学物理系
速度间的关系:
v人对地 = v人对车 + v车对地
v 为绝对速度(质点相对于地面(参考系S)的速度) v '为相对速度(质点相对于车(参考系S)的速度) u 为牵连速度(参考系S相对于S平动的速度)
伽利略速度变换 太原理工大学物理系
速度间的关系: 加速度间的关系:
解:车在前进的过程中,雨 相对于车向后下方运动,使 雨不落在木板上,挡板最上 端处的雨应飘落在木板的最 左端的左方。 l h
45 v车地 v雨地
v雨车
45
5(m/s)
v车地
v雨地
太原理工大学物理系
例3:在相对地面静止的坐标系内,A、B两船都 以2m/s的速率匀速行驶,A船沿x轴正向,B船沿y 轴正向,今在A船上设置与静止坐标系方向相同 的坐标系,求:在A船上看B船的速度。 解:以地为固定参照系,A为动参照系,B船为运
动物体,则有
由伽利略速度变换得 vB地 vBA v A地 v BA v B地 v A地 2 j 2i 2i 2 j
太原理工大学物理系
第一章质点运动学小结
四个物理量: 三种坐标系:直角坐标系;自然坐标系;极坐标系
两类问题:已知运动方程确定质点的速度和加速度。
已知质点运动的加速度和初始条件求速 度、运动方程。
相对运动:
伽利略速度变换
太原理工大学物理系
a a a0
du a0 0 dt
若
u const.
则
加速度关系变为
a a
太原理工大学物理系
讨论
1.以上结论是在绝对时空观下得出的 牛顿绝对时空观:长度测量和时间测量的绝对性
绝对时空观只在 u << c 时才成立。
2.注意区分“速度叠加”与“速度变换” 速度叠加是同一参考系中,一个质点的速度和其 分速度间的关系(矢量合成)。 速度变换涉及有相对运动的两个参考系,和参考 系间的相对速度有关。 太原理工大学物理系
