5.5 车辆振动模型
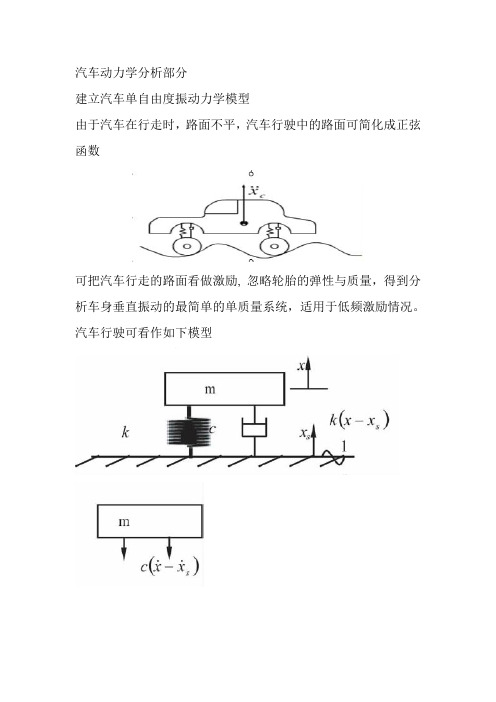
建立汽车单自由度振动力学模型
B a
1 (2 ) 2 (1 2 ) 2 (2 ) 2
以ξ为参数, 由前面式画出的幅频响应曲线及相频响应曲线如图
由图看到,当频率比λ=
2 时,无论阻尼比ξ为多少, 2 时,振幅
振幅B 恒等于支承运动振幅 a;当λ> 增加阻尼反而使振幅 B 增大。
B 小于 a,
在工程机械中超过允许范围的振动影响着本身的正常运行及寿 命,还造成环境污染,有效的隔离振动是相当重要的问题。一类 是用隔振器将振动着的机械与地基隔离开,称为积极隔振;另一 类是将需要保护的设备用隔振器与振动着的地基隔开, 称为消极 隔振。 两种方法的原理是类似的, 隔振效果可以用传递率TR 度 量, 将图2的幅频响应曲线的纵坐标β改为TR, 则得到TR 随 频率比λ的变化规律的特性曲线。 从曲线中看到,只有当λ>
cx
s
,相位比 xs 超前
2
由常微分方程
cx kx p 0 sin t m x
c k 2 n , n2 m 将方程 (4) 的两端同除以质量m, 并且令 m
其中ξ为相对阻尼系数, n 为相应的无阻尼系统的固有频率, 则方程(4)改写为:
2 n x n2 x x
由于支承的运动,质量块受到的弹性恢复力为 k(x-xs),阻尼力为 c( x c xs ),根据达朗伯原理可得如下的运动微分方程:
xs
(2)
由(1) (2) 得
由于支承运动而使质量块 m 受到得激振力由两部分组成, 一部分是由弹簧传递过来得 kxs, 相位与 xs 相同;另一部分是由阻尼器传递过来的
汽车动力学分析部分 建立汽车单自由度振动力学模型 由于汽车在行走时,路面不平,汽车行驶中的路面可简化成正弦 函数
四自由度汽车振动模型分析

四自由度汽车振动模型分析四自由度汽车振动模型是一种用于描述汽车在行驶过程中的振动响应的数学模型。
它通常用于研究汽车的悬挂系统和底盘结构的振动特性,并根据振动特性进行优化设计。
本文将从四自由度汽车振动模型的基本原理、振动模型的建立以及参数标定的方法进行详细分析。
在建立振动模型之前,我们需要对汽车的主要振动特征进行分析。
主要振动特征包括车体的垂直运动、前后悬挂系统的纵向运动和横向运动。
这些振动特征可以通过实验测试或模拟仿真得到。
一般来说,四自由度汽车振动模型包括车体的垂直运动、车体的俯仰运动、前轮的纵向运动和后轮的纵向运动。
其中,车体的垂直运动和俯仰运动是通过车体的弹簧-阻尼系统描述的,前轮和后轮的纵向运动是通过悬挂系统的弹簧-阻尼系统描述的。
具体而言,四自由度汽车振动模型可以用以下方程描述:1.车体的垂直运动:m₁ẍ₁+c₁(x₁-x₂)+k₁(x₁-x₂)+c₂(x₁-x₄)+k₂(x₁-x₄)=F其中m₁是车体的质量,x₁是车体的垂直位移,c₁和k₁分别是车体和前悬挂系统的阻尼和刚度,c₂和k₂分别是车体和后悬挂系统的阻尼和刚度,F是作用在车体上的外力。
2.车体的俯仰运动:m₂ẍ₂+c₁(x₂-x₁)+k₁(x₂-x₁)=0其中m₂是车体的质量,x₂是车体的俯仰角,c₁和k₁分别是车体和前悬挂系统的阻尼和刚度。
3.前轮的纵向运动:m₃ẍ₃+c₃(x₃-x₁)+k₃(x₃-x₁)+c₄(x₃-x₄)+k₄(x₃-x₄)=0其中m₃是前轮的质量,x₃是前轮的纵向位移,c₃和k₃分别是前悬挂系统和车体的阻尼和刚度,c₄和k₄分别是前悬挂系统和后悬挂系统的阻尼和刚度。
4.后轮的纵向运动:m₄ẍ₄+c₄(x₄-x₃)+k₄(x₄-x₃)=0其中m₄是后轮的质量,x₄是后轮的纵向位移,c₄和k₄分别是后悬挂系统和前悬挂系统的阻尼和刚度。
根据以上方程,我们可以得到一个四自由度的运动方程组,可以通过求解该方程组得到汽车的振动响应。
基于虚拟样机技术的车辆振动模态测试

基于虚拟样机技术的车辆振动模态测试newmaker1 引言随着生活水平的提高,人们对汽车综合性能的要求也日益提高。
其中,减轻振动强度,降低噪声水平,提高乘车舒适性是最重要的内容之一,而且正受到越来越多的重视。
这就使得优化汽车系统的动态特性,控制振动和噪声成为非常突出的问题。
目前,模态分析技术已经成为解决这些问题的重要技术手段。
模态分析技术是指通过振动模态试验获得表征结构动态特性的模态参数的一种动态分析方法。
但是通过物理实验对车辆进行振动模态测试是一项耗时耗力且费用高昂的测试方法。
相比之下,基于虚拟样机技术的汽车振动模态测试技术则以其快捷方便实用的特点而越来越被人们所重视和采用。
通过虚拟样机技术对汽车总体动态性能和各系统之间的相互影响等进行直观而且全面的仿真分析、评价和改进,从而尽可能缩短设计周期,提高设计质量、降低设计成本。
目前,人们已利用虚拟样机技术对工程中的大量问题进行了相应研究。
本文利用多体动力学仿真分析软件ADAMS 建立汽车多体动力学模型,并在此基础上通过ADAMS/Vibration 模块对车辆模型进行模态测试。
利用ADAMS/Vibration 振动分析模块,可以把不同的子系统装配起来进行线性振动分析,并可以通过ADAMS 后处理工具把结果以图表或动画的形式显示出来,包括绘制和动画显示受迫振动和频率响应函数,生成模态坐标列表及显示其它的时间和频率数据。
2 ADAMS/vibrat ion 模态测试流程在使用ADAMS/Vibration 进行车辆振动模态测试时,主要步骤如图1 所示。
其中,输入通道用来绘制频率响应函数及设置激振器,而激振器用来对车辆系统模型产生激励。
输出通道用以检测系统的频率响应,并可以在频域内直接给出测试结果。
3 ADAMS 车辆模型汽车模型主要由前后悬架、轮胎、座椅和转向系等子系统组成,按照实际车辆各零部件的相对位置和约束关系组装成整车系统。
整车包含24 个运动部件和34 个约束副,最后共有12 个自由度,并且验证模型正确没有过约束。
四自由度汽车振动模型分析

四自由度汽车振动模型分析作者:文/张泽鹏李洋徐海升来源:《时代汽车》 2018年第10期摘要:本文以普通乘用车为例,将汽车简化成四自由度振动模型,根据牛顿第二定律求出系统的运动微分方程并利用MATLAB求解得到该振动系统的固有频率和主振型,最终绘制出振幅比随路面激励频率变化的曲线。
关键词:主振型;固有频率;MATLAB1振动模型的建立与分析1.1振动模型的建立选取一辆乘用车,各参数和数值在表1中给出,为了分析方便做出如下假设:(1)车身是质量分布均匀的刚体。
(2)两侧车轮的运动状态在任何时刻都相同。
(3)车身仅做垂直于地面的上下振动zc和绕质心的俯仰θ。
(4)车轮仅做上下振动Z1,Z2。
基于以上假设并将将该车简化为四自由度的振动模型如图1所示。
1.2根据牛顿第二定律对四自由度模型进行受力分析3主要结论(1)根据图2和图3可以得知,在后轮的激励对车身垂直振动的影响较大,前轮的激励对车身俯仰振动的影响较大。
(2)路面激励为4.6Hz时,车身垂直振动zc与后轮路面激励的振幅比达到最大值,为1.645,与前轮路面激励的振幅比达到最大值,为1.063。
(3)路面激励为4.8Hz时,车身俯仰角与后轮路面激励振幅比达到最大值,为0.7842;路面激励为4.6Hz时,车身俯仰角与前轮路面激励振幅比达到最大值,为1.650。
(4)根据幅频特性曲线可知,在行车过程中避免路面激励出现在[3Hz,8.7Hz]的区间内可有效提高舒适性。
参考文献:[1]詹长书,吕文超.汽车悬架的二自由度建模方法及分析[J].拖拉机与农用运输车,2010,37(06):9-11+15.[2]张眷红.基于MATLAB的汽车振动系统仿真卟机械工程与自动化,2008.。
汽车五自由度建模

汽车五自由度建模Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】汽车振动大作业一、汽车悬架系统振动模型汽车是一个复杂的振动系统,在振动分析的建模过程当中,要根据所分析的问题对汽车进行简化,建立相应的模型。
现在考虑汽车车身悬架的五自由度模型,如下图1所示,该模型主要考虑左右车辙的不平度差异和较小的轮胎阻尼而得到的,该模型中主要有车身的垂直、俯仰两个自由度和前后车轴质量两个垂直自由度,汽车座椅一个垂直自由度,系统共五个自由度,其中车身质量的垂直、俯仰两个自由度的振动对系统平顺性的影响较大,假设车身是具有垂直和俯仰两个自由度的刚体,其车身的质量和转动惯量分别为:h h I m 和,前后车轮质量、悬架参数和轮胎刚度的符合前加入了分别表示前(front)和后(rear)的下标“f ”和“r ”,如图1示:图1 五自由度汽车悬架系统图1中:1z 表示前轮转动位移自由度;2z 表示车体垂直位移自由度;3z 1z 表示后轮转动位移自由度;4z 俯仰转动位移自由度;5z 表示驾驶员座椅垂向自由度;1m 表示驾驶员座椅质量;2m 表示车体质量;3)(m f m =表示前轮质量;4)(m r m =表示后轮质量;1k 表示座椅弹簧刚度;5,4,3,2k k k k 悬架弹簧刚度;1c 表示座椅弹簧阻尼;5,4,3,2c c c c 表示悬架弹簧阻尼;a 表示车身质心至前轴距离;b 车身质心至后轴距离,)(),(r F f F 分别为前后轮随机激励力。
二、运动微分方程由图1可得到下述理论值:(1) 系统的动能为: )(212121212121325125524423222211I m z m z m z m z I z m z m T i i i ==++++=∑= (1-2)(2) 系统的势能为:255244232532324223121))((21))((21)(21)(21)(21r F z k f F z k bz z z k az z z k dz z z k V -+-++-++-++-=(1-3) (3) 系统阻尼耗散的能量:55554454332353325332224232423111213121))(())(())(())(())((z c r F z c z c f F z c z bc z c z c z b z zc z dc z c z c z b z zc z dc z c z c zd z zc C ----+-+--+-+--+-+--= (1-4)由拉格朗日运动方程:可得到多自由度的运动微分方程:式中:表一 汽车结构参数取汽车结构参数如表一所示,则可求得系统的质量矩阵,阻尼矩阵,刚度矩阵分别为:由特征方程0)(2=Φ-M K ω求得固有频率与振型。
推荐-多自由度汽车振动特性建模与分析 精品

目录目录 (3)摘要 (3)A BSTRACT (4)1 前言 (5)1.1课题研究的意义 (5)1.2相关领域发展历史和发展趋势 (5)1.3汽车振动的建模方法 (6)1.4主要研究内容 (7)2 悬架工作过程分析 (9)2.1悬架的功用 (9)2.2悬架的组成 (9)2.3汽车悬架的分类 (11)2.4汽车悬架工作过程 (13)3 MATLAB/SIMULINK简介 (14)4路面激励的时域模型 (16)4.1路面不平度的功率谱密度 (16)4.2路面激励的时域模型 (17)5汽车悬架的五自由度模型 (20)5.1汽车模型简化的假设 (20)5.2五自由度动力学模型 (20)5.3系统动力学方程 (21)5.4路面激励时域模型 (23)5.5悬架特性五自由度仿真模型 (24)5.5某汽车振动仿真结果及分析 (26)6 悬架特性分析与评价 (31)6.1汽车行驶速度对平顺性的影响分析 (31)6.2路面不平度对平顺性的影响分析 (32)6.3悬架弹性元件刚度对平顺性的影响分析 (34)6.4悬架减振器阻尼对平顺性的影响分析 (39)7 结论 (42)总结与体会 (46)谢辞 (46)参考文献 (47)多自由度汽车振动特性建模与分析摘要汽车平顺性是汽车的主要性能之一。
它的优劣直接关系到驾驶员的驾驶舒适性和乘员的舒适性。
如何提高汽车平顺性已成为汽车设计人员越来越关心的问题。
随着随机振动理论的发展,计算机仿真也大量运用到汽车性能分析当中。
本文基于汽车振动动力学分析方法,建立五自由度汽车振动模型。
该五自由度模型的五个自由度包括纵向两车轮的两个自由度、车身的两个自由度和驾驶员一个自由度。
汽车振动模型的输入有路面不平度、车速。
因此,本次采用白噪声法以白噪声作为输入建立了A、B、C、D各级路面模型。
通过Matlab/ simulink 软件建立仿真模型,以某汽车参数为基础仿真得到了汽车驾驶员加速度、悬架动挠度和车轮动载荷的仿真结果,这样得到了汽车平顺性与车速、路面不平度、悬架参数的关系。
基于MATLAB的汽车直线加速工况下振动模型分析
基于MATLAB的汽车直线加速工况下振动模型分析汽车在直线加速工况下面临着振动问题,这对于车辆的性能和乘坐舒适度都会产生一定影响。
因此,针对这一问题,我们可以利用MATLAB进行振动模型的分析,以便更好地了解振动的原因和解决方案。
在进行振动模型分析之前,首先需要了解汽车在直线加速工况下的运动特性。
汽车在直线加速时,受到动力所产生的加速度和阻力的影响,会引起车身的振动。
这种振动主要是由质量的不平衡、悬挂系统的刚度和阻尼失效等因素引起的。
因此,我们需要建立一个合理的振动模型,来描述这些因素对汽车振动的影响。
在MATLAB中,可以利用多种数学方法和工具箱来建立汽车振动模型。
其中一种常用的方法是使用有限元分析(FEA)技术来进行振动分析。
有限元方法基于连续介质力学原理,将结构划分为各种小的有限元,通过建立节点和单元的连接关系来描述结构的振动。
这样就可以利用MATLAB提供的FEA工具箱来进行汽车振动的模拟和分析。
在进行有限元模型分析之前,首先需要建立汽车的几何模型。
可以通过CAD软件将汽车的主要构件进行绘制,然后导入MATLAB中进行后续的处理。
可以使用MATLAB提供的CAD工具箱来进行CAD文件的读取和处理。
接下来,需要对汽车的材料特性和悬挂系统参数进行建模。
汽车的材料特性可以通过实验或者文献数据进行获取。
而悬挂系统的参数需要进行测量或者仿真分析。
可以使用MATLAB提供的参数优化和曲线拟合工具箱来进行参数的优化和拟合。
建立好汽车的几何模型和参数后,就可以使用MATLAB的FEA工具箱进行振动分析了。
可以通过在汽车结构上加入初始激励和加载条件,来模拟直线加速工况下的振动响应。
然后使用MATLAB提供的振动分析函数,如固有频率分析、模态分析和频域响应分析等,来分析振动的模态特性和响应情况。
在振动模型分析过程中,还可以考虑不同控制策略和系统参数对振动的影响。
可以利用MATLAB提供的控制系统工具箱和优化算法来进行参数的优化和系统性能的改善。
基于主动悬架四自由度汽车振动模型分析
基于主动悬架四自由度汽车振动模型分析汽车振动是指汽车行驶过程中,由于路面不平或车身运动引起的车辆产生的振动。
振动会对行驶安全、乘坐舒适度和车辆寿命等方面产生重要影响。
因此,对汽车振动进行分析和控制是汽车工程中的重要课题之一主动悬架是一种利用控制力来改变车辆振动特性的技术,通过控制悬架系统中的阻尼器以及悬架的刚度等参数,可以实现对车辆振动的主动控制。
主动悬架系统一般由传感器、控制器和执行机构组成,它能够根据车辆的运动状态和路面信息,即时调整悬架参数,以达到减小车辆振动和提高乘坐舒适度的目的。
主动悬架四自由度模型是一种简化的车辆振动模型,它考虑了车辆的垂直振动、悬架横向振动、车辆侧倾和悬架纵向振动等主要因素。
该模型的四个自由度分别是车身垂直振动、车身侧倾、前悬架横向振动和后悬架横向振动。
通过对该振动模型进行分析,可以得到车辆在不同工况下的振动特性,进而进行优化设计和控制策略的制定。
在进行主动悬架四自由度汽车振动模型分析时,通常会考虑以下几个方面:1.车辆参数的确定:包括车辆的质量、悬挂和弹簧刚度、阻尼器阻尼系数等。
这些参数对于车辆的振动特性具有重要影响,需要根据实际情况进行测量或估算。
2.路面输入的建模:路面不平度是车辆振动的主要激励源,在模型中通常通过一维或多维随机过程来描述。
利用加速度传感器测量路面不平度数据,并通过傅里叶变换等方法进行频谱分析和合成,得到对车辆振动的激励。
3.悬架系统的建模:主动悬架系统可以通过控制器对悬架刚度和阻尼进行调节,以改变车辆的振动特性。
悬架系统的建模需要考虑悬架的结构特性、传感器和执行机构的动力学等因素。
4.系统响应的求解:通过对振动模型进行数学描述和求解,可以得到车辆在不同工况下的振动响应,如车身加速度、车身倾角、悬架位移等。
这些响应结果可以用于评估车辆的振动性能,并帮助制定合适的悬架控制策略。
基于主动悬架四自由度汽车振动模型分析可以帮助分析车辆振动特性、设计优化主动悬架系统、制定振动控制策略等。
采用多目标遗传算法对五自由度车辆振动模型优化
采用多目标遗传算法对五自由度车辆振动模型优化黄小兵【摘要】This paper deals with the serious seat vibration problem in vehicle driving process. A multi -objective genetic algorithm was used in the optimization for five-degree of freedom vehicle vibration. Considering the five conflict functions in vibration model, a new multi-objective genetic algorithm was presented. The five-degree of freedom vehicle model was built and the five different objective functions including seat acceleration, forward tire velocity, rear tire velocity, relative displacement between sprung mass and forward tire and relative displacement between sprung mass and rear tire were optimized. Four different pairs of these five objective functions have been selected for 2-objective optimization processes. The optimization results were presented in graphical means,and compared with the classical one. The optimization results shown a little seat acceleration when the vehicle over a bump. Using multi-objective genetic algorithm in the optimization for five-degree of freedom vehicle can reduce the seat vibration when the vehicle is over a road obstacle.%针对当前车辆在行驶过程中座椅振动比较大问题,采取多目标遗传算法对五自由度车辆振动模型进行优化.提出了一个新的多目标遗传算法,同时考虑五自由度车辆振动模型相互冲突的五个函数;建立五自由度车辆振动模型,通过对5个不同目标函数进行优化,分别为座椅加速度、前轮速度、后轮速度、簧载质量和前轮的相对位移及簧载质量和后轮的相对位移,从这些目标函数中选出不同四对函数用于2-目标优化处理;通过图形展示2-目标优化处理结果,并与以往研究结果形成鲜明对比.优化结果显示,车辆经过地面隆起物时,座椅产生的加速度较小.采用多目标遗传算法对五自由度车辆振动模型优化后,车辆在行驶过程中经过地面障碍物时,座椅振动较小.【期刊名称】《机械设计与制造》【年(卷),期】2017(000)008【总页数】4页(P65-68)【关键词】多目标;遗传算法;振动模型;优化【作者】黄小兵【作者单位】攀枝花学院机械工程学院,四川攀枝花 617000【正文语种】中文【中图分类】TH16;U46随着国内经济的的快速发展,人们的生活水平也在不断的提高。
汽车五自由度建模
汽车振动大作业一、汽车悬架系统振动模型汽车是一个复杂的振动系统,在振动分析的建模过程当中,要根据所分析的问题对汽车进行简化,建立相应的模型。
现在考虑汽车车身悬架的五自由度模型,如下图1所示,该模型主要考虑左右车辙的不平度差异和较小的轮胎阻尼而得到的,该模型中主要有车身的垂直、俯仰两个自由度和前后车轴质量两个垂直自由度,汽车座椅一个垂直自由度,系统共五个自由度,其中车身质量的垂直、俯仰两个自由度的振动对系统平顺性的影响较大,假设车身是具有垂直和俯仰两个自由度的刚体,其车身的质量和转动惯量分别为:h h I m 和,前后车轮质量、悬架参数和轮胎刚度的符合前加入了分别表示前(front)和后(rear)的下标“f ”和“r ”,如图1示:I(h) m2m(f)m(r)Z(b)abz4z5F(f)F(r)z2z3m1z1k1k2k3k4k5c1c2c3c4c5d图1 五自由度汽车悬架系统图1中:1z 表示前轮转动位移自由度;2z 表示车体垂直位移自由度;3z 1z 表示后轮转动位移自由度;4z 俯仰转动位移自由度;5z 表示驾驶员座椅垂向自由度;1m 表示驾驶员座椅质量;2m 表示车体质量;3)(m f m =表示前轮质量;4)(m r m =表示后轮质量;1k 表示座椅弹簧刚度;5,4,3,2k k k k 悬架弹簧刚度;1c 表示座椅弹簧阻尼;5,4,3,2c c c c 表示悬架弹簧阻尼;a 表示车身质心至前轴距离;b 车身质心至后轴距离,)(),(r F f F 分别为前后轮随机激励力。
二、运动微分方程由图1可得到下述理论值: (1) 系统的动能为:)(212121212121325125524423222211I m z m z m z m z I z m z m T i i i ==++++=∑=(1-2)(2) 系统的势能为:255244232532324223121))((21))((21)(21)(21)(21r F z k f F z k bz z z k az z z k dz z z k V -+-++-++-++-=(1-3)(3) 系统阻尼耗散的能量:55554454332353325332224232423111213121))(())(())(())(())((z c r F z c z c f F zc z bc z c z c z b z zc z dc z c z c z b z zc z dc z c z c zd z zc C ----+-+--+-+--+-+--= (1-4)由拉格朗日运动方程:)5,,2,1(0)()( ==-∂∂+∂∂-∂∂i F z Vz T z T dt d Qi ii i可得到多自由度的运动微分方程:)()()()(t F t Kz t z C t z M =++式中:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=543210000000000000000000m m m m m M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+-+---++-------++---=533343223232221232113232132111110000c c bc c c c ac c bc ac c b c a c d bc ac dc dc c c bc ac dc c c c c dc c c C⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+-+---++-------++---=5333422232322212321132321321111100000k k ak k k k ak k bk ak k c k a k d bk ak dk dk k k bk ak dk k k k k dk k k K表一 汽车结构参数汽车结构参数数值1m —驾驶员座椅质量kg 65 2m —车体质量kg 7084m —右前、左前轮胎质量 kg 80 5m —左后、右后轮胎质量kg 80)(h I —转动惯量 21060m kg ⋅1k —座椅弹簧刚度m N /23071 32,k k —右前、左前悬架弹簧刚度 m N /20292 54,k k —左后、右后悬架弹簧刚度m N /128701c —座椅弹簧阻尼11500-⋅⋅m s N5432,,,c c c c —悬架弹簧阻尼11000-⋅⋅m s Na —车身质心至前轴距离m 5.1b —车身质心至后轴距离m 75.0d -座椅到质心距离m 1875.0取汽车结构参数如表一所示,则可求得系统的质量矩阵,阻尼矩阵,刚度矩阵分别为:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=800000080000001060000007080000065M⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡----------=14808602898919326001490521521920292028989152195570939882432619326202923988262689230710043262029223071K⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡----------=100001500100000100075010000150075023.286575.46825.2811000100075.468350015000025.28115001500C由特征方程0)(2=Φ-M K ω求得固有频率与振型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
路面输入除采用 Gq (ω) 外,还可以采用 Gq (ω)和 Gq& (ω)。 & & 相应地, 相应地,幅频特性要采用 H( jω) 2&~q 和 H( jω) &z&~q& 。 & & & z
2
即
G&& (ω) = H ( jω) &&~q Gq (ω) & z z &
2
G&& (ω) = H ( jω) &&~q Gq (ω) && z z &&
2
2
p ~ qi
Gij ( jω ) H ( jω ) z
p ~q j
5.5 车辆振动模型
(七)汽车四自由度系统(双输入) 汽车四自由度系统(双输入) 4)悬挂质量分配系数ε=1时任一点 的垂直振动加速度功率 )悬挂质量分配系数 时任一点P的垂直振动加速度功率 谱
4)悬架与轮胎的刚度比γ的影响
轮胎与悬架的刚度比γ 轮胎与悬架的刚度比 的影响规律: 的影响规律:
5.5 车辆振动模型
(七)汽车四自由度系统(双输入) 汽车四自由度系统(双输入) 1)任一点P垂直振动位移功率谱求解概述 )任一点 垂直振动位移功率谱求解概述 z
zp
c
lp
ϕ
Iy
Gx ( jω ) = H * ( jω ) Gq ( jω ) H ( jω )
G = m2 g
F [ Fd / G] 1 F [&&] z = & & F [ q] g F [ q]
& 因此, 因此,ω0和ζ对 Fd / G − q 幅频特性的影响与& − q & z &
幅频特性的影响,从变化趋势上讲完全一样。 幅频特性的影响,从变化趋势上讲完全一样。
3)悬架弹簧的动挠度
fd = z − q
其中,路面输入的均方根谱如下: 其中,路面输入的均方根谱如下: 均方根谱如下
G (ω) = ( 2π/ ω) G ( n ) n2u q 0 0 q 2 Gq (ω) = 2π Gq ( n0 ) n0 u & 2 Gq (ω) = 2πω Gq ( n0 ) n0 u &&
5.5 车辆振动模型
(一)振动模型的简化 1)四轮汽车的七自由度模型 )
5.5 车辆振动模型
(一)振动模型的简化 2)四轮汽车的四自由度模型 )
车身对称于 x(I ) = y(I ) xoz平面、
条件? 条件?
5.5 车辆振动模型
(一)振动模型的简化 3)四轮汽车的两个二自由度模型 )
将悬挂质量m 将悬挂质量 2简化为三个集中质 量,应满足的三个条件 1)总质量保持不变 )
2 ω0 = K / m2
思考:ω0代表车身部分的偏频, 思考: 代表车身部分的偏频, 那么当路面激励频率接近 路面激励频率接近ω 那么当路面激励频率接近ω0时, 车轮与车身振动幅值的大小关 系?
5.5 车辆振动模型
(五)车身与车轮双自由度系统振型分析(单输入) 车身与车轮双自由度系统振型分析(单输入) 振型分析 2)主频率 )
注:在分析某一参数影响时,其余3个参数保持不变。 在分析某一参数影响时,其余3个参数保持不变。
1)车身固有频率f0的影响
的影响规律: 固有频率f0的影响规律:
2)车身部分阻尼比ζ的影响
车身部分阻尼比ζ的 影响规律:
3)车身与车轮部分质量比µ的影响
车身与车轮部分质量比µ 车身与车轮部分质量比 的影响规律: 的影响规律:
条件? 条件?
5.5 车辆振动模型
评价指标计算( (二)车身单自由度系统评价指标计算(单输入) 车身单自由度系统评价指标计算 单输入) 前提条件:位移坐标的原点? 前提条件:位移坐标的原点? 1)力学模型 ) 2)频率响应函数 ) 3)评价指标 ) ①车身振动加速度均方值 ②悬架弹簧动挠度均方值 ③车轮与地面相对动载荷均方值
1 2 1 2 KKt 2 2 2 ω = ωt + ω0 m ωt + ω0 − 2 4 m2m1
2 1、 2
(
)
(
)
例
设某一汽车质量比 µ = m2 /m1 = 10 ,
刚度比 γ = Kt /K = 9,求ω1、ω2与ω0关系? 关系
ω1 = 0.95ω0 < ω0 < ωt < ω2 = 1.001ωt
2)沿x方向质心位置不变 ) 方向质心位置不变
3)转动惯量Iy保持不变 )转动惯量
5.5 车辆振动模型
(一)振动模型的简化 3)四轮汽车的两个二自由度模型 )
ε=1
条件? 条件?
5.5 车辆振动模型
(一)振动模型的简化 4)四轮汽车的两个单自由度模型 )
激振频率较小, 激振频率较小,只需 考虑车身的低频振动
= Q /ω = Q = Q ⋅ω
双对数坐标系中,路面输入功率谱曲线特性 速度功率谱
斜率为0:1 斜率为
与频率无关,“白 与频率无关, 噪声” 噪声”信号
Gq (ω) = Q &
位移功率谱
斜率为- 斜率为-1:1
Gq (ω) = Q / ω
斜率为1:1 斜率为
加速度功率谱
Gq& (ω) = Qω &
5.5 车辆振动模型
(七)汽车四自由度系统(双输入) 汽车四自由度系统(双输入) 3)悬挂质量分配系数ε=1时的振动方程 )悬挂质量分配系数 时的振动方程
zp
lp
z1
zc
a b
z2
u
ϕ
C
①z1, z2表达式 , ②动力学方程
P
Iy
k1
c1
L
k2
c2
q2
q1
③偏频 ④主频率与主振型
5.5 车辆振动模型
由于 Gq ( ω) 为一“白噪声”,所 为一“白噪声” &
方根谱 G&& (ω) z
& z 1)车身加速度 && 对路面速度输入 q 的幅频特性分析
100
ζ=0.25 ζ=0.5 f0=2Hz
思考: 对 思考:ζ对共振峰值有 影响, 何影响,对高频段振 动加速度的影响? 动加速度的影响?
&& z & q
5.5 车辆振动模型
(五)车身与车轮双自由度系统振型分析(单输入) 车身与车轮双自由度系统振型分析(单输入) 振型分析 3)振型 )
当激振频率ω接近 当激振频率 接近ω1 接近 (即接近ω0)时,车身质 即接近 量产生低频共振, 量产生低频共振,按一阶 主振型振动,车身质量 主振型振动,车身质量m2 的振幅比车轮质量m 的振幅比车轮质量 1的振 当激振频率ω接近ω2 幅大将近10倍,称为车身 大将近 倍 称为车身 (即接近ωt)时,车轮质量 型振动。 型振动。 产生高频共振, 产生高频共振,按二阶主振 型振动,车轮质量 型振动,车轮质量m1的振幅 比车身质量m 的振幅大将近 比车身质量 2的振幅大将近 车轮型振动。 100倍,称为车轮型振动。 倍 称为车轮型振动
2
对上式开根号,得到输入、输出均方根谱之间的关系 对上式开根号,得到输入、输出均方根谱之间的关系 均方根谱
H ( jω) Gq (ω) &&~q z G&z& (ω) = H ( jω) &z&~q Gq (ω) & & & H ( jω) &z&~q& Gq& (ω) &
& fd 对 q 幅频特性的分析
F [ fd ] F [ z− q] F [ z] fd = = = −1 q F [ q] F [ q] F [ q]
0:1 2:1
fd 1 fd = & q ω q
斜率减1
0:1 2:1
1:1
-1:1
思考: 和阻尼比ζ 思考:悬架固有频率 f0 和阻尼比ζ对 fd 有何 影响? 影响?
4)悬架系统固有频率f0与阻尼比ζ的选择
思考: 思考:悬架系统固有频率 f0 和阻尼比ζ对车身振动加速 度及悬架动挠度的影响有何不同? 度及悬架动挠度的影响有何不同?
[ 值的实用范围, 悬架系统 f 0、fs、f d ]值的实用范围,fs为静挠度
车 型 轿车 货车 大客车 越野汽车 f0/Hz 1.1~1.2 1.5~2 1.2~1.8 1.3~2
速度输入信号与输出信号均方根谱之间的关系 速度输入信号与输出信号均方根谱之间的关系 输出信号均方根谱之间
G&& (ω) = H ( jω) &&~q Gq (ω) & z z &
取对数
lg
(
G&& (ω) = lg H ( jω) &&~q + lg z z &
) (
) (
Gq (ω) &
)
以在双对数坐标系中 G&& (ω) 与 H(jω) &z&~q & z 的图形完全相同, 的图形完全相同,只是在双对数坐标 上移动 lg Gq (ω) 。 & 因此,可以用响应量对速度输入的幅 因此,可以用响应量对速度输入的幅 速度输入 H ( jω) &&~q 定性分析响应的均 频特性 z & 。
5.5 车辆振动模型
(七)汽车四自由度系统(双输入) 汽车四自由度系统(双输入) 2)悬挂质量分配系数ε=1时的各频响函数 时的各频响函数 z p )悬挂质量分配系数
