平行线与相交线几何证明题专项训练
(完整版)相交线平行线专题证明

40、如图,已知AB∥CD,试再添上一个条 件,使∠1=∠2成立。(要求给出两个以上 答案)
29、已知:如图,AD是一条直线,∠1=65°, ∠2=115°.求证:BE∥CF.
30、如图,CD∥AB,∠DCB=70°, ∠CBF=20°,∠EFB=130°,问直线EF与 AB有怎样的位置关系,为什么?
31、(1)已知AB∥CD,下列各图中的∠ABE、∠E、∠CDE 三个角之间各有什么关系?填入下列括号内,并选择一个 你自己喜欢的图加以证明。
3 F
C
6、已知,如图,AD∥BC,∠B=70°,∠C =60°,求∠CAE的度数.(写理由)
、如图,已知,AC∥DE,DC∥FE,CD平 分∠ACB,求证:EF平分∠BED.
A
D
F
3
4 5
1 2
B
E
C
8、如图,∠AOB是∠BOC的补角,OD平分 ∠AOB、OE平分∠BOC,求∠DOE的度数。
37、经过平移,△ABC的边AB移到了EF, 作出平移后的三角形,你能给出两种作法 吗?请表述出来。
38、如图,AB∥CD,需增加什么条件才能使 ∠1=∠2成立?至少举出两种并证明。
39、(1)已知AB∥CD,EF∥MN,∠1=115°, 求∠2和∠4的度数;
(2)本题隐含着一个规律,请你根据(1)的结 果进行归纳,试着用文字表述出来;
21、 如图,在△ABC中,CD⊥AB于点D, F G⊥AB 于点G, E D//BC。
试说明:∠EDC =∠B FG
22、已知:如图,AB∥CD,AP平分∠BAC, CP平分∠ACD,求∠APC的度数.
人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题(含答案)

人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题1、如图,已知∠2=∠3,∠C=∠D,求证:∠A=∠F.证明:∵∠2=∠3,∠1=∠2,∴∠1=∠3.∴DB∥CE.∴∠DBA=∠C.∵∠D=∠C,∴∠D=∠DBA.∴DF∥AC.∴∠A=∠F.2、如图,已知EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD的度数.解:∵EF∥AD,∴∠2=∠3(两直线平行,同位角相等).∵∠1=∠2,∴∠1=∠3(等量代换).∴AB∥DG(内错角相等,两直线平行).∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).3、如图,∠1=115°,∠2=50°,∠3=65°,EG为∠NEF的平分线.求证:AB∥CD,EG∥FH.证明:∵∠1=115°,∴∠FCD=180°-∠1=180°-115°=65°.∵∠3=65°,∴∠FCD=∠3.∴AB∥CD.∵∠2=50°,∴∠NEF=180°-∠2=180°-50°=130°.∵EG为∠NEF的平分线,∴∠GEF=12∠NEF=65°.∴∠GEF=∠3.∴EG∥FH.4、如图,已知∠B=∠D,∠E=∠F,判断BC与AD的位置关系,并说明理由.解:BC∥AD,理由:∴BE∥FD.∴∠B=∠BCF.又∵∠B=∠D,∴∠BCF=∠D.∴BC∥AD.5、如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.求证:AD平分∠BAC.证明:∵AD⊥BC,EG⊥BC,∴∠ADC=∠EGC=90°.∴AD∥EG.∴∠1=∠2,∠E=∠3.∵∠E=∠1,∴∠2=∠3.∴AD平分∠BAC.6、如图,B,C,E三点在一条直线上,A,F,E三点在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.证明:∵AB∥CD,∴∠4=∠BAE.∴∠3=∠BAE.∵∠1=∠2,∴∠1+∠CAF=∠2+∠CAF,即∠BAE=∠CAD.∴∠3=∠CAD.∴AD∥BE.7、如图,已知AB∥CD,试判断∠B,∠BED和∠D之间的关系,并说明理由.解:∠BED=∠B+∠D.理由如下:过点E作EF∥AB,则∠B=∠BEF.∵AB∥CD,∴EF∥CD.∴∠DEF=∠D.∵∠BED=∠BEF+∠DEF,∴∠BED=∠B+∠D.8、如图,∠AEF+∠CFE=180°,∠1=∠2,EG与HF平行吗?为什么?解:平行.理由:∵∠AEF+∠CFE=180°,∴AB∥CD.∴∠AEF=∠EFD.∴∠AEF -∠1=∠EFD -∠2,即∠GEF =∠HFE.∴EG ∥HF.9、如图,A ,B ,C 三点在同一直线上,∠1=∠2,∠3=∠D ,试判断BD 与CF 的位置关系,并说明理由.解:BD ∥CF.理由如下:∵∠1=∠2,∴AD ∥BF.∴∠D =∠DBF.∵∠3=∠D ,∴∠3=∠DBF.∴BD ∥CF.10、如图,∠ABC =∠ADC ,BF ,DE 分别是∠ABC ,∠ADC 的平分线,∠1=∠2,试说明:DC ∥AB.解:∵BF ,DE 分别是∠ABC ,∠ADC 的平分线,∴∠3=12∠ADC ,∠2=12∠ABC. ∵∠ABC =∠ADC ,∴∠3=∠2.∵∠1=∠2,∴∠1=∠3.∴DC∥AB.11、如图,AD平分∠BAC,AD⊥BC于D,点E,A,C共线,∠DAC=∠EFA,延长EF 交BC于点G.求证:EG⊥BC.证明:∵AD平分∠BAC,∴∠DAC=∠DAB.又∵∠DAC=∠EFA,∴∠DAB=∠EFA.∴AD∥EG.∴∠ADC=∠EGD.∵AD⊥BC,∴∠ADC=90°.∴∠EGD=90°.∴EG⊥BC.12、已知AB∥CD,点E为AB,CD之外任意一点.(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;(2)如图2,探究∠CDE与∠B,∠BED的数量关系,并说明理由.解:(1)∠B=∠BED+∠D.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠BEF=∠B,∠D=∠DEF.∵∠BEF=∠BED+∠DEF,∴∠B=∠BED+∠D.(2)∠CDE=∠B+∠BED.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠B+∠BEF=180°,∠CDE+∠DEF=180°.又∵∠DEF=∠BEF-∠BED,∴∠CDE+∠BEF-∠BED=∠B+∠BEF,即∠CDE=∠B+∠BED.13、如图,把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′和C′的位置上,ED′与BC的交点为G.若∠EFG=50°,求∠1,∠2,∠3的度数.解:根据折叠的性质可知,∠DEF=∠D′EF,∠EFC=∠EFC′.∵∠EFG=50°,∴∠EFC=180°-50°=130°.∴∠EFC′=∠EFC=130°.∴∠3=∠EFC′-∠EFG=130°-50°=80°.∵AD∥BC,∴∠DEF=∠EFG=50°.∴∠DED′=2∠DEF=100°.∴∠1=180°-∠DED′=180°-100°=80°.∵AD∥BC,∴∠1+∠2=180°.∴∠2=180°-∠1=100°.故∠1=80°,∠2=100°,∠3=80°.14、如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.解:(1)证明:∵AE⊥BC,FG⊥BC,∴AE∥GF.∴∠2=∠A.∵∠1=∠2,∴∠1=∠A.∴AB∥CD.(2)∵AB∥CD,∴∠D+∠CBD+∠3=180°.∵∠D =∠3+60°,∠CBD =70°,∴∠3=25°.∵AB ∥CD ,∴∠C =∠3=25°.15、(1)如图1,AB ∥CD ,则∠E +∠G 与∠B +∠F +∠D 有何关系?(2)如图2,若AB ∥CD ,又能得到什么结论?请直接写出结论.解:(1)过点E 作EM ∥AB ,过点F 作FN ∥AB ,过点G 作GH ∥CD. ∵AB ∥CD ,∴AB ∥EM ∥FN ∥GH ∥CD.∴∠1=∠B ,∠2=∠3,∠4=∠5,∠6=∠D.∴∠1+∠2+∠5+∠6=∠B +∠3+∠4+∠D ,即∠BEF +∠FGD =∠B +∠EFG +∠D.(2)∠B +∠F 1+∠F 2+…+∠F n -1+∠D =∠E 1+∠E 2+…+∠E n .16、已知E ,F 分别是AB ,CD 上的动点,P 也为一动点.(1)如图1,若AB ∥CD ,求证:∠P =∠BEP +∠PFD ;(2)如图2,若∠P =∠PFD -∠BEP ,求证:AB ∥CD ;(3)如图3,AB ∥CD ,移动E ,F ,使∠EPF =90°,作∠PEG =∠BEP ,则∠AEG∠PFD =2.证明:(1)过点P作PG∥AB,则∠EPG=∠BEP.∵AB∥CD,∴PG∥CD.∴∠GPF=∠PFD.∴∠EPF=∠EPG+∠FPG=∠BEP+∠PFD.(2)过点P作PQ∥AB,则∠QPE=∠BEP.∵∠EPF=∠PFD-∠BEP,∴∠PFD=∠EPF+∠BEP=∠EPF+∠QPE=∠FPQ. ∴DC∥PQ.∴AB∥CD.。
完整版相交线与平行线证明题专项训练

1如图,已知 AB // CD, /仁/3,试说明AC // BD.7、已知,如图15,/ ACB = 60°,/ ABC = 500,BO 、CO 分别平分/ ABC 、/ ACB ,EF 是经过点 0且平行于BC 的直 线,求/ BOC的度数。
8 已知:如图 2— 99,AD // BC ,/仁/2,Z 3= / 4 . DE 与CF 平行吗?为什么?相交线与平行线证明题专项训练 5、如图, 什么?AB // CD,直线EF 交AB 、CD 于点G 、H.如果GM 平分/ BGF,HN 平分/ CHE ,那么,GM 与HN 平行吗?为2、如图, 已知/ BAF = 50 °,/ ACE = 140°, CD 丄CE ,能判断DC // AB 吗?为什么?6、 女口图,/ 1 = Z 2,AC 平分/ DAB 试说明:DC//AB.BB4、如图, AB // CD,AD // BC, / A=3 / B.求/ A 、 / B 、/ C 、/ D 的度数.3、如图,已知 CD 丄AD ,DA 丄AB ,/ 1 = Z 2 则DF 与AE 平行吗?为什么?9、已知:如图AB/CD,EF交A求:/ BHF的度数。
B 于G,交CD 于F, FH 平分/ EFD,交AB 于H,/ AGE=50012、已知一个角的余角的补角比这个角的补角的一半大90°,则这个角的度数等于多少度?13、如图:已知AD// BE, /仁/ 2,请说明/ A=Z E的理由.14、已知,如图,BCE、AFE是直线, AB // CD , / 1 = / 2,/ 3=/ 4。
求证:AD //BE。
10、如图,直线AB、CD 相交于点O , OA 平分/ COE,/ COE : Z EOD=4 : 5,求/ BOD 的度数。
/ 1 =/ ACB,1/ CAB = 2 / BAD,试说明AD // BC .15、已知如图,直线AB、CD相交于B16、已知:如图/ 1= / 2,/ C=/D,O , OE 平分/ BOD , OF 平分/ COB,/ 2: / 1 = 4:1,求/ AOF 的度数。
相交线与平行线基础证明训练题
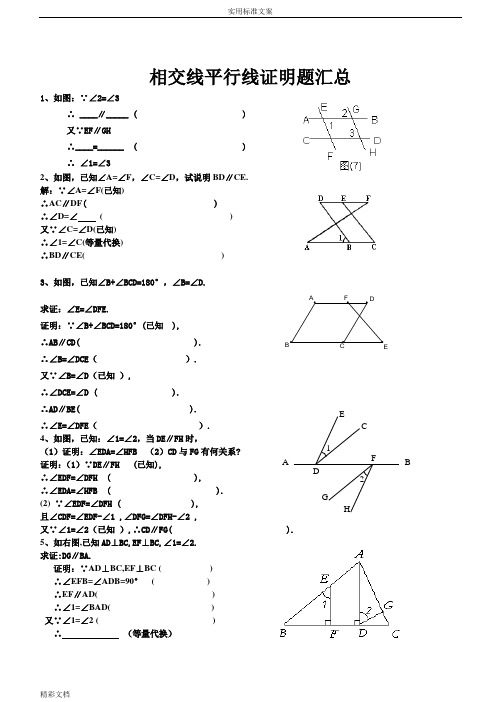
1、如图:∵∠2=∠3∴ ____∥_____ ( ) 又∵EF ∥GH∴____=______ ( ) ∴ ∠1=∠32、如图,已知∠A=∠F ,∠C=∠D ,试说明BD ∥CE. 解:∵∠A=∠F(已知)∴AC ∥DF ( )∴∠D=∠ ( ) 又∵∠C=∠D(已知) ∴∠1=∠C(等量代换)∴BD ∥CE( ) 3、如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.证明:∵∠B+∠BCD=180°(已知 ), ∴AB ∥CD( ). ∴∠B=∠DCE ( ). 又∵∠B=∠D (已知 ),∴∠DCE=∠D ( ). ∴AD ∥BE( ).∴∠E=∠DFE ( ). 4、如图,已知:∠1=∠2,当DE ∥FH 时,(1)证明:∠EDA=∠HFB (2)CD 与FG 有何关系?证明:(1)∵DE ∥FH (已知),∴∠EDF=∠DFH ( ),∴∠EDA=∠HFB ( ). (2) ∵∠EDF=∠DFH ( ), 且∠CDF=∠EDF-∠1 ,∠DFG=∠DFH-∠2 ,又∵∠1=∠2(已知 ),∴CD ∥FG( ). 5、如右图,已知AD ⊥BC,EF ⊥BC,∠1=∠2. 求证:DG ∥BA.证明:∵AD ⊥BC,EF ⊥BC ( ) ∴∠EFB=∠ADB=90° ( ) ∴EF ∥AD( ) ∴∠1=∠BAD( ) 又∵∠1=∠2 ( ) ∴ (等量代换)A B ECGHF12DG H K EDC BA ∴DG ∥BA.( )6、如图:已知:AD ⊥BC 于D ,EF ⊥BC 于F ,∠1=∠3,求证 :AD 平分∠BAC 。
证明:∵AD ⊥BC EG ⊥BC 于F (已知) ∴AD ∥EF ( ) ∴∠1=∠E ( ) ∠2=∠3( )又∵∠3=∠E (已知) ∴∠1=∠2( )∴AD 平分∠BAC ( )7、如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=30°,试说明AB ∥CD. 证明:∵EG ⊥AB (已知)∴∠EGK=90°( ),∴ 在ΔEGK 中∠E+∠EKG=90°( ),又∵∠E=30°( ) ∴∠EKG=600 又∵∠CHF=600 ∴∠EKG=∠CHF∴AB ∥CD.( )。
平行线与相交线几何证明题专项训练及答案

平行线与相交线几何证明题专项训练及答案证明题1:平行线与等角线的性质问题描述在平面内给出一组平行线和一条相交线,证明以下性质:如果该相交线与任意一条平行线均成相等角,则该相交线与其它平行线也成相等角。
证明过程已知条件设给出的平行线为l1 和 l2,给出的相交线为l3。
根据已知条件,相交线l3与平行线l1成相等角,即∠A = ∠D(角度A在l1上,角度D在l3上)。
证明目标要证明相交线l3与平行线l2成相等角,即∠B = ∠E(角度B在l2上,角度E在l3上)。
证明过程1.假设相交线l3与平行线l2不成相等角,即∠B ≠ ∠E。
2.在l2上取一点F,并作垂线FG与l1相交于G点。
3.连接点E和G,并延长线段EG与l1和l2相交于H 点。
4.根据平行线的性质,得到∠D = ∠F(对应角相等)和∠A = ∠G(同旁内角相等)。
5.在△DGF和△AEG中,根据三角形内角和定理,得到∠D + ∠F + ∠G = 180°和∠A + ∠E + ∠G = 180°。
6.结合前述结果,得到∠D + ∠F = ∠A + ∠E。
7.根据已知条件,得到∠A = ∠D。
8.结合步骤6和7的结果,得到∠F = ∠E。
9.根据角度相等的定义,得到∠B = ∠E,即相交线l3与平行线l2也成相等角,证明完毕。
答案根据以上证明过程,可以得出结论:如果相交线与一组平行线成等角,那么相交线与其它平行线也成等角。
证明题2:平行线的封闭性问题描述在平面内给出一组平行线,证明以下性质:如果两条平行线的一个夹角与另外一条平行线的一个角相等,则这两条平行线也相等。
证明过程已知条件设给出的平行线为l1 和 l2,给出的夹角为∠A(角度A在l1和l2之间)。
根据已知条件,∠A = ∠B(角度B在l1和另外一条平行线l3之间)。
证明目标要证明l1 = l2,即两条平行线相等。
证明过程1.假设l1 ≠ l2,即l1和l2不相等。
证明题七年级下册

证明题七年级下册一、相交线与平行线证明题。
1. 如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠2 : ∠1 = 4:1,求∠AOF的度数。
证明:设∠1 = x,因为∠2:∠1 = 4:1,则∠2 = 4x。
因为OE平分∠BOD,所以∠DOE=∠1 = x。
又因为∠2+∠DOE = 180°(邻补角之和为180°),即4x + x=180°,5x = 180°,解得x = 36°。
所以∠COE=180° - ∠1=180° - 36° = 144°。
因为OF平分∠COE,所以∠COF=(1)/(2)∠COE=(1)/(2)×144° = 72°。
∠AOC = ∠1 = 36°(对顶角相等)所以∠AOF=∠AOC + ∠COF = 36°+72° = 108°。
2. 已知:如图,AB∥CD,∠1 = ∠2,求证:AM∥CN。
证明:因为AB∥CD,所以∠EAB = ∠ACD(两直线平行,同位角相等)。
又因为∠1 = ∠2,所以∠EAB - ∠1=∠ACD - ∠2,即∠MAC = ∠NCA。
所以AM∥CN(内错角相等,两直线平行)3. 如图,已知∠1 = ∠2,∠C = ∠D,求证:∠A = ∠F。
证明:因为∠1 = ∠2,∠1 = ∠3(对顶角相等),所以∠2 = ∠3。
所以DB∥EC(同位角相等,两直线平行)。
所以∠D = ∠4(两直线平行,同位角相等)。
又因为∠C = ∠D,所以∠C = ∠4。
所以DF∥AC(内错角相等,两直线平行)。
所以∠A = ∠F(两直线平行,内错角相等)二、三角形证明题。
4. 在△ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于F。
求证:AF=(1)/(3)AC。
证明:过点D作DG∥BF交AC于G。
人教版七年级下册数学第5章相交线与平行线证明题专题训练
人教版七年级下册数学第5章 相交线与平行线 证明题专题训练1.如图,直线AB 与直线CD 相交于点O ,OE ⊥OF ,且OA 平分⊥COE . (1)若⊥DOE =50°,求⊥AOE ,⊥BOF 的度数.(2)设⊥DOE =α,⊥BOF =β,请探究α与β的数量关系(要求写出过程).2.如图,直线AB 和CD 相交于点O ,OE 把⊥AOC 分成两部分,且⊥AOE ⊥⊥EOC =2⊥3,OF 平分⊥BOE . (1)若⊥BOD =65°,求⊥BOE .(2)若⊥AOE =12⊥BOF ﹣10°,求⊥COE .3.已知如图,直线AB 、直线CD 相交于点O ,OE 是AOD ∠内的一条射线,且OE CD ⊥,:1:2AOE AOC ∠∠=. (1)求BOD ∠的度数;(2)如图2,射线OM 平分AOD ∠,射线ON 在BON ∠内部,且23BON BOM ∠=∠,求DON ∠的度数.4.如图,⊥1+⊥2=180°,⊥C =⊥D .求证:AD ⊥BC .5.如图,FCG B ∠=∠,180DEF D +=︒∠∠,则AB 与EF 平行吗?为什么?6.已知,如图,ABC ADC ∠=∠,BF 、DE 分别平分ABC ∠与ADC ∠,且13∠=∠.求证://AB DC .7.如图,点A 在CF 上,46BAF ∠=︒,136ACE ∠=︒,CE DG ⊥于点C .问 //DG AB 吗?为什么?8.如图,//AB CD ,//CD EF ,//BC ED ,70B ∠=︒,求C ∠,D ∠和E ∠的度数.9.将一副直角三角板按如图所示的方式放置,60B ∠=︒,45E ∠=︒,75AFD ∠=︒.求证://AE BC .10.如图,已知180BAD ADC ∠+∠=︒,AE 平分BAD ∠,交CD 于点F ,交BC 的延长线于点E ,DG 交BC 的延长线于点G ,CFE AEB ∠=∠. (1)若87B ∠=︒,求DCG ∠的度数;(2)AD 与BC 是什么位置关系?请说明理由;(3)若DAB α∠=,DGC β∠=,直接写出α,β满足什么数量关系时AE DG ∥.11.如图,已知射线AM ⊥BN ,连结AB ,点C 是射线BN 上的一个动点(与点B 不重合),AD ,AE 分别平分⊥BAC 和⊥CAM ,交射线BN 于点D ,E . (1)试说明:⊥ACB =2⊥AEB ;(2)若⊥ADB ﹣⊥BAD =45°,求⊥AEB 的度数.12.如图所示,点B 、E 分别在AC 、DF 上,BD 、CE 均与AF 相交,A F ∠=∠,C D ∠=∠,求证:12∠=∠.13.如图,⊥ENC +⊥CMG =180°,AB ⊥CD . (1)求证:⊥2=⊥3.(2)若⊥A =⊥1+70°,⊥ACB =42°,则⊥B 的大小为______.14.已知:如图,ABC 中,点D 、E 分别在AB 、AC 上,EF 交DC 于点F ,32180∠+∠=︒ ,1B ∠=∠. (1)求证:∥DE BC ;(2)若DE 平分ADC ∠,33B ∠=∠,求2∠的度数.15.如图,点D ,E 分别在AB 和AC 上,DE BC ∥,30DBE ∠=︒,25EBC ∠=︒,求BDE ∠的度数.16.如图,已知,A ADE C E ∠=∠∠=∠. (1)若3,EDC C ∠=∠求C ∠的度数; (2)求证://BE CD .17.已知:如图,CDG B ∠=∠,AD BC ⊥于点D ,EF BC ⊥于点F ,试判断1∠与2∠的关系,并说明理由.(写出推理依据)18.已知:如图,⊥BAP+⊥APD =180°,⊥1 =⊥2.求证:AE⊥PF.19.如图,AE⊥BC,FG⊥BC,⊥1=⊥2,求证:AB⊥CD.20.如图,AB⊥DE,C为BD上一点,⊥A=⊥BCA,⊥E=⊥ECD,求证:CE⊥CA.21.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分⊥ADC交BC于点E,点F为线段CD延长线上一点,⊥BAF=⊥EDF(1)求证:⊥DAF=⊥F;(2)在不添加任何辅助线的情况下,请直接写出所有与⊥CED互余的角.22.已知AB⊥CD,点E为AB,CD之外任意一点.(1)如图1,探究⊥BED与⊥B,⊥D的数量关系,并说明理由;(2)如图2,探究⊥CDE与⊥B,⊥E的数量关系,并说明理由.参考答案:1.解:⊥⊥DOE=50°,⊥⊥COE=180°-⊥DOE=180°-50°=130°,⊥OA平分⊥COE,⊥⊥AOE=12⊥COE=12×130°=65°,⊥OE⊥OF,⊥⊥EOF=90°,⊥⊥BOF=180°-⊥AOE-⊥EOF=180°-65°-90°=25°;(2)解:⊥⊥DOE=α,⊥⊥COE=180°-⊥DOE=180°-α,⊥OA平分⊥COE,⊥⊥AOE=12⊥COE=12(180°-α)=90°-12α,⊥OE⊥OF,⊥⊥EOF=90°,⊥⊥BOF=β=180°-⊥AOE-⊥EOF=180°-(90°-12α)-90°=12α,即α=2β.2.解:⊥⊥AOC与⊥BOD是对顶角,⊥⊥AOC=⊥BOD=65°.⊥⊥AOE:⊥EOC=2:3,⊥⊥AOE=25⊥AOC=26°.⊥⊥BOE=180°-⊥AOE=180°-26°=154°;(2)解:设⊥AOE=2x,⊥EOC=3x.⊥⊥AOE=12⊥BOF-10°,⊥⊥BOF=4x+20°.⊥OF平分⊥BOE,⊥⊥BOE=2⊥BOF=8x+40°.⊥⊥AOE +⊥BOE =2x +8x +40°=180°. ⊥x =14°. ⊥⊥COE =3x =42°. 3.解:⊥OE ⊥CD , ⊥⊥COE =90°, ⊥⊥AOE :⊥AOC =1:2, ⊥⊥AOC =90°×23=60°,⊥⊥BOD =⊥AOC =60°; (2)由(1)可知:⊥BOD =60°,⊥⊥AOD =180°-⊥BOD =180°-60°=120°, ⊥OM 平分⊥AOD , ⊥⊥AOM =12 ×120°=60°,⊥⊥BOM =180°-⊥AOM =180°-60°=120°, ⊥⊥BON =23 ⊥BOM =23×120°=80°,⊥⊥DON =⊥BON -⊥BOD =80°-60°=20°. 4.证明:⊥⊥1+⊥2=180°,⊥2+⊥AED =180°, ⊥⊥1=⊥AED , ⊥DE ⊥AC , ⊥⊥D =⊥DAF , ⊥⊥C =⊥D , ⊥⊥DAF =⊥C , ⊥AD ⊥BC . 5.解:AB 与EF 平行, 理由:⊥FCG B ∠=∠, ⊥//AB DC ,⊥180DEF D +=︒∠∠, ⊥//EF DC ,6.证明:BF ,DE 分别平分ABC ∠与ADC ∠21ABC ∴∠=∠,22ADC ∠=∠ ABC ADC ∠=∠ 12∠∠∴=13∠=∠23∴∠=∠//AB CD ∴.7.解://DG AB ,理由如下. ⊥CE CD ⊥, ⊥90DCE ∠=︒, ⊥136ACE ∠=︒,⊥36013690134ACD ∠=︒-︒-︒=︒, ⊥46BAF ∠=︒,⊥180********BAC BAF ∠=︒-∠=︒-︒=︒, ⊥ACD BAC ∠=∠, ⊥//DG AB . 8.//AB CD ,//CD EF ,////AB CD EF ∴,70C B ∴∠=∠=︒,E D ∠=∠,又//BC DE , 180C D ∴∠+∠=︒,⊥⊥D =110°,110E ∴∠=︒.答:C ∠,D ∠和E ∠的度数分别是70︒、110︒、110︒. 9.解:由直角三角板的性质可得: ⊥C=30°,⊥⊥AFD=⊥C+⊥CDF=75°,⊥⊥CDF=⊥E , ⊥AE⊥BC . 10.解:⊥180BAD ADC ∠+∠=︒, ⊥AB CD ∥, ⊥87B DCG ∠=∠=︒. (2)解:AD 与BC 是的位置关系为:AD BC ∥,理由如下: ⊥AE 平分BAD ∠, ⊥BAE DAE ∠=∠, ⊥180BAD ADC ∠+∠=︒, ⊥AB CD ∥, ⊥BAE CFE ∠=∠, ⊥AEB CFE ∠=∠, ⊥⊥AEB =⊥BAE =⊥DAE , ⊥AD BC ∥. (3)解:α与β的数量关系为:12αβ=,理由如下:当AE DG ∥时,AEB DGC β∠=∠=,由(2)中推导可知,1122AEB EAD BAD α∠=∠=∠=,⊥12αβ=. 11.解:⊥AE 平分⊥CAM2.CAM EAM ∴∠=∠,AM BN ∥,.CAM ACB EAM AEB ∴∠=∠∠=∠2.ACB AEB ∴∠=∠(2) 解:,AM BN ∥,.CAM ACB ADB DAM ∴∠=∠∠=∠⊥AD 平分⊥BAC.BAD CAD ∴∠=∠45,ADB BAD ︒∠-∠=45.DAM CAD ︒∴∠-∠= 45.CAM ACB ︒∴∠=∠= 由(1)知,2,ACB AEB ∠=∠22.5.AEB ︒∴∠= 12.证明:⊥A F ∠=∠, ⊥AC DF ∥, ⊥ABD D ∠=∠, 又⊥C D ∠=∠, ⊥ABD C ∠=∠, ⊥DB CE ∥, ⊥13∠=∠, ⊥23∠∠=, ⊥12∠=∠. 13.(1)证明:⊥⊥ENC +⊥CMG =180°,⊥CMG =⊥FMN , ⊥⊥ENC +⊥FMN =180°, ⊥FG ⊥ED , ⊥⊥2=⊥D , ⊥AB ⊥CD , ⊥⊥3=⊥D , ⊥⊥2=⊥3;(2)解:⊥AB ⊥CD ,⊥⊥A +⊥ACD =180°,⊥⊥A =⊥1+70°,⊥ACB =42°,⊥⊥1+70°+⊥1+42°=180°,⊥⊥1=34°,⊥AB ⊥CD ,⊥⊥B =⊥1=34°.故答案为:34°.14.解:(1)⊥32180∠+∠=︒,⊥2+⊥DFE =180°, ⊥⊥3=⊥DFE ,⊥EF //AB ,⊥⊥ADE =⊥1,又⊥1B ∠=∠,⊥⊥ADE =⊥B ,⊥DE //BC ,(2)⊥DE 平分ADC ∠,⊥⊥ADE =⊥EDC ,⊥DE //BC ,⊥⊥ADE =⊥B ,⊥33B ∠=∠⊥⊥5+⊥ADE +⊥EDC =3B B B ∠+∠+∠=180°, 解得:36B ∠=︒,⊥⊥ADC =2⊥B =72°,⊥EF //AB ,⊥⊥2=⊥ADC =180°-108°=72°,15.解:⊥30DBE ∠=︒,25EBC ∠=︒,⊥⊥ABC =⊥DBE +⊥EBC =55°,⊥DE ⊥BC ,⊥⊥BDE +⊥ABC =180°,⊥⊥BDE =180°-⊥ABC =125°.16.(1)A ADE ∠=∠,//ED AC ∴,180EDC C ∴∠+∠=︒.3EDC C ∠=∠ ,3180C C ∴∠+∠=︒,45C ∴∠=︒ ;(2)A ADE ∠=∠,//ED AC ∴,ABE E ∴∠=∠.C E ∠=∠,ABE C ∴∠=∠,//BE CD ∴ .17.CDG B ∠=∠DG AB ∴1DAB ∴∠=∠ 又AD BC ⊥于点D ,EF BC ⊥于点FAD EF ∴2DAB ∴∠=∠12∠∠∴=18.证明:⊥⊥BAP +⊥APD =180°⊥AB⊥CD⊥⊥BAP=⊥CPA⊥⊥1 =⊥2⊥⊥BAP-⊥1=⊥CPA-⊥2,即⊥EAP=⊥FPA ⊥AE⊥PF19.证明:如图,设BC 与AE 、GF 分别交于点M 、N.⊥AE⊥BC,FG⊥BC,⊥⊥AMB=⊥GNB=90°,⊥AE⊥FG,⊥⊥A=⊥1;又⊥⊥2=⊥1,⊥⊥A=⊥2,⊥AB⊥CD.20.证明⊥AB⊥DE,⊥⊥B+⊥D=180°,⊥⊥A=⊥BCA,⊥E=⊥ECD,⊥⊥B=180°-2⊥BCA,⊥D=180°-2⊥ECD,⊥(180°-2⊥BCA)+(180°-2⊥ECD)=180°,⊥⊥BCA+⊥ECD=90°,⊥⊥ACE=90°,⊥CE⊥CA.21.解:(1)⊥AB⊥BC于点B,DC⊥BC于点C,⊥⊥B+⊥C=180°,⊥AB⊥CF,⊥⊥BAF+⊥F=180°,又⊥⊥BAF=⊥EDF,⊥⊥EDF+⊥F=180°,⊥ED⊥AF,⊥⊥ADE=⊥DAF,⊥EDC=⊥F,⊥DE平分⊥ADC,⊥⊥ADE=⊥CDE,⊥⊥DAF=⊥F;(2)⊥⊥C=90°,⊥⊥CED+⊥CDE=90°,⊥⊥CED与⊥CDE互余,又⊥⊥ADE=⊥DAF=⊥EDC=⊥F,⊥与⊥CED互余的角有⊥ADE,⊥CDE,⊥F,⊥FAD.22.解:(1)⊥B=⊥BED+⊥D.理由如下:过点E作EF⊥AB.又⊥AB⊥CD,⊥EF⊥AB⊥CD.⊥⊥BEF=⊥B,⊥D=⊥DEF.⊥⊥BEF=⊥BED+⊥DEF,⊥⊥B=⊥BED+⊥D.(2)⊥CDE=⊥B+⊥BED.理由如下:过点E作EF⊥AB.又⊥AB⊥CD,⊥EF⊥AB⊥CD.⊥⊥B+⊥BEF=180°,⊥CDE+⊥DEF=180°.又⊥⊥DEF=⊥BEF-⊥BED,⊥⊥CDE+⊥BEF-⊥BED=⊥B+⊥BEF,即⊥CDE=⊥B+⊥BED.。
人教版七年级数学相交线与平行线证明题专项训练
人教版七年级数学相交线与平行线证明题专项训练1.已知AB∥CD,∠1=∠3,证明AC∥BD。
根据平行线内角和定理,∠1+∠2=180°,∠3+∠4=180°,又∠1=∠3,因此∠2=∠4,即AB与CD的对应内角相等,因此AB与CD平行。
同理可证AC与BD平行。
2.已知CD⊥AD,DA⊥AB,∠1=∠2,问DF与AE是否平行。
根据垂直线的性质,∠1和∠2是直角,因此AD与AB垂直。
根据平行线内角和定理,∠2+∠3=180°,因此∠3=90°-∠2,又∠1=∠2,因此∠4=∠3,即DF与AE的对应内角相等,因此DF与AE平行。
3.已知AB∥CD,AD∥BC,∠A=3∠B,求∠A、∠B、∠C、∠D的度数。
根据平行线内角和定理,∠A+∠B=180°,∠C+∠D=180°,又∠A=3∠B,因此4∠B=180°,∠B=45°,∠A=135°。
同理可得∠C=135°,∠D=45°。
4.已知AB∥CD,直线EF交AB、CD于点G、H,如果GM平分∠BGF,HN平分∠CHE,那么,GM与HN平行吗?为什么?根据平行线内角和定理,∠BGF+∠FGM=180°,∠CHE+∠EHN=180°,又GM与HN分别平分这两个角,因此∠XXX∠XXX,即GM与HN的对应角相等,因此GM与HN平行。
5.已知∠ACB=60,∠ABC=50,BO、CO分别平分∠ABC、∠ACB,EF是经过点O且平行于BC的直线,求∠BOC的度数。
根据平分角的性质,∠XXX∠OCB=30°,又根据平行线内角和定理,∠BOC+∠OBC+∠OCB=180°,因此∠BOC=120°。
6.已知AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50,求∠BHF的度数。
根据平行线内角和定理,∠AGE+∠BGF=180°,又XXX∠EFD,因此∠XXX∠HFE,又∠AGE=50,因此∠HFE=50,因此∠BHF=180°-∠BGF-∠XXX°。
平行线与相交线证明题专项(最终五篇)
平行线与相交线证明题专项(最终五篇)第一篇:平行线与相交线证明题专项证明题专练二、两组平行线的证明题【找出连接两组平行线的角】1.已知:如图,CD平分∠ACB,AC∥DE,∠DCE=∠FEB,求证:EF平分∠DEB.1、如图已知,AB∥CD.AF,CF分别是∠EAB、∠ECD的角平分线,F是两条角平分线的一、平行线之间的基本图交点;求证:∠F= 1B2∠AEC.E FCDB2、已知AB//CD,此时∠A、∠AEF、∠EFC和∠C的关系又如何?你能找出其中的规律吗? ED3、将题变为如下图:AB//CD此时∠A、∠AEF、∠EFD和∠D的关系又如何?你能找出其中的规律吗?CD4、如图,AB//CD,那么∠A、∠C与∠AEC有什么关系? ECDEC E B3、已知:如图2-96,DE⊥AO于E,BO⊥AO,FC⊥AB于C,∠1=∠2,求证:DO⊥AB.三、两组平行线构造平行四边形1.已知:如图,AB是一条直线,∠C = ∠1,∠2和∠D互余,BE⊥FD于G.求证:AB∥CD .2、如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.DF42A(第22B 题)C五、寻找角之间的关系1、如图2-97,已知:∠1=∠2,∠3=∠4,∠5=∠6.求证:AD∥BC.2、已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4。
求证:AD∥BE。
D3.如图12,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1 +∠2 = 90°.求证:(1)AB∥CD;(2)∠2 +∠3 = 90°.六、翻折图103、如图,M、N、T和A、B、C分别在同一直线上,且∠1=∠3,∠P=∠T,求证:∠M=∠R。
四、证特殊角1、AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则∠AEC的度数是.图7 图82、AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作PF⊥EP垂足为P,若∠PEF=30,则∠PFC=_____.3、如图,已知:DE∥AC,CD平分∠ACB,EF平分∠DEC,∠1与∠2互余,求证:DG∥EF.A1、如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为.2、如图(1),已知矩形ABCD,将△BCD沿对角线BD折叠,记点C的对应点为C′,若D5.如图已知直线a∥b,AB平分∠MAD,AC平分∠NAD,DE⊥AC 于E,求证:∠1=∠2.∠ADC′=20°,则∠DBC=的度数为。
