利用matlab进行微积分的计算共28页文档
实验一B Matlab基本操作与微积分计算
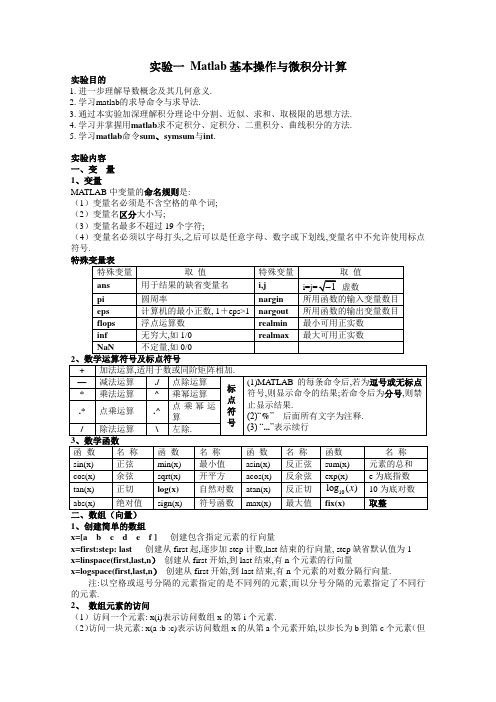
实验一Matlab基本操作与微积分计算实验目的1.进一步理解导数概念及其几何意义.2.学习matlab的求导命令与求导法.3.通过本实验加深理解积分理论中分割、近似、求和、取极限的思想方法.4.学习并掌握用matlab求不定积分、定积分、二重积分、曲线积分的方法.5.学习matlab命令sum、symsum与int.实验内容一、变量1、变量MATLAB中变量的命名规则是:(1)变量名必须是不含空格的单个词;(2)变量名区分大小写;(3)变量名最多不超过19个字符;(4)变量名必须以字母打头,之后可以是任意字母、数字或下划线,变量名中不允许使用标点符号.1、创建简单的数组x=[a b c d e f ]创建包含指定元素的行向量x=first:step: last创建从first起,逐步加step计数,last结束的行向量, step缺省默认值为1x=linspace(first,last,n)创建从first开始,到last结束,有n个元素的行向量x=logspace(first,last,n)创建从first开始,到last结束,有n个元素的对数分隔行向量.注:以空格或逗号分隔的元素指定的是不同列的元素,而以分号分隔的元素指定了不同行的元素.2、数组元素的访问(1)访问一个元素: x(i)表示访问数组x的第i个元素.(2)访问一块元素: x(a :b :c)表示访问数组x的从第a个元素开始,以步长为b到第c个元素(但不超过c),b可以为负数,b缺损时为1.(3)直接使用元素编址序号: x ([a b c d]) 表示提取数组x的第a、b、c、d个元素构成一个新的数组[x (a) x (b) x(c) x(d)].3、数组的运算(1)标量-数组运算数组对标量的加、减、乘、除、乘方是数组的每个元素对该标量施加相应的加、减、乘、除、乘方运算.设:a=[a1,a2,…,an], c=标量, 则:a+c=[a1+c,a2+c,…,an+c]a .*c=[a1*c,a2*c,…,an*c]a ./c= [a1/c,a2/c,…,an/c](右除)a .\c= [c/a1,c/a2,…,c/an] (左除)a .^c= [a1^c,a2^c,…,an^c]c .^a= [c^a1,c^a2,…,c^an](2)数组-数组运算当两个数组有相同维数时,加、减、乘、除、幂运算可按元素对元素方式进行的,不同大小或维数的数组是不能进行运算的.设:a=[a1,a2,…,an], b=[b1,b2,…,bn], 则:a +b= [a1+b1,a2+b2,…,an+bn]a .*b= [a1*b1,a2*b2,…,an*bn]a ./b= [a1/b1,a2/b2,…,an/bn]a .\b=[b1/a1,b2/a2,…,bn/an]a .^b=[a1^b1,a2^b2,…,an^bn]三、矩阵1、矩阵的建立矩阵直接输入:从“[ ” 开始,元素之间用逗号“,”(或空格),行之间用分号“;”(或回车),用“ ]”结束.特殊矩阵的建立:a=[ ] 产生一个空矩阵,当对一项操作无结果时,返回空矩阵,空矩阵的大小为零.b=zeros (m,n) 产生一个m行、n列的零矩阵c=ones (m,n) 产生一个m行、n列的元素全为1的矩阵d=eye (m,n) 产生一个m行、n列的单位矩阵eye (n) %生成n维的单位向量eye (size (A)) %生成与A同维的单位阵2、矩阵中元素的操作(1)矩阵A的第r行A(r,:)(2)矩阵A的第r列A(:,r)(3)依次提取矩阵A的每一列,将A拉伸为一个列向量A(:)(4)取矩阵A的第i1~i2行、第j1~j2列构成新矩阵:A(i1:i2, j1:j2)(5)以逆序提取矩阵A的第i1~i2行,构成新矩阵:A(i2:-1:i1,:)(6)以逆序提取矩阵A的第j1~j2列,构成新矩阵:A(:, j2:-1:j1 )(7)删除A的第i1~i2行,构成新矩阵:A(i1:i2,:)=[ ](8)删除A的第j1~j2列,构成新矩阵:A(:, j1:j2)=[ ](9)将矩阵A和B拼接成新矩阵:[A B];[A;B]3、矩阵的运算(1)标量-矩阵运算同标量-数组运算.(2)矩阵-矩阵运算a. 元素对元素的运算,同数组-数组运算.(A/B %A右除B; B\A %A左除B)b. 矩阵运算:矩阵加法:A+B矩阵乘法:A*B方阵的行列式:det(A)方阵的逆:inv(A)方阵的特征值与特征向量:[V,D]=eig[A] A 的转置 A’ A 的n 次幂A^n 四、导数及偏导数计算 1.学习matlab 命令.建立符号变量命令sym 和syms 调用格式: x=sym(‘x’), 建立符号变量x ;syms x y z , 建立多个符号变量x,y,z ; matlab 求导命令diff 调用格式:diff (函数()f x ) , 求()f x 的一阶导数()f x ';diff (函数()f x , n ) , 求()f x 的n 阶导数()()n f x (n 是具体整数); diff (函数(,)f x y ,变量名x ), 求(,)f x y 对x 的偏导数f x∂∂; diff (函数(,)f x y , 变量名x ,n ) ,求(,)f x y 对x 的n 阶偏导数n n fx∂∂;matlab 求雅可比矩阵命令jacobian ,调用格式:jacobian ([(,,)f x y z ;(,,)g x y z ;(,,)h x y z ], [,,x y z ])给出: f f f x y z gg g x y z h h h xyz ⎛⎫∂∂∂ ⎪∂∂∂ ⎪ ⎪∂∂∂⎪∂∂∂ ⎪ ⎪∂∂∂ ⎪∂∂∂⎝⎭2.求一元函数的导数. (1)()y f x =的一阶导数. 例1.1 设()x f x e =,用定义计算(0)f '. 解:()f x 在某一点0x 的导数定义为极限: 000()()limx f x x f x x∆→+∆-∆我们记h x =∆,输入命令:syms h;limit((exp(0+h)-exp(0))/h,h,0) 得结果:ans=1.可知(0)1f '= 例1.2 求ln(sin )y x =的导数. 解: 输入命令:dy_dx=diff(log(sin(x))). 得结果:dy_dx=cos(x)/sin(x).在matlab 中,函数x ln 用log(x)表示,而log10(x)表示x lg .例1.3 求下列函数的导数: %利用matlab 命令diff 一次可以求出若干个函数的导数.1.1y =2.22cos 2cos2y x x =+.3.xy sin 34=.4.xy ln ln 4=. 解: 输入命令:a=diff([sqrt(x^2- 2*x+5),cos(x^2)+2*cos(2*x),4^(sin(x)),log(log(x))]). 得结果:a=[1/2/(x^2-2*x+5)^(1/2)*(2*x-2), -2*sin(x^2)*x-4*sin(2*x), 4^sin(x)*cos(x)*log(4), 1/x/log(x)].由本例可以看出,matlab 函数是对矩阵或向量进行操作的,a(i)表示向量a 的第i 个分量.函数向量的第i 个函数的导数为导数向量中对应的元素。
MATLAB教程【5】微积分

Z=trapz(x,y) 计算 对x的梯形积分,其中 、y定义函数关系 计算y 的梯形积分, 定义函数关系y=f(x)。 的梯形积分 其中x、 定义函数关系 。 Z=trapz(x,y,dim) 对dim指定的 的维进行积分。 指定的y的维进行积分 指定的 的维进行积分。
1.4.7 数 值 积 分
一、数值积分的基本原理
b b
I1 = ∫ f ( x)dx, I 2 = ∫ p ( x)dx
a a
f(b)
T=
b−a [ f (a ) + f (b )] 2
梯形公式
f(a)
将积分区间[a,b]划分为 等份,步长 划分为n等份 将积分区间 划分为 等份, h=(b-a)/n,xk=a+bk构造求积公式 构造求积公式
( I n = ( b − a )∑ C k n ) f ( x k ) k =0 n
牛顿 − 柯特斯公式
a
b n = 1即梯形公式, n = 2时为辛普生公式 即梯形公式,
b−a a+b S= [ f (a ) + 4 f ( ) + f ( b )] 6 2
1.4.7 数 值 积 分
二、数值积分的实现 1、梯形积分:对矢量、矩阵和多维列阵进行梯形积分 、梯形积分:对矢量、 Z=trapz(y) 计算 的数值梯形积分,步长默认为 ,若不是 而是 , 计算y 的数值梯形积分,步长默认为1,若不是1 而是h,
例:用不同的方法求函 数 f ( x )的数值导数并作图 f ( x) = f '( x) = x 3 + 2 x 2 − x + 12 + 6 x + 5 + 5 x + 2 3x2 + 4x − 1 2 x + 2 x − x + 12
第3讲 MATLAB在微积分中的应用

2)求数值解的方法 1. 欧拉方法 若步长h较小,则可用差商近似代替导数,即 y ( x + h) − y ( x ) y '( x) ≈ h 于是便得公式 yi +1 ≈ yi + hf ( xi , yi ) , i = 0,1, L , n − 1. y0 = y ( x0 ) 此法称为欧拉方法。
例7 用MATLAB软件求微分方程 du = 1+ u2 dt 的通解; 例8 用MATLAB软件求微分方程 d 2 y dy 2 + 4 + 29 y = 0 dx dx y(0) = 0, y ' (0) = 15 的特解。
例9 用MATLAB软件求微分方程组 dx dt = 2 x − 3 y + 3z dy = 4 x − 5 y + 3z dt dz dt = 4 x − 4 y + 2 z 的通解.
2. 改进的欧拉方法 对方程y ' = f ( x, y )两边从xi到xi +1积分,再利用梯形公式,得 y ( xi +1 ) − y ( xi ) = ∫
xi +1 xi
f ( x, y ( x )) dx
xi +1 − xi ≈ [ f ( xi , y ( xi )) + f ( xi +1 , y ( xi +1 ))] 2 h 于是有公式: yi +1 ≈ yi + [ f ( xi , yi ) + f ( xi +1 , yi +1 )], y0 = y ( x0 ) 2 上式中右边yi +1的值可用欧拉方法计算,即有 yi +1 = yi + hf ( xi , yi ) i = 0,1, L , n − 1. h yi +1 = yi + 2 [ f ( xi , yi ) + f ( xi +1 , yi +1 )] 此法称为改进的欧拉方法。
第2讲 MATLAB微积分中的应用

返回
clear; [a,b]=solve('3*x-y=1','x+y=3','x,y')
返回
2.3 导数 help diff (P35)
第三讲 MATLAB在微积
分中的应用
返回
2.1 极限
(1)limit(f,x,a):计算当变量x趋近于常数a时,
(2)
f(x)函数的极限值;
(2) limit(f,x,a,‘right’):‘right’表示变量x从右边 趋近于a;
(3) limit(f,x,a,‘left’): ‘left’表示变量x从左边 趋近于a
diff(f,x):以x为自变量,对符号表达式f求一阶导数; diff(f,x,n):以x为自变量,对符号表达式s求n阶导数。
返回
例1 设y = xe3x, 求y' , y (5).
syms x; y='x*exp(3*x)'; y1=diff(y,x); % 1阶导数 y5=diff(y,x,5); % 5阶导数 y1,y5
例2 求3次方程x3 x 3 = 0的所有根.
roots([1,0,-1,-3])
返回
>>roots([1,0,-1,-3]) ans =
1.6717 -0.8358 + 1.0469i -0.8358 - 1.0469i >>
返回
Matlab微积分问题计算机求解实验

>> q2=quad('quad1',0,1)
【例】求exp(-x2)在[0,1]上的积分。
数值积分
3、编写被积函数表达式,函数名为f=@(x).exp(-x.^2);
>> q2=quad(f,0,1)
数值积分
(2)梯形法(被积函数由一个表格定义)
trapz函数采用梯形法求取数值积分,适用于由表格形式定义的函数关系的求定积分问题,求值速度快, 但精度差。
syms x; f=abs(x)/x;%给出待展开的函数 xx=[-pi:pi/200:pi]; xx=xx(xx~=0); xx=sort([xx,-eps,eps]);
Fourier级数的Matlab程序
yy=subs(f,x,xx);%计算f(x)的值 for i=1:20
[A,B,F]=fseries(f,x,n); y=subs(F,x,xx); subplot(4,5,n); plot(xx,yy);%画出f(x)的图像 hold on plot(xx,y);%画出Fourier级数的图像 end
K ex2dx 0
计算积分
21
( x1)2
练习:
e 2 dx,
0 2
e2t 2 x 2 1
dx
cost (2 x 2 3 x 1)2
符号求和
symsum(u,n,n0,nn): symsum(f,a,b): 关于默认变量求和
例:计算级数
S 1 及其前100项的部2 分和 n n 1
>> syms n; f=1/n^2;
>> S=symsum(f,n,1,inf)
>> S100=symsum(f,n,1,100)
第七章 MATLAB微积分数值计算

相同维数的向量U,且 1 U1 2 ( V4 4V3 5V2 2V1 ) h 1 U i 2 (Vi 1 2Vi Vi 1 ), (1 i n) h 1 U n 2 (2Vn 5Vn 1 4Vn 2 Vn 3 ) h 默认的步长为1。 U=4*del2(V,h1,h2),对矩阵V,横向(x方向)以步长h1,纵向(y方
diff调用格式为:
Dy=diff(Y):计算向量Y的向前差分,并把结果赋值给向量Dy Dy(i)=Y(i+1)-Y(i),i=1,2,…,n-1。注意向量Dy元素个数比Y少一个
Dy=diff(Y,n):计算向量Y的n阶向前差分。注意向量Dy元素个数比Y少n个.例如:
diff(Y,2)=diff(diff(Y))=DX(i+1)-DX(i)= Y(i+2)-2Y(i+1)+Y(i) , i=1,2 ……n-2。
计算积分,可以采取逐步缩小步长h的办法。即先任
取步长h进行计算,然后取较小步长 h’ 进行计算,如果两
次计算结果相差较大,则取更小步长进行计算,如此下去, 直到相邻两次计算结果相差不大为止,取最小步长算出的 结果作为积分值。这种方法称为变步长积分法。 利用两种步长计算积分时,通常取h’=h/2 。而每次
x
4
精度为O(∆X4)的高阶中心差分算法
yi yi yi yi 2 8 yi 1 8 yi 1 yi 2 12 x yi 2 16 yi 1 30 yi 16 yi 1 yi 2 12 x
2
yi 3 8 yi 2 13 yi 1 13 yi 1 8 yi 2 yi 3 8 x
7.1 数值微分 7.2 数值积分 7.3 常微分方程的数值解法
Matlab在微积分中的应用
Matlab 在微积分中的应用命令1 极限函数 limit格式 limit(F,x,a) %计算符号表达式F=F(x)的极限值,当x →a 时。
limit(F,a) %用命令findsym(F)确定F 中的自变量,设为变量x ,再计算F 的极限值,当x →a 时。
limit(F) %用命令findsym(F)确定F 中的自变量,设为变量x ,再计算F 的极限值,当x →0时。
limit(F,x,a,'right')或limit(F,x,a,'left') %计算符号函数F 的单侧极限:左极限x →a - 或右极限x →a+。
例3-25>>syms x a t h n;>>L1 = limit((cos(x)-1)/x)>>L2 = limit(1/x^2,x,0,'right')>>L3 = limit(1/x,x,0,'left')>>L4 = limit((log(x+h)-log(x))/h,h,0)>>v = [(1+a/x)^x, exp(-x)];>>L5 = limit(v,x,inf,'left')>>L6 = limit((1+2/n)^(3*n),n,inf)计算结果为:L1 =L2 =infL3 =-infL4 =1/xL5 =[ exp(a), 0]L6 =exp(6)命令2 导数(包括偏导数)函数 diff格式 diff(S,'v')、diff(S,sym('v')) %对表达式S 中指定符号变量v 计算S 的1阶导数。
diff(S) %对表达式S 中的符号变量v 计算S 的1阶导数,其中v=findsym(S)。
diff(S,n) %对表达式S 中的符号变量v 计算S 的n 阶导数,其中v=findsym(S)。
第三章-matlab求解微积分
第三章 微积分的数学实验3.1极限与一元微积分3.1.1 初等运算1.定义单个或多个符号变量:syms x y z t ;定义单个符号变量或者符号函数还可以用单引号定义,如x=’x ’,f=’sin(x^2)+2*x-1’。
符号表达式的反函数运算g=finverse(f),g 是返回函数f 的反函数。
例1 求sin(1)y x =-的反函数>>syms x>>y=sin(x-1); g=finverse(y),结果为 g=1+asin(t)2. f actor(f) 因式分解函数f3.Collect(f) 对函数f 合并同类项4. expand(f) 将函数f 表达式展开5. simple(f) 找出表达式的最简短形式(有时需要用2次)6. roots (p )对多项式p 求根函数。
7. solve(F) 一般方程的求根函数例2 解方程2510x x +-=解 >>syms x>>solve(x^2+5*x-1)结果为x =[ -5/2+1/2*29^(1/2) -5/2-1/2*29^(1/2)]8.fzero(f,x0)或fzero(f,[a,b]) 在初始点x0处开始或在区间[a,b]上搜索函数的零点,f(a)与f(b)需要符号相反。
3.1.2 Matlab计算函数的极限函数形式:1)limit(F,x,a),求函数F在 x ->a时的极限。
2)limit(F,a),默认其中的变量为极限变量.3)limit (F),默认其中的变量为极限变量且趋向于0.4)limit(F,x,a,'right')或limit(F,x,a,’left') 求函数F在x->a时的右、左极限.例3 >>syms x a t h; %syms作用是申明x,a,t,h是符号变量,不需先赋值再调用。
>>limit(sin(x)/x) %结果为 1>>limit((x-2)/(x^2-4),2) %结果为 1/4>>limit((1+2*t/x)^(3*x),x,inf) %结果为 exp(6*t)>>limit(1/x,x,0,'right') %结果为 inf>>limit(1/x,x,0,'left') %结果为 -inf>>limit((sin(x+h)-sin(x))/h,h,0) %结果为 cos(x)>>v = [(1 + a/x)^x, exp(-x)];limit(v,x,inf,'left') %结果为[exp(a),0]3.1.3 Matlab计算导数与微分1.一元导数和微分diff函数用以计算函数的微分和导数,相关的函数语法有下列4个:diff(f) 返回f对预设独立变量的一次导数值diff(f,'t')或diff(f,t) 返回f对独立变量t的一次导数(值)diff(f,n) 返回f对预设独立变量的n阶导数(值)diff(f,'t',n) 或diff(f,t,n)返回f对独立变量t的n阶导数(值)这里尽管自变量已经作为符号变量,可以不用syms说明,但是在具体执行diff(f)、diff(f,'t')和diff(f,t)会出现差异,有的能够执行,有的不能够,有的执行符号微分,有的执行数值微分,所以比较麻烦。
微积分问题的MATLAB求解
0-1规划(bintprog)
非线性最小二乘 lsqnonlin lsqcurvefit
其他规划ga gamultiobj simulannealbnd patternsearch threshacceptbnd 上下界 约束 fminbnd fmincon lsqnonlin lsqcurvefit
fun
H
A,b
Aeq,beq vlb,vub X0 x1,x2 options
A矩阵和b向量分别为线性不等式约束: linprog,quadprog,fgoalattain, fmincon,fminimax AX≤b中的系数矩阵和右端向量 Aeq矩阵和beq向量分别为线性等式约 束Aeq*X=beq中的系数矩阵和右端向量 X的下限和上限向量 迭代初始点坐标 函数最小化的区间 优化选项参数结构 linprog,quadprog,fgoalattain, fmincon,fminimax linprog,quadprog,fgoalattain, fmincon,fminimax,lsqcurvefit, lsqnonlin 除fminbnd外所有函数 fminbnd 所有优化函数
内寻找一个近似零点。 solve(f)求解表达式f的代数方程,求解变量为默认变量。 solve(f,x)求解变量为x sovle(f1,f2,...,fn,x1,x2,...,xn)求解f1,f2,...,fn表示的代数方程组。
例如:
三. 微商的计算
3.1符号导数
diff函数用于对符号表达式求导数,该函数的调用形式为: diff(f)没有指定变量和导数阶数,系统按照findsym函数指示的默认变量求一阶导数 diff(f,x) diff(f,n)按findsym函数指示的默认变量求n阶导数,n必须为正整数。 diff(f,x,n)
利用matlab进行微积分的计算
Matlab的微积分符号运算都可以对数组进行。
函数的积分 积分符号运算的基本语句 int(F); %求函数表达式F的不定积分 int(F,v); %求函数表达式F关于变量v的不定积分 int(F,a,b); %求函数表达式F在区间[a,b]上的定积分 int(F,v,a,b); %求函数表达式F在区间[a,b]上的关于变量v的 定积分
elapsed time is 17.471170 seconds. s=
53362913282294785045591045624042980409652472280384260097101349248456268889497101757 50609790198503569140908873155046809837844217211788500946430234432656602250210027842 563285208140554494121044251014267277029477471270891796396777961045322469242686646888 828158207198489710511079687324931915552939701750893156451997608573447301418328401172 44122806490743077037366831700558002936592350885893602352858528081607595747378366554 13175508131522517/712886527466509305316638415571427292066835886188589304045200199115 432408758111149947644415191387158691171781701957525651298026406762100925146587100430 513107268626814320019660997486274593718834370501543445252373974529896314567498212823 69562328237940110688092623177088619795407912477545580493264757378299233527517967352 48042463638051137034331214781746850878453485678021888075373249921995672056932029099 390891687487672697950931603520000
