4第四章非理想流动
合集下载
化学反应:第四章 非理想流动

4.1 反应器中的返混现象与停留时间分布
第四章 非理想流动
实际的工业装置
在实际的工业装置中由于物料在反应器内的流 动速率不均匀、或因内部构件的影响造成物料出现 与主体流动方向相反的逆向流动、死角等都会导致 偏离理想流动。
对于所有偏离平推流和全混流的流动模式 统称为非理想流动。
本章将利用停留时间分布定量地对非理想流动 进行讨论,并考察这些非理想流动对反应器性能的 影响。
4.1 反应器中的返混现象与停留时间分布
第四章 非理想流动
假如示踪剂改用红色流体,连续检测出口中红色
流体的浓度,如果将观测的时间间隔缩到非常小,
得到的将是一条连续的停留时间分布曲线。
4.1 反应器中的返混现象与停留时间分布
(1) 停留时间分布密度函数的定义
第四章 非理想流动
定义:在稳定连续流动系统中,同时进入反应器的N 个流体粒子中,其停留时间介于t~t+dt的那部分粒 子dN占总粒子数N的分率记作:
第四章 非理想流动
1. 停留时间分布密度函数E(t)
实验: 在连续反应器内,如果在某一瞬间 (t = 0) 极快地 向入口物流中加入 100 个红色粒子,同时在系 统的出口处记下不同时间间隔流出的红色粒子数, 结果如下表。
4.1 反应器中的返混现象与停留时间分布
第四章 非理想流动
以时间 t 为横坐标,出口流中红色粒子数为 纵坐标,将上表作图如下:
流体的流动速率和方向带有一定的随机性。反应器内的流动状态实际是 随机变化的。
根据概率理论,我们可以借用两种概率分布以定量地描绘物料在流动系统中的 停留时间分布,这两种概率分布就是停留时间分布密度函数 E (t)和停留时间 分布函数 F (t)。
4.1 反应器中的返混现象与停留时间分布
非理想流动.ppt

停留时间分布的数学描述
数学期望:所有质点停留时间的“加权平均值”
tm t
tE(t)dt
0
E(t)dt
tE(t)dt
0
t dF(t) dt 0 dt
1
tdF (t )
0
0
E(t)dt=dF(t) F(t):所有停留时间为0—t的质点所占的分率 F(t+dt):所有停留时间为0—t+dt的质点所占的分率
如果假定红色粒子和主流体之间除了颜色的差别以外,其余所有性质都完全 相同,那么就可以认为这100个粒子的停留时间分布就是主流体的停留时间分 布。
停留时间分布的数学描述
N N
停留时间为 t t t的物料量 t 0时瞬间进入反应器的物 料量
以时间t为横坐标,出口流中红色粒子数为纵坐标,将上表作图:
t
1
tmE(t) tm dt 2 0 tm tmE(t) tm dt 1
1
t 2E(t)dt 2
tE(t)dt 1
t2 0 m
tm 0
1 t2
t 2E(t)dt 1
0
m
2t
2
m
t 2E(t)dt t 2
0
m
t2
2
t2
/t2 m
F(t)
t
t
F (t) C(t)dt 0
C(t)dt
0
C(t)dt
0
可直接测得
几种流型的停留时间分布函数 与分布密度
活塞流模型 全混流模型
化学反应工程第四章习题答案

3||2(t3E(t)3tE(t)5tE(t)7)tE(t)9
3
=vt =0.86.187 =4.95(m)
°02-2
=°t E(t)dt -t
2G
2
= 47.25 -(6.187)=8.971
8.971
2
(6.187)
= 0.234
73. 某反应器用示踪法测其流量,
不可逆反应,此反应若在活塞流反应器中进行,转化率为 出口转化率。
据如下:
t(min)
0
5
10
15
20
25
30
35
G(g/i)
0
3
5
5
4
2
1
0
2 2试根据实验数据确定E(t)曲线的方差G和二二。 解:首先对实验数据进行一致性检验,此时应满足:
M80
CAdtCo100
0v00.8
5
CAdt [0-2(5-41)- 4(3 - 5 - 2 -0)]=100
03
•••实验数据的一致性检验是满足的。
03
72.有一管式反应装置经脉冲示踪法实验测得如下表所示的数:
V(0=0.8 m3/min;m=80kg;「.C0=80/0.8=100
t(分)
0
2
4
6
8
10
12
14
16
3
CX (kg/m)
0
6.5
12.5
12.5
10
5.0
2.5
1.0
0
2 _ 2试根据表列数据确定该装置的有效容积V、平均停留时间t、方差匚t和二戈
,则表明混合〕
不均匀。
(1)
36.微观流体混合的混合态称为
3
=vt =0.86.187 =4.95(m)
°02-2
=°t E(t)dt -t
2G
2
= 47.25 -(6.187)=8.971
8.971
2
(6.187)
= 0.234
73. 某反应器用示踪法测其流量,
不可逆反应,此反应若在活塞流反应器中进行,转化率为 出口转化率。
据如下:
t(min)
0
5
10
15
20
25
30
35
G(g/i)
0
3
5
5
4
2
1
0
2 2试根据实验数据确定E(t)曲线的方差G和二二。 解:首先对实验数据进行一致性检验,此时应满足:
M80
CAdtCo100
0v00.8
5
CAdt [0-2(5-41)- 4(3 - 5 - 2 -0)]=100
03
•••实验数据的一致性检验是满足的。
03
72.有一管式反应装置经脉冲示踪法实验测得如下表所示的数:
V(0=0.8 m3/min;m=80kg;「.C0=80/0.8=100
t(分)
0
2
4
6
8
10
12
14
16
3
CX (kg/m)
0
6.5
12.5
12.5
10
5.0
2.5
1.0
0
2 _ 2试根据表列数据确定该装置的有效容积V、平均停留时间t、方差匚t和二戈
,则表明混合〕
不均匀。
(1)
36.微观流体混合的混合态称为
第四章非理想流动反应器(201204)

Vc(t )dt c(t ) F (t ) Vc()dt c()
降 阶 法
(不讲)
c(0)
c(0) c(t)
c0(t) 0
t=0 输入曲线
0 t
响应曲线
t
Vc(t )dt Vc(0) dt
停留时间大于 t 的示踪剂量 示踪剂输入量
t→t +dt
1-F(t)
c( t ) F (t ) 1 c ( 0)
t E (t )t t
2 t 2 0 2
• 取样为等时间间隔时: (t t ) E (t ) t t E (t ) t t E (t )t E (t )t
2 2 2 t
2
t E (t ) t E (t )
2
2
(4)无因次化对比时间及函数
(4) 脉冲法和阶跃法的比较
脉冲法 阶跃法
示踪剂 注入方 法
在原有的流股中加入 示踪剂,不改变原流 股流量
可直接测得
将原有流股换成流量与 其相同的示踪剂流股
dF (t ) dC (t ) E(t ) dt C0 dt
E(t)
F(t)
C (t )dt F (t ) C (t )dt C (t )dt
0
E(t )dt 1
• 停留时间分布函数F(t):停留时间0-t范围内的物料(停留 时间小于t的质点)占进料的分率。 t 有: t=0, F(t)=0, t=∞, F(t)=1,F(t)是单调增函数
F (t ) E(t )dt
0
在某一时间t时, E(t)和F(t)之间的关系为: dF (t ) t E(t ) F (t ) E(t )dt dt 0
第4章非理想流动反应器设计PPT课件
脉冲法阶跃法第2节停留时间分布的示踪剂并保持混合物的流量仍为v同时在出口处测定示踪剂浓度c随时间t的变化第2节停留时间分布脉冲注入出口应答第2节停留时间分布时间内注入示踪剂的总量为mmol出口处浓度随时间变化为ctdt时间间隔内出口处流出的示踪剂量占总示踪剂量的dt时间间隔内流出物料量为dn则在此时间间隔内流出的物料占进料物料第2节停留时间分布示踪剂的停留时间分布就是物料质点的停留时间分布即
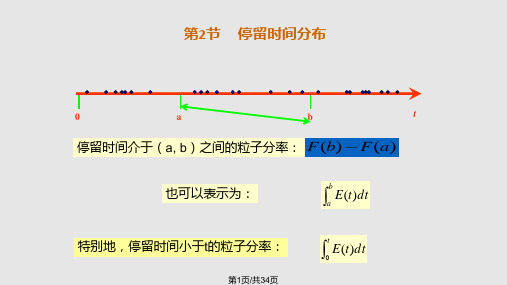
第2节 停留时间分布
0
a
b
t
停留时间介于(a, b)之间的粒子分率: F (b) F (a)
也可以表示为:
b
a E(t)dt
特别地,停留时间小于t的粒子分率:
第1页/共34页
t
0 E(t)dt
第2节 停留时间分布
(1)归一化(normalizing)性质
E(t)dt 1 0
(2)F(t)、E(t)的关系
c0
t=0 脉冲注入
t
第6页/共34页
0 出口应答
第2节 停留时间分布
✓ 设Δt0时间内注入示踪剂的总量为m(mol),出口处浓度随时间变化为c(t), 在示踪剂注入后t -t+dt时间间隔内,出口处流出的示踪剂量占总示踪剂量的 分率:
✓ 若 t+d在t时注间入间示隔踪内剂,的流同出时物,料流量入为反ddN应NN器,的示则踪物在剂料此量时v为间0Nc间m(,t隔)在d内t注,入流示出踪的剂物后料的占t-进料
0
c( ti )ti
t
0
c( ti )
F(t )
0
• 在等时间间隔取样时:
c( ti )
0
第10页/共34页
第2节 停留时间分布
• 阶跃法
第2节 停留时间分布
0
a
b
t
停留时间介于(a, b)之间的粒子分率: F (b) F (a)
也可以表示为:
b
a E(t)dt
特别地,停留时间小于t的粒子分率:
第1页/共34页
t
0 E(t)dt
第2节 停留时间分布
(1)归一化(normalizing)性质
E(t)dt 1 0
(2)F(t)、E(t)的关系
c0
t=0 脉冲注入
t
第6页/共34页
0 出口应答
第2节 停留时间分布
✓ 设Δt0时间内注入示踪剂的总量为m(mol),出口处浓度随时间变化为c(t), 在示踪剂注入后t -t+dt时间间隔内,出口处流出的示踪剂量占总示踪剂量的 分率:
✓ 若 t+d在t时注间入间示隔踪内剂,的流同出时物,料流量入为反ddN应NN器,的示则踪物在剂料此量时v为间0Nc间m(,t隔)在d内t注,入流示出踪的剂物后料的占t-进料
0
c( ti )ti
t
0
c( ti )
F(t )
0
• 在等时间间隔取样时:
c( ti )
0
第10页/共34页
第2节 停留时间分布
• 阶跃法
第四章 非理想流动模型 答案

0
t20 10tic 2c ii tm 2171 2 1 2 6 .4 61.4272.5275736.374256.31480(s2)
0
无因次方差
θ2tm 2t2217428.5 020.01990.02 ( 接近 PFR )
求平均转化率
(1) 根据一级反应转化率的本征动力学公式: 在该反应器出口处的平均转化率为
F ( t ) 5 0 0 0 .0 0 2 e x p ( 0 .0 0 2 t ) d t e x p ( 0 .0 0 2 t) 5 0 0
2 0 0
2 0 0
11 e 0 .4 e 0 .6 7 0 0 .3 6 8 0 .3 0 2 3 0 .2 %
E(t)
0 .0 0 2 4 0 .0 0 2 2 0 .0 0 2 0 0 .0 0 1 8 0 .0 0 1 6 0 .0 0 1 4 0 .0 0 1 2 0 .0 0 1 0 0 .0 0 0 8 0 .0 0 0 6 0 .0 0 0 4 0 .0 0 0 2 0 .0 0 0 0
第四章 非理想流动模型 答案
② 停留时间在0 ~ tm 的物料所占总料量的百分数为
F (tm )0 tm E (t)d t 0 .0 0 2 0 tm e x p ( 0 .0 0 2 t) d t ( tm= 500 s )
5 0 0 e x p ( 0 .0 0 2 t) d ( 0 .0 0 2 t) e x p ( 0 .0 0 2 t)5 0 0
0
1 0
c i 0 0 0 0 .1 0 .5 1 0 .0 8 .0 4 .0 0 0 2 2 .6
i 1
1 0
t ic i 0 0 0 1 4 .4 9 6 .0 2 4 0 0 2 3 0 4 1 3 4 4 0 0 6 1 5 8 .4
第四章. 非理想流动[1]
![第四章. 非理想流动[1]](https://img.taocdn.com/s3/m/ec0f2f87e53a580216fcfe1c.png)
12
4.1.2 概率函数的定义与性质
4.1.2.1 RTD密度函数E(t)的定义与性质 • (1)定义:流体以稳定流量进入设备而 不发生化学变化时,任意瞬间(记为t=0) 进入设备的数量为N的流体微元中,从出 口流出的停留时间介于tt+dt的流体微 N d 元数占总数的分率 N ,用统计规律的概 率方法表示时为概率密度与随机变量的 N d 变化值的乘积E(t)dt,即 N =E(t) dt。为时间的函数,称RTD密度函数。
E t dt 1
t 0
t 0
N
即
0
E t dt 1
(4-1)式
15
②E(t)t的图形
图中直方阴影的面 积dS=E(t)dt,密度随 时间的变化曲线与 横坐标围城的面积 是无数个小直方面 积的加和,即
S dS E t dt 1
i
i
13
对离散型数据:(Ni/N)=E(t)t,或:
N i N E t t
因此上述实验(t1=t2==2)得:
N i N
0 100
2 100 6 100 12 100
18 100
22 100
17 100 17 200
12 100
6 100
4 100 4 200
4
(4). 三种理想反应器RTD的定性说明 • BSTR.间歇操作,无流型可言,故不存在 停留时间分布问题; • PFR. 所有流体微元停留时间相同,集中 在同一时间点=VR/V0,就是说PFR的 RTD是均一的或RTD范围集中在一点。 • CSTR.流体微元停留时间从0应有尽 有,RTD范围最宽。
24
4.1.2 概率函数的定义与性质
4.1.2.1 RTD密度函数E(t)的定义与性质 • (1)定义:流体以稳定流量进入设备而 不发生化学变化时,任意瞬间(记为t=0) 进入设备的数量为N的流体微元中,从出 口流出的停留时间介于tt+dt的流体微 N d 元数占总数的分率 N ,用统计规律的概 率方法表示时为概率密度与随机变量的 N d 变化值的乘积E(t)dt,即 N =E(t) dt。为时间的函数,称RTD密度函数。
E t dt 1
t 0
t 0
N
即
0
E t dt 1
(4-1)式
15
②E(t)t的图形
图中直方阴影的面 积dS=E(t)dt,密度随 时间的变化曲线与 横坐标围城的面积 是无数个小直方面 积的加和,即
S dS E t dt 1
i
i
13
对离散型数据:(Ni/N)=E(t)t,或:
N i N E t t
因此上述实验(t1=t2==2)得:
N i N
0 100
2 100 6 100 12 100
18 100
22 100
17 100 17 200
12 100
6 100
4 100 4 200
4
(4). 三种理想反应器RTD的定性说明 • BSTR.间歇操作,无流型可言,故不存在 停留时间分布问题; • PFR. 所有流体微元停留时间相同,集中 在同一时间点=VR/V0,就是说PFR的 RTD是均一的或RTD范围集中在一点。 • CSTR.流体微元停留时间从0应有尽 有,RTD范围最宽。
24
化学反应:第四章 非理想流动

4.1 反应器中的返混现象与停留时间分布
早混和迟混的影响
第四章 非理想流动
早混
晚混
即使两反应体系的空时相同,由于反应混合的迟早不同,反应结果也不相 同。
4.1 反应器中的返混现象与停留时间分布
二、 停留时间分布的定量描述
第四章 非理想流动
• 一种流动对应着一定的停留时间分布 • 一种停留时间分布对应着不同的流动 • 停留时间分布用概率分布的概念来定量描述。
E(t
)dt
0
tE(t
)dt
2 t
0
t
2
E(t
)dt
t
2
无因次方差与方差的关系
2
2 t
t
2
4.1 反应器中的返混现象与停留时间分布
三、停留时间分布的实验测定
第四章 非理想流动
• 物理示踪信号响应技术:
采用一种易于检测的无化学反应活性的物质 按一定的输入方式加入稳定的流动系统(输 入信号),通过观测该示踪物质在系统出口 浓度随时间的变化(响应信号)来确定系统 物料的停留时间分布。
dN E(t)dt N
E(t)被称为停留时间分布密度函数。
4.1 反应器中的返混现象与停留时间分布
(2) 停留时间分布密度函数曲线
第四章 非理想流动
以 E(t) 纵轴,t 为横轴,作图,得到 E(t) 对 t 的停留时间分布密度函数曲线,如下图。
E(t) E(t)dt
dt
t
4.1 反应器中的返混现象与停留时间分布
4.1 反应器中的返混现象与停留时间分布
第四章 非理想流动
1. 平均停留时间(数学期望)
它是指整个物料在设备内的停留时间,而不是个 别质点的停留时间。所有质点停留时间的“加权平 均值”
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. E(t)和F(t)之间的关系
F(t) tdN tE(t)dt
0N 0
分布函数是密度函 数的可变上限积分
E(t) dF (t) 密度函数是分布函数的一阶导数
dt
t 0 F (0 ) 0 ;
t F ( )0E (t)d t 1 .0
4.1.2 停留时间分布的实验测定
• 停留时间分布通常由实验测定,主要的方法 是应答技术,即用一定的方法将示踪物加到反 应器进口,然后在反应器出口物料中检验示踪 物信号,以获得示踪物在反应器中逗留的时间 分布规律的实验数据。
在反应器入口处
c0 t 0
c0
t
c
t 0 t 0
在切换成含示踪剂的流体后,t-dt~t时间间隔内示
踪剂流出系统量为Qc(t)dt ,这部分示踪剂在系统内的
停留时间必定小于或等于t,任意的dt时间间隔内流入
系统的示踪剂量为Qc(∞)dt ,由F(t)定义可得
F(t)QQcc( t)ddtt cc( t)
提出可能的流动模型,并根据停留时间分布测定的 实验数据来确定所提出的模型中所引入的模型参数; • 3、结合反应动力学数据通过模拟计算来预测反应结 果; • 4、通过一定规模的热模实验来验证模型的准确性。
4.2.1 常见的几种流动模型
一、 理想流动模型
1. 平推流模型
根据平推流的定义,同时进入系统的流体粒子也 同时离开系统,即平推流反应器不改变输入信号的 形状,只将其信号平移一个位置。
0
Z/2
Z
1、平推流模型 基本假设:物料质点沿同一方向以同一流速流动。 基本特征:参数在同一径向上相同,所有物料质点在 反应器中的停留时间都相同,反应器内无返混。
• 2、全混流模型
FCAA00 Q0QT00
• 基本假设:加入反应器的物
T0
料能在瞬间与存留物料混合。
• 基本特征:反应器内各处参 TC,out
1、脉冲示踪法
实验方法:用极短的时间,在定常态操作的系统入 加入一定量的示踪剂,同时在系统的出口处检测示 踪剂浓度的变化。 测量方法:热导法,电导法,放射性同位素示踪。
示踪剂脉冲注入
主流体 Q0
C0(t)
δ(t)
系统 Vr
示踪剂检测 Q
C(t)
面积=C0
t=0 t
0
t
脉冲法测定停留时间分布
Q•E(t)•dt = V•c(t)•dt
阶跃法的特点 由实验数据直接求得F(t) 示踪过程易于实现 示踪剂量大 由F(t)求E(t)涉及求导的数值计算
4.1.3 停留时间分布函数的数字特征
为了对不同的停留时间函数进行定量比较,通 常是比较其特征值。常用的特征值有数学期望和 方差。
1.数学期望(平均停留时间)
t
tE(t)dt
0
E(t)dt
0 E()d 1
无因次化方差
2 0 ( 1 )2 E ()d 0 (t 1 )2 E (t)d t
12 0(tt)2E(t)dt2t2
2
2 t
t2
可推知:平推流
2
0
全混流
2
1
例: 由脉冲法测定某反应器的响应曲线结果如下:
t(min) 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7
Ft dFt
0 1Ft
1t
0
dt
ln1Ft1t
ln1[F(t)]t
对恒容:
t
t
t
t
Ft1e 1e F
Et
dFt
1
t
e
1 e
dt
t
Ee
t • 将 代为 则有:
1
E
(t)
t
t 1
e
t0 tt
0
t
0 t0 F(t) 1e1 t t
1 t
无因次化 F () 1 e x p [ ] E () e x p [ ]
(8)
C0 2t1 t2t3
t3
……
第N釜流出的物料中示踪剂浓度为:
2. 全混流模型
考察有效体积为Vr、进料体积流量为Q的全混流 反应器,若在某一瞬间t=0,将流体切换成流量相同 的含有示踪剂的流体,同时检测流出物料中示踪剂 浓度变化。
含示踪剂流体C0 Q 流体
Q
检测C
全混流的停留时间分布
单位时间内流入、流出反应器的示踪剂量分别
为QC0、 QC 单位时间内反应器内示踪剂的累积量 为 d V r ,C 因此有:
Vr
数均相同,且等于出口物料
G
参数,各物料颗粒在反应器
CA T
FA Q T G TC,in
内具有一定的停留时间分布, 返混最大。
全混流反应器
实际的工业装置
在实际的工业装置中由于物料在反应器内的流动 速率不均匀、或因内部构件的影响造成物料出现与 主体流动方向相反的逆向流动、死角等都会导致偏 离理想流动。
E(t)
F(t)
1
1.0
0
t
t
0
tt
单位时间内反应器内示踪剂做物料衡算得:
输入 v0cA0
输出 v0cA
积累 dVR dctAVRddA ct
VRddcAtv0cA0v0cAv0cA0cA
dcA dt
Vv0RcA0cA
cA0
cA
即:
d
cA cA0
1
cA cA0
dt
Ft cA
cA0
积分:
ddF tt1Ft
解式(5)一阶线性微分方程得:
以及
C2
exp(t )[C0 t2 t1t2
tC]
t 0C 2 0 C 0
C2 t exp( t )
C0 t1 t2
t2
(6)
对第三全混流区(i=3) 应有: t0 C30
vC2 vC3
dV3C3 dt
(7)
解式(7)一阶线性微分方程并整理得:
C3 t2 exp( t )
• 模型法:通过对复杂的实际过程的分析,进 行合理的简化,然后用一定的数学方法予 以描述,使其符合实际过程的规律性,此 即所谓的数学模型,然后加以求解。
• 在建立流动模型时通常采用下述四个步骤: • 1、通过冷态模型实验测定装置的停留时间分布; • 2、根据所得的有关E(t)或F(t)的结果通过合理的简化
c A 0 25 22 27 26 22 19 15 10 7 4 3 3 1 0
计算 t5mi时n的 Ft,Et和 t
解:
7
cAdt cAdt 81.333300E t 源自 c AcA 81.3333
c A dt
0
Et 4 0.0492
t5 81.3333
t
Ft Etdt
0
F t
流动模型与滞留区、沟流和短路等作 不同的组合。 本节讲述三种非理想流动模型。
(一) 多级混合模型(N为模型参数)
多釜串联模型是用N个全混釜串联来模拟一个 实际的反应器。N为模型参数。
1.模型假定条件:① 每一级内为全混流; ② 级际间无返混; ③ 各釜体积相同
2.多釜串联模型的停留时间分布
设反应器总体积为Vr,并假想由N个体积相等的全混釜串联 组成,釜间无任何返混。若对系统施加脉冲示踪后,作示踪
对于所有偏离平推流和全混流的流动模式统 称为非理想流动。
本章将定量地对非理想流动进行讨论,并考察这 些非理想流动对反应器性能的影响。
4.1.1 非理想流动与停留时间分布
• 一、偏离理想流动的模型
• 1、对平推流的偏离:
•
不是均匀速度,发生涡流
•
存在径向流速分布
•
催化剂填充不均匀
• 2、对全混留的偏离:
dt
v(C 0 C )d (V d r tC )d [C d /tC 0]1(1 C C 0)
F (t)C d F (t)1 [1 F (t)]
C 0
d t
F (t) d F (t) 1td tln [1 F (t)] t
0 1 F (t) 0
F(t)1exp[t]
E (t) d F d t(t) d d t[1 e x p ( t)] 1 e x p ( t)
E(t) t t t
F(t)
1
t t0 tt
t
t t
E(t)tt0
tt tt
E()1 0
1 1
F(t) 10
tt t t
F()
0 1
1 1
统计特征值: 1 20
2 0
表明所有的流体粒子在反应器内的停留时间相同。 方差越小,说明分布越集中,分布曲线就越窄,停留 时间分布方差等于零这一特征说明系统内不存在返混。
tE(t)dt
0
0
ttdF (t)d t F(t)1td(tF )
0 dt
F(t)0
t
tE(t)t E(t)t
tE(t) E(t)
2.方差(对均值的二次矩)
t20 (t E t)(2 t)E d (tt)dt0 (tt)2E (t)dt0 t2E (t)dtt2 0
若
2 t
越小,则偏离程度越小,对于平推流
示踪剂 加入量
在t~t+dt 间自系统出口处 流出的示踪剂量
停留时间介于t~t+dt间的示踪剂的量
E t Vc t
Q
Q
Vct 0
dt
E
t
ct
0
c
t
dt
2 阶跃示踪法
含示踪剂流体Q
C(∞)
流体 Q 切换
C(∞)
系统 Vr
示踪剂检测
Q
