力学平衡稳定性(动画)稳定平衡、不稳定平衡和随遇平衡
12.2 静力学系统平衡位置的确定及稳定性判断
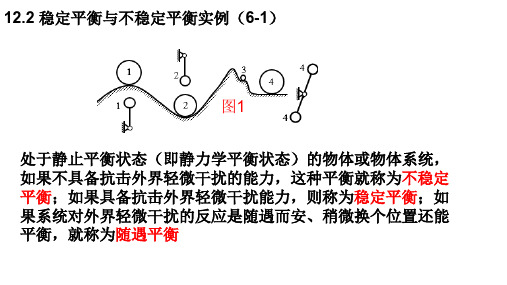
12.2 稳定平衡与不稳定平衡实例(6-1)图1处于静止平衡状态(即静力学平衡状态)的物体或物体系统,如果不具备抗击外界轻微干扰的能力,这种平衡就称为不稳定平衡;如果具备抗击外界轻微干扰能力,则称为稳定平衡;如果系统对外界轻微干扰的反应是随遇而安、稍微换个位置还能平衡,就称为随遇平衡例题对于第12.1节例题12.1-2,(1)假设系统不是在θ=30°位置,而是在任意角θo位置,即θ=θo位置保持静止平衡状态,求力偶M的值;(2)该例题计算结果表明,M=3.75mgL时系统能够在θ=30°位置保持静力学平衡状态,请问这属于哪种类型的平衡?图2(1)W (θ)=M (θ-θo )-7.5mgL (cos θo -cos θ)从功函数表达式可知,系统运动初始位置不同时功函数也不同,但只是相差一个常数.为什么?W ′(θ)=M -7.5mgL sin θ,令W ′(θo )=0得:M =7.5mgL sin θo ,系统在θ=θo 位置静止平衡时M =7.5mgL sin θo .W(θ)=3.75mgL [(θ-π/6)-2(cos30°-cos θ)] 1W(θ)=M(θ-π/6)-7.5mgL(cos30°-cos θ)3M =3.75mgL 24θo =30°图2假设3.75mgL =10W(θ)= 3.75mgL [(θ-π/6)-2(cos30°-cos θ)]4结论:本系统在30°位置的平衡是稳定平衡,在150°位置的平图3图4图2图5有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)12.2 不稳定平衡实例(6-2)图1处于静止平衡状态(即静力学平衡状态)的物体或物体系统,如果不具备抗击外界轻微干扰的能力,这种平衡就称为不稳定平衡;如果具备抗击外界轻微干扰能力,则称为稳定平衡;如果系统对外界轻微干扰的反应是随遇而安、稍微换个位置还能平衡,就称为随遇平衡例12.1-4、求图示无重组合梁支座A的约束力.图2图4解把A 铰用外力等效替代,设系统从静止开始加速运动(C 铰向下),系统运动至任意位置时动能及力系作功:图3图2θF αM αF F αw A sin sin )()(21438++-=⇒θr F αM αr F αr F αw DK BJ BA A sin sin sin )(21++-=56CD BC :sin :sin =αθαθsin sin 117=⇒αθθααd d F M F F w A ⋅++-=⇒cos 4cos )38()(' 21ααθθcos 11cos 7=⋅⇒d d 00令=)('w 2114118183F M F F A --=得:θF αM αF F αw A sin sin )()(21438++-=⇒6789W(α)=M (α-sinα)11图2图3图4假设M =100W(α)=M (α-sinα)11图2图3图4结论:图2所示系统为不稳定平衡图51112.2 静力学系统平衡位置的确定及稳定性判断(6-3)图1处于静止平衡状态(即静力学平衡状态)的物体或物体系统,如果不具备抗击外界轻微干扰的能力,这种平衡就称为不稳定平衡;如果具备抗击外界轻微干扰能力,则称为稳定平衡;如果系统对外界轻微干扰的反应是随遇而安、稍微换个位置还能平衡,就称为随遇平衡定理12.2-1单自由度物体系统运动过程中力系对系统做的功是系统参数的一元函数,该函数(即功函数)的驻点位置与系统运动起始位置无关;功函数的所有驻点位置都是系统能够保持静止平衡状态的位置,系统在这些位置静止时所受力系都是平衡力系,而在除此以外的其他任何位置,系统静止时所受力系都不是平衡力系.系统在功函数极大值位置的平衡是稳定平衡,在功函数常量位置的平衡是随遇平衡.在其他驻点位置的平衡是不稳定平衡.如何确定功函数的极大值、极小值位置?设q o 位置是功函数w(q)的驻点位置,即w ′(q o )=0,那么系统在q o 位置可处于静止平衡状态,则有:1)当w ″(q o )<0时q o 位置是功函数的极大值位置,系统在该处的平衡是稳定平衡;2)当w ″(q o )>0时q o 位置是功函数的极小值位置,系统在该处的平衡是不稳定平衡;3)当w ″(q o )=0时q o 位置是功函数的驻点但不一定是极值位置,要考察更高阶导数才能确定.25x y =25x y -=35x y =45x y =例12.2-1 图示细杆OA、AB长度都为L,OA杆上作用有力偶M, A铰销钉上作用有竖直力F1, 滑块B上有水平力F2 ,不计构件自重.图示θ=30°时系统处于静止平衡状态,求力偶M大小,并判断平衡的稳定性.图2)cos 22(sin )(21θθθθL L F L F M w -⋅-⋅-=θθθsin 2cos )(' 21L F L F M w ⋅--=θθθcos 2sin )('' 21L F L F w ⋅-=0) 30(' =︒w L F F M )2/3(21+=⇒解令系统从θ=0位置开始运动,OA 杆逆时针转动,功函数:0)30(''>︒w 2132F F >⇒不稳定平衡;0)30(''<︒w 2132F F <⇒稳定平衡;0)30('' =︒w 2132F F =⇒0 sin 2 cos ''' 3021≠⋅+=︒=θθθL F L F w 无极值,不稳定平衡.123456789图2例12.1-1 匀质圆轮半径为r,质量为m1,受到力偶M作用。
动力学中的平衡与稳定性分析

动力学中的平衡与稳定性分析动力学是研究物体在作用力下的运动规律的学科,平衡和稳定性是动力学中一个重要的概念。
平衡指的是物体处于稳定的状态,不受到任何干扰而保持静止或匀速直线运动;稳定性则是指物体在一定偏离平衡位置范围内具有恢复力,能够迅速回到平衡状态。
动力学中的平衡分为静态平衡和动态平衡。
静态平衡是指物体处于静止状态,不受到任何作用力或受到的作用力相互抵消,使得物体维持在一个静止的位置。
在静态平衡下,物体所受的合力和合力矩均为零。
动态平衡则是指物体以一定的速度作匀速直线运动,所受的合力和合力矩仍然为零。
静态平衡和动态平衡都是稳定的状态,只是物体的运动方式不同。
稳定性是指物体在平衡位置附近能够恢复到原来的平衡状态的性质。
平衡位置是指物体受到作用力后停留的位置。
在稳定平衡下,物体受到微小的扰动后会发生回归,恢复到原来的平衡状态。
稳定性的分析可以通过偏微分方程或者相图分析进行。
在偏微分方程方法中,通过对物体受到的外力和物体的位移关系进行微分,得到稳定性的判据。
相图分析则是通过将物体受力和受力矩绘制成相图,根据相图的形状来判断物体的稳定性。
在动力学中,稳定性分为两种类型:线性稳定和非线性稳定。
线性稳定是指物体在平衡位置附近的位移和受力之间呈线性关系,即物体经过微小的扰动后能够回到平衡位置。
非线性稳定则是指物体在平衡位置附近的位移和受力之间不呈线性关系,但仍具备稳定性。
非线性稳定包括了相位稳定、周期稳定和混沌。
相位稳定是指物体在一定范围内变化时,其周期在一致的范围内波动。
周期稳定则是指物体在一定周期内波动,并能在周期内完成一定的运动规律。
混沌是指物体在一定范围内的微弱扰动会导致突然的不可预测的运动变化,常常出现在非线性系统中。
总结起来,动力学中的平衡与稳定性分析涉及物体在作用力下的运动规律以及物体所处的稳定状态。
平衡可分为静态平衡和动态平衡,稳定性分为线性稳定和非线性稳定。
通过偏微分方程和相图分析可以对动力学系统的稳定性进行分析。
(完整版)物理竞赛讲义(四)一般物体的平衡、稳度

郑梁梅高级中学高一物理竞赛辅导讲义第四讲:一般物体的平衡、稳度【知识要点】(一)一般物体平衡条件受任意的平面力系作用下的一般物体平衡的条件是作用于物体的平面力系矢量和为零,对与力作用平面垂直的任意轴的力矩代数和为零,即:ΣF=0ΣM=0若将力向x、y轴投影,得平衡方程的标量形式:ΣF x=0 ΣF y=0 ΣM z=0(对任意z轴)(二)物体平衡种类(1)稳定平衡:当物体受微小扰动稍微偏离平衡位置时,有个力或力矩使它回到平衡位置这样的平衡叫稳定平衡。
特点:处于稳定平衡的物体偏离平衡位置的重心升高。
(2)不稳定平衡:当物体受微小扰动稍微偏离平衡时,在力或力矩作用下物体偏离平衡位置增大,这样的平衡叫不稳定平衡。
特点:处于不稳定平衡的物体偏离平衡位置时重心降低。
(3)随遇平衡:当物体受微小扰动稍微偏平衡位置时,物体所受合外力为零,能在新的平衡位置继续平衡,这样的平衡叫随遇平衡。
特点:处于随遇平衡的物体偏离平衡位置时重心高度不变。
(三)稳度:物体稳定程度叫稳度。
一般来说,使一个物体的平衡遭到破坏所需的能量越多,这个平衡的稳度越高;重心越低,底面积越大,物体稳度越高。
一般物体平衡问题是竞赛中重点和难点,利用ΣF=0和ΣM=0二个条件,列出三个独立方程,同时通过巧选转轴来减少未知量简化方程是处理这类问题的一般方法。
对于物体平衡种类问题只要求学生能用重心升降法或力矩比较法并结合数学中微小量的处理分析出稳定的种类即可。
这部分问题和处理复杂问题的能力,如竞赛中经常出现的讨论性题目便是具体体现,学生应重点掌握。
【典型例题】【例题1】如图所示,匀质管子AB长为L,重为G,其A端放在水平面上,而点C则靠在高h=L/2的光滑铅直支座上,设管子与水平面成倾角=45°,处于平衡时,它与水平面之间的动摩擦因数的最小值。
【例题2】如图代表某一竖直平面,在其面内有两根均匀细杆AB 和BC ,质量相同,长度分别为,它们共同接触水平地面,端点记为B ,各自的另一端A 和C 分别靠在相对21l l 、的两堵竖直墙上。
大学物理中的力学平衡物体的平衡与稳定性

大学物理中的力学平衡物体的平衡与稳定性大学物理中的力学平衡:物体的平衡与稳定性在大学物理学习中,力学平衡是一个基本概念,也是我们研究物体静止与稳定性的重要工具。
了解物体的平衡与稳定性对于我们理解力学规律、应用于实际问题具有重要意义。
本文将详细介绍大学物理中的力学平衡、物体的平衡以及稳定性,并从实例角度加深理解。
物体的平衡分析物体的平衡可以分为两种情况:平衡在一维的情况称为一维平衡,平衡在三维的情况称为三维平衡。
一维平衡在一维平衡中,物体的平衡状态仅需考虑物体在水平方向上的力平衡。
假设物体在水平面上,当物体受到力的合力为零时,物体处于一维平衡状态。
这个概念比较容易理解,就像在一个水平的桌面上放置一个书本,只有当受到的外力合力为零时,书本才能保持静止不动。
三维平衡在三维平衡中,物体同时受到多个方向的力作用,物体的平衡状态需要考虑力的合力以及力矩平衡。
力矩的概念涉及到物体的旋转,当物体受到的合力矩为零时,物体处于平衡状态。
例如,如果我们将一个木块放在桌子的边缘,只有当木块受到的合力矩为零时,它才能保持在桌子上不掉下来。
稳定性分析物体的稳定性是指物体在平衡状态下,受到干扰时能否返回原始的平衡位置。
根据稳定性的不同,物体可以分为稳定平衡、不稳定平衡和部分稳定平衡。
稳定平衡当物体在平衡位置附近发生微小偏移时,回归平衡位置的趋势增强,我们称这种平衡状态为稳定平衡。
例如,将一个圆球放在一个U型凹槽中,无论它发生微小偏移,都会回归到凹槽的底部,保持原有平衡。
不稳定平衡当物体在平衡位置附近发生微小偏移时,回归平衡位置的趋势减弱,甚至偏移越大越不容易回归平衡位置,我们称这种平衡状态为不稳定平衡。
例如,将一个圆球放在一个尖顶上,即使微小的偏移也会导致圆球离开尖顶,不再保持平衡。
部分稳定平衡部分稳定平衡是介于稳定平衡和不稳定平衡之间的状态。
当物体在平衡位置附近发生微小偏移时,回归平衡位置的趋势存在,但其强度较弱。
例如,将一个圆锥形物体放置在一个斜面上,当它发生轻微偏移时,可能会回到原位,但在较大偏移时可能会滚落。
力学系统中的平衡与不平衡状态研究

力学系统中的平衡与不平衡状态研究力学系统是物体或物体集合的组合,它们之间通过力的作用相互联系。
在力学系统中,平衡和不平衡是两种重要的状态。
平衡状态指的是系统内部各个部分的力相互抵消,没有产生任何运动或变形的趋势。
而不平衡状态则是指系统内部存在未抵消的力,从而导致系统发生运动或变形。
平衡状态是力学系统的稳定状态之一。
在平衡状态下,系统内部的各个部分的力之和为零,物体不会发生运动或变形。
这种平衡可以是静态平衡或动态平衡。
静态平衡是指物体处于静止状态,不受外力的作用。
动态平衡则是指物体处于匀速直线运动状态,受到的合外力为零。
平衡状态是力学系统的一种稳定状态,它使得物体能够保持相对稳定的位置或状态。
不平衡状态是力学系统的另一种重要状态。
在不平衡状态下,系统内部存在未抵消的力,物体会发生运动或变形。
不平衡状态可以分为静态不平衡和动态不平衡。
静态不平衡是指物体处于静止状态,但受到的合外力不为零,从而导致物体发生形变。
动态不平衡则是指物体处于加速运动状态,受到的合外力不为零,导致物体发生运动。
研究力学系统中的平衡与不平衡状态对于理解物体的运动和变形规律具有重要意义。
通过研究平衡状态,可以探究物体如何保持相对稳定的位置或状态。
这对于设计和构建稳定的结构、机器和设备至关重要。
例如,在建筑工程中,研究平衡状态可以帮助我们设计出稳定的建筑结构,防止倒塌和损坏的发生。
在机械工程中,研究平衡状态可以帮助我们设计出平衡的机械装置,提高机器的性能和效率。
而研究不平衡状态则可以揭示物体的运动和变形规律。
通过研究不平衡状态,可以了解物体在受到外力作用下的运动轨迹和变形方式。
这对于预测和控制物体的运动和变形具有重要意义。
例如,在交通工程中,研究不平衡状态可以帮助我们预测车辆在不同路况下的运动轨迹,从而提高交通流量的效率和安全性。
在航天工程中,研究不平衡状态可以帮助我们预测航天器在不同引力场中的运动轨迹,从而实现精确的航天任务。
除了对实际应用具有重要意义外,研究力学系统中的平衡与不平衡状态还可以深化对物理规律的理解。
压杆稳定的概念及三种平衡状态-PPT

cr s
a s
b
令
2
a s
b
2 (小柔度杆)
cr s
令 1
2E p
目录
表 1 直线公式的系数 a 和 b
材料 低碳钢 优质碳钢 硅钢 铬钼钢 铸铁 强铝 松木
a(MPa) 304 461 578
980.7 332.2
373 28.7
b(MPa) 1.12 2.568 3.744 5.296 1.454 2.15 0.19
(b): 木杆的横截面与(a)相同,高为 1.4m(细长压杆),当压力为 0.1KN时杆被压弯,导致破坏。
(a)和(b)竟相差60倍,为什么?
(a)
(b)
平衡的三种状态
稳定平衡状态
随遇平衡状态
不稳定平衡状态
平衡刚性圆球受干扰力,刚球离开原位置;干扰力撤消:
稳定平衡 —— 凹面上,刚球回到原位置; 随遇平衡 —— 平面上,刚球在新位置上平衡; 不稳定平衡 —— 凸面上,刚球不回到原位置,
压杆的稳定校核 已知拖架D处承受载荷 例题F=10kN。AB杆外径D=50mm, 内径d=40mm,材料为Q235钢, E[=n2st0]0=G3P。a,校核A=B1杆01 0的,稳定性。
解: CD梁
MC 0
F 2000 FN sin 30 1500
得 FN 26.6kN
AB杆
l 1
dx
x l, v
B
Ak 0
Asin kl B coskl
cos kl 0
kl (2n 1) (n 1,2)
2 k2 F
EI
F
(2n
1)2
(2l)2
2 EI
取 n=1, 得:
《物体平衡的稳定性》 讲义

《物体平衡的稳定性》讲义在我们的日常生活和物理学的研究中,物体平衡的稳定性是一个十分重要的概念。
理解物体平衡的稳定性,对于解释许多自然现象、解决工程问题以及保障我们的日常生活安全都具有重要意义。
首先,我们来明确一下什么是物体的平衡。
当一个物体所受到的合力为零,同时合力矩也为零的时候,这个物体就处于平衡状态。
简单来说,就是物体在这种状态下既不发生平动,也不发生转动。
然而,平衡状态还可以进一步细分为稳定平衡、不稳定平衡和随遇平衡三种类型。
稳定平衡是指当物体受到微小的扰动而偏离平衡位置后,能够自动地恢复到原来的平衡位置。
比如一个放在碗底的小球,当我们稍微推它一下,它会晃动几下然后回到碗底原来的位置。
这是因为在稳定平衡状态下,物体偏离平衡位置时,其重力势能会增加,从而产生一个使物体回到平衡位置的恢复力。
不稳定平衡则与稳定平衡相反。
当物体处于不稳定平衡状态时,一旦受到微小的扰动,就会加速偏离原来的平衡位置,而无法回到原位。
一个常见的例子是把一个小球放在倒置的碗顶,轻轻一碰,小球就会滚落下来。
在这种情况下,物体偏离平衡位置时,重力势能反而降低,没有恢复力使其回到原来的位置。
随遇平衡则是指物体在受到扰动偏离平衡位置后,能够在新的位置保持平衡。
比如一个水平放置的圆柱体,无论它在水平面上滚动到哪个位置,都能保持平衡。
那么,是什么因素决定了物体处于哪种平衡状态呢?一个关键的因素是物体的重心位置和支撑面的关系。
对于一个有固定支撑的物体,如果其重心在支撑面所围成的区域内,那么物体通常处于稳定平衡状态。
比如说,一个底面积较大的金字塔,由于其重心较低且在底座范围内,所以非常稳定。
反之,如果物体的重心在支撑面之外,那么物体往往处于不稳定平衡状态。
像一个细长的杆子竖直放置,重心很高且容易超出支撑范围,就很不稳定。
此外,物体的质量分布也会影响平衡的稳定性。
质量分布越均匀,物体越容易保持平衡的稳定性。
比如一个质量均匀的圆盘,比起质量分布不均匀的形状,更容易保持平衡。
力学平衡稳定性稳定平衡、不稳定平衡和随遇平衡 ppt课件

设 想 此 时 有 一 个 偏 离 平 衡 态 的 虚 变 动 , 则 有 :
S1S2S0
2
平 衡 态 的 条 件 是 : 1S0(平 衡 判 据 ) 2S0( 稳 定 性 判 据 )
由 热 力 学 第 一 、 二 定 律 :
dUTdSdW 系
1
等熵、无外功的系统过程:
在等温不做功的情况下: dF 0
由此可得: 等温不做功的系统中进行的过程, 系统的自由能绝不会增加,而平衡 对应于自由能F取最小值的宏观态
若将系统对外做功分为膨胀功与非膨胀功,有: dW系 PdV dW系
有之前1式:
dU TdS dW系 作勒让德变换:
dG SdT VdP dW系
同理分析:
T T P P
(热平衡条件) (力学平衡条件) (相平衡条件)
将 稳 定 性 判 据 2 U 0 应 用 于 热 力 学 系 统 :
2 U 2 S U 2 V S 2 2 S 2 U V SV V 2 U 2 SV 2 0
写成二次型的形式
由2式,同时T
=
U S
V
:
2U
S2
V
T S
V
T U
V
U S
V
T CV
0
( T 0 ) C V d Q 系 d T V 0
具体分析
热平衡时: T系 =Ta
由系统内部的涨落,使得: T系>Ta
此 时 ,热 量 从 系 统 传 向 外 界 , 则 : dQ系0
代入热平衡稳定性条件:
U1U2U0
2
1U0 (平衡判据) 2U0(平衡稳定性判据)
热力学势 平衡判据 (熵除外)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
由2式,同时T
=
U S
V
:
2U
S
2
V
T S
V
T U
V
U S
V
T CV
0
(T 0)
CV
dQ系
dT
0
V
具体分析
热平衡时: T系 = T a
由系统内部的涨落,使得: T系 > T a
此时,热量从系统传向外界,则: dQ系 0
代入热平衡稳定性条件:
CV dQ系 dT V 0 dT 0
热力学势
基本关系式
条件
相应关系式
U
等熵
dU dW系
dU TdS dW系
等熵不做功
dU 0
F
dF SdT dW系
等温 等温不做功
dF dW系
dF 0
G
等温等压
dG dW系
dG SdT VdP dW系
等温等压无非 膨胀功
dG 0
H
等熵等压
dH dW系
dH TdS VdP dW系 等熵等压无非
最大功原理
热力学第一定律:
dU dQ dW系 有关系式:
TdS dQ 得:
dU TdS dW系
1
利用勒让德变换,得:
dF SdT dW系
若为可逆等温过程 dT 0,由1得:
dF dW系 (可逆等温过程)
若经历的是不可逆等温过程,则由1 得:
dF dW系 (不可逆等温过程)
dG SdT VdP dW系
同理分析:
dG dG
dW系 dW系
(可逆等温等压过程) (不可逆等温等压过程)
最大功原理:
系统在可逆的等温等压过程中所做
非膨胀功最大
在等温等压无非膨胀功条件下: dG 0 (等温等压无非膨胀功)
所以: 在等温等压无非膨胀功的系统发生 过程中,自由焓G绝不会增加,平衡态 对应于自由焓具有最小值的宏观态
2G 0 2H 0
2S 0
平衡判据: 1S 0
应用于孤立系统各部分中,可得:
T T P P
(热平衡条件) (力学平衡条件) (相平衡条件)
将稳定性判据 2U 0应用于热力学系统:
2U
2U S 2
V
S
2
2
2U SV
SV
2U V 2
S
V
2
0
写成二次型的形式
最大功原理: 在可逆等温过程中系统所做功 最大,由此得最大功原理。
在等温不做功的情况下: dF 0
由此可得: 等温不做功的系统中进行的过程, 系统的自由能绝不会增加,而平衡 对应于自由能F取最小值的宏观态
若将系统对外做功分为膨胀功与非膨胀功,有: dW系 PdV dW系
有之前 1 式:
dU TdS dW系 作勒让德变换:
2U S
2U
V
S 2
V
2U
SV
2U
SV
S
2U
V
V
2
S
根据线性代数,正定二次型系数有下列条件:
2U
S
2
V
0
2
2U
S 2
V
2U
SV
2U
S
V
2U
D
U S
V
, UV
S
DS,V 0
V
2
S
DT, P DS,V 0
DT, P DT,V
DT, P DT ,V
P S
V T
T V
T
CV
(P
V )T
因为 T 0,CV 0
则
(P V )T 0
所以: T 1 V (P V )T 0
最终得:
CTV
0 0
热平衡稳定性条件 力学平衡稳定性条件
焓H
同理分析: dH 0 等熵等压无非膨胀功)
即: 在满足以上条件的系统发生的过程中, 焓决不会增加,平衡态对应于焓具有 最小值的宏观态
总结:
在三种不同的条件下,系统分别向F、G、H 减小 的方向变化,平衡态分别对应于F、G、H的最小值
注意: 在绝热过程中没有最大功原理,因为绝热过程中有 dU = dW系
膨胀功
dH 0
平衡的稳定性条件
平衡的稳定性判据和条件
考虑孤立系统 可知该过程总是向熵增加的方向进行,有:
dS 0 因而达到平衡态后,熵有最大值,且不变化。
设想此时有一个偏离平衡态的虚变动,则有:
S 1S 2S 0
2
平衡态的条件是: 1S 0 (平衡判据) 2S 0(稳定性判据)
由热力学第一、二定律:
dU TdS dW系
1
等熵、无外功的系统过程:
U 1U 2U 0
2
1U 0 (平衡判据) 2U 0 (平衡稳定性判据)
热力学势 平衡判据 (熵除外)
U
1U 0
F
1F 0
G
1G 0
H
1H 0
S
1S 0
平衡稳定 性判据
2U 0
2F 0
系统会因为放热而降温回到热平衡 反之:
CV 0 dT 0, 系统会因为放热而升温偏离热平衡
结论:CV 0保证了系统的热平衡稳定性
2U
S 2
V
2U
SV
2U
SV
2U
D
U S
V
, UV
S
V
2
S
DS,V
DT, P DS,V 0 3
由3式:
DT, P DS,V
