数模竞赛最优化题目
历年数模题(最优化部分)

MCM2013 A题
建立一个模型以展示不同形状的平底锅在边缘处的热量分 布情况,锅的形状由矩形渐变到圆形(即要考虑两个形状 之间的其他形状)。 假设 1、对于矩形的锅,宽与高的比为W/L. 2、每个锅的面积为A 3、在烤箱中预先设定两个均匀分布的烤台。 建立一个模型可以用来在以下条件中选出最佳形状的锅 1、使得可以适应空间的锅的数量最大化 2、使得锅内的热量最大可能地均匀分布 3、综合考虑条件1和2,权重分别设为p 和 (1- p),举例 说明随着权值P以及宽高比W/L的变化,结果将如何变化。
CUMCM 2010 C题
输油管的布置
某油田计划在铁路线一侧建造两家炼油厂,同时在铁路线上增建一个 车站,用来运送成品油。由于这种模式具有一定的普遍性,油田设计 院希望建立管线建设费用最省的一般数学模型与方法。 1. 针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形,提 出你的设计方案。在方案设计时,若有共用管线,应考虑共用管线费 用与非共用管线费用相同或不同的情形。 2. 设计院目前需对一更为复杂的情形进行具体的设计。两炼油厂的具 体位置由附图所示,其中A厂位于郊区(图中的I区域),B厂位于城 区(图中的II区域),两个区域的分界线用图中的虚线表示。图中各 字母表示的距离(单位:千米)分别为a = 5,b = 8,c = 15,l = 20。
CUMCM 2012 B题 (原题很长,有缩减)
给出小屋外表面光伏电池的铺设方案,使小屋的全 年太阳能光伏发电总量尽可能大,而单位发电量的 费用尽可能小,并计算出小屋光伏电池35年寿命期 内的发电总量、经济效益(当前民用电价按0.5元 /kWh计算)及投资的回收年限。 在同一表面采用两种或两种以上类型的光伏电池组 件时,同一型号的电池板可串联,而不同型号的电 池板不可串联。在不同表面上,即使是相同型号的 电池也不能进行串、并联连接。应注意分组连接方 式及逆变高等教育学费标准探讨
数学建模比赛题目

数学建模比赛题目
数学建模比赛的题目通常涉及现实生活中的问题,需要参赛者运用数学方法和计算机技术来解决。
以下是一些可能的数学建模比赛题目示例:
1. 城市交通流量预测:给定一个城市的交通流量数据,要求参赛者预测未来的交通流量,以便为城市规划和交通管理提供依据。
2. 股票价格预测:给定历史股票价格数据,要求参赛者预测未来的股票价格变动,以便为投资者提供参考。
3. 天气预报:给定历史气象数据,要求参赛者预测未来的天气状况,以便为农业、航空和旅游等行业提供依据。
4. 人口增长预测:给定一个国家或地区的人口数据,要求参赛者预测未来的人口增长趋势,以便为政府制定政策和规划提供依据。
5. 物流优化:给定一个物流网络和相关数据,要求参赛者优化物流路线和资源分配,以便降低成本和提高效率。
6. 医疗数据分析:给定医院的医疗数据和病例信息,要求参赛者分析病情趋势和患者特征,以便为医疗研究和治疗提供依据。
7. 能源消耗预测:给定一个地区的能源消耗数据,要求参赛者预测未来的能源需求,以便为政府和企业制定能源政策和规划提供依据。
8. 机器学习算法设计:给定一组数据和任务,要求参赛者设计一种机器学习算法来解决该任务,例如分类、回归或聚类等。
这些题目只是数学建模比赛的一部分示例,实际上比赛的题目非常多样化,可以根据实际情况进行设计。
数学建模《最优化问题》

2c1 rc2
c2 c2 c3
2c1r Q rT c2
c2 c3 记 c3
不 允 许 缺 货
T T ,
Q
Q
1
T ' T , Q' Q
c3
c3 1
T T , Q Q
允许 缺货 模型
2c1 c2 c3 T rc2 c3
利润 Q=R-C=pw -C 求 t 使Q(t)最大 Q(10)=660 > 640
Q(t ) (8 gt)(80 rt ) 4t
4r 40g 2 t =10 rg
10天后出售,可多得利润20元
敏感性分析
4r 40g 2 t rg
研究 r, g变化时对模型结果的影响 • 设g=0.1不变
其中 c1,c2,c3, t1, ,为已知参数
模型求解
dC 0 dx
求 x使 C(x)最小
b 0
c1t12 2c2t1 x 2c32
dB dt
x
t1
t2 t
结果解释
• / 是火势不继续蔓延的最少队员数
结果 解释
c1t1 2c2t1 x 2c32
允许缺货的存贮模型
当贮存量降到零时仍有需求r, 出现缺货,造成损失.
q Q r
Q rT1
t
原模型假设3:贮存量降到零 T1 B T 时Q件立即生产出来(或立即到 0 货). 现假设3:允许缺货, 每天每件缺货损失费 c3 , 缺货需补足. 一周期 c2 贮存费 一周期 c 3 缺货费
A
T1
0
7.1
存贮模型
2023年全国数学建模题目

2023年全国数学建模题目
一、优化模型
题目:全球能源分配优化问题
问题描述:全球各国对能源的需求不断增长,而能源资源有限。
为了实现可持续发展,需要优化全球能源分配,确保各国都能获得适量的能源供应。
请运用优化模型和方法,设计一个全球能源分配方案,以满足各国能源需求,并尽量减少能源浪费和环境污染。
二、统计分析
题目:社交媒体用户行为分析
问题描述:社交媒体平台上积累了大量用户数据,包括用户发布的内容、关注对象、互动情况等。
请运用统计分析方法,分析社交媒体用户的偏好、行为模式和社交网络结构,为相关企业提供营销策略建议。
三、机器学习
题目:基于机器学习的文本分类问题
问题描述:文本数据包括各种主题,如政治、经济、文化等。
请运用机器学习算法,对给定的文本数据进行分类,并评估分类效果。
同时,请探讨如何提高分类准确率和泛化能力。
四、预测模型
题目:商品价格预测问题
问题描述:商品价格受到多种因素的影响,如市场需求、生产成本、政策因素等。
请运用预测模型和方法,预测未来一段时间内某种商品的价格走势,为投资者和企业提供决策依据。
五、决策分析
题目:企业投资决策问题
问题描述:企业需要在多个项目中做出投资决策,以实现利润最大化。
请运用决策分析方法,评估各项目的风险和收益,为企业制定最优投资策略。
六、系统动力学
题目:城市交通拥堵问题研究
问题描述:城市交通拥堵是一个复杂的问题,涉及多个因素之间的相互作用。
请运用系统动力学方法,建立城市交通拥堵问题的动力学模型,分析各因素之间的因果关系和动态变化规律,提出缓解交通拥堵的策略建议。
数模竞赛最优化题目

(规划设计题)
1以县局X1及其所辖的16个支局Z1,Z2,……,Z16为研究对象,假设区级第一班次邮车08:00到达县局X1,区级第二班次邮车16:00从县局X1再出发返回地市局D,若每辆县级邮车最多容纳65袋邮件,试问最少需要多少辆邮车才能满足该县的邮件运输需求?同时,为提高邮政运输效益,应如何规划邮路和如何安排邮车的运行?(邮件量见表2,空车率=(邮车最大承运的邮件量(袋)-邮车运载的邮件量(袋))/邮车最大承运的邮件量(袋),单车由于空车率而减少的收入为(空车率*2元/公里))
3如果调度室在列车到达前两小时能够获取列车的相关信息,请利用这些信息制定可行的列车编组调度方案,使每班的中时尽量少,发出的车辆尽量多。
4如果因自然灾害导致S3以南的铁路中断,需要将有关的车辆转向东方向经E4向南绕行,请你们给出相应的调度方案,并计算相应每班的中时。
5假设编组完成的列车都能及时发出,按照你们的编组调度方案分析研究该编组站一天24小时最多能编组完成多少车辆,相应每班的中时是多少?即根据所建立模型进一步分析该编组站能否再提高资源的利用率和运行效率。
6目前我国的铁路资源紧张,需大于求,如何改进编组调度方案,才使得现有的铁路设施有更高的利用率,产生更高效益,谈谈建议和意见。
2采用尽可能少、尽可能短的邮路可以减少邮政部门车辆和人员等的投入,从而显著降低全区邮政运输网的总运行成本。考虑投入车况较好的邮车,通常每条邮路只需要一辆邮车即能满足运载能力要求,试问应如何构建该地区的邮政运输网络(县的划分不能变更),请你给出邮路规划和邮车调度方案。请注意邮车的调度必须满足上文中有关该地区的邮政运输流程及时限规定。(每条邮路的运行成本为3元/公里)
3考虑到部分县与县交界地带的支局,其邮件由邻县县局负责运送可能会降低全区的运行成本,带来可观的经济效益。若允许在一定程度上打破行政区域的限制,你能否给出更好的邮路规划和邮车调度方案?(在此同样不必考虑邮车的运载能力的限制,每条邮路的运行成本为3元/公里)
数学建模竞赛中的部分优化问题

路、公路运输,铺设一条
火车站 公路 管道
450 里程(km)
A1
钢管管道 A1 A2 A15 (沿管道建有公路)
优化建模
钢厂的产量和销价(1单位钢管=1km管道钢管)
钢厂i
1
2
3
4
产量上限 si 销价 pi (万元)
800 800 160 155
1000 155
2000 160
钢厂产量的下限:500单位钢管 1单位钢管的铁路运价
, tani
D yi0 xi0
or
i
3
2
, tani
yi0 xi0
,
,
yi0
v sin i
, if
i
3
2
, tani
yi0 xi0
or 3
2
i
2 , tani
yi0 D xi0
整理: 其中:
fij (t) zij 2 bij zij cij .
290 30 S7
S2
1200
S3
690 720
S4
690
170 520
160 130 88
A18
160
320 A20
100 70 30
70 260
A21
S6
A19
110
190
62
20 20
A15
500
1100
202
S1
A16
42
20
12
A17
462
70 10
S5 10
220
420
数学建模优化问题经典练习
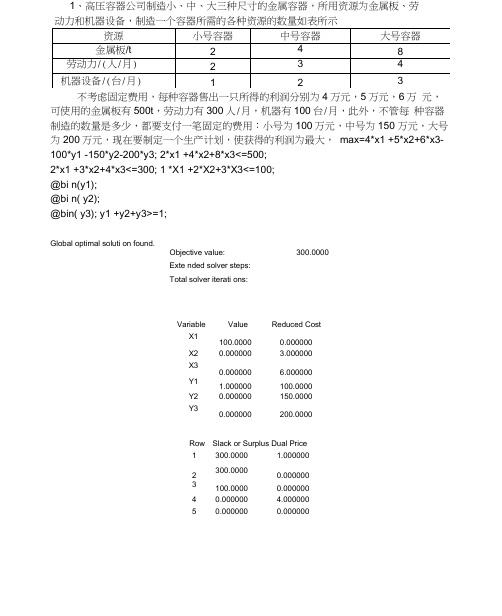
1、高压容器公司制造小、中、大三种尺寸的金属容器,所用资源为金属板、劳 动力和机器设备,制造一个容器所需的各种资源的数量如表所示不考虑固定费用,每种容器售出一只所得的利润分别为4万元,5万元,6万 元,可使用的金属板有500t ,劳动力有300人/月,机器有100台/月,此外,不管每 种容器制造的数量是多少,都要支付一笔固定的费用:小号为100万元,中号为150 万元,大号为200万元,现在要制定一个生产计划,使获得的利润为最大, max=4*x1 +5*x2+6*x3-100*y1 -150*y2-200*y3; 2*x1 +4*x2+8*x3<=500; 2*x1 +3*x2+4*x3<=300; 1 *X1 +2*X2+3*X3<=100; @bi n(y1); @bi n( y2);@bin( y3); y1 +y2+y3>=1; Global optimal soluti on found.Objective value: Exte nded solver steps: Total solver iterati ons:Variable Value Reduced Cost X1 100.0000 0.000000 X2 0.000000 3.000000 X3 0.000000 6.000000 Y1 1.000000 100.0000 Y2 0.000000 150.0000 Y30.000000200.0000Row 1 Slack or Surplus Dual Price 300.0000 1.000000 2 300.0000 0.000000 3 100.0000 0.000000 4 0.000000 4.000000 50.0000000.000000300.00002、安排4个人去做4项不同的工作,每个工人完成各项工作所消耗的时间(单位:分钟)如表:(2) 如果在(1)中在增加一项工作E,甲、乙、丙、丁四人完成工作E的时间分别为17,20,15,16分钟,那么应指派这四人干哪四项工作,使得这四人总的消耗时间为最少?min =20*x11 + 19*x12+20*x13+28*x14+18*x21 +24*x22+27*x23+20*x24+26*x31 +16*x32+15*x33+18*x34+17*x41 +20*x42+24*x43+19*x44;x11+x12+x13+x14=1;x21+x22+x23+x24=1;x31+x32+x33+x34=1;x41+x42+x43+x44=1;x11+x21+x31+x41=1;x12+x22+x32+x42=1;x13+x23+x33+x43=1;x14+x24+x34+x44=1;@bin (x11);@bin (x12);@bin (x13);@bin (x14);@bin (x21);@bin (x22);@bin (x23);@bin (x24);@bin (x31);@bin (x32);@bin (x33);@bin (x34);@bin (x41);@bin (x42);@bin (x43); @bin (x44);Global optimal solution found. Objective value: 71.00000Extended solver steps 0 Total solver iterations:Variable Value Reduced Cost X11 0.000000 20.00000 X12 1.000000 19.00000 X13 0.000000 20.00000 X14 0.000000 28.00000 X21 0.000000 18.00000 X22 0.000000 24.00000 X23 0.000000 27.00000 X24 1.000000 20.00000 X31 0.000000 26.00000 X32 0.000000 16.00000 X33 1.000000 15.00000 X34 0.000000 18.00000 X41 1.000000 17.00000 X42 0.000000 20.00000 X430.000000 24.00000 X440.00000019.00000Row Slack or Surplus Dual Price 1 71.00000 2 0.000000 3 0.000000 4 0.000000 5 0.000000 6 0.000000 7 0.000000 8 0.000000 90.000000min =20*x11 +19*x12+20*x13+28*x14+17*x15+18*x21 +24*x22+27*x23+20*x24+20 *x25+26*x31 +16*x32+15*x33+18*x34+15*x35+17*x41 +20*x42+24*x43+19*x44+1 6*x45; x11+x12+x13+x14+x15=1; x21+x22+x23+x24+x25=1; x31+x32+x33+x34+x35=1;-1.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000x41+x42+x43+x44+x45=1;x11 +x21 +x31 +x41 <=1;x12+x22+x32+x42<=1;x13+x23+x33+x43v=1;x14+x24+x34+x44<=1;x15+x25+x35+x45<=1;@bin (x11);@bin (x12);@bin (x13);@bin (x14);@bin (x15);@bin (x21);@bin (x22);@bin (x23);@bin (x24);@bin (x25);@bin (x31);@bin (x32);@bin (x33);@bin (x34);@bin (x35);@bin (x41);@bin (x42);@bin (x43);@bin (x44);@bin (x45);Objective value: 68.00000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX11 0.000000 20.00000X12 1.000000 19.00000X13 0.000000 20.00000X14 0.000000 28.00000X15 0.000000 17.00000X21 1.000000 18.00000X22 0.000000 24.00000X23 0.000000 27.00000X24 0.000000 20.00000X25 0.000000 20.00000X31 0.000000 26.00000X320.000000 16.00000X33 1.000000 15.00000X340.000000 18.00000X35 0.000000 15.00000X41 0.000000 17.00000X42 0.000000 20.00000X43 0.000000 24.00000X44 0.000000 19.00000X451.000000 16.00000DualRow Slack or Surplus Prii1 68.00000 -1.0000002 0.000000 0.0000003 0.000000 0.00000040.000000 0.00000050.000000 0.0000006 0.000000 0.00000070.000000 0.0000008 0.000000 0.0000009 1.000000 0.00000010 0.000000 0.0000003、一个公司考虑到北京、上海、广州和武汉四个城市设立库房,这些库房负责向华北、华中、华南三个地区供货,每个库房每月可处理货物1000件。
中国研究生数学建模竞赛题目

中国研究生数学建模竞赛题目
以下是中国研究生数学建模竞赛的一些题目示例:
1. 非线性规划问题:给定某工厂的生产和成本数据,要求优化产量和成本之间的关系,使得产量最大化同时成本最小化。
2. 最优调度问题:某电力公司需要安排多个发电机组的启动和停止时间,以满足不同时间段的电力需求和节约燃料成本等条件。
3. 网络流问题:某物流中心需要将多个物品从供应商通过不同的物流通道送达多个目的地,要求建立一个最优的运输方案,使得总运输时间最短。
4. 高等数学问题:给定一个复杂函数模型,要求推导该函数的极值点、驻点和拐点,并分析函数在不同区间的增减性和凹凸性。
5. 随机过程问题:某金融交易市场的交易量数据呈现随机波动,要求建立一个合适的随机模型,进行交易风险评估和预测。
6. 图论问题:某城市的交通网络由多个节点和边组成,要求分析城市中的交通拥堵情况,找到最短路径和最少换乘的出行方案。
以上只是一些示例题目,实际的竞赛题目会根据具体的考查内
容和难度设置。
每年竞赛的题目都会有所变化,考察的内容也会涵盖数学的不同领域和应用实践。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3考虑到部分县与县交界地带的支局,其邮件由邻县县局负责运送可能会降低全区的运行成本,带来可观的经济效益。若允许在一定程度上打破行政区域的限制,你能否给出更好的邮路规划和邮车调度方案(在此同样不必考虑邮车的运载能力的限制,每条邮路的运行成本为3元/公里)
4县局选址的合理与否对构建经济、快速的邮政运输网络起到决定性的作用。假设图2中县局X1,……,X5均允许迁址到本县内任一支局处,同时原来的县局弱化为普通支局。设想你是该地区网运部门负责人,请你重新为各个县局选址,陈述你的迁址理由并以书面材料形式提交省局网运处。
3如果调度室在列车到达前两小时能够获取列车的相关信息,请利用这些信息制定可行的列车编组调度方案,使每班的中时尽量少,发出的车辆尽量多。
4如果因自然灾害导致S3以南的铁路中断,需要将有关的车辆转向东方向经E4向南绕行,请你们给出相应的调度方案,并计பைடு நூலகம்相应每班的中时。
5假设编组完成的列车都能及时发出,按照你们的编组调度方案分析研究该编组站一天24小时最多能编组完成多少车辆,相应每班的中时是多少即根据所建立模型进一步分析该编组站能否再提高资源的利用率和运行效率。
2008
C
货运列车的编组调度问题
经济类
(规划设计类)
1试设计快速自动实现车辆编组调度方案的优化模型或算法,并给出附件2中车辆可行的编组方案(包括解体程序、轨道编号、车辆数量、集结程序、新列车的组成等),主要使每班的中时尽量地少。
2发往S1的货物和军用物资都为特别专供货物,需要保障优先运送。如果要求装载这类物资的车辆必须在2小时内发出(即中时不超过2小时);同时发往地震灾区(向西方向某些车站)的救灾货物车辆要求中时不超过1小时,请你们给出相应的调度方案,并计算相应每班的中时。
经济类
(规划设计题)
1以县局X1及其所辖的16个支局Z1,Z2,……,Z16为研究对象,假设区级第一班次邮车08:00到达县局X1,区级第二班次邮车16:00从县局X1再出发返回地市局D,若每辆县级邮车最多容纳65袋邮件,试问最少需要多少辆邮车才能满足该县的邮件运输需求同时,为提高邮政运输效益,应如何规划邮路和如何安排邮车的运行(邮件量见表2,空车率=(邮车最大承运的邮件量(袋)-邮车运载的邮件量(袋))/邮车最大承运的邮件量(袋),单车由于空车率而减少的收入为(空车率*2元/公里))
98B灾情巡视的最佳路线图论、组合优化
00B钢管订购和运输组合优化、运输问题
01B公交车调度问题多目标规划
03B露天矿生产的车辆安排整数规划、运输问题
04A奥运会临时超市网点设计统计分析、数据处理、优化
04B电力市场的输电阻塞管理数据拟合、优化
07B 公交车问题 多目标规划、动态规划、图
2007
邮政运输网络中的邮路规划和邮车调度
6目前我国的铁路资源紧张,需大于求,如何改进编组调度方案,才使得现有的铁路设施有更高的利用率,产生更高效益,谈谈建议和意见。
