自动控制原理 第二版(孟庆明)答案
自动控制原理第二版6-7-8章习题及详解
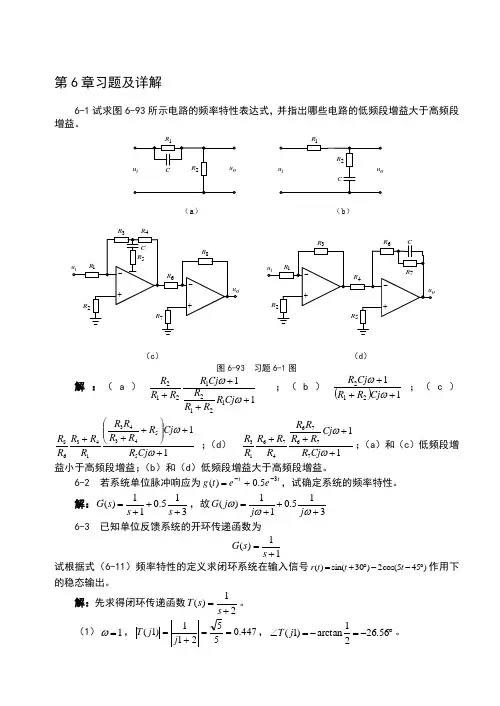
第6章习题及详解6-1 试求图6-93所示电路的频率特性表达式，并指出哪些电路的低频段增益大于高频段增益。
（a ） （b ）R R（c ） （d ）图6-93 习题6-1图解：（a ）1112121212++++ωωCj R R R R Cj R R R R ；（b ）()11212+++ωωCj R R Cj R ；（c ）1155434314368++⎪⎪⎭⎫ ⎝⎛+++ωωCj R Cj R R R R R R R R R R ；（d ） 117767647613++++ωωCj R Cj R R R R R R R R R ；（a ）和（c ）低频段增益小于高频段增益；（b ）和（d ）低频段增益大于高频段增益。
6-2 若系统单位脉冲响应为t t e e t g 35.0)(--+=，试确定系统的频率特性。
解：315.011)(+++=s s s G ，故315.011)(+++=ωωωj j j G 6-3 已知单位反馈系统的开环传递函数为11)(+=s s G 试根据式（6-11）频率特性的定义求闭环系统在输入信号()sin(30)2cos(545)r t t t =+︒--︒作用下的稳态输出。
解：先求得闭环传递函数21)(+=s s T 。
（1）1=ω，447.055211)1(==+=j j T ，︒-=-=∠56.2621arctan )1(j T 。
（2）5=ω，186.02929251)5(==+=j j T ，︒-=-=∠20.6825arctan )5(j T 。
故)2.1135cos(372.0)44.3sin(447.0)(︒--︒+=∞→t t t y t 。
6-4 某对象传递函数为s e Ts s G τ-+=11)( 试求：(1)?该对象在输入()sin()u t t ω=作用下输出的表达式，并指出哪部分是瞬态分量； (2)?分析T 和τ增大对瞬态分量和稳态分量的影响；(3)?很多化工过程对象的T 和τ都很大，通过实验方法测定对象的频率特性需要很长时间，试解释其原因。
自动控制原理与应用答案解析第二版_课后答案解析
第二章习题课 (2-11d)
2-11d 求系统的闭环传递函数 。
解: (1)
R(s) G1 + G2
C(s)
_
HG2
R(s)
_
C(s) G1 + G2
L1 H
C(s) R(s)
= (G1+G2
)
1 1+G2H
(2) L1=-G2H P1=G1 Δ1 =1
P2=G2 Δ2 =1
第二章习题课 (2-11e)
C(s)=
(s2+4s+2) (s+1)(s+2)
=1+
2 s+2
-
1 s+1
c(t)=δ (t)+2e-2t+e-t
第二章习题课 (2-10)
2式R-1(，s0) 试已- R画知(sG出)系1 -系统统G1的+2的G微G3G动1分G2G-2态G6方+3G结GG程-432GG构组46G图G5的3C并拉(s求)氏G传4变C递(s换) RC((函解ss))R=数:(s1)。+CRG- ((ss3)GX)X[GGX112(7(-1GX2(ssXs())3)s6=(=1--)s(G+GR{=s)=)R81GG((GGsGs(C2))3s236(]GG)G((s-ssG)1CG)4)1[[(XX=G2GXXsC7(3-)2Gs2((1G(5--2()ss(sGs+4G[))s8))(GG-)G1s-C3-15()7-GG(Gs(X+(1ss)GsGG)6)64[3)GG(3G(-3sG2sGG55G)G7)(4X2s(G8GG3GGG)s3(X3])5s7G86(573-)s(GC]s)4})]((8GsGG(s)14)7(C]s-C)(Gs(s)8))
自动控制原理(非自动化类)习题答案_第二版(孟庆明)
自动控制原理（非自动化类）习题答案第一章习题1-1（略）1-2（略）1-3解：受控对象：水箱液面。
被控量：水箱的实际水位h c 执行元件：通过电机控制进水阀门开度，控制进水流量。
比较计算元件：电位器。
测量元件：浮子，杠杆。
放大元件：放大器。
工作原理：系统的被控对象为水箱。
被控量为水箱的实际水位h 。
给定值为希望水位h （与电位器设定c r 电压u r 相对应，此时电位器电刷位于中点位置）。
当h c =h r 时，电位器电刷位于中点位置，电动机不工作。
一但h c ≠h r 时，浮子位置相应升高（或电动机通过减速器使阀门的开度减小（或增大），以使水箱水位达到希望值h r 。
出水h rh c水位自动控制系统的职能方框图1-4解：受控对象：门。
执行元件：电动机，绞盘。
放大元件：放大器。
受控量：门的位置测量比较元件：电位计工作原理：系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时，桥式电位器测量电路产生偏差电压，经放大器放大后，驱动电动机带动绞盘转动，使大门向上提起。
同时，与大门连在一起的电位器电刷上移，直到桥式电位器达到平衡，电动机停转，开门开关自动断开。
反之，当合上关门开关时，电动机带动绞盘反转，使大门关闭。
开(闭)门的位置门实际仓库大门自动控制开（闭）的职能方框图1-5解：系统的输出量：电炉炉温给定输入量：加热器电压被控对象：电炉_大门位置绞盘电动机放大器电位器_浮子杠杆水箱阀门减速器电动机放大器电位器放大元件：电压放大器，功率放大器，减速器比较元件：电位计测量元件：热电偶职能方框图：给定炉温炉温—第二章习题2-1解：对微分方程做拉氏变换：⎧X 1(s )=R (s )−C (s )+N 1(s )⎪⎪X 2(s )=K 1X 1(s )⎪X 3(s )=X 2(s )−X 5(s )⎨⎪TsX 4(s )=X 3(s )⎪X 5(s )=X 4(s )−K 2N 2(s )⎪⎪K X (s )=s 2C (s )+sC (s )⎩35绘制上式各子方程的方块图如下图所示：N 1(s)R(s)+X 1(s)X 2(s)X 3(s)X 1(s)X 2(s)--C(s)X 5(s)N 2(s)X 3(s)X 4(s)X 5(s)C(s)X 4(s)-X 5(s)将方块图连接起来，得出系统的动态结构图：N 2(s)N 1(s)+X 1(s)_C(s)R(s)X 2(s)X 3(s)X 4(s)X 5(s)K 1K 3C (s )/R (s )=，Ts 3+(T +1)s 2+s +K K 13--K 3K 11s 2+s1TsK 2K 31Ts1s 2+sK 2K 1热电偶电炉加热器电机功率放大电压放大电位器C (s )/N 1(s )=C (s )/R (s )，K 2K 3TsC (s )/N (s )=−2Ts 3+(T +1)s 2+s +K K 132-2解：对微分方程做拉氏变换⎧X 1(s )=K [R (s )−C (s )]⎪⎪X 2(s )=⎜sR (s )⎪(s +1)X 3(s )=X 1(s )+X 2(s )⎨⎪(Ts +1)X 4(s )=X 3(s )+X5(s )⎪C (s )=X (s )−N (s )4⎪⎪⎩X 5(s )=(Ts +1)N (s )绘制上式各子方程的方块如下图：X 2(s)R(s)X 1(s)R(s)X 2(s)X 1(s)X 3(s)-C(s)X 5(s)N(s)N(s)X 5(s)—X 3(s)X 4(s)X 4(s)C(s)将方块图连接得出系统的动态结构图：N(s)X 2(s)X 5(s)—C(s)R(s)X 1(s)X 3(s)X 4(s)⎜s K+K +⎜s =(s +1)(Ts +1)(s +1)(Ts +1)=C (s )R (s )k Ts 2+(T +1)s +(K +1)1+(s +1)(Ts +1)C (s )N (s )=02-3解：（过程略）C (s )1C (s )=G 1+G 2(a)=R (s )ms 2+fs +K(b)R (s )1+G G −G G +G G −G G 13142324-K1Ts +11s +1τsTs+1Ts1Ts +1τsK1s +1C (s )=G 2+G 1G 2C (s )=G 1−G 2(c)(d)R (s )1+G 1+G 2G 1R (s )1−G 2G 3C (s )=G 1G 2G 3G 4(e)R (s )1+G 1G 2+G 2G 3+G 3G 4+G 1G 2G 3G 42-4解：（1）求C/R ，令N=0G (s )=K 1K 2K 3s (Ts +1)K 1K 2K 3G (s )C (s )/R (s )==1+G (s )Ts 2+s +K K K 123求C/N ，令R=0，向后移动单位反馈的比较点K 3K 2)Ts +1=K n K 3s −K 1K 2K 3G n C (s )/N (s )=(K −G K n n 1K K Ts 2+s +K K K s 1+32K 1231Ts +1s（2）要消除干扰对系统的影响C (s )/N (s )=K n K 3s −K 1K 2K 3G n=0Ts 2+s +K K K 123K n s G (s )=n K 1K 22-5解：（a ）（1）系统的反馈回路有三个，所以有3∑La=L 1+L 2+L 3=−G 1G 2G 5−G 2G 3G 4+G 4G 2G 5a =1三个回路两两接触，可得⊗=1−∑La=1+G 1G 2G 5+G 2G 3G 4−G 4G 2G 5（2）有两条前向通道，且与两条回路均有接触，所以P 1=G 1G 2G 3,⊗1=1P 2=1,⊗2=1（3）闭环传递函数C/R 为C =G 1G 2G 3+1R 1+G 1G 2G 5+G 2G 3G 4−G 4G 2G 5（b ）（1）系统的反馈回路有三个，所以有3∑La=L 1+L 2+L 3=−G 1G 2−G 1−G 1a =1三个回路均接触，可得⊗=1−∑L a=1+G 1G 2+（2）有四条前向通道，且与三条回路均有接触，所以P 1=G 1G 2,⊗1=1P 2=G 1,⊗2=1P 3=G 2,⊗3=1P 4=−G 1,⊗4=1（3）闭环传递函数C/R 为C =G 1G 2+G 1+G 2−G 1=G 1G 2+G 2R 1+G 1G 2+2G 11+G 1G 2+2G 12-6解：用梅逊公式求，有两个回路，且接触，可得⊗=1−∑La=1+G 1G 2G 3+G 2，可得C (s )=G 1G 2G 3+G 2G 3C (s )=C (s )/R (s )R (s )1+G 1G 2G 3+G 2N 1(s )(1+G 2)G 3C (s )=−1⋅(1+G 1G 2G 3+G 2)=−1C (s )=N 2(s )1+G 1G 2G 3+G 21+G 1G 2G 3+G 2N 3(s )E (s )=1+G 2−G 2G 3E (s )=−C (s )=−G 2G 3−G 1G 2G 3R (s )1+G 1G 2G 3+G 2N 1(s )N 1(s )1+G 1G 2G 3+G 2E (s )=−C (s )−(1+G 2)G 3E (s )=−C (s )==1N 2(s )N 2(s )1+G 1G 2G 3+G 2N 3(s )N 3(s )第三章习题103-1解：（原书改为G (s )=）0.2s +1采用K 0,K H 负反馈方法的闭环传递函数为10K 0⎫(s )=C (s )=K G (s )1+10K H =R (s )01+G (s )K 0.2s +1H1+10K H要使过渡时间减小到原来的0.1倍，要保证总的放大系数不变，则：（原放大系数为10，时间常数为0.2）10K 0⎧=10⎧K =10⎪0⎨1+10K ⇒⎨H⎩K =0.9⎪H 1+10K =10⎩H3-2解：系统为欠阻尼二阶系统（书上改为“单位负反馈……”，“已知系统开环传递函数”）⎛%=e −⎩/1−⎩⋅100%=1.3−1⋅100%21t p ==0.11−⎩2⎤n解得：⎤=33.71n⎩=0.358所以，开环传递函数为：113647.1G(s)==s(s+24.1)s(0.041s+1) 3-3解：（1）K=10s−1时：100G(s)=s2+10s⎤2=100n2⎩⎤=10n解得：⎤n=10,⎩=0.5,⎛%=16.3%,t p=0.363（2）K=20s−1时：200G(s)=s2+10s⎤2=200n2⎩⎤=10n解得：⎤n=14.14,⎩=0.354,⎛%=30%,t p=0.238结论，K增大，超调增加，峰值时间减小。
自动控制原理答案_第二版(孟庆明)讲解
课后答案网，用心为你服务！大学答案--- 中学答案--- 考研答案--- 考试答案最全最多的课后习题参考答案，尽在课后答案网（）！Khdaw团队一直秉承用心为大家服务的宗旨，以关注学生的学习生活为出发点，旨在为广大学生朋友的自主学习提供一个分享和交流的平台。
爱校园（）课后答案网（）淘答案（）自动控制原理（非自动化类）习题答案第一章 习题1-1（略） 1-2（略） 1-3 解：受控对象：水箱液面。
被控量：水箱的实际水位 h c 执行元件：通过电机控制进水阀门开度，控制进水流量。
比较计算元件：电位器。
测量元件：浮子，杠杆。
放大元件：放大器。
工作原理：系统的被控对象为水箱。
被控量为水箱的实际水位 h 。
给定值为希望水位 h （与电位器设定 c r 电压 u r 相对应，此时电位器电刷位于中点位置）。
当 h c = h r 时，电位器电刷位于中点位置，电动机不工作。
一但 h c ⎺ h r 时，浮子位置相应升高（或降低），通过杠杆作用使电位器电刷从中点位置下移（或上移），从而给电动机提供一定的工作电压，驱动 电动机通过减速器使阀门的开度减小（或增大），以使水箱水位达到希望值 h r 。
水位自动控制系统的职能方框图1-4 解：受控对象：门。
执行元件：电动机，绞盘。
放大元件：放大器。
受控量：门的位置 测量比较元件：电位计工作原理：系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时，桥式电位器测量电路产生偏差电压，经放大器放大后，驱动电动机带动绞盘转动， 使大门向上提起。
同时，与大门连在一起的电位器电刷上移，直到桥式电位器达到平衡，电动机停转，开 门开关自动断开。
反之，当合上关门开关时，电动机带动绞盘反转，使大门关闭。
开(闭)门门实际 仓库大门自动控制开（闭）的职能方框图1-5 解：系统的输出量：电炉炉温 给定输入量：加热器电压 被控对象：电炉放大元件：电压放大器，功率放大器，减速器 比较元件：电位计 测量元件：热电偶 职能方框图：第二章 习题2-1 解：对微分方程做拉氏变换：♣ X 1 (s ) = R (s ) C (s ) + N 1 (s ) ♠ ♠ X 2(s ) = K 1 X 1 (s )♠ X 3 (s ) = X 2 (s ) X 5 (s )♦ ♠TsX 4 (s ) = X 3 (s )♠ X 5 (s ) = X 4 (s ) K 2 N 2 (s )♠ ♠K X (s ) = s 2C (s ) + sC (s ) ♥3 5 绘制上式各子方程的方块图如下图所示：1(s)3(s)5(s)K 1K 3C (s ) / R (s ) = ， Ts 3 + (T + 1)s 2+ s + K K 1 3C (s ) / N 1 (s ) = C (s ) / R (s ) ，K 2 K 3Ts C (s ) / N (s ) = 2Ts 3 + (T + 1)s 2 + s + K K 1 32-2 解：对微分方程做拉氏变换♣ X 1 (s ) = K [R (s ) C (s )] ♠♠ X 2 (s ) = ⎜ sR (s )♠(s + 1) X 3 (s ) = X 1 (s ) + X 2 (s )♦♠(Ts + 1) X 4 (s ) = X 3 (s ) + X 5 (s ) ♠C (s ) = X (s ) N (s ) 4 ♠ ♠♥ X 5 (s ) = (Ts + 1) N (s )绘制上式各子方程的方块如下图：⎜ s K+ K + ⎜ s = (s + 1)(Ts + 1) (s + 1)(Ts + 1) = C (s ) R (s ) k Ts 2+ (T + 1)s + (K + 1) 1 + (s + 1)(Ts + 1)C (s ) N (s ) =2-3 解：（过程略） C (s ) 1 C (s ) =G 1 + G 2 (a)= R (s ) ms 2+ fs + K(b)R (s ) 1 + G G G G + G G G G 1 3 1 4 2 3 2 4C (s ) =G 2 + G 1G 2C (s ) = G 1G 2 (c)(d)R (s ) 1 + G 1 + G 2G 1R (s ) 1 G 2G 3C (s ) =G 1G 2G 3G 4 (e)R (s ) 1 + G 1G 2 + G 2G 3 + G 3G 4 + G 1G 2G 3G 42-4 解 ：（1）求 C/R ，令 N=0G (s ) = K 1K 2 K3s (Ts + 1)K 1K 2 K 3 G (s )C (s ) / R (s ) = = 1 + G (s ) Ts 2 + s + K K K 1 2 3求 C/N ，令 R=0，向后移动单位反馈的比较点K 3K 2 ) Ts + 1 = K n K 3s K 1K 2 K 3G n C (s ) / N (s ) = (K G K n n 1K K Ts 2 + s + K K K s 1 + 3 2K 1 2 3 1 Ts + 1 s（2）要消除干扰对系统的影响C (s ) / N (s ) = K n K 3 s K 1K 2 K 3G n= 0Ts 2 + s + K K K 1 2 3K n sG (s ) = nK 1K 22-5 解：（a ）（1）系统的反馈回路有三个，所以有3La= L 1 + L 2 + L 3 = G 1G 2G 5 G 2G 3G 4 + G 4G 2G 5a =1三个回路两两接触，可得 ⊗ = 1La= 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5（2）有两条前向通道，且与两条回路均有接触，所以P 1 = G 1G 2G 3 , ⊗1 = 1 P 2 = 1, ⊗2 = 1（3）闭环传递函数 C/R 为C =G 1G 2G 3 + 1 R 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5（b ）（1）系统的反馈回路有三个，所以有3La= L 1 + L 2 + L 3 = G 1G 2 G 1 G 1a =1三个回路均接触，可得 ⊗ = 1La= 1 + G 1G 2 + 2G 1（2）有四条前向通道，且与三条回路均有接触，所以P 1 = G 1G 2 , ⊗1 = 1 P 2 = G 1 , ⊗2 = 1 P 3 = G 2 , ⊗3 = 1 P 4 = G 1 , ⊗4 = 1（3）闭环传递函数 C/R 为C = G 1G 2 + G 1 + G 2 G 1 = G 1G 2 + G 2 R 1 + G 1G 2 + 2G 1 1 + G 1G 2 + 2G 12-6 解：用梅逊公式求，有两个回路，且接触，可得 ⊗ = 1La= 1 + G 1G 2G 3 + G 2 ，可得C (s ) = G 1G 2G 3+ G 2G 3 C (s ) = C (s ) / R (s )R (s ) 1 + G 1G 2G 3 + G 2 N 1 (s )(1 + G 2 )G 3C(s ) = 1⋅ (1 + G 1G 2G 3 + G 2 )= 1C(s ) = N 2 (s ) 1 + G 1G 2G 3 + G 2 1 + G 1G 2G 3 + G 2 N 3 (s )E (s ) =1 + G2 G 2G3 E (s )= C (s ) = G 2G 3 G 1G 2G 3 R (s ) 1 + G 1G 2G 3 + G 2N 1 (s ) N 1 (s ) 1 + G 1G 2G 3 + G 2 E(s ) = C (s ) (1 + G 2 )G 3E (s ) = C (s )= = 1 N 2 (s ) N 2 (s ) 1 + G 1G 2G 3 + G 2 N 3 (s ) N 3 (s )第三章 习题103-1 解：（原书改为 G (s ) =）0.2s + 1采用 K 0 , K H 负反馈方法的闭环传递函数为10K 0⎫ (s ) = C (s ) = K G (s )1 + 10K H = R (s ) 01 + G (s )K 0.2 s + 1H 1 + 10K H要使过渡时间减小到原来的 0.1 倍，要保证总的放大系数不变，则：（原放大系数为 10，时 间常数为 0.2）10K 0♣ = 10 ♣ K = 10 ♠0 ♦1 + 10K ® ♦ H♥K = 0.9♠ H 1 + 10K = 10 ♥H 3-2 解：系统为欠阻尼二阶系统（书上改为“单位负反馈……”，“已知系统开环传递函数”）⎛ % = e⎩⋅100% = 1.3 1 ⋅100%1t p == 0.1解得：⎤n = 33.71 ⎩ = 0.358所以，开环传递函数为：1136 47.1G (s ) = = s (s + 24.1) s (0.041s + 1)3-3 解：（1） K = 10s 1时：100G (s ) = s 2+ 10s⎤ 2 =100 n 2⎩⎤n = 10解得：⎤n = 10, ⎩ = 0.5, ⎛ % = 16.3%, t p = 0.363 （2） K = 20s 1 时：200 G (s ) = s 2+ 10s⎤ 2 = 200n 2⎩⎤n = 10解得：⎤n = 14.14, ⎩ = 0.354, ⎛ %=30%, t p = 0.238结论，K 增大，超调增加，峰值时间减小。
自动控制原理答案完全版_第二版(孟庆明)
自动控制原理（非自动化类）习题答案第一章 习题1-1（略） 1-2（略） 1-3 解：受控对象：水箱液面。
被控量：水箱的实际水位 h c 执行元件：通过电机控制进水阀门开度，控制进水流量。
比较计算元件：电位器。
测量元件：浮子，杠杆。
放大元件：放大器。
工作原理：系统的被控对象为水箱。
被控量为水箱的实际水位 h 。
给定值为希望水位 h （与电位器设定 c r 电压 u r 相对应，此时电位器电刷位于中点位置）。
当 h c = h时，电位器电刷位于中点位置，电动机不工作。
一但 h ⎺ h 时，浮子位置相应升高（或降低） 1-4 解：当合上开门开关时，桥式电位器测量电路产生偏差电压，经放大器放大后，驱动电动机带动绞盘转动， 使大门向上提起。
同时，与大门连在一起的电位器电刷上移，直到桥式电位器达到平衡，电动机停转，开 门开关自动断开。
反之，当合上关门开关时，电动机带动绞盘反转，使大门关闭。
开(闭)门门实际 仓库大门自动控制开（闭）的职能方框图1-5 解：系统的输出量：电炉炉温 给定输入量：加热器电压 被控对象：电炉放大元件：电压放大器，功率放大器，减速器 比较元件：电位计 测量元件：热电偶 职能方框图：第二章 习题2-1 解：对微分方程做拉氏变换：♣ X 1 (s ) = R (s ) C (s ) + N 1 (s ) ♠ ♠ X 2(s ) = K 1 X 1 (s )K 1K 3C (s ) / R (s ) = ， Ts 3 + (T + 1)s 2+ s + K K 1 3C (s ) / N 1 (s ) = C (s ) / R (s ) ，K 2 K 3Ts C (s ) / N (s ) = 2Ts 3 + (T + 1)s 2 + s + K K 1 32-2 解：对微分方程做拉氏变换♣ X 1 (s ) = K [R (s ) C (s )] ♠♠ X 2 (s ) = ⎜ sR (s )♠(s + 1) X 3 (s ) = X 1 (s ) + X 2 (s )♦♠(Ts + 1) X 4 (s ) = X 3 (s ) + X 5 (s ) ♠C (s ) = X (s ) N (s ) 4 ♠ ♠♥ X 5 (s ) = (Ts + 1) N (s )⎜ s K+ K + ⎜ s = (s + 1)(Ts + 1) (s + 1)(Ts + 1) = C (s ) R (s ) k Ts 2+ (T + 1)s + (K + 1) 1 + (s + 1)(Ts + 1)C (s ) N (s ) =2-3 解：（过程略） C (s ) 1 C (s ) =G 1 + G 2 (a)= R (s ) ms 2+ fs + K(b)R (s ) 1 + G G G G + G G G G 1 3 1 4 2 3 2 4C (s ) =G 2 + G 1G 2C (s ) = G 1G 2 (c)(d)R (s ) 1 + G 1 + G 2G 1R (s ) 1 G 2G 3C (s ) =G 1G 2G 3G 4 (e)R (s ) 1 + G 1G 2 + G 2G 3 + G 3G 4 + G 1G 2G 3G 42-4 解 ：（1）求 C/R ，令 N=0G (s ) = K 1K 2 K3s (Ts + 1)K 1K 2 K 3 G (s )C (s ) / R (s ) = = 1 + G (s ) Ts 2 + s + K K K 1 2 3求 C/N ，令 R=0，向后移动单位反馈的比较点K 3K 2 ) Ts + 1 =C (s ) / N (s ) = (K G K n n 1K K s 1 + 3 2K （22-5 解：（a ）（12G 5G 2G 5（21 123 1 P2 = 1, ⊗2 = 1（3）闭环传递函数 C/R 为C =G 1G 2G 3 + 1 R 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5（b ）（1）系统的反馈回路有三个，所以有3La= L 1 + L 2 + L 3 = G 1G 2 G 1 G 1a =1三个回路均接触，可得 ⊗ = 1La= 1 + G 1G 2 + 2G 1（2）有四条前向通道，且与三条回路均有接触，所以P 1 = G 1G 2 , ⊗1 = 1 P 2 = G 1 , ⊗2 = 1 P 3 = G 2 , ⊗3 = 1 P 4 = G 1 , ⊗4 = 1（3）闭环传递函数 C/R 为C = G 1G 2 + G 1 + G 2 G 1 = G 1G 2 + G 2 R 1 + G 1G 2 + 2G 1 1 + G 1G 2 + 2G 12-6 解：用梅逊公式求，有两个回路，且接触，可得 ⊗ = 1La= 1 + G 1G 2G 3 + G 2 ，可得C (s ) = G 1G 2G 3+ G 2G 3 C (s ) = C (s ) / R (s )R (s ) 1 + G 1G 2G 3 + G 2 N 1 (s )(1 + G 2 )G 3C(s ) =C(s ) = N 2 (s ) 1 + G G G + G N (s )E (s ) =R (s ) E(s ) N 2 (s ) 3-1 采用 K 要使过渡时间减小到原来的 0.1 倍，要保证总的放大系数不变，则：（原放大系数为 10，时 间常数为 0.2）10K 0♣ = 10 ♣ K = 10 ♠0 ♦1 + 10K ® ♦ H♥K = 0.9♠ H 1 + 10K = 10 ♥H 3-2 解：系统为欠阻尼二阶系统（书上改为“单位负反馈……”，“已知系统开环传递函数”）⎛ % = e⎩⋅100% = 1.3 1 ⋅100%1t p == 0.1解得：⎤n = 33.71 ⎩ = 0.358所以，开环传递函数为：1136 47.1G (s ) = = s (s + 24.1) s (0.041s + 1)3-3 解：（1） K = 10s 1时：100G (s ) = s 2+ 10s⎤ 2 =100 n 2⎩⎤n = 10解得：⎤n = 10, ⎩ = 0.5, ⎛ % = 16.3%, t p = 0.363 （2） K = 20解得：⎤n =结论，K 3-4 解：（1）a. ⎩ = 0.1,⎤ n 3.5 t = = 7s s⎩⎤ nb. ⎩ = 0.1,⎤ =10s 1 时， n ⎛ % = e ⎩⋅100% = 72.8%3.5 t = = 3.5s s⎩⎤ nc. ⎩ = 0.1,⎤ =1s 1 时， n⎛ % = e ⎩⋅100% = 72.8%3.5 t = = 35s s⎩⎤ n⎩ = 0.5,⎤ = 5s 1时，(2) n ⎛ % = e ⎩⋅100% = 16.3%3.5 t = = 1.4s s⎩⎤ n(3) 讨论系统参数：⎩ 不变，⎛ % 不变；⎩ 不变，⎤n 增加，则 t s 减小；⎤n 不变，⎩ 增加， 则⎛ % 减小， t s 减小3-5 解：（1） （a ）用劳思判据s 3 s 2 s 1 s 0系统稳定。
自动控制原理答案(第二版)+中国电力出版社
第二部分古典控制理论基础习题详解一 概述2-1-1 试比较开环控制系统和闭环控制系统的优缺点。
【解】：控制系统优点缺点开环控制简单、造价低、调节速度快调节精度差、无抗多因素干扰能力闭环控制抗多因素干扰能力强、调节精度高结构较复杂、造价较高2-1-2试列举几个日常生活中的开环和闭环控制系统的例子，并说明其工作原理。
【解】：开环控制——半自动、全自动洗衣机的洗衣过程。
工作原理：被控制量为衣服的干净度。
洗衣人先观察衣服的脏污程度，根据自己的经验，设定洗涤、漂洗时间，洗衣机按照设定程序完成洗涤漂洗任务。
系统输出量（即衣服的干净度）的信息没有通过任何装置反馈到输入端，对系统的控制不起作用，因此为开环控制。
闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。
工作原理：以卫生间蓄水箱蓄水量控制为例，系统的被控制量（输出量）为蓄水箱水位（反应蓄水量）。
水位由浮子测量，并通过杠杆作用于供水阀门（即反馈至输入端），控制供水量，形成闭环控制。
当水位达到蓄水量上限高度时，阀门全关（按要求事先设计好杠杆比例），系统处于平衡状态。
一旦用水，水位降低，浮子随之下沉，通过杠杆打开供水阀门，下沉越深，阀门开度越大，供水量越大，直到水位升至蓄水量上限高度，阀门全关，系统再次处于平衡状态。
2-1-3 试判断下列微分方程所描述的系统属何种类型（线性、非线性；定常、时变）。
【解】：（1）线性定常系统；（2）线性时变系统；（3）非线性定常系统；（4）线性定常系统。
122-1-4 根据题2-1-1图所示的电动机速度控制系统工作原理图：（1）将a ，b 与c ，d 用线连接成负反馈系统；（2）画出系统方框图。
【解】：（1）a -d 连接，b -c 连接。
（2）系统方框图题2-1-4解图抽头移动，电动机获得一个正电压，通过齿轮减速器传递，使阀门打开，从而增加入水流量使水位上升，当水位回到给定值时，电动机的输入电压又会回到零，系统重新达到平衡状态。
《自动控制原理》第二版课后习题答案
k (x x ) f ( dx1 dy )
（1）
1
1
dt dt
对B点有
f ( dx1 dy ) k y dt dt 2
（2）
联立式（1）、（2）可得：
dy k1k2 y k1 dx dt f (k1 k2 ) k1 k2 dt
电压。
在正常情况下，炉温等于某个期望值T °C，热电偶的输出电压u f 正好等于给定电压ur 。 此时， ue ur u f 0 ，故u1 ua 0 ，可逆电动机不转动，调压器的滑动触点停留在某 个合适的位置上，使uc 保持一定的数值。这时，炉子散失的热量正好等于从加热器吸取的热
量，形成稳定的热平衡状态，温度保持恒定。
第一章 自动控制的一般概念 习题及答案
1-1 根据题 1-15 图所示的电动机速度控制系统工作原理图，完成： (1) 将 a，b 与 c，d 用线连接成负反馈状态； (2) 画出系统方框图。
解 （1）负反馈连接方式为： a d ， b c ；
（2）系统方框图如图解 1-1 所示。
1-2 题 1-16 图是仓库大门自动控制系统原理示意图。试说明系统自动控制大门开、闭的 工作原理，并画出系统方框图。
图 1-16 仓库大门自动开闭控制系统
1
解 当合上开门开关时，电桥会测量出开门位置与大门实际位置间对应的偏差电压，偏 差电压经放大器放大后，驱动伺服电动机带动绞盘转动，将大门向上提起。与此同时，和大 门连在一起的电刷也向上移动，直到桥式测量电路达到平衡，电动机停止转动，大门达到开 启位置。反之，当合上关门开关时，电动机带动绞盘使大门关闭，从而可以实现大门远距离 开闭自动控制。系统方框图如图解 1-2 所示。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失)，则出现以下
自动控制原理第二版课后答案(孟庆明)
自动控制原理第二版课后答案(孟庆明)目录第一章 (1)第二章 (2)第三章 (5)第四章 (15)第五章 (18)第六章 (27)1-1（略） 1-2（略） 1-3 解：受控对象：水箱液面。
被控量：水箱的实际水位 h c 执行元件：通过电机控制进水阀门开度，控制进水流量。
比较计算元件：电位器。
测量元件：浮子，杠杆。
放大元件：放大器。
工作原理：系统的被控对象为水箱。
被控量为水箱的实际水位 h 。
给定值为希望水位 h （与电位器设定 c r 电压 u r 相对应，此时电位器电刷位于中点位置）。
当 h c = h r 时，电位器电刷位于中点位置，电动机不工作。
一但 h c ⎺ h r 时，浮子位置相应升高（或降低），通过杠杆作用使电位器电刷从中点位置下移（或上移），从而给电动机提供一定的工作电压，驱动 电动机通过减速器使阀门的开度减小（或增大），以使水箱水位达到希望值 h r 。
水位自动控制系统的职能方框图1-4 解：受控对象：门。
执行元件：电动机，绞盘。
放大元件：放大器。
受控量：门的位置 测量比较元件：电位计工作原理：系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时，桥式电位器测量电路产生偏差电压，经放大器放大后，驱动电动机带动绞盘转动， 使大门向上提起。
同时，与大门连在一起的电位器电刷上移，直到桥式电位器达到平衡，电动机停转，开 门开关自动断开。
反之，当合上关门开关时，电动机带动绞盘反转，使大门关闭。
开(闭)门门实际 仓库大门自动控制开（闭）的职能方框图1-5 解：系统的输出量：电炉炉温 给定输入量：加热器电压 被控对象：电炉第一章放大元件：电压放大器，功率放大器，减速器比较元件：电位计 测量元件：热电偶 职能方框图： 2-1 解：对微分方程做拉氏变换：♣ X 1 (s ) = R (s ) C (s ) + N 1 (s ) ♠ ♠ X 2(s ) = K 1 X 1 (s )♠ X 3 (s ) = X 2 (s ) X 5 (s ) ♦♠TsX 4 (s ) = X 3 (s )♠ X 5 (s ) = X 4 (s ) K 2 N 2 (s ) ♠ ♠K X (s ) = s 2C (s ) + sC (s ) ♥3 5 绘制上式各子方程的方块图如下图所示：(s)3(s)5(s)K 1K 3C (s ) / R (s ) = ， Ts 3 + (T + 1)s 2+ s + K K 1 3第二章C (s ) / N 1 (s ) = C (s ) / R (s ) ，K 2 K 3Ts C (s ) / N (s ) = 2Ts 3 + (T + 1)s 2 + s + K K 1 32-2 解：对微分方程做拉氏变换♣ X 1 (s ) = K [R (s ) C (s )]♠♠ X 2 (s ) = ⎜ sR (s )♠(s + 1) X 3 (s ) = X 1 (s ) + X 2 (s ) ♦♠(Ts + 1) X 4 (s ) = X 3 (s ) + X 5 (s ) ♠C (s ) = X (s ) N (s ) 4 ♠ ♠♥ X 5 (s ) = (Ts + 1) N (s )绘制上式各子方程的方块如下图：⎜ s K+ K + ⎜ s = (s + 1)(Ts + 1) (s + 1)(Ts + 1) = C (s ) R (s ) k Ts 2+ (T + 1)s + (K + 1) 1 + (s + 1)(Ts + 1)C (s )N (s ) =0 2-3 解：（过程略） C (s ) 1 C (s ) =G 1 + G 2 (a)=R (s ) ms 2 + fs + K(b)R (s ) 1 + G G G G + G G G G 1 3 1 4 2 3 2 4C (s ) = G 2 + G 1G 2 C (s ) = G 1 G 2 (c)(d)R (s ) 1 + G 1 + G 2G 1R (s ) 1 G 2G 3C (s ) =G 1G 2G 3G 4 (e)R (s ) 1 + G 1G 2 + G 2G 3 + G 3G 4 + G 1G 2G 3G 42-4 解 ：（1）求 C/R ，令 N=0G (s ) =K 1K 2 K 3s (Ts + 1)K 1K 2 K 3 G (s )C (s ) / R (s ) = = 1 + G (s ) Ts 2 + s + K K K 1 2 3 求 C/N ，令 R=0，向后移动单位反馈的比较点K 3K 2 ) Ts + 1 = K n K 3 s K 1K 2 K 3G n C (s ) / N (s ) = (K G K n n1 K K Ts2 + s + K K K s 1 +3 2 K 1 2 31Ts + 1 s（2）要消除干扰对系统的影响C (s ) / N (s ) = K n K 3 s K 1K 2 K 3G n= 0Ts 2 + s + K K K 1 2 3K n sG (s ) = nK 1K 22-5 解：（a ）（1）系统的反馈回路有三个，所以有3La= L 1 + L 2 + L 3 = G 1G 2G 5 G 2G 3G 4 + G 4G 2G 5a =1三个回路两两接触，可得 ⊗ = 1La= 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5（2）有两条前向通道，且与两条回路均有接触，所以P 1 = G 1G 2G 3 , ⊗1 = 1 P 2 = 1, ⊗2 = 1（3）闭环传递函数 C/R 为C =G 1G 2G 3 + 1 R 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5（b ）（1）系统的反馈回路有三个，所以有3La= L 1 + L 2 + L 3 = G 1G 2 G 1 G 1a =1三个回路均接触，可得 ⊗ = 1La= 1 + G 1G 2 + 2G 1（2）有四条前向通道，且与三条回路均有接触，所以P 1 = G 1G 2 , ⊗1 = 1 P 2 = G 1 , ⊗2 = 1 P 3 = G 2 , ⊗3 = 1 P 4 = G 1 , ⊗4 = 1（3）闭环传递函数 C/R 为C = G 1G 2 + G 1 + G 2 G 1 = G 1G 2 + G 2 R 1 + G 1G 2 + 2G 1 1 + G 1G 2 + 2G 12-6 解：用梅逊公式求，有两个回路，且接触，可得 ⊗ = 1La= 1 + G 1G 2G 3 + G 2 ，可得C (s ) = G 1G 2G 3 + G 2G 3C (s ) = C (s ) / R (s )R (s ) 1 + G 1G 2G 3 + G 2 N 1 (s ) (1 + G 2 )G 3C(s ) = 1⋅ (1 + G 1G 2G 3 + G 2 )= 1C(s ) = N 2 (s ) 1 + G 1G 2G 3 + G 2 1 + G 1G 2G 3 + G 2 N 3 (s )E (s ) =1 + G2 G 2G3 E (s ) = C (s ) =G 2G 3 G 1G 2G 3 R (s ) 1 + G 1G 2G 3 + G 2N 1 (s ) N 1 (s ) 1 + G 1G 2G 3 + G 2E(s ) = C (s )(1 + G 2 )G 3 E (s )= C (s )= = 1 N 2 (s ) N 2 (s ) 1 + G 1G 2G 3 + G 2 N 3 (s ) N 3 (s )103-1 解：（原书改为 G (s ) =）0.2s + 1采用 K 0 , K H 负反馈方法的闭环传递函数为10K 0⎫ (s ) =C (s ) = K G (s )1 + 10K H = R (s ) 0 1 + G (s )K 0.2s + 1H1 + 10K H要使过渡时间减小到原来的 0.1 倍，要保证总的放大系数不变，则：（原放大系数为 10，时 间常数为 0.2）10K 0♣ = 10 ♣ K = 10 ♠0 ♦1 + 10K ® ♦ H♥K = 0.9 ♠ H 1 + 10K = 10 ♥ H3-2 解：系统为欠阻尼二阶系统（书上改为“单位负反馈……”，“已知系统开环传递函数”）⎛ % = e⎩⋅100% = 1.3 1 ⋅100%1t p == 0.1第三章解得：⎤n = 33.71 ⎩ = 0.358所以，开环传递函数为：1136 47.1G (s ) = = s (s + 24.1) s (0.041s + 1)3-3 解：（1） K = 10s 1时：100G (s ) = s 2+ 10s⎤ 2 =100 n 2⎩⎤n = 10解得：⎤n = 10, ⎩ = 0.5, ⎛ % = 16.3%, t p = 0.363 （2） K = 20s 1 时：200 G (s ) = s 2+ 10s⎤ 2 = 200 n2⎩⎤n = 10解得：⎤n = 14.14, ⎩ = 0.354, ⎛ %=30%, t p = 0.238结论，K 增大，超调增加，峰值时间减小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三个回路均接触，可得 1 La 1 G1G2 2G1
4
（2）有四条前向通道，且与三条回路均有接触，所以
（3）闭环传递函数 C/R 为
P1 G1G2 , 1 1 P2 G1, 2 1 P3 G2 , 3 1 P4 G1, 4 1
C G1G2 G1 G2 G1 G1G2 G2
系统稳定。 3-8 解：系统闭环特征方程为：
劳思表：
0.01s3 2 s2 s K 0
s3
0.01
1
s2
2 K
s1 2 0.01K 2
s0
K
当 2 0, 2 0.01K 0, K 0 时系统稳定 2
稳定域为： 0, 0 K 200
3-9 解：（1）
解法一、因为 1，属于Ⅰ型无差系统，开环增益 K 10 ，故当 r(t) 1(t) 时， ess 0 ；
输入 r (t )
t2
1(t )
时，
R(s)
2 s3
, ess
lim
s 0
sE s
lim
s0
s 1
使大门向上提起。同时，与大门连在一起的电位器电刷上移，直到桥式电位器达到平衡，电动机停转，开 门开关自动断开。反之，当合上关门开关时，电动机带动绞盘反转，使大门关闭。
开闭门
的位置
_
电位器
放大器
电动机
绞盘
大门
门实际 位置
1-5 解： 系统的输出量：电炉炉温 给定输入量：加热器电压 被控对象：电炉
仓库大门自动控制开（闭）的职能方框图
电压 ur 相对应，此时电位器电刷位于中点位置）。
当 hc hr 时，电位器电刷位于中点位置，电动机不工作。一但 hc hr 时，浮子位置相应升高（或
降低），通过杠杆作用使电位器电刷从中点位置下移（或上移），从而给电动机提供一定的工作电压，驱动
电动机通过减速器使阀门的开度减小（或增大），以使水箱水位达到希望值 hr 。
（2）有两条前向通道，且与两条回路均有接触，所以
（3）闭环传递函数 C/R 为
P1 G1G2G3, 1 1 P2 1, 2 1
C
G1G2G3 1
R 1 G1G2G5 G2G3G4 G4G2G5
（b） （1）系统的反馈回路有三个，所以有
3
La L1 L2 L3 G1G2 G1 G1
当 r (t )
t 1(t) 时， ess
1 K
0.1；当 r(t)
t 2 1(t) 时， ess
。
解法二、系统的闭环特征方程为：
劳思表：
0.05s3 0.6s2 s 10 0
s3 0.05 1 s2 0.6 10 s1 1
6 s0 10
9
系统稳定。
Es
E i R
(s)R(s)
1
1 G(s)
/
N2 (s)
Ts3
(T
K 2 K3Ts 1)s2 s
K1K3
2-2 解：对微分方程做拉氏变换
X1(s) K[R(s) C(s)] X 2 (s) sR(s) (s 1) X 3(s) X1(s) X 2 (s) (Ts 1) X 4 (s) X 3 (s) X5 (s) C (s) X4 (s) N (s) X5 (s) (Ts 1)N (s)
s0 K
若系统稳定，则： 3 K 1 0, K 0 4
解得 K 4 3
3-7 解：
(a) 系统传递函数：
10(s 1)
s3 21s2 10s 10
劳斯表：
8
s3
1 10
s2 21 10
s1 200 / 21 0
s0 10 0
系统稳定。
(b) 系统传递函数：
10
s2 101s 10
劳思表：
s2 1 10 s1 101 0 s0 10
X (s)K
5 3
(s) X 5 (s)
X 4 (s) K2 N2 s2C(s) sC
(
s)
绘制上式各子方程的方块图如下图所示：
N1(s)
R(s)
+ X1(s)
X1(s)
X2(s)
-
K1
C(s) N2(s)
X2(s)
X3(s) 1
Ts
X4(s)
K2
X4(s)
X5(s)
- X5(s)
K3
将方块图连接起来，得出系统的动态结构图：
G(s) K1K2 K3 s(Ts 1)
C (s)
/
R(s)
G(s) 1 G(s)
Ts
2
K1K2 K3 s K1K2K3
求 C/N，令 R=0，向后移动单位反馈的比较点
K3
C(s) /
N (s)
(Kn
Gn
K1
K2 s
)
1
Ts K3
Ts
1
1 K1
K2 s
K n K3s K1K2 K3Gn Ts2 s K1K2K3
绘制上式各子方程的方块如下图：
R(s)
X1(s) R(s)
K
-
C(s)
X5(s)
X3(s)
1
X4(s)
Ts 1
X4(s)
X2(s) X1(s)
s
τ
N(s) N(s)
— C(s)
s
X2(s)
1 s 1
X3(s)
X5(s) T
将方块图连接得出系统的动态结构图：
X2(s) τs
R(s)
X1(s)
K
-
1 X3(s) s 1
G1 G2
R(s) 1 G1G3 G1G4 G2G3 G2G4
3
(c) C(s) G2 G1G2 R(s) 1 G1 G2G1
(d) C(s) G1 G2 R(s) 1G2G3
(e) C(s)
G1G2G3G4
R(s) 1 G1G2 G2G3 G3G4 G1G2G3G4
2-4 解 ：（1）求 C/R，令 N=0
s4
3
52
s3 10 1 0
s2 4.7 2
s1 3.2553 0
s0
2
7
10 1 0
10 D1 10, D2 3
1 5
47, D3
3
5
2 153
0 10 1
10 1 0 0
3 5 20
D4 0
10
1
306 0
（其实 D4 不必计算，因为 D3 0 ）
0 3 52
系统不稳定。 3-6 解：（1）系统闭环特征方程为
2 n
200
2n 10
解得：n 14.14, 0.354, %=30%, tp 0.238
结论，K 增大，超调增加，峰值时间减小。 3-4 解：（1）
a. 0.1, n 5s1 时， b. 0.1, n 10s1 时， c. 0.1, n 1s1 时，
% e / 12 100% 72.8%
hr
电位器
_
放大器
电动机
减速器
浮子 杠杆
阀门
出水
水箱
hc
1-4 解： 受控对象：门。 执行元 件：电动机，绞盘。 放大 元件：放大器。
水位自动控制系统的职能方框图
受控量：门的位置 测量比较元件：电位计
工作原理：系统的被控对象为大门。被控量为大门的实际位置。输入量为希望的大门位置。 当合上开门开关时，桥式电位器测量电路产生偏差电压，经放大器放大后，驱动电动机带动绞盘转动，
1
放大元件：电压放大器，功率放大器，减速器 比较元件：电位计 测量元件：热电偶 职能方框图：
给定 炉温
电 位器
电压放大
功率 放大
电机
加 热器
电炉
炉温
—
热 电偶
第二章 习题
2-1 解：对微分方程做拉氏变换：
X1(s) R(s) C(s) N1(s) X 2 (s) K1 X1(s)
X3 (s) X 2 (s) X5 (sT) sX 4 (s) X3 (s)
1101K00KH 1 10K H
10 10
KKH0
10 0.9
3-2 解：系统为欠阻尼二阶系统（书上改为“单位负反馈„„”，“已知系统开环传递函数”）
% e / 12 100% 1.3 1 100% 1
t p n
0.1 1 2
5
解得：
n 33.71 0.358
3-1 解：（原书改为 G(s) 10 ） 0.2s 1
采用 K0 , KH 负反馈方法的闭环传递函数为
10K0
(s)
C (s) R(s)
K
0
1
G(s) G(s)K
H
1 10 K H 0.2 s 1
1 10 K H
要使过渡时间减小到原来的 0.1 倍，要保证总的放大系数不变，则：（原放大系数为 10，时 间常数为 0.2）
则 % 减小， ts 减小
3-5 解：（1） （a）用劳思判据
系统稳定。 （b）用古尔维茨判据
s3 1 9 s2 20 100 s1 4 0 s0 100
系统稳定。 （2） （a）用劳思判据
系统不稳定。 （b）用古尔维茨判据
20 100
D1 20, D2 1
80 9
20 100 0
D3 1 9 0 8000 0 20 100
C(s) C(s) / R(s) N1 (s)
C(s) 1 (1 G1G2G3 G2 ) 1
N3 (s)
1 G1G2G3 G2
E(s) C(s) G2G3 G1G2G3 N1(s) N1(s) 1 G1G2G3 G2