主成分回归能消除多重共线性吗?
多重共线性的处理(主成分回归方法)-瑟嘉

本文主要是对多重共线性的处理(主成分回归法)的介绍。
1.思路:
A:确定是否存在共线
B:找出多重共线的自变量
C:用主成分回归法。
2:具体操作:
1)一般的书都有共线性的判断指标。
这里就省略了(^_^)
2)找出多多重共线性的自变量:
以下是具体操作:
在spss,regresion―――statistic中有个
Collinearty dagnostics,它就可以判断哪些变量是否存在共线性。
如,给出它的一个实例:
【变异构成(V ariance Proportion):回归模型中各项(包括常数项)的变异被各主成分所解释的比例,即各主成分对模型中各项的贡献。
如果模型中某个主成分对2个或多个自变量的贡献均较大(大于0.5),者这几个自变量贡献。
】
上面例子可以看出,x4,x6之间存在共线性。
3)主成分回归。
这个包括3部分:
A:找到主成分:用上面确定了有共线的几个变量拿来做成分分析,保留主成分得分。
(这个在factor中,应该狠容易实现吧,那我就省略了,^_^)
B:回归分析:将A步骤求得的主成分得分,与其他的自变量(没共线性的其他自变量)拿来做回归分析,当然会得到回归模型。
(MODEL,代表)
C:用那些共线性变量,来替换MODEL中的主成分变量.
(因为可以用主成分回归系数,根据主成分的表达式,很容易用自变量代替主成分)。
主成分回归克服多重共线性的R语言实现

主成分回归克服多重共线性的R语言实现作者:汪朋来源:《科技资讯》2015年第28期摘要:多重共线性是回归分析中容易出现的一类重要问题,现有的克服多重共线性的方法有很多,这其中主成分回归是非常有效的一种,但该方法计算复杂,必须借助于计算软件才能完成。
为此,本文在已有R函数的基础上,通过自编一定的R函数和代码,探讨了应用R语言实现主成分回归的过程。
最后的案例表明,通过R语言实现主成分回归来克服模型的多重共线性,过程简单,效果明显,且容易被学习者和应用者掌握。
关键词:主成分回归多重共线性 R语言中图分类号:文献标识码:A 文章编号:1672-3791(2015)03(b)-0000-001引言回归模型是应用最为广泛的统计模型之一,常被用来处理多变量间相依关系问题,而多重共线性问题是回归分析中一个非常棘手的问题,最早是R.Frisch提出。
大量实践表明,当模型存在严重的多重共线性时,模型的参数估计变得不够稳定,甚至出现估计的回归系数与其实际意义不相符,模型的显著性检验和预测功能失效等严重后果。
正因如此,从20世纪六七十年代至今,人们提出了多种方法来克服模型的多重共线性,比较常用的有逐步回归法、岭回归法和主成分回归法等。
逐步回归法是剔除变量,容易造成信息损失和结构分析的预期目的难以实现的问题;岭回归法要求选择比较准确的岭参数,而岭参数的选择主观性很强;相比之下,主成分回归法通过将自变量分解成几个不相关的主成分,能完全克服模型的多重共线性,且选择的主成分能基本上概括原变量的信息,使得主成分回归法成为克服多重共线性中的一种较为有效的方法,但该方法计算复杂,需要借助于计算软件才能完成。
目前主流的统计软件虽一般提供了主成分分析的功能,都基本上没有直接实现主成分回归的模块,因此,本文在R语言提供的主成分分析的函数的基础上,通过自编相关的函数,来探讨如何快速简便地运用主成分回归法克服回归模型的多重共线性。
二、主成分回归法的R语言实现过程主成分回归法是利用主成分分析找到解释变量的若干个主成份,由于主成份之间是互不相关的,因此考虑将被解释变量关于这些主成份进行回归,可以消除模型的多重共线性。
基于主成分回归的企业物流成本多元线性预测模型研究

基于主成分回归的企业物流成本多元线性预测模型研究随着现代物流技术的逐步发展,企业的物流成本越来越成为一个重要的成本项目。
为了准确地预测物流成本,合理规划物流成本预算,企业需要建立一个科学的成本预测模型。
基于主成分回归的企业物流成本多元线性预测模型,可以通过主成分分析,将多个相关性较高的指标合并成一个主成分,从而简化了成本预测模型中的多元线性回归分析。
本文通过对基于主成分回归的企业物流成本多元线性预测模型的研究进行浅析,探讨其优缺点及运用范围。
一、主成分回归的理论基础主成分回归(Principal Component Regression, PCR)是将主成分分析(Principal Component Analysis,PCA)与多元回归分析相结合的一种预测模型。
多元回归模型是指依据多个自变量和一个因变量之间的函数关系,来预测因变量的取值的模型。
主成分分析则是一种在数据预处理中使用的数据降维技术,它可以经过数学转换,将相关性较高的多个指标合并成一个主成分,从而减少数据的冗余信息。
如此一来,我们通过主成分分析可以减少自变量间的相关性,从而研究多个自变量与因变量之间的关系。
将主成分分析与多元回归分析相结合,即可构建主成分回归模型。
该模型的优点在于能够聚焦于重要的自变量,排除高相关性多余自变量的干扰。
二、基于主成分回归的企业物流成本预测模型企业物流成本预测的关键是确定影响物流成本的指标及其权重。
传统的多元线性回归模型通常基于回归系数,难以识别关键自变量。
而基于主成分回归的模型,既可以避免多重共线性的问题,又可以通过主成分权值修正各自变量的权重,有效降低了计算维度。
因此,基于主成分回归的企业物流成本预测模型是一个相对准确和有实际应用价值的预测模型。
对于企业物流成本这一指标,长期来看,常常受到运费、包装、仓储、物流设施等影响。
若用传统的多元线性回归模型来预测企业物流成本,可能出现自变量之间的共线性问题。
在多元回归分析中,如果自变量之间相关程度过高,则会影响模型可靠性,因为模型无法确定某个自变量和因变量之间真实的关系。
主成分回归多重共线性
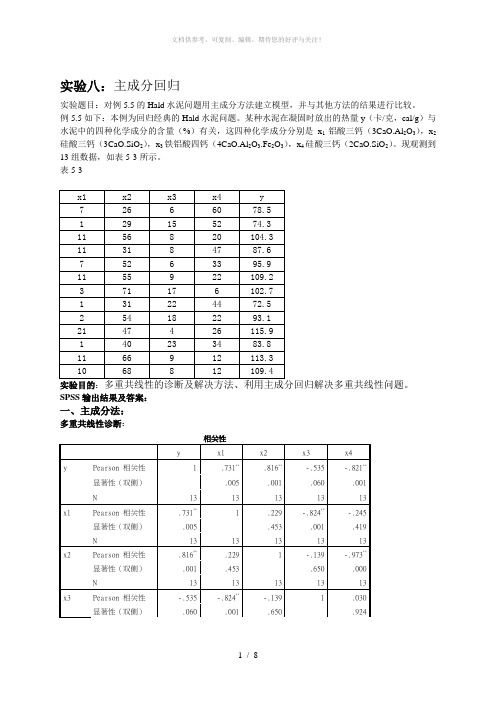
实验八:主成分回归实验题目:对例5.5的Hald水泥问题用主成分方法建立模型,并与其他方法的结果进行比较。
例5.5如下:本例为回归经典的Hald水泥问题。
某种水泥在凝固时放出的热量y(卡/克,cal/g)与水泥中的四种化学成分的含量(%)有关,这四种化学成分分别是x1铝酸三钙(3CaO.Al2O3),x2硅酸三钙(3CaO.SiO2),x3铁铝酸四钙(4CaO.Al2O3.Fe2O3),x4硅酸三钙(2CaO.SiO2)。
现观测到13组数据,如表5-3所示。
表5-3实验目的:SPSS输出结果及答案:一、主成分法:多重共线性诊断:N 13 13 13 13 13 x4 Pearson 相关性-.821**-.245 -.973**.030 1显著性(双侧).001 .419 .000 .924N 13 13 13 13 13**. 在 .01 水平(双侧)上显著相关。
由表可知,x1,x2,x4的相关性都比较大,较接近,所以存在多重共线性主成分回归:解释的总方差成份初始特征值提取平方和载入合计方差的 % 累积 % 合计方差的 % 累积 %1 2.236 55.893 55.893 2.236 55.893 55.8932 1.576 39.402 95.294 1.576 39.402 95.2943 .187 4.665 99.959 .187 4.665 99.9594 .002 .041 100.000 .002 .041 100.000提取方法:主成份分析。
输出结果显示有四个特征根,最大的是λ1=2.236,最小的是λ4=0.002。
方差百分比显示第一个主成分Factor1的方差百分比近56%的信息量;前两个主成分累计包含近95.3%的信息量。
因此取两个主成分就已经足够。
由于前两个主成分的方差累计已经达到95.3%,故只保留前两个主成分。
成份矩阵a成份1 2 3 4x1 .712 -.639 .292 .010x2 .843 .520 -.136 .026x3 -.589 .759 .275 .011x4 -.819 -.566 -.084 .027提取方法:主成分a.已提取了 4 个成份。
主成分回归分析

例3.10 影响电的需求量的指标有:(1)钢的产 量x1;(2)生铁产量x2;(3)钢材产量x3;(4)有色金 属产量x4;(5)原煤产量x5;(6)水泥产量x6;(7)机 械工业总产值x7;(8)化肥产量x8;(9)硫酸产量 x9;(10)烧碱产量x10;(11)棉纱产量x11共11个 指标。收集了23年的指标值,建立发电站需求 模型。(数据见spssex/ex310)
Y* X * e X *UU e 令 U Y * Z e
Y* Zcc e (c 1,2,...,q)
Y* 1Z1 2Z2 ...qZq
ˆc ZcZc 1 ZcY *
1
2
1 z1 y *1 1
4、再考虑最小特征根对应的特征向量, 找出绝对值最大的特征向量,剔除与之 对应的变量。
直至满足给定条件时停止。
5、将因变量与剩余变量作标准 化后的y与主成分的回归方程。 离差平方和分解:
yi* y 2
yi* yˆi* 2
归平方和。 找出偏回归平方和最小的主成分,其系 数向量中,最大的Uij所对应的自变量被 剔除。 找出次小的偏回归平方和,类似做之 最后将y*与剩下自变量做回归。
推荐阅读
期刊名及期数
财经研究 2002.1
数量经济技术经济研 究 2003.6
数量经济技术经济研 究 2003.12 统计研究 2004.2
Z1=0.3145*zx1+0.3027*zx2+0.3100*zx3+0.2782*zx 4+0.2518*zx5+0.3110*zx6+0.3116*zx7+0.3075*zx8 +0.3034*zx9+0.3145*zx10+0.3050*zx11
主成分分析多元回归分析

基于数据分析的决策更加科学和客观,能 够减少主观偏见和误判,提高决策的质量 和效果。
02 主成分分析
主成分分析的基本原理
降维思想
主成分分析是一种降维技术,通过线性变换将原始数据变 换为一组各维度线性无关的表示,可用于提取数据的主要 特征分量,常用于高维数据的降维。
方差最大化
主成分分析旨在找到数据中的主成分,这些主成分能够最 大化投影后的方差,从而保留数据中的主要变化性。
的。
02
去除多重共线性
在多元回归分析中,自变量之间可能存在高度相关,导致模型估计失真。
主成分分析可以提取出相互独立的主成分,作为多元回归模型的自变量,
从而消除多重共线性的影响。
03
降低维度
对于高维数据,直接进行多元回归分析可能面临维度灾难问题。主成分
分析通过降维技术,将高维数据转换为低维数据,使得多元回归分析更
聚类等任务的输入特征。
异常检测
通过计算数据在主成分上的投 影距离,可识别出偏离正常数
据模式的异常点。
03 多元回归分析
多元回归分析的基本原理
多元线性回归模型
通过建立一个包含多个自变量的线性方程,来预测因变量的值。模型形式为 Y=β0+β1X1+β2X2+…+βnXn,其中Y为因变量,X1, X2, …, Xn为自变量,β0, β1, β2, …, βn为回归系数。
研究不足与展望
在主成分分析中,我们通常需要选择 主成分的数量。然而,在实际应用中 ,如何选择合适的主成分数量是一个 具有挑战性的问题。未来研究可以进 一步探讨主成分数量的选择标准和方 法。
在多元回归分析中,模型的假设检验 和诊断是非常重要的步骤。然而,在 实际应用中,由于数据的不完整性和 复杂性,模型的假设可能无法满足。 未来研究可以进一步探讨如何在不满 足假设的情况下进行稳健的回归分析 。
回归分析中的多重共线性问题及解决方法(七)
回归分析是统计学中常用的一种方法,它用于研究自变量和因变量之间的关系。
然而,在实际应用中,经常会遇到多重共线性的问题,这给回归分析带来了一定的困难。
本文将讨论回归分析中的多重共线性问题及解决方法。
多重共线性是指独立自变量之间存在高度相关性的情况。
在回归分析中,当自变量之间存在多重共线性时,会导致回归系数估计不准确,标准误差增大,对因变量的预测能力降低,模型的解释能力受到影响。
因此,多重共线性是回归分析中需要重点关注和解决的问题之一。
解决多重共线性问题的方法有很多种,下面将介绍几种常用的方法。
一、增加样本量增加样本量是解决多重共线性问题的一种方法。
当样本量足够大时,即使自变量之间存在一定的相关性,也能够得到较为稳健的回归系数估计。
因此,可以通过增加样本量来减轻多重共线性对回归分析的影响。
二、使用主成分回归分析主成分回归分析是一种常用的处理多重共线性问题的方法。
主成分回归分析通过将原始自变量进行线性变换,得到一组新的主成分变量,这些主成分变量之间不存在相关性,从而避免了多重共线性问题。
然后,利用这些主成分变量进行回归分析,可以得到更为准确稳健的回归系数估计。
三、岭回归岭回归是一种经典的解决多重共线性问题的方法。
岭回归通过对回归系数施加惩罚项,从而减小回归系数的估计值,进而降低多重共线性对回归分析的影响。
岭回归的思想是在最小二乘估计的基础上加上一个惩罚项,通过调节惩罚项的系数来平衡拟合优度和模型的复杂度,从而得到更为稳健的回归系数估计。
四、逐步回归逐步回归是一种逐步选择自变量的方法,可以用来解决多重共线性问题。
逐步回归可以通过逐步引入或剔除自变量的方式,来得到一组最优的自变量组合,从而避免了多重共线性对回归系数估计的影响。
以上所述的方法都可以用来解决回归分析中的多重共线性问题。
在实际应用中,应该根据具体的情况选择合适的方法来处理多重共线性问题,从而得到准确可靠的回归分析结果。
总之,多重共线性是回归分析中需要重点关注的问题,通过合适的方法来处理多重共线性问题,可以得到更为准确稳健的回归系数估计,从而提高回归分析的预测能力和解释能力。
用主成分法解决多重共线性问题
用主成分法解决多重共线性问题一、多重共线性的表现线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系。
看似相互独立的指标本质上是相同的,是可以相互代替的,但是完全共线性的情况并不多见,一般出现的是在一定程度上的共线性,即近似共线性。
二、多重共线性的后果1.理论后果多重共线性是因为变量之间的相关程度比较高。
按布兰查德认为, 在计量经济学中, 多重共线性实质上是一个“微数缺测性”问题,就是说多重共线性其实是由样本容量太小所造成,当样本容量越小,多重共线性越严重。
多重共线性的理论主要后果:(1)完全共线性下参数估计量不存在;(2)近似共线性下OLS估计量非有效;(3)模型的预测功能失效;(4)参数估计量经济含义不合理2.现实后果(1)各个解释变量对指标最后结论影响很难精确鉴别;(2)置信区间比原本宽,使得接受假设的概率更大;(3)统计量不显著;(4)拟合优度的平方会很大;(5)OLS估计量及其标准误对数据微小的变化也会很敏感。
三、多重共线性产生的原因1.模型参数的选用不当,在我们建立模型时如果变量之间存在着高度的相关性2. 由于研究的经济变量随时间往往有共同的变化趋势,他们之间存在着共性。
例如当经济繁荣时,反映经济情况的指标有可能按着某种比例关系增长3. 滞后变量。
滞后变量的引入也会产生多重共线行,例如本期的消费水平除受本期的收入影响之外,还有可能受前期的收入影响,建立模型时,本期的收入水平就有可能和前期的收入水平存在着共线性。
四、多重共线性的识别1.方差扩大因子法( VIF)一般认为如果最大的VIF超过10,常常表示存在多重共线性。
2.容差容忍定法如果容差(tolerance)<=0.1,常常表示存在多重共线性。
3. 条件索引条件索引(condition index)>10,可以说明存在比较严重的共线性。
五、多重共线性的处理方法处理方法有多重增加样本容量、剔除因子法、PLS(偏最小二乘法)、岭回归法、主成分法。
偏最小二乘回归
偏最小二乘回归偏最小二乘回归(Partial Least Squares Regression,简称PLSR)是一种主成分回归方法,旨在解决多元线性回归中自变量数目较多,且存在共线性或多重共线性的问题。
本文将介绍偏最小二乘回归的原理、应用案例以及优缺点。
1. 偏最小二乘回归原理偏最小二乘回归是基于多元线性回归的一种方法,通过压缩自变量的空间,将高维的自变量转化为低维的潜在变量,从而避免了多重共线性的问题。
在偏最小二乘回归中,我们定义两个主成分,其中第一个主成分能最大化自变量与因变量之间的协方差,而第二个主成分垂直于第一个主成分,以此类推。
2. 偏最小二乘回归应用案例偏最小二乘回归在众多领域都有广泛的应用。
以下是一些常见的应用案例:2.1 化学分析在化学领域中,我们常常需要使用红外光谱仪等仪器进行样本的分析。
然而,由于样本中存在大量的杂质,导致光谱数据存在共线性等问题。
通过偏最小二乘回归可以降低样本数据的维度,提取出有用的信息,从而准确地进行化学成分的分析。
2.2 生物医学在生物医学领域中,研究人员常常需要通过大量的生理指标预测某种疾病的发生风险。
然而,由于生理指标之间存在相互关联,使用传统的线性回归模型时,很容易出现共线性的问题。
通过偏最小二乘回归,可以降低指标的维度,减少共线性对预测结果的影响,提高疾病预测的准确性。
2.3 金融领域在金融领域中,偏最小二乘回归也有广泛的应用。
例如,在股票市场的分析中,研究人员常常需要通过一系列宏观经济指标预测股票的涨跌趋势。
然而,这些指标之间往往存在较强的相关性,导致传统的回归模型难以提取出有效的信息。
通过偏最小二乘回归,可以从多个指标中提取出潜在的主成分,预测股票的涨跌趋势。
3. 偏最小二乘回归的优缺点3.1 优点(1)解决了多重共线性问题:偏最小二乘回归通过降低自变量的维度,有效地解决了多重共线性问题,提高了模型的稳定性和准确性。
(2)提取了潜在的主成分:通过偏最小二乘回归,我们可以从高维的自变量中提取出潜在的主成分,这些主成分更具有解释性,有助于理解自变量与因变量之间的关系。
主成分回归分析
05
主成分回归分析的未来发展与展望
算法改进与优化ຫໍສະໝຸດ 算法并行化利用多核处理器或分布式计算环境,将主成分回归分析算法并行 化,以提高计算效率和准确性。
优化特征选择
研究更有效的特征选择方法,自动确定主成分的数量,减少计算复 杂度和过拟合的风险。
集成学习与机器学习
结合集成学习、深度学习等机器学习方法,改进主成分回归分析的 模型性能和泛化能力。
跨领域应用拓展
生物医学研究
将主成分回归分析应用于生物医学领域,如基因表达数据分析、 疾病预测和个性化医疗。
金融市场分析
利用主成分回归分析对金融市场数据进行降维和预测,为投资决 策提供支持。
环境监测与保护
将主成分回归分析应用于环境监测数据,评估环境质量、预测污 染趋势,为环境保护提供科学依据。
数据隐私与安全问题
02
主成分解释性差
03
对异常值敏感
提取的主成分可能难以直观地解 释其含义,导致模型的可解释性 降低。
主成分分析对异常值较为敏感, 异常值可能会对主成分的提取造 成影响。
03
主成分回归分析的步骤
数据预处理
数据清洗
去除异常值、缺失值和重复值,确保数据质量。
数据转换
对数据进行标准化或归一化处理,使不同量纲的 数据具有可比性。
保留信息
通过主成分分析,可以保留原始自变 量中的大部分信息,避免了信息损失。
主成分回归分析的优势与局限性
• 改善共线性:对于存在高度共线性的自变 量,主成分回归分析能够消除共线性影响, 提高模型的稳定性和预测能力。
主成分回归分析的优势与局限性
01
假设限制
主成分回归分析要求因变量与主 成分之间存在线性关系,对于非 线性关系的数据可能不太适用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
法得 到 了学者 们 的重 视 , 者 手 头有 的 8本 包 含 有 作
多重 共线 性 内容 的《 量 经 济 学 》 材 中 , 6本 提 计 教 有
到 主 成 分 回 归 , 中 有 3本 作 了 比较 详 细 的 论 其 述 [9 1,] [ 8 0[蚰 。 ]- 3 ] 。早 在 1 9 9 6年 , 惠 文 和 王 朱 韵华 就指 出 : 目前 , 些研 究文 献 提 出 , “ 一 利用 主成
一
、
引 言
中 ,00 2 1 年期 间“ 名 ” 20 - 0 1 题 中含 有“ 主成 分 回归 ”
的论 文 就有 1 1篇之 多 。 2
在 计 量 经 济模 型 的应 用 中 , 重共 线 性 问题 是 多 经 常碰 到 的 , 别是 当解释 变量 的个 数较 多 时 , 特 常常 会 存 在严 重 的多重 共线 性 。当存在 严重 的 多重共 线
二 、 拟 计 算 的模 型及 计 算 方 法 模
为比较主成分 回归估计与普通最小二乘估计的
误 差 大小 , 作者 选取 了大 量 的模型 进行 了模 拟计 算 , 本 文 选择 3 假设 模 型予 以说 明 。 17 — 1 9 年 个 取 98 98 全 国居 民消费 额 X ( 元 ) 政 府 消 费 额 z ( 元 ) 亿 、 z亿 、 铁路 客 运 量 z ( 人 ) 来 华 旅 游 入 境 人 数 - ( 。万 、 z 万
模型1各种回归估计量的均值标准差与误差标准差表最小二乘回归或5个主成分回归系数b0b1b2b3b4b5均值99389005990099500020150015036标准差58036006150327200060116296182误差标准差580370061503272000601162961781个主成分回归系数15均值13336004190165800060255410974标准差608260001000039000010006102604误差标准差3391200182006590003601056403392个主成分回归系数25均值13430004190165800060255310974标准差43181000100004000410007602604误差标准差5514200182006590005601056403403个主成分回归系数35均值10751004900187700020181610742标准差55129000910028000580093603936误差标准差5563600143009200005900988427634个主成分回归系数45均值10076004400186400020158413078标准差57780015700282000600111861053误差标准差577820022400909000600112164003模型2各种回归估计量的均值标准差与误差标准差表最小二乘回归或5个主成分回归系数b0b1b2b3b4b5均值19990139701627012000021228464标准差577530061503242000600114394597误差标准差577500615032420006001143946051个主成分回归系数15均值10623004590181700060279912027标准差600620001000038000010005902538误差标准差1262300941002200126202600903052个主成分回归系数25均值5591004190166101015040341216标准差435480001000039000420007602539误差标准差1505300981000730019003834916393个主成分回归系数35均值2299008810308401226007610650标准差545870008900274000580091703
叶 宗裕
( 江师范大学 经济与管理学院 , 江 金 华 3 1 0 ) 浙 浙 2 0 4 摘要 : 主成 分 回归方法 已得到广泛应 用 , 但该方 法是否 能减小参 数估 计 的误 差 , 理论上 并没 有明确 的结 论 。以 3个假设模型为例 , 运用模拟计算 的方 法对主成 分 回归方 法进行 了研究 , 发现主成分 回归估计 的误差
可能 比普通最小二 乘估计更 小 , 可能更 大 , 也 依赖 于实际 的模 型。
关键词 : 主成 分 回归 ; 拟计算 } 模 偏倚 ; 误差
中图 分 类 号 : 1 O2 2 文 献 标 志码 : A 文 章 编 号 :0 7 3 1 (0 20 一O 1 一O 10 - 1 6 2 1 )3 0 6 5
二 乘估 计 的误 差?实 际 上这在计 量 经济学 文献 中并
没有 给 出 明确 的结 论 , 目前 也 不 可 能给 出严 密 的逻
OL S估 计 量 的 准 确 度 大 大 下 降 。估 计 量 的标 准 差 增 大会 导致 估计 量 的 t 计 量 值 减 小 , 很 可 能 使 统 这 原 来 显著 的 t 变 成 不 显 著 的 , 值 即容 易 将 有 重 要 影
也 可 能更 大 。
的变 化也 可能 使 估 计 值 发 生 很 大 变 化 。可 以看 出 , 严重 的多重共 线 性 使 OI S估计 量 标 准 差 急 剧 增 大
是最 根本 的问题 。对 多 重 共 线性 问题 , 今 为止 还 迄 没有 理想 的解 决 方 法 。最 近几 年 来 , 主成 分 回归 方
关 系模型为以下 3 : 种
作者简 介: 叶宗裕 , , 男 浙江江 山人 , 教授 , 研究方 向: 统计学 与计 量经济学 。
1 6
叶宗裕 : 主成分 回归能消除多重共线性吗 ?
模 型 1Y :
一
10 0+ 0 0 xn+ 0 1 2一 0 .6 . x 0 0 2 3 + 0 1 x t 1 x5+ 地 . 0 xr . 5 4+ 5 I () 1
分分析消除多重共线性 的作用 , 这实际上是一种错 误观念 。事实上 , 无论是从数量上还是从方向上 , 主
成分 分析 都无 法 消除 变量 的多重共 线 性”4。但 是 , [ ] 主 成分 回归方 法 还 是 被广 泛应 用 , 中国 期 刊全 文 在
人)民 7 期
V0 7 No 3 L2 .
统 计 与 信 息 论 坛
Sai is& Ifr t nF r m tt t sc nomai ou o
21 0 2年 3月
Ma, 2 1 r ,0 2
【 计理 论与 方法】 统
主 成 分 回 归能 消除 多重 共 线性 吗 ?
同时, y关 于 z , 。…,s 将 z , 用普通最/ - 乘 b 法 回归求得系数估计值 b, . b 。 ob . 容易知道 , ' 当 m=5 , 时 主成分回归与最小二乘 回归 的估计值相
引 自文献[] 1 中的例 3 。 l 、tX 之间的相关 —6X 、 z 、s
系数都在 0 9 .3以上 , 说明解释变量之间存在严重 的
多重 共线 性 。 设 被解 释 变 量 Y与 解 释 变量 之 间 的 假
数据库和中国优秀博 士硕 士学位论 文全文数据库
收稿 日期 :0 1 O 6 2 1 —1 一2
性 时 , S估 计 量 的 方 差 和 标 准 差 急 剧 增 大 , OL 即
我 们 不禁 要 问 , 成 分 回归 是 否 能够 解 决 多重 主 共线 性 问题 , 使 模 型参 数 的估 计 更加 准确 吗 ? 即 能
用 主成 分 回归所 估计 参数 的误 差是 否小 于普通 最小
响 的变量 误认 为不 显 著 的变量 , 会导致 OL 还 S估 计 量对 样本 数据 的变化 非 常 敏感 , 即样 本 数 据 有 微 小
辑 推导 。对 这类 问 题 , 模 拟计 算 的方 法 进行 研 究 用
能收到很好的效果 , 能使我们对一些计量经济学方
法 有更 深 入 的认 识 。作 者 运 用 模 拟 计 算 的方 法 对 1 0多个各 种 不 同的假设 模 型进 行 了研 究 , 现 主 成 发 分 回归估计 的误差 可 能 比普通 最 小 二 乘 估计 更 小 ,
