单项式多项式概念讲解.
单项式和多项式的例子

单项式和多项式的例子
在代数学中,单项式和多项式是常见且重要的概念。
单项式是指只含有一个项的代数表达式,而多项式则是含有两个或多个项的代数表达式。
本文将通过一些具体的例子来说明单项式和多项式的定义和特点。
首先,我们来看一个单项式的例子。
假设有一个代数表达式:
3x^2。
这个表达式只含有一个项,项中的系数为3,指数为2。
因此,3x^2是一个单项式。
在这个例子中,x^2是变量的平方,3是系数。
单项式可以含有任意多个变量和常数的乘积,但只能有一个变量的某个次幂,且系数只能是实数。
接下来,我们再来看一个多项式的例子:2x^3+4x^2-5x+
1。
这个表达式含有四个项,分别是2x^3、4x^2、-5x和1。
在这个例子中,每个项都是一个单项式。
多项式可以由多个单项式相加或相减而得到。
每个单项式的指数可以是正整数、负整数或零,每个单项式可以有不同的系数。
单项式和多项式在代数学中有着广泛的应用。
它们可以用来表示各种数学关系和问题,并且在解方程、因式分解、多项式运算等方面具有重要作用。
通过对单项式和多项式的研究和掌握,我们可以更好地理解和运用代数学知识。
总结起来,单项式是指只含有一个项的代数表达式,而多项式是含有两个或多个项的代数表达式。
它们在代数学中起着重要的作用,并且可以通过各种例子来进一步理解其定义和特点。
希望通过本文所提供的例子,读者对单项式和多项式有更加清晰的认识。
代数式整式单项式多项式的概念

代数式整式单项式多项式的概念嘿,朋友们,今天咱们来聊聊那些看似复杂的代数式、整式、单项式和多项式。
别紧张,听起来高大上,其实就像咱们平时聊聊天一样。
代数式,顾名思义,就是用字母组合成的一种表达式。
听起来是不是有点晦涩?别担心,咱们就把它当成一个神秘的拼图,每块拼图都有它的价值。
你可以把数字当作是坚固的砖块,而字母呢,就是这些砖块之间的连接线。
它们一起构建了我们日常生活中许多数学现象,比如说,计算购物的总价,或者说规划旅行的距离。
整式,就是那种没有分母的代数式。
你看,它就像是一种豪华套餐,所有的东西都在一个大盘子里。
比如,咱们可以看到 (3x + 5) 这样的整式,简单又好懂。
只要你不把这个大盘子里的东西搞得七零八落,它就会很乖巧地待在那里,等着你去利用。
想象一下,整式就像一个乖孩子,永远在你的掌控之中,不会像那些让人头疼的分式和根式那样来回折腾。
再说说单项式,嘿,这可有意思了!单项式就是只有一个项的代数式,像极了独自喝饮料的小伙伴。
想象一下,(7y^2) 就是一个典型的单项式,简单明了,就像你路边看到的那家小摊,只卖一种饮料,纯粹而不复杂。
它的特点就是专一,专心致志地为某个变量服务。
你要是把单项式比作一个人的话,那绝对是个一心一意的小家伙,绝不会在意那些旁的花花草草。
然后我们来聊聊多项式。
多项式就像一个派对,里面有很多个项。
你看看 (2x^3 + 3x^2 x + 4),这简直就是个热闹的大家庭!每个项就像家庭成员,各自有各自的性格,有的高调、有的低调,却又和谐共处。
多项式的魅力就在于它的多样性,像是你去超市购物,总能找到各种你喜欢的东西。
这些项之间的相互作用会产生出许多有趣的效果,真的是让人耳目一新!你说,代数式、整式、单项式和多项式,怎么就能在我们的生活中扮演如此重要的角色呢?想想你每天的开销,购物清单上的每一项其实都可以用代数式来表示。
你要买三斤苹果,每斤五块钱,那就是 (3 times 5 = 15) 的整式。
单项式多项式概念讲解

单项式与多项式的概念1、单项式的有关概念(1)单项式:由数与字母或字母与字母相乘组成的代数式。
单独的一个数或字母.........也叫做单项式。
例如:a x abx n m a ,9,4,,,332-注意:单项式不含加减运算,只含字母与字母或字母的乘法〔包括乘方〕运算 (2)单项式的系数:单项式中数字因数叫做这个单项式的系数。
例如:单项式227,21xy y x -的系数分别是7,21-,当单项式系数是1或-1时,“1〞通常省略不写,如ab 就是ab ⋅1,系数是1;n -就是n ⋅-1,系数是-1.(3)单项式的次数〔指数〕:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
如x 4的次数是1,z y x 323的次数是2+3+1=6;数学的次数是0,如3,-9等可以当作0次单项式。
一个单项式的次数是几就叫做几次单项式,如2231b a 中,a 与b 的指数和为4,那么2231b a 是四次单项式。
例1:指出以下各单项式的系数和次数7,,5,332322y x bc a ab a π- 提示:圆周率π是常数,当单项式中含有π时,π是单项式的系数,且在计算单项式的次数时应注意不要加上π的指数。
2、多项式的有关概念(1)多项式:几个单项式的和叫做多项式。
其中,每个单项式叫做多项式的项,不含字母的项叫做常数项。
如5232+-x x 是多项式,它的项分别是23x ,x 2-和5,其中5是常数项。
(2)多项式的次数:多项式里次数最高的项的次数就是这个多项式的次数。
如23224+-x y 的次为是3,即“32x 〞的次数。
一个多项式中含有几项,最高次数是几次就叫几次几项式。
如66234+-y y 叫做四次三项式。
在多项中,含有字母的项的次数是几次就叫做几次项。
如5232-+-b ab b a 中,b a 23就是它的三次项,二次项是ab 2-,一次项是b ,常数项是-5.〔3〕多项式的排列:把一个多项式按某一个字母的指数从大到小的顺序排列叫降幂排列;反之,那么称为升幂排列。
第二章 第一节 单项式和多项式
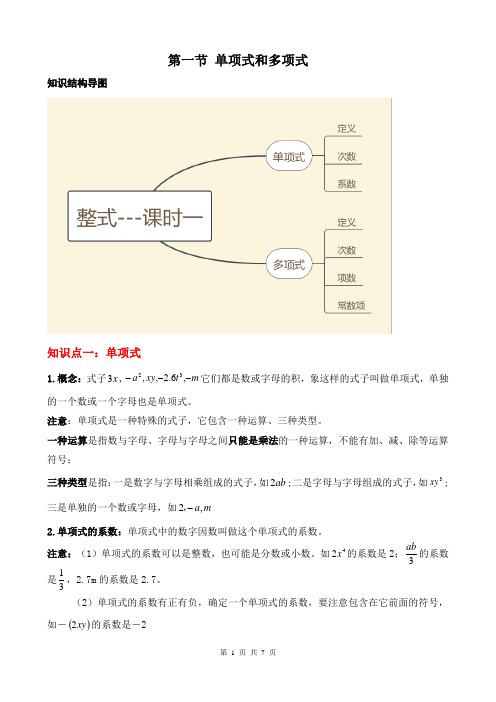
第一节 单项式和多项式知识结构导图知识点一:单项式1.概念:式子x 3,m t xy a ---,6.2,,32它们都是数或字母的积,象这样的式子叫做单项式,单独的一个数或一个字母也是单项式。
注意:单项式是一种特殊的式子,它包含一种运算、三种类型。
一种运算是指数与字母、字母与字母之间只能是乘法的一种运算,不能有加、减、除等运算符号;三种类型是指:一是数字与字母相乘组成的式子,如ab 2;二是字母与字母组成的式子,如3xy ;三是单独的一个数或字母,如m a ,2-,2.单项式的系数:单项式中的数字因数叫做这个单项式的系数。
注意:(1)单项式的系数可以是整数,也可能是分数或小数。
如42x 的系数是2;3ab 的系数是31,2.7m 的系数是2.7。
(2)单项式的系数有正有负,确定一个单项式的系数,要注意包含在它前面的符号,如-()xy 2的系数是-2(3)对于只含有字母因素的单项式,其系数是1或-1,不能认为是0,如-2xy 的系数是-1;2xy 的系数是1。
(4)表示圆周率的π,在数学中是一个固定的常数,当它出现在单项式中时,应将其作为系数的一部分,而不能当成字母。
如2πxy 的系数就是2π3单项式的次数:一个单项式中,所有字母的指数和叫做这个单项式的次数。
注意:(1)计算单项式的次数时,应注意是所有字母的指数和,不要漏掉字母指数是1的情况。
如单项式z y x 342的次数是字母z y x ,,的指数和,即4+3+1=8,而不是7次,应注意字母Z 的指数是1而不是0.(2)单项式是一个单独字母时,它的指数是1,如单项式m 的指数是1,单项式是单独的一个常数时,一般不讨论它的次数。
(3)单项式的指数只和字母的指数有关,与系数的指数无关。
如单项式-43242z y x 的次数是2+3+4=9而不是13次。
(4)单项式通常根据单项式的次数进行命名。
如x 6是一次单项式,xyz 2是三次单项式。
例题:下列说法正确的是( )A .单项式23x -的系数是3-B .单项式3242π2ab -的次数是7 C .1x是单项式 D .单项式可能不含有字母检测:1、判断下列各代数式是不是单项式?若是,写出它的系数与次数。
单项式与多项式

2x 3y n-1 是关于x、y的 例2.如果(m+1) 6次单项式,则m、n应满足什么条件?
类型二:确定单项式的系数和次数
3 例1.多项式2 -9x y 2+7x 2 y3-x 4-x 的次数 是( ) A、 15次 B、 6次 C 、 5次 D 、4次
8
类型二:确定单项式的系数和次数
例2. 如果5x n +(m-1)x+6是关于x的三次二项 式,求m 2 - n 2 的值.
知识点回顾
概念:由数字或字母的积组成的式子叫单项式, 单独的一个数或一个字母也是单项式 系数:单项式中的数字因数
单项式 整式
次数:单项式中所有字母指数的和 概念:几个单项式的和
多项式
项:多项式里每个单项式叫这个多项式的项, 不包含字母的项叫常数项 次数:单项式中所有字母指数的和
概念辨析
1.下列代数式中,哪些是整式?哪些是单项式?哪些 是多项式?
x 2
解:单项式有: 多项式有: 整式有:
s t
1 x +y
2x+y
2a + b 3
概念辨析
2.下列多项式各由哪些项组成?各是几次多项式?
3x-7
3
x -3x+4
ab-a -1正确: ①1x ②-1x ③a ×3 ④a ÷2 ⑤ 1 1 xy 2 m的系数为1,次数为0 4 2πr的系数是2,次数为2
类型二:确定单项式的系数和次数
2 -k 不包xy项, 例3. 若多项式x2 +3(k-1)xy+y 求k的值.
类型一:确定单项式的系数和次数
例1填空:
(1)b的系数是______,次数是_______;
(2) 单项式310m6系数是____,次数是____;
第三单元 第1讲 单项式和多项式的认识 教师版

单项式和多项式的认识1、理解代数式,单项式,多项式以及整式的含义.2、会区分单项式和多项式,知道什么是项什么是系数.1、单项式和多项式的区分.2、单项式,多项式的系数次数问题.1.代数式的概念:用基本的运算符号(运算包括加、减、乘、除、乘方与开方等)把数和表示数的字母连接起来的式子叫做代数式.单独的一个数或一个字母也是代数式.【注意】代数式中可以含有加、减、乘、除、乘方、开方等运算符号,不可含有"="、"≠"、">"、"<"等表示相等或不等关系的符号.代数式的书写要求:①数与字母、字母与字母相乘时常省略“×”号或用“⋅”.【注意】数字与数字相乘,仍使用"×",不用"⋅",更不能省略乘号.②数字通常写在字母前面.③当字母前面的数字为1或−1时,把数字1省略.④带分数与字母相乘时要化成假分数.⑤相同的字母的积用乘方表示.⑥在代数式中出现除法运算时,一般要书写成分数的形式.⑦在实际问题中需用单位时,若代数式的最后结果含有加、减运算,则需要把整个式子用括号括起来,再写单位,否则可直接写单位.列代数式:把问题中与数量有关的词语,用含有数、字母和运算符号的式子表示出来,这就是列代数式.单项式的定义:数或字母的积叫做单项式,单独的一个数或一个字母也是单项式.【注意】如果含有分母,分母中是数字的式子是单项式,分母中含有字母的式子不是单项式.单项式的系数:单项式中的数字因数叫做这个单项式的系数.单项式表示数字与字母相乘时,通常把数写在前面.【注意】①一个单项式只含有字母因数,它的系数就是1或-1.②一个单项式只含有数字因数,它的系数就是它本身.③负数作系数时,应包括前面的符号.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.【注意】①一个单项式只含有数字因数且非0,它的次数是0.②一个单项式的次数是几,这个单项式就是几次单项式.多项式的定义:几个单项式的和叫做多项式.其中,每个单项式叫做多项式的项,不含字母的项叫做常数项。
单,多项式讲义

单项式、多项式讲义 知识点梳理概念:单项式:即由_____与______的乘积组成的代数式称为单项式。
单独_________或___________也是单项式,如a ,5。
一个单项式中,_____________的指数的和叫做这个单项式的次数;单项式中的数字因数称为这个单项式的________①圆周率π是常数; ②单项式次数只与字母指数有关。
书写要求:1.数字写在字母的前面,省略乘号。
[5a 、16xy ]2.单项式分母不能为字母。
(否则为分式,不为单项式)3.π是常数,所以应作为系数。
4.若系数是带分数,要化成假分数。
[x 27x 213=] 5.但一个单项式的系数是1或-1时,“1”通常省略不写。
如[(-1)ab ]写成[ -ab ]6.在单项式中字母不可以做分母,分子可以。
7.常数的次数为0。
多项式:几个单项式的和叫做多项式。
每个单项式叫做多项式的项.不含字母的项,叫做常数项。
个多项式含有几项,就叫几项式.多项式里,次数最高项的次数,就是这个多项式的次数.特别注意: (2)多项式的每一项都包括它前面的符号。
典型例题例1判断下列各代数式哪些是单项式?(1)21+x ; (2)abc ; (3)b 2; (4)-5ab 2; (5)y ; (6)-xy 2; (7)-5。
变式:2x ,-4x , 31a +0.5b , 32xy, x 1,m ,-ab ,-21. 例2指出以下单项式的系数:3x 2,-0.6x 2y 3z ,a 2b ,-2.15ab 3,-m 3,0.12h .变式:下面各题的判断是否正确(1)-7xy 3的系数是7; (2)-x 2y 3与x 3没有系数;(3)-ab 3c 6的次数是0+3+6; (4)-a 3的系数是-1;(5)-32x 2y 3的次数是7; (6)2∏r 2h 的系数是2。
能力提升一、判断题.(对的打“∨”,错的打“×”)1.x 是单项式.( )2.6不是单项式.( )3.m 的系数是0,次数也是0.( )4.单项式4πxy 的系数是4π,次数是2.( ) 二、填空题.5.x 2yz 的系数是________,次数是________.6.-372ab 的系数是______,次数是_______. 7.如果单项式-2x 2y n 与单项式a 4b 的次数相同,则n =________.8.写出系数为5,含有x 、y 、z 三个字母且次数为4的所有单项式,它们分别是____ ___.三、选择题.9.下列各式中单项式的个数是( ).3x ,x +1,-212,-1,0.72,42a x xy -. A .2个 B .3个 C .4个 D .5个10.单项式-x 2yz 2的系数、次数分别是( ). 0.2 B .0.4 C .-1,5 D .1,4典型例题例1:指出下列多项式的项和次数:(1)3x -1+3x 2; (2)4x 3+2x -2y 2。
单项式多项式概念讲解

单项式多项式概念讲解单项式与多项式的概念1、单项式的有关概念(1)单项式:由数与字母或字母与字母相乘组成的代数式。
单独的一个数或字母.........也叫做单项式。
例如:a x abx n m a ,9,4,,,332- 注意:单项式不含加减运算,只含字母与字母或字母的乘法(包括乘方)运算(2)单项式的系数:单项式中数字因数叫做这个单项式的系数。
例如:单项式227,21xy y x -的系数分别是7,21-,当单项式系数是1或-1时,“1”通常省略不写,如ab 就是ab ⋅1,系数是1;n -就是n ⋅-1,系数是-1.(3)单项式的次数(指数):一个单项式中,所有字母的指数的和叫做这个单项式的次数。
如x 4的次数是1,z y x 323的次数是2+3+1=6;数学的次数是0,如3,-9等可以当作0次单项式。
一个单项式的次数是几就叫做几次单项式,如2231b a 中,a 与b 的指数和为4,则2231b a 是四次单项式。
之,则称为升幂排列。
例 2 、已知多项式y x xy 514322--,试按下列要求将其重新排列(1)按字母x 作降幂排列;(2)按字母y 作升幂排列3、整式的概念单项式与多项式统称为整式判断一个式子是不是整式应注意几点(1)分母不含字母;(2)根号里面不含字母①单项式②多项式4、几种约定俗成的读与写 (1)字母与数字相乘,或字母与字母相乘,乘号不用“⨯”,而是用“⋅”,或省略不写,如“a 4乘以b ”可写成“b a ⋅4”或“ab 4”。
但数字与数字相乘一般用“⨯”,且不得省略,如“34⨯”不能简写成“43”或“34⋅”(2)字母与数字相乘,一般数字写在字母之前,如“n m 235”不要写成“352n m ”;系数为带分数的,一般写成假分数,如“213与2x 的积”写成“227x ”而不写成“2213x ”,以免造成混淆。
(3)多项式中,“a 与b 的差”是指“b a -”,而不是“a b -”“a 、b 的平方和”是指“22b a+”,而不是“2b a +” “a 与b 的平方的差”是指“2b a -”,而不是“22b a -”“a 与b 的差的立方”是指“3)(b a -”,而不是“3b a -”例1:指出下列各式中,哪些是单项式,哪些是多项式,哪些是整式?π2222222,5,52,71,19,3,,r R x x x x n m xy b a x y x -+--++-+例2、多项式5)13(72++-+x n kx xm 是关于x 的三次三项式,并且一次项系数为-7,求m+n-k 的值变式:已知多项式63512212--+-+x xy y x m 是六次四项式,单项式m n y x -523与该多项式的次数相同,那么m 、n 的值分别为( )A 、5,3B 、3,2C 、2,1D 、0,21例3、(1)某班共有x 个学生,其中女生人数占45%,用代数式表示该班的男生人数是(2)某商品的原价为100元,如果经过两次降价,且每次降价的百分率都是m ,那么该商品现在的价格是 元(结果用含m 的代数式表示)课堂训练1、多项式134223--y x x是几次几项式;并说出最高次项和常数项是什么?2、把多项式3322543y x xy y x -+-重新排列;(1)按y 的降幂排列;(2)按x 的升幂排列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单项式与多项式的概念
1、单项式的有关概念
(1)单项式:由数与字母或字母与字母相乘组成的代数式。
单独的一个数或字母也叫做单项式。
例如:3a,-m2n,abx,4x3,9,a
注意:单项式不含加减运算,只含字母与字母或字母的乘法(包括乘方)运算
(2)单项式的系数:单项式中数字因数叫做这个单项式的系数。
例如:单项式1
2
x2y,-7x y2
的系数分别是1
2
,-7,当单项式系数是1或-1时,“1”通常省略不写,如ab就是1⋅ab,
系数是1;-n就是-1⋅n,系数是-1.
(3)单项式的次数(指数):一个单项式中,所有字母的指数的和叫做这个单项式的次数。
如4x的次数是1,3x2y3z的次数是2+3+1=6;数学的次数是0,如3,-9等可以当作0次单项式。
11
一个单项式的次数是几就叫做几次单项式,如a2b2中,a与b的指数和为4,则a2b2是
33
四次单项式。
例1:指出下列各单项式的系数和次数
aπx2y3
-,5ab2,a2bc3,
37
提示:圆周率π是常数,当单项式中含有π时,π是单项式的系数,且在计算单项式的次数时应注意不要加上π的指数。
2、多项式的有关概念
(1)多项式:几个单项式的和叫做多项式。
其中,每个单项式叫做多项式的项,不含字母的项叫做常数项。
如3x2-2x+5是多项式,它的项分别是3x2,-2x和5,其中5是常数
项。
(2)多项式的次数:多项式里次数最高的项的次数就是这个多项式的次数。
如2y4-3x2+2的次为是3,即“2x3”的次数。
一个多项式中含有几项,最高次数是几次就叫几次几项式。
如2y4-6y3+6叫做四次三项式。
在多项中,含有字母的项的次数是几次就叫做几次项。
如3a2b-2ab+b-5中,3a2b 就是它的三次项,二次项是-2ab,一次项是b,常数项是-5.
(3)多项式的排列:把一个多项式按某一个字母的指数从大到小的顺序排列叫降幂排列;反之,则称为升幂排列。
例2、已知多项式3xy2-4x2-列;(2)按字母y作升幂排列1
5
y,试按下列要求将其重新排列(1)按字母x作降幂排
3、整式的概念
单项式与多项式统称为整式
判断一个式子是不是整式应注意几点(1)分母不含字母;(2)根号里面不含字母
整式
①单项式
②多项式
代
数
式
分式
根式
4、几种约定俗成的读与写
(1)字母与数字相乘,或字母与字母相乘,乘号不用“⨯”,而是用“⋅”,或省略不写,如“4a乘以b”可写成“4a⋅b”或“4ab”。
但数字与数字相乘一般用“⨯”,且不得省略,如“4⨯3”不能简写成“43”或“4⋅3”
(2)字母与数字相乘,一般数字写在字母之前,如“35m2n”不要写成“m2n35”;系数
为带分数的,一般写成假分数,如“3171
与x2的积”写成“x2”而不写成“3x2”,以222
免造成混淆。
(3)多项式中,“a与b的差”是指“a-b”,而不是“b-a”
“a、b的平方和”是指“a2+b2”,而不是“a+b2”
“a与b的平方的差”是指“a-b2”,而不是“a2-b2”
“a与b的差的立方”是指“(a-b)3”,而不是“a-b3”
例1:指出下列各式中,哪些是单项式,哪些是多项式,哪些是整式?
a+b15R2-r2
x2+y2,-x,,9x y+1,m2n,2x2-x-5,,
37x2+xπ
例2、多项式7x m+kx2-(3n+1)x+5是关于x的三次三项式,并且一次项系数为-7,求m+n-k的值
变式:已知多项式-1
5
x2y m+1+xy2-3x2-6是六次四项式,单项式3x2n y5-m与该多项式
的次数相同,那么m、n的值分别为()
A、5,3
B、3,2
C、2,1
D、0,1 2
例3、(1)某班共有x个学生,其中女生人数占45%,用代数式表示该班的男生人数是(2)某商品的原价为100元,如果经过两次降价,且每次降价的百分率都是m,那么该商品现在的价格是元(结果用含m的代数式表示)
课堂训练
1、多项式4x3-3x2y2-1是几次几项式;并说出最高次项和常数项是什么?
((
2、把多项式3x2y-4x y2+x3-5y3重新排列;1)按y的降幂排列;2)按x的升幂排列。
3、(3m-2)x2y n+1是关于x、y的系数为1的5次单项式,则m-n2的值
4、已知多项式-数相同,求m、n 1
5
x2y m+1+xy2-3x3-6是六次四项式,单项式3x2n y5-m与该多项式的次
5、已知4a4b m与-7
2
a n+3b2是同类项,求m、n的值
31
6、已知3x m-1-2x m+1-6x m+是关于x的三次四项式,求当x=-时,这个多项式的值
42
7、若当x=1时代数式ax3+bx+7的值为4,则当x=-1时,代数式ax3+bx+7
10、x 已-知 a x 、b 1 互2[3相反(5 -,4c,d )]} 的值。
,m 的绝对值是 2,若 x = 2a + 2b
8、代数式 3x 2 - 4 x + 6 的值为 9,则 x 2 - 4 3
x + 6 的值。
9、一个三位数,把它百位上的数字与个位上的数字对调,得到一个新的三位数,试说明原
来的三位数与新的三位数的差一定能被 11 整除。
1 求 5 {
2 + - 为 x + 数 x 互为倒数 + cd - m 2, m 2。
