材料力学002第二章轴向拉压与剪切
材料力学(机械类)第二章 轴向拉伸与压缩

二
章
拉伸压缩与剪切
1
பைடு நூலகம்
§2-1
轴向拉伸与压缩的概念和实例
轴向拉伸——轴力作用下,杆件伸长 (简称拉伸) 轴向压缩——轴力作用下,杆件缩短 (简称压缩)
2
拉、压的特点:
1.两端受力——沿轴线,大小相等,方向相反 2. 变形—— 沿轴线
3
§2-2 轴向拉伸或压缩时横截面上的内力和应力
1 、横截面上的内力
A3
2
l1 l2 y AA3 A3 A4 sin 30 tan 30 2 1.039 3.039mm
A
A A4
AA x2 y2 0.6 2 3.039 2 3.1mm
40
目录
例 2—5 截面积为 76.36mm² 的钢索绕过无摩擦的定滑轮 F=20kN,求刚索的应力和 C点的垂直位移。 (刚索的 E =177GPa,设横梁ABCD为刚梁)
16
§2-4
材料在拉伸时的力学性能
材料的力学性能是指材料在外力的作用下表现出的变 形和破坏等方面的特性。
现在要研究材料的整个力学性能(应力 —— 应变):
从受力很小
破坏
理论上——用简单描述复杂
工程上——为(材料组成的)构件当好医生
17
一、 低碳钢拉伸时的力学性能 (含碳量<0.3%的碳素钢)
力均匀分布于横截面上,σ等于常量。于是有:
N d A d A A
A A
得应力:
N A
F
FN
σ
10
例题2-2
A 1
45°
C
2
02第02章 轴向拉压应力与剪切.

四、拉压杆的强度计算
1、极限应力、许用应力
⑴、极限应力(危险应力、失效应力):材料发生破坏或产生过 大变形而不能安全工作时的最小应力值。“σjx”(σu、σ0)
⑵、许用应力:构件安全工作时的最大应力。“〔σ〕”
jx
n
(其中n为安全系数值>1)
⑶安全系数取值考虑的因素: (1)给构件足够的安全储备。
F
28
cos cos2
F
sin
2
sin
2
2、符号规定
n
p
⑴、α:斜截面外法线与x轴的夹角。
x 轴正向逆时针转到 n 轴“α”规定为正值;
x 轴正向顺时针转到 n 轴“α”规定为负值。 ⑵、σα:同“σ”的符号规定
⑶、τα:在保留段内任取一点,如果“τα”对其点之矩为顺 时针方向规定为正值,反之为负值。
aAB 1000 31.6mm
60KN
40KN
BC
X 40kN 100kN
37
例:
B
Y
FNAB
33000 0
A
300
C
F
FNAC
X
F
已知:三角架 ABC 的〔σ〕=120 MPa,AB 杆为 2 根 80*80*7 的等边角钢,AC 为 2 根 10 号槽钢,AB、AC 两杆的夹角为300 。
5、应力的计算公式:
由 lim FN dFN 0 dA
可得
dA
A
FN
由于“均布”,可得
dA
A
FN
A FN
FN ——轴向拉压杆横截面上正应力的计算公式
A
25
6、拉压杆内最大的正应力:
等直杆: max
材料力学第2章 拉伸 压缩 剪切

[ ]
s
ns
强度条件:
FN = [ ] A
安全系数的确定
1)
2)
材质情况
载荷情况
3)
4)
计算精度
零件工作情况
5)
对自重的要求
例2 某拉伸试验机的结构示意图如图所示,试验机 的CD杆与试件AB材料相同,其ζp=200MPa, ζs=240MPa, ζb=400MPa。试验机最大拉力为 100kN。 (1) 用这一试验机作拉断试验时, 试件直径最大可达多大?
D
2 M A 2 FCD a F 2a 0 FCD 2a 4Fa l EA EA
FCD 2 2F
8 2Fa B 2 2l EA
例2:图为一简单托架,BC杆为圆钢,横截面直径 d=20mm,BD杆为8号槽钢,E=200MPa,试 求B点的位移。设F=60kN。 FN2 3/5-FN1=0 FN2 4/5-F=0 FN2=5F/4=75kN FN1=3F/4=45kN BB1=Δ ll=0.86×10-3m BB2=Δ l2=0.732×10-3m
FN 1
2F [ ] A 31
3 1 F [ ] A 21.86( kN ) 2
FN 2
例: 杆系结构如图所示,已知杆AB、AC 材料相
同,[ζ]=160MPa,载荷F=20kN,试设计杆
的横截面面积。
B
30o 45o
FN 1 sin 30 FN 2 sin 45
l BD
FNBD l1 1.05 10 4 m EA1
l DC 0.52 104 m lCA 0.52 104 m
l AB l BD l DC lCA 1.05 104 m
材料力学 第二章 轴向拉压、剪切挤压
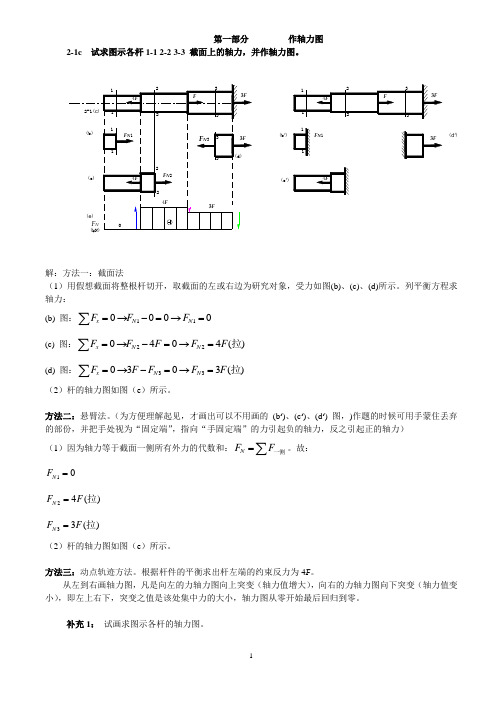
第一部分 作轴力图2-1c 试求图示各杆1-1 2-2 3-3 截面上的轴力,并作轴力图。
(b ')(c ')F N 1(d ')解:方法一:截面法(1)用假想截面将整根杆切开,取截面的左或右边为研究对象,受力如图(b)、(c)、(d)所示。
列平衡方程求轴力: (b) 图:110000xN N F F F =→-=→=∑ (c) 图:220404()xN N FF F F F =→-=→=∑拉 (d) 图:330303()xN N FF F F F =→-=→=∑拉(2)杆的轴力图如图(e )所示。
方法二:悬臂法。
(为方便理解起见,才画出可以不用画的 (b ‘)、(c ‘)、(d ‘) 图,)作题的时候可用手蒙住丢弃的部份,并把手处视为“固定端”,指向“手固定端”的力引起负的轴力,反之引起正的轴力) (1)因为轴力等于截面一侧所有外力的代数和:N F F=∑一侧。
故:10N F = 24()N F F =拉 33()N F F =拉(2)杆的轴力图如图(e )所示。
方法三:动点轨迹方法。
根据杆件的平衡求出杆左端的约束反力为4F 。
从左到右画轴力图,凡是向左的力轴力图向上突变(轴力值增大),向右的力轴力图向下突变(轴力值变小),即左上右下,突变之值是该处集中力的大小,轴力图从零开始最后回归到零。
补充1: 试画求图示各杆的轴力图。
(c ')(e ')(d ')(kN)20455(f)(kN)205455(f ')题5-1aF NF N解:方法一:截面法(1)用假想截面将整根杆切开,取截面的右边为研究对象,受力如图(b)、(c)、(d)、(e)所示。
列平衡方程求轴力: (b) 图:11020020()xN N F F F kN =→-=→=∑拉(c) 图:2202025020255()xN N FF F kN =→--=→=-=-∑压(d) 图:330202550020255045()xN N F F F kN =→-+-=→=-+=∑拉 (e) 图:440202550400202550405()xN N FF F kN =→-+--=→=-+-=∑拉(2)杆的轴力图如图(f )所示。
材料力学第2章-拉伸、压缩与剪切

第2章 拉伸、压缩与剪切1、轴向拉伸与压缩概念:作用于杆件上的外力合力的作用线与杆件轴线重合,杆件变形是沿轴线方向的伸长或缩短。
2、直杆轴向拉伸或压缩时横截面上的内力与应力内力:把拉伸时的轴力(轴力背向截面)为正,压缩时轴力(轴力指向截面)为负。
应力:平面假设(变形前原为平面的横截面,变形后仍保持为平面且仍垂直于轴线。
)规定:拉应力为正,压应力为负。
AF A dA F N A N =⇒==⎰σσσ 式中N F 为轴力,A 为横截面面积,σ为正应力。
3、直杆轴向拉伸或压缩时斜截面上的应力ασσα2cos = αστα2sin 2= 式中ασ和ατ分别为斜截面的正应力和切应力,σ为横截面的正应力,α为斜截面与横截面的夹角。
4、材料拉伸时的力学性能 应变:ll ∆=ε l ∆为伸长量,l 为原始长度。
(1)弹性阶段:应力σ与应变ε成正比,即εσE =。
其中E 为与材料有关的比例常数,为弹性模量。
直线部分的最高点a 所对应的应力p σ为比例极限。
b 点所对应的应力e σ为弹性极限。
(2)屈服阶段:通常把下屈服极限称为屈服极限或屈服点,用s σ表示。
其是衡量材料强度的重要指标。
(3)强化阶段:强化阶段中的最高点e 所对应的应力b σ是材料能承受的最大应力,称为强度极限。
其是衡量材料强度的另一重要指标。
(4)局部变形阶段:某一局部的横向尺寸急剧缩小,形成缩颈现象。
伸长率:%1001⨯-=ll l δ 塑性材料:%5>δ 脆性材料:%5<δ 断面收缩率:%1001⨯-=A A A ψ A 为原始横截面积,1A 为最小横截面积 5、材料压缩时的力学性能低碳钢压缩时的弹性模量E 和屈服极限s σ与拉伸时相同。
但是得不到强度极限。
铸铁的抗压强度极限比抗拉极限高5~4倍。
6、失效、安全因数和强度计算脆性材料断裂时的应力是强度极限b σ,塑性材料屈服时的应力是屈服极限s σ,这二者是构件失效时的极限应力。
材料力学 第二章拉伸、压缩与剪切

根据轴力图可以显示各段轴力的大小以及各段的变形是拉伸或压缩
9
§2-2 轴向拉伸或压缩时横截面上的内力与应力
2.应力
轴力的大小并不能用来判断杆件是否有足够的强度,如:
F
F
F
F
细杆先被拉断,说明拉杆的强度不仅与轴力的大小有关,还 与拉杆的的横截面有关,所以必须用横截面上的应力来度量 杆件的受力程度。
3
§2-1 轴向拉伸与压缩的概念与实例
1.轴向拉伸与压缩的实例
2.拉伸压缩动画示范
5
§2-1 轴向拉伸与压缩的概念与实例
3.拉伸与压缩的受力特点
作用于杆件上的外力合力的作用线与杆件的轴 线重合,杆件变形是沿轴线方向伸长或缩短的。
6
§2-2 轴向拉伸或压缩时横截面上的内力与应 力
F1 FN1 0 FN1 F1 2.62 KN (压力)
F1 F2 FN2 0 FN2 F1 F2 1.32KN(压力)
FN 2 F3 0 FN 2 F3 1.32 KN (压力)
8
§2-2 轴向拉伸或压缩时横截面上的内力与应力
轴力图:用平行于杆件轴线的坐标表示横截面的位置, 用垂直于杆件轴线的坐标表示横截面上轴力的数值,从 而绘出表示轴力沿杆轴变化规律的图线。
铸铁压缩时,仍在较小在变形下
突然破裂,破坏断面的法线与轴
线大致成45°角。表明沿斜截面
相对错动而破坏。抗压强度约比
抗拉强度高4-5倍。
24
§2-7 失效、安全因数和强度计算
一、失效 构件因强度、刚度、稳定性等原因不能正常工作。 强度条件引起的失效: 脆性材料制成的构件在拉应力下,当变形很小时就突然断裂; 塑性材料制成的构件在拉断之前已经出现塑性变形,由于不 能保持原有的形状和尺寸,它已经不能正常工作。断裂与出现 塑性变形统称为失效。
【可编辑全文】材料力学-第二章-拉压与剪切
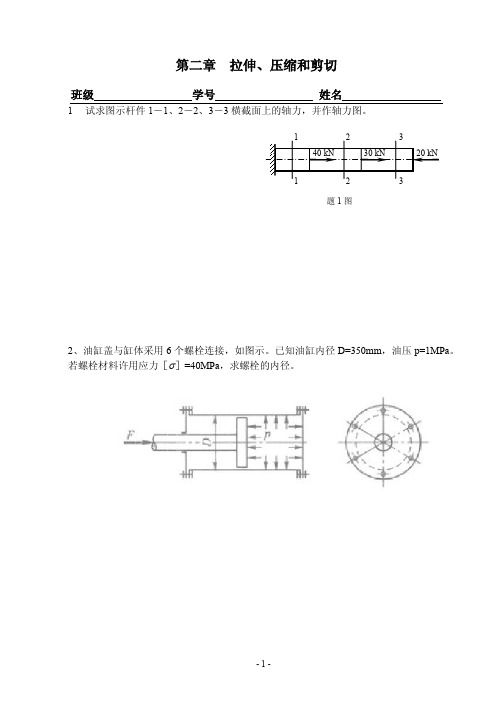
班级 学号 姓名1 试求图示杆件1-1、2-2、3-3横截面上的轴力,并作轴力图。
2、油缸盖与缸体采用6个螺栓连接,如图示。
已知油缸内径D=350mm ,油压p=1MPa 。
若螺栓材料许用应力[ ]=40MPa ,求螺栓的内径。
题1图140 kN 30 kN20 kN122 33班级 学号 姓名3 图示木制桁架受水平力P 作用。
已知P=80kN[][]MPa MPa 10,8==压拉σσ,试设计AB 、AD 两杆的横截面积。
4 图示结构,杆1、2的横截面均为圆形,直径分别为d 1=30mm , d 2=20mm 。
两杆材料相同,许用应力[σ]=160MPa ,在节点A 处受铅直力P=80kN 。
试校核结构的强度。
A B C D P60° 60° 30° 30°BC A P 12 30° 45°班级学号 姓名5、某铣床工作台进给油缸如图示,缸内油压p=2MPa ,油缸内径D=75mm ,活塞杆直径 d=18mm 。
已知活塞材料的许用应力[σ]=50MPa ,试校核活塞杆的强度。
6、简易吊车如图所示。
AB 为木杆,横截面积 21cm 100=A ,许用压应力[]MPa 71=σ。
BC 为钢杆,横截面积22cm 6=A ,许用拉应力[]MPa 1602=σ。
试求许可吊重F 。
F30°AB C木杆 钢杆第二章 拉伸、压缩和剪切班级 学号 姓名7、 图示拉杆沿斜截面m -m 由两部分胶合而成。
设在胶合面上许用拉应力[]MPa 100=σ,许用切应力[]MPa 50=τ,并设胶合面的强度控制杆件的拉力。
试问:为使杆件承受最大拉力F ,α角的值应为多少?若杆件横截面面积为4cm 2,并规定α≤60°,试确定许可载荷F 。
8、变截面杆如图所示。
已知:21cm 8=A ,22cm 4=A , GPa 200=E 。
试求杆的总伸长l ∆。
002-材料力学_轴向拉压

σ
F FN
σ =
FN A
拉应力为正 压应力为负
拉压杆横截面上正应力计算公式
公式适用于轴载作用的杆件。 公式适用于轴载作用的杆件。 变截面杆或分布轴载作 用下横截面正应力计算
σ ( x) =
FN ( x ) A( x )
2.2 拉压杆的应力
二、斜截面上的应力
σ F σ
τ= σ
σ
2
σ
τ=
2
σ
F
2 σ τ= 2
ρgπ
l
ξ )2
叠加原理适用
FN (0) = F
FN (l ) = ( F + P)
dFN ( x) ρgπ 2 d1 (d 2 d1 ) d d ρgπ d d = [d1 + 2 x + ( 2 1 )2 x2 ] = (d1 + 2 1 x) 2 = p( x) dx 4 l l 4 l
单向(单轴) 单向(单轴)应力状态
σ
2
σ τ = 2 σ
2
2
讨论任一方位截面上的应力及与横截面上应 作顺时针转动的趋势为正。 切应力以使隔离体有作顺时针转动的趋势为正。 力的关系, 力的关系,斜截面上各处法向线应变和切应 σ max = σ 0 = σ τ0 = 0 横截面上 变相同,即变形是均匀的。 变相同,即变形是均匀的。因此内力均匀分 σ min = σ 90 = 0 τ 90 = 0 布。 纵截面上 σ Fα = ∫ Aoα p α dAτ max p ατ ∫ Aα=dA = p α σ α = σ = = A F
2.1 拉压杆的内力 轴力及轴力图
横截面是杆件内最有代表性的截面, 横截面是杆件内最有代表性的截面, 其上的内力可用截面法求出。 其上的内力可用截面法求出。 由隔离体的平衡条件截面上只 有截面法向的内力分量 FN(x), ), 轴力。 称为轴力 称为轴力。 由 ∑ Fx = FN ( x) F = 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)理论与实际的差异。
28
2、强度条件: max
等直杆: max
FN max A
变直杆:
max
FN A
m a x
3、强度计算:
(1)、校核强度——已知:F、A、〔σ〕。求: max
18
一、应力的概念 截面某点处内力分布的密集程度 在大多数情形下,工程构件的内力并非均匀分布,集度 的定义不仅准确而且重要,因为“破坏”或“失效”往往从 内力集度最大处开始。Biblioteka 191、一般受力杆: F1
m
F3
F2
F1 F2
F4
m
△FT △F
c
△A
△FN
(1)、定义:
pm
F A
——ΔA上的平均应力
20
3
4
5
6
受力简图: F
F
FN1
FN1
F
F
FN2
FN2
二、轴向拉压的概念:
(1)受力特点:作用于杆两端的外力合力作用线与 杆轴线重合。
(2)变形特点:杆沿轴线方向伸长或缩短。 7
§2-2 轴向拉压杆的内力和内力图
一、外力和内力的概念 1.外力:一个物体对另一个物体的相互作用力(荷载、支反力)。 2.内力:物体内部各粒子之间的相互作用力。 附加内力:由外力作用而引起的物体内部各粒子之间相互作
9
三、轴向拉压杆的内力
1—1
1.外力——F
F
F
F
FN
2.内力——FN (轴力) (1)轴力的大小:(截面法确定)
①截开。 ②代替,用内力“FN”代替。 ③平衡, ∑X=0, FN-F=0, FN=F。
10
(2)轴力的符号规定:原则—根据变形 拉伸—拉力,其轴力为正值。方向背离所在截面。 压缩—压力,其轴力为负值。方向指向所在截面。
26
9、圣维南原理: 作用于杆上的外力可以用其等效力系代替,但替换后外
力作用点附近的应力分布将产生显著影响,且分布复杂,其 影响范围不超过杆件的横向尺寸。
10、注意的问题
(1) 公式中各值单位要统一
N m2
Pa
N mm2 MPa
(2) “FN”代入绝对值,在结果后面可以标出“拉”、“压”。
27
O x
FN
q(x) x
–
k L2 2
FN(x)
FN (x)
x kxdx 1 kx2
0
2
FN
(x)max
1 2
k L2
17
§2-3 轴向拉压杆的应力和强度计算
问题提出: 2F
2F
F
F
F
F
1. 内力大小不能全面衡量构件强度的大小。 2. 构件的强度由两个因素决定:
①内力在截面分布集度应力; ②材料承受荷载的能力。
三、拉压杆的强度计算
1、极限应力、许用应力
⑴、极限应力(危险应力、失效应力):材料发生破坏或产生过
大变形而不能安全工作时的最小应力值。“σjx”(σu、σ0)
⑵、许用应力:构件安全工作时的最大应力。“〔σ〕”
jx
n
(其中n为安全系数值>1)
⑶安全系数取值考虑的因素: (1)给构件足够的安全储备。
24
3、平面假设:变形前的横截面,变形后仍为平面且各横截面 沿杆轴线作相对平移
4、应力的分布规律——均布 F
5、应力的计算公式:
由 lim FN dFN 0 dA
可得
dA
A
FN
由于“均布”,可得
dA
A
FN
A FN
FN ——轴向拉压杆横截面上正应力的计算公式
A
25
6、拉压杆内最大的正应力:
1
第二章 轴向拉压应力与剪切
§2-1 工程实例和基本概念 §2-2 轴向拉压杆的内力和内力图 §2-3 轴向拉压杆的应力和强度计算 §2-4 材料在拉压时的力学性质 §2-5 应力集中的概念
拉压部分小结 §2-6剪切与挤压的强度计算
2
§2-1 工程实例和基本概念
一、工程实例: 活塞杆、厂房的立柱、工程桁架等。
F+N
F-N
11
(3)轴力图:轴力沿轴线变化的图形
①取坐标系
FN
②选比例尺
③正值的轴力画在 x 轴的上侧,
+
负值的轴力画在 x 轴的下侧。
x
(4)轴力图的意义
①反映出轴力与截面位置变化关系,较直观; ②确定出最大轴力的数值及其所在横截面的位置,即确定 危险截面位置,为强度计算提供依据。
12
(5)注意的问题
①在截开面上设正的内力方向。 ②采用截面法之前,不能将外力简化、平移。
F
F
P
F
FN
FN
13
[例1] 图示杆的A、B、C、D点分别作用着大小为5F、8F、4F、 F 的力,方向如图,试画出杆的轴力图。
OA
BC
D
FA
FB
FC
FD
FN1 A
BC
D
FA
FB
FC
FD
解: 求OA段内力FN1:设截面如图
X 0 FN1 FA FB FC FD 0
2、轴向拉压杆:
m
FN
F
——ΔA上的平均正应力
lim FN dFN
F
0 dA
——C点处的正应力
ΔA △FN
C
σ
二、轴向拉压杆横截面上正应力的确定 推导的思路:实验→变形规律→应力的分布规律→应力的
计算公式 22
1、实验: 变形前
受力后
F
F
23
2、变形规律: 横向线——仍为平行的直线,且间距增大。 纵向线——仍为平行的直线,且间距减小。
p lim F dF
A0 dA
F1
——C点处的总应力
F2
τp
c
σ
lim FN dFN ——“正应力”
0 dA
lim FT dFT
0 dA
——“切应力”(剪应力)
(2)单位:
N m2
Pa
——帕斯卡(帕)
103 Pa 1KPa 千帕 106 Pa 1MPa 兆帕 109 Pa 1GPa 吉2帕1
等直杆: max
FN max A
变直杆: max
FN A
m a x
7、正应力的符号规定——同内力 拉伸——拉应力,为正值,方向背离所在截面。 压缩——压应力,为负值,方向指向所在截面。
8、公式的使用条件 (1) 轴向拉压杆 (2) 除外力作用点附近以外其它各点处。 (范围:不超过杆的横向尺寸)
用力的改变量(材料力学中的内力)。
8
二、内力的确定——截面法(基本方法) 1、截开—欲求哪个截面的内力,就假想的将杆从此截面截开, 杆分为两部分。 2、代替—取其中一部分为研究对象,移去另一部分,把移去 部分对留下部分的相互作用力用内力代替。 3、平衡—利用平衡条件,列出平衡方程,求出内力的大小。
FN1 5F 8F 4F F 0 FN1 2F 14
15
OA FA
轴
力 图
FN
2F
如
右
图
示
BC
D
FB
FC
FD
5F F
3F
x
16
[例2] 图示杆长为L,受分布力 q = kx 作用,方向如图,试画出
杆的轴力图。 q(x)
解:x 坐标向右为正,坐标原点在
x
自由端。
L
取左侧x 段为对象,内力FN(x)为:
