§3.3平面直角坐标系导学案
平面直角坐标系(第3课时)导学案
2.2 平面直角坐标系（ 3）学习目标：1、关于给定图形，会选择适合的平面直角坐标系，写出它的顶点坐标 , 领会能够用坐标刻画一个简单图形；2、会经过成立适合的平面直角坐标系，确立实质问题中物体的地点，形成数形联合意识；3、在运用数学表述和解决问题的过程中，认识数学拥有抽象、谨慎和应用宽泛的特色，领会数学价值，形成谨慎务实的科学态度。
课前准备： A4 纸一张，等边三角形纸板温故而知新1、请在右图所示平面直角坐标系中描出以下各点：A(3,0),B(-2,0),C(0,3),D(0,-4),E(3,2),F(3,-3),G(-2,2)H(4,4),M(-5,-5)2、你能将以上点进行适合的分类吗？说说你的想法。
3、如图，边长为 3 的正方形 ABCD, 请成立适合的平面直角坐标系，并写出各极点的坐标。
B A解：以为原点，分别以、所在直线为 x 轴，y 轴，C D 成立直角坐标系，此时各极点的坐标分别是(提示：平面直角坐标系离不开原点、X 轴、 Y 轴，所以在题目中要说明）讲堂研究：活动 1：聚焦目标一★小试牛刀我能行：1、你还能够如何成立平面直角坐标系？看看哪个小组的方法多？A A AB B BC D C D C D2、对照不一样的成立平面直角坐标系的方法,你更喜爱哪一种 ?说说你的见解 .★八仙过海我会做4.如图，长方形形ABCD 中，AB 是 4，BC 是 6，成立适合的平面直角坐标系，并直接写出各个极点的坐标。
ABC D★贯通融会我会讲5.(1) 关于边长为 4 的正△ ABC ，成立适合的平面直角坐标系，写出各个极点的坐标 .(提示：平面直角坐标系中点的坐标确实定方法)(2)如图 Rt △ABC 中, AC=BC=2 ，成立适合的平面直角坐标系，并直接写出 A、B、 C 三个点的坐标。
活动 2：聚焦目标二、三★火眼金睛我会用A CB6、我班甲、乙两女同学都参加了学校组织的啦啦操活动，甲同学站在大院里当时跳啦啦操的地点，对你说，假如将我的地点看作原点，那乙同学的地点就是（-3 ，-2），你能找见乙同学当时跳舞的地点吗？甲●7、在一次“寻宝”游戏中，寻宝人已经找到了坐标为（-2，1）和（2，1）的两个标记物 A,B ，而且知道藏宝地址的坐标（ 1，-1），除别的不知道其余信息。
平面直角坐标系导学案
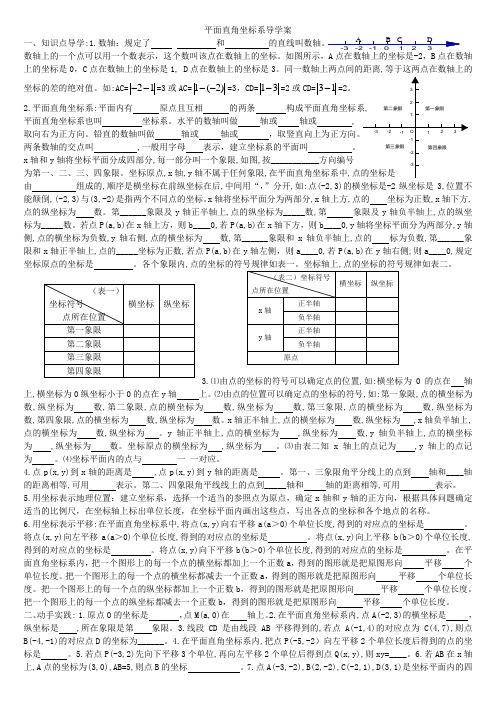
平面直角坐标系导学案一、知识点导学:1.数轴：规定了和的直线叫数轴。
数轴上的一个点可以用一个数表示，这个数叫该点在数轴上的坐标。
如图所示，A点在数轴上的坐标是-2，B点在数轴上的坐标是0，C点在数轴上的坐标是1, D点在数轴上的坐标是3。
同一数轴上两点间的距离,等于这两点在数轴上的坐标的差的绝对值。
如:AC=21--=3或AC=1(2)--=3，CD=13-=2或CD=31-=2。
2.平面直角坐标系:平面内有原点且互相的两条构成平面直角坐标系平面直角坐标系也叫坐标系。
水平的数轴叫做轴或轴或 ,取向右为正方向。
铅直的数轴叫做轴或轴或，取竖直向上为正方向。
两条数轴的交点叫 ,一般用字母表示，建立坐标系的平面叫。
x轴和y轴将坐标平面分成四部分,每一部分叫一个象限,如图,按___________方向编号为第一、二、三、四象限。
坐标原点,x轴,y轴不属于任何象限,在平面直角坐标系中,由组成的,顺序是横坐标在前纵坐标在后,中间用“，”分开,如:点(-2,3)的横坐标是-2纵坐标是3,位置不能颠倒,(-2,3)与(3,-2)是指两个不同点的坐标。
x轴将坐标平面分为两部分,x轴上方,点的坐标为正数,x轴下方,点的纵坐标为数。
第______象限及y轴正半轴上,点的纵坐标为_____数,第象限及y轴负半轴上,点的纵坐标为_____数。
若点P(a,b)在x轴上方，则b____0,若P(a,b)在x轴下方，则b____0,y轴将坐标平面分为两部分,y轴侧,点的横坐标为负数,y轴右侧,点的横坐标为数,第______象限和x轴负半轴上,点的标为负数,第______象限和x轴正半轴上,点的_____坐标为正数,若点P(a,b)在y轴左侧，则a____0,若P(a,b)在y轴右侧,则a____0,规定坐标原点的坐标是。
各个象限内,点的坐标的符号规律如表一。
坐标轴上,点的坐标的符号规律如表二。
3.⑴由点的坐标的符号可以确定点的位置,如:横坐标为0的点在轴上,横坐标为0纵坐标小于0的点在y轴上。
平面直角坐标系教案15篇
平面直角坐标系教案平面直角坐标系教案15篇在教学工作者开展教学活动前，很有必要精心设计一份教案，教案是教学活动的依据，有着重要的地位。
我们应该怎么写教案呢？以下是小编帮大家整理的平面直角坐标系教案，欢迎阅读，希望大家能够喜欢。
平面直角坐标系教案1一教材分析１、教材的地位与作用本节课的教学内容是义务教育课程标准实验教科书，七年级下册第6.1.2节平面直角坐标系又称笛卡儿坐标。
平面直角坐标系是图形与数量之间的桥梁，有了它我们便可以把几何问题转化为代数问题，也可以把代数问题转化为几何问题。
本章内容从数的角度刻画了第五章有关平移的内容，对学生以后的学习起到铺垫作用，6.1.2节平面坐标系主要是介绍如何建立平面坐标系，如何确定点的坐标和由点的坐标寻找点的位置，以及平面坐标系中特殊部位点的坐标特征，根据学生的接受能力，我把本内容分为２课时，这是第一课时，主要介绍如何建立坐标系和在给定的坐标系中确定点的坐标。
２、教学目标根据新课标要求，数学的教学不仅要传授知识，更要注重学生在学习中所表现出来的情感态度，帮助学生认识自我、建立信心。
知识能力：①认识平面直角坐标系，了解点与坐标的对应系；②在给定的直角坐标系中，能由点的位置写出点坐标。
数学思考：①通过寻找确定位置，发展初步的空间观念；②通过学习用坐标的位置，渗透数形结合思想解决问题：通过运用确定点坐标，发展学生的应用意识。
情感态度：①通过建立平面直角坐标系和确定坐标系中点的坐标，培养学生合作交流与探索精神；②通过介绍数学家的故事，渗透理想和情感的教育。
３、重难点根据本章知识内容以及学生对坐标横纵坐标书写易出错误，确定本节重难点为：重点：认识平面坐标系难点：根据点的位置写出点的坐标一、教法分析针对学初一学生的年龄特点和心理特征，以及他们现有知识水平，通过科学家发现点的坐标形成的经过启迪学生思维，通过小组合作与交流及尝试练习，促进学生共同进步，并用肯定和激励的言语鼓舞、激励学生。
《平面直角坐标系》教案及导学案
【学习目标】
1、认识平面直角坐标系，在给定的直角坐标系中，能根据坐标描出点的位置，能由点的位置写出点的坐标；
2、能根据实际条件建立适当的平面直角坐标系。
【学习重点】正确建立平面直角坐标系，根据坐标描出点的位置，由点的位置确定点的坐标的。
【学法指导】从熟悉的数轴为起点，了解数轴上点的坐标的定义，从而建立点与坐标的对应关系。
类比着利用数轴确定直线上点的位置的方法，探究出由两条相互垂直、原点重合的数轴建立了平面直角坐标系。
坐标平面内点与坐标的对应关系，相似于数轴上点与坐标的对应关系。
这样对点与坐标的对应关系顺利地实现由一维到二维的过渡。
点的坐标是用有序数对（列数在前，排数在后）表示的，利用有序数对就可以确定点的位置。
【学习过程】。
人教版数学《平面直角坐标系》导学案
人教版数学《平面直角坐标系》导学案人教版数学《平面直角坐标系》导学案人教版数学《平面直角坐标系》导学案1.会判断点的坐标在哪个象限。
2.能根据坐标在平面直角坐标系中描出点的坐标。
一、板书课题同学们，我们继续来学习6.1.2平面直角坐标系(板书)。
二、出示目标(一)过渡语：学习目标是什么?请看投影：(二)屏幕显示学习目标1.会判断点的坐标在哪个象限。
2.能根据坐标在平面直角坐标系中描出点的坐标。
三、自学指导(一)过渡语：怎样才能当堂达到学习目标呢?请大家按照指定认真自学。
(二)出示自学指导自学指导认真看课本(P42思考下面至P43练习前)○1思考四个象限中横坐标﹑纵坐标各有什么特点;○2仿照例中找点A的方法，描出点B﹑C﹑D﹑E的坐标;③解答P43探究中的问题。
如有疑问，可以小声问同学或举手问老师。
6分钟后，比谁会根据坐标描出点的位置四、先学(一)学生看书，教师巡视，督促每一位学生认真紧张地自学。
(二)检测1、过渡语：看完的同学请举手?会用平面直角坐标系的同学请举手?好，下面就比一比，看谁能仿照例题做出检测题。
2、检测题：P43 2.3、学生练习，教师巡视。
(收集错误进行二次备课)五、后教(一)：自由更正请同学们认真看堂上板演的内容，如果有错误或不同解法的请上来更正或补充。
(二)讨论、归纳评：1、描点这些点描的对吗?我们先来看这个点L(-5，-3)第一步干什么?引导学生说出：在x轴上找出表示-5的'点，也就是：在x轴上找出表示横坐标的点(师板书)。
第二步干什么?引导学生说出：在y轴上找出表示纵坐标的点(师板书)第三步干什么?引导学生说出：过两个点分别坐x轴、y轴的垂线。
第四步干什么?描点，写坐标。
2、象限点R在第几象限?这个象限的点有什么特点?引导学生说出：横坐标大于0，纵坐标大于0.师板书：第一象限(+，+)同理评出第二、三、四象限、及这些象限点的特点。
第二现象(-，+);第三象限(-，-);第四象限(+，-)(师板书)点M(4,0)在第几象限?为什么?引导学生说出：坐标轴上的点不属于任何象限。
平面直角坐标系教案全
第三章平面直角坐标系集体备课：（共7课时）教材内容本章内容包括平面直角坐标系及有关概念，点的坐标，用坐标表示地理位置和平移等。
实际生活中常用有序实数对表示位置，由此引出平面直角坐标系，建立点与有序实数对的对应关系，从而把数和形结合起来。
用坐标法表示地理位置体现了直角坐标系在实际生活中的应用。
用坐标表示地理位置，可以通过建立直角坐标系，绘制出一个区域内地点分布的平面示意图来完成。
用坐标表示平移，从数的角度刻画了第五章有关平移的内容，主要研究了两方面的问题，一方面探讨点或图形的平移引起的点或图形顶点坐标的变化规律，另一方面探讨点或图形顶点坐标的有规律变化引起的点或图形的平移。
此外，用极坐标表示一个地点的地理位置，在本章最后的“数学活动”中有所渗透。
教案目标〔知识与技能〕1、能利用有序数对来表示点的位置；２会画出平面直角坐标系，能建立适当的直角坐标系描述物体的位置；３、在给定的直角坐标系中，会根据坐标描出点的位置，由点的位置写出它的坐标。
〔过程与方法〕1、经历画坐标系、描点，由点找坐标的过程和图形的坐标变化与图形平移之间关系的探索过程，发展学生的形象思维能力与数形结合意识；2、通过平面直角坐标确定地理位置，提高学生解决问题的能力。
〔情感、态度与价值观〕明确数学理论来源于实践，反过来又能指导实践，数与形是可以相互转化的，进一步发展学生的辩证唯物主义思想。
重点难点在平面直角坐标糸中，由已知点的坐标确定这一点的位置，由已知点的位置确定这一点的坐标和平面直角坐标系的应用是重点；建立坐标平面内点与有序实数对之间的一一对应关系和由坐标变化探求图形之间的变化是难点。
课时分配6.1平面直角坐标系……………………………………… 3课时6.2 坐标方法的简单应用…………………………………2课时本章小结……………………………………………………2课时3.1平面直角坐标系（1）〔教案目标〕理解有序数对的意义，能利用有序数对表示物体的位置。
平面直角坐标系导学案14页word文档
第六章 平面直角坐标系课题：6.1.1 有序数对【学习目标】理解有序数对的意义，了解平面上确定点的常用方法. 【学习重点】理解有序数对及平面内确定点的方法. 【学习难点】利用有序数对表示平面内的点. 【学习过程】 一、自主学习1. 数轴：画一条数轴，并在数轴上表示0，2，-5，0.25；2、数轴上的点与实数 对应，即数轴上的每一个点可以用 来表示，每一个实数也可以用 来表示。
3、 方位角：(1)如右图，点A 在点O 的 ;,则点B 在点 O 的 ;点C 在点 O 的 ;(2)在图上作出点O 的南偏东20º的OM 边。
小结：直线上一点（数轴上一点）可以用_____________________来确定他的位置 二、自主研究（一）平面内点的确定 1、行列定位法（坐标定位法）（1）.去电影院看电影需买票，如果你买的票是6排3号，在电影院如何准确地找到这个位置呢？一般来说，先找 再找 。
如果另有一人的票是3排6号，两人是同一个座位吗？为什么？（1）图5-2是广州市地图简的一部分，你如何介绍“广州起义烈士陵园”所在区域？（2）如果“广州火车站”在B3区，则“广州起义烈士陵园”所在区域为，（3）“省政府”所在区域为。
（2有序数对：其中各个数表示的含义，我们把这种有的个数a与b组成的数对，叫做有序数对,记作。
利用有序数对，可以很准确地表示出平面内一个点的位置。
三、典例讲解例1、1.如图1所示,一方队正沿箭头所指的方向前进, A的位置为三列四行,表示为(3,4),那么B 的位置是 ( )A.(4,5)B.(5,4)C.(4,2)D.(4,3)2.如图1所示,B左侧第二个人的位置是 ( )A.(2,5)B.(5,2)C.(2,2)D.(5,5)3.如图1所示,如果队伍向北前进,那么A(3,4)西侧第二个人的位置是 ( )A.(4,1)B.(1,4)C.(1,3)D.(3,1)4.如图1所示,(4,3)表示的位置是 ( )A.AB.BC.CD.D5.小张看电影，买了一张8排10号的电影票，用有序实数对可表示为，如果变换有序数对的位置，所表示的位置和原来的位置（填“相同”或“不同”）.6.如图所示,A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?7. 如图，甲处表示2街与5巷的十字路口，乙处表示5街与2巷的十字路口，如果用（2，5）表示甲处的位置，那么“（2，5）（3，5）（4，5）（5，5）（5，4）（5，3）（5，2）”表示从甲处到乙处的一条路线，请你画出这条从甲处到乙处的路线.8 我们规定向东和向北方向为正，如向东走4米，再向北走6米，记作（4，6），则向西走5米，再向北走3米，记作___________；数对（－2，－6）表示_________________________________.例2、如图（7题的图），从甲到已不走回头线有几种走法？四、知识运用1.如图1所示,进行“找宝”游戏,如果宝藏藏在(3,3)字母牌的下面, 那么应该在字母的下面寻找.2.如图2所示,如果点A的位置为(3,2),那么点B的位置为______, 点C 的位置为______,点D和点E的位置分别为DCBA三行六行六列五列四列三列二列一列______,_______.3.如图3所示,如果点A 的位置为(1,2),那么点B 的位置为_______,点C 的位置为_______.4.如图所示,请说出图中物体的位置.5.如图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法? 请分别写出这些路线. 6 .如图是某城市市区的一部分示意图，对市政府来说： （1） 北偏东60的方向有哪些单位？要想确定单位的位置。
八年级数学《平面直角坐标系》导学案
第六讲平面直角坐标系【知识要点】1、坐标平面内的点和有序实数对一一对应已知点P(x，y)，它的横坐标x和纵坐标y的顺序是不能任意交换的，A(3，2)和B(2，3)表示两个不同的点．对于坐标平面内的任意一点P，存在唯一的一对有序实数(x，y)和它对应；反过来，对于任意一对有序实数(x，y)，在坐标平面内有唯一的P点和它对应．这里，(x，y)称为点P的坐标，x是横坐标，y是纵坐标，x写在前，y写在后．2、各象限内坐标的符号点P（x，y）在第一象限内，则x＞0，y＞0，反之亦然．点P（x，y）在第二象限内，则x＜0，y＞0，反之亦然．点P（x，y）在第三象限内，则x＜0，y＜0，反之亦然．点P（x，y）在第四象限内，则x ＞0，y＜0，反之亦然．3、特殊点的坐标x轴上点的纵坐标为零，即(x，0)，如果某点的坐标为(x，0)，则它在x轴上．y轴上点的横坐标为零，即(0，y)，如果某点的坐标为(0，y)，则它在y轴上．第一、三象限角平分线上点的横坐标和纵坐标相等，即(x，x)，如果点的坐标为(x，x)，则它必定在一、三象限角平分线上．第二、四象限角平分线上点的横坐标和纵坐标互为相反数，即(x，－x)，如果点的坐标为(x，－x)，则它在二、四象限角平分线上．原点的坐标是(0，0)，反之，坐标是(0，0)的点是原点．4、对称点关于x轴对称的两个点的横坐标相等，纵坐标互为相反数．关于y轴对称的两点的横坐标互为相反数，纵坐标相等．关于原点对称的两点的横坐标纵坐标都互为相反数．如果一个点的坐标为(a ，b )，那么这个点关于x 轴、y 轴、原点的对称点分别是(a ，－b )，(－a ，b )，(－a ，－b )．它的逆命题亦成立．5、点P (x ，y )到两坐标轴的距离点P(x ，y )到x 轴和y 轴的距离分别是|y |和|x |． 点P(x ，y )【典型例题】专题一 、象限与字母的范围例1、点)2,1(2+-b a A 在坐标轴上,则 。
平面直角坐标系自主学习导学案
平面直角坐标系
学习目标
二次备课1．领会实际模型中确定位置的变化，会正确画出平面直角坐标系。
理
解平面直角坐标系的有关概念。
2．理解平面内点的坐标的意义。
会在给定的直角坐标系中根据点的坐
标标出点的位置，会根据点的位置写出点的坐标。
3．使学生了解平面上的点与有序实数对的一一对应关系。
学习重难点
1．理解并掌握平面直角坐标系的有关概念。
2．在给定的直角坐标系中，根据点的坐标标出点的位置，会根据点的
位置写出点的坐标。
学习过程
自学质疑
1．想一想：在教室里怎样确定自己的位置？
2．上电影院看电影，电影票上至少要有
几个数字才能确定你的位置？
3．怎样表示平面内的点的位置？
互动探究
生活中，我们常要描述各种目标的位置。
如图4-3，如果将北京（东、西）路和中山（南、北）路看成2条互相垂
直的数轴，十字路口为它们的公共原点，那么中山北路西边50m可记为-50，
北京西路北边30m 可记为+30，音乐喷泉的位置就可以用一对实数（-50，
30）来描述。
给出定义
精讲点拨
例1．在直角坐标系中，描出下列各点的位置。
A （3，1）
B （－2，4）
C （－4，－2）
D （3，－2）
E （0，1）
F （－4，0）
O （0，0） G （1，3） H （4，－2）
矫正反馈
迁移应用
写出图中的多边形ABCDEF 各个顶点的坐标。
【板书设计】
0-2-121-2-12
1。
《平面直角坐标系》导学案 人教七下数学
7.1．2 平面直角坐标系【学习目标】1．认识平面直角坐标系，了解平面直角坐标系的概念并会平面直角坐标系. 2. 了解点的坐标的意义，会用坐标表示点，能画出点的坐标位置.3. 在平面直角坐标系中能由点的位置确定点的坐标或由点的坐标确定点的位置. 【学习重点与难点】1.学习重点：了解点的坐标的意义，会用坐标表示点，能画出点的坐标位置；2.学习难点：在平面直角坐标系中能由点的位置确定点的坐标或由点的坐标确定点的位置. 【学习过程】 一、温故知新1．数轴的三要素是_________、_________、____________.3．根据下图，你能正确说出各个象棋子的位置吗？二、自主探究（一）预习自我检测（阅读课本思考并完成以下问题）1. 数轴上的点可以用 个数来表示,这个数叫做这个点的坐标.反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了. 2、思考：类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?3.新知学习：如何用一对实数来表示平面内的位置呢？早在1637年以前，法国数学家笛卡儿受到了经、纬线的启发，地理上的经纬度是以赤道和本初子午线为标准的，这两条线从局部上看是平面内互相垂直的两条直线.所以笛卡儿在平面内画两条 的数轴，其中水平的数轴叫 （或 ）取向右为正方向，铅直的数轴叫 （或 ），取向 为正方向，X 轴或Y 轴统称为 ，它们的交点是 ，这个平面叫做坐标平面.这就是今天要研究的笛卡儿的平面直角坐标系.三、合作探究点的坐标重点：x轴或横轴，y轴或纵轴，原点，单位长度，两条数轴互相垂直，箭头.1. 如何在平面直角坐标系中表示一个点？A（3，4）的表示方法：A点在x轴上的坐标为，A点在y轴上的坐标为，A点在平面直坐标系中的坐标为，记作：A (___,___)图1 图2请你写出图1中点B,C,D的坐标：B(___,___),C(___,___),D(___,___).归纳：1.我们用___________表示平面上的点，这对数叫____.表示方法为（a,b）.a是点对应______上的数值，b是点在______上对应的数值.注意：轴上的坐标写在前面.2.思考：原点O的坐标是( ___ ，___ ),x轴上的纵坐标都是 , y轴上的横坐标都是 .3.新知运用：在平面直角坐标系（图2）中描出下列各点：A(4,5), B(-2,3), C(-4,-1), D(2.5,-2), E(0,-4),四、达标测试1．点（-3，2）在第______象限；点（2，-3）在第______象限．2．点（p，q）既在x轴上，又在y轴上，则p=______；q=_________．3．点M(a,0)在＿＿＿轴上；点N(0,b)在＿＿＿轴上.4.坐标平面内下列各点中，在x轴上的点是（）A、（0，3）B、)0,3(- C、)2,1(- D、)3,2(--5.在方格纸上有A、B两点，若以B点为原点建立直角坐标系，则A点坐标为（2，5），若以A点为原点建立直角坐标系，则B点坐标为（）A．（-2，-5） B．（-2，5） C．（2，-5） D．（2，5）6.坐标平面内下列各点中，在x轴上的点是（）A、（0，3）B、)0,3(- C、)2,1(- D、)3,2(--7．已知x 轴上的点P 到y 轴的距离为3，则点P 的坐标为（ ） A （3,0） B （0,3） C （0,3）或（0,-3） D （3,0）或（-3,0） 8．在平面直角坐标系中，点（-1，m2+1）一定在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限9.如图3式边长分别为8和6的长方形，试建立适当的坐标系表示顶点A 、B 、C 、D 的坐标.五、我的感悟：这节课我的最大收获是： 我不能解决的问题是：__________ ____________________________________ _____________________________ ____________________________________ _____________________________ 六、课后反思：D C B。
§3.2平面直角坐标系导学案
子洲三中 “双主”高效课堂 导学案2014-2015学年第一学期 姓名： 组名： 使用时间2014年 月 日一、教学目标：1．理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念； 2．认识并能画出平面直角坐标系；3．能在给定的直角坐标系中，由点的位置写出它的坐标。
二、教学过程第一环节 感受生活中的情境，导入新课同学们，你们喜欢旅游吗？ 假如你到了某一个城市旅游，那么你应怎样确定旅游景点的位置呢？下面给出一张某市旅游景点的示意图，根据示意图（图5－6），回答以下问题： （1） 你是怎样确定各个景点位置的？（2） “大成殿”在“中心广场”南、西各多少个格？“碑林”在“中心广场”北、东各多少个格？（3） 如果以“中心广场”为原点作两条互相垂直的数轴，分别取向右、向上的方向为数轴的正方向，一个方格的边长看做一个单位长度，那么你能表示“碑林”的位置吗？“大成殿”的位置呢？在上一节课，我们已经学习了许多确定位置的方法，这个问题中，大家看用哪种方法比较合适？第二环节 分类讨论，探索新知1．平面直角坐标系、横轴、纵轴、横坐标,纵坐标、原点的定义和象限的划分。
学生自学课本，理解上述概念。
2．例题讲解例1 写出图中的多边形ABCDEF 各顶点的坐标。
3．想一想 在例1中，（1）点B 与点C 的纵坐标相同，线段BC 的位置有什么特点？（2）线段CE 位置有什么特点？（3）坐标轴上点的坐标有什么特点？年 级科 目课 题主 备 人 备 课 方 式负责人（签字） 审核领导（签字） 序号 八（3） 数学§3.2.1平面直角坐标系乔智AB CD E FO 11x y由B （0，－3），C （3，－3）可以看出它们的纵坐标相同，即B ，C 两点到X 轴的距离相等，所以线段BC 平行于横轴（x 轴），垂直于纵轴（y 轴）。
第三环节 学有所用.补充：1．在下图中，确定A ，B ，C ，D ，E ，F ，G 的坐标。
AB CDEF1y x2．如下图，求出A ，B ，C ，D ，E,F 的坐标。
平面直角坐标系导学案
课题：平面直角坐标系（1）课型：新授课 小主人：___________ 学习小组：_______ 导学案编号：_15 _一、课前抽测求出下列自变量的取值范围：①13-=x y ②1+=x x y ③43-+=x x y【学习目标】1．认识并能画出平面直角坐标系，能根据点的坐标描出点的位置及由点的位置写出点的坐标；（重点） 2．通过探究，理解并掌握平面直角坐标系各象限内点的特征。
（难点）二、新知探究知识点1．平面直角坐标系：1、数轴的三要素是：_________、_________、_________。
数轴上的点与实数________________。
2、平面直角坐标系的构成：在平面上，由两条__________重合、互相_________且具有_________的数轴，构成平面直角坐标系。
水平的数轴称为__________，习惯上取_______为正方向；竖直的数轴称为____________，习惯上取_________为正方向；两坐标轴的交点为平面直角坐标系的__________。
3、平面直角坐标系中，任意一点都可以用____________________来表示。
知识点2．点的坐标：1、已知点的位置写坐标：有了平面直角坐标系，平面内任意一点都可以用一对有序实数来表示。
例如：图中的点A ，从A 分别向x 轴和y 轴作垂线，垂足分别为,M N ，点M 在x 轴上对应的数为3，称为点A 的横坐标；点N 在y 轴上对应的数为4，称为点A 纵坐标。
用小括号，将___________写在前，__________写在后，中间用“逗号”分开，得到一对有序实数(3,4)，称为点A 的坐标，这时点A 可记作A (3,4)。
例１：请写出图中B 、C 、D 、E 和原点O 的坐标。
2、已知点的坐标确定点的位置：如果给你一个坐标(4,5)P -，则先在x 轴上找到表示4-的点，过这个点作x 轴的垂线；再在y 轴上找到表示5的点，过这个点作y轴的垂线，两条垂线的交点为(4,5)P -。
3.3.3点到直线的距离导学案
§3.3.3-3.3.4点到直线的距离与两条平行直线间的距离编写：陈文钦 学号 组次： 姓名______________一、知识回顾与导入：1、两点间距离公式_______________________.2、求点A(2,1)、B(5,-1)间的距离。
二、思考1：什么是点到直线的距离？思考2：点P （2,-3）到x 轴、y 轴的距离分别是_______、_______;思考3：点P （2,-3）到直线y=2、x=2的距离是________、_______(画图)思考：如何求点A （1，2）到直线2x+y-8=0的距离。
你的过程：探究：在平面直角坐标系中，如果已知点0P 的坐标为),(00y x ，怎样用点的坐标和直线的方程直接求点到直线0:=++C By Ax l 的距离呢?参见书本推导你的结论：点0P 到直线0:=++C By Ax l 的距离公式为：三、课本例题例5求点P （-1，2）到直线l ：3x=2的距离例6 已知点A(1,3),B(3,1),C(-1,0),求三角形ABC 的面积四．小组讨论/如果直线21//l l ,如何求1l 与2l间的距离转化思想为：点线间的距离课本P108例7小结：1.平面内一点P(00,x y ) 到直线Ax+By+C=0的距离公式是2200B A CBy Ax d +++= 当A=0或B=0时,公式仍然成立。
2.两平行直线间的距离可以转化为点到直线的距离（采用与x ，y 轴的交点）限时训练编写：陈文钦学号组次：姓名______________基础过关题1.求坐标原点到直线3x+2y-26=0的距离.2.求点P（-1，2）到直线2x+y-10=0的距离.3.求点P（-1,2）到直线l:3x=2的距离.4.求点P（-1,2）到直线l:3y=2的距离.课本110页A组第9题，B组第2、4题；知识加餐1、动点P在直线x+y-4=0上，O为原点,则︱OP︱的最小值为( )A 10B 22C 6D 22、点P为x轴上一点，点P到直线3x-4y+6=0的距离为6,则点P的坐标为（）A（8,0） B（8,0）或（-12,0） C（-12,0） D（6,0）3．过点P(1,2)作一条直线，使A(2,3)，B(4，－5)到它的距离相等，则这条直线的方程是()A．4x＋y－6＝0 B．x＋4y－6＝0C．2x＋3y－7＝0或x＋4y－6＝0 D．3x＋2y－7＝0或4x＋y－6＝04、点（2，3）到直线2x+4y+a=0的距离为1，则实数a的值为____________。
平面直角坐标系导学案
1.掌握各个象限点的符号特征； 2.应用各个象限点的符号特征解决问题。
学习重点：各个象限点的符号特征 学习难点：应用各个象限点的符号特
征解决问题
学习过程：一.我回顾
1. （ ）组成平面直角坐标系，水平的数 轴称为（ ）轴或（ ），习惯上取向右的方 向为正方向；竖直的数轴为（ ）轴或 （ ），取向上的方向为正方向；两坐标轴 的交点为平面直角坐标系的（ ）。 2.画一个平面直角坐标系，并标出各个象限 的名称.
五.谈谈你的收获：
六.当堂测试：
1.已知点P（-a --1，∣a∣+1）一定在（ ） A.第一象限 B. 第二象限 C第三象限 D第四象限 2.已知点P（m+3，m+1）在直角坐标系的x轴上， 则P点的坐标为（ ） A（2,0） B（0,2） C（4,0） D(0,-4) 3.若点A（a，b）在第二象限，则点B（-a，-b） 在第-------象限 4.第二象限内的点p(a,b)满足∣a∣=2，a+b=3,则 p点坐标是---------- 5.已知点P（2-a，3a+6）到两坐标轴的距离相等， 求P点的坐标
1.若点A（a-1，a）在第二象限，则点B（a，1-a）在第-------象限 2.若点P（m，1-2m）的横坐标与纵坐标互为相反数，则点P一定在--------- 3.若点P（a，b）在第三象限，则点Q（-ab，a+b）在第-------象限.
四.提升能力：
教师点拨：
同学们今后在做有关点的坐标的问题时，我们一 定要在掌握了各个象限点的坐标的特征的基础上， 认真全面考虑问题，才能作出正确解答.
2
y
第二象限
5 4 3 2 1
平面直角坐标系导学案
象马6491543287532(街)(巷)2354114532AB O C6045。
1麻城市春蕾学校导学稿七年级数学备课组 撰稿人：蔡晓东 审稿人：郑强 周锦华课题：7.1.1有序数对【学习目标】：1.通过现实情景感受利用有序数对表示位置的广泛性，能利用有序数对来表示位置.2.让学生感受到可以用数量表示图形位置，形成数形结合的意识.3.感受数学源于生活.【学习重点】：理解有序数对的意义和作用 【学习难点】：用有序数对表示平面内的点的位置 【学习方法】：引导自学,合作交流 【学习过程】：、一、预习导学(预习课本第39-40页)1.你能在数轴上找到表示6的点吗？2.地埋图册上有一处写着“北纬44.2°，东经125.7°”，你能在地球仪上找到这个位置吗？3.你买了一张8排6号的电影票，你能很快找到自己的座位吗？ 分析以上情景，他们分别利用哪些数据找到位置的。
二、学习研讨问题1：在看电影时,同学都会根据电影票上的“排数”和“号数”准确地“对号入座”。
右边是某电影院的座位示意图,你能指出4排4号，6排4号和6排6号的位置吗(分别记为A 、B)?问题2：由“排数”和“号数”这两个数字就能找到你的位子，用1个数能找到吗？问题3：在电影院里确定你的座位，如果用（2，7）表示第2排第7号的座位，那么（5，8）表示什么意思？它与（8，5）的意义相同吗？问题4：要确定一个位置必须要有几个数，数字的顺序不同意义一样吗？概念：我们把这种有顺序的两个数a 与b 组成的数对叫做有序数对（ordered pair ）,记作（a,b ）。
它可以很准确的表示出一个位置。
三、练习巩固：问题1：如图所示的马所处的位置为（2，3）． （1）你能表示图中象所处的位置吗？（2）写出马下一步可以到达的位置。
方法指导：（1）由马的位置可知：列数在前，行数在后；（2）中国象棋中的规则是“马”走日，“象”飞田。
问题2：如图是某市交通网络图，邮局位于2街与4巷的十字路口，学校位于6街1巷的十字路口，如果用（2，4）表示邮局的位置，张老师想去邮局发一份快递，请你用有序数对写出他从学校到邮局的最近路线。
高中数学《平面直角坐标系》导学案
§1.1平面直角坐标系1，知识与技能：回顾在平面直角坐标系中刻画点的位置的方法2，能力与与方法：体会坐标系的作用3，情感、态度与价值观：通过观察、探索、发现的创造性过程，培养创新意识。
【重点、难点】\教学重点：体会直角坐标系的作用教学难点：能够建立适当的直角坐标系,解决数学问题二、学习过程【情景创设】运动会的开幕式上常常有大型团体操的表演，其中不断变化的背景图案是由看台上座位排列整齐的人群不断翻动手中的一本画布构成的。
要出现正确的背景图案，需要缺点不同的画布所在的位置。
【导入新课】1.直角坐标系(1)数轴①定义：规定了原点、正方向和_________的直线.②对应关系：数轴上的点与_____之间一一对应.(2)直角坐标系①定义：在同一个平面上相互垂直且有公共原点的两条数轴构成平面直角坐标系，简称直角坐标系.②相关概念：数轴的正方向：水平放置的数轴_____的方向、水平放置的数轴_____ 的方向分别是数轴的正方向.x轴或横轴：坐标轴_____的数轴.y轴或纵轴：坐标轴_____的数轴.坐标原点：坐标轴的__________.③对应关系：平面直角坐标系内的点与_________________之间一一对应.④公式：设平面直角坐标系中，点P1(x1，y1)，P2(x2，y2)，线段P1P2的中点为两点间的距离公式AB=___________________中点P的坐标公式d = ___________________三、典例分析典例1】已知△ABC的边AB长为2a，若BC的中线为定长m，求顶点C的轨迹方程. 【变式拓展】若圆x2+y2=1经过变换φ′后得到曲线22x yC1, 2516'+=：求变换φ′的坐标变换公式.四、总结反思方法技巧:与伸缩变换相关问题的处理方法(1)已知变换前的曲线方程及伸缩变换，求变换后的曲线方程的方法：利用伸缩变换用(x′，y′)表示出(x，y)，代入变换前的曲线方程.(2)已知变换后的曲线方程及伸缩变换，求变换前的曲线方程：利用伸缩变换用(x，y)表示(x′，y′)，代入变换后的曲线方程.五、随堂检测1.求将椭圆22x y1259+=按φ:1x x51y y3⎧'=⎪⎪⎨⎪'=⎪⎩，变换后的曲线围成图形的面积.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
子洲三中 “双主”高效课堂 导学案
2014-2015学年第一学期 姓名： 组名： 使用时间2014年 月 日
年 级
科 目
课 题
主 备 人
备 课 方 式 负责人（签字） 审核领导（签字） 序号 八（3） 数学 §3.3轴对称与坐标变化 乔智
一、教学目标：
1、在同一直角坐标系中，感受图形上点的坐标变化与图形的轴对称变换之间的关系．
2、经历图形坐标变化与图形轴对称之间关系的探索过程，发展形象思维能力和数形结合意识。
二、教学过程
有了坐标系，图像上的点就对应着坐标了，反过来坐标就可以反应点了。
相应地，点的运动变化自然导致坐标的变化，坐标的变化也可以从数量的角度反应图形的变化。
不妨先研究我们熟悉的轴对称。
活动1：探索两个关于坐标轴对称的图形的坐标关系
1.在如图所示的平面直角坐标系中，第一、二象限内各有一面小旗。
两面小旗之间有怎样的位置关系？对应点A 与A 1的坐标又有什么特点？其它对应的点也有这个特点吗？
2.在右边的坐标系内，任取一点，做出这个点关于y 轴对称的点，看看两个点的坐标有什么样的位置关系，说说其中的道理。
变式。
发展
3.如果关于x 轴对称呢？
在这个坐标系里作出小旗ABCD 关于x 轴的对称图形，它的各个顶点的坐标与原来的点的坐标有什么关系？
归纳。
概括
4.关于x 轴对称的两点，它们的横坐标 ，纵坐标 ；
关于y 轴对称的两点，它们的横坐标 ，纵坐标 。
运用。
巩固
5.已知点P(2a-3，3)，点A （－1，3b+2），
（1）如果点P 与点A 关于x 轴对称，那么a+b= ； （2）如果点P 与点A 关于y 轴对称，那么a+b= 。
活动2：探索坐标变化引起的图形变化
反过来，坐标具有上述关系的点，一定关于坐标轴对称吗？我们先做几个具体的，找找经验。
１（1）在平面直角坐标系中依次连接下列各点：（0，0），（5，4），（3，0），（5，1），（5，-1），
（3，0），（4，-2），（0，0），你得到了一个怎样的图案？
（2）将所得图案的各个顶点的纵坐标保持不变，横坐标分别乘以-1，顺次连接这些点，你会得到怎样的图案？这个图案与原图案又有怎样的位置关系呢？
变式。
拓展
2.如果1（1）中所得图案的各个顶点的横坐标保持不变，纵坐标分别变为原来的-1倍，顺次连接所得的点，你会得到怎样的图案？这个图案与原图案有怎样的位置关系呢？ *3。
如果纵坐标、横坐标都分别变为原来的-1倍，得到的图形与原来的图形又有怎样的关系呢？说说你的判断和理由。
归纳。
概括
4.横坐标相同、纵坐标相反的两点， ； 横坐标相反、纵坐标相同的两点， 。
运用。
巩固
5.五个点的坐标如下：A(-1,2),B(1,2),C(2，-1)，D(-1，-2),E(2,1)，其中关于x 轴对称的点有 ，关于y 轴对称的有 。
活动3：反思小结 1.你有哪些收获？
2.要画一个和已知图形的成轴对称的图形,你有哪些方法,与同伴交流.
活动4：自主反馈
1. 已知A 、B 两点的坐标分别是(－2，3)和(2，3），则下面四个结论：
①A 、B 关于x 轴对称；②A 、B 关于y 轴对称；③A 、B 关于原点对称；④A 、B 之间的距离为4，其中正确的有( )
A ．1个
B ．2个
C ．3个
D ．4个
*2.一束光线从点Ａ（３，３）出发，经过ｙ轴上点Ｃ反射后经过点Ｂ（１，０）则光线从Ａ点到Ｂ点经过的路线长是（ ）。
Ａ．４ Ｂ．５ Ｃ．６ Ｄ．７
批改日期 月 日。