四川省成都市第七中学2019届高三一诊模拟考试理科综合答案
2019届四川省成都市第七中学高三上学期一诊模拟考试理综试卷精英版
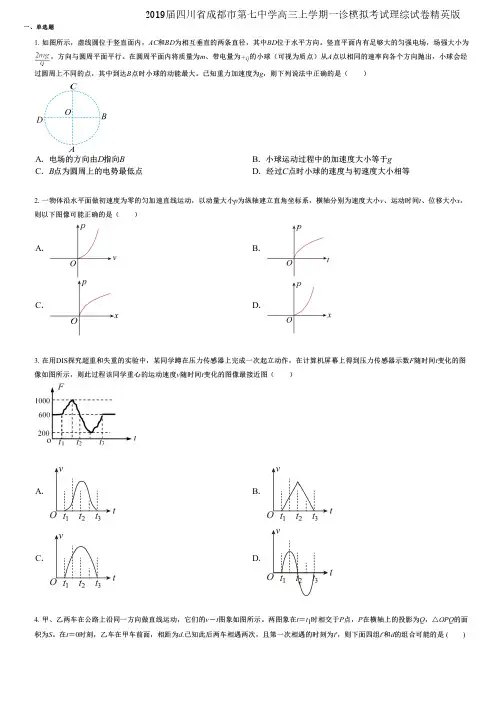
一、单选题1. 如图所示，虚线圆位于竖直面内，AC 和BD 为相互垂直的两条直径，其中BD 位于水平方向。
竖直平面内有足够大的匀强电场，场强大小为，方向与圆周平面平行。
在圆周平面内将质量为m、带电量为的小球（可视为质点）从A 点以相同的速率向各个方向抛出，小球会经过圆周上不同的点，其中到达B 点时小球的动能最大。
已知重力加速度为g，则下列说法中正确的是（ ）A ．电场的方向由D 指向BB ．小球运动过程中的加速度大小等于gC ．B 点为圆周上的电势最低点D ．经过C 点时小球的速度与初速度大小相等2. 一物体沿水平面做初速度为零的匀加速直线运动，以动量大小p 为纵轴建立直角坐标系，横轴分别为速度大小v 、运动时间t 、位移大小x ，则以下图像可能正确的是（ ）A．B．C．D．3. 在用DIS 探究超重和失重的实验中，某同学蹲在压力传感器上完成一次起立动作，在计算机屏幕上得到压力传感器示数F 随时间t 变化的图像如图所示，则此过程该同学重心的运动速度v 随时间t变化的图像最接近图（ ）A．B．C．D．4. 甲、乙两车在公路上沿同一方向做直线运动，它们的v －t 图象如图所示。
两图象在t ＝t 1时相交于P 点，P 在横轴上的投影为Q ，△OPQ 的面积为S 。
在t ＝0时刻，乙车在甲车前面，相距为d .已知此后两车相遇两次，且第一次相遇的时刻为t ′，则下面四组t ′和d 的组合可能的是 ( )2019届四川省成都市第七中学高三上学期一诊模拟考试理综试卷精英版二、多选题A ．t ′＝t 1，d ＝SB ．t ′＝t 1，d＝S C ．t ′＝t 1，d ＝S D ．t ′＝t 1，d＝S5. 如图所示，从倾角为θ的斜面上A 点，以水平速度v 0抛出一个小球，不计空气阻力，它落到斜面上B点时所用的时间为（ ）A．B．C．D．6. 质量为的物块，置于水平地面上。
在水平力F 的作用下由静止开始运动，F 与时间t 的关系如图所示。
【精品】四川省成都市第七中学2019届高三一诊模拟考试理科综合试题(答案)
【精品】成都七中2019届高中毕业班一诊模拟理科综合本试卷分选择题和非选择题两部分。
满分300 分，考试时间150 分钟。
注意事项：1. 答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上。
2. 答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号。
3. 答非选择题时，必须使用0. 5 毫米黑色签字笔，将答案书写在答题卡规定的位置上。
4. 所有题目必须在答题卡上作答，在试题卷上答题无效。
5. 考试结束后，只将答题卡交回。
可能用到的原子量：H-1C-12N-14 0-16Na-23 Ba-137第I卷（共126 分〉有一项是符合题目一、选择题z本题共13个小题，每小题6分。
在每小题给出的四个选项中，只要求的。
1. 下列有关生物体中分子和结构的叙述，正确的是A.多糖和脂肪都是由许多单体连接成的多聚体 B.RNA 聚合酶与mRNA 的基本组成单位相同c.质粒与T2 噬菌体的DNA 都能携带遗传信息D.激素、神经递质与抗体都能向细胞传递信息2. 下列有关生物学实验及研究的叙述，正确的是A. 用人体的成熟红细胞为实验材料可诊断镰刀型细胞贫血症B. 用差速离心法可分离叶绿体中色素和细胞质中各种细胞器c. 用同位素标记法跟踪氨基酸可研究性激素合成和分泌过程D.用澳靡香草酌蓝水溶液可检测乳酸链球菌细胞呼吸的产物3. 下列关于正常人体生命活动调节的叙述，正确的是A. 甲状腺激素含量减少时，机体通过反馈调节促进下丘脑和垂体的分泌活动B.渗透压升高时，抗利尿激素分泌增加使肾小管和集合管对水的通透性增加c.寒冷环境下，机体通过皮肤毛细血管收缩减少散热使散热量低于炎热环境D.血糖浓度升高时，膜岛素能直接参与骨髓肌细胞中葡萄糖合成糖原的过程4. 下列有关兴奋的产生、传导和传递的叙述，正确的是A.神经纤维处于静息状态时，膜内K＋与N旷的比值低于产生兴奋时 B.突触后膜一定是神经元的树突末梢形成的，且有神经递质的受体c.突触小体一定是神经元轴突末梢膨大形成的，可以释放神经递质 D.兴奋在神经纤维上的传导和神经元之间的传递都是电信号的形式5. SP8 噬菌体侵染枯草杆菌后，将产生的mRNA 与分开的SP8--DNA 的每条单链混合并进行核酸分子的杂交实验，检测发现mRNA 只和其中一条富含嘿岭碱基的DNA 链形成杂交分子。
四川省成都七中2019届高三模拟考试理科综合试题及答案
成都七中 2018-2019 学年下期高三热身理综考试题（最后一卷）注意事项：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3.全部答案在答题卡上完成，答在本试题上无效。
4.考试结束后，将本试题和答题卡一并交回。
可能用到的相对原子质量：H-1 C-12 O-16 Na-23 第Ⅰ卷（选择题共126 分）一、选择题：本大题共13 小题，每小题6 分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．下列有关细胞物质的叙述，正确的是（）A.脂质具有构成生物膜、调节代谢和储存能量等生物学功能B.组成蛋白质、核酸、糖原的单体都具有多样性C.核糖体与酶、抗体、激素、神经递质的合成都有关D.DNA 是主要的遗传物质，可通过噬菌体侵染细菌的实验来证明2．下列有关生物实验的叙述，正确的是（）A.对培养液中的酵母菌进行计数时，先将培养液滴入计数室，然后盖好盖玻片在显微镜下计数B.“体验制备细胞膜的方法”实验中，需用血液加适量的生理盐水制备新鲜的红细胞稀释液C.“探究生长素类似物促进扦插枝条生根的最适浓度”的正式实验中，需要用蒸馏水作对照组D.“探究温度对酶的酶活性的影响”实验中，将酶与底物混合后再进行保温3．癌胚抗原（CEA）和甲胎蛋白（AFP）是人胚胎时期机体合成的两种糖蛋白，出生后其含量很快下降，但某些癌症患者血液中的CEA 或AFP 含量远超正常值。
下列说法错误的是（）A.CEA 、AFP 的合成属于吸能反应B.CEA 或AFP 含量超过正常值时，可确诊为癌症C.体内某些细胞的大量增殖会使CEA 、AFP 含量升高D.控制CEA 、AFP 合成的基因，碱基排列顺序有差异4．下列有关人体内环境和稳态调节的叙述，正确的是（）A．大量出汗后只补充水，血浆渗透压会升高B．免疫系统的作用与机体维持内环境稳态无关C．温度下降时甲状腺激素会定向运输给产热器官D．内环境稳态遭到破坏必将引起细胞代谢紊乱5．下列有关染色体、DNA 、基因、脱氧核苷酸的说法，正确的是（）A.一个基因含有许多个脱氧核苷酸，基因的特异性是由脱氧核苷酸的比例决定的B.基因是具有遗传效应的DNA 片段，不是4 种碱基对的随机排列C.在DNA 分子结构中，脱氧核苷酸的排列构成了DNA 分子的基本骨架D.染色体是DNA 的主要载体，一条染色体上含有2 个DNA 分子6．某自由交配的种群在Ⅰ、Ⅱ、Ⅲ时间段都经历多次繁殖过程，定期随机抽取100 个个体，测得基因型为AA 、aa 的个体数量变化曲线如图所示。
2019届四川省成都市第七中学高三一诊模拟考试数学(理)试题(word版)
2019届四川省成都市第七中学高三一诊模拟考试数学（理）试题（考试时间：120分钟 试卷满分：150分）一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.若随机变量()23,X N σ，且()50.2P X ≥=，则()15P X <<=（ ）A.0.6B.0.5C.0.4D.0.32.函数()2ln 1y x =+的图象大致是（ ）A. B.C. D.3.“牟合方盖”是我国古代数学家刘徽在探求球体体积时构造的一个封闭几何体，它由两个等径正贯的圆柱体的侧面围成，其直视图如图（其中四边形是为体现直观性而作的辅助线）.当“牟合方盖”的正视图和侧视图完全相同时，其俯视图为（ ）A. B.C. D.4.设i 是虚数单位，复数z 满足()13z i z -=+，则z 的虚部为（ ） A.1B.-1C.-2D.25.执行下边的算法程序，若输出的结果为120，则横线处应填入（ ）A.6k <B.6k ≤C.6k ≥D.6k >6.设实数,x y 满足242210x y x y x -≤⎧⎪+≤⎨⎪-≥⎩，则1y x +的最大值是（ ）A.-1B.12C.1D.327.“22log log a b >”是“11a b<”的（ ） A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件8.函数()sin cos 6f x x x x π⎛⎫=∙+ ⎪⎝⎭的图象的一条对称轴方程是（ ） A.12x π=B.6x π=C.4x π=D.3x π=9.将多项式656510a x a x a x a ++++…分解因式得()()52x x m -+，m 为常数，若57a =-，则0a =（ ） A.-2B.-1C.1D.210.已知正三棱锥的高为6，侧面与底面成60︒的二面角，则其内切球（与四个面都相切）的表面积为（ ） A.4πB.16πC.36πD.64π11.设,,a b c 分别是ABC ∆的内角,,A B C 的对边，已知()()()()sin sin sin b c A C a c A C ++=+-，设D是边BC 的中点，且ABC ∆()AB DA DB ∙+等于（ ） A.2B.4C.-4D.-212.如果{}n a 不是等差数列，但若k N *∃∈，使得212k k k a a a +++=，那么称{}n a 为“局部等差”数列.已知数列{}n x 的项数为4，记事件A ：集合{}{}1234,,,1,2,3,4,5x x x x ⊆，事件B ：{}n x 为“局部等差”数列，则条件概率()|P B A =（ ） A.415B.730C.15D.16二、填空题：本题共4小题，每小题5分，共20分.13.某学校初中部共120名教师，高中部共180名教师，其性别比例如图所示，已知按分层抽样方法得到的工会代表中，高中部女教师有6人，则工会代表中男教师的总人数为________.14.设抛物线2:12C y x =的焦点为F ，准线为l ，点M 在C 上，点N 在l 上，且()0FN FM λλ=>，若4MF =，则λ的值为________.15.设0a >，0b >，e 为自然对数的底数，若12e a e x b dx x -+=⎰，则211a b++的最小值是________.16.若函数()232,02,0x a x f x x ax x +⎧-≤⎪=⎨-+>⎪⎩有三个不同的零点，则实数a 的取值范围是________.三、解答题：共70分.解答应写出文字说明，证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生依据要求作答. 17.正项等比数列{}n a 中，已知34a =，426a a =+.()Ⅰ求{}n a 的前n 项和n S ；()Ⅱ对于()Ⅰ中的n S ，设1n b S =，且()1n n n b b S n N *+-=∈，求数列n b 的通项公式.18.“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”……江南梅雨的点点滴滴都流润着浓烈的诗情.每年六、七月份，我国长江中下游地区进入持续25天左右的梅雨季节，如图是江南Q 镇2009～2018年梅雨季节的降雨量（单位：mm ）的频率分布直方图，试用样本频率估计总体概率，解答下列问题：()Ⅰ“梅实初黄暮雨深”.假设每年的梅雨天气相互独立，求Q 镇未来三年里至少有两年梅雨季节的降雨量超过的概率；()Ⅱ“江南梅雨无限愁”.在Q 镇承包了20亩土地种植杨梅的老李也在犯愁，他过去种植的甲品种杨梅，平均每年的总利润为28万元.而乙品种杨梅的亩产量m （kg /亩）与降雨量之间的关系如下面统计表所示，又知乙品种杨梅的单位利润为320.01m -⨯（元/kg ），请你帮助老李排解忧愁，他来年应该种植哪个品种的杨梅可以使利润ξ（万元）的期望更大？（需说明理由）；19.已知椭圆()222210x y a b a b +=>>的离心率为2，且经过点()2,0A .()Ⅰ求椭圆的标准方程；()Ⅱ设O 为椭圆的中线，点()2,0D -，过点A 的动直线l 交椭圆于另一点B ，直线l 上的点满足4OB OC ∙=，求直线BD 与OC 的交点P 的轨迹方程.20.如图，在多面体ABCDE 中，AC 和BD 交于一点，除EC 以外的其余各棱长均为2.()Ⅰ作平面CDE 与平面ABE 的交线l ，并写出作法及理由； ()Ⅱ求证：平面BDE ⊥平面ACE ；()Ⅲ若多面体的体积为2，求直线DE 与平面BCE 所成角的正弦值.21.已知函数()sin 2cos 2f x x x x ax =+++，其中a 为常数.()Ⅰ若曲线()y f x =在0x =处的切线在两坐标轴上的截距相等，求a 的值； ()Ⅱ若对[]0,x π∀∈，都有()2f x ππ<<，求a 的取值范围.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.[选修4-4：坐标系与参数方程]在平面直角坐标系xOy 中，曲线C 的参数标方程为t tt tx e ey e e--⎧=+⎪⎨=-⎪⎩（其中t 为参数），在以O 为极点、x 轴的非负半轴为极轴的极坐标系（两种坐标系的单位长度相同）中，直线l的极坐标方程为sin 3πρθ⎛⎫-= ⎪⎝⎭()Ⅰ求曲线C 的极坐标方程；()Ⅱ求直线l 与曲线C 的公共点P 的极坐标.23.[选修4-5：不等式选讲]已知函数()21f x x x =-+，且,,a b c R ∈.()Ⅰ若2a b c ++=，求()()()f a f b f c ++的最小值； ()Ⅱ若1x a -<，求证：()()()21f x f a a -<+.第七中学2019届高三一诊模拟考试数学（理）试题参考答案一、选择题1-5:ADBCC 6-10: DABDB 11、12：AC 二、填空题13.12 14.3 15.8316.(]34， 三、解答题17.解：()Ⅰ设正项等比数列{}n a 的公比为()0q q >，则 由34a =及426a a =+得446q q=+，化简得22320q q --=，解得2q =或12q =-（舍去）.于是1241a q==，所以122112n n n S -==--，n N *∈. ()Ⅱ由已知111b S ==，()121n n n n b b S n N *+-==-∈，所以当2n ≥时，由累加法得()()()()()12111221122211n n n n n n n b b b b b b b b n -----=-+-++-+=+++--+……()12122212n n n n --=-+=--.又11b =也适合上式，所以{}n b 的通项公式为2n n b n =-，n N *∈.18.解：()Ⅰ频率分布直方图中第四组的频率为()11000.0020.0040.0030.1-⨯++=. 江南Q 地区在梅雨季节时降雨量超过350mm 的概率为500.0030.10.25⨯+=. 所以Q 地区未来三年里至少有两年梅雨季节的降雨量超过350mm 的概率为2323331119151444646432C C ⎛⎫⎛⎫⎛⎫⨯+-+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（或0.15625）. ()Ⅱ根据题意，总利润为()20320.01m m -（元），其中500,700,600,400m =. 所以随机变量ξ（万元）的分布列如下表.故总利润ξ（万元）的数学期望270.2350.431.20.322.40.1 5.414.09.36 2.2431E ξ=⨯+⨯+⨯+⨯=+++=（万元）.因为31>28，所以老李来年应该种植乙品种杨梅，可使总利润的期望更大.19.解：()Ⅰ因为椭圆的离心率c e a ==，且2a =，所以c =又2222b a c =-=.故椭圆的标准方程为22142x y +=. ()Ⅱ设直线l 的方程为2x ty =+（当t 存在时，由题意0t ≠），代入2224x y +=，并整理得()22240ty ty ++=.解得242B t y t -=+，于是224222B B t x ty t -=+=+，即222424,22t t B t t ⎛⎫-- ⎪++⎝⎭.设()002,C ty y +，则()()2230002224224842222t tyty t t y OB OC t t t -+---∙=+=+++. 由已知得4OB OC ∙=，得232084248t t y t --=+，解得04y t -=，于是42,C t -⎛⎫- ⎪⎝⎭.()* 又()2,0D -，此时2284,22t DB t t -⎛⎫= ⎪++⎝⎭，42,OC t -⎛⎫=- ⎪⎝⎭. 所以221616022DB OC t t -∙=+=++，于是DB OC ⊥. 故直线BD 与OC 的交点P 的轨迹是以OD 为直径的圆（除去,O D 两点）. 又当t 不存在时，,,,B C D P 四点重合，此时()2,0P -也满足题意. 于是点P 的轨迹方程是()220x x y ++=，即()22200x y x x ++=≠.或解：（()*前相同）由,B D 两点的坐标可得直线BD 的方程为()22ty x -=+. 又由点C 坐标可得直线OC 的方程为2y x t=. 两式相乘，消去参数t 得()22y x x =-+.（如果只求出交点P 的坐标，此步不得分） 又当t 不存在时，,,,B C D P 四点重合，此时()2,0P -也满足题意. 故直线BD 与OC 的交点的轨迹方程()22200x y x x ++=≠.20.解：()Ⅰ过点E 作AB （或CD ）的平行线，即为所求直线l .AC 和BD 交于一点，,,,A B C D ∴四点共面.又四边形ABCD 边长均相等. ∴四边形ABCD 为菱形，从而//AB DC .又AB ⊄平面CDE ，且CD ⊂平面CDE ，//AB ∴平面CDE .AB ⊂平面ABE ，且平面ABE 平面CDE l =，//AB l ∴.()Ⅱ()Ⅱ证明：取AE 的中点O ，连结OB ，OD .AB BE =，DA DE =，OB AE ⊥∴，OD AE ⊥.又OB OD O =，AE ⊥∴平面OBD ，BD ⊂平面OBD ，故AE BD ⊥.又四边形ABCD 为菱形，AC BD ⊥∴.又AE AC A =，BD ⊥∴平面ACE .又BD ⊂平面BDE ，∴平面BDE ⊥平面ACE .()Ⅲ解：由222E ABCD E ABD D ABE V V V ---===，即1D ABE V -=.设三棱锥D ABE -的高为h，则112132h ⎛∙∙= ⎝，解得h =又3DO =DO ⊥∴平面ABE .建立如图的空间直角坐标系O xyz -，则()0,1,0A -，)B，(D ，()0,1,0E .(BC AD ==∴，()0BE =，.由0y y ⎧=⎪-=得，平面BCE 的一个法向量为()1,3,1n =-. 又(0,1,DE =，于是cos ,DE n <>==.故直线DE 与平面BCE 所成角的正弦值为5. 21.解：()Ⅰ求导得()cos sin f x x x x a '=-+，所以()0f a '=. 又()04f =，所以曲线()y f x =在0x =处的切线方程为4y ax =+. 由切线在两坐标轴上的截距相等，得44a-=，解得1a =-即为所求. ()Ⅱ对[]0,x π∀∈，()sin 0f x x x ''=-<，所以()f x '在[]0,π区间内单调递减.（1）当0a ≤时，()()00f x f a ''<=≤，所以()f x 在区间[]0,π内单调递减，故()()f x f a ππ>=，由()f x π>恒成立，得1a ≥，这与0a ≤矛盾，故舍去.（2）当a π≥时，()()0f x f a ππ''>=-≥，所以()f x 在区间[]0,π内单调递增，故()()()0f f x f π<<，即()4f x a π<<，由()2f x ππ<<恒成立得a π≤，结合a π≥得a π=.（3）当0a π<<时，因为()00f a '=>，()0f a ππ'=-<，且()f x '在[]0,π区间上单调递减，结合零点存在定理可知，存在唯一()00,x π∈，使得()00f x '=，且()f x 在区间[]00,x 内单调递增，在区间[]0,x π内单调递减.故()()(){}min 0,f x f fπ>，由()f x π>恒成立知，()04f π=≥，()f a πππ=≥，所以1a π≤<. 又()f x 的最大值为()00000sin 2cos 2f x x x x ax =+++，由()00f x '=得000sin cos a x x x =-， 所以()20000002sin 2cos cos 2f x x x x x x =+-+.设()()22sin 2cos cos 20g x x x x x x x π=+-+<<，则()2s i n 0g xx x '=>，所以()g x 在区间[]0,π内单调递增，于是()()2g x g ππ<=，即()20f x π<.所以不等式()2f x π<恒成立. 综上所述，所求a 的取值范围是[]1,π.22.解：()Ⅰ消去参数t ，得曲线C 的直角坐标方程()2242x y x -=≥.将cos x ρθ=，y sin ρθ=代入224x y -=，得()222cos4sin ρθθ-=.所以曲线C 的极坐标方程为2cos 2444ππρθθ⎛⎫=-<< ⎪⎝⎭.()Ⅱ将l 与C 的极坐标方程联立，消去ρ得242cos 23sin πθθ⎛⎫-=⎪⎝⎭.展开得()22223cos cos sin 2cos sin θθθθθθ-+=-.因为cos 0θ≠，所以23tan 10θθ-+=.于是方程的解为tan θ=，即6πθ=.代入sin 3πρθ⎛⎫-=⎪⎝⎭ρ=P 的极坐标为6π⎛⎫ ⎪⎝⎭.23.解：()Ⅰ由柯西不等式得，()22221433a b c a b c ++≥++=（当且仅当23a b c ===时取等号），所以()()()()()222473133f a f b f c a b c a b c ++=++-+++≥+=，即()()()f a f b f c ==的最小值为73； ()Ⅱ因为1x a -<，所以()()()()2211f x f a x a x a x a x a x a -=---=-∙+-<+-()()()()212112121x a a x a a a a =-+-≤-+-<++=+，故结论成立.- 11 -。
2019届四川省成都市第七中学高三一诊模拟数学(理)试卷及答案解析
4．考试结束后,请将本试题卷和答题卡一并上交。
一、单选题
1．若随机变量 ,且 ,则
A．0.6 B．0.5 C．0.4 D．0.3
2．函数 的图象大致是
A． B．
C． D．
3．“牟合方盖”是我国古代数学家刘徽在探求球体体积时构造的一个封闭几何体,它由两个等径正贯的圆柱体的侧面围成,其直视图如图（其中四边形是为体现直观性而作的辅助线）.当“牟合方盖”的正视图和侧视图完全相同时,其俯视图为
C．充要条件 D．既不充分也不必要条件
8．函数 的图象的一条对称轴方程是
A． B． C． D．
9．将多项式 分解因式得 , 为常数,若 ,则
A．-2 B．-1 C．1 D．2
10．已知正三棱锥的高为6,侧面与底面成 的二面角,则其内切球（与四个面都相切）的表面积为
A． B． C． D．
11．设 分别是 的内角 的对边,已知 ,设 是边 的中点,且 的面积为 ,则 等于
Ⅰ “梅实初黄暮雨深” 假设每年的梅雨天气相互独立,求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率；
Ⅱ “江南梅雨无限愁” 在Q镇承包了20亩土地种植杨梅的老李也在犯愁,他过去种植的甲品种杨梅,平均每年的总利润为28万元 而乙品种杨梅的亩产量 亩 与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为 元 ,请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅可以使总利润 万元 的期望更大？ 需说明理由
降雨量
亩产量
500
700
600
400
19．已知椭圆 的离心率为 ,且经过点 .
成都七中 2019 届 高中毕业班高考模拟题-理科综合(答案)
，从初态到最低点，
根据动能定理可知： k t 20．AC 【解析】以正离子为研究对象，由动能定理得
돀 ，解得外力做功：
，D 正确
， 时间内通过的总电量为
，
喷出的总质量为
。由动量定理可知正离子所受平均冲量
，由以上式
子可得
，根据牛顿第三定律可知，发动机产生的平均推力
，故 A 正确。
21．BC 设导轨与金属杆之间的动摩擦因数为μ，根据共点力的平衡条件可得：F-μmg=BIL，而
m/s2，加速度不变，
D 错误。 19．BD A. 因为重力做正功，所以重力势能减小了 mgL，A 错误
B.根据题意克服电场力做功： 电
，所以电势能增加 2mgL，B 正确
C.因为缓慢移动，所以小球动能不变，但是重力势能减小了，所以机械能减小，C 错误
D. 初态小球静止，根据平衡可知：sin
，所以电场力：
(2)①> ΔH1+ΔH2
② 32 1.56
htቀ tht
th
(MPa)2
③催化剂显著降低了 C10H12→C10H8 的活化能，反应生成的 C10H12 很快转变为 C10H8，
C10H12 不能积累 35．（15 分，除标注外，每空 2 分）
(1)
（2 分） 2（1 分）
(2)①A 能形成分子间氢键，B 分子间只存在范德华力
射性同位素 tO注入人体，进行医学检查时，人体呼吸沉积的量很小，对人体造成的影响很小，
检查过程安全，D 错误．故选 A.
15．D 16．A
17．D
A. 由 P=UI 可知，额定电流 I=P/U=180/36=5A，故 A 错误；
B. 电量 q=10Ah=10×3600=3.6×104C，故 B 错误；
2019届四川省成都市第七中学高三上学期一诊模拟考试理综试卷真题汇编版
一、单选题二、多选题1. 小丽同学乘坐轻轨列车欣赏重庆轨道环线沿途风光，看到一幢幢高楼向后退去，她选的参考系是（ ）A ．列车B ．地面C ．高楼2. 下列说法正确的是（ ）A ．物体做曲线运动时，速度一定在改变B ．做曲线运动的物体受到的合外力可能为零C ．物体在恒力作用下不可能做曲线运动D ．做曲线运动的物体在某一时刻加速度可能与速度同方向3.如图所示，人竖直站在自动扶梯的水平踏板上，随扶梯一起匀速斜向下运动．以下分析正确的是（ ）A ．人受到重力和支持力的作用B ．人受到摩擦力的方向水平向左C ．人受到重力、支持力和摩擦力的作用D ．人受到与速度方向相同的合外力4. 下列射线本质上由电子构成的是（ ）A ．射线B ．射线C ．射线D ．射线5. 屈原在长诗《天问》中发出了“日月安属?列星安陈?”的旷世之问，这也是中国首次火星探测工程“天问一号”名字的来源。
“天问一号”探测器的发射时间要求很苛刻，必须在每次地球与火星会合之前的几个月、火星相对于太阳的位置领先于地球特定角度的时候出发。
火星与地球几乎在同一平面内沿同一方向绕太阳近似做匀速圆周运动。
如图所示，不考虑火星与地球的自转，且假设火星和地球的轨道平面在同一个平面上，相关数据见下表，则根据提供的数据可知（ ）质量半径绕太阳做圆周运动的周期地球MR 1年火星约0.1M 约0.5R 约1.9年A ．在火星表面附近发射飞行器的速度至少为7.9km/sB ．地球与火星从第1次会合到第2次会合的时间约为2.1年C ．火星到太阳的距离约为地球到太阳的距离的1.9倍D ．火星表面的重力加速度与地球表面的重力加速度之比约为3：56. 下列说法正确的是（ ）2019届四川省成都市第七中学高三上学期一诊模拟考试理综试卷真题汇编版三、实验题A ．图甲实验利用“放大法”观察玻璃瓶的微小形变B ．图乙水杯随圆盘一起匀速圆周转动，受重力、支持力、静摩擦力和向心力C ．图丙货物被起重机竖直向上匀速提起过程中，所受合外力不做功，机械能增加D ．图丁自动卸货车始终静止在地面上， 车用在液压机作用下倾角缓慢增大且货物始终没有下滑，该过程中车厢对货物的支持力逐渐变大且做正功7. 如图所示，C 为中间插有电介质的电容器，a 和b 为其两极板；a 板接地；P 和Q 为两竖直放置的平行金属板，在两板间用绝缘线悬挂一带电小球；P 板与b 板用导线相连，Q 板接地．开始时悬线静止在竖直方向，在b 板带电后，悬线偏转了角度α．在以下方法中，能使悬线的偏角α变大的是A ．缩小a 、b 间的距离B ．加大a 、b 间的距离C ．取出a 、b 两极板间的电介质D ．换一块形状大小相同、介电常数更大的电介质8. 如图所示，带电荷量为的球1固定在倾角为光滑绝缘斜面上的a 点，其正上方L 处固定一电荷量为的球2，斜面上距a 点L 处的b 点有质量为m 的带电球3，球3与一端固定的绝缘轻质弹簧相连并在b 点处于静止状态。
四川省成都市第七中学2019届高三第一次诊断性检测数学(理)试题(解析版)
2019年四川省成都七中高考数学一诊试卷（理科）一、选择题（本大题共12小题，共60.0分）1.若随机变量～，且，则A. B. C. D.【答案】A【解析】解：随机变量～，且，．故选：A．由已知结合正态分布曲线的对称性即可求解．本题考查正态分布曲线的特点及曲线所表示的意义，考查正态分布中两个量和的应用，考查曲线的对称性，属于基础题．2.函数的图象大致是A. B. C. D.【答案】D【解析】解：函数的定义域为R，，故排除A，C；，当时，，可知在上为减函数，排除B．故选：D．由函数的定义域及排除A，C，再由导数研究单调性排除B，则答案可求．本题考查函数的图象及图象变换，训练了利用导数研究函数的单调性，是中档题．3.“牟合方盖”是我国古代数学家刘徽在探求球体体积时构造的一个封闭几何体，它由两等径正贯的圆柱体的侧面围成，其直观图如图其中四边形是为体现直观性而作的辅助线当“牟合方盖”的正视图和侧视图完全相同时，其俯视图为A. B. C. D.【答案】B【解析】解：根据几何体的直观图：由于直观图“牟合方盖”的正视图和侧视图完全相同时，该几何体的俯视图为有对角线的正方形．故选：B．直接利用直观图“牟合方盖”的正视图和侧视图完全相同，从而得出俯视图形．本题考查的知识要点：直观图和三视图之间的转换，主要考查学生的空间想象能力和转化能力，属于基础题型．4.设i是虚数单位，复数z满足，则z的虚部为A. 1B.C.D. 2【答案】C【解析】解：由，得，即．的虚部为．故选：C．把已知等式变形，再由复数代数形式的乘除运算化简得答案．本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．5.执行如图的算法程序，若输出的结果为120，则横线处应填入A.B.C.D.【答案】C【解析】解：模拟程序的运行，可得，执行循环体，，执行循环体，，执行循环体，，执行循环体，，执行循环体，，由题意，此时，不满足条件，退出循环，输出S的值为120．可得横线处应填入的条件为．故选：C．分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出变量S的值，要确定进入循环的条件，可模拟程序的运行，用表格对程序运行过程中各变量的值进行分析，不难得到题目要求的结果．算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视程序填空也是重要的考试题型，这种题考试的重点有：分支的条件循环的条件变量的赋值变量的输出其中前两点考试的概率更大此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．6.设实数x，y满足，则的最大值是A. B. C. 1 D.【答案】D【解析】解：画出满足条件的平面区域，如图示：而的几何意义表示过平面区域内的点与点的连线的斜率，由，解得：，，故选：D．画出约束条件的可行域，利用目标函数的几何意义，求解即可．本题主要考查线性规划的应用以及直线斜率的求解，利用数形结合是解决本题的关键．7.“”是“”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】D【解析】解：，推不出，推不出，“”是“”的既不充分也不必要条件．故选：D．首先转化，然后根据充分条件和必要条件的定义进行判断即可．本题主要考查充分条件和必要条件的判断，根据充分条件和必要条件的定义是解决本题的关键．8.函数的图象的一条对称轴方程是A. B. C. D.【答案】B【解析】解：．由，得，，当时，，即函数的对称轴为，故选：B．利用两角和差的余弦公式结合辅助角公式进行化简，结合三角函数的对称性进行求解即可．本题主要考查三角函数的对称性，利用辅助角公式将函数进行化简是解决本题的关键．9.将多项式分解因式得，m为常数，若，则A. B. C. 1 D. 2【答案】D【解析】解：由，，可得：，解得，即为：，时，，故选：D．由两，通过，求出m，然后利用二项式定理求解即可．本题考查了二项式定理的应用，考查了推理能力与计算能力，属于中档题．10.已知正三棱锥的高为6，侧面与底面成的二面角，则其内切球与四个面都相切的表面积为A. B. C. D.【答案】B【解析】解：过顶点V做平面ABC是正三棱锥，为中心，过O做，垂足为D，连接VD，则为侧面与底面成的二面角，侧面与底面成的二面角，，，，，，．，为内切球的半径．，内切球的表面积．故选：B．过顶点V做平面ABC，过O做，垂足为D，连接VD，则为侧面与底面成的二面角，从而，分别求出OD、AB、VD的长，由此利用等体积法求解．本题考查棱锥的外接球球半径的求法，解题时要认真审题，仔细解答，注意合理地进行等价转化．11.设a，b，c分别是的内角A，B，C的对边，已知，设D是BC边的中点，且的面积为，则等于A. 2B. 4C.D.【答案】A【解析】解：，，，，，，，，故选：A．先根据正余弦定理求出，，再将，化为，后用数量积可得．本题考查了平面向量数量积的性质及其运算，属基础题．12.如果不是等差数列，但若，使得，那么称为“局部等差”数列已知数列的项数为4，记事件A：集合2，3，4，，事件B：为“局部等差”数列，则条件概率A. B. C. D.【答案】C【解析】解：由已知数列{x n}的项数为4，记事件A：集合{x1，x2，x3，x4}{1，2，3，4，5}，则事件A的基本事件为：，，，，，共5个，在满足事件A的条件下，事件B：{x n}为“局部等差”数列有，共1个，即条件概率P（B|A）=，故选：C．由即时定义可得：事件A的基本事件为：，，，，，共5个，在满足事件A的条件下，事件B：{x n}为“局部等差”数列有，共1个，由条件概率可得：P（B|A）=，得解．本题考查了对即时定义的理解及条件概率，属中档题．二、填空题（本大题共4小题，共20.0分）13.某学校初中部共120名教师，高中部共180名教师，其性别比例如图所示，已知按分层抽样抽方法得到的工会代表中，高中部女教师有6人，则工会代表中男教师的总人数为______．【答案】12【解析】解：高中部女教师有6人，占，则高中部人数为x，则，得人，即抽取高中人数15人，则抽取初中人数为人，则男教师有人故答案为：12根据高中女教师的人数和比例，先求出抽取高中人数，然后在求出抽取初中人数即可得到结论．本题主要考查分层抽样的应用，根据人数比例以及男女老少人数比例建立方程关系是解决本题的关键．14.设抛物线C：的焦点为F，准线为l，点M在C上，点N在l上，且，若，则的值为______．【答案】3【解析】解：根据题意画出图形，如图所示；抛物线，焦点，准线为；设，，则，解得，；，，又，，解得．故答案为：3．根据题意画出图形，结合图形求出抛物线的焦点F和准线方程，设出点M、N的坐标，根据和求出的值．本题考查了抛物线的方程与应用问题，也考查了平面向量的坐标运算问题，是中档题．15.设，，c为自然对数的底数，若，则的最小值是______．【答案】【解析】解：，，则，即，由基本不等式得，则，当且仅当，即当时，等号成立，因此，的最小值为．故答案为：．利用定积分计算出，经过配凑得出，将代数式与代数式相乘，利用基本不等式可得出的最小值．本题考查定积分的计算，同时也考查了利用基本不等式求最值，解决本题的关键在于对代数式进行合理配凑，考查计算能力，属于中等题．16.若函数有三个不同的零点，则实数a的取值范围是______．【答案】【解析】解：由题意函数可知：函数图象的左半部分为单调递增指数函数的部分，有一个零点，函数图象的右半部分为开口向上的3次函数的一部分，必须有两个零点，，，如上图，要满足题意：，，可得，解得．综合可得，故答案为：．由题意可得需使指数函数部分与x轴有一个交点，3次函数的图象由最小值并且小于0，x大于0的部分，只有两个交点．本题考查根的存在性及根的个数的判断，数形结合是解决问题的关键，属中档题．三、解答题（本大题共7小题，共82.0分）17.正项等比数列中，已知，．Ⅰ求的前n项和；Ⅱ对于Ⅰ中的，设，且，求数列的通项公式．【答案】解：Ⅰ正项等比数列的公比设为q，已知，，可得，，解得，，即；Ⅱ，且，可得．【解析】Ⅰ正项等比数列的公比设为q，运用等比数列的通项公式，解方程可得首项和公比，即可得到所求求和；Ⅱ由，结合数列的分组求和和等比数列的求和公式，计算可得所求和．本题考查等比数列的通项公式和求和公式的运用，考查数列的恒等式和求和方法：分组求和，考查方程思想和运算能力，属于基础题．18.“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”江南梅雨的点点滴滴都流润着浓洌的诗情每年六、七月份，我国长江中下游地区进入持续25天左右的梅雨季节，如图是江南Q镇～年梅雨季节的降雨量单位：的频率分布直方图，试用样本频率估计总体概率，解答下列问题：Ⅰ“梅实初黄暮雨深”假设每年的梅雨天气相互独立，求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率；Ⅱ“江南梅雨无限愁”在Q镇承包了20亩土地种植杨梅的老李也在犯愁，他过去种植的甲品种杨梅，平均每年的总利润为28万元而乙品种杨梅的亩产量亩与降雨量之间的关系如下面统计表所示，又知乙品种杨梅的单位利润为元，请你帮助老李排解忧愁，他来年应该种植哪个品种的杨梅可以使总利润万元的期望更大？需说明理由【答案】解：Ⅰ频率分布直方图中第四组的频率为，则江南Q镇在梅雨季节时降雨量超过350mm的概率为，所以Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率为或；Ⅱ根据题意，总利润为元，其中，700，600，400；所以随机变量万元的分布列如下图所示；则总利润万元的数学期望为万元，因为，所以老李来年应该种植乙品种杨梅，可使总利润的期望更大．【解析】Ⅰ由频率分布直方图计算对应的频率，利用频率估计概率，求出对应的概率值；Ⅱ根据题意计算随机变量的分布列和数学期望，比较得出结论和建议．本题考查了频率分布直方图和离散型随机变量的分布列应用问题，是中档题．19.已知椭圆的离心率为，且经过点．Ⅰ求椭圆的标准方程；Ⅱ设O为椭圆的中心，点，过点A的动直线l交椭圆于另一点B，直线l上的点C满足．，求直线BD与OC的交点P的轨迹方程．【答案】解：Ⅰ椭圆的离心率，且，，，椭圆的标准方程为，Ⅱ设直线l的方程为当t存在时，由题意，代入，并整理可得，解得，于是，即，设，，解得，于是，，，，，，直线BD与OC的交点P的轨迹是以OD为直径的圆除去O，D两点，轨迹方程为，即，【解析】Ⅰ根据椭圆的离心率和，即可求出椭圆的方程，Ⅱ设直线l的方程为当t存在时，由题意，代入，并整理可得，求出点B的坐标，根据向量的运算求出点C的坐标，再根据向量的运算证明，即可求出点P的轨迹方程本题考查直线与椭圆的位置关系的综合应用，椭圆的方程的求法，考查转化思想以及计算能力，函数与方程的思想的应用．20.如图，在多面体ABCDE中，AC和BD交于一点，除EC以外的其余各棱长均为2．Ⅰ作平面CDE与平面ABE的交线l并写出作法及理由；Ⅱ求证：平面平面ACE；Ⅲ若多面体ABCDE的体积为2，求直线DE与平面BCE所成角的正弦值．【答案】解：Ⅰ过点E作或的平行线，即为所求直线l．理由如下：和BD交于一点，，B，C，D四点共面，又四边形ABCD边长均相等，四边形ABCD为菱形，从而，又平面CDE，且平面CDE，平面CDE，平面ABE，且平面平面，．证明：Ⅱ取AE的中点O，连结OB，OD，，，，，，平面OBD，平面OBD，，又四边形ABCD是菱形，，又，平面ACE，又平面BDE，平面平面ACE．解：Ⅲ由多面体ABCDE的体积为2，得，，设三棱锥的高为h，则，解得，，平面ABE，以O为原点，OB为x轴，OE为y轴，OD为z轴，建立如图所示的空间直角坐标系，则，0，，0，，1，，1，，1，，1，，设平面BCE的法向量y，，则，取，得，设直线DE与平面BCE所成角为，则．直线DE与平面BCE所成角的正弦值为．【解析】Ⅰ过点E作或的平行线，即为所求直线由AC和BD交于一点，得A，B，C，D四点共面，推导出四边形ABCD为菱形，从而，进而平面CDE，由此推导出．Ⅱ取AE的中点O，连结OB，OD，推导出，，从而平面OBD，进而，由四边形ABCD是菱形，得，从而平面ACE，由此能证明平面平面ACE．Ⅲ由，得，求出三棱锥的高为，得平面ABE，以O为原点，OB为x轴，OE为y轴，OD为z轴，建立如图所示的空间直角坐标系，利用向量法能求出直线DE与平面BCE 所成角的正弦值．本题考查两平面的交线的求法，考查面面垂直的证明，考查线面角的正弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题．21.已知函数，其中a为常数．Ⅰ若曲线在处的切线在两坐标轴上的截距相等，求a之值；Ⅱ若对，都有，求a的取值范围．【答案】解：Ⅰ函数的导数为，由题意可得，，可得切线方程为，即有，解得；Ⅱ若对，，在递减，当时，，在递减，，由恒成立，可得，与矛盾；当时，，在递增，可得即，由恒成立，可得且，可得；当时，，，且在递减，可得存在，，在递增，在递减，故，由恒成立，可得，，可得，又的最大值为，由，，可得，设，，，可得在递增，即有，即，不等式恒成立，综上可得a的范围是．【解析】Ⅰ求得的导数，可得切线的斜率和切点，由题意可得a的方程，解方程可得a；Ⅱ若对，，在递减，讨论，，，结合函数的单调性和不等式恒成立思想，以及函数零点存在定理，构造函数法，即可得到所求范围．本题考查导数的运用：求切线方程和单调性、极值和最值，考查函数零点存在定理和分类讨论思想方法，以及各种函数法，考查化简整理的运算能力，属于难题．22.在平面直角坐标系xOy中曲线C的参数方程为其中t为参数在以O为极点、x轴的非负半轴为极轴的极坐标系两种坐标系的单位长度相同中，直线l的极坐标方程为．Ⅰ求曲线C的极坐标方程；Ⅱ求直线l与曲线C的公共点P的极坐标．【答案】解：Ⅰ平面直角坐标系xOy中曲线C的参数方程为其中t为参数，曲线C的直角坐标方程为，，将，代入，得曲线C的直角坐标方程为，，将，代入，得，曲线C的极坐标方程为Ⅱ将l与C的极坐标方程联立，消去，得，，，，方程的解为，即，代入，得，直线l与曲线C的公共点P的极坐标为【解析】Ⅰ由曲线C的参数方程求出曲线C的直角坐标方程，由此能求出曲线C的极坐标方程．Ⅱ将l与C的极坐标方程联立，得，从而，进而方程的解为，由此能求出直线l与曲线C的公共点P的极坐标．本题考查曲线的极坐标方程的求法，考查直线与曲线的公共点的极坐标的求法，考查直角坐标方程、参数方程、极坐标方程的互化等基础知识，考查运算求解能力，是中档题．23.已知函数，且a，b，．Ⅰ若，求的最小值；Ⅱ若，求证：．【答案】解：Ⅰ由柯西不等式可得，当且仅当时取等号，即；，即的最小值为．证明：Ⅱ，，故结论成立【解析】Ⅰ根据柯西不等式即可求出最小值，Ⅱ根据绝对值三角不等式即可证明．本题考查了柯西不等式和绝对值三角形不等式，考查了转化和化归的思想，属于中档题．。
四川省成都七中2019届高三一诊模拟考试理综试题
成都七中2019届高三一诊模拟考试理综化学试卷1、下列说法中，正确的是( )A ．气象环境报告中新增的“PM2.5”是对一种新分子的描述B ．化学反应能够制造出新的物质，同时也能制造出新的元素C ．“光化学烟雾”、“硝酸型酸雨”的形成都与氮氧化合物有关D ．明矾[KAl(SO 4)2·12H 2O]常用于自来水的净化、杀菌消毒2、下列叙述正确的是（ ）A ．将SO 2通入酸性高锰酸钾溶液中，溶液褪色，说明SO 2具有漂白性B ．相同温度下，完全中和相同PH 、相同体积的氨水和NaOH 溶液，所需相同浓度的盐酸体积相等C ．0.1mol·L －1的酸式盐NaHA 溶液中，c (Na +)＝0.1mol·L －1≥c (A 2-)D ．向KI 溶液中加入氯化银，沉淀逐渐变黄色，说明同温下)AgCl ()AgI (SP SP K K3、二氧化碳和钠在一定条件下可制得金刚石，其化学方程式为3CO 2+4Na ＝2X+C （金刚石）。
设N A 为阿伏加德罗常数的值，下列有关此反应的叙述中，不正确．．．的是（ ） A ．1molC （金刚石）中含有C —C 键数目为2N AB ．当有0.4molNa 参与反应时，被还原的CO 2为0.3N AC ．金刚石与石墨互为同素异形体D ．X 的化学式为Na 2CO 34、下列实验现象或结论错误的是（ ）D 向Na2S溶液中滴入足量ZnSO4溶液有白色沉淀生成，再加入几滴CuSO4溶液沉淀由白色转化为黑色，说明溶度积（Ksp）：ZnS>CuS5、下列反应的离子方程式正确的是（）A．Fe3O 4与稀硝酸反应：Fe3O4+8H+=Fe2++2Fe3++4H 2OB．向硝酸银溶液中逐滴滴入稀氨水直至过量：Ag++2NH3·H2O=[Ag(NH3)2]++2H2OC．Ca(HCO3)2与过量Ca(OH)2溶液反应：Ca2++2HCO3-+2OH-=CaCO3↓+CO32-+2H2OD．Na2S溶液呈碱性：S2-+2H2O H2S+2OH-6、已知A、B为单质，C为化合物，他们之间存在如下转化关系：则下列说法中正确的是①若C溶于水后得到强碱溶液，则A可能是Na②若向C溶液中逐滴加入NaOH溶液的过程中溶液中出现白色沉淀并逐渐溶液至消失，则A可能是Al③若C的溶液遇NaHCO3固体，放出CO2气体，则A可能是H2④若C的溶液中滴加KSCN溶液显红色，则B可能为Fe⑤若C的溶液中滴加NaOH溶液有蓝色沉淀生成，则B可能为CuA．①②③B．②④C．③⑤D．①④⑤7、某同学设计如下实验测量m g铜银合金样品中铜的质量分数：下列说法中不正确的是( )A.收集到的V L气体全为NOB.过滤用到的玻璃仪器是：烧杯、漏斗、玻璃棒C.操作Ⅱ应是洗涤D.铜的质量分数为：(143.5V-22.4w)/100.4m8、X、Y、Z、W为原子序数依次增大的4种短周期元素，已知：①X与Z、Y与W分别同族；②X、Z、W分别与Y都可组成两种中学常见的化合物；③Y的阴离子与Z的阳离子的核外电子排布相同；④这4种元素的单质中有一种易溶于CS2溶剂。
精品解析：【全国百强校】四川省成都市第七中学2019届高三一诊模拟考试数学(理)试题(解析版)
第七中学2019届高三一诊模拟考试数学（理）试题注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。
2．选择题答案使用2B铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。
3．考生必须按照题号在答题卡各题号相对应的答题区域内(黑色线框)作答,写在草稿纸上、超出答题区域或非题号对应的答题区域的答案一律无效。
4．保持卡面清洁，不折叠，不破损。
5．做选考题时，考生按照题目要求作答，并用2B铅笔在答题卡上把所选题目对应的题号涂黑。
一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若随机变量，且，则（）A. 0.6B. 0.5C. 0.4D. 0.3【答案】A【解析】【分析】根据随机变量X服从正态分布N（3，σ2），看出这组数据对应的正态曲线的对称轴x=3，根据正态曲线的特点，即可得到结果．【详解】∵随机变量X服从正态分布N（3，σ2），∴对称轴是x=3．∵P（X≥5）=0.2，∴P（1＜X＜5）=1﹣2P（X≥5）=1﹣0.4=0.6．故选：A．【点睛】本题考查正态曲线的形状认识，从形态上看，正态分布是一条单峰、对称的曲线，其对称轴为x=μ，并在x=μ时取最大值从x=μ点开始，曲线向正负两个方向递减延伸，不断逼近x轴，但永不与x轴相交，因此说曲线在正负两个方向都是以x轴为渐近线的．2.函数的图象大致是（）A. B.C. D.【答案】D【解析】【分析】先判断函数为偶函数，再根据特殊点的函数值即可判断．【详解】因为满足偶函数f（﹣x）=f（x）的定义，所以函数为偶函数，其图象关于y轴对称，故排除B，又x=0时，y=0，排除A、C，故选D.【点睛】本题考查了函数的图象的识别，一般常用特殊点的函数值、函数的奇偶性和函数的单调性来排除，属于基础题．3.“牟合方盖”是我国古代数学家刘徽在探求球体体积时构造的一个封闭几何体，它由两个等径正贯的圆柱体的侧面围成，其直视图如图（其中四边形是为体现直观性而作的辅助线）.当“牟合方盖”的正视图和侧视图完全相同时，其俯视图为（）A. B.C. D.【答案】B【解析】【分析】相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．根据三视图看到方向，可以确定三个识图的形状，判断答案．【详解】∵相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．∴其正视图和侧视图是一个圆，俯视图是从上向下看，相对的两个曲面在同一个圆柱的侧面上，∴俯视图是有2条对角线且为实线的正方形，故选：B．【点睛】本题很是新颖，三视图是一个常考的内容，考查了空间想象能力，属于中档题．4.设是虚数单位，复数满足，则的虚部为（）A. 1B. -1C. -2D. 2【答案】C【解析】【分析】令z=a+bi(a,b，将其代入，化简即可得出．【详解】令z=a+bi，代入，（a-1+bi）= a+3+bi，,，故选C.【点睛】本题考查了复数相等的概念及运算法则、虚部的定义，考查了计算能力，属于基础题．5.执行下边的算法程序，若输出的结果为120，则横线处应填入（）A. B. C. D.【答案】C【解析】【分析】由题意知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得结果．【详解】模拟执行算法程序，可得：S=1，k=1，不满足条件，S=1，k=2，不满足条件，S=2，k=3，不满足条件，S=6，k=4，不满足条件，S=24，k=5，不满足条件，S=120，k=6，此时i满足条件，退出循环，输出S的值为120；所以横线处应填写的条件为，故选C.【点睛】本题考查了程序框图的应用问题，属于直到型循环结构，当循环的次数不多，或有规律时，常采用模拟循环的方法解答．6.设实数满足，则的最大值是（）A. -1B.C. 1D.【答案】D【解析】【分析】由约束条件确定可行域，由的几何意义，即可行域内的动点与定点P（0，-1）连线的斜率求得答案．【详解】由约束条件，作出可行域如图，联立，解得A（），的几何意义为可行域内的动点与定点P（0，-1）连线的斜率，由图可知，最大．故答案为：．【点睛】本题考查简单的线性规划，考查了数形结合的解题思想方法，属于中档题型．7.“”是“”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】【分析】利用对数函数的单调性即可判断出结论．【详解】⇒a>b>0 ⇒，但满足的如a=-2,b=-1不能得到，故“”是“”的充分不必要条件.故选A.【点睛】本题考查了对数函数的单调性、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．8.函数的图象的一条对称轴方程是（）A. B. C. D.【答案】B【解析】【分析】将函数表达式展开合并，再用辅助角公式化简，得f（x）=sin（2x+）-．再根据正弦函数对称轴的公式，求出f（x）图象的对称轴方程.【详解】f（x）==sinx=sin2x-=sin2x+-=sin（2x+）-，∴f（x）=sin（2x+）-，令2x+=(k,解得x=(k,k=0时，，故选B.【点睛】本题考查了三角函数的化简与三角函数性质，运用了两角和差的正余弦公式和二倍角公式，属于中档题．9.将多项式分解因式得，m为常数，若，则A. B. C. 1 D. 2【答案】D【解析】【分析】由可得=5m-2=-7,m=-1，.【详解】因为的通项公式为，=x+（-2）=(5m-2)，=5m-2，又，5m-2=-7,m=-1,=2，故选D.【点睛】本题考查了二项式定理的应用，考查了推理能力与计算能力，属于中档题．10.已知正三棱锥的高为6，侧面与底面成的二面角，则其内切球与四个面都相切的表面积为A. B. C. D.【答案】B【解析】【分析】过点P作PD⊥平面ABC于D，连结并延长AD交BC于E，连结PE，△ABC是正三角形，AE是BC边上的高和中线，D为△ABC的中心．由此能求出棱锥的全面积，再求出棱锥的体积，设球的半径为r，以球心O为顶点，棱锥的四个面为底面把正三棱锥分割为四个小棱锥，利用等体积能求出球的表面积．【详解】如图，过点P作PD⊥平面ABC于D，连结并延长AD交BC于E，连结PE，△ABC是正三角形，∴AE是BC边上的高和中线，D为△ABC的中心．∴为侧面与底面所成的二面角的平面角，∴=∵PD=6，∴DE=2,PE=4, AB=12,∴S △ABC=×（12）2=36，S△PAB=S△PBC=S△PCA==24．∴S 表=108.设球的半径为r，以球心O为顶点，棱锥的四个面为底面把正三棱锥分割为四个小棱锥，∵PD=6，∴V P﹣ABC=•36•6=72．则由等体积可得r==2，∴S球=4π22=16π．故选B.【点睛】本题考查棱锥的内切球的半径的求法，棱锥全面积和体积的求法，考查球的表面积公式，解题时要认真审题，注意空间思维能力的培养．11.设a，b，c分别是的内角A，B，C的对边，已知，设D是BC边的中点，且的面积为，则等于A. 2B. 4C.D.【答案】A【解析】【分析】利用三角形内角和定理可得．由正弦定理可得b2+c2﹣a2=bc，由余弦定理可得cosA=，结合范围A∈（0，π）可得A的值，结合的面积求得bc,将利用向量加减法运算转化为,即可求得结果.【详解】∵，，∴由正弦定理可得：，整理可得：b2+c2﹣a2=-bc，∴由余弦定理可得：cosA=，∴由A∈（0，π），可得：A=，又的面积为，即,∴bc=4,又=-=-=-===-bccosA=2.故选A.【点睛】本题主要考查了向量加减法的运算、数量积的运算，综合运用了正弦定理，余弦定理，三角形面积公式，考查了转化思想和计算能力，属于中档题．12.如果不是等差数列，但若，使得，那么称为“局部等差”数列.已知数列的项数为4，记事件：集合，事件：为“局部等差”数列，则条件概率（）A. B. C. D.【答案】C【解析】【分析】分别求出事件与事件的基本事件的个数，用=计算结果.【详解】由题意知，事件共有=120个基本事件，事件“局部等差”数列共有以下24个基本事件，（1）其中含1，2，3的局部等差的分别为1，2，3，5和5，1，2，3和4，1，2，3共3个，含3，2，1的局部等差数列的同理也有3个，共6个.含3，4，5的和含5，4，3的与上述（1）相同，也有6个.含2，3，4的有5，2，3，4和2，3，4，1共 2个，含4，3，2的同理也有2个.含1，3，5的有1，3，5，2和2，1，3，5和4，1，3，5和1，3，5，4共4个，含5，3，1的也有上述4个，共24个，=.故选C.【点睛】本题主要考查了条件概率的求法，综合运用了等差数列与集合的知识，理解题意是解决此类题的关键.二、填空题：本题共4小题，每小题5分，共20分.13.某学校初中部共120名教师，高中部共180名教师，其性别比例如图所示，已知按分层抽样方法得到的工会代表中，高中部女教师有6人，则工会代表中男教师的总人数为________.【答案】12【解析】【分析】利用分层抽样中的比例，可得工会代表中男教师的总人数．【详解】∵高中部女教师与高中部男教师比例为2：3，按分层抽样方法得到的工会代表中，高中部女教师有6人，则男教师有9人，工会代表中高中部教师共有15人，又初中部与高中部总人数比例为2：3，工会代表中初中部教师人数与高中部教师人数比例为2：3，工会代表中初中部教师总人数为10，又∵初中部女教师与高中部男教师比例为7：3，工会代表中初中部男教师的总人数为10×30%=3；∴工会代表中男教师的总人数为9+3=12，故答案为12．【点睛】本题考查对分层抽样的定义的理解，考查识图能力与分析数据的能力，考查学生的计算能力，比较基础．14.设抛物线的焦点为，准线为，点在上，点在上，且，若，则的值（）A. B. 2 C. D. 3【答案】D【解析】【分析】过M向准线l作垂线，垂足为M′，根据已知条件，结合抛物线的定义得==，即可得出结论．【详解】过M向准线l作垂线，垂足为M′，根据已知条件，结合抛物线的定义得==，又∴|MM′|=4，又|FF′|=6，∴==，.故选：D．【点睛】本题考查了抛物线的定义标准方程及其性质、向量的共线，考查了推理能力与计算能力，属于中档题．15.设，，c为自然对数的底数，若，则的最小值是______．【答案】【解析】【分析】运算=1，将变形，利用分母的和为定值，将乘以，利用基本不等式即可求得结果.【详解】=1，，.故答案为.【点睛】本题考查了“乘1法”与基本不等式的性质，考查了微积分基本定理，积分的运算，属于中档题．16.若函数有三个不同的零点，则实数的取值范围是_____．【答案】【解析】【分析】由题意可将函数有三个不同的零点转化为函数y=a与有三个不同的交点，结合图象求出实数a的取值范围．【详解】由题意可将函数有三个不同的零点转化为函数y=a与有三个不同的交点，如图所示：当时，的图象易得，当时，函数g(x)=，==0，x=1,在区间(0，1)上单调递减，在区间(1，)上单调递增，如图所示：有三个不同的交点，a≤4故答案为：【点睛】本题主要考查函数的零点与方程的根的关系，体现了化归与转化、数形结合的数学思想，属于中档题．三、解答题：共70分.解答应写出文字说明，证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生依据要求作答.17.正项等比数列中，已知，．Ⅰ求的前n项和；Ⅱ对于Ⅰ中的，设，且，求数列的通项公式．【答案】【解析】【分析】利用等比数列通项公式列出方程组，求出a1=1，q=2，由此能求出{a n}的前项和．（2）由，直接利用累加法求出{b n}的通项．【详解】设正项等比数列的公比为，则由及得，化简得，解得或（舍去）.于是，所以，.由已知，，所以当时，由累加法得，.又也适合上式，所以的通项公式为，.【点睛】本题考查数列通项公式、数列的前n项和的求法，考查累加法求通项等基础知识，考查运算求解能力，是中档题．18.“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”江南梅雨的点点滴滴都流润着浓洌的诗情每年六、七月份，我国长江中下游地区进入持续25天左右的梅雨季节，如图是江南Q镇年梅雨季节的降雨量单位：的频率分布直方图，试用样本频率估计总体概率，解答下列问题：Ⅰ“梅实初黄暮雨深”假设每年的梅雨天气相互独立，求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率；Ⅱ“江南梅雨无限愁”在Q镇承包了20亩土地种植杨梅的老李也在犯愁，他过去种植的甲品种杨梅，平均每年的总利润为28万元而乙品种杨梅的亩产量亩与降雨量之间的关系如下面统计表所示，又知乙品种杨梅的单位利润为元，请你帮助老李排解忧愁，他来年应该种植哪个品种的杨梅可以使总利润万元的期望更大？需说明理由【答案】乙【解析】【分析】由频率分布直方图可求出降雨量超过的概率，利用独立重复试验的概率公式计算三年里至少有两年梅雨季节的降雨量超过的概率.根据题意，列出随机变量（万元）的分布列并求期望，与甲品种的平均值作比较得出结论.【详解】频率分布直方图中第四组的频率为.江南地区在梅雨季节时降雨量超过的概率为.所以地区未来三年里至少有两年梅雨季节的降雨量超过的概率为（或0.15625）.根据题意，总利润为（元），其中.所以随机变量（万元）的分布列如下表.故总利润（万元）的数学期望（万元）.因为31>28，所以老李来年应该种植乙品种杨梅，可使总利润的期望更大.【点睛】本题考查频率分布直方图的应用，离散型随机变量的期望的求法，考查计算能力．19.已知椭圆的离心率为，且经过点．Ⅰ求椭圆的标准方程；Ⅱ设O为椭圆的中心，点，过点A的动直线l交椭圆于另一点B，直线l上的点C满足．，求直线BD与OC的交点P的轨迹方程．【答案】【解析】【分析】（1）利用椭圆C：的离心率为，且经过点M（2，0），可求椭圆的几何量，从而可求椭圆方程；（2）直线方程与椭圆方程联立，利用韦达定理，求得B点坐标，结合求出C的坐标，写出BD、OC的直线方程，利用消参法求轨迹.【详解】因为椭圆的离心率，且，所以.又.故椭圆的标准方程为.设直线的方程为（当存在时，由题意），代入，并整理得.解得，于是，即.设，则.由已知得，得，解得，于是.又，由两点的坐标可得直线的方程为.又由点坐标可得直线的方程为.两式相乘，消去参数得.（如果只求出交点的坐标，此步不得分）又当不存在时，四点重合，此时也满足题意.故直线与的交点的轨迹方程.【点睛】本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查直线过定点，正确运用韦达定理是关键．20.如图，在多面体ABCDE中，AC和BD交于一点，除EC以外的其余各棱长均为2．Ⅰ作平面CDE与平面ABE的交线l并写出作法及理由；Ⅱ求证：平面平面ACE；Ⅲ若多面体ABCDE的体积为2，求直线DE与平面BCE所成角的正弦值．【答案】见解析见解析【解析】【分析】由题意可得平面，由线面平行的性质作出交线即可.取的中点，连结，.由条件可证得平面，故.又.平面.从而平面平面.利用等体积法求得三棱锥的高，通过建立空间坐标系，利用空间向量法求线面角. 【详解】过点作（或）的平行线，即为所求直线.和交于一点，四点共面.又四边形边长均相等.四边形为菱形，从而.又平面，且平面，平面.平面，且平面平面，.取的中点，连结，.，，，.又，平面，平面，故.又四边形为菱形，.又，平面.又平面，平面平面.由，即.设三棱锥的高为，则，解得.又，平面.建立如图的空间直角坐标系，则，，，.，.由得，平面的一个法向量为.又，于是.故直线与平面所成角的正弦值为.【点睛】本题考查证明线面平行的方法，求二面角的大小，找出二面角的平面角是解题的关键和难点．21.已知函数，其中为常数.若曲线在处的切线在两坐标轴上的截距相等，求的值；若对，都有，求的取值范围.【答案】【解析】【分析】（1）求出切点坐标，写出切线方程，利用切线在两坐标轴上的截距相等，求得a即可．（2）对a分类讨论，易判断当或当时，在区间内是单调的，根据单调性得出结论，当时，在区间内单调递增，在区间内单调递减，故，又因为，成立.而的最大值为，将最大值构造新函数，通过导函数的符号判断函数的单调性求解函数的最值，然后求解结果．【详解】求导得，所以.又，所以曲线在处的切线方程为.由切线在两坐标轴上的截距相等，得，解得即为所求.对，，所以在区间内单调递减.①当时，，所以在区间内单调递减，故，由恒成立，得，这与矛盾，故舍去.②当时，，所以在区间内单调递增，故，即，由恒成立得，结合得.③当时，因为，，且在区间上单调递减，结合零点存在定理可知，存在唯一，使得，且在区间内单调递增，在区间内单调递减.故，由恒成立知，，，所以.又的最大值为，由得，所以.设，则，所以在区间内单调递增，于是，即.所以不等式恒成立.综上所述，所求的取值范围是.【点睛】本题考查导数的几何意义及利用导数研究函数的单调性以及函数的最值的求法，构造新函数以及二次导数是解决函数恒成立问题常用的方法，考查转化思想以及计算能力．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]22.在平面直角坐标系中，曲线的参数标方程为（其中为参数），在以为极点、轴的非负半轴为极轴的极坐标系（两种坐标系的单位长度相同）中，直线的极坐标方程为.求曲线的极坐标方程；求直线与曲线的公共点的极坐标.【答案】【解析】【分析】（1）先将曲线C的参数标方程化为普通方程，再利用极坐标与直角坐标的互化，把普通方程化为极坐标方程；（2）将与的极坐标方程联立，求出直线l与曲线C的交点的极角，代入直线的极坐标方程即可求得极坐标．【详解】消去参数，得曲线的直角坐标方程.将，代入，得.所以曲线的极坐标方程为.将与的极坐标方程联立，消去得.展开得.因为，所以.于是方程的解为，即.代入可得，所以点的极坐标为.【点睛】本题考查曲线的极坐标方程与普通方程的互化，直线的极坐标方程与曲线极坐标方程联立求交点的问题，考查计算能力．[选修4-5：不等式选讲]23.已知函数，且.若，求的最小值；若，求证：.【答案】见解析【解析】【分析】由柯西不等式将中的变为，求得的最小值.因为，又，故再结合绝对值三角不等式证得结论成立.【详解】由柯西不等式得，（当且仅当时取等号），所以，即的最小值为；21 因为，所以，故结论成立.【点睛】本题考查了利用柯西不等式求最值，考查了利用绝对值三角不等式证明的问题，属于中等题.。
四川省成都七中2019届高三模拟考试理科综合试题及答案
成都七中2018-2019学年下期高三热身理综考试题（最后一卷）注意事项：1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3.全部答案在答题卡上完成，答在本试题上无效。
4.考试结束后，将本试题和答题卡一并交回。
可能用到的相对原子质量：H-1 C-12 O-16 Na-23第Ⅰ卷（选择题共126分）一、选择题：本大题共13小题，每小题6分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．下列有关细胞物质的叙述，正确的是（）A. 脂质具有构成生物膜、调节代谢和储存能量等生物学功能B. 组成蛋白质、核酸、糖原的单体都具有多样性C. 核糖体与酶、抗体、激素、神经递质的合成都有关D. DNA 是主要的遗传物质，可通过噬菌体侵染细菌的实验来证明2．下列有关生物实验的叙述，正确的是（）A. 对培养液中的酵母菌进行计数时，先将培养液滴入计数室，然后盖好盖玻片在显微镜下计数B. “体验制备细胞膜的方法”实验中，需用血液加适量的生理盐水制备新鲜的红细胞稀释液C. “探究生长素类似物促进扦插枝条生根的最适浓度”的正式实验中，需要用蒸馏水作对照组D. “探究温度对酶的酶活性的影响”实验中，将酶与底物混合后再进行保温3．癌胚抗原（CEA)和甲胎蛋白（AFP)是人胚胎时期机体合成的两种糖蛋白，出生后其含量很快下降，但某些癌症患者血液中的CEA 或AFP 含量远超正常值。
下列说法错误的是（）A. CEA、AFP 的合成属于吸能反应B. CEA 或AFP 含量超过正常值时，可确诊为癌症C. 体内某些细胞的大量增殖会使CEA、AFP 含量升高D. 控制CEA、AFP 合成的基因，碱基排列顺序有差异4．下列有关人体内环境和稳态调节的叙述，正确的是（）A．大量出汗后只补充水，血浆渗透压会升高B．免疫系统的作用与机体维持内环境稳态无关C．温度下降时甲状腺激素会定向运输给产热器官D．内环境稳态遭到破坏必将引起细胞代谢紊乱5．下列有关染色体、DNA、基因、脱氧核苷酸的说法，正确的是（）A. 一个基因含有许多个脱氧核苷酸，基因的特异性是由脱氧核苷酸的比例决定的B. 基因是具有遗传效应的DNA 片段，不是4 种碱基对的随机排列C. 在DNA 分子结构中，脱氧核苷酸的排列构成了DNA 分子的基本骨架D. 染色体是DNA 的主要载体，一条染色体上含有2 个DNA 分子6．某自由交配的种群在Ⅰ、Ⅱ、Ⅲ时间段都经历多次繁殖过程，定期随机抽取100 个个体，测得基因型为AA、aa 的个体数量变化曲线如图所示。
四川省成都七中2019届高中毕业班一诊模拟理综物理试卷(有答案)
2019.12.14一诊模拟试题14-17为单选，18-21为多选14. 下列说法不正确的是（ ）A.重心、合力等概念的建立都体现等效替代的思想B.根据速度定义式t x v ∆∆=，当∆t 非常非常小时，tx ∆∆就可以表示物体在t 时刻的瞬时速度，该定义应用了极限思想方法。
C 、在不需要考虑物体本身的大小和形状时，用质点来代替物理的方法叫假设。
D 、在探究加速度、力和质量三者的关系时，先保持质量不变研究加速度与力的关系，再保持力不变研究加速度与质量的关系，该实验应用了控制变量法15.如图所示，清洗楼房光滑玻璃的工人常用一根绳子将自己悬在空中，工人及其装备的总重量为G ，悬绳对工人的拉力大小为F 1 ，墙壁对工人的总弹力大小为 F 2，若保持这个姿势，工人增加悬绳的长度缓慢下移，则（ ）A 、F 1 逐渐变小B 、 F 2逐渐变大C 、F 1 与 F 2的合力变小D G 、F 1与 F 2的合力变小16、发射月球探测卫星要经过多次变轨，如图I 是某次月球探测卫星发射后在近地轨道，II 、III 是两次变轨后的转移轨道，O 点是II 、III 轨道的近地点，Q 、P 分别是II 、III 轨道的远地点，则下列说法正确的是（ ）A 、在三个轨道上，卫星在O 点的速度相同B 、在三个轨道上，卫星在O 点的加速度相同C 、卫星在Q 点的机械能等于在P 点的机械能D 、卫星在Q 点的机械能大于在P 点的机械能17.在如图所示的电路中，R1˃r ,将滑动变阻器的R 的滑片从位置a 向下滑动到位置b 的过程，电路均处于稳定状态，下列判断正确的是（ ）A 、电源的输出功率P 增大B 、灯泡L 的亮度变亮C 、电容器C 所带电荷量Q 增大D 、电阻R 1消耗的热功率P 1减小18. 一粒钢珠从静止状态开始开始自由下落，然后陷入泥潭中。
若把在空中下落的过程称为过程I ，进入泥潭直到停止的过程称为II ，则 （ ）A 、过程I 中钢珠的动量的改变量等于重力的冲量B 、过程II 中阻力的冲量的大小等于过程I 中重力的冲量的大小C 、过程II 中钢珠的动量的改变量等于零D 、I 、II 两个过程中合外力的总冲量等于零。
【100所名校】2019届四川省成都市第七中学高三一诊模拟考试数学(理)试题(解析版)
第1页（共6页） 第2页（共6页） 2019届四川省成都市第七中学 高三一诊模拟考试数学（理）试题 数学 注意事项： 1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。
2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4．考试结束后，请将本试题卷和答题卡一并上交。
一、单选题 1．若随机变量 ，且 ，则 A ．0.6 B ．0.5 C ．0.4 D ．0.3 2．函数 的图象大致是 A ． B ． C ． D ． 3．“牟合方盖”是我国古代数学家刘徽在探求球体体积时构造的一个封闭几何体，它由两个等径正贯的圆柱体的侧面围成，其直视图如图（其中四边形是为体现直观性而作的辅助线）.当“牟合方盖”的正视图和侧视图完全相同时，其俯视图为A ．B ．C ．D ． 4．设 是虚数单位，复数 满足 ，则 的虚部为 A ．1 B ．-1 C ．-2 D ．2 5．执行下边的算法程序，若输出的结果为120，则横线处应填入 A ． B ． C ． D ． 6．设实数 满足 ，则 的最大值是 A ．-1 B ． C ．1 D ． 7．“ ”是“ ”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 8．函数 的图象的一条对称轴方程是 A ． B ． C ． D ． 9．将多项式 分解因式得 ， 为常数，若 ，则 A ．-2 B ．-1 C ．1 D ．2 10．已知正三棱锥的高为6，侧面与底面成 的二面角，则其内切球（与四个面都相切）的表面积为 A ． B ． C ． D ． 11．设 分别是 的内角 的对边，已知 ，设 是边 的中点，且 的面积为 ，则 等于 A ．2 B ．4 C ．-4 D ．-2 此卷只装订不密封班级姓名准考证号考场号座位号12．如果不是等差数列，但若，使得，那么称为“局部等差”数列.已知数列的项数为4，记事件：集合，事件：为“局部等差”数列，则条件概率A．B．C．D．13．设抛物线的焦点为，准线为，点在上，点在上，且，若，则的值A．B．2 C．D．3二、填空题14．某学校初中部共120名教师，高中部共180名教师，其性别比例如图所示，已知按分层抽样方法得到的工会代表中，高中部女教师有6人，则工会代表中男教师的总人数为________.15．设，，为自然对数的底数，若，则的最小值是________.16．若函数有三个不同的零点，则实数的取值范围是_____．三、解答题17．正项等比数列中，已知，.求的前项和；对于中的，设，且，求数列的通项公式.18．“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”江南梅雨的点点滴滴都流润着浓洌的诗情每年六、七月份，我国长江中下游地区进入持续25天左右的梅雨季节，如图是江南Q镇～年梅雨季节的降雨量单位：的频率分布直方图，试用样本频率估计总体概率，解答下列问题：Ⅰ“梅实初黄暮雨深”假设每年的梅雨天气相互独立，求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率；Ⅱ“江南梅雨无限愁”在Q镇承包了20亩土地种植杨梅的老李也在犯愁，他过去种植的甲品种杨梅，平均每年的总利润为28万元而乙品种杨梅的亩产量亩与降雨量之间的关系如下面统计表所示，又知乙品种杨梅的单位利润为元，请你帮助老李排解忧愁，他来年应该种植哪个品种的杨梅可以使总利润万元的期望更大？需说明理由19．已知椭圆的离心率为，且经过点.求椭圆的标准方程；设为椭圆的中线，点，过点的动直线交椭圆于另一点，直线上的点满足，求直线与的交点的轨迹方程.20．如图，在多面体中，和交于一点，除以外的其余各棱长均为2.第3页（共6页）第4页（共6页）作平面与平面的交线，并写出作法及理由；求证：平面平面；若多面体的体积为2，求直线与平面所成角的正弦值.21．已知函数，其中为常数.若曲线在处的切线在两坐标轴上的截距相等，求的值；若对，都有，求的取值范围.22．在平面直角坐标系中，曲线的参数标方程为（其中为参数），在以为极点、轴的非负半轴为极轴的极坐标系（两种坐标系的单位长度相同）中，直线的极坐标方程为.求曲线的极坐标方程；求直线与曲线的公共点的极坐标.23．已知函数，且.若，求的最小值；若，求证：.第5页（共6页）第6页（共6页）2019届四川省成都市第七中学高三一诊模拟考试数学（理）试题数学答案参考答案1．A【解析】【分析】根据随机变量X服从正态分布N（3，σ2），看出这组数据对应的正态曲线的对称轴x=3，根据正态曲线的特点，即可得到结果．【详解】∵随机变量X服从正态分布N（3，σ2），∴对称轴是x=3．∵P（X≥5）=0.2，∴P（1＜X＜5）=1﹣2P（X≥5）=1﹣0.4=0.6．故选：A．【点睛】本题考查正态曲线的形状认识，从形态上看，正态分布是一条单峰、对称的曲线，其对称轴为x=μ，并在x=μ时取最大值从x=μ点开始，曲线向正负两个方向递减延伸，不断逼近x轴，但永不与x轴相交，因此说曲线在正负两个方向都是以x轴为渐近线的．2．D【解析】【分析】先判断函数为偶函数，再根据特殊点的函数值即可判断．【详解】因为，满足偶函数f（﹣x）=f（x）的定义，所以函数为偶函数，其图象关于y轴对称，故排除B，又x=0时，y=0，排除A、C，故选D.【点睛】本题考查了函数的图象的识别，一般常用特殊点的函数值、函数的奇偶性和函数的单调性来排除，属于基础题．3．B【解析】【分析】相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．根据三视图看到方向，可以确定三个识图的形状，判断答案．【详解】∵相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．∴其正视图和侧视图是一个圆，俯视图是从上向下看，相对的两个曲面在同一个圆柱的侧面上，∴俯视图是有2条对角线且为实线的正方形，故选：B．【点睛】本题很是新颖，三视图是一个常考的内容，考查了空间想象能力，属于中档题．4．C【解析】【分析】令z=a+bi(a,b，将其代入，化简即可得出．【详解】令z=a+bi，代入，（a-1+bi）= a+3+bi，,，故选C.【点睛】本题考查了复数相等的概念及运算法则、虚部的定义，考查了计算能力，属于基础题．5．C【解析】【分析】由题意知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得结果．【详解】答案第1页（共16页）答案第2页（共16页）模拟执行算法程序，可得：S=1，k=1，不满足条件，S=1，k=2，不满足条件，S=2，k=3，不满足条件，S=6，k=4，不满足条件，S=24，k=5，不满足条件，S=120，k=6，此时i满足条件，退出循环，输出S的值为120；所以横线处应填写的条件为，故选C.【点睛】本题考查了程序框图的应用问题，属于直到型循环结构，当循环的次数不多，或有规律时，常采用模拟循环的方法解答．6．D【解析】【分析】由约束条件确定可行域，由的几何意义，即可行域内的动点与定点P（0，-1）连线的斜率求得答案．【详解】由约束条件，作出可行域如图，联立，解得A（，），的几何意义为可行域内的动点与定点P（0，-1）连线的斜率，由图可知，最大．故答案为：．【点睛】本题考查简单的线性规划，考查了数形结合的解题思想方法，属于中档题型．7．A【解析】【分析】利用对数函数的单调性即可判断出结论．【详解】a>b>0 ，但满足的如a=-2,b=-1不能得到，故“”是“”的充分不必要条件.故选A.【点睛】本题考查了对数函数的单调性、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．8．B【解析】【分析】将函数表达式展开合并，再用辅助角公式化简，得f（x）=sin（2x+）-．再根据正弦函数对称轴的公式，求出f（x）图象的对称轴方程.【详解】f（x）==sinx=sin2x-=sin2x+-=sin（2x+）-，∴f（x）=sin（2x+）-，令2x+=(k,解得x=(k,k=0时，，故选B.【点睛】答案第3页（共16页）答案第4页（共16页）本题考查了三角函数的化简与三角函数性质，运用了两角和差的正余弦公式和二倍角公式，属于中档题．9．D【解析】【分析】由，可得=5m-2=-7,m=-1，.【详解】因为的通项公式为，=x+（-2）=(5m-2)，=5m-2，又，5m-2=-7,m=-1,（）（）=2，故选D.【点睛】本题考查了二项式定理的应用，考查了推理能力与计算能力，属于中档题．10．B【解析】【分析】过点P作PD⊥平面ABC于D，连结并延长AD交BC于E，连结PE，△ABC是正三角形，AE是BC边上的高和中线，D为△ABC的中心．由此能求出棱锥的全面积，再求出棱锥的体积，设球的半径为r，以球心O为顶点，棱锥的四个面为底面把正三棱锥分割为四个小棱锥，利用等体积能求出球的表面积．【详解】如图，过点P作PD⊥平面ABC于D，连结并延长AD交BC于E，连结PE，△ABC是正三角形，∴AE是BC边上的高和中线，D为△ABC的中心．∴为侧面与底面所成的二面角的平面角，∴=∵PD=6，∴DE=2,PE=4, AB=12,∴S△ABC=×（12）2=36，S△PAB=S△PBC=S△PCA==24．∴S表=108.设球的半径为r，以球心O为顶点，棱锥的四个面为底面把正三棱锥分割为四个小棱锥，∵PD=6，∴V P﹣ABC=•36•6=72．则由等体积可得r==2，∴S球=4π22=16π．故选B.【点睛】本题考查棱锥的内切球的半径的求法，棱锥全面积和体积的求法，考查球的表面积公式，解题时要认真审题，注意空间思维能力的培养．11．A【解析】【分析】利用三角形内角和定理可得．由正弦定理可得b2+c2﹣a2=bc，由余弦定理可得cosA=，结合范围A∈（0，π）可得A的值，结合的面积求得bc,将利用向量加减法运算转化为,即可求得结果.【详解】∵，，∴由正弦定理可得：（），整理可得：b2+c2﹣a2=-bc，∴由余弦定理可得：cosA=，∴由A∈（0，π），可得：A=，又的面积为，即,∴bc=4,又=-=-=-===-bccosA=2.故选A.【点睛】本题主要考查了向量加减法的运算、数量积的运算，综合运用了正弦定理，余弦定理，三角形面积公式，考查了转化思想和计算能力，属于中档题．答案第5页（共16页）答案第6页（共16页）12．C【解析】【分析】分别求出事件与事件的基本事件的个数，用=（）计算结果.【详解】由题意知，事件共有=120个基本事件，事件：“局部等差”数列共有以下24个基本事件，（1）其中含1，2，3的局部等差的分别为1，2，3，5和5，1，2，3和4，1，2，3共3个，含3，2，1的局部等差数列的同理也有3个，共6个.含3，4，5的和含5，4，3的与上述（1）相同，也有6个.含2，3，4的有5，2，3，4和2，3，4，1共2个，含4，3，2的同理也有2个.含1，3，5的有1，3，5，2和2，1，3，5和4，1，3，5和1，3，5，4共4个，含5，3，1的也有上述4个，共24个，=.故选C.【点睛】本题主要考查了条件概率的求法，综合运用了等差数列与集合的知识，理解题意是解决此类题的关键.13．D【解析】【分析】过M向准线l作垂线，垂足为M′，根据已知条件，结合抛物线的定义得==，即可得出结论．【详解】过M向准线l作垂线，垂足为M′，根据已知条件，结合抛物线的定义得==，又，∴|MM′|=4，又|FF′|=6，∴==，.故选：D．【点睛】本题考查了抛物线的定义标准方程及其性质、向量的共线，考查了推理能力与计算能力，属于中档题．14．12【解析】【分析】利用分层抽样中的比例，可得工会代表中男教师的总人数．【详解】∵高中部女教师与高中部男教师比例为2：3，按分层抽样方法得到的工会代表中，高中部女教师有6人，则男教师有9人，工会代表中高中部教师共有15人，又初中部与高中部总人数比例为2：3，工会代表中初中部教师人数与高中部教师人数比例为2：3，工会代表中初中部教师总人数为10，又∵初中部女教师与高中部男教师比例为7：3，工会代表中初中部男教师的总人数为10×30%=3；∴工会代表中男教师的总人数为9+3=12，故答案为12．【点睛】本题考查对分层抽样的定义的理解，考查识图能力与分析数据的能力，考查学生的计算能力，比较基础．15．【解析】【分析】运算=1，将变形，利用分母的和为定值，将乘以，利用基本不等式即可求得结果.答案第7页（共16页）答案第8页（共16页）【详解】=（）1，，.故答案为.【点睛】本题考查了“乘1法”与基本不等式的性质，考查了微积分基本定理，积分的运算，属于中档题．16．，【解析】【分析】由题意可将函数有三个不同的零点转化为函数y=a与（）有三个不同的交点，结合图象求出实数a的取值范围．【详解】由题意可将函数有三个不同的零点转化为函数y=a与（）有三个不同的交点，如图所示：当时，的图象易得，当时，函数g(x)=，==0，x=1, 在区间(0，1)上单调递减，在区间(1，)上单调递增，如图所示：有三个不同的交点，＜a≤4故答案为：，【点睛】本题主要考查函数的零点与方程的根的关系，体现了化归与转化、数形结合的数学思想，属于中档题．17．【解析】【分析】利用等比数列通项公式列出方程组，求出a1=1，q=2，由此能求出{a n}的前项和．（2）由，直接利用累加法求出{b n}的通项．【详解】设正项等比数列的公比为，则由及得，化简得，解得或（舍去）.于是，所以，.由已知，，所以当时，由累加法得，.又也适合上式，所以的通项公式为，.【点睛】本题考查数列通项公式、数列的前n项和的求法，考查累加法求通项等基础知识，考查运算求解能力，是中档题．18．乙【解析】【分析】由频率分布直方图可求出降雨量超过的概率，利用独立重复试验的概率公式计算三年里至少有两年梅雨季节的降雨量超过的概率.根据题意，列出随机变量（万元）的分布列并求期望，与甲品种的平均值作比较得出结论.【详解】频率分布直方图中第四组的频率为.江南地区在梅雨季节时降雨量超过的概率为.所以地区未来三年里至少有两年梅雨季节的降雨量超过的概率为（或0.15625）.答案第9页（共16页）答案第10页（共16页）根据题意，总利润为（元），其中.所以随机变量（万元）的分布列如下表.故总利润（万元）的数学期望（万元）.因为31>28，所以老李来年应该种植乙品种杨梅，可使总利润的期望更大.【点睛】本题考查频率分布直方图的应用，离散型随机变量的期望的求法，考查计算能力．19．【解析】【分析】（1）利用椭圆C：＞＞的离心率为，且经过点M（2，0），可求椭圆的几何量，从而可求椭圆方程；（2）直线方程与椭圆方程联立，利用韦达定理，求得B点坐标，结合求出C的坐标，写出BD、OC的直线方程，利用消参法求轨迹.【详解】因为椭圆的离心率，且，所以.又.故椭圆的标准方程为.设直线的方程为（当存在时，由题意），代入，并整理得.解得，于是，即.设，则.由已知得，得，解得，于是.又，由两点的坐标可得直线的方程为.又由点坐标可得直线的方程为.两式相乘，消去参数得.（如果只求出交点的坐标，此步不得分）又当不存在时，四点重合，此时也满足题意.故直线与的交点的轨迹方程.【点睛】本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查直线过定点，正确运用韦达定理是关键．20．见解析见解析【解析】【分析】由题意可得平面，由线面平行的性质作出交线即可.取的中点，连结，.由条件可证得平面，故.又.平面.从而平面平面.利用等体积法求得三棱锥的高，通过建立空间坐标系，利用空间向量法求线面角.【详解】过点作（或）的平行线，即为所求直线.和交于一点，四点共面.又四边形边长均相等.四边形为菱形，从而.又平面，且平面，平面.平面，且平面平面，.取的中点，连结，.，，，.又，平面，平面，故.又四边形为菱形，.又，平面.又平面，平面平面.由，即.设三棱锥的高为，则，解得.又，平面.建立如图的空间直角坐标系，则，，，.答案第11页（共16页）答案第12页（共16页）。
四川省成都市2019届高三第一次诊断性检测理科综合试题及答案
成都市2019届高三第一次诊断性检测理科综合可能用到的相对原子质量：H-1 C-12 O-16 Na-23 Mg-24 S-32 Cl-35.5 Fe-56 Co-59第Ⅰ卷(共126分)一、选择题本题共13个小题，每小题6分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.下列生物实验方法能达到实验目的的是A.用斐林试剂鉴别细胞中的单糖和二糖B用台盼蓝染色鉴别区分死细胞和活细胞C用健那绿染色观察线粒体中DNA的分布D.用重铬酸钾检测人体细胞无氧呼吸的产物2.下列关于细胞中某些重要化合物的叙述，正确的是A.细胞中合成DNA时都以DNA作为模板B细胞中合成ATP时都由细胞呼吸提供能量C.催化蛋白质水解的酶都只能在细胞内起作用D细胞质基质和线粒体中都有[H]的产生和消耗3.下列关于细胞中生物膜的叙述，错误的是A.生物膜上的蛋白质对细胞的增殖分化过程有影响B生物膜的信息交流功能与能量转换功能可相互影响C.生物膜上的多糖分子具有识别、运输和保护等重要功能D.生物膜的流动镶嵌模型体现了结构与功能相适应的观点4.科学家发现，神经细胞释放的乙酰胆碱可刺激血管内皮细胞产生一氧化氮，一氧化氮会引起平滑肌松弛使血管扩张，从而增强血液流动。
下列叙述正确的是A.突触前膜释放乙酰胆碱时需要载体蛋白协助B.血管内皮细胞的细胞膜上具有乙酰胆碱受体C.血管内皮细胞产生的一氧化氮属于神经递质D.乙酰胆碱能催化血管内皮细胞合成一氧化氮5.下图表示某种生物细胞内基因表达的部分过程(④代表核糖体，⑤代表多肽链)。
下列叙述正确的是A.①②链之间和②③链之间的碱基配对方式完全不同B.②链中的G和③链中的G都代表鸟嘌呤核糖核苷酸C.基因中的遗传信息通过③链传递到⑤需要RNA参与D.一个核糖体通常可结合多条③链以提高⑤的合成速率6.为了研究赤霉素和放线菌素D(一种转录抑制剂)对大麦种子中淀粉酶生成量的影响，研究人员利用去胚的大麦种子进行了相关实验，结果如下表。
2019届四川省成都市第七中学高三上学期一诊模拟考试理综试卷提分版
一、单选题1. 在物理学的研究及应用过程中涉及诸多的思想方法，如理想化、模型化、放大、极限思想，控制变量、猜想、假设、类比、比值法等等．以下关于所用思想方法的叙述不正确的是（）A ．在不需要考虑物体本身的大小和形状时，用质点来代替物体的方法是假设法B．速度的定义式，采用的是比值法；当趋近于0时， 就可以表示物体在t 时刻的瞬时速度，该定义应用了极限思想C ．在探究电阻、电压和电流三者之间的关系时，先保持电压不变研究电阻与电流的关系，再保持电流不变研究电阻与电压的关系，该实验应用了控制变量法D ．如图示的三个实验装置，这三个实验都体现了放大的思想2. 如图所示，一导线弯成直径为d 的半圆形闭合回路，虚线MN 右侧有磁感应强度为B 的匀强磁场，方向垂直于回路所在的平面．回路以速度v 向右匀速进入磁场，直径CD 始终与MN 垂直．从D 点到达边界开始到C点进入磁场为止，下列说法中正确的是A ．感应电流方向为顺时针方向B ．CD 段直导线始终不受安培力C ．感应电动势的最大值E =BdvD ．感应电动势的平均值=πBdv3. 一卫星绕某一行星做匀速圆周运动，其高度恰好与行星半径相等，线速度大小为v 。
而该行星的环绕周期（即沿行星表面附近飞行的卫星运行的周期）为T 。
已知引力常量为G ，则这颗行星的质量为（ ）A．B．C．D．4. 人造地球卫绕地球做匀速圆周运动，其轨道半径为R ，线速度为，周期为T ，若使卫星周期变为2T ，可能的方法有（ ）A ．R不变，使线速度变为B ．不变，使轨道半径变为2RC ．轨道半径变为D ．以上方法均不可以5. 黄浦滨江滑板公园的一根滑道如图所示，小吕同学从静止开始沿斜面下滑，经圆弧滑道至A 点起跳。
此过程中可将人视为质点，不计摩擦力及空气阻力，以滑道最低点所在平面为零势能面，人的重力势能E p 、动能E k 与水平位移x的关系图像正确的是（ ）A．B．2019届四川省成都市第七中学高三上学期一诊模拟考试理综试卷提分版二、多选题三、实验题C．D．6. 下列说法正确的是（ ）A ．饱和汽压与分子密度有关，与温度无关B ．一定质量的理想气体向真空自由膨胀时，体积增大，熵增大C ．雨伞伞面上有许多细小的孔，却能遮雨，是因为水的表面张力作用D ．如果附着层的液体分子比液体内部的分子稀疏，这样的液体与固体之间表现为不浸润E ．用油膜法估测分子大小，如果油膜没有充分展开，测出来的分子大小将偏小7. 如图所示，甲、乙、丙是绕地球做匀速圆周运动的3艘飞船，下列说法正确的是（）A ．丙开动发动机向后瞬时喷气后，其势能不变B ．丙开动发动机向后瞬时喷气后的一段时间内，可能沿原轨道追上同一轨道上的乙C ．甲受稀薄气体的阻力作用后，其动能增大、势能减小D ．甲受稀薄气体的阻力作用后，阻力做功大小与引力做功大小相等8. 如图，竖直面内有半径为的四分之一光滑圆弧轨道BC，固定在光滑的水平地面上，且圆弧轨道最低点与水平地面相切。