第七章 对流换热
ch7.对流换热

努塞尔数 斯坦顿数
Nu x hx St x Rex Pr c p v0
Re x
20:30:50
v0 x
Chapter 7 对流换热
17
7.2 流过平板时的对流换热(数学分析法)
1 0.664Pr 3 1 2 Re L
平均值
Nu
2 St Pr 3
0.664Re L
1 2
n
自然对流换热 模型实验确定待定系数
20:30:51
C m n
31
Chapter 7 对流换热
7.3.2 相似原理在对流换热中的应用
2、 定性温度、定型尺寸、特征速度 定性温度 流体温度 tf or (tf1+tf2)/2;
热边界层平均温度
壁面温度 特征速度 流体速度; tw 。
(tf+fw)/2;
q t f t w A t
q ht f t w A
20:30:50 Chapter 7 对流换热
h t
12
7.1 对流换热的基本概念 对流换热系数计算式
t q y
y 0
q ht f t w
t t y 0 y y h t f tw t
l2〞
l3′ A1′
l1′ h′ A2′ l2′
l3〞
h〞 A1〞 A2〞 l1〞
20:30:51
Chapter 7 对流换热
22
7.3.1 相似原理
2) 现象相似的条件
⑴ 相似的前提条件(必要条件)
① 同类物理现象 用同一方程描述。例如:流体在管道中流动;流体绕流平板。 ② 几何条件相似 因为所有具体现象都发生在一定的几何空间内。
对流换热

(c) 流体物性
主要有、CP、、、a ,可综合为普朗特准数:
Pr CP a
(d) 换热面的形状、尺寸和放置位置。
• 窑炉中因温度甚高,火焰、烟气及炉衬对物料的传 热主要靠辐射传热,对流传热在窑内所占比重不大;
• 一般认为:在800℃以上、炉内气体只靠自然通风 流动时,对流换热 仅占5%以下,可以忽略其影响;
2.2.2 对流换热
2.2.2.1 概述
对流换热——是指流体(气体或液体,在窑炉
中主要指空气、燃气与烟气)与固体壁面直接
接触时彼此之间的换热过程。
w
y
右图中: 边界层温降很大——导热; 主流区温降很小——对流; 对流换热 = 导热 +对流 换热面积 ⊥传热方向
ˆx
tw • ل ئر
د
ˆ ق
Q (tw t f ) F
其中:tw、tf——分别为壁面、流体的温度,℃ F——换热面积,m2;
——对流换热系数,指单位时间内、
温差等于1 °C时,单位面积的传 热量,W/(m2·℃)
描述对流换热,须用一组微分方程:
描写换热 过程的
(1) 表面换热微分方程:
t
F
• 目前,由于高速喷嘴的采用,气体运动速度大,使 对流传热大大加强,对流换热就不容忽视。
如:某冶金炉,炉气温度760 ℃,加热钢件到700℃,
当炉气流速分别为6m/s和18m/s时,对流换热系数 分别为10.8 kCal/m2.h. ℃和22.6 k2对流换热基本定律——牛顿冷却定律
1 3
[W/m2·ºC]
层流:
=A
(
t
)
1 4
对流换热基本方程课件

相似理论与量纲分析
相似理论
相似理论是研究两个或多个物理现象之间相似性的理论。在对流换热问题中,如 果两个物理现象的相似准则数相等,则它们之间的对流换热过程具有相似性。
量纲分析
量纲分析是一种通过比较不同物理量之间的量纲关系来研究物理现象的方法。在 对流换热问题中,可以利用量纲分析来确定影响对流换热的无量纲参数,从而简 化对流换热问题的研究。
THANKS FOR WATCHING
感谢您的观看
对流换热基本方程课件
目 录
• 引言 • 对流换热基本概念 • 对流换热基本方程推导 • 对流换热基本方程求解方法 • 对流换热强化技术及应用案例 • 总结与展望
01 引言
对流换热现象
01
02
03
定义
对流换热是指流体与固体 壁面之间由于温度差异引 起的热量传递过程。
分类
对流换热可分为自然对流 和强制对流两种形式。
对流换热研究有助于降低设备能耗、 减少废热排放,对于环境保护和可持 续发展具有积极作用。
对流换热基本方程重要性
描述对流换热过程
对流换热基本方程是描述对流换 热过程中热量传递、流体流动及 物性参数变化等规律的基础工具
。
指导工程实践
掌握对流换热基本方程有助于工程 师在设计、优化和运行工程设备时 做出合理决策,提高设备性能和经 济性。
推动理论研究
对流换热基本方程是研究对流换热 机理、探索新现象和新规律的基础 ,对于推动传热学及相关领域理论 研究具有重要意义。
02 对流换热基本概念
对流换热定义及分类
对流换热定义
对流换热是指流体与固体表面之间的 热量传递过程,其中流体可以是气体 或液体,固体表面可以是各种形状和 材料的壁面。
第7章对流换热

外掠流动 沿流动方向的 边界层外的主
纵向距离x
流速度u∞
管内流动 Re<2300——稳定的层流 Re>104 ——旺盛紊流
2300<Re<104——过渡流
外掠平壁 Rex<6×104——稳定的层流 Rex=(3~5)×105——过渡到紊流
15
一、层流流动
稳定流动情况下,粘性流体以均匀流速流入管道时壁面逐渐形 成边界层。管内流动时边界层厚度逐渐增加,并最后汇集于管道 中心。当流体再往前推进时,管内速度分布不再改变而形成充分 发展的流动 。
拉普拉斯算子在直角坐标系中代表
Du p 2u 2 (divV) X
D x
3 x
幻灯片 16
▲若流体的密度也是常数,则divV=0
粘性力
Du p 2u X D x
流体单位体 积的惯性力
单位体积的压力
体积力
原则上,据三个方向的动量方程式和连续性方程式可以结合 边界条件求解四个未知数u、v、w 和p。
但由于纳维——斯托克斯方程是非线性的微分方程组,只有少 数几种经简化后的情况可求得分析解,大量的尚依赖于数值解。 此外,流体的物性和压力都可能与温度有关,必须引进能量方程 式,并进一步考虑温度场和速度场之间的关联。
6
三、能量方程
微元控制体积单位时间内流 体通过控制体边界面净导入的 热量-总和,加上单位时间内界 面上作用的各种力对流体所作 的功,等于控制体积内流体总能 的时间变化率。
v
u y
w u z
Fx
dxdydz
控制体所受的力
可分为表面力Fs 和体积力Fb 两类
剪应力
du
冶金传输原理-第7章 对流换热ppt课件

该定律指明,实验时,必须测量出相似准数所包含的一切量。
2、相似第二定律——现象相似的条件
判断相似的充分必要 条件
凡是同一现象,如果定解条件相似,而且由定解条件的物 理量所组成的相似准数在数值上相等,则这些现象必定相似。
该定律指明,实验时,为了保证模型与实物现象相似,必须使 定解条件相似,而且,由定解条件组成的决定性准数在数值上要相 等。
7.3 热边界层概念
对流换热时,流体与壁面间存在传热温差。用细小的高灵敏的
测温元件测出的温度沿壁面y方向的变化如下图所示。
热边界层——壁面附近形成的
y
温度急剧变化的流体簿层。
y 0处,T TW;
相对过余温度
T-TW 0.99处,热边界层外缘。 T TW
T
热边界层T厚 :热度 边界层外
缘到壁面的距离。
7.4 相似理论基础
三、相似理论求解物理方程
1、粘性流体的动量平衡方程
沿x方向的纳维尔——斯托克斯方程为
ux t
ux
ux x
uy
uy y
uz
uz z
1Px2xu2x
2ux y2
2ux z2
gx
2、相似转换解相似准数
(3.46)
(‘)——实际物体的运动 (“)——实验室模型的运动
u'x t'
u'x
hA T
联立以上两式,得:
T
h
(7.3)
T y
y0
式(7.3)即为对流换热微分方 程式,该式描述了h与流体温度场的 关系。
7.2 对流换热微分方程组 7.2.1 连续性微分方程
(3.27)或(7.4)式
7.2.2 动量微分方程 (3.47)式
对流换热概念
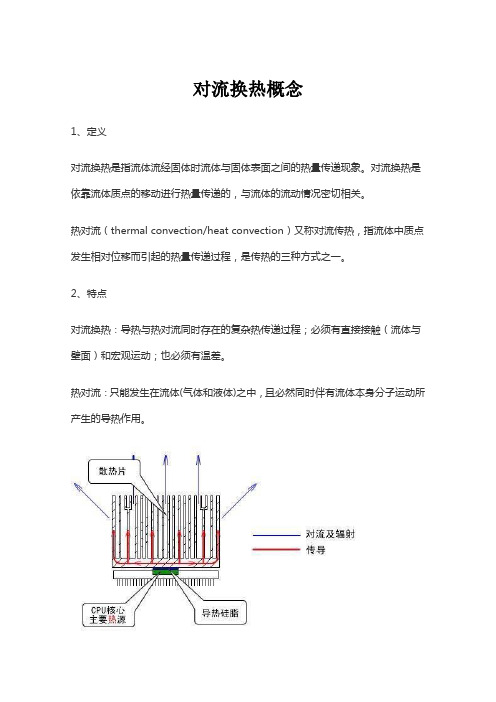
对流换热概念
1、定义
对流换热是指流体流经固体时流体与固体表面之间的热量传递现象。
对流换热是依靠流体质点的移动进行热量传递的,与流体的流动情况密切相关。
热对流(thermal convection/heat convection)又称对流传热,指流体中质点发生相对位移而引起的热量传递过程,是传热的三种方式之一。
2、特点
对流换热:导热与热对流同时存在的复杂热传递过程;必须有直接接触(流体与壁面)和宏观运动;也必须有温差。
热对流:只能发生在流体(气体和液体)之中,且必然同时伴有流体本身分子运动所产生的导热作用。
3、形式
对流换热:流体各部分因温度引起的密度差所形成的运动称为自然对流;由风机、泵等所驱动的流体运动称为受迫对流。
相应的换热过程分别称为自然对流换热和受迫对流换热。
热对流:自然对流;强迫对流和湍流,其中以湍流的热传递速率最高。
自然对流是由温度不均匀而引起流体内压强或密度不均匀,从而导致循环流动。
如煮水时水的上下循环流动。
对流换热

Pr
1/ 3
( ) 1 .0 2 5 a
1
1/ 3
Pr
1/ 3
它反映了速度边界层与温度边界层的相对大小,反映了流体动量传 递能力和热量传递能力的相对大小。
(4)格拉晓夫准则: g tl Gr 2
3
格拉晓夫准则的 数值反映了浮升 力和粘性力的相 对大小。
式中: — 流体的容积膨胀系数 ,1/K. 理想气体时为1/T, 蒸气、液体时实验测出,查表格. L —壁面定型尺寸, Δt—Δt = tw-t f ν—运动粘度
v
u y
u
2
y
2
1 dp
dx
2 2
u
t x
v
t y
a
t y
伯努利方程:
dp dx
u
du
dx
u x
v y
0
u
u x
v
u y
1 dp
dx
a
2
u y
2
2
u
t x
v
t y
t y
2
层流边界层对流换 热微分方程组: 3个方程、3个未知 量:u、v、t,方程 封闭
牛顿型流体:服从
u y
定律的流体。
非牛顿型流体:血液、泥浆、油漆等。
综上所述,表面传热系数是众多因素的函数:
h f (u , t w , t f , , c p , , , , l )
5-1
Hale Waihona Puke 当粘性流体 在壁面上流动时, 由于粘性的作用, t qx 流体的流速在靠 y w,x 近壁面处随离壁 面的距离的缩短 牛顿冷却公式:q x h x t w t f x 而逐渐降低;在 贴壁处被滞止, 处于无滑移状态 t t hx (即:y=0, u=0) tw tf x y w ,x tx y w,x 形成速度变化很 大的贴壁流体薄 注意:与第三类边界条件的区别,一类,二类? 层.
第7章_相变对流传热讲解

5、6、蒸气过热与液膜过冷
(只要对潜热项进行适当修正即可) 蒸汽过热: r" r c p,v (tv ts ) 液膜过冷:
r ' r 0.68c p (ts tw ) r (1 0.68Ja)
7.3.2 膜状凝结传热的强化
1. 基本原则: 尺量减薄液膜厚度(膜层热阻是主要热阻) 2. 强化技术——增加尖突物、及时排液 (1)采用高效冷凝面——原理:利用表面张力使肋顶 或沟槽脊背的液膜拉薄,从而增强换热。 ①低肋高、小节距横管;②锯齿管; (2)使液膜在下流过程中分段泄出或采用其他加速排 泄的措施,保持开始段δ较薄的条件 ——①加泄出罩; ②顺液流方向开沟槽的竖管 (3)采用微肋管(强化管内换热)
1、不凝结气体的影响 影响机理:
(1)冷壁面附近形成一不凝结气体层,增加了一项热阻 (2)不凝结气体的存在使壁面附近的蒸气分压下降,相
应的饱和温度下降,从而使凝结换热的驱动力下降
影响结果:使表面传热系数大大下降,换热削弱 影响程度:与压力、热负荷、运动速度等有关 例:纯净水蒸汽膜状凝结,h=5820-11630W/m•℃, 含有1%空气时,实验证明 h值将下降60%左右
7-2 膜状凝结分析解及计算关联式
主要内容:分析求解思路、求解结果、适用条件(场合)
7.2.1 努塞尔蒸气层流膜状凝结分析解(1916年提出) 1、基本依据:液膜热阻为过程的主要热阻 2、简化假设(详见P303) (1)常物性; (3)忽液膜惯性力; (7)ρ v<< ρ l; (2)蒸汽静止; (4)汽液界面无温差,tδ=ts; (8)液膜表面平整无波动。
7-5 大容器沸腾传热的实验关联式
一 、大容器饱和核态沸腾
表面传热系数或热流密度的计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7 对流换热7.0 本章主要内容导读本章讨论对流换热问题,首先介绍对流换热的相关基本概念——对流换热的机理、数学描述方法和主要研究方法,然后介绍两类无相变的对流换热——强制对流换热和自然对流换热,主要内容如图7-1所示。
图7-1 第七章主要内容导读7.1 对流换热基本概念7.1.1对流换热机理如前所述,实际工程中经常遇到的对流问题是对流换热问题,它是导热与热对流共同作用的结果。
由于流体的热运动强化了传热,通过对流流体的传热速率比通过静止流体导热的传热速率高得多。
并且,流体速度越快,传热速率越高。
理论上,对流换热可以通过牛顿冷却公式求解,即=αQ∆Ft与导热中的导热系数λ不同,对流换热系数α不是物性参数,因此对流换热过程和相应的对流换热系数受到许多因素的影响,这些影响因素可以分为如下五类。
(1)流体流动产生的原因。
根据流动产生的原因,对流换热可以分为强制对流换热与自然对流换热两大类。
前者由泵、风机或其它外部动力源的作用引起,后者通常由流体各个部分温度不同产生的密度差引起。
两种流动产生的原因不同,流体中的速度场、对流换热规律和换热强度均不一样。
通常强制对流换热的流速高、换热系数α大;(2)流体有无相变。
在流体没有相变时对流换热中的热量传输由流体显热的变化实现,在有相变的换热过程中(如沸腾或凝结),流体相变热(潜热)的释放或吸收常常起主要作用,流体的物性、流动特性和换热规律均与无相变时不同。
一般同一种流体在有相变时的换热强度远大于无相变时的强度;(3)流体的流动状态。
根据动量传输知识,粘性流体存在着两种不同的流态——层流和湍流。
层流时流体微团沿着主流方向作有规则的分层流动,湍流时流体各部分之间发生剧烈的混合。
因此,在其它条件相同时湍流换热的强度明显强于层流换热的强度;(4)换热表面的几何因素。
这里的几何因素指换热表面的形状、大小、换热表面与流体运动方向的相对位置以及换热表面的状态(光滑或粗糙)。
这些几何因素都将影响流体在壁面上的流动状况,从而影响到对流换热。
例如,管内强制对流换热与流体横掠圆管的强制对流换热中的流动是截然不同的,前者是内流中的管内流动,后者是外流中的外掠圆管流动。
这两种不同流动条件下的换热规律有明显差异。
在自然对流中不仅几何形状,几何布置对流动也有决定性影响,同样的水平壁面在热面朝上散热时的流动与热面朝下散热时的流动有显著差异,它们的换热规律也不一样;(5)流体的物理性质。
流体的物理性质对对流换热有很大影响。
以无相变的强制对流换热为例,流体的密度ρ、动力粘度μ、比热c、导热系数λ等都会影响流体中速度的分布及热量的传输,从而影响对流换热。
例如,内冷发电机的冷却介质从空气改成水可以提高发电机的出力,就是利用了水的物理性质有利于强化对流换热的特点。
流体物理性质对对流换热的具体影响见教材第十一章。
对流换热最主要的任务是确定对流换热系数α,即寻求不同条件下对流换热系数与各种影响因素之间的函数关系。
通过量纲分析,这种函数关系可以转化为几种相似准数之间的函数关系,即对流换热准数方程。
7.1.2对流换热数学描述7.1.2.1对流换热方程简介对流换热与导热和热辐射不同,它涉及流体的运动,因此对流换热的数学描述方程中不仅包括与热量传输有关的能量守恒方程,还包括与动量传输有关的质量守恒方程和动量守恒方程,即连续性方程和纳维-斯托克斯方程。
由于对流换热问题中有六个相关物理量:三维速度(v x、v y、v z)、压强p、温度t和对流换热系数α,因此对流换热数学描述中还有一个补充方程——对流换热微分方程。
7.1.2.2对流换热能量微分方程对流换热能量微分方程是能量守恒定律的微分形式,它描述了流体的温度分布。
直角坐标下的对流换热能量微分方程可以表示为。
)(222222zt y t x t a z t v y t v x t v t z y x ∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂τ 公式中的a 为流体的热扩散率。
对流换热能量微分方程的应用条件为——不可压缩牛顿流体、无内热源、物性保持不变、流速较低、忽略粘性耗散热。
公式左侧第一项为非稳态项,其它项的和为对流项,反映对流对对流换热的影响,公式右侧为扩散项,反映导热对对流换热的影响。
对流换热能量微分方程的具体推导过程见教材第十一章。
利用随体导数和哈密顿算符的概念,上式也可以表示为t a t2d d ∇=τ7.1.2.3对流换热微分方程图7-2给出了对流换热过程中在物体壁面附近的热量传输情况。
显然,流体在物体壁面处的导热热通量与对流热通量相等,即t q y t q q x x ∆==⎪⎪⎭⎫⎝⎛∂∂-==αλconv wcond公式中的αx 是x 位置处的局部对流换热系数。
图7-2 对流换热过程中的热量传输示意图上式可以重新表示为w⎪⎪⎭⎫⎝⎛∂∂∆-=y t t x λα 该公式称为对流换热微分方程,它揭示了对流换热系数与流体温度场之间的关系。
在工程计算中常用的是平均对流换热系数,它与局部对流换热系数的关系为⎰⎰==Lx F x x L or FF 0d 1d 1αααα例7-1A 根据局部换热系数计算平均换热系数对于流过表面极为粗糙平板的流动,局部对流换热系数αx 的实验结果满足以下关系式1.0)(-=ax x x α其中a 是系数(单位为W/m 1.9·K),x 为从平板前缘计算的距离。
(1)对于长度为x 的平板,写出平均对流换热系数α与局部对流换热系数αx 之间的关系;(2)定性的绘制出α和αx 随x 的变化关系。
例7-1A 图解: (1)平均对流换热系数可表示为x x L x ax x x a x ax x x L ααα11.111.19.0d )(1d 11.09.001.00==⎪⎪⎭⎫ ⎝⎛===--⎰⎰ (2)α和αx 随x 的变化关系如图所示。
7.1.2.4对流换热求解方法上述对流换热能量微分方程、对流换热微分方程和连续性方程、纳维-斯托克斯方程共同构成了描述对流换热的对流换热微分方程组。
组成方程组的六个方程求解六个变量从理论上来说完全可行,但是实际上存在许多困难,这一点在动量传输中求解连续性方程和纳维-斯托克斯方程时已经有所描述。
目前对上述对流换热微分方程组有以下几种求解方法:(1)分析法(analytical method)。
主要包括两种情况:根据边界层理论、采用数量级分析法获得边界层对流换热微分方程组,然后给出分析解和采用积分近似解法获得近似解,求解过程与动量传输中外部流动的边界层求解方法类似。
(2)实验法(experimental method)。
根据量纲分析方法的指导通过实验获得对流换热准数方程,是目前最主要的对流换热求解方法。
(3)数值法(numerical method)。
通过计算机模拟获得数值解,近年来发展迅速的对流换热求解方法。
(4)类比法(analogy method)。
通过将热量传输与动量传输进行类比获得对流换热的解,早期对流换热研究中的主要研究方法。
7.1.3对流换热准数方程 7.1.3.1对流换热准数方程的推导例7-1 对流换热准数方程的推导对于一般的无相变对流换热问题,对流换热系数可表示为()t g L c v f p ∆=βμρλα,,,,,,其中L 称为定型尺寸,βgΔt 在自然对流换热中起相当于强制对流换热中速度v 的作用。
利用量纲分析方法获得对流换热准数方程。
解:(1)根据题意有()t g L c v f p ∆=βμρλα,,,,,,因此有 8=n(2)写出各物理量的量纲2-1-1-3-2-1-231-1-3-1LT L T ML MLT ΘL T ML LT T M ΘΘ∆-tg L c v pβμρλα因此有4==m j即基本量纲和基本物理量的数量均为4。
(3)计算k 值4=-=j n k取v 、λ、μ和L 作为基本物理量,存在4个无量纲量π。
(4)计算无量纲量π并作相应变换44444333332222211111)(D C B A D C B A D C B A p D C B A L v t g L v L v c L v μλβπμλρπμλπμλαπ∆====即0004443424444144400003333333333331300002122322222222220000111131311111111][[T][L][M]][]T []L []M [][][[T][L][M]][]T []L []M [][][[T][L][M]][]T []L []M [][][[T][L][M]][]T []L []M [][Θ=Θ=Θ=Θ=Θ=Θ=Θ=Θ=-----+-+++----+-++-++------+-+++------+-+++B C B A D C B A C B B C B A D C B A C B B C B A D C B A C B B C B A D C B A C B ππππ 因此有14040424131303130212120*********===-==-=====-====-==D C B A D C B A D C B A D C B A即24321vtL g RevL Pra c Nu Lp ∆========βπμρπνλμπλαπ 对π4进行处理有Gr tL g vL v tL g =∆=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛∆=⨯=2322214modified,4νβμρβπππ (5)根据0),,,(4321=ππππf写出最终关系式),,(Pr Gr Re F Nu =上式就是对流换热的准数方程。
7.1.3.2对流换热准数方程中准数的物理意义对流换热准数方程中涉及四个准数:努塞尔数Nu 、雷诺数Re 、格拉晓夫数Gr 和普朗特数Pr 。
根据努塞尔数Nu 的定义式有w ww f w ⎪⎭⎫ ⎝⎛∂∂=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∂⎪⎪⎭⎫ ⎝⎛--∂==Y ΘL y t t t t L Nu λα 即努塞尔数为壁面处的法向无量纲过余温度梯度。
此外,努塞尔数还可以表示为condconv /q q L t tL Nu =∆∆==λαλα 因此,努塞尔数的大小表示对流换热相对于相同流体层导热的增强程度。
努塞尔数越大,对流换热效果越明显。
有时需要用到局部努塞尔准数Nu x ,其表达式为λαLNu x x =从形式上看努塞尔数Nu 与比渥数Bi 完全相同,但二者的物理意义明显不同。
此外,努塞尔数中的λ为流体的导热系数,而且公式中的对流换热系数α一般属于未知物理量,努塞尔数通常属于待定准数。
而比渥数中的λ为导热物体的导热系数,而且公式中的对流换热系数α一般为已知物理量,比渥数通常属于已定准数。
