八年级上册数学考试重点难题集

合集下载

八年级上册数学考试重点难题集

八年级上册数学考试重点难题集1．实数m＝20053－2005,下列各数中不能整除m的是（）（A）2006（B）2005（C）2004（D）20032．a,b,c,d是互不相等的正整数,且abcd＝441,那么a＋b＋c＋d的值是（）（A）30（B）32（C）34（D）363．三角形三边的长都是正整数,其中最长边的长为10,这样的三角形有（）（A）55种（B）45种（C）40种（D）30种4．一个凸多边形截去一个角后形成的多边形的内角和是2520°,则原多边形的边数是（）（A）14（B）15（C）15或16（D）15或16或175．Let a be integral part of and b be its decimal part．Let c be the integral part of and d be the decimal part.．if ad －bc＝m,the（）（A）－2＜m＜－1（B）－1＜m＜0（C）0＜m＜1（D）1＜m＜2（英汉词典：integral part 整数部分；decimal part 小数部分）6．对a,b,定义运算“＊”如下：a＊b＝已知3＊m＝36,则实数m等于（）（A）2（B）4（C）±2（D）4或±27．将连续自然数1,2,3,…,n（n≥3）的排列顺序打乱,重新排列成a1,a2,a3,…,an．若(a1－1)(a2－2)(a3－3)…(an－n)恰为奇数,则（）（A）一定是偶数（B）一定是奇数（C）可能是奇数,也可能是偶数（D）一定是2m－1（m是奇数）。

八年级上册数学重难点总结

八年级上册数学重难点总结一、三角形。

1. 重点。

- 三角形的三边关系：任意两边之和大于第三边，任意两边之差小于第三边。

这一关系常用于判断三条线段能否组成三角形，以及在已知三角形两边长度时求第三边的取值范围。

例如，已知三角形的两边长分别为3和5，则第三边x的取值范围是2 < x < 8。

- 三角形内角和定理：三角形内角和为180°。

可以利用这个定理求解三角形中未知角的度数。

如在三角形ABC中，已知∠A = 50°，∠B = 60°，则∠C=180° - 50° - 60° = 70°。

- 三角形的角平分线、中线和高的概念及性质。

角平分线将角平分，中线将对边平分，高与对边垂直。

- 等腰三角形的性质与判定。

性质包括两腰相等、两底角相等、三线合一（底边上的高、中线、角平分线重合）；判定方法是根据定义（有两边相等的三角形是等腰三角形）或者等角对等边（有两个角相等的三角形是等腰三角形）。

- 等边三角形的性质与判定。

性质有三边相等、三个角都是60°；判定可以根据定义（三边相等的三角形是等边三角形）、三个角都相等的三角形是等边三角形或者有一个角是60°的等腰三角形是等边三角形。

2. 难点。

- 三角形全等的判定。

全等三角形的判定定理有SSS（边边边）、SAS（边角边）、ASA（角边角）、AAS（角角边）、HL（直角、斜边、直角边，适用于直角三角形）。

难点在于准确找出全等的条件，尤其是在复杂图形中，容易混淆条件或者遗漏条件。

例如，在证明两个三角形全等时，可能会误将SSA（边边角）当作全等的判定条件。

- 等腰三角形性质与判定的综合应用。

例如在一些几何证明题中，需要先判定一个三角形是等腰三角形，然后再利用等腰三角形的性质来求解其他问题，这就要求对等腰三角形的判定和性质有深入的理解并且能够灵活运用。

- 利用三角形的相关知识解决实际问题。

八年级上册数学考试重点难题集

1. 如右图，一只蚂蚁从点O 出发，在扇形OAB 的边缘沿着OABO 的路线匀速爬行一周，设蚂蚁的爬行时间为t ，蚂蚁与O 点的距离为s ，则s 关于t 的函数图象大致是（）A. B. C. D.2. 如图，等边△ABC 中，点D 、E 分别在边AB ，BC 上，把△BDE 沿直线DE 翻折，使点B 落在'B处，'DB 、'EB 分别与边AC 交于点F 、G 。

若∠ADF=80度，则∠EGC= o。

3. 一次函数y=kx-6的图象经过第三象限，且它与两条坐标轴构成的直角三角形面积等于9，则K= 。

4．如图，直线y=-x+5与坐标轴交于点A 、B ，在线段AB 上（不包括端点）任取一点P ，过点P 分别作PM ⊥x 轴，PN ⊥y 轴，则长方形PMON 的周长为。

5.随着网络时代的到来，很多家庭都接入了网络，电信局规定了拨号入网的两种收费方式，用户可以任意选择其中之一：A （计时制）：05.0元／分；B （全月制）：54元／月（限一部个人住宅电话入网）。

此外，B 种上网方式要加收通信费02.0元／分。

(1)（4分）设某用户某月上网的时间为x 小时，两种方式的费用分别为1y （元）、2y （元），写出1y 、2y 与x 之间的函数关系式； (2)（2分）画出两个函数的图象；(3)（3分）请你帮该用户选择哪种方式上网更省钱？AA DBCE'B FGxh/EDB C′ F CD ′ A第6题 6．如图，把一个长方形纸片沿EF 折叠后，点D ，C 分别落在D ′，C ′的位置．若∠EFB ＝65°，则∠AED ′ 等于（）A ．70°B ．65°C ．50°D ．25°7．如图，将一个等腰直角三角形按图示方式依次翻折，若DE ＝a ，则下列说法正确的个数有（）①DC ′平分∠BDE ； ②BC 长为a )22(+；③△B C ′D 是等腰三角形； ④△CED 的周长等于BC 的长。

八年级上册数学期中考试难题集

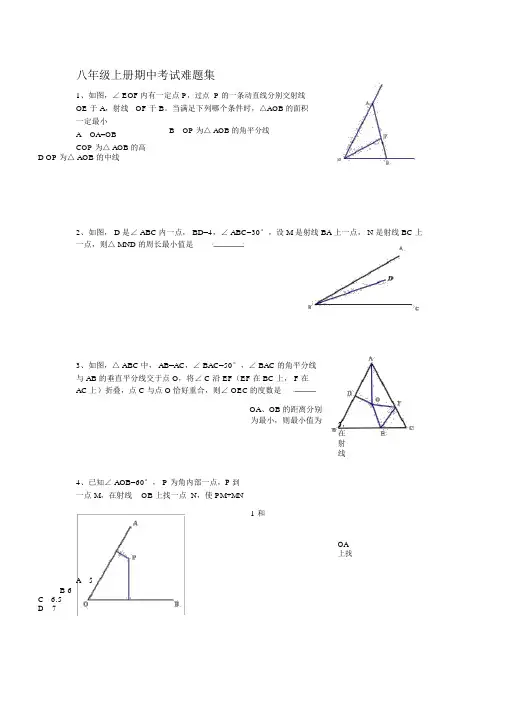
八年级上册期中考试难题集1、如图，∠ EOF内有一定点P，过点 P 的一条动直线分别交射线OE 于 A，射线OF 于 B。

当满足下列哪个条件时，△AOB 的面积一定最小A OA=OB B OP 为△ AOB 的角平分线C OP 为△ AOB 的高D OP为△ AOB 的中线2、如图， D 是∠ ABC 内一点， BD=4，∠ ABC=30°，设 M 是射线 BA 上一点， N 是射线 BC 上一点，则△ MND 的周长最小值是3、如图，△ ABC 中， AB=AC，∠ BAC=50°，∠ BAC 的角平分线与 AB 的垂直平分线交于点 O，将∠ C 沿 EF（EF 在 BC 上， F 在AC 上）折叠，点 C 与点 O 恰好重合，则∠ OEC的度数是4、已知∠ AOB=60°， P 为角内部一点，P 到一点 M，在射线OB 上找一点 N，使 PM+MN OA、OB 的距离分别为最小，则最小值为1 和5，在射线OA上找A 5B 6C 6.5D 75、已知△ ABC 的两边长为3、 7.△ DEF的三边为3、 3x-2、 2x-1，当△ ABC 与△ DEF 全等时，x的值可能为6、△ ABC 为直角三角形，∠ C=90°， AC=4，CB=3， AB=5，BD 为△ ABC的中线， AE 平分∠BAC交 BD 于 E，则 E 到 BC的距离为7、、已知：如图（ 1），在△ ABC中，∠ ABC=2∠ ACB，点 H 是 BC中点，过点 H 作 DH⊥于 H 且与 BA 延长线相交于点 D（1）图（1）中存在连接两点的线段等于DB，请画出此线段并说明理由（2）如图（ 1），当∠ B=45°时，三条线段 AB、 AD、 BC之间存在 BC=AB+2AD，请给出证明（3）如图（2），当∠ B=36°时，三条线段 AB、AD、BC之间又存在何种确定的等量关系？请写出结论并证明8、如图 1，在平面直角坐标系中，已知A（ -5,0）、 C（ 0， -4），点 B 在 y 轴正半轴上，满足S△ABC20 ，点P（m，0），（-4<m<0），线段PB绕点P顺时针旋转90°至PD（1）求证： OB=OC（2）求点 D 的坐标（3）如图 2，连接 CD 并延长交 x 轴于点 E，求证：∠ PDC=45° +∠ PBO9、在直角坐标系中，A 点的坐标为（a，0），B 点的坐标为（ 0，b），E 点的坐标为（ 0，-b），a ba2144 (c4)2C 点的坐标为（ c， 0）且 a、 b、 c 满足 a 120（1）求 a、 b、 c 的值（2）如图，点 M 为射线 OA 上 A 点右侧一动点，过点M 作 MN⊥EM 交直线 AB 于 N，连BM，问是否存在点 M ，使S△ABC 3S△AMB，若存在，求M 点的坐标，若不存在，2请说明理由。

初二数学难题30道

初二数学难题30道1. 解析几何：在直角坐标系中，点A(2, 3)，点B(1, 2)，求线段AB的中点坐标。

2. 代数方程：解方程 2x + 5 = 3x 4。

3. 函数问题：给定函数 f(x) = x^2 2x + 1，求 f(3) 的值。

4. 不等式求解：解不等式 5x 2 > 3。

5. 平行四边形：已知平行四边形ABCD，AB = 6cm，BC = 8cm，求对角线AC的长度。

6. 解析几何：在直角坐标系中，点A(1, 2)，点B(3, 4)，求线段AB的长度。

7. 代数方程：解方程 3x^2 4x + 1 = 0。

8. 函数问题：给定函数 g(x) = 2x + 3，求 g(2) 的值。

9. 不等式求解：解不等式 2x 5 < 1。

10. 平行四边形：已知平行四边形ABCD，AB = 7cm，BC = 9cm，求对角线BD的长度。

11. 解析几何：在直角坐标系中，点A(4, 5)，点B(2, 1)，求线段AB的长度。

12. 代数方程：解方程 4x^2 9x + 2 = 0。

13. 函数问题：给定函数 h(x) = x^3 3x^2 + 2x，求 h(1) 的值。

14. 不等式求解：解不等式3x + 4 ≤ 7。

15. 平行四边形：已知平行四边形ABCD，AB = 8cm，BC = 10cm，求对角线AC的长度。

16. 解析几何：在直角坐标系中，点A(3, 2)，点B(1, 1)，求线段AB的中点坐标。

17. 代数方程：解方程 5x 3 = 2x + 7。

18. 函数问题：给定函数 f(x) = x^2 + 4x + 4，求 f(0) 的值。

19. 不等式求解：解不等式4x 8 ≥ 2。

20. 平行四边形：已知平行四边形ABCD，AB = 9cm，BC = 11cm，求对角线BD的长度。

21. 解析几何：在直角坐标系中，点A(2, 3)，点B(1, 4)，求线段AB的长度。

22. 代数方程：解方程 6x^2 5x 1 = 0。

初二数学上册试卷难题

一、选择题（每题5分，共50分）1. 已知函数f(x) = x^2 - 4x + 3，那么f(2)的值为（）A. 1B. 3C. 5D. 72. 在直角坐标系中，点A(-3, 2)，点B(2, 4)，那么线段AB的中点坐标为（）A. (-1, 3)B. (1, 3)C. (1, -1)D. (-1, -1)3. 若一个等差数列的前三项分别为a，b，c，且a + b + c = 15，那么该数列的公差为（）A. 1B. 2C. 3D. 54. 已知一个梯形的上底长为3cm，下底长为5cm，高为4cm，那么该梯形的面积为（）A. 14cm^2B. 16cm^2C. 18cm^2D. 20cm^25. 若一个三角形的三边长分别为3，4，5，那么该三角形是（）A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等腰三角形6. 已知一次函数y = kx + b的图象经过点(1, 2)，且与y轴的交点坐标为(0, 3)，那么该函数的解析式为（）A. y = 2x + 3B. y = 3x + 2C. y = 2x - 3D. y = 3x - 27. 若一个平行四边形的对角线长度分别为5cm和10cm，那么该平行四边形的面积为（）A. 25cm^2B. 50cm^2C. 75cm^2D. 100cm^28. 已知一个圆的半径为r，那么该圆的面积为（）A. πr^2B. 2πr^2C. 3πr^2D. 4πr^29. 若一个正方形的边长为a，那么该正方形的对角线长度为（）A. aB. a√2C. 2aD. 2a√210. 已知一个等腰三角形的底边长为6cm，腰长为8cm，那么该三角形的面积为（）A. 24cm^2B. 32cm^2C. 40cm^2D. 48cm^2二、填空题（每题5分，共50分）1. 已知等差数列的前三项分别为1，3，5，那么该数列的公差为______。

2. 若一个梯形的上底长为4cm，下底长为6cm，高为3cm，那么该梯形的面积为______cm^2。

八上数学全册重难点题型 85个必考考点

八上数学全册重难点题型 85个必考考点一、长方形和平行四边形1. 长方形和平行四边形的性质2. 长方形和平行四边形的周长和面积计算3. 长方形和平行四边形的应用题二、三角形1. 三角形内角和定理2. 三角形外角和定理3. 三角形边长关系定理4. 三角形面积计算5. 三角形的相似和全等三、直角三角形1. 直角三角形的性质2. 直角三角形的勾股定理3. 直角三角形的应用题四、折线及其特殊角关系1. 折线的特殊角关系2. 折线的性质和应用题五、多边形1. 多边形的性质2. 多边形的周长和面积计算3. 多边形的等腰三角形应用六、圆1. 圆的性质2. 圆的周长和面积计算3. 圆的切线、弦、弧等特殊性质4. 圆的应用题七、空间图形1. 空间图形的性质2. 空间图形的体积和表面积计算3. 空间图形的应用题八、数列1. 等差数列的性质和求和公式2. 等比数列的性质和求和公式3. 数列的应用题九、逻辑推理与证明1. 数学归纳法2. 尝试证明与反证法3. 推理错误定位与分析十、数据统计1. 统计数据的整理和呈现2. 统计数据的分析与应用3. 数据统计的实际问题解决十一、平面直角坐标系1. 平面直角坐标系的性质2. 点、中点、斜率、距离等概念3. 平面直角坐标系中的方程与函数以上为八年级上学期数学全册的重难点题型的必考考点，详细内容涵盖了几何、代数和数学方法等多个知识点，对学生的数学能力和解题思维提出了很高的要求。

希望同学们认真复习，扎实掌握这些必考考点，为学业的成功打下坚实的基础。

八年级数学全册的重难点题型的必考考点涵盖了多个知识点，涉及几何、代数和数学方法等各个方面。

这些考点对学生的数学能力和解题思维提出了很高的要求。

下面我们将继续扩展讨论这些考点，并为同学们提供更详细的学习指导。

十二、解析几何1. 点与直线的位置关系2. 直线与直线的位置关系3. 角平分线、垂直平分线等特殊线段的性质4. 解析几何的应用题在解析几何中，同学们需要理解和熟练掌握点与直线的位置关系，比如点在直线的同侧、异侧和上线段的延长线上等。

八年级上数学试卷难度较高

一、选择题（每题4分，共20分）1. 已知一元二次方程x^2-3x+2=0的解为x1和x2，则x1+x2的值为（）A. 1B. 2C. 3D. 42. 若|a|=3，|b|=5，则|a-b|的最大值为（）A. 2B. 3C. 4D. 83. 在△ABC中，∠A=60°，∠B=45°，则∠C的度数为（）A. 60°B. 75°C. 120°D. 135°4. 已知正方形的对角线长为10cm，则该正方形的面积为（）A. 25cm^2B. 50cm^2C. 100cm^2D. 200cm^25. 若a、b是方程x^2-2ax+a^2=0的两个实数根，则a的值为（）A. 1B. 2C. 0D. -1二、填空题（每题5分，共20分）6. 若x^2-5x+6=0的两根分别为x1和x2，则x1+x2=________，x1x2=________。

7. 在等腰三角形ABC中，AB=AC，∠B=40°，则∠C的度数为________。

8. 若一个数的绝对值是5，则这个数是________或________。

9. 若方程x^2+px+q=0的判别式为p^2-4q=0，则方程的两个实数根互为________。

10. 在△ABC中，若∠A=50°，∠B=70°，则∠C的度数为________。

三、解答题（共40分）11. （10分）已知方程x^2-4x+3=0，求证：方程的两个实数根互为相反数。

12. （10分）已知等腰三角形ABC中，AB=AC，∠B=40°，求∠A和∠C的度数。

13. （10分）若一个数的绝对值是8，求这个数。

14. （10分）已知方程x^2-3x+2=0，求证：方程的两个实数根互为倒数。

四、附加题（10分）15. （10分）已知等边三角形ABC中，AB=BC=AC，求∠A的度数。

答案：一、选择题1. B2. D3. B4. C5. B二、填空题6. 5 37. 80°8. ±59. 倒数10. 60°三、解答题11. （1）方程x^2-4x+3=0可分解为(x-1)(x-3)=0，所以x1=1，x2=3。

(完整)八年级上册数学期末考试难题精选

八年级上册数学期末考试难题精选分式：一：如果,求证11++a ab 11++b bc 11++c ac解：原式11++a ab a ab abc a ++ababc bc a ab ++211++a ab a ab a ++1ab a ab++111++++a ab a ab二：已知a 1b 1)(29b a +，则a b b a等于多少？解：a 1b 1)(29b a +ab ba +)(29b a +(b a +)2ab2a ab 2b ab（22b a +）abab b a 22+25a b b a 25三：一个圆柱形容器的容积为立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管２倍的大水管注水。

向容器中注满水的全过程共用时间分。

求两根水管各自注水的速度。

解：设小水管进水速度为，则大水管进水速度为。

由题意得：t x v x v =+82 解之得：t vx 85=经检验得：tvx 85=是原方程解。

∴小口径水管速度为t v 85，大口径水管速度为tv25。

四：联系实际编拟一道关于分式方程2288+=xx 的应用题。

要求表述完整，条件充分并写出解答过程。

解略五：已知＝222y x xy -、＝2222y x y x -+，用“”或“－”连结、,有三种不同的形式，、、，请你任取其中一种进行计算，并简求值，其中：：。

解：选择一：22222222()()()xy x y x y x yM N x y x y x y x y x y++++=+==--+--，当x ∶y ∶时，52x y =，原式572532y yy y +=-．选择二：22222222()()()xy x y x y y xM N x y x y x y x y x y+----=-==--+-+，当x ∶y ∶时，52x y =，原式532572y yy y -=-+．选择三：22222222()()()x y xy x y x yN M x y x y x y x y x y+---=-==--+-+，当x ∶y ∶时，52x y =，原式532572y yy y -=+．反比例函数：一：一张边长为正方形的纸片，剪去两个面积一定且一样的小矩形得到一个“”图案如图所示．小矩形的长（）与宽（）之间的函数关系如图所示：（）求与之间的函数关系式；（）“”图案的面积是多少？（）如果小矩形的长是≤≤，求小矩形宽的范围.解：（）设函数关系式为xky =∵函数图象经过（，） ∴102k = ∴， ∴xy 20= （）∵xy 20=∴， ∴2162022162=⨯-=-=xy S S E 正（）当时，310620==y当时，351220==y∴小矩形的长是≤≤，小矩形宽的范围为cm y 31035≤≤二：是一个反比例函数图象的一部分，点(110)A ，，(101)B ，是它的两个端点．（）求此函数的解析式，并写出自变量x 的取值范围；（）请你举出一个能用本题的函数关系描述的生活实例．解：（）设k y x =，(110)A Q ，在图象上，101k∴=，即11010k =⨯=， 10y x∴=，其中110x ≤≤；（）答案不唯一．例如：小明家离学校10km ，每天以km/h v 的速度去上学，那么小明从家去学校所需的时间10t v=．三：如图，⊙和⊙都与轴和轴相切，圆心和圆心都在反比例函数1y x=的图象上，则图中阴影部分的面积等于 .答案：π²π四：如图，已知正比例函数和反比例函数的图像都经过点（－，1-），且（1-，－）为双曲线上的一点，为坐标平面上一动点，垂直于轴，垂直于轴，垂足分别是、．（）写出正比例函数和反比例函数的关系式；（）当点在直线上运动时，直线上是否存在这样的点，使得△与△面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（）如图，当点在第一象限中的双曲线上运动时，作以、为邻边的平行四边形，解：（）设正比例函数解析式为y kx =，将点（2-，1-）坐标代入得12k =，所以正比例函数解析式为12y x =图同样可得，反比例函数解析式为2y x= （）当点在直线上运动时，设点的坐标为1()2Q m m ，，于是211112224OBQ S OB BQ m m m △=?创=，而1(1)(2)12OAP S △=-?=，所以有，2114m =，解得2m =±所以点的坐标为1(21)Q ，和2(21)Q ，-- （）因为四边形是平行四边形，所以＝，＝，而点（1-，2-）是定点，所以的长也是定长，所以要求平行四边形周长的最小值就只需求的最小值．因为点在第一象限中双曲线上，所以可设点的坐标为2()Q n n，，由勾股定理可得222242()4OQ n n n n=+=-+，所以当22()0n n -=即20n n -=时，2OQ 有最小值，又因为为正值，所以与2OQ 同时取得最小值，所以有最小值．由勾股定理得＝5，所以平行四边形周长的最小值是2()2(52)254OP OQ +=+=+．五：如图，在平面直角坐标系中，直线与轴和轴分别交于点、点，与反比例函数一罟在第一象限的图象交于点(，)、点(，)．过点作上轴于，过点作上轴于． ()求，的值；()求直线的函数解析式；勾股定理：一：清朝康熙皇帝是我国历史上对数学很有兴趣的帝王．近日，•西安发现了他的数学专著，其中有一文《积求勾股法》，它对“三边长为、、的整数倍的直角三角形，已知面积求边长”这一问题提出了解法：“若所设者为积数（面积），以积率六除之，平方开之得数，再以勾股弦各率乘之，即得勾股弦之数”．用现在的数学语言表述是：“若直角三角形的三边长分别为、、的整数倍，•设其面积为，则第一步：6Sm ；第三步：分别用、、乘以，得三边长”．（）当面积等于时，请用康熙的“积求勾股法”求出这个直角三角形的三边长；（）你能证明“积求勾股法”的正确性吗？请写出证明过程．解：m1502566S == 所以三边长分别为：×，×，×；（）证明：三边为、、的整数倍，设为倍，则三边为，，，•而三角形为直角三角形且、为直角边．其面积12（）·（），所以6S ，6S （取正值），即将面积除以，然后开方，即可得到倍数．二：一张等腰三角形纸片，底边长，底边上的高长．．现沿底边依次从下往上裁剪宽度均为的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是( )．第张．第张．第张．第张答案：三：如图，甲、乙两楼相距米，甲楼高米，小明站在距甲楼米的A 处目测得点A 与甲、乙楼顶B C 、刚好在同一直线上，且与相距350米，若小明的身高忽略不计，则乙楼的高度是米．答案：米四：恩施州自然风光无限，特别是以“雄、奇、秀、幽、险”著称于世．著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧，50km AB A =，、B 到直线X 的距离分别为10km 和40km ，要在沪渝高速公路旁修建一服务区P ，向A 、B 两景区运送游客．小民设计了两种方案，图（）是方案一的示意图（AP 与直线X 垂直，垂足为P ），P 到A 、B 的距离之和1S PA PB =+，图（）是方案二的示意图（点A 关于直线X 的对称点是A '，连接BA '交直线X 于点P ），P 到A 、B 的距离之和2S PA PB =+．（）求1S 、2S ，并比较它们的大小；米乙甲米？米（）请你说明2S PA PB =+的值为最小；（）拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直，建立如图（）所示的直角坐标系，B 到直线Y 的距离为30km ，请你在X 旁和Y 旁各修建一服务区P 、Q ，使P 、A 、B 、Q 组成的四边形的周长最小．并求出这个最小值．解:⑴图（）中过作⊥,垂足为,则＝,又＝,∴＝在△ 中，＝＝ ∴＝ ∴ ＝24022=+BC CP ＝10240+⑵图（）中，过作⊥′垂足为，则′＝，又＝∴'＝4110504022=+ 由轴对称知：＝' ∴＝'＝4110 ∴1S ﹥2S()如图（），在公路上任找一点,连接'，由轴对称知＝' ∴＝'﹥' ∴＝'为最小（）过作关于轴的对称点', 过作关于轴的对称点'，图（）图（）图（）连接'',交轴于点, 交轴于点,则即为所求过'、 '分别作轴、轴的平行线交于点, ''＝5505010022=+∴所求四边形的周长为55050+五：已知：如图，在直角梯形中，∥，∠＝°，⊥于点，交于点，交的延长线于点，且AE AC =．（）求证：BG FG =；（）若2AD DC ==，求的长．解：（）证明：90ABC DE AC ∠=Q °，⊥于点F ，ABC AFE ∴∠=∠．AC AE EAF CAB =∠=∠Q ，， ABC AFE ∴△≌△AB AF ∴=．连接AG ，＝＝，Rt Rt ABG AFG ∴△≌△． BG FG ∴=．（）解：∵＝⊥，1122AF AC AE ∴==． 30E ∴∠=°． 30FAD E ∴∠=∠=°，AF ∴=AB AF ∴==四边形：一：如图，△、△、△均为直线同侧的等边三角形.() 当≠时，证明四边形为平行四边形；() 当时，顺次连结、、、四点所构成的图形有哪几类？直接写出构成图形的类型和相应的条件.解：() ∵△、△为等边三角形，∴，，∠∠°.∴∠∠.∴△≌△.∴ .又∵△为等边三角形，∴ .∴.同理可得 .∴四边形是平行四边形.() 构成的图形有两类，一类是菱形，一类是线段.当图形为菱形时，∠≠°（或与不重合、△不为正三角形）当图形为线段时，∠°（或与重合、△为正三角形）.二：如图，已知△是等边三角形，、分别在边、上，且，连结并延长至点，使，连结、和。

八年级上册重点难点试题

CBAOD八年级上册重点难点试题1、多项式 1a 42+加上一个单项式后,使它构成一个平方式,那么加上的单项式可以是____(填一个即可) 2、若 224x 9y kxy +- 是一个完全平方式，则k 的值是_______3.已知034106m 22=++++n m n ，则m+n=_______ 4、若分式 11x 2--x 的值为0，则x 的值为_________5、对于实数a 、b ，现用“☆”定义新运算：a ☆b ＝a 3－ab ，那么将多项式a ☆4因式分解，其结果为_________ 6. 某红外线遥控器发出的红外线波长为0.000000904 m ，用科学记数法表示这个数是______ 7.若等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的顶角为__________ 8、等腰三角形一腰上的高与另一腰的夹角为40度，则它的顶角为______9、等腰三角形的周长是18cm ，其中一边长为4cm ，其它两边长分别为 ______________ 10.(1)已知a-b=2,ab=3,则=+22a b _______ (2)已知21a =+a ，则221a a+=______ 11、把分式mnn+m 中的都扩大4倍，那么分式的值（） A 、缩小为原来的41B 、扩大为原来的4倍C 、不变D 、无法确定12、下列各式中，正确的有（）A 1个B 2个C 3个D 4个13、 b a b a b 23496a +- 分解因式的正确结果是（）A. a ²b(a ²-6a+9)B. a ²b(a+3)(a-3)C. b(a ²-3)D. a ²b(a-3) ² 14、下列各式从左到右的变形中，是因式分解的为（）. A 、；B 、；C 、； D 、15、若|a －2|＋b 2－2b ＋1＝0，则a ＝__________，b ＝__________16、△ABC 的三边长分别a 、b 、c ，且a+2ab ＝c+2bc ，△ABC 的形状为___________ 17、如下图，MP 、NQ 分别垂直平分AB 、AC 且BC=6cm ，则△APQ 的周长为___________cm 18、如下图，在△ABC 中，∠C 是直角，AD 平分∠BAC ，交BC 于点D;如果AB ＝8，CD ＝2，那么△ABD 的面积等于______ 19.如下图，AB ＝AC ，AC 的垂直平分线DE 交AC 于D ，交AB 于E ，BC ＝6，△CDB 的周长为15，则AC ＝________．20.如上图，O 是△ABC 中∠ABC 和∠ACB 的平分线的交点，OD ∥AB 交BC 于D ，OE ∥AC 交BC 于E ，若BC=10㎝，则△ODE 的周长等于21．等腰三角形一腰上的中线把这个三角形的周长分成15㎝和12㎝，则这个三角形的底边长为 cm ．A B E DC FAC22.一个正多边形的一个外角等于它的一个内角的13，这个正多边形是______边形 23、△ABC 中，BO 、CO 分别平分∠ABC 、∠ACB(1)若∠A=70°，则∠BOC= (2)若∠BOC=120°，∠A= 24.如图，有三种卡片，其中边长为a 的正方形卡片1张，边长为a ，b 的长方形卡片6张，边长为b 的正方形卡片 9张，用这16张卡片拼成一个无空隙的正方形，则这个正方形的边长是___________25.如图，小亮从A 点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，……照这样走下去，他第一次回到出发地A点时，一共走了__________米26.若a+b=3，则22a +4ab+22b －6的值为_________27.(1)已知则（2）201520145.132）（）（-∙=_______ 28.已知关于x 的方程 x223x -=--mx 无解,则m 的值为__________ 29.当时，关于的方程无解。

初二数学难题带答案上学期

初二数学难题带答案（上学期）一、选择题（每小题3分，共30分）1. 如图，△ ABD^A CDB下面四个结论中，不正确的是（）A.A ABC ffiA CDB的面积相等B . △ABD ffiA CDB的周长相等C.Z A+Z ABD=Z C+Z CBD D AD// BC 且AD= BC,第1 题图）, 第2题图）, 第3题图）, 第4题图）2. 如图，小强利用全等三角形的知识测量池塘两端M N的距离，如果△ PQ3△NMO则只需测出其长度的线段是（）A. POB. PQC. MOD. MQ3.如图，BE±AC于点D,且AD= CD BD= ED,则Z ABC= 54°，则Z E=（） A. 25° B. 27° C. 30° D. 45°4. （2014?南昌）如图，AB// DE AC// DF, AO DF,下列条件中不能判断△ ABC^△DEF的是（）A. AB= DEB.Z B=Z EC. EF= BCD. E F // BC5. 如图，Z 1 = Z 2，Z 3=Z 4，则下面结论中错误的是（）A.A ADC^A BCD B △ABD^A BAC C △ABO^A COD D △AOD^ BOC ,第5题图）, 第6题图）, 第7题图）6. 如图，在△ ABC中, A吐AC,点E, F是中线AD上的两点，则图中可证明为全等三角形的有（）A. 3对B . 4对C . 5对D . 6对7. 如图，在△ ABC中, Z ACB= 90°，沿CD折叠△ CBD使点B恰好落在AC边上的点E处，若Z A= 22°，则Z BDC等于（）A 44°B 60°C 67°D 77°8. 如图，DEIBC于点E,且BE= CE AB+ AO 15,则厶ABD的周长为（） A．15 B．20 C．25 D．309. 如图，AB丄B C, BE!AC, Z 1 = Z 2, AD= AB 则（）A.Z 1 = Z EFDB. BE= ECC. BF- DF= CDD. FD// BC,第8题图）, 第9题图）, 第10题图）10 .如图，在△ ABC中, AD是Z BAC的平分线，DEI AC于E, DF! AB于F,且FB= CE则下列结论：①DE= DF,②AE=AF,③BD= CD④AD!BC.其中正确的个数有（）A. 1个B . 2个C . 3个D . 4个二、填空题（每小题3分，共24分）1 1 .在厶ABC中, A吐8, AO6,贝U BC边上的中线AD的取值范围是12.若厶ABC^A EFG 且Z B= 60°,Z FGE-Z E= 56°，则Z A= _______________度．13 .如图，A吐DB Z ABD=Z CBE请你添加一个适当的条件______________ 使厶ABC^A DBE.（只需添加一个即可）14. 如图，A吐AC AD= AE / BAG=/ DAE / 1= 25°,/ 2 = 30°，则/ 3= ,第13题图） , 第14 题图） , 第15 题图） , 第16题图） , 第17题图）15. 如图，在Rt△ ABC中,/ AC= 90°, BC= 2 cm, CDLAB,在AC上取一点E,使EC= BC,过点E作EF±AC交CD的延长线于点F,若EF= 5 cm,则AE= cm.16. 如图，在Rt△ ABC中,/ C= 90°, AC= 10 cm, BC= 5 cm, —条线段PQ=AB P, Q两点分别在线段AC和AC的垂线AX上移动，则当AF= __________ 时，才能使厶ABC ffiA APQ全等.17. 如图，已知△ ABC中,/ ABC / ACB的角平分线交于点O,连接AO并延长交BC于D, OH L BC于H,若/ BA（= 60° , OH= 5 cm ,则/ BAD= _____ ，点O到AB的距离为________ cm.18. 已知点A, B的坐标分别为（2 , 0）, （2 , 4）,以A, B , P为顶点的三角形与△ ABO全等,写出一个符合条件的点P的坐标：三、解答题（共66 分）19. （6 分）如图,在厶ABC^P^ DCE中 , AB// DC A吐DC BC= CE 且点B, C,E 在一条直线上.求证：/ A=/ D.20. （8 分）如图，点B在射线AE上 , / CAE=Z DAE / CBE=Z DBE求证：AC = AD.21. （10分）如图,E是/ AOB的平分线上一点,EC丄OA EDLOB垂足为C, D,连接CD交OE于 F.求证：（1）OC= OD （2）DF = CF.22. （10 分）如图,在Rt△ ABC中 , / AC= 90°，点D, F分别在AB AC上 , CF= CB连接CD将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.（1）求证：△ BCD^A FCE⑵若EF/ CD求/ BD C的度数.23. （10 分）如图AB=DC AD=BC DE=BF 求证：BE=DF.24. （10分）如图,已知：/ B=/ C= 90° , M是BC的中点,DM平分/ ADC. 求证：（1）AM 平分/ DAB；（2）AD= AB＋CD.25. （12分）如图,在/ AOB的两边OA OB上分别取OM= ON / OM=/ OND DN 和EM相交于点C, CD= CE.求证：点C在/ AO B的平分线上.第12 章检测题参考答案1. C2.B3.B4.C5.C6.D7.C8.A9.D 10.D 11.1 v AD< 712.32 13. /C=/ E 14.55° 15. 3 16.5 cm 或10 cm 17.30°；518. (0 4)或(4 0)或(4 4)( 答其中一个即可)19. v AB// DC, •••/ B=/ DCE又：A吐DC BC= CE , /•△ ABC^ADCE(SAS) •••/ A=/ D20. v/ CBE=Z DBE •- 180°-/ CB= 180°—/ DBE 即/ AB(=Z ABD 在厶ABC?3ABD中, / CA=/ DAE AB= AB / AB(=/ ABD •△ABC^A ABD(ASA) • AC= AD21. (1) v EC L OA EDL OB •/ OC=/ OD= 90°,在厶OCE ffiA ODE中, /Ed EDO / CO旨/ DOE OE= OE :. △ OCE^ ODE(AAS) /• 0C= OD (2) 在厶COF ffiA DOF中, OC= OD / CO昌/ DOE OF= OF, :. △ COF^A DOF(SAS)二DF= CF22. (1) vZ ACB= 90°, / DCE= 90°, /-Z ACB-Z AC亠/DCE-Z ACD 即/ BC亠/ FCE在厶 BCD ffiA FCE中,BO CF, Z BCD^Z FCE DC= CE •/△BCD ◎△ FCE(SAS)(2) v EF// CD /Z E=Z D CE= 90°, /Z BDC=Z E= 90°23. 连接BD.v AD= BC A吐CD BD= BD ABD^A CDB(SSS) , /Z ADB=Z DBC /•180°—Z ADB= 180°-Z DBC /Z BDE=Z DBF 在厶BDE ffiA DBF 中,DE=BF, Z BD吕Z DBF DB= BD BDE^A DBF(SAS) / BE= DF24. (1)过M作MH L AD于H , v DIM平分Z ADC MCL DC MH L AD, / CM= HM 又v BM= CM / MHh BM v MHL AD, MBL AB / AM平分Z DAB (2) vZ CDMk Z HDM/Z CM匡Z HMD 又v DC L MC DHL MH / DC= DH 同理：AB= AH, v AD =DH^AH, / AD= AB+ CD25. 在△MOE^A NOD中, Z OM EZ OND OM= ON Z MO EZ NOD /△MO專△NOD(ASA) / OD= OE v CD= CE OC E OC / △OCI^A OCE(SSS) /Z DOC =Z EOC即C在Z AOB的平分线上以上资料来源可靠，专业可信，将助您更好的提升办公效率。

八年级上学期数学重难点突破汇总V0.2

八年级上学期数学重难点突破汇总V0.2一．选择题（共7小题）1．如图，在△ABC中，∠B+∠C＝α，按图进行翻折，使B'D∥C'G∥BC，B'E∥FG，则∠C'FE的度数是（）A．B．90°﹣C．α﹣90°D．2α﹣180°2．如图，等腰直角△ABC中，∠BAC＝90°，AD⊥BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M 为EF的中点，延长AM交BC于点N，连接DM，NE．下列结论：①AE＝AF；②AM⊥EF；③△AEF是等边三角形；④DF＝DN，⑤AD∥NE．其中正确的结论有（）A．1个B．2个C．3个D．4个3．如图，点P是∠AOB的角平分线OC上一点，PN⊥OB于点N，点M是线段ON上一点．已知OM＝3，ON＝5，点D为OA上一点若满足PD＝PM，则OD的长度为（）A．3B．5C．5和7D．3和74．如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D为BC的中点，点E、F分别在AB、AC上，且∠EDF ＝90°，下列结论：①△DEF是等腰直角三角形；②AE＝CF；③△BDE≌△ADF；④BE+CF＝EF．其中正确的是（）A．①②④B．②③④C．①②③D．①②③④5．如图，AP，CP分别是四边形ABCD的外角∠DAM，∠DCN的平分线，设∠ABC＝α，∠APC＝β，则∠ADC 的度数为（）A．180°﹣α﹣βB．α+βC．α+2βD．2α+β6．如图，已知等边三角形ABC，点D为线段BC上一点，以线段DB为边向右侧作△DEB，使DE＝CD，若∠ADB ＝m°，∠BDE＝（180﹣2m）°，则∠DBE的度数是（）A．（m﹣60）°B．（180﹣2m）°C．（2m﹣90）°D．（120﹣m）°7．如图，在△ABC中，高AD和BE交于点H，且∠1＝∠2＝22.5°，下列结论正确的有（）①∠1＝∠3；②BD+DH＝AB；③2AH＝BH；④若CD＝，则BH＝3；⑤若DF⊥BE于点F，则AE﹣DF＝FH．A．①②④B．①②⑤C．②③④D．③④⑤二．填空题（共12小题）8．如图，Rt△ABC中，∠C＝90°．E为AB中点，D为AC上一点，BF∥AC交DE的延长线于点F．AC＝6，BC＝5．则四边形FBCD周长的最小值是．9．如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝4，△ABC的面积是．10．如图，∠C＝90°，AC＝20，BC＝10，AX⊥AC，点P和点Q同时从点A出发，分别在线段AC和射线AX 上运动，且AB＝PQ，当AP＝时，以点A，P，Q为顶点的三角形与△ABC全等．11．已知：如图，BD为△ABC的角平分线，且BD＝BC，E为BD延长线上的一点，BE＝BA，过E作EF⊥AB，F为垂足，下列结论：①△ABD≌△EBC；②∠BCE+∠BCD＝180°；③AD＝EF＝EC；④BA+BC＝2BF，其中正确的结论有（填序号）．12．在非直角三角形ABC中，∠A＝40°，高BD和高CE所在的直线相交于点H，则∠BHC＝ °．13．在四边形ABCD中，∠ADC与∠BCD的角平分线交于点E，∠DEC＝115°，过点B作BF∥AD交CE于点F，CE＝2BF，∠CBF＝∠BCE，连接BE，S△BCE＝4，则CE＝．14．如图，已知等腰△ABC，AB＝AC，∠BAC＝120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP＝OC，下面结论：①∠APO＝∠ACO；②∠APO+∠PCB＝90°；③PC＝PO；④AO+AP ＝AC；其中正确的有．（填上所有正确结论的序号）15．如图，在△ABC中，∠ABC＝60°，CD＝，CD是△ABC的一条高线．若E，F分别是CD和BC上的动点，则BE+EF的最小值为．16．在直角坐标系中，已知A（6，0）、F（3，0），C（0，2），在△AOC的边上取两点P、Q（点Q是不同于点F的点），若以O、P、Q为顶点的三角形与△OFP全等，则符合条件的点P的坐标为．17．如图，任意画一个∠BAC＝60°的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD相交于点P，连接AP，有以下结论：①∠BPC＝120°；②AP平分∠BAC；③AD＝AE；④PD＝PE；⑤BD+CE＝BC；其中正确的结论为．（填写序号）18．如图，在△ABC中，∠ABC：∠ACB：∠CAB＝5：6：7，点M在BA的延长线上，点N在BC的延长线上，DA平分∠CAM，DC平分∠ACN，连接BD，则∠BDC﹣∠ADB＝度．19．若关于x的方程＝无解，则a的值是．三．解答题（共21小题）20．如图，在四边形ABCD中，∠DAB＝∠ABC＝90°，AD∥BC，AB＝BC，E是AB的中点，CE⊥BD．（1）求证：BE＝AD；（2）求证：AC是线段ED的垂直平分线：（3）△DBC是等腰三角形吗？并说明理由．21．如图，CE、CB分别是△ABC、△ADC的中线，且AB＝AC．求证：CD＝2CE．22．【问题背景】在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且∠EAF ＝60°，试探究图1中线段BE、EF、FD之间的数量关系．【初步探索】小亮同学认为：延长FD到点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，则可得到BE、EF、FD之间的数量关系是．【探索延伸】在四边形ABCD中如图2，AB＝AD，∠B+∠D＝180°，E、F分别是BC、CD上的点，∠EAF＝∠BAD，上述结论是否任然成立？说明理由．【结论运用】如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角（∠EOF）为70°，试求此时两舰艇之间的距离．23．如图，一个直角三角形纸片的顶点A在∠MON的边OM上移动，移动过程中始终保持AB⊥ON于点B，AC⊥OM于点A．∠MON的角平分线OP分别交AB、AC于D、E两点．（1）点A在移动的过程中，线段AD和AE有怎样的数量关系，并说明理由．（2）点A在移动的过程中，若射线ON上始终存在一点F与点A关于OP所在的直线对称，判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形？（3）若∠MON＝45°，猜想线段AC、AD、OC之间有怎样的数量关系，只写出结果即可．不用证明．24．如图，已知△ABC是等边三角形，且AE＝CD，AD、BE相交于P，BQ⊥AD于Q．（1）求证：△ABE≌△CAD；（2）求∠PBQ的度数；（2）求证：BP＝2PQ．25．如图1，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，（1）连接AQ、CP交于点M，则在P、Q运动的过程中，∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数；（2）何时△PBQ是直角三角形？（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数．26．如图，过∠AOB平分线上一点C作CD∥OB交OA于点D，E是线段OC的中点，请过点E画直线分别交射线CD、OB于点M、N，探究线段OD、ON、DM之间的数量关系，并证明你的结论．27．如图1，△ABC与△ADE都是以点A为顶点的等腰三角形，且∠BAC＝∠DAE，BD⊥AD，ED的延长线交BC于点F，探究线段BF与CF的数量关系，并说明理由．（如果你经过思考后不能找到问题的答案，可选择以下两个问题来完成）①将△ABC与△ADE改为等边三角形，其他条件不变，如图2．②将原题改为探究线段BD与EC的数量关系．28．有公共顶点A的△ABD，△ACE都是的等边三角形．（1）如图1，将△ACE绕顶点A旋转，当E，C，B共线时，求∠BCD的度数；（2）如图2，将△ACE绕顶点A旋转，当∠ACD＝90°时，延长EC角BD于F，①求证：∠DCF＝∠BEF；②写出线段BF与DF的数量关系，并说明理由．29．在△ABC中，BD是△ABC的角平分线，点E在射线DC上，EF⊥BC于点F，EM平分∠AEF交直线AB于点M．（1）如图1，点E在线段DC上，若∠A＝90°，∠M＝α．①∠AEF＝；（用含α的式子表示）②求证：BD∥ME；（2）如图2，点E在DC的延长线上，EM交BD的延长线于点N，用等式表示∠BNE与∠BAC的数量关系，并证明．30．阅读下面材料：小明遇到这样一个问题：如图1，在△ABC中，AD平分∠BAC，∠ABC＝2∠C．求证：AC＝AB+BD；小明通过思考发现，可以通过“截长、补短”两种方法解决问题：方法一：如图2，在AC上截取AE，使得AE＝AB，连接DE，可以得到全等三角形，进而解决问题．方法二：如图3，延长AB到点E，使得BE＝BD，连接DE，可以得到等腰三角形，进而解决问题．（1）根据阅读材料，任选一种方法证明AC＝AB+BD，根据自己的解题经验或参考小明的方法，解决下面的问题；（2）如图4，四边形ABCD中，E是BC上一点，EA＝ED，∠DCB＝2∠B，∠DAE+∠B＝90°，探究DC、CE、BE之间的数量关系，并证明．31．如图①，在Rt△ABC中，∠C＝90°，BC＝9cm，AC＝12cm，AB＝15cm，现有一动点P，从点A出发，沿着三角形的边AC→CB→BA运动，回到点A停止，速度为3cm/s，设运动时间为ts．（1）如图（1），当t＝时，△APC的面积等于△ABC面积的一半；（2）如图（2），在△DEF中，∠E＝90°，DE＝4cm，DF＝5cm，∠D＝∠A．在△ABC的边上，若另外有一个动点Q，与点P同时从点A出发，沿着边AB→BC→CA运动，回到点A停止．在两点运动过程中的某一时刻，恰好△APQ≌△DEF，求点Q的运动速度．32．阅读下列材料并解答问题：在一个三角形中，如果一个内角的度数是另一个内角度数的3倍，那么这样的三角形我们称为“梦想三角形”例如：一个三角形三个内角的度数分别是120°，40°，20°，这个三角形就是一个“梦想三角形”．反之，若一个三角形是“梦想三角形”，那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍．（1）如果一个“梦想三角形”有一个角为108°，那么这个“梦想三角形”的最小内角的度数为．（2）如图1，已知∠MON＝60°，在射线OM上取一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（点C不与O、B重合），若∠ACB＝80°．判定△AOB、△AOC是否是“梦想三角形”，为什么？（3）如图2，点D在△ABC的边上，连接DC，作∠ADC的平分线交AC于点E，在DC上取一点F，使得∠EFC+∠BDC＝180°，∠DEF＝∠B．若△BCD是“梦想三角形”，求∠B的度数．33．如图，△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，点P从A点出发沿A﹣C路径向终点C运动；点Q 从B点出发沿B﹣C﹣A路径向终点A运动．点P和Q分别以每秒1cm和3cm的运动速度同时开始运动，其中一点到达终点时另一点也停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．则点P运动时间为多少时，△PEC与△QFC全等？34．在等腰三角形ABC中，∠ABC＝90度，D是AC边上的动点，连结BD，E、F分别是AB、BC上的点，且DE⊥DF．（1）如图1，若D为AC边上的中点．①填空：∠C＝，∠DBC＝；②求证：△BDE≌△CDF．（2）如图2，D从点C出发，点E在PD上，以每秒1个单位的速度向终点A运动，过点B作BP∥AC，且PB＝AC＝4，点E在PD上，设点D运动的时间为t秒（0≤t≤4）在点D运动的过程中，图中能否出现全等三角形？若能，请直接写出t的值以及所对应的全等三角形的对数，若不能，请说明理由．35．如图，已知△ABC中，AB＝AC＝10cm，BC＝8cm，点D为AB的中点．如果点P在线段BC上以3cm/s的速度由点B向C点运动，同时，点Q在线段CA上由点C向A点运动．（1）若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由．（2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？36．如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形△AOB，点C为x正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边三角形△CBD，连接DA并延长，交y轴于点E．（1）求证：△OBC≌△ABD．（2）在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数；如果变化，请说明理由．（3）当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？37．如图，△ABC中，AB＝BC＝CA，∠A＝∠ABC＝∠ACB，在△ABC的顶点A，C处各有一只小蚂蚁，它们同时出发，分别以相同速度由A向B和由C向A爬行，经过t（s）后，它们分别爬行到了D，E处，设DC与BE的交点为F．（1）证明△ACD≌△CBE；（2）小蚂蚁在爬行过程中，DC与BE所成的∠BFC的大小有无变化？请说明理由．38．如图，在平面直角坐标系中，直线l过点M（3，0），且平行于y轴．（1）如果△ABC三个顶点的坐标分别是A（﹣2，0），B（﹣1，0），C（﹣1，2），△ABC关于y轴的对称图形是△A1B1C1，△A1B1C1关于直线l的对称图形是△A2B2C2，写出△A2B2C2的三个顶点的坐标；（2）如果点P的坐标是（﹣a，0），其中0＜a＜3，点P关于y轴的对称点是P1，点P1关于直线l的对称点是P2，求PP2的长．39．在等边△ABC的两边AB、AC所在直线上分别有两点M、N，D为△ABC外一点，且∠MDN＝60°，∠BDC ＝120°，BD＝DC．探究：当M、N分别在直线AB、AC上移动时，BM、NC、MN之间的数量关系及△AMN 的周长Q与等边△ABC的周长L的关系．（1）如图1，当点M、N边AB、AC上，且DM＝DN时，BM、NC、MN之间的数量关系是；此时＝；（2）如图2，点M、N在边AB、AC上，且当DM≠DN时，猜想（I）问的两个结论还成立吗？若成立请直接写出你的结论；若不成立请说明理由．（3）如图3，当M、N分别在边AB、CA的延长线上时，探索BM、NC、MN之间的数量关系如何？并给出证明．40．在△DEF中，DE＝DF，点B在EF边上，且∠EBD＝60°，C是射线BD上的一个动点（不与点B重合，且BC≠BE），在射线BE上截取BA＝BC，连接AC．（1）当点C在线段BD上时，①若点C与点D重合，请根据题意补全图1，并直接写出线段AE与BF的数量关系为；②如图2，若点C不与点D重合，请证明AE＝BF+CD；（2）当点C在线段BD的延长线上时，用等式表示线段AE，BF，CD之间的数量关系（直接写出结果，不需要证明）．。

八年级上册数学重点难点

八年级上册数学重点难点
八年级上册数学的重点和难点可能因教材版本和学生具体情况而有所不同，但一般来说，以下是一些可能被认为是重点和难点的知识点：
重点：
1. 函数：函数是八年级数学中的一个重要概念，要求学生掌握函数的性质、图像和运算。

2. 三角形：三角形是几何学中的基础图形，要求学生掌握三角形的性质、全等和相似等知识点。

3. 勾股定理：勾股定理是几何学中一个非常重要的定理，要求学生掌握其证明和应用。

4. 一次函数：一次函数是函数中的基础类型，要求学生掌握其图像、性质和运算。

5. 分式：分式是代数中的基础知识点，要求学生掌握其性质、运算和化简。

难点：
1. 函数图像：函数的图像是理解函数性质的重要手段，但学生往往难以理解和掌握。

2. 三角形全等和相似：三角形全等和相似的判定条件比较复杂，学生容易混淆。

3. 勾股定理的证明：勾股定理的证明过程比较繁琐，学生不易理解和掌握。

4. 分式的化简：分式的化简需要学生掌握一定的运算技巧和代数变换，难度较大。

5. 二次根式的化简：二次根式的化简需要学生掌握一定的运算技巧和代数变换，难度较大。

总的来说，重点和难点知识点的掌握需要学生多做练习、勤于思考，并在学习中不断积累经验。

初二数学上册重难点考点

十一章全等三角形
11.1全等三角形
重点：全等形和全等三角形的概念及全等三角形的表示方法，全等三角形的性质难点：准确找出全等三角形的对应边和对应角
考点：运用全等三角形的性质解决线段的长度问题和角度问题，
利用全等变换解决几何问题，全等三角形的面积问题
11.2三角形全等的判定
重点：判定三角形全等的方法:角边角(ASA)、角角边（AAS）、HL （直角三角形）
难点：灵活运用三角形全等的性质解决线段或角相等的问题
考点：通过判定三角形全等与多边形综合题
11.3角的平分线的性质
重点：角的平分线的性质及判定，作出已知角的平分线
难点：用角的平分线的性质求线段相等，角的度数，角的平分线性质的综合运用考点：角的平分线的性质与三角形全等，线段垂直平分线及圆等其他几何知识相互渗透
十二章轴对称
12.1轴对称
重点：轴对称与轴对称图形，线段垂直平分线，画轴对称图形或成轴对称的两个图形的对称轴
难点：轴对称和轴对称图形的性质
考点：轴对称变换与旋转知识的综合
12.2作轴对称图形
重点：作轴对称图形
难点：用坐标表示轴对称
考点：轴对称变换及关于坐标轴对称的点的坐标，轴对称与平移、中心对称、旋转的综合
12.3 等腰三角形
重点：等腰三角形的有关概念及性质，等腰三角形的判定，等边三角形及其性质，等边三角形的判定，含30°角的直角三角形的性质
难点：有关等腰三角形的综合运用
考点：等腰三角形及等边三角形的性质和判定及探究性问题。

八年级上册数学《全等三角形难题集》

1倍长中线�线段�造全等 1、已知�如图�A D 是△A B C 的中线�B E 交A C 于E �交A D 于F �且 A E =E F �求证�A C =B F ABCDE F分析�要求证的两条线段A C 、B F 不在两个全等的三角形中�因此证A C =B F 困难�考虑能否通过辅助线把A C 、BF 转化到同一个三角形中�由A D 是中线�常采用中线倍长法�故延长A D 到G �使D G =A D �连B G �再通过全等三角形和等线段代换即可证出。

2、已知在△A B C 中�A D 是B C 边上的中线�E 是A D 上一点�且B E =A C �延长B E 交A C 于F �求证�A F =E F F EDABC提示�倍长A D 至G �连接B G �证明ΔB D G ≌ΔC D A三角形B E G 是等腰三角形3、已知�如图△A B C 中�A B =5�A C =3�则中线A D 的取值范围是_________. D CBA4、在△A B C 中,A C =5,中线A D =7�则A B 边的取值范围是( ) A 、1<A B <29 B 、4<A B <24 C 、5<A B <19 D 、9<A B <195、已知�A D 、A E 分别是△A B C 和△A B D 的中线�且BA =B D � 求证�A E =21ACABCDE6、如图�△A B C 中�B D =D C =A C �E 是D C 的中点�求证�AD 平分∠B AE . E D C BA7、已知C D =A B �∠B D A =∠B A D �A E 是△A B D 的中线�求证�∠C =∠B A EABCDE提示�倍长A E 至F �连结D F 证明ΔA B E ≌ΔF D E �S A S � 进而证明ΔA D F ≌ΔA D C �S A S �8、如图23�△A B C 中�D 是B C 的中点�过D 点的直线G F 交A C 于F �交A C 的平行线B G 于G 点� D E ⊥D F �交A B 于点E �连结E G 、E F .⑴求证�B G =C F ⑵请你判断B E +C F 与E F 的大小关系�并说明理由。

部编数学八年级上册专题01三角形六大重难题型(期末真题精选)(解析版)含答案

专题01 三角形六大重难题型一．中线分周长（分类讨论）1．如图，已知BD 是△ABC 的中线，AB ＝5，BC ＝3，且△ABD 的周长为12，则△BCD 的周长是 10　．试题分析：先根据三角形的中线、线段中点的定义可得AD ＝CD ，再根据三角形的周长公式即可求出结果．答案详解：解：∵BD 是△ABC 的中线，即点D 是线段AC 的中点，∴AD ＝CD．实战训练∵AB＝5，△ABD的周长为12，∴AB+BD+AD＝12，即5+BD+AD＝12．解得BD+AD＝7．∴BD+CD＝7．则△BCD的周长是BC+BD+CD＝3+7＝10．所以答案是：10．2．已知AD是△ABC的中线，若△ABD与△ACD的周长分别是17和15，△ABC的周长是22，则AD的长为　5　．试题分析：根据三角形的周长公式列式计算即可得解．答案详解：解：∵△ABD与△ACD的周长分别是17和15，∴AB+BC+AC+2AD＝17+15＝32，∵△ABC的周长是22，∴AB+BC+AC＝22，∴2AD＝32﹣22＝10，∴AD＝5．所以答案是：5．3．如图所示，AD是△ABC的中线．若AB＝7cm，AC＝5cm，则△ABD和△ADC的周长的差为　2　cm．试题分析：根据三角形中线的定义得到BD＝CD，求得△ABD和△ACD的周长差＝（AB+AD+BD）﹣（AC+AD+CD）＝AB﹣AC，于是得到结论．答案详解：解：∵AD是BC边上的中线，∴BD＝CD，∴△ABD和△ACD的周长差＝（AB+AD+BD）﹣（AC+AD+CD）＝AB﹣AC，∵AB＝7cm，AC＝5cm，∴△ABD和△ACD的周长差＝7﹣5＝2cm．所以答案是：2．二．中线之等分面积4．如图，已知△ABC 中，点D 、E 分别是边BC 、AB 的中点．若△ABC 的面积等于8，则△BDE 的面积等于（）A ．2B ．3C ．4D ．5试题分析：根据三角形的面积公式即可得到结论．答案详解：解：∵点D 是边BC 的中点，△ABC 的面积等于8，∴S △ABD =12S △ABC ＝4，∵E 是AB 的中点，∴S △BDE =12S △ABD =12×4＝2，所以选：A ．5．已知：如图所示，在△ABC 中，点D ，E ，F 分别为BC ，AD ，CE 的中点，且S △ABC ＝4cm 2，则阴影部分的面积为　1　cm 2．试题分析：易得△ABD ，△ACD 为△ABC 面积的一半，同理可得△BEC 的面积等于△ABC 面积的一半，那么阴影部分的面积等于△BEC 的面积的一半．答案详解：解：∵D 为BC 中点，根据同底等高的三角形面积相等，∴S △ABD ＝S △ACD =12S △ABC =12×4＝2（cm 2），同理S △BDE ＝S △CDE =12S △BCE =12×2＝1（cm 2），∴S △BCE ＝2（cm 2），∵F 为EC 中点，∴S △BEF =12S △BCE =12×2＝1（cm 2）．所以答案是1．三．三角形的高的辨别6．如图，△ABC中，AD⊥BC于D，点E在CD上，则图中以AD为高的三角形有　6　个．试题分析：由于AD⊥BC于D，图中共有6个三角形，它们都有一边在直线CB上，由此即可确定以AD为高的三角形的个数．答案详解：解：∵AD⊥BC于D，而图中有一边在直线CB上，且以A为顶点的三角形有6个，∴以AD为高的三角形有6个．所以答案是：6．7．如图，△ABC中，BC边所在直线上的高是线段　AD　．试题分析：根据三角形的高的概念解答即可．答案详解：解：△ABC中，BC边所在直线上的高是线段AD，所以答案是：AD四．多边形的内角和与外角和8．若一个多边形的内角和是540°，则这个多边形是　五　边形．试题分析：根据多边形的内角和公式求出边数即可．答案详解：解：设多边形的边数是n，则（n﹣2）•180°＝540°，解得n＝5，所以答案是：五．9．如图，∠A+∠B+∠C+∠D+∠E+∠F的值是（）A．240°B．360°C．540°D．720°试题分析：根据四边形的内角和及三角形的外角定理即可求解．答案详解：解：如图，AC、DF与BE分别相交于点M、N，在四边形NMCD中，∠MND+∠CMN+∠C+∠D＝360°，∵∠CMN＝∠A+∠E，∠MND＝∠B+∠F，∴∠A+∠B+∠C+∠D+∠E+∠F＝360°，所以选：B．10．一个多边形的内角和等于1260°，从它的一个顶点出发，可以作对角线的条数是（）A．4B．6C．7D．9试题分析：设这个多边形的边数为n，根据多边形的内角和定理得到（n﹣2）×180°＝1260°，然后解方程即可．答案详解：解：设这个多边形的边数为n，∴（n﹣2）×180°＝1260°，解得n＝9，∴这个多边形为九边形；从这个多边形的一个顶点出发共有：9﹣3＝6（条）．所以选：B．五．三角形的内角和11．如图，在△ABC中，D是AC上一点，E是AB上一点，BD，CE相交于点F，∠A＝60°，∠ABD＝20°，∠ACE＝35°，则∠EFD的度数是（）A．115°B．120°C．135°D．105°试题分析：由△ABD的内角和为180°，可以求∠ADB，由△AEC内角和为180°，可以求∠AEC，再根据四边形AEFD内角和为360°，可求∠EFD．答案详解：解：在△AEC中，∠A+∠ACE+∠AEC＝180°，∴∠AEC＝180°﹣∠A﹣∠ACE＝180°﹣60°﹣35°＝85°，在△ABD中，∠A+∠ABD+∠ADB＝180°，∴∠ADB＝180°﹣∠A﹣∠ABD＝180°﹣60°﹣20°＝100°，在四边形AEFD中，∠A+∠AEC+∠ADB+2∠EFD＝360°，∴∠EFD＝360°﹣∠A﹣∠AEC﹣∠ADB＝360°﹣60°﹣85°﹣100°＝115°，所以选：A．12．如图，△ABC中，∠BAC＞∠B，∠C＝70°，将△ABC折叠，使得点B与点A重合，折痕PD 分别交AB、BC于点D、P，当△APC中有两个角相等时，∠B的度数为（）A．35°或20°B．20°或27.5°C．35°或25°或32.5°D．35°或20°或27.5°试题分析：分三种情况，利用三角形的内角和定理、等腰三角形的性质先求出∠APC的度数，再利用折叠的性质和三角形的内角和定理求出∠B．答案详解：解：由折叠的性质知：∠BPD＝∠APD=12∠BPA，∠BDP＝∠ADP＝90°．当AP＝AC时，∠APC＝∠C＝70°，∵∠BPD=12（180°﹣∠APC）＝55°，∴∠B＝90°﹣55°＝35°；当AP＝PC时，∠PAC＝∠C＝70°，则∠APC＝40°．∵∠BPD=12（180°﹣∠APC）＝70°，∴∠B＝90°﹣70°＝20°；当PC＝AC时，∠APC＝∠PAC，则∠APC＝55°．∵∠BPD=12（180°﹣∠APC）＝62.5°，∴∠B＝90°﹣62.5°＝27.5°．所以选：D．13．如图，∠ABD，∠ACD的角平分线交于点P，若∠A＝48°，∠D＝10°，则∠P的度数为（）A．19°B．20°C．22°D．25°试题分析：延长PC交BD于E，根据角平分线的定义可得∠1＝∠2，∠3＝∠4，再根据三角形的内角和定理可得∠A+∠1＝∠P+∠3，然后根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠5，整理可得∠P=12（∠A﹣∠D），然后代入数据计算即可得解．答案详解：解：如图，延长PC交BD于E，∵∠ABD，∠ACD的角平分线交于点P，∴∠1＝∠2，∠3＝∠4，由三角形的内角和定理得，∠A+∠1＝∠P+∠3①，在△PBE中，∠5＝∠2+∠P，在△DCE中，∠5＝∠4﹣∠D，∴∠2+∠P＝∠4﹣∠D②，①﹣②得，∠A﹣∠P＝∠P+∠D，∴∠P=12（∠A﹣∠D），∵∠A＝48°，∠D＝10°，∴∠P=12（48°﹣10°）＝19°．所以选：A．14．如图，在△ABC中，∠B＝28°，将△ABC沿直线m翻折，点B落在点D的位置，则∠1﹣∠2的度数是（）A．42°B．46°C．52°D．56°试题分析：根据折叠得出∠D＝∠B＝28°，根据三角形的外角性质得出∠1＝∠B+∠BEF，∠BEF ＝∠2+∠D，求出∠1＝∠B+∠2+∠D即可．答案详解：解：∵∠B＝28°，将△ABC沿直线m翻折，点B落在点D的位置，∴∠D＝∠B＝28°，∵∠1＝∠B+∠BEF，∠BEF＝∠2+∠D，∴∠1＝∠B+∠2+∠D，∴∠1﹣∠2＝∠B+∠D＝28°+28°＝56°，所以选：D．15．如图，将△ABC沿DE、HG、EF翻折，三个顶点均落在点O处，若∠1＝131°，则∠2的度数为（）A．49°B．50°C．51°D．52°试题分析：先根据折叠性质得：∠HOG＝∠B，∠DOE＝∠A，∠EOF＝∠C，根据三角形内角和为180°和周角360°求出结论．答案详解：解：由折叠得：∠HOG＝∠B，∠DOE＝∠A，∠EOF＝∠C，∵∠A+∠B+∠C＝180°，∴∠HOG+∠DOE+∠EOF＝180°，∵∠1+∠2+∠HOG+∠DOE+∠EOF＝360°，∴∠1+∠2＝180°，∵∠1＝131°，∴∠2＝180°﹣131°＝49°，所以选：A．16．如图，在△ABC中，∠1＝100°，∠C＝80°，∠2=12∠3，BE平分∠ABC交AD于E，求∠4的度数．试题分析：首先根据三角形的外角的性质求得∠3，再根据已知条件求得∠2，进而根据三角形的内角和定理求得∠ABD，再根据角平分线的定义求得∠ABE，最后根据三角形的外角的性质求得∠4．答案详解：解：∵∠1＝∠3+∠C，∠1＝100°，∠C＝80°，∴∠3＝20°，∵∠2=12∠3，∴∠2＝10°，∴∠ABC＝180°﹣100°﹣10°＝70°，∵BE平分∠ABC，∴∠ABE＝35°，∵∠4＝∠2+∠ABE，∴∠4＝45°．17．如果在直角三角形中，一个锐角是另一个锐角的3倍，那么这个三角形中最小的一个角等于　22.5　度．试题分析：在直角三角形中，设最小的锐角的度数为x，则另一个锐角的度数则为3x．由“直角三角形的两个锐角互余”的性质知，x+3x＝90°．通过解方程即可求得x的值．答案详解：解：在直角三角形中，设最小的锐角的度数为x，则另一个锐角的度数则为3x．则x+3x＝90°，即4x＝90°，解得，x＝22.5°，即这个直角三角形中最小的一个角等于22.5°．所以答案是：22.5．六．新定义类18．新定义：在△ABC中，若存在最大内角是最小内角度数的n倍（n为大于1的正整数），则称△ABC为“n倍角三角形”．例如，在△ABC中，若∠A＝90°，∠B＝60°，则∠C＝30°，因为∠A最大，∠C最小，且∠A＝3∠C，所以△ABC为“3倍角三角形”．（1）在△DEF中，若∠E＝40°，∠F＝60°，则△DEF为“　2　倍角三角形”．（2）如图，在△ABC中，∠C＝36°，∠BAC、∠ABC的角平分线相交于点D，若△ABD为“6倍角三角形”，请求出∠ABD的度数．试题分析：（1）根据三角形内角和定理求出∠D，根据n倍角三角形的定义判断；（2）根据角平分线的定义、三角形内角和定理求出∠ADB，n倍角三角形的定义分情况讨论计算，得到答案．答案详解：解：（1）在△DEF中，∠E＝40°，∠F＝60°，则∠D＝180°﹣∠E﹣∠F＝80°，∴∠D＝2∠E，∴△DEF为“2倍角三角形”，所以答案是：2；（2）∵∠C＝36°，∴∠BAC+∠ABC＝180°﹣36°＝144°，∵∠BAC、∠ABC的角平分线相交于点D，∴∠DAB=12∠BAC，∠DBA=12∠ABC，∴∠DAB+∠DBA=12×144°＝72°，∴∠ADB＝180°﹣72°＝108°，∵△ABD为“6倍角三角形”，∴∠ADB＝6∠ABD或∠ADB＝6∠BAD，当∠ADB＝6∠ABD时，∠ABD＝18°，当∠ADB＝6∠BAD时，∠BAD＝18°，则∠ABD＝180°﹣108°﹣18°＝54°，综上所述，∠ABD的度数为18°或54°．19．在△ABC中，若存在一个内角角度是另外一个内角角度的n倍（n为大于1的正整数），则称△ABC为n倍角三角形．例如，在△ABC中，∠A＝80°，∠B＝75°，∠C＝25°，可知∠B＝3∠C，所以△ABC为3倍角三角形．（1）在△ABC中，∠A＝80°，∠B＝60°，则△ABC为　2　倍角三角形；（2）若锐角三角形MNP是3倍角三角形，且最小内角为α，请直接写出α的取值范围为　22.5°＜α＜30°　．（3）如图，直线MN与直线PQ垂直相交于点O，点A在射线OP上运动（点A不与点O重合），点B在射线OM上运动（点B不与点O重合）．延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F，若△AEF为4倍角三角形，求∠ABO 的度数．试题分析：（1）由∠A＝80°，∠B＝60°，可求∠C的度数，发现内角之间的倍数关系，得出答案，（2）△DEF是3倍角三角形，必定有一个内角是另一个内角的3倍，然后根据这两个角之间的关系，分情况进行解答，（3）首先证明∠EAF＝90°，分两种情形分别求出即可．答案详解：解：（1）∵∠A＝80°，∠B＝60°，∴∠C＝180°﹣∠A﹣∠B＝40°，∴∠A＝2∠C，∴△ABC为2倍角三角形，所以答案是：2；（2）∵最小内角为α，∴3倍角为3α，由题意可得：3α＜90°，且180°﹣4α＜90°，∴最小内角的取值范围是22.5°＜α＜30°．所以答案是22.5°＜α＜30°．（3）∵AE平分∠BAO，AF平分∠AOG，∴∠EAB＝∠EAO，∠OAF＝∠FAG，∴∠EAF＝∠EAO+∠OAF=12（∠BAO+∠OAG）＝90°，∵△EAF是4倍角三角形，∠F显然大于∠E,∴∠E=14×90°或15×90°，∵AE平分∠BAO，OE平分∠BOQ，∴∠E=12∠ABO，∴∠ABO＝2∠E，∴∠ABO＝45°或36°．20．在△ABC中，若存在一个内角角度，是另外一个内角角度的n倍（n为大于1的正整数），则称△ABC为n倍角三角形．例如，在△ABC中，∠A＝80°，∠B＝75°，∠C＝25°，可知∠B＝3∠C，所以△ABC为3倍角三角形．（1）在△ABC中，∠A＝55°，∠B＝25°，则△ABC为　4　倍角三角形；（2）若△DEF是3倍角三角形，且其中一个内角的度数是另外一个内角的余角的度数的13，求△DEF的最小内角；（3）若△MNP是2倍角三角形，且∠M＜∠N＜∠P＜90°，请直接写出△MNP的最小内角的取值范围．试题分析：（1）由∠A＝55°，∠B＝25°，可求∠C的度数，发现内角之间的倍数关系，得出答案，（2）△DEF是3倍角三角形，必定有一个内角是另一个内角的3倍，然后根据这两个角之间的关系，分情况进行解答，（3）可设未知数表示2倍角三角形的各个内角，然后列不等式组确定最小内角的取值范围．答案详解：解：（1）∵∠A＝55°，∠B＝25°，∴∠C＝180°﹣∠A﹣∠B＝100°，∴∠C＝4∠B，所以答案是：4（2）设最小的内角为x°，则3倍角为3x°①当最小的内角的度数是3倍内角的余角的度数的13时，即：x=13（90°﹣3x），解得：x＝15°②3倍内角的度数是最小内角的余角的度数的13时，即：3x=13（90°﹣x），解得：x＝9°，因此，△DEF的最小内角是9°或15°．（3）设∠M的度数为x，则其它的两个角分别为2x，（180°﹣3x），由∠M＜∠N＜∠P＜90°可得：2x＜90°且180°﹣3x＜90°且2x≠180°﹣3x∴30°＜x＜45°且x≠36°．答：△MNP的最小内角的取值范围是30°＜x＜45°且x≠36°．21．若△ABC中刚好有∠B＝2∠C，则称此三角形为“可爱三角形”，并且∠A称作“可爱角”．现有一个“可爱且等腰的三角形”，那么聪明的同学们知道这个三角形的“可爱角”应该是（）A．45°或36°B．72°或36°C．45°或72°D．45°或36°或72°试题分析：分设三角形底角为α，顶角为2α或设三角形的底角为2α，顶角为α，根据三角形的内角和为180°，得出答案．答案详解：解：①设三角形底角为α，顶角为2α，则α+α+2α＝180°，解得：α＝45°，②设三角形的底角为2α，顶角为α，则2α+2α+α＝180°，解得：α＝36°，∴2α＝72°，∴三角形的“可爱角”应该是45°或72°，所以选：C．22．若三角形满足一个角α是另一个角β的3倍，则称这个三角形为“智慧三角形”，其中α称为“智慧角”．在有一个角为60°的“智慧三角形”中，“智慧角”是　60或90　度．试题分析：根据“智慧三角形”及“智慧角”的意义，列方程求解即可．答案详解：解：在有一个角为60°的三角形中，①当另两个角分别是100°、20°时，“智慧角”是60°；②α+β＝120°且α＝3β，∴α＝90°．，即“智慧角”是90°．所以答案是：60或90．。

初二数学上册月考难点知识全汇总，月考必备！

初二数学上册月考难点知识全汇总，月考必备！一转眼初二的同学已经学习一个月了，今天，老师整理了初二数学的重难点，希望在月考前可以帮助到大家！八年级数学上册重要知识点第一章勾股定理1、勾股定理直角三角形两直角边a，b的平方和等于斜边c的平方，即a2+b2=c2。

2、勾股定理的逆定理如果三角形的三边长a，b，c有这种关系，那么这个三角形是直角三角形。

3、勾股数满足的三个正整数，称为勾股数。

常见的勾股数组有：（3，4，5）；（5，12，13）；（8，15，17）；（7，24，25）；（20，21，29）；（9，40，41）；……（这些勾股数组的倍数仍是勾股数）第二章实数 1、实数的概念及分类①实数的分类②无理数无限不循环小数叫做无理数。

在理解无理数时，要抓住“无限不循环”这一时之，归纳起来有四类：•开方开不尽的数，如√7 ,3√2等；•有特定意义的数，如圆周率π，或化简后含有π的数，如π /₃+8等；•有特定结构的数，如0.1010010001…等;•某些三角函数值，如sin60°等•2、实数的倒数、相反数和绝对值①相反数实数与它的相反数是一对数（只有符号不同的两个数叫做互为相反数，零的相反数是零），从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果a与b互为相反数，则有a+b=0，a=-b，反之亦成立。

②绝对值在数轴上，一个数所对应的点与原点的距离，叫做该数的绝对值。

|a|≥0。

0的绝对值是它本身，也可看成它的相反数，若|a|=a，则a≥0；若|a|=-a，则a≤0。

③倒数如果a与b互为倒数，则有ab=1，反之亦成立。

倒数等于本身的数是1和-1。

0没有倒数。

④数轴规定了原点、正方向和单位长度的直线叫做数轴（画数轴时，要注意上述规定的三要素缺一不可）。

解题时要真正掌握数形结合的思想，理解实数与数轴的点是一一对应的，并能灵活运用。

⑤估算3、平方根、算数平方根和立方根①算术平方根一般地，如果一个正数x的平方等于a，即x2=a，那么这个正数x就叫做a的算术平方根。

八年级上册数学考试重点难题集

1，某大型超市从生产基地购进一批水果,运输过程中质量损失5%，假设不计超市其他费用。

(1）如果超市在进价的基础上提高5%作为售价，那么请你通过计算说明超市是否亏本；(2)如果超市至少要获得20%的利润，那么这种水果的售价最低应提高百分之几?（结果精确到0。

1％）解：假设水果总质量m,进价为p,那么运输后出去质量损失水果质量为(1—5%）m = 0.95m （1) 成本为 mp ，销售额 0。

95m ＊(1+5%）p = 0.95＊1.05mp = 0.9975mp < mp 所以赔本（2）假设售价提高x%，因为要获得20%的利润,所以销售额为（1+20％）mp = 1。

2mp 实际销售额 0.95m ＊(1+x%）p = 1.2mp 0.95 ＊（1+x ％) = 1.2x% = 1。

2/0。

95 - 1 = （1.2 — 0.95) / 0.95 =0。

25/0.95 = 25/95 = 5/19 = 0.263 = 26.3％,2. 如右图，一只蚂蚁从点O 出发，在扇形OAB 的边缘沿着O B A O ---的路线匀速爬行一周，设蚂蚁的爬行时间为t ，蚂蚁与O 点的距离为s ，则s 关于t 的函数图象大致是（ ▲ C ）A. B. C 。

D 。

3。

如图，等边ABC ∆中，点D 、E 分别在边AB ，BC 上,把BDE ∆沿直线DE 翻折，使点B 落在'B处，'DB 、'EB 分别与边AC 交于点F 、G 。

若oADF 80=∠，则=∠EGC ▲80° o4．将直线42+-=x y 向上平移2个单位，所得直线解析式是 y=—2x+6 ，将直线OABO t s O t s O t s O tsA DBCE'B FG42+-=x y 向右平移2个单位，所得直线的解析式是y=-2x+8。

5。

一次函数6+=kx y 的图象经过第三象限,且它与两条坐标轴构成的直角三角形面积等于9，则=k 2 ▲ .解：一次函数y=kx+6的图象经过第三象限，则k ＞0，令y=0，得x=-6\k ，则一次函数的图象与x 轴交点坐标为（-6\k ，0）， ∴面积=|—6\k|＊6\2=9 解得：k=2． 6．如图，直线5+-=x y 与坐标轴交于点A 、B , 在线段AB 上(不包括端点)任取一点P ，过点P 分别作x PM ⊥轴，y PN ⊥轴，则长方形PMON 的周长为 50 ▲ 。

八年级上册数学期末考试难题精选

向容器中注满水的全过程共用时间分。

求两根水管各自注水的速度。

解：设小水管进水速度为，则大水管进水速度为。

由题意得：t xvx v =+82解之得：t v x 85= 经检验得：tvx 85=是原方程解。

∴小口径水管速度为t v 85，大口径水管速度为tv25。

四：联系实际编拟一道关于分式方程2288+=xx 的应用题。

要求表述完整，条件充分并写出解答过程。

解略五：已知＝222y x xy -、＝2222y x y x -+，用“”或“－”连结、,有三种不同的形式，、、，请你任取其中一种进行计算，并简求值，其中：：。

解：选择一：22222222()()()xy x y x y x yM N x y x y x y x y x y++++=+==--+--，当x ∶y ∶时，52x y =，原式572532y yy y +=-．选择二：22222222()()()xy x y x y y xM N x y x y x y x y x y+----=-==--+-+，当x ∶y ∶时，52x y =，原式532572y yy y -=-+．选择三：22222222()()()x y xy x y x yN M x y x y x y x y x y+---=-==--+-+，当x ∶y ∶时，52x y =，原式532572y yy y -=+．反比例函数：一：一张边长为正方形的纸片，剪去两个面积一定且一样的小矩形得到一个“”图案如图所示．小矩形的长（）与宽（）之间的函数关系如图所示：（）求与之间的函数关系式；（）“”图案的面积是多少？（）如果小矩形的长是≤≤，求小矩形宽的范围.解：（）设函数关系式为xk y =∵函数图象经过（，） ∴102k=∴， ∴xy 20=（）∵xy 20=∴， ∴2162022162=⨯-=-=xy S S E 正（）当时，310620==y 当时，351220==y∴小矩形的长是≤≤，小矩形宽的范围为cm y 31035≤≤ 二：是一个反比例函数图象的一部分，点(110)A ，，(101)B ，是它的两个端点．（）求此函数的解析式，并写出自变量x 的取值范围；（）请你举出一个能用本题的函数关系描述的生活实例．解：（）设k y x =，(110)A ，在图象上，101k∴=，即11010k =⨯=， 10y x∴=，其中110x ≤≤；（）答案不唯一．例如：小明家离学校10km ，每天以km/h v 的速度去上学，那么小明从家去学校所需的时间10t v=．三：如图，⊙和⊙都与轴和轴相切，圆心和圆心都在反比例函数1y x=的图象上，则图中阴影部分的面积等于 .答案：π²π四：如图，已知正比例函数和反比例函数的图像都经过点（－，1-），且（1-，－）为双曲线上的一点，为坐标平面上一动点，垂直于轴，垂直于轴，垂足分别是、．（）写出正比例函数和反比例函数的关系式；（）当点在直线上运动时，直线上是否存在这样的点，使得△与△面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（）如图，当点在第一象限中的双曲线上运动时，作以、为邻边的平行四边形，求平行四边形周长的最小值．解：（）设正比例函数解析式为y kx =，将点（2-，1-）坐标代入得12k =，所以正比例函数解析式为12y x = 同样可得，反比例函数解析式为2y x = （）当点在直线上运动时，设点的坐标为1()2Q m m ，，于是211112224OBQ S OB BQm m m △=?创=，而1(1)(2)12OAP S △=-?=，A BO xy图xyBA OMQP图xyBCAOMPQ所以有，2114m =，解得2m =±所以点的坐标为1(21)Q ，和2(21)Q ，-- （）因为四边形是平行四边形，所以＝，＝，而点（1-，2-）是定点，所以的长也是定长，所以要求平行四边形周长的最小值就只需求的最小值．因为点在第一象限中双曲线上，所以可设点的坐标为2()Q n n，，由勾股定理可得222242()4OQ n n n n=+=-+，所以当22()0n n -=即20n n -=时，2OQ 有最小值，又因为为正值，所以与2OQ 同时取得最小值，所以有最小值．由勾股定理得＝5，所以平行四边形周长的最小值是2()2(52)254OP OQ +=+=+．五：如图，在平面直角坐标系中，直线与轴和轴分别交于点、点，与反比例函数一罟在第一象限的图象交于点(，)、点(，)．过点作上轴于，过点作上轴于．()求，的值；()求直线的函数解析式；勾股定理：一：清朝康熙皇帝是我国历史上对数学很有兴趣的帝王．近日，•西安发现了他的数学专著，其中有一文《积求勾股法》，它对“三边长为、、的整数倍的直角三角形，已知面积求边长”这一问题提出了解法：“若所设者为积数（面积），以积率六除之，平方开之得数，再以勾股弦各率乘之，即得勾股弦之数”．用现在的数学语言表述是：“若直角三角形的三边长分别为、、的整数倍，•设其面积为，则第一步：6S＝；第二步：m ；第三步：分别用、、乘以，得三边长”．（）当面积等于时，请用康熙的“积求勾股法”求出这个直角三角形的三边长；（）你能证明“积求勾股法”的正确性吗？请写出证明过程．解：（）当时，m1502566S ==，所以三边长分别为：×，×，×；（）证明：三边为、、的整数倍，设为倍，则三边为，，，•而三角形为直角三角形且、为直角边．其面积12（）·（），所以6S ，6S （取正值），即将面积除以，然后开方，即可得到倍数．二：一张等腰三角形纸片，底边长，底边上的高长．．现沿底边依次从下往上裁剪宽度均为的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是( )．第张．第张．第张．第张答案：三：如图，甲、乙两楼相距米，甲楼高米，小明站在距甲楼米的A 处目测得点A 与甲、乙楼顶B C 、刚好在同一直线上，且与相距350米，若小明的身高忽略不计，则乙楼的高度是米．答案：米四：恩施州自然风光无限，特别是以“雄、奇、秀、幽、险”著称于世．著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧，50km AB A =，、B 到直线X 的距离分别为10km 和40km ，要在沪渝高速公路旁修建一服务区P ，向A 、B 两景区运送游客．小民设计了两种方案，图（）是方案一的示意图（AP 与直线X 垂直，垂足为P ），P 到A 、B 的距离之和1S PA PB =+，图（）是方案二的示意图（点A 关于直线X 的对称点是A '，连接BA '交直线X 于点P ），P 到A 、B 的距离之和2S PA PB =+．（）求1S 、2S ，并比较它们的大小；（）请你说明2S PA PB =+的值为最小；（）拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直，建立如图（）所示的直角坐标系，B 到直线Y 的距离为30km ，请你在X 旁和Y 旁各修建一服务区P 、Q ，使P 、A 、B 、Q 组成的四边形的周长最小．并求出这个最小值．图（）图（）A '图（）米乙甲米？米解:⑴图（）中过作⊥,垂足为,则＝,又＝,∴＝在△ 中，＝＝ ∴＝ ∴ ＝24022=+BC CP ＝10240+⑵图（）中，过作⊥′垂足为，则′＝，又＝∴'＝4110504022=+ 由轴对称知：＝' ∴＝'＝4110 ∴1S ﹥2S()如图（），在公路上任找一点,连接'，由轴对称知＝' ∴＝'﹥' ∴＝'为最小（）过作关于轴的对称点', 过作关于轴的对称点'，连接'',交轴于点, 交轴于点,则即为所求过'、 '分别作轴、轴的平行线交于点, ''＝5505010022=+∴所求四边形的周长为55050+五：已知：如图，在直角梯形中，∥，∠＝°，⊥于点，交于点，交的延长线于点，且AE AC =．（）求证：BG FG =；PBAQYB'A'（）若2AD DC ==，求的长．解：（）证明：90ABC DE AC ∠=°，⊥于点F ，ABC AFE ∴∠=∠．AC AE EAF CAB =∠=∠，， ABC AFE ∴△≌△AB AF ∴=．连接AG ，＝＝，Rt Rt ABG AFG ∴△≌△． BG FG ∴=．（）解：∵＝⊥，1122AF AC AE ∴==． 30E ∴∠=°． 30FAD E ∴∠=∠=°，3AF ∴=． 3AB AF ∴==．四边形：一：如图，△、△、△均为直线同侧的等边三角形. () 当≠时，证明四边形为平行四边形；() 当时，顺次连结、、、四点所构成的图形有哪几类？直接写出构成图形的类型和相应的条件.解：() ∵△、△为等边三角形，∴ ，，∠ ∠ °.∴∠ ∠. ∴△ ≌△. ∴ .又∵△为等边三角形， ∴ . ∴ . 同理可得 . ∴四边形是平行四边形.() 构成的图形有两类，一类是菱形，一类是线段. 当图形为菱形时，∠ ≠°（或与不重合、△不为正三角形）当图形为线段时，∠ °（或与重合、△为正三角形）.二：如图，已知△是等边三角形，、分别在边、上，且，连结并延长至点，使，连结、和。

八年级上册数学考试重点难题集

八年级上册数学考试重点难题集

八年级上册数学重难点总结

八年级上册数学考试重点难题集

八年级上册数学期中考试难题集

初二数学难题30道

初二数学上册试卷难题

八上数学 全册重难点题型 85个必考考点

八年级上数学试卷难度较高

(完整)八年级上册数学期末考试难题精选

八年级上册重点难点试题

初二数学难题带答案上学期

八年级上学期数学重难点突破汇总V0.2

八年级上册数学重点难点

初二数学上册重难点 考点

八年级上册数学《全等三角形难题集》

部编数学八年级上册专题01三角形六大重难题型(期末真题精选)(解析版)含答案

初二数学上册月考难点知识全汇总，月考必备！

八年级上册数学考试重点难题集

八年级上册数学期末考试难题精选

八上数学全册重难点题型 85个必考考点

初二数学上册重难点考点