14-反弯点法、D值法、侧移例题
合集下载
zA框架结构在水平荷载下的计算(反弯点法和D值法)
的方便，假定同层各节点转角相同。 ②假定同层各节点的侧移相同。 这一假定，实际上是忽略了框架梁的
轴向变形。这与实际结构差别不大。
33
（二）柱的抗侧刚度D值
柱 D 值计算
D V
计算假定 例 ：柱 AB 的 D 值计算
层间侧移△相等 ，
剪切角为 u j
hj
梁、柱结点转角相等，设为
计算柱与相邻柱线刚度相同 ic 与柱B端相交的梁的线刚度为
y 0 —标准反弯点高度比，由附表2.1-2.2查取； y1 —上、下层梁刚度不等时的修正值，由附表2.3查取； y 2 y 3 —上、下层层高不等时的修正值，由附表2.4查取。
48
（三）确定柱反弯点高度比y
１.标准反弯高度比y０ 标准反弯点高度比是在各层等高、各跨相等、 各层梁和柱线刚度都不改变时框架在水平荷载作 用下的反弯点高度比。 按该框架总层数n，所在楼层数j以及梁柱线 刚度比K查附表2.1、附表2.2。 在查取y0时，风荷载（均布水平荷载）作用下 和水平地震作用（三角形荷载）下应采用相应的 表格。
h上、h下——上层、下层层高
51
（三）确定柱反弯点高度系数y
4.反弯点高度
Y yh
当 反 弯 点 高 度 为 0≤ Ｙ ≤ ｈ 时 ， 反 弯点在本层；当Ｙ>ｈ时，本层无反点， 反弯点在上层；当Ｙ<0时，反弯点在下 层。
52
（四）确定柱端弯矩
上端弯矩
M
t ij
Vij
h1 y
下端弯矩
M
b ij
由此也可以看出，反弯点法是有一定的适用范 围的，即框架梁、柱的线刚度之比应不小于3。
5
水平荷载作用下框 架的变形情况：
当梁刚度无限 大时，水平荷载作 用下框架的变形情 况：节点转角为0， 各节点水平位移相 同。
轴向变形。这与实际结构差别不大。
33
（二）柱的抗侧刚度D值
柱 D 值计算
D V
计算假定 例 ：柱 AB 的 D 值计算
层间侧移△相等 ，
剪切角为 u j
hj
梁、柱结点转角相等，设为
计算柱与相邻柱线刚度相同 ic 与柱B端相交的梁的线刚度为
y 0 —标准反弯点高度比，由附表2.1-2.2查取； y1 —上、下层梁刚度不等时的修正值，由附表2.3查取； y 2 y 3 —上、下层层高不等时的修正值，由附表2.4查取。
48
（三）确定柱反弯点高度比y
１.标准反弯高度比y０ 标准反弯点高度比是在各层等高、各跨相等、 各层梁和柱线刚度都不改变时框架在水平荷载作 用下的反弯点高度比。 按该框架总层数n，所在楼层数j以及梁柱线 刚度比K查附表2.1、附表2.2。 在查取y0时，风荷载（均布水平荷载）作用下 和水平地震作用（三角形荷载）下应采用相应的 表格。
h上、h下——上层、下层层高
51
（三）确定柱反弯点高度系数y
4.反弯点高度
Y yh
当 反 弯 点 高 度 为 0≤ Ｙ ≤ ｈ 时 ， 反 弯点在本层；当Ｙ>ｈ时，本层无反点， 反弯点在上层；当Ｙ<0时，反弯点在下 层。
52
（四）确定柱端弯矩
上端弯矩
M
t ij
Vij
h1 y
下端弯矩
M
b ij
由此也可以看出，反弯点法是有一定的适用范 围的，即框架梁、柱的线刚度之比应不小于3。
5
水平荷载作用下框 架的变形情况：
当梁刚度无限 大时，水平荷载作 用下框架的变形情 况：节点转角为0， 各节点水平位移相 同。
剪力法反弯法D值法
y y0 y1 y2 y3 h
h 2 y 或 h 2 3
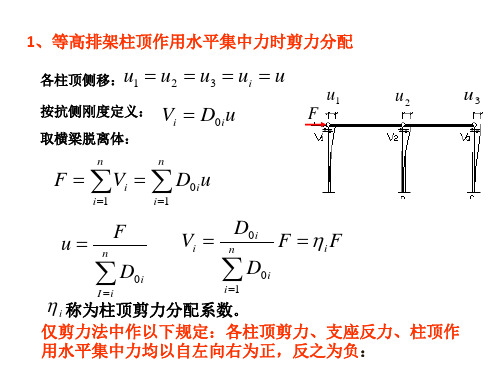
1、等高排架柱顶作用水平集中力时剪力分配
各柱顶侧移：u1
u2 u3 ui u
按抗侧刚度定义： 取横梁脱离体：
Vi D0i u
n
F
u1
u2
u3
F Vi D0i u
i 1 i 1
n
u
F
D
I i
n
Vi
D0i
F
0i
D
i 1
n
F i F
0i
i 称为柱顶剪力分配系数。
j1 j 2 jm j
Vjk ijk hj
V j Fi
i j
n
j
Vj
k
1
m
12ijk
Vjk
ijk ijk k
1
m
Vj
k 1, 2, ,m
hj
2
各柱剪力分配：
j
3、—改进反弯点法（D值法）
柱的抗侧刚度
D
MBA F
12ic D jk 2 hj
E
H hj
B
MAB
A
G
V jk
D jk
D
k 1
m
Vj
jk
各柱剪力分配：
C
式计算。 柱侧向刚度修正系数 c
位 置 边 简 图 柱 中 柱
K
K i2 i4 2ic i2 ic
i2 ic
简 图
K
K i1 i2 i3 i4 2ic i1 i2 ic
d值法,反弯点法-文档资料
D0 12 ic h2
同样，因柱的上、下端都不转动，故除底层柱外，其他各层柱的反 弯点均在柱中点（h/2）；底层柱由于实际是下端固定，柱上端的约束刚 度相对较小，因此反弯点向上移动，一般取离柱下端2/3柱高处为反弯点 位置，即取yh= 2 h 3 用反弯点法计算框架结构内力的要点与D值法相同。
现讨论底层柱的D值。
c
0 .5 K 2K
同理，当底层柱的下端为铰接时，可得
0.5K 1 2K
c
底层柱D值计算图式
综上所述，各种情况下柱的侧向刚度 D 值中系数 c 及梁柱线刚度比 K 按下表所列公 式计算。 柱侧向刚度修正系数 c
位 置 边 简 图 柱 中 柱
K
K i2 i4 2ic
c
3
反弯点法
由上述分析可见，D值法考虑了柱两端节点转动对其侧向刚度和反弯 点位置的影响，因此，此法是一种合理且计算精度较高的近似计算方法， 适用于一般多、高层框架结构在水平荷载作用下的内力和侧移计算。
当梁的线刚度比柱的线刚度大很多时（例如ib/ic>3），梁柱节点的 转角很小。如果忽略此转角的影响，则水平荷载作用下框架结构内力的 计算方法，尚可进一步简化，这种忽略梁柱节点转角影响的计算方法称 为反弯点法。 在确定柱的侧向刚度时，反弯点法假定各柱上、下端都不产生转动， c 即认为梁柱线刚度比为无限大。将趋近于无限大代入D值法 的公式， c 可得 =1。因此，由式可得反弯点法的柱侧向刚度，并用D0表示为：
标准反弯点位置简化求解
（2）上、下横梁线刚度变化时反弯点高度比的修正值 y1 若与某层柱相连的上、下横梁线刚度不同，则其反弯点位置 不同于标准反弯点位置 ynh，其修正值为 y1h，如图所示。y1 的分析 方法与 yn 相仿，计算时可由附表 7.4 查取。 由附表 7.4 查 y1 时，梁柱线刚度比 K 仍按表 4.4.1 所列公式确定。 当 i1 i2 i3 i4 时，取 1 (i1 i2 ) /(i3 i4 ) ，则由 1 和 K 从附表 7.4 查出 y1，这时反弯点应向上移动，y1 取正值；当 i3 i4 i1 i2 时， 取 1 (i3 i4 ) /(i1 i2 ) ， 由 1 和 K 从附表 7.4 查出 y1， 这时反弯点应 向下移动，故 y1 取负值。 对底层框架柱，不考虑修正值 y1。
同样，因柱的上、下端都不转动，故除底层柱外，其他各层柱的反 弯点均在柱中点（h/2）；底层柱由于实际是下端固定，柱上端的约束刚 度相对较小，因此反弯点向上移动，一般取离柱下端2/3柱高处为反弯点 位置，即取yh= 2 h 3 用反弯点法计算框架结构内力的要点与D值法相同。
现讨论底层柱的D值。
c
0 .5 K 2K
同理，当底层柱的下端为铰接时，可得
0.5K 1 2K
c
底层柱D值计算图式
综上所述，各种情况下柱的侧向刚度 D 值中系数 c 及梁柱线刚度比 K 按下表所列公 式计算。 柱侧向刚度修正系数 c
位 置 边 简 图 柱 中 柱
K
K i2 i4 2ic
c
3
反弯点法
由上述分析可见，D值法考虑了柱两端节点转动对其侧向刚度和反弯 点位置的影响，因此，此法是一种合理且计算精度较高的近似计算方法， 适用于一般多、高层框架结构在水平荷载作用下的内力和侧移计算。
当梁的线刚度比柱的线刚度大很多时（例如ib/ic>3），梁柱节点的 转角很小。如果忽略此转角的影响，则水平荷载作用下框架结构内力的 计算方法，尚可进一步简化，这种忽略梁柱节点转角影响的计算方法称 为反弯点法。 在确定柱的侧向刚度时，反弯点法假定各柱上、下端都不产生转动， c 即认为梁柱线刚度比为无限大。将趋近于无限大代入D值法 的公式， c 可得 =1。因此，由式可得反弯点法的柱侧向刚度，并用D0表示为：
标准反弯点位置简化求解
（2）上、下横梁线刚度变化时反弯点高度比的修正值 y1 若与某层柱相连的上、下横梁线刚度不同，则其反弯点位置 不同于标准反弯点位置 ynh，其修正值为 y1h，如图所示。y1 的分析 方法与 yn 相仿，计算时可由附表 7.4 查取。 由附表 7.4 查 y1 时，梁柱线刚度比 K 仍按表 4.4.1 所列公式确定。 当 i1 i2 i3 i4 时，取 1 (i1 i2 ) /(i3 i4 ) ，则由 1 和 K 从附表 7.4 查出 y1，这时反弯点应向上移动，y1 取正值；当 i3 i4 i1 i2 时， 取 1 (i3 i4 ) /(i1 i2 ) ， 由 1 和 K 从附表 7.4 查出 y1， 这时反弯点应 向下移动，故 y1 取负值。 对底层框架柱，不考虑修正值 y1。
反弯点法和D值法的应用
风或地震对框架结构的水平作用，一般可简化为作用于框架节点上的水平力。
其定性的弯矩图如图a所示：各杆的弯矩图是直线形，且一般都有一个反弯点。
若能求出各柱反弯点位置及各柱分配到的层间剪力，则各梁、柱的内力很容易计算。
框架变形图如图b所示：（1）若忽略构件的轴向变形，则同一层内各节点具有相同的侧向位移和层间位移；（2）框架上部各节点均有转角；（3）各节点的层间位移和转角越靠下层越大。
一、反弯点法反弯点法的关键，一是确定反弯点的位置；二是确定每层各柱的剪力。
为简化计算，进行如下假定：◆在确定反弯点位置时，假定柱上端与下端的转角相等（底层柱除外，其下端为0）；◆在确定同层各柱剪力分配时，假定节点转角为零，即认为梁的线刚度为无穷大。
◆梁端弯矩可由节点平衡条件求出，并按节点左右梁的线刚度进行分配。
根据以上假定有：（一）反弯点位置由假定（1）有：底层柱反弯点近似为距柱下端2/3底层层高处，其余层柱反弯点位于层高的中点；（二）柱的侧移刚度D。
侧移刚度D。
是表示柱上下端产生单位相对水平位移时，在柱顶所需施加的水平剪力。
根据假定（2）各柱无转角，只有层间位移，则如图所示，柱顶剪力，则柱的侧移刚度为：（3-4）（三）同层各柱剪力的确定现以n层，每层有m个柱子的框架为例，说明第j层各柱剪力的分配。
将框架沿第j层各柱的反弯点处切开以剪力和轴力,得计算简图如图所示。
根据水平力平衡条件有：（3-5）（3-6）（3-7）根据假定（2），同层各柱的层间侧移Δ相等，将式（3-7）代入式（3-6）有：（3-8）将上式代入（3-7）有，j层任一柱k分配的剪力为：（3-9）即同层各柱剪力按各柱间的侧移刚度比进行分配。
（四）柱端弯矩根据假定（1）有：底层柱：上端：（3-10）下端：（3-11）上部各层柱：（3-12）（五）梁端弯矩根据假定（3），由节点弯矩平衡（图），梁端弯矩为：（3-13）（3-14）（六）梁的剪力以各梁为脱离体，将梁的左右弯矩之和除以该梁的跨长，得梁的剪力。
框架结构在水平荷载下的计算反弯点法和D值法
M DH M DC 1.4 9k2N
MDH19 .42kN
MDC19.42kN
MGH16.67kN
DH (1.5)
G
MGC ? MGC52.04kN
MGK ?
C
G (1.7)
MGK30.56kN B
F
MGF65.93KN
(2.4)
A
E
M G K(M G H M G)F 1 .7 1 .0 1 .03.5 0k6N
a
A B 则 D jk V 1 h ji2 c2 2 K K ,
K,K ib 2 K 2 ic
B
b l
a
b
D jk
12 ic hj2
l
框架梁的线刚度无穷大时
，
1,
D
12ic hj 2
同理可推导底层柱 D 值
0.5K,Kib
2K
ic
B
b
hj
a
39 A
（二）柱的抗侧刚度D值
柱的抗侧刚度D值
D
12ic h2
式中
h—层高
ic —柱的线刚度，ic EIc /h ； E—柱混凝土弹性模量； I c —柱截面惯性矩； —与梁柱刚度比有关有刚度修正系数
40
i2 ic
i4
K i2 i4 2ic
i2 ic
K i2 ic
M G C (M G H M G)F 1 .7 1 .7 1 .05.0 2k4N
M (0.8)
K (1.0)
J (1.2)
I
31
二、改进反弯点法－Ｄ值法
当框架的高度较大、层数较多时，柱 子的截面尺寸一般较大，这时梁、柱的线 刚度之比往往要小于3，反弯点法不再适 用。进行框架内力计算，就必须对反弯点 法进行改进——改进反弯点（D值）法。
MDH19 .42kN
MDC19.42kN
MGH16.67kN
DH (1.5)
G
MGC ? MGC52.04kN
MGK ?
C
G (1.7)
MGK30.56kN B
F
MGF65.93KN
(2.4)
A
E
M G K(M G H M G)F 1 .7 1 .0 1 .03.5 0k6N
a
A B 则 D jk V 1 h ji2 c2 2 K K ,
K,K ib 2 K 2 ic
B
b l
a
b
D jk
12 ic hj2
l
框架梁的线刚度无穷大时
，
1,
D
12ic hj 2
同理可推导底层柱 D 值
0.5K,Kib
2K
ic
B
b
hj
a
39 A
（二）柱的抗侧刚度D值
柱的抗侧刚度D值
D
12ic h2
式中
h—层高
ic —柱的线刚度，ic EIc /h ； E—柱混凝土弹性模量； I c —柱截面惯性矩； —与梁柱刚度比有关有刚度修正系数
40
i2 ic
i4
K i2 i4 2ic
i2 ic
K i2 ic
M G C (M G H M G)F 1 .7 1 .7 1 .05.0 2k4N
M (0.8)
K (1.0)
J (1.2)
I
31
二、改进反弯点法－Ｄ值法
当框架的高度较大、层数较多时，柱 子的截面尺寸一般较大，这时梁、柱的线 刚度之比往往要小于3，反弯点法不再适 用。进行框架内力计算，就必须对反弯点 法进行改进——改进反弯点（D值）法。
d值法,反弯点法
向下移动，故 y1 取负值。 对底层框架柱，不考虑修正值 y1。
梁刚度变化时反弯点的修正
（3）上、下层层高变化时反弯点高度比的修正值 y2 和 y3 当与某柱相邻的上层或下层层高改变时，柱上端或下端的约束刚度
发生变化，引起反弯点移动，其修正值为 y2h 或 y3h。y2，y3 的分析方法 也与 yn 相仿，计算时可由附表 7.5 查取。
现讨论底层柱的D值。
c
0.5 K 2K
同理，当底层柱的下端为铰接时，可得
c
0.5K 1 2K
底层柱D值计算图式
综上所述，各种情况下柱的侧向刚度 D 值中系数 c 及梁柱线刚度比 K 按下表所列公
式计算。
柱侧向刚度修正系数 c
边柱
中柱
位置
简图
K
简图
K
c
一般层
K i2 i4 2ic
框架第2层脱离体图
（2）框架柱的侧向刚度——D值：一般规则框架中的柱
DV
K 2K
12ic h2源自c12ic h2
c
2
K K
框架柱侧向刚度计算公式
c 称为柱的侧向刚度修正系数，它反映了节点转动降低了 柱的侧向刚度，而节点转动的大小则取决于梁对节点转动的约束 程度。K ，c 1 这表明梁线刚度越大，对节点的约束能力 越强，节点转动越小，柱的侧向刚度越大。
计算方法，尚可进一步简化，这种忽略梁柱节点转角影响的计算方法称 为反弯点法。
在确定柱的侧向刚度时，反弯点法假定各柱上、下端都不产生转动， 即认为梁柱线刚度比为无限大。将趋近于无限大代入D值法 的公c 式， 可得 =1。 c因此，由式可得反弯点法的柱侧向刚度，并用D0表示为：
D值法
2、计算各柱分配的剪力
3、计算柱的反弯点高度 4、确定柱端弯矩，然后按结点平衡和梁的转动 刚度确定梁端弯矩。
Dik Vik Vi Dik
五、D值法与反弯点法的区别
反弯点法的基本假定是横梁刚度要比柱大得 多，因而结点只有侧移而无转角；D值法却要考 虑转角的影响。另外，反弯点法假定二层以上的 反弯点在柱高的中点，D值法要考虑结点转动引 起反弯点位置的变化。
V AB
12 K c 6ic 12 K c 2 ( ) ( ) h h h
(ｅ )
把(ｄ)代入(ｅ)，得
12 K c k 12 K c k VAB 2 h 2k h 2k 12 K c D VAB 2 h k 表3-1 2k
； 2、柱AB及相邻上下柱的线刚度均为KC，且它们 的弦转角均为ψ。
由结点A的平衡条件，
M
A
0 ，得，
M AB M AG M AC M AE 0(a ) M AB 2 K c (2 3 ) 6 K c ( ) M AG 2 K b 4 (2 ) 6 K b 4 M AC 2 K c (2 3 ) 6 K c ( ) M AE 2 K b 3 (2 ) 6 K b 3 6(2 K c K b 3 K b 4 ) 12 K c (2 K c K b 3 K b 4 ) 2 K c (ｂ)
当框架横梁的线刚度为无穷大，即，则 α=1 。由此 可知， α 是考虑框架结点转动对柱侧翼刚度的影响 系数。 2、底层柱的侧移刚度
12 K c D VAB 2 h 0.5 k 2k
三、确定柱反弯点高度比
影响柱反弯点高度的主要因素是柱上下端的约 束条件。反弯点移向转角较大的一端，也就是约束 刚度较小的一端。 影响柱两端约束刚度的主要因素是∶ A、结构总层数及该层所在位置； B、梁柱线刚度比； C、荷载形式∶ D、上层以下层梁刚1 y 2 y3
《d值法,反弯点法》课件
2
d值法求解
应用d值法计算结构的稳定系数，并分析结果。
3
反弯点法求解
使用反弯点法评估结构的稳定性，并与d值法结果进行比较。
总结与结论
总结d值法和反弯点法的特点和应用场景，强调合理选择方法的重要性。
反弯点法：原理与应用
1 原理解释
2 工程应用
介绍反弯点法的理论基础， 如何确定结构的弯曲和垂 直稳定性。
讲解反弯点法在不同工程 领域中的应用，包括建筑 结构和地下工程。
3 优点与局限
比较反弯点法与d值法的 优点和局限性，提供选择 合适方法的指导。
案例分析：d值法 vs 反弯点法
1
问题描述
给定一个结构问题，需要评估其稳定性。
《d值法,反弯点法》PPT 课件
d值法的介绍和原理，讲解如何使用d值法评估工程结构的稳定性。详细介绍d 值法的计算步骤和应用领域。
பைடு நூலகம்
应用举例：d值法
桥梁设计
使用d值法评估桥梁的稳定性，确保能够承受预期荷载。
土质工程
应用d值法来确定土层的稳定性，指导土工设计。
高层建筑
利用d值法评估高层建筑的抗震性能，确保结构安全。