偏心拉伸实验
3.偏心拉伸(08)

偏心拉伸试验
学院_________专业_________班_________实验组别_______实验者姓名_______________
实验日期_______________年_________月_________日实验室温度___________℃
批改时间____________ 报告成绩______________ 批阅人______________
一、实验原理(接桥方法设计:a测量轴力图及计算公式,b测量弯矩图及计算公式)
二、实验设备
电阻应变仪型号名称____________________________
实验装置名称____________________________
量具名称____________________________ 精度________mm
三、实验基本数据
四、实验测量数据和处理结果
五、回答思考题中提出的问题
(1)不同的桥路方式对测量结果有无影响?
(2)电阻应变仪无显示或数据不稳定,是什么原因造成的?该如何调整?(3)简述实验心得,或试验中你觉得应该注意的事项。
偏心拉伸实验(指导书)

偏心拉伸实验一. 实验目的1.测定如图2所示试件, 沿A-A 加载时, 即偏心拉伸时的拉应力和弯曲应力。
2.测定如图2所示试件, 沿A-A 加载时, 即偏心拉伸时, 横截面中性轴位置。
3. 与理论值进行比较分析二. 实验仪器和设备1. 拉压实验装置一台2. YJ-4501静态数字电阻应变仪一台3. 偏心拉伸试件一根(已粘贴好应变片)三. 实验原理拉压实验装置见图1, 它由座体1, 蜗轮加载系统2, 支承框架3, 移动横梁4, 传感器5和测力仪6等组成。
通过手轮调节传感器和移动横梁中间的距离, 将万向接头和已粘贴好应变片的偏心试件(见图2), 安装在上、下夹具中间。
若载荷作用在试件的对称轴线上, 则此时试件横截面上只有拉应力, 应力FSσ=F 为作用在试件上的力, S 为试件横截面面积。
若沿A-A 加载, 则此时试件受偏心拉伸, 横截面上即有拉应力, 也有弯曲应力, 应力ZF M y S I σ=± M 为0.02F, IZ 为形心轴惯性矩, y 为距形心轴距离(见图3)。
偏心试件弹性模量为70GN/m 2。
偏心试件上共粘贴有6片应变片, 粘贴位置如图2所示, 并已两两串联连接, 见图4(a )。
另有一个补偿块, 补偿块上共粘贴四片应变片, 其中绿色线为两片应变片串联连接线, 见图2(b )。
四. 实验步骤1.首先将偏心试件安装至拉压实验装置的上、下夹具间, 并通过试件对称轴。
2. 接通测力仪电源, 将测力仪开关置开。
3. 将应变片按图5串联单臂半桥接线法接至应变仪各通道上。
4.检查应变仪灵敏系数是否与应变片一致, 若不一致, 重新设置。
5. 实验:a. 加初始载荷, 初载菏取0.3KN, 将应变仪各通道置零(可反复进行)。
b. 加载荷至1.3KN, 记录各通道应变读数。
c. 载荷退至0.3KN, 记录各通道应变读数, 不为零时需重新置零。
d.再次加载至1.3KN, 记录各通道应变读数。
偏心拉伸实验报告

偏心拉伸实验报告实验目的,通过偏心拉伸实验,研究材料在拉伸过程中的变形和破坏特性,了解材料的力学性能。
实验原理,偏心拉伸是指在拉伸试样上施加偏心载荷,使试样在拉伸过程中产生偏心变形,从而引起试样的非均匀应变和破坏。
在偏心拉伸实验中,试样的拉伸变形主要包括轴向拉伸变形和偏心变形。
轴向拉伸变形是指试样在拉伸过程中发生的均匀拉伸变形,而偏心变形是指试样在偏心载荷作用下产生的非均匀应变和破坏。
通过对试样的偏心拉伸实验,可以研究材料的屈服特性、断裂特性和应变硬化特性。
实验步骤:1. 准备拉伸试样和拉伸设备;2. 在拉伸试样上标定偏心位置;3. 施加偏心载荷,进行偏心拉伸实验;4. 记录试样的拉伸变形和破坏情况;5. 分析实验数据,得出结论。
实验结果:通过偏心拉伸实验,我们观察到试样在偏心载荷作用下发生了非均匀应变和破坏。
试样的偏心变形导致了试样的局部应变集中,最终导致试样的破坏。
在实验中,我们还观察到试样的屈服特性和断裂特性,得出了材料的力学性能参数。
实验结论:偏心拉伸实验结果表明,材料在拉伸过程中会出现非均匀应变和破坏,偏心变形是导致试样破坏的主要原因之一。
通过偏心拉伸实验,我们可以了解材料的力学性能,为材料的设计和应用提供参考。
实验意义:偏心拉伸实验对于研究材料的力学性能具有重要意义,可以为工程结构的设计和材料的选择提供依据。
通过对材料的偏心拉伸实验,可以评估材料的抗拉强度、屈服特性和断裂特性,为工程实践提供参考。
总结:偏心拉伸实验是研究材料力学性能的重要手段,通过实验可以了解材料在拉伸过程中的变形和破坏特性。
偏心拉伸实验结果对于材料的设计和应用具有重要意义,可以为工程结构的设计和材料的选择提供依据。
希望通过本次实验,能够更深入地了解材料的力学性能,为工程实践提供更多的参考和支持。
偏心拉伸体会

偏心拉伸体会
测定偏心拉伸时的最大正应力,验证叠加原理的正确性。
学习拉弯组合变形时分别测量各内力分量产生的应变成分的方法。
测定偏心拉伸试样的弹性模量E和偏心距E。
进一步学习用应变仪测量微应变的组桥原理和方法,并能熟练掌握、灵活运用发挥主观能动性去做实验、完成试验报告。
实验过程中要多思考,思考实验每一步的用途以及为什么这么做。
在有限的课堂时间内投入到无限的学习思考中去。
实验报告的完成不能仅仅认为完成老师给的模板上提出的问题就行,
比如老师要求做相应的数值模拟,不应该只是把数值模拟的图弄上去,应该明白老师要求数值模拟的意义何在。
必须分析数值模拟的结果,再和实验结果相比较,思考两种方法的不同,相互检验,互相补充。
但我们最开始甚至做一条曲线,都不进行描述,这样都属于没有发挥主观能动性。
偏心拉伸实验

实验三偏心拉伸实验一、实验目的1. 测量试件在偏心拉伸时横截面上的最大正应变;2. 测定中碳钢材料的弹性模量E;3. 测定试件的偏心距e;二、实验设备与仪器1. 微机控制电子万能试验机;2. 电阻应变仪;3. 游标卡尺。
三、试件中碳钢矩形截面试件, (如图所示)。
截面的名义尺寸为h×b = (7.0×30)mm2 , 。
四、实验原理和方法试件承受偏心拉伸载荷作用, 偏心距为e。
在试件某一截面两侧的a点和b点处分别沿试件纵向粘贴应变片Ra和Rb ,则a点和b点的正应变为:εa =εp +εM +εt(1)εb =εp εM +εt(2)式中: εp——轴向拉伸应变εM ——弯曲正应变εt ——温度变化产生的应变有分析可知, 横截面上的最大正应变为:εmax =εp +εM (3)根据单向拉伸虎克定律可知: pA P E ε=(4)试件偏心距e 的表达式为:PEW e Z M ⋅⋅=ε (5)可以通过不同的组桥方式测出上式中的εmax 、εp 及εM, 从而进一步求得弹性模量E 、最大正应力和偏心距e 。
1.测最大正应变εmax组桥方式见图二。
(1/4桥;2个通道)εmax =εp +εM=(εp +εM +εt ) -εt=εa -εt (6)2.测拉伸正应变εp全桥组桥法(备有两个温补片), 组桥方式见图三。
)(21)]()[(21b t t a t M P t t t M P P εεεεεεεεεεεεε+--=+-+--++= (7)将εp 代入式(4), 即可求得材料的弹性模量E 。
3.测偏心矩e半桥组桥法, 组桥方式见图四。
)(21)]()[(21b a t M P t M P M εεεεεεεεε+=+--++=(8)将εM 代入式(5)即得到试件的偏心距e:为了尽可能减小实验误差, 实验采用多次重复加载的方法。
可参考如下加载方案: P0=6KN, Pmax=16KN, (P=10KN, N=4。
偏心拉伸实验
ep
P M
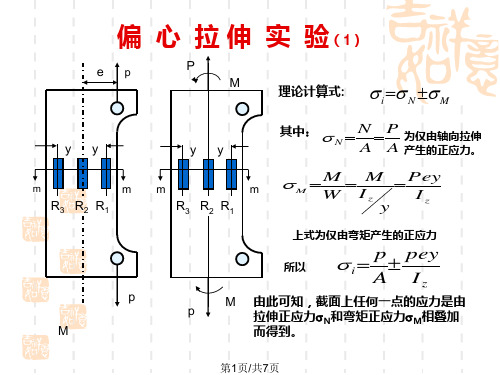
理论计算式: i N M
yy
yy
其中:
N
N A
P A
为仅由轴向拉伸 产生的正应力。
m
m
R3 R2 R1
p M
m
m
R3 R2 R1
M
M W
M Iz y
Pey Iz
上式为仅由弯矩产生的正应力
所以
i
p A
pey Iz
M 由此可知,截面上任何一点的应力是由
p
拉伸正应力N和弯矩正应力M相叠加
▪ 二、电阻应变片的功能
▪ 三、桥路联接的基本关系式及其特性:
▪
仪=1-2+3-4
▪ ① 半桥外补偿 、 ② 全桥外补偿、
③全桥自补偿、 ④ 半桥自补偿、
第4页/共7页
偏 心 拉 伸 实 验 (5)
四、电阻应变测量中的温度补偿问题。 五、机测实验的主要用途
① 主要用来测试金属材料的强度极限、刚 度等机械性质。
而得到。
第1页/共7页
偏 心 拉 伸 实 验(2)
x
p M
当用实验的方法测量这种组合 Rt 变形的任一点的应力时,可采用半
D… C…
桥共用外补偿的联接方法,如右图 示。
B…
yy
此时由电阻应变仪读得应变
仪得应变数仪为由拉伸引起的 R1 ( R2、R3 )
A…
123
m
R3 R2 R1
y 线应变N和由弯矩引起的线应
m 变M的叠加的结果. 即:仪 =(N±M+εt)-εt
半桥外补偿的 接线图
此时实际应变实=仪=N±M。
M p
由虎克定律得;
实验六 偏心拉伸实验

实验六 偏心拉伸实验一、实验目的1. 测定偏心拉伸时的最大正应力,验证叠加原理的正确性2. 分别测定偏心拉伸时由拉力和弯矩所产生的应力。
3. 测定弹性模量E 。
4.测定偏心距e 。
二、实验设备1. 组合变形电测综合实验装置(自制);2. 电阻应变测力仪;三、实验原理和方法偏心拉伸试件,如下图所示。
在外载荷作用下,其轴力F N =F ,弯矩M=F ×e,其中e 为偏心距。
根据叠加原理,得横截面上的应力为单向应力状态,其理论计算公式为拉伸应力和弯曲应力的代数和。
即20F 6M =A bh σ± 试件应变片的布置方法如上图所示,R 1和R 2分别为试件两侧面上的两个对称点,则1F =Mεεε-2F =M εεε+式中F ε——轴力引起的拉伸应变;M ε——弯矩引起的应变。
该实验采用全桥对臂的方式测轴力引起的应变,采用半桥方式测弯矩引起的应变。
四、实验步骤1. 设计好本实验所需的各类数据表格。
2. 测量试件尺寸。
3. 拟定加载方案。
4. 根据试件的分布情况和提供的设备条件确定最佳贴片、组桥方案并接线。
5. 分4-6级加载实验。
记录不同载荷时应变仪的度数应变d ε,并随时检查应变仪的度数变化量d ε∆是否符合线性变化。
6. 实验结束,卸载、关闭电源,拆线整理所有设备,清理试验现场,将所有仪器、设备复原。
五、实验结果处理1. 基本参数。
如图(a)所示,h=30 b=5 k=2.182. 实验过程中采集的数据。
表(b ) 测量M ε时应变与加载数据表表(c)各测点处应变数据的处理()F N ∆()F εμε∆()M εμε∆500 16 -31 500 17 -31.5 500 19.5 -31.5 500 15 -3150016.5 -30 ()εμε16.8-313、所用试件的弹性模量为660500198.41501016.810F F E Gpa A ε--===⨯⨯⨯ 4、偏心距为()293362198.410510*********.2366500Z M MEW Ebh e mmF Fεε---⨯⨯⨯⨯⨯⨯⨯====⨯5、应力计算实验值 9-6E =198.41016.810=3.33312MPa F σε=⨯⨯⨯9-6M E =198.4103110=6.1504MPa σε=⨯⨯⨯max 9.48352F M Mpa σσσ=+=理论值()3max263350065009.23109.48667150105103010Z F M Mpa A W σ----⨯⨯⨯=+=+=⨯⨯⨯⨯ 相对误差为0.003%。
偏心拉伸实验报告实验结论

偏心拉伸实验报告实验结论偏心拉伸实验报告实验结论引言:偏心拉伸实验是一种常见的力学实验,用以研究材料在受拉力作用下的变形和破坏特性。
通过施加偏心拉力,可以模拟实际工程中材料所承受的不均匀受力情况,从而更好地了解材料的力学性能。
本文将总结偏心拉伸实验的结果,并得出实验结论。
实验设计:本次实验采用了标准的偏心拉伸试验机,选取了不同种类的材料进行测试,包括金属、塑料和复合材料。
每种材料都进行了多组试验,以确保结果的准确性和可靠性。
在实验过程中,我们记录了拉伸载荷、试样长度和试样断裂位置等数据。
实验结果:在所有的实验中,我们观察到了以下现象和结果:1. 材料的断裂位置:在偏心拉伸实验中,材料的断裂位置通常会出现在试样的较薄部分。
这是由于拉伸力的作用,使得试样的较薄部分承受的应力较大,从而导致破坏。
这一现象在金属和塑料试样中尤为明显,而在复合材料试样中稍微有所不同,可能会出现在不同的位置。
2. 材料的断裂形态:不同材料在偏心拉伸实验中的断裂形态也有所不同。
金属试样通常会出现拉伸断裂,即试样在拉伸力作用下逐渐拉长,最终发生断裂。
塑料试样则可能会出现拉断或剪切断裂,取决于材料的特性和结构。
复合材料试样的断裂形态更加多样,可能会同时出现拉伸、剪切和撕裂等多种破坏方式。
3. 材料的应力-应变曲线:通过对实验数据的分析,我们得到了材料的应力-应变曲线。
在拉伸阶段,材料的应变随着拉伸力的增加而线性增长,直至达到极限强度。
此后,材料开始发生塑性变形,应变增长速率逐渐减慢,直至材料最终断裂。
不同材料的应力-应变曲线形状和特点有所差异,这与材料的组成、结构和加工方式等有关。
实验结论:通过以上实验结果的观察和分析,我们得出以下结论:1. 材料的断裂位置受到拉伸力的影响,较薄部分承受的应力较大,容易破坏。
2. 不同材料在偏心拉伸实验中的断裂形态各异,金属试样通常呈现拉伸断裂,塑料试样可能出现拉断或剪切断裂,而复合材料试样的破坏方式更加多样。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验名称:直梁弯曲实验
(四点弯)
学号 姓名
实验时间:2010年05 月 19 日
试件编号
试验机编
号
计算机编
号
应变仪编号
百
分
表编号
同组
实验地点: 12 12 12 12
教师
实验三 偏心拉伸实验
一、实验目的
1.测量试件在偏心拉伸时横截面上的最大正应变m ax ε; 2.测定中碳钢材料的弹性模量E ; 3.测定试件的偏心距e ;
二、实验设备与仪器
1.微机控制电子万能试验机; 2.电阻应变仪; 3.游标卡尺。
三、试件
中碳钢矩形截面试件,(如图所示)。
截面的名义尺寸为h ×b = (7.0×30)mm 2 ,MPa s 360=σ。
四、实验原理和方法
试件承受偏心拉伸载荷作用,偏心距为e 。
在试件某一截面两侧的a 点和b 点处分别沿试件纵向粘贴应变片R a 和R b ,则a 点和b 点的正应变为:
εa =εp +εM +εt (1) εb =εp -εM +εt (2)
式中: εp ——轴向拉伸应变
εM ——弯曲正应变
图一 试件示意图 h R a
R b
b
t
εt ——温度变化产生的应变
有分析可知,横截面上的最大正应变为:
εmax =εp +εM (3)
根据单向拉伸虎克定律可知:
p
A P E ε=
(4)
试件偏心距e 的表达式为:
P
E
W e Z M ⋅⋅=
ε (5)
可以通过不同的组桥方式测出上式中的εmax 、εp 及εM ,从而进一步求得弹性模量E 、最大正应力max σ和偏心距e 。
1、测最大正应变εmax
组桥方式见图二。
(1/4桥;2个通道)
εmax =εp +εM
=(εp +εM +εt ) -εt
=εa -εt (6)
2、测拉伸正应变εp
全桥组桥法(备有两个温补片),组桥方式见图三。
)(2
1
)]
()[(21
b t t a t M P t t t M P P εεεεεεεεεεεεε+--=+-+--++= (7)
将εp 代入式(4),即可求得材料的弹性模量E 。
3、测偏心矩e
半桥组桥法,组桥方式见图四。
)(2
1
)]()[(2
1
b a t M P t M P M εεεεεεεεε+=+--++=
(8)
将εM 代入式(5)即得到试件的偏心距e :
图二
图三
图四
为了尽可能减小实验误差,实验采用多次重复加载的方法。
可参考如下加载方案:P0=6KN,P max=16KN, P=10KN,N=4。
五、实验步骤
1.设计实验所需各类数据表格;
2.测量试件尺寸;
测量试件三个有效横截面尺寸,取其平均值作为实验值。
3.拟定加载方案;初始载荷为6KN,应变仪清零,一次加到16KN,记录应变仪读数。
4.试验机准备、试件安装和仪器调整;
5.确定各项要求的组桥方式、接线和设置应变仪参数;K=2.08;R=120Ω
6.检查及试车;
检查以上步骤完成情况,然后预加一定载荷,再卸载至初载荷以下,以检查试验机及应变仪是否处于正常状态。
7.进行试验;
将载荷加至初载荷,记下此时应变仪的读数或将读数清零。
重复加载,每重复一次,记录一次应变仪的读数。
实验至少重复四次,如果数据稳定,重复性好即可。
8.数据通过后,卸载、关闭电源、拆线并整理所用设备。
六、试验结果处理
试件宽L=30.03mm,厚H=7.82mm
1,最大正应变增量 N N
n
t a ∑=-∆=1
max )
(εεε=375×10-6 。
2,材料的弹性模量∑=∆⋅
⋅∆=
N
n
p A N
P E 1
ε
εp =207.65×10-6 ,A=L ×H ,△P=10 kN ,
代入上式得,E=205.1 GPa.
3, 试件的偏心距N
P E
W e Z N
n M
⋅∆⋅⋅∆=
∑=1
ε
,
εM =167.25×10-6
,Wz =HL 2
6
代入上式可得:偏心距 e =4.03 mm。
