实验二 偏心拉伸实验
偏心拉伸实验报告实验结论

偏心拉伸实验报告实验结论偏心拉伸实验报告实验结论引言:偏心拉伸实验是一种常见的力学实验,用以研究材料在受拉力作用下的变形和破坏特性。
通过施加偏心拉力,可以模拟实际工程中材料所承受的不均匀受力情况,从而更好地了解材料的力学性能。
本文将总结偏心拉伸实验的结果,并得出实验结论。
实验设计:本次实验采用了标准的偏心拉伸试验机,选取了不同种类的材料进行测试,包括金属、塑料和复合材料。
每种材料都进行了多组试验,以确保结果的准确性和可靠性。
在实验过程中,我们记录了拉伸载荷、试样长度和试样断裂位置等数据。
实验结果:在所有的实验中,我们观察到了以下现象和结果:1. 材料的断裂位置:在偏心拉伸实验中,材料的断裂位置通常会出现在试样的较薄部分。
这是由于拉伸力的作用,使得试样的较薄部分承受的应力较大,从而导致破坏。
这一现象在金属和塑料试样中尤为明显,而在复合材料试样中稍微有所不同,可能会出现在不同的位置。
2. 材料的断裂形态:不同材料在偏心拉伸实验中的断裂形态也有所不同。
金属试样通常会出现拉伸断裂,即试样在拉伸力作用下逐渐拉长,最终发生断裂。
塑料试样则可能会出现拉断或剪切断裂,取决于材料的特性和结构。
复合材料试样的断裂形态更加多样,可能会同时出现拉伸、剪切和撕裂等多种破坏方式。
3. 材料的应力-应变曲线:通过对实验数据的分析,我们得到了材料的应力-应变曲线。
在拉伸阶段,材料的应变随着拉伸力的增加而线性增长,直至达到极限强度。
此后,材料开始发生塑性变形,应变增长速率逐渐减慢,直至材料最终断裂。
不同材料的应力-应变曲线形状和特点有所差异,这与材料的组成、结构和加工方式等有关。
实验结论:通过以上实验结果的观察和分析,我们得出以下结论:1. 材料的断裂位置受到拉伸力的影响,较薄部分承受的应力较大,容易破坏。
2. 不同材料在偏心拉伸实验中的断裂形态各异,金属试样通常呈现拉伸断裂,塑料试样可能出现拉断或剪切断裂,而复合材料试样的破坏方式更加多样。
偏心拉伸实验

D图2-2R 图2-1实验二 偏心拉伸实验一、实验目的1.测定偏心拉伸试样材料的弹性模量E 。
2.测定偏心拉伸试样的偏心距e 。
3.学习组合载荷作用下由内力产生的应变成份分别单独测量的方法。
二、设备和仪器(同§7) 三、试样采用图2-1所示的铝合金偏心拉伸试样,Ra 和Rb 为沿应变方向粘贴的应变片,另外有两枚粘贴在与试样材质相同但不受载荷的铝块上的应变片,供全桥测量时组桥之用。
尺寸b=24mm ,t=5mm 。
四、试验原理 由电测原理知:1234du εεεεε=-+-(I-7)式中du ε为仪器读数。
从此式看出:相邻两臂应变符号相同时,仪器读数互相抵销;应变符号相异时,仪器读数绝对值是两者绝对值之和。
相对两臂应变符号相同时,仪器读数绝对值是两者绝对值之和;应变符号相异时,仪器读数互相抵销。
此性质称为电桥的加减特性。
利用此特性,采取适当的布片和组桥,可以将组合载荷作用下各内力产生的应变成份分别单独测量出来,且减少误差,提高测量精度。
从而计算出相应的应力和内力。
——这就是所谓内力素测定。
图2-1中Ra 和Rb 的应变均由拉伸和弯曲两种应变成份组成,即() ()a F M b F M a b εεεεεε=+=-式中Fε和M ε分别为拉伸和弯曲应变的绝对值。
若如图2-2组桥,则由(I-7)、(a )和(b )式得2du a b F εεεε=+=若如图2-3组桥,则由(I-7)、(a )和(b )式得2du a b M εεεε=-=通常将仪器读出的应变值与待测应变值之比称为桥臂系数。
故上述两种组桥方法的桥臂系数均为2。
为了测定弹性模量E ,可如图2-2组桥,并等增量加载,即0(1,2,,5)i F F i F i =+⋅∆=末级载荷5F 不应使材料超出弹性范围。
初载荷F 时应变仪调零,每级加载后记录仪器读数图2-3dui ε,用最小二乘法计算出弹性模量E :52151i duii iFE bti αε==⋅∆=⋅∑∑ (2-1)式中α为桥臂系数。
偏心拉伸或压缩(材料力学课件)

建筑结构的偏心拉伸或压缩分析
建筑结构的偏心拉伸或压缩分析是确保结构安全的重要环节 。在设计和施工过程中,需要考虑材料的力学性能、结构的 几何形状和载荷分布等因素,以评估结构的稳定性和安全性 。
在进行建筑结构的偏心拉伸或压缩分析时,需要使用专业的 分析软件和实验设备,如有限元分析软件和材料试验机等, 以获得准确的计算结果和实验数据。
偏心拉伸或压缩时,材料内部产 生应力分布不均匀,最大应力出 现在截面的中心,最小应力出现
在截面的边缘。
偏心拉伸时,中心部位受到拉应 力,边缘部位受到压应力;偏心 压缩时,中心部位受到压应力,
边缘部位受到拉应力。
应力分布与材料的弹性模量、泊 松比和截面形状等因素有关。
材料在偏心拉伸或压缩下的应变
在偏心拉伸或压缩过程中,材料会发生应变,表现为截面尺寸和形状的变化。
偏心拉伸或压缩(材料力学课 件)
• 偏心拉伸或压缩的基本概念 • 材料在偏心拉伸或压缩下的行为 • 偏心拉伸或压缩的强度分析
• 偏心拉伸或压缩的实验研究 • 偏心拉伸或压缩的工程应用
01
偏心拉伸或压缩的基本概念
定义与特性
定义
偏心拉伸或压缩是指物体在受到不均 匀分布的拉伸或压缩载荷作用时,其 中心轴线与载荷作用线不重合,导致 物体产生弯曲和扭转的现象。
机械设备的偏心拉伸或压缩分析
机械设备的偏心拉伸或压缩分析是确保设备正常运行的关 键环节。在设计和制造过程中,需要考虑材料的力学性能 、设备的运行环境和载荷分布等因素,以评估设备的稳定 性和可靠性。
在进行机械设备的偏心拉伸或压缩分析时,需要使用专业 的分析软件和实验设备,如有限元分析软件和疲劳试验机 等,以获得准确的计算结果和实验数据。
THANKS
偏心拉伸实验报告

偏心拉伸实验报告偏心拉伸实验报告引言:偏心拉伸实验是一种常见的力学实验,通过施加不同的偏心距离和拉伸力来研究材料的力学性能。
本实验旨在探究材料在偏心拉伸条件下的应力-应变关系,并分析其对材料的影响。
实验目的:1. 研究材料在偏心拉伸条件下的应力-应变关系;2. 掌握偏心拉伸实验的操作方法;3. 分析偏心拉伸对材料性能的影响。
实验原理:偏心拉伸实验是一种静态拉伸实验,通过施加不同的偏心距离,使拉伸力不再作用于材料的几何中心,而是偏离几何中心。
这样的拉伸方式可以模拟材料在实际应用中受到的偏心力作用,从而更真实地反映材料的力学性能。
实验装置:1. 偏心拉伸试验机:用于施加拉伸力和控制偏心距离;2. 试样夹具:用于夹持试样,保证试样在拉伸过程中的稳定性;3. 应变计:用于测量试样在拉伸过程中的应变;4. 数据采集系统:用于记录和分析实验数据。
实验步骤:1. 准备试样:根据实验要求,选择合适的试样材料和尺寸,并进行必要的加工和标记;2. 安装试样:将试样夹持在试验机上,确保试样的几何中心与试验机的拉伸轴线重合;3. 施加拉伸力:通过试验机控制系统,逐渐施加拉伸力,同时记录拉伸力和应变数据;4. 调整偏心距离:在拉伸过程中,通过调整试验机的偏心距离,使拉伸力不再作用于试样的几何中心;5. 记录数据:在拉伸过程中,及时记录拉伸力和应变数据,并保证数据的准确性和可靠性;6. 结束实验:根据实验要求,停止拉伸,并将试样从试验机上取下。
实验数据处理:1. 绘制应力-应变曲线:根据实验数据,绘制应力-应变曲线,分析材料在偏心拉伸条件下的力学性能;2. 计算材料的屈服强度和抗拉强度:根据应力-应变曲线,计算材料的屈服强度和抗拉强度,评估材料的抗拉性能;3. 分析偏心拉伸对材料性能的影响:根据实验结果,分析偏心拉伸对材料的强度、韧性、断裂形态等性能的影响。
实验结果与讨论:通过偏心拉伸实验,我们得到了材料在不同偏心距离下的应力-应变曲线。
实验二 偏心拉伸实验(精品文档)_共6页

实验二偏心拉伸实验力学-聂灿亮一.实验目的1. 测定弹性模量; E2. 测定偏心距;e3. 将测得的弹性模量与偏心距分别与理论值进行对比,计算相对误差;4. 分析误差产生原因。
二.实验设备和仪器1. 静态电阻应变仪;2. 带孔拉伸实验杆件。
三.实验原理与分析1. 偏心拉伸试件为低碳钢矩形截面构件,其受力截面如下图所示:2. 在外荷载作用下,有轴力和弯矩,大小分别为:N M,,试件变形是拉伸和弯矩的组合变形,其正N F =M Fe =应力及相应应变为 在试件左侧面:(1)'2''2616N N N Fe A W bh bh N Fe E E bh bh σσε⎧=-=-⎪⎪⎨⎛⎫⎪==- ⎪⎪⎝⎭⎩在试件左侧面:(2)''2''''2616N M N FeA W bh bh N Fe E E bh bh σσε⎧=+=+⎪⎪⎨⎛⎫⎪==+ ⎪⎪⎝⎭⎩3. 试件应变片布置如图四所示。
和分别为试件两侧面上1R 2R 的两个对称点,则可测得:(3)'1''2N MN Mεεεεεεεε⎧==-⎪⎨==+⎪⎩其中,为轴力引起的拉伸应变;为弯矩引起的应变,N εM ε由上式可得:(4)1221=22N M εεεεεε+⎧⎪⎪⎨-⎪=⎪⎩4. 根据以上各式,可计算出弹性模量、偏心距。
E e 四. 实验步骤1. 设计好本实验所需的各类数据表格;2. 测量试件尺寸;3. 确定加载方案:本实验按逐级1000N ,初试1000N ,最大2000N 加载;4. 采用合适的接线方案,调整好所用设备和仪器;5. 进行试验,并记录数据;6. 完成试验后,关闭电源,将设备和仪器恢复到初始状态。
五. 数据分析与处理1. 实验数据记录与处理根据(3)(4)公式计算出N M εε、荷载/N1000 2000 /(1e-6) 1ε-33 -68 /(1e-6)2ε91 200 /(1e-6)N ε29 66 /(1e-6)M ε621342. 计算弹性模量(=4.8mm, =30mm ): E b h 综合(1)(2)(3)式解得’ 33100010239.44.83029=200010210.04.83066N Gpa Gpa F E bh Gpa Gpaε⎧⨯=⎪⎪⨯⨯=⎨⎪⨯=⎪⨯⨯⎩取平均值得: 239.4+210.0=224.72E Gpa =3. 计算偏心距e 结合(1)(2)(3)(4)式以及表格所记录处理的数据得, 23223224.7 4.830621010.0361000=6224.7 4.8301341010.8462000z MM mm mm EW Ebh e FF mm mmεε⎧⨯⨯⨯⨯=⎪⎪⨯==⎨⨯⨯⨯⎪⨯=⎪⨯⎩取平均值得: 10.03+10.84=10.43mm 2e =4. 与理论值相对误差计算弹性模量: , E 1227.4206100%10.38%206d -=⨯=偏心距:e 210.4310.00100% 4.3%10.00d -=⨯=5. 误差分析(1)做实验时由于孔径不是与拉钩完全紧密咬合,加载时会导致上下拉力不是完全共线;(2) 刚开始加载时试件会有些微摆动;(3)由于孔径的大小不好测量,所以在测量时会产生读数误差;(4)计算对无理小数的近似计算,会产生计算误差。
实验一、二 拉伸实验
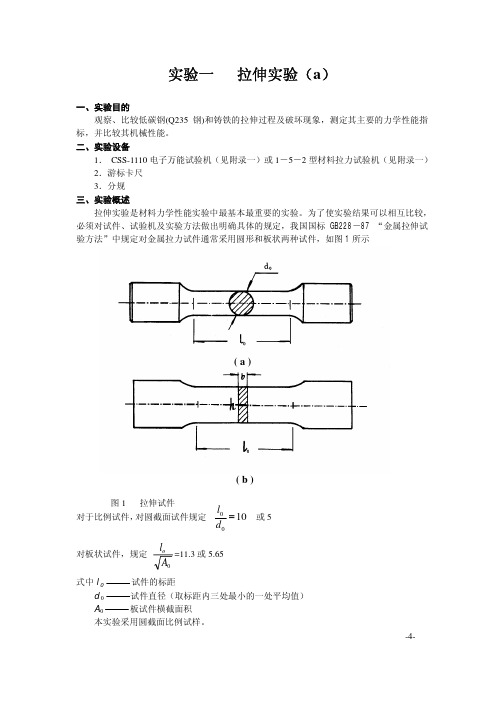
后的标距部分长度 l1 和拉断后颈缩处的最小直径 d1 。由以下两式算得其主要塑性指标:
延伸率:
δ = l1 − l0 ×100% l0
截面收缩率:ψ = Ao − A1 ×100% Ao
式中,A1 为试件拉断后,颈缩处之最小截面积 l0 为试件之原始标距长度 l1 为试件拉断后标距长度
移位法示意图
7. 观察破坏现象并画下破坏断口的草图。
8. 测量断后数据。试件拉断后,按计算机要求回答和输入断后数据,观察计算机自动
处理的力学性能指标,分析结果是否合理,如果合理,则存盘和打印结果;如不合理,可用
手动方法对实验结果进行修正,还可通过再现实验(所编号 LXY),观察该实验的结果,打
印该实验报告。
三、实验记录与结果
1.试件尺寸
材 标距
料 l0 (mm)
横截面Ⅰ
(1) (2) 平均
直径 d 0 (mm)
横截面Ⅱ (1) (2) 平均
最小横截面面
横截面Ⅲ
积 A0 (mm2 )
(1) (2) 平均
钢
铸 铁 2. 实验数据
屈服载荷 材
料 ps (kN)
最大载荷
pb (kN)
拉断后标距
l1 (mm)
颈缩处直径
一截面进行测量,每一横截面沿互垂方向各测一次取其平均值,再用所得的三个数据中的最 小值计算试件的横截面面积。
3. 检查机器,选择度盘并配上相应摆锤。将试件夹装在上夹头中,转动齿杆调整度盘 零点,再把试件夹在下夹头中,最后将自动绘图装置调整好。
4.经教师检查后开动机器进行实验。实验过程中,注意观察自动绘图装置、载荷刻度 盘及试件的变形,特别是弹性、屈服、强化和颈缩各阶段的特征,注意记录 Ps 及 Pb。试件
偏心拉伸实验报告

偏心拉伸实验报告偏心拉伸实验报告一、实验目的本实验旨在研究材料在偏心拉伸条件下的力学性能表现,以获取材料的应力-应变曲线,并对材料的强度、塑性和韧性等关键性能指标进行评估。
通过本实验,有助于我们更深入地理解材料在复杂应力状态下的行为,为工程实践提供重要的理论依据。
二、实验原理偏心拉伸实验是一种常用的材料力学性能试验方法,主要用来模拟材料在复杂应力状态下的行为。
在偏心拉伸实验中,试样的一端被固定,而另一端受到拉伸载荷的作用。
与常规拉伸实验不同,偏心拉伸实验中试样的轴向应力分布不均匀,具有较高的应力梯度,因此可以更好地模拟实际工程中材料的受力状态。
三、实验步骤1.试样制备根据实验要求,选择合适的材料和尺寸规格,制备标准拉伸试样。
考虑到偏心拉伸的特殊性,试样的形状和尺寸需要满足相关标准。
试样制备完成后,应对其进行严格的检查,确保其符合实验要求。
2.实验装置进行偏心拉伸实验需要使用专门的实验装置,主要包括:拉伸机、夹具、偏心轮等。
实验装置应具备高精度和高稳定性,以确保实验结果的准确性和可重复性。
3.实验操作将试样安装在实验装置上,并确保试样的中心线与偏心轮的旋转轴重合。
然后,对试样施加一定的预载,以消除试样与夹具、偏心轮之间的接触间隙。
在预载完成后,逐渐增加拉伸载荷,并记录试样的变形量和对应的载荷。
4.数据处理与分析根据实验数据,绘制试样的应力-应变曲线,并对关键性能指标进行计算和分析。
这些指标包括:强度、塑性和韧性等。
对实验结果进行深入分析,可以对材料的力学性能有更全面的了解。
四、实验结果及数据分析1.应力-应变曲线通过偏心拉伸实验,我们获得了材料的应力-应变曲线。
曲线图反映了材料在拉伸过程中的应力分布和应变情况。
从曲线上可以看出,随着拉伸载荷的增加,材料的应力也逐渐增大。
同时,材料发生了一定程度的塑性变形。
2.性能指标分析根据应力-应变曲线,我们可以计算出材料的强度、塑性和韧性等性能指标。
这些指标是评估材料在复杂应力状态下的重要依据。
拉伸测试实验报告

一、实验目的1. 熟悉拉伸测试实验的原理和操作方法;2. 掌握拉伸测试仪器的工作原理和操作步骤;3. 通过实验测定材料的弹性模量、屈服强度、抗拉强度、伸长率等力学性能指标;4. 分析实验结果,了解材料在不同应力状态下的力学行为。
二、实验原理拉伸测试实验是一种常用的力学性能测试方法,用于测定材料在拉伸过程中的应力-应变关系。
实验原理如下:1. 根据胡克定律,在弹性范围内,材料的应力与应变呈线性关系,即σ = Eε,其中σ为应力,E为弹性模量,ε为应变;2. 材料在拉伸过程中,当应力达到一定值时,材料发生屈服,应力不再随应变线性增加;3. 材料在拉伸过程中,当应力达到最大值时,材料发生断裂,应力降至零;4. 伸长率是指材料在拉伸过程中长度增加的百分比,即ΔL/L×100%,其中ΔL为材料拉伸后的长度变化,L为材料原始长度。
三、实验仪器与设备1. 电子万能材料试验机:用于施加拉伸力,测量应力;2. 拉伸试样:根据实验要求加工成不同规格的试样;3. 拉伸夹具:用于固定试样,保证试样在拉伸过程中的稳定性;4. 游标卡尺:用于测量试样原始长度和拉伸后的长度;5. 计算器:用于计算实验数据。
四、实验步骤1. 准备试样:根据实验要求加工试样,确保试样表面平整、光滑;2. 安装试样:将试样安装在拉伸夹具上,确保试样固定牢固;3. 设置试验参数:根据实验要求设置试验机参数,如拉伸速度、最大载荷等;4. 进行拉伸测试:启动试验机,对试样进行拉伸测试;5. 记录实验数据:在拉伸过程中,记录试样断裂时的载荷、原始长度、拉伸后的长度等数据;6. 实验数据整理:将实验数据整理成表格,便于后续分析。
五、实验结果与分析1. 计算材料力学性能指标:(1)弹性模量E = F / (Aε),其中F为拉伸力,A为试样横截面积,ε为应变;(2)屈服强度σs = F / A,其中F为屈服载荷;(3)抗拉强度σb = F / A,其中F为断裂载荷;(4)伸长率ΔL/L×100%,其中ΔL为材料拉伸后的长度变化,L为材料原始长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二偏心拉伸实验
力学-聂灿亮
一.实验目的
1.测定弹性模量E;
2.测定偏心距e;
3.将测得的弹性模量与偏心距分别与理论值进行对比,计算相
对误差;
4.分析误差产生原因。
二.实验设备和仪器
1.静态电阻应变仪;
2.带孔拉伸实验杆件。
三.实验原理与分析
1.偏心拉伸试件为低碳钢矩形截面构件,其受力截面如下图所
示:
2.在外荷载作用下,有轴力N和弯矩M,大小分别为:
N F =,M Fe =,试件变形是拉伸和弯矩的组合变形,其正
应力及相应应变为 在试件左侧面:
'2'
'2616N N N Fe A W bh bh
N Fe E E bh bh σσε⎧=-=-⎪⎪⎨⎛⎫
⎪==- ⎪⎪⎝⎭⎩
(1) 在试件左侧面:
''2''
''2616N M N Fe
A W bh bh
N Fe E E bh bh σσε⎧=+=+⎪⎪⎨⎛⎫
⎪==+ ⎪⎪⎝⎭⎩
(2) 3. 试件应变片布置如图四所示。
1R 和2R 分别为试件两侧面上的两个对称点,则可测得:
'
1''
2N M
N M
εεεεεεεε⎧==-⎪⎨==+⎪⎩ (3) 其中,N ε为轴力引起的拉伸应变;M ε为弯矩引起的应变,由上式可得:
1221
=2
2
N M εεεεεε+⎧⎪⎪⎨-⎪=⎪⎩ (4)
4. 根据以上各式,可计算出弹性模量E 、偏心距e 。
四. 实验步骤
1. 设计好本实验所需的各类数据表格;
2. 测量试件尺寸;
3. 确定加载方案:本实验按逐级1000N ,初试1000N ,最大
2000N 加载;
4. 采用合适的接线方案,调整好所用设备和仪器;
5. 进行试验,并记录数据;
6. 完成试验后,关闭电源,将设备和仪器恢复到初始状态。
五. 数据分析与处理
1. 实验数据记录与处理
根据(3)(4)公式计算出N M εε、
2. 计算弹性模量E (b =4.8mm, h =30mm ): 综合(1)(2)(3)式解得
3
3
100010239.44.83029
=200010210.04.83066
N Gpa Gpa F E bh Gpa Gpa
ε⎧⨯=⎪⎪⨯⨯=⎨⎪⨯=⎪⨯⨯⎩’ 取平均值得:239.4+210.0
=224.72
E Gpa = 3. 计算偏心距e
结合(1)(2)(3)(4)式以及表格所记录处理的数据得
2322
3224.7 4.83062
1010.0361000
=6224.7 4.8301341010.8462000z M
M mm mm EW Ebh e F
F mm mm
εε⎧⨯⨯⨯⨯=⎪⎪⨯=
=⎨⨯⨯⨯⎪⨯=⎪⨯⎩
,
取平均值得: 10.03+10.84
=10.43mm 2
e =
4. 与理论值相对误差计算
弹性模量E : 1227.4206
100%10.38%206
d -=
⨯=, 偏心距e : 210.4310.00
100% 4.3%10.00
d -=
⨯= 5. 误差分析
(1)
做实验时由于孔径不是与拉钩完全紧密咬合,加载时会导致上下拉力不是完全共线;
(2) 刚开始加载时试件会有些微摆动;
(3) 由于孔径的大小不好测量,所以在测量时会产生读数误差; (4)
计算对无理小数的近似计算,会产生计算误差。
六. 试验总结与注意事项
1. 学会了如何去测量一个拉伸试件的偏心距;
2. 将公式推导与实验相结合,从不同路径验证理论上的正确性;
3. 本实验是非破坏实验,注意不要损坏试件;
4. 施加荷载时,应保证荷载作用位置的准确。
