数学建模作业5
北工大数学建模作业5
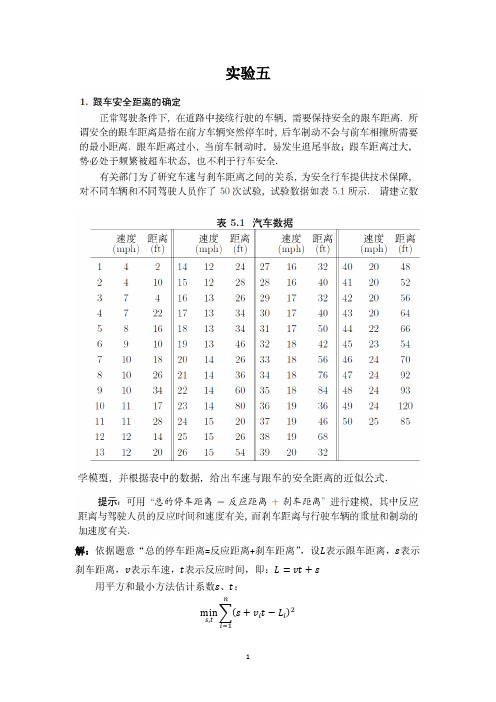
实验五解：依据题意“总的停车距离=反应距离+刹车距离”，设L表示跟车距离，s表示刹车距离，v表示车速，t表示反应时间，即：L=vt+s用平方和最小方法估计系数s、t：min s,ts+v i t−L i2 ni=1将50组实验数据代入计算并取最优解，相应的LINGO程序如下图1-1所示：图1-1（详细如下）model:sets:quantity/1..50/:v,L;endsetsdata:v= 4 4 7 7 8 9 10 10 10 11 11 12 12 12 12 13 13 13 13 14 14 14 14 15 15 15 16 16 17 17 17 18 18 18 18 19 19 19 20 20 20 20 20 22 23 24 24 24 24 25;L= 2 10 4 22 16 10 18 26 34 17 28 14 20 24 28 26 34 34 46 26 36 60 80 20 26 54 32 40 32 40 50 42 56 76 84 36 46 68 32 48 52 56 64 66 54 70 92 93 120 85;enddatamin=@sum(quantity:(s+v*t-L)^2);@free(s);@free(t);endLINGO程序计算结果截取如下图1-2所示：图1-2由计算结果可知：平方和最小时，s=-17.57909，t=3.932409。
即,L=3.932409v−17.57909解：依据题意设第一个作业点为坐标原点，即（0, 0）点。
则第二个作业点的坐标为（75，330），第三个作业点的坐标为（-225, -40）。
设两个临时机场的位置坐标分别为A x a，y a、B x b，y b，A机场给三个作业点提供的油料分别为a1、a2、a3，B机场给三个作业点提供的油料分别为b1、b2、b3，要求每月从机场到作业点的吨公里数最少，建立数学模型：目标函数为：Min L=a1x a2+y a2+b1x b2+y b2+a2x a−752+y a−3302+b2x b−752+y b−3302+a3x a+2252+y a+402+b3x b+2252+y b+402约束条件为：a1+b1=25a2+b2=14a3+b3=34相应的LINGO程序如下图2-1所示：图2-1（不是很清晰，详细见下）min=a1*(xa^2+ya^2)^0.5+b1*(xb^2+yb^2)^0.5+a2*((xa-75)^2+(ya-330)^2)^0 .5+b2*((xb-75)^2+(yb-330)^2)^0.5+a3*((xa+225)^2+(ya+40)^2)^0.5+b3*((x b+225)^2+(yb+40)^2)^0.5;a1+b1=25;a2+b2=14;a3+b3=34;@free(xa);@free(xb);@free(ya);@free(yb);LINGO程序运行结果如下图2-2所示：图2-2由计算结果可知：临时机场A建立的位置坐标为（0, 0）处，机场B建立的位置坐标为（-225，-40）处时，并且A机场给第1个作业点提供油料25t，给第2个作业点提供14t，给第3个作业点提供0t；机场B给第1个作业点提供0t，给第2个作业点提供0t，给第三个作业点提供34t，这种方案下每月的吨公里数最少为4737.816。
数学建模第五次作业
1.区间估计解：R程序：X <- c(1067, 919, 1196, 785, 1126, 936, 918, 1156, 920, 948);n <- length(X);xb <- mean(X);S2 <- var(X);S <- sqrt(S2);T = (xb-1000)/(S/sqrt(n));结果：mean df a b1 997.1 9 902.9965 1091.203p-value=0.5270268由此可知：置信区间为902.996到1096.203，该批灯泡能使用1000小时以上的概率为52.70268%。
2.假设检测I解：假设H0<=225，H1>225此问题是单边检验输入数据，调用函数t.test()R程序：X<-c(220, 188, 162, 230, 145, 160, 238, 188,247,113,126, 245, 164, 231, 256, 183, 190, 158,224,175)t.test(X, alternative = "greater", mu = 225)结果：data: Xt = -3.4783, df = 19, p-value = 0.9987alternative hypothesis: true mean is greater than 22595 percent confidence interval:175.8194 Infsample estimates:mean of x192.15由此可知：P值为0.9987，不能拒绝原假设，接受H0，即认为油漆工人的血小板计数与正常成年男子有差异，油漆作业对人体血小板计数有影响。
3.假设检测II解：（1）两总体方差相同模型选择t检验法R程序：X<-c(113,120,138,120,100,118,138,123)Y<-c(138,116,125,136,110,132,130,110)t.test(X, Y, alternative = "less", var.equal=TRUE)t.test(X, Y, alternative = "less")结果：Two Sample t-testdata: X and Yt = -0.566, df = 14, p-value = 0.2902alternative hypothesis: true difference in means is less than 095 percent confidence interval:-Inf 7.12812sample estimates:mean of x mean of y121.250 124.625（2）两总体方差不同模型R程序：X<-c(113,120,138,120,100,118,138,123)Y<-c(138,116,125,136,110,132,130,110)var.test(X, Y)结果：F test to compare two variancesdata: X and YF = 1.2278, num df = 7, denom df = 7, p-value = 0.7935alternative hypothesis: true ratio of variances is not equal to 195 percent confidence interval:0.2458103 6.1327511sample estimates:ratio of variances1.227800（3）成对数据模型R程序：X<-c(113,120,138,120,100,118,138,123)Y<-c(138,116,125,136,110,132,130,110)var.test(X, Y, alternative = "less", exact=F)结果：F test to compare two variancesdata: X and YF = 1.2278, num df = 7, denom df = 7, p-value = 0.6033alternative hypothesis: true ratio of variances is less than 195 percent confidence interval:0.000000 4.649733sample estimates:ratio of variances1.227800由此可知：（1）p=0.29(2)p=0.79(3)p=0.60，置信区间（1）>（2）>（3）。
数学建模第五章作业
第五章作业1.解（3）给定样条在左右端点的一阶导数的三次样条123456789-50510三次样条（给定样条在左右端点的一阶导数)样条的一阶导函数样条的二阶导函数样条的三阶导函数图1 绘制图1的MATLAB 脚本如下：x=[0,1,3,6,8,9];y=[-1,3,1,2,0,2,4,1]; pp=csape(x,y,'complete'),pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4); d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3); d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2); d3s=@(t,tj,c)6.*c(1).*ones(size(t)); for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c); v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c); plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold on endlegend('三次样条（给定样条在左右端点的一阶导数)','样条的一阶导函数',...'样条的二阶导函数','样条的三阶导函数') y1=[3,1,2,0,2,4];plot(x,y1,'ko'),hold off命令窗口显示的结果为 pp =form: 'pp'breaks: [0 1 3 6 8 9] coefs: [5x4 double] pieces: 5 order: 4 dim: 1 ans =1.4903 -2.4903 -1.00003.0000 -0.4879 1.9807 -1.5097 1.0000 0.1795 -0.9469 0.5580 2.0000 -0.0157 0.6691 -0.2754 0 -0.7874 0.5749 2.2126 2.0000 计算结果说明该三次样条的分段多项式形式为321.4903 2.49033,x x x --+ 01x ≤≤ 320.4879(1) 1.9807(1) 1.5097(1)1,x x x --+---+ 13x ≤≤()s x = 320.1795(3)0.9469(3)0.5580(3)2,x x x ---+-+ 36x ≤≤320.0157(6)0.6691(6)0.2754(6),x x x --+--- 68x ≤≤ 320.7874(8)0.5749(8) 2.2126(8)2,x x x --+-+-+ 89x ≤≤（4）给定样条在左右端点的二阶导数的三次样条123456789-3-2-11234三次样条（给定样条在左右端点的二阶导数)样条的一阶导函数样条的二阶导函数样条的三阶导函数图2 绘制图2的MATLAB 脚本如下x=[0,1,3,6,8,9];y=[0,3,1,2,0,2,4,0]; pp=csape(x,y,'second'),pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4); d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3); d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2); d3s=@(t,tj,c)6.*c(1).*ones(size(t)); for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c); v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c); plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold on endlegend('三次样条（给定样条在左右端点的二阶导数)','样条的一阶导函数',...'样条的二阶导函数','样条的三阶导函数') y1=[3,1,2,0,2,4];plot(x,y1,'ko'),hold off 命令窗口显示的结果为 pp =form: 'pp'breaks: [0 1 3 6 8 9] coefs: [5x4 double] pieces: 5 order: 4 dim: 1 ans =0.5134 0 -2.5134 3.0000 -0.4018 1.5402 -0.9732 1.0000 0.1754 -0.8706 0.3661 2.0000 -0.0741 0.7084 -0.1204 0 -0.0880 0.2639 1.8241 2.0000计算结果说明该三次样条的分段多项式形式为30.5134 2.51343,x x -+ 01x ≤≤ 320.4018(1) 1.5402(1)0.9732(1)1,x x x --+---+ 13x ≤≤()s x = 320.1754(3)0.8706(3)0.3661(3)2,x x x ---+-+ 36x ≤≤320.0741(6)0.7084(6)0.1204(6),x x x --+--- 68x ≤≤ 320.0880(8)0.2639(8) 1.8241(8)2,x x x --+-+-+ 89x ≤≤ （4）按照非结点方法得到的三次样条123456789-4-3-2-1012345三次样条（非结点方法)样条的一阶导函数样条的二阶导函数样条的三阶导函数图3 绘制图3的MATLAB 脚本如下x=[0,1,3,6,8,9];y=[3,1,2,0,2,4]; pp=csape(x,y,'not-a-knot'),pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4); d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3); d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2); d3s=@(t,tj,c)6.*c(1).*ones(size(t)); for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c); v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c); plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold on endlegend('三次样条（非结点方法)','样条的一阶导函数',... '样条的二阶导函数','样条的三阶导函数') plot(x,y,'ko'),hold off 命令窗口显示的结果为form: 'pp'breaks: [0 1 3 6 8 9] coefs: [5x4 double] pieces: 5 order: 4 dim: 1ans =-0.3240 2.1291 -3.8052 3.0000 -0.3240 1.1573 -0.5188 1.0000 0.1633 -0.7864 0.2229 2.0000 -0.0700 0.6833 -0.0866 0 -0.0700 0.2633 1.8066 2.0000 计算结果说明该三次样条的分段多项式形式为320.3240 2.1291 3.80523,x x -++-+ 01x ≤≤ 320.3240(1) 1.1573(1)0.5188(1)1,x x x --+---+ 13x ≤≤()s x = 320.1633(3)0.7864(3)0.2229(3)2,x x x ---+-+ 36x ≤≤320.0700(6)0.6833(6)0.0866(6),x x x --+--- 68x ≤≤ 320.0700(8)0.2633(8) 1.8066(8)2,x x x --+-+-+ 89x ≤≤（5）周期的三次样条123456789-10-551015三次样条（周期的)样条的一阶导函数样条的二阶导函数样条的三阶导函数图4 绘制图4的MATLAB 脚本如下x=[0,1,3,6,8,9];y=[3,1,2,0,2,4]; pp=csape(x,y,'periodic'),pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4); d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3); d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2); d3s=@(t,tj,c)6.*c(1).*ones(size(t)); for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c); v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c); plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold on endlegend('三次样条（周期的)','样条的一阶导函数',... '样条的二阶导函数','样条的三阶导函数') plot(x,y,'ko'),hold off 命令窗口显示的结果为 pp =form: 'pp'breaks: [0 1 3 6 8 9] coefs: [5x4 double] pieces: 5order: 4 dim: 1ans =1.9961 -3.7833 -0.2127 3.0000 -0.52962.2048 -1.7912 1.0000 0.1754 -0.9728 0.6728 2.0000 0.0537 0.6061 -0.4272 0 -1.5706 0.9285 2.6421 2.0000计算结果说明该三次样条的分段多项式形式为321.9961 3.78330.21273,x x x --+ 01x ≤≤ 320.5296(1) 2.2048(1) 1.7912(1)1,x x x --+---+ 13x ≤≤()s x = 320.1754(3)0.9728(3)0.6728(3)2,x x x ---+-+ 36x ≤≤320.0537(6)0.6061(6)0.4272(6),x x x -+--- 68x ≤≤ 321.5706(8)0.9285(8) 2.6421(8)2,x x x --+-+-+ 89x ≤≤ 2.解:问题分析：由题意，本题只需结合给出的10个结点坐标，分别利用多项式插值、分段线条插值、三次样条插值方法，借助Matlab 完成加工所需数据得到所求的图像，再利用复化梯形求积公式求得机翼断面的面积即可。
数学建模课后习题作业
【陈文滨】1、在稳定的椅子问题中，如设椅子的四脚连线呈长方形，结论如何？【模型假设】（1）椅子四条腿一样长，椅脚与地面接触处视为一点，四脚的连线呈长方形．（2）地面高度是连续变化的，沿任何方向都不会出现间断 (没有像台阶那样的情况)，即从数学的角度看，地面是连续曲面．这个假设相当于给出了椅子能放稳的必要条件．（3）椅子在任何位置至少有三只脚同时着地．为保证这一点，要求对于椅脚的间距和椅腿的长度而言，地面是相对平坦的．因为在地面上与椅脚间距和椅腿长度的尺寸大小相当的范围内，如果出现深沟或凸峰(即使是连续变化的)，此时三只脚是无法同时着地的。
【模型建立】在上述假设下，解决问题的关键在于选择合适的变量，把椅子四只脚同时着地表示出来．首先，引入合适的变量来表示椅子位置的挪动．生活经验告诉我们，要把椅子通过挪动放稳，通常有拖动或转动椅子两种办法，也就是数学上所说的平移与旋转变换．然而，平移椅子后问题的条件没有发生本质变化，所以用平移的办法是不能解决问题的．于是可尝试将椅子就地旋转，并试图在旋转过程中找到一种椅子能放稳的情形．注意到椅脚连线呈长方形，长方形是中心对称图形，绕它的对称中心旋转180度后，椅子仍在原地．把长方形绕它的对称中心O旋转，这可以表示椅子位置的改变。
于是，旋转角度θ这一变量就表示了椅子的位置．为此，在平面上建立直角坐标系来解决问题．如下图所示，设椅脚连线为长方形ABCD，以对角线AC所在的直线为x轴，对称中心O为原点，建立平面直角坐标系．椅子绕O点沿逆时针方向旋转角度θ后，长方形ABCD转至A1B1C1D1 的位置，这样就可以用旋转角θ（0≤θ≤π）表示出椅子绕点O旋转θ后的位置．其次，把椅脚是否着地用数学形式表示出来．我们知道，当椅脚与地面的竖直距离为零时，椅脚就着地了，而当这个距离大于零时，椅脚不着地．由于椅子在不同的位置是θ的函数，因此，椅脚与地面的竖直距离也是θ的函数．由于椅子有四只脚，因而椅脚与地面的竖直距离有四个，它们都是θ的函数．而由假设(3)可知，椅子在任何位置至少有三只脚同时着地，即这四个函数对于任意的θ，其函数值至少有三个同时为0．因此，只需引入两个距离函数即可．考虑到长方形ABCD是中心对称图形，绕其对称中心 O沿逆时针方向旋转180°后，长方形位置不变，但A,C和B,D对换了．因此，记A、B两脚与地面竖直距离之和为f（θ），C、D两脚与地面竖直距离之和为g（θ），其中θ∈[0，π]，从而将原问题数学化。
数学建模第五次作业题答案
答：1、模型假设：（1）银行具备实现任意投资上述五种证券的能力，且无意外情况的发生（如：银行倒闭，证券不存在等）。
（2）以上五种证券的相关属性不会发生改变，且银行的投资范围仅为以上列表中进行选择。
（3）银行投资的在上述五种证券中做出的各种方案都是可行的，即理想化模型。
（4）实施投资的相关方案在对应期限内有效并必须履行。
数学模型截图：程序代码截图：运行结果截图：敏感性分析报告截图：第1问建模结果评价：证券A投资2.182百万元，C投资7.364百万元,E投资0.454百万元；税后最大收益为0.298百万元。
2、数学模型：由第1问结果可知，在Dual Price给出的数据来看：资金每增加1百万元，收益增加0.0298百万元。
所以以大于2.75%的利率街道1百万元的资金的利息，所以应该借贷。
对于1的模型，修改资金总和10百万元增加为不超过11百万元，重新建模计算即可。
程序代码截图：运行结果截图：第2问建模结果评价：证券A投资2.40百万元,C投资8.10百万元,E投资0.50百万元；税后最大收益为0.328百万元，也就是说：经理应该贷款，可以提高收益。
第3问建模结果评价：由第1问的建模结果数据Dual Price可分析得：A证券的税前收益的范围为[3.0%,4.65%],而目标函数最优解不变即得，A增加为4.5%，投资不变；C证券的税前收益范围为[4.89%,8.46%],再由目标函数最优解不变可以推出，C减少为4.8%，投资应该改变的。
答：模型假设：（1）商家具备每次订购的商品都能够在商品保质期内售完的能力。
（2）供应商具备商家售完后新订购的商品能够及时补货的能力。
（3）新订购的商品应该在上一批次商品完全售完后才补进。
（4）不考虑意外情况（如商品质量不过关、商店倒闭等）的发生。
（5）由于存储费的设立，考虑第一批产品不收取存储费。
（6）假设x为每次购进新商品的件数，f(x)为每一批商品销售所获总利润，g(x)为平均每件商品所获的利润。
大学生数学建模例题之五
彩票发行方案的优化设计摘要本文通过对所给方案的分析，建立了彩票问题的优化模型，据此对现行各方案进行了比较和评判，并针对地区经济发展状况设计出了一种“更好”的方案。
论文首先介绍了风险决策中的效用理论，对彩民购买彩票的心态进行了分析，结合模糊数学中隶属度的概念，确定出了彩民的心理曲线，即效用函数。
它反映了彩票对彩民的吸引力，也体现了彩民对待风险的态度和地区的经济发展水平，可作为评价方案合理性的定量指标。
在客观概率尺度下，按照彩民的平均收入水平，对已知的29种方案分别做出判断，结果表明，排在前两位的分别是31选7和32选7。
其次，根据效用理论中存在着主观概率，即人们主观认可的事件发生概率与客观概率是不一致的，以及彩票信息在人群中的传播效应，建立了确定“更好”方案的三个优化模型。
其一，基于客观概率意义下的优化模型；其二，主观概率意义下的优化模型；第三，依据放射性元素的衰减原理，研究了彩票信息在人群中传播的影响效应，建立了信息衰减模型。
由于三个模型都是大规模非线性规划，难以直接求解，为此，我们设计了针对本问题的模拟退34选，但奖金设置不同火算法，运用Matalab软件求得了问题的全局最优解，最优方案均为6（见论文）。
最后，在分析所得结果的基础上，指出了三个模型的优缺点。
根据我们的研究成果，分别给彩票管理部门和彩民提出了一些参考建议。
1、问题的重述常见的彩票销售规则主要有“传统型”和“乐透型”两类，以“传统型”为例：先从6组0-9号球中摇出6个基本号码，每组摇出一个，然后从0-4号球中摇出一个特别号码，构成中奖号码。
投注者从0-9十个号码中任选6个基本号码（可重复），从0－4中选一个特别号码，构成一注，根据单注号码与中奖号码相符的个数多少及顺序确定中奖等级。
“乐透型”有多种不同的形式，奖金的设置也很灵活。
彩票的返奖比例一般为销售总额的50%，低项奖数额固定，高项奖按比例分配，但一等奖单注保底金额60万元，封顶金额500万元，各高项奖额的计算方法为：[(当期销售总额 ×总奖金比例) -低项奖总额 ]×单项奖比例现在的问题是：1、评价题目给出的现有方案的合理性；2、设计一种更好的方案，据此给彩票发行部门提出建议；3、给报纸写一篇短文，供彩民参考。
汽选购问题数学建模-5
假定3种型号的汽车（相当于3个方案）供选购，记做S1、S2、S3，3个属性（评价指标）为价格、性能和款式，依次记为x1、x2、x3，具体数据如下表。
性能、款式，满分为10分，打分表格中数据表示每个方案Si对属性xj的取值，也称属性值（指标观测值）。
表一的数据我们可以用（原始）决策矩阵表示为指标观测值--> 决策矩阵决策矩阵的获得一般有两种途径，一种是直接通过测量或调查得到，如表1中的价格，这是偏于客观（定量）的方法；另一种是由决策者或请专家评定，这偏主观（定性）的方法。
8.2.2 决策矩阵的规范化决策矩阵的每一列表示各方案对某一属性的属性值，由于通常各属性的物理意义各不相同，在下一步分析之前，需将决策矩阵规范化。
进行规范化时首先需要区分效益型属性（极大型指标）和费用型属性（极小型指标），前者指属性值越大，该属性对决策的重要程度越高，后者正相反。
汽车选购中的属性x2 ,x3 是效益型的，而x1是费用型的，三个属性中两个是效益型的，故将全部属性值统一为效益型的。
汽车选购中的属性x2 ,x3 是效益型的，而x1是费用型的，三个属性中两个是效益型的，故将全部属性值统一为效益型的。
用取倒数的方法可将汽车选购中的决策矩阵重新表示为：一致化处理无量纲化处理方法：模一化：列向量单位化按“列”进行处理，保证每一列的处理方法统一。
汽车选购的决策矩阵X经过(1)(2)(3)式标准化后分别通过计算与观察，经过规范化后的决策矩阵，每个数值都是介于0、1之间，消除了各个指标量纲的影响。
经过此处理，决策矩阵的各个属性值就处于同一数量级，适合进行成对比较。
8.2.3 属性权重的确定信息熵法各个指标对于决策目标的影响程度称为属性权重（权重系数），用来表示评价指标(j=1, 2, …, m)的权重系数，则应有。
属性权重的确定也有偏于主观和客观两种方法，偏于主观的方法可以由决策者根据决策目的和经验先验地给出，如层次分析法中利用比较矩阵的最大特征值对应的特征向量来作为权重，这里不再赘述。
数学建模答案 (5)
一、解释下列词语，并举例说明(每小题满分5分，共15分)1．模型模型是系统知识的抽象表示。
我们不能仅仅通过语言来描述一个系统，也不能仅仅通过记忆来记录关于系统的知识。
知识是通过某种媒介来表达的，这种媒介所表达的内容就是模型。
而知识形成媒介的过程就是建模，或者称为模型化。
通常模型可以使用多种不同的媒介来表达，比如纸质或电子文档、缩微模型/原型、音像制品等等。
而表达模型的体现方式也是多种多样的，常见的有图表、公式、原型、文字描述等等。
2．数学模型由数字、字母、或其他数学符号组成的，描述现实对象（原型）数量规律的数学结构。
具体地说，数学模型也可以描述为：对于现实世界的一个特定对象，为了一个特定的目的，根据特有的内在规律，做出一些简化假设后，运用适当的数学工具，得到的一个数学结构称之为数学模型.如概率的功利化定义。
3．抽象模型通过人们对原型的反复认识，将获取的知识以经验的形式直接存储在大脑中的模型称之谓思维模型。
从实际的人、物、事和概念中抽取所关心的共同特性，忽略非本质的细节把这些特性用各种概念精确地加以描述。
二、简答题（每小题满分8分，共24分）1．模型的分类按照模型替代原型的方式，模型可以简单分为形象模型和抽象模型两类.形象模型：直观模型、物理模型、分子结构模型等;抽象模型：思维模型、符号模型、数学模型等。
2．数学建模的基本步骤1）建模准备：确立建模课题的过程；2）建模假设：根据建模的目的对原型进行抽象、简化。
有目的性原则、简明性原则、真实性原则和全面性原则；3）构造模型：在建模假设的基础上，进一步分析建模假设的各条款，选择恰当的数学工具和构造模型的方法对其进行表征，构造出根据已知条件和数据，分析模型的特征和模型的结构特点，设计或选择求解模型的数学刻划实际问题的数学模型.；4）模型求解：构造数学模型之后，方法和算法，并借助计算机完成对模型的求解；5）模型分析：根据建模的目的要求，对模型求解的数字结果，或进行稳定性分析，或进行系统参数的灵敏度分析，或进行误差分析等。
数学建模(合)大作业
学生实验报告实验时间：2017 学年第 2 学期专业班级：信息与计算科学1502班____ （学号）：庞云杰（20155653）_______2017年 03月21日实验名称实验一：用MATLAB求解线性规划问题实验地点信息楼121 实验日期2017.03.21学时2一、实验目的1．了解线性规划的基本容2.熟悉MATLAB软件求解线性规划问题的基本命令3.学习灵敏分析问题的思维方法二、实验容三、实验作业P226,1和3任选一1．问题分析：确定种植最佳土地分配，即每种等级耕地分别种植水稻、大豆、玉米的面积2．模型建立：1)令分别为I II III三等耕地上种植的水稻面积，令分别为III III三等耕地上种植的大豆面积，令分别为I II III三等耕地上种植的玉米面积且令为xi（1<=i<=9）面积的耕地上的产量为ci.2)目标函数：总产量最大，即max=3)约束条件非负条件：最低产量限制：耕地面积恒定：综上数学模型为：在MATLAB中调试>>clc>>c=[11 9.5 9 8 6.8 6 14 12 10];A=[-11 -9.5 -9 0 0 0 0 0 00 0 0 -8 -6.8 -6 0 0 00 0 0 0 0 0 -14 -12 -10];b=[-190;-130;-350];F=[1 0 0 1 0 0 1 0 00 1 0 0 1 0 0 1 00 0 1 0 0 1 0 0 1];>>FF=[100;300;200];>>G=[0;0;0;0;0;0;0;0;0];>>GG=[];>> [x,fval]=linprog(c,A,b,F,FF,G,GG) Optimization terminated.x =17.27270.000082.7273300.0000165.00000.00000.000035.0000fval =4.2318e+003即：值分别17.27270.00.082.7273300.0165.00.00..0，此时才能使总产量最大。
数学建模习题-第五章
习 题1、对于节传染病的SIR 模型证明；①若σ/10>s ，则)(t i 先增加，在σ/1=s 处达到最大 ，然后减少并趋于零；)(t s 单调减少至∞s 。
②若σ/10<s ，则)(t i 单调减少并趋于零，)(t s 单调减少至∞s 。
2、对于传染病的SIR 模型证明(20)~(22)式。
3、在节经济增长模型中，为了适用于不同的对象可将产量函数)(t Q 折算成现金，仍用)(t Q 表示。
考虑到物价上升因素我们记物价上升指数为)(t p (设1)0(=p )。
则产品的表面价值)(t y 、实际价值)(t Q 和物价指数)(t p 之间满足)(t y =)()(t P t Q 。
①导出)(t y 、)(t Q 、)(t p 的相对增长率之间的关系，并作解释。
②设雇佣工人数目为)(t L ，每个工人工资为)(t W ，企业的利润简化为从产品的收入)(t y 中扣除工人的工资和固定的成本。
利用节的（5）式讨论，企业应雇佣多少工人能使利润最大。
4、在节的房室模型中证明方程（3）对应的齐次方程通解如（4）、（5）式所示，说明方程的两个特征根α和β一定是负实根。
5、模仿节建立的二室模型建立一室模型（只有中心室），在快速静脉注射、恒速静脉滴注（持续时间为τ）和口服或肌肉注射3种给药方式下求解血药浓度，并画出浓度曲线图。
6、利用上题建立的一室模型，讨论按固定时间间隔T 每次给予固定剂量D 的多次重复给药方式。
为了维持药品的疗效和保证机体的安全，要求血药浓度C 控制在（21,C C ）范围内。
设中心室容积V 为已知。
① 在快速静脉注射的多次重复给药方式下，写出血药浓度表达式并作图，讨论怎样确定T 和D 使血药浓度的变化满足上述要求。
② 在恒速静脉滴注和口服（或肌肉注射）的多次重复给药方式下，给出血药浓度变化的简图，并在这两种方式选择一种来讨论确定T 和D 的问题。
7、在节香烟过滤嘴模型中，① 设800=M 毫克，801=l 毫米，202=l 毫米，02.0=b （1/秒），08.0=β（1/秒），50=v 毫米/秒，3.0=a ，求Q 和21/Q Q 。
数学建模案例分析5.建模案例：最佳灾情巡视路线
建模案例：最佳灾情巡视路线这里介绍1998年全国大学生数学模型竞赛B题中的两个问题.一、问题今年夏天某县遭受水灾.为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视.巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线.1．若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的路线.2．假定巡视人员在各乡（镇）停留时间T=2h，在各村停留时间t=1h，汽车行驶速度V=35km/h.要在24h内完成巡视，至少应分几组；给出这种分组下最佳的巡视路线.乡镇、村的公路网示意图见图1.图1二、假设1．汽车在路上的速度总是一定，不会出现抛锚等现象；2．巡视当中，在每个乡镇、村的停留时间一定，不会出现特殊情况而延误时间；3．每个小组的汽车行驶速度完全一样；4．分组后，各小组只能走自己区内的路，不能走其他小组的路（除公共路外）.三、模型的建立与求解将公路网图中，每个乡（镇）或村看作图中的一个节点，各乡（镇）、村之间的公路看作图中对应节点间的边，各条公路的长度（或行驶时间）看作对应边上的权，所给公路网就转化为加权网络图，问题就转化为在给定的加权网络图中寻找从给定点O 出发，行遍所有顶点至少一次再回到O 点，使得总权（路程或时间）最小，此即最佳推销员回路问题.在加权图G 中求最佳推销员回路问题是NP —完全问题，我们采用一种近似算法求出该问题的一个近似最优解，来代替最优解，算法如下：算法一 求加权图G （V ，E ）的最佳推销员回路的近似算法：1． 用图论软件包求出G 中任意两个顶点间的最短路，构造出完备图),(E V G ''，()E y x '∈∀,， ()(),,G x y mind x y ω=；2． 输入图G '的一个初始H 圈；3． 用对角线完全算法产生一个初始H 圈；4． 随机搜索出G '中若干个H 圈，例如2000个；5． 对第2、3、4步所得的每个H 圈，用二边逐次修正法进行优化，得到近似最佳H 圈；6． 在第5步求出的所有H 圈中，找出权最小的一个，此即要找的最佳H圈的近似解.由于二边逐次修正法的结果与初始圈有关，故本算法第2、3、4步分别用三种方法产生初始圈，以保证能得到较优的计算结果.问题一 若分为3组巡视，设计总路程最短且各组尽可能均衡的巡视路线.此问题是多个推销员的最佳推销员回路问题.即在加权图G 中求顶点集V 的划分12,,,n V V V ，将G 分成n 个生成子图[][][]12,,...,n G V G V G V ，使得（1）顶点i V O ∈, i =1，2，3,…,n ；（2）()G V V n i i== 1 ；（3）()()(),m ax m ax i j i ji i C C C ωωαω-≤，其中i C 为i V 的导出子图[]i V G 中的最佳推销员回路，()i C ω为i C 的权，i ，j =1，2，3,…,n ；（4）()1ni i C ω=∑取最小.定义 称()()(),0m ax m ax i j i ji i C C C ωωαω-=为该分组的实际均衡度.α为最大容许均衡度.显然100≤≤α，0α越小，说明分组的均衡性越好.取定一个α后，0α与α满足条件（3）的分组是一个均衡分组.条件（4）表示总巡视路线最短.此问题包含两方面：第一，对顶点分组；第二，在每组中求最佳推销员回路，即为单个推销员的最佳推销员问题.由于单个推销员的最佳推销员回路问题不存在多项式时间内的精确算法，故多个推销员的问题也不存在多项式时间内的精确算法.而图中节点数较多，为53个，我们只能去寻求一种较合理的划分准则，对图１进行粗步划分后，求出各部分近似最佳推销员回路的权，再进一步调整，使得各部分满足均衡性条件（3）.图2 O点到任意点的最短路图（单位：km）从O点出发去其他点，要使路程较小应尽量走O点到该点的最短路.故用图论软件包求出O点到其余顶点的最短路，这些最短路构成一棵以O为树根的树，将从O点出发的树枝称为干枝，见图2，从图中可以看出，从O点出发到其它点共有6条干枝，他们的名称分别为①，②，③，④，⑤，⑥.根据实际工作的经验及上述分析，在分组时应遵从以下准则：准则一：尽量使同一干枝及其分枝上的点分在同一组；准则二：应将相邻的干枝上的点分在同一组；准则三：尽量将长的干枝与短的干枝分在同一组.由上述分组准则，我们找到两种分组形式如下：分组一：（⑥，①），（②，③），（⑤，④）；分组二：（①，②），（③，④），（⑤，⑥）．显然分组一的方法极不均衡，故考虑分组二.对分组二中每组顶点的生成子图，用算法一求出近似最优解及相应的巡视路线.使用算法一时，在每个子图所构造的完备图中，取一个尽量包含图2中树上的边的H圈作为其第2步输入的初始圈.分组二的近似解见表1.因为该分组的均衡度0α=()()()121,2,3241.9125.5m ax 241.9i i C C C ωωω=--==54.2%所以此分法的均衡性很差.为改善均衡性，将第Ⅱ组中的顶点C ，2，3，D ，4分给第Ⅲ组（顶点2为这两组的公共点），重新分组后的近似最优解见表2.因该分组的均衡度=0α()311,2,3216.4191.1m ax 216.4i i C C C ωωω=--==11.69%所以这种分法的均衡性较好.问题二 当巡视人员在各乡（镇）、村的停留时间一定，汽车的行驶速度一定，要在24h 内完成巡视，至少要分几组及最佳的巡视路线.由于T =2h ，t =1h ，V =35km/h ，需访问的乡镇共有17个，村共有35个.计算出在乡（镇）及村的总停留时间为17⨯2h+35h=69h ，要在24h 内完成巡回，若不考虑行走时间，有: 2469<i (i 为分的组数).得i 最小为4，故至少要分4组.由于该网络的乡（镇）、村分布较为均匀，故有可能找出停留时间尽量均衡的分组，当分4组时各组停留时间大约为69h 17.254=h ，则每组分配在路途上的时间大约为24h-17.25h=6.75h.而前面讨论过，分三组时有个总路程599.8km 的巡视路线，分4组时的总路程不会比599.8km 大太多，不妨以599.8km 来计算.路上时间约为599.8h 1735=h ，若平均分配给4个组，每个组约需417h=4.25h〈6.75h ，故分成4组是可能办到的.现在尝试将顶点分为4组.分组的原则：除遵从前面准则一、二、三外，还应遵从以下准则：准则四：尽量使各组的停留时间相等.用上述原则在图2上将图分为4组，同时计算各组的停留时间,然后用算法一算出各组的近似最佳推销员巡回，得出路线长度及行走时间，从而得出完成巡视的近似最佳时间.用算法一计算时，初始圈的输入与分3组时同样处理.这4组的近似最优解见表3.加框的表示此点只经过不停留.该分组实际均衡度0α==-74.2269.2174.22 4.62%可以看出，表3分组的均衡度很好，且完全满足24h 完成巡视的要求.。
数学建模作业(举例)05
作业：P 201.举出一个实例说明建立数学模型的必要性，包括实际问题的背景，建模目的，需要大体上什么样的模型以及怎样应用这种模型CUMC M2002A题车灯线光源的优化设计安装在汽车头部的车灯的形状为一旋转抛物面，车灯的对称轴水平地指向正前方，其开口半径36毫米，深度21．6毫米。
经过车灯的焦点，在与对称轴相垂直的水平方向，对称地放置一定长度的均匀分布的线光源。
要求在某一设计规范标准下确定线光源的长度。
该设计规范在简化后可描述如下。
在焦点F正前方25米处的A点放置一测试屏，屏与FA垂直，用以测试车灯的反射光。
在屏上过A点引出一条与地面相平行的直线，在该直线A点的同侧取B点和C点，使AC二2AB：2．6米。
要求C点的光强度不小于某一额定值(可取为1个单位)，B点的光强度不小于该额定值的两倍(只须考虑一次反射)。
请解决下列问题(1)在满足该设计规范的条件下，计算线光源长度，使线光源的功率最小。
(2)对得到的线光源长度，在有标尺的坐标系中画出测试屏上反射光的亮区(3)讨论该设计规范的合理性。
车灯线光源的优化设计王伟叶，姜文华，吴家麒指导老师：曹沅(复旦大学数学系，上海200433)编者按：本文的一个有点是能从入射角等于反射角，入射向量，入射点处抛物面的法向量和反射向量共面以及抛物面方程三组方程出发应用数学软件详细算出光源上一点射向抛物面时，可能有几个反射点(反射光线)可以反射到C点(类似的B点)，尽管没有指出有可能会有三个反射点。
本文的另一个优点是能对本文所作的近似假设的合理性作比较仔细的分析。
本文在计算亮区时能用两种方法计算并作了比较。
摘要：本文首先将车前灯线光源的优化设计问题通过合理的假设、近似和数学推理归结为一个求函数最值的模型，进而通过Matlab的符号计算和绘图功能求解。
得到了切合实际的解答，其次对该长度的光源在测试屏上产生的反射光亮斑用两种不同的方法进行了绘制，最后对题中所提及的设计规范进行了分析，阐述了其合理性。
《数学建模》习题及参考答案 第五章 微分方程模型
第五章部分习题1. 对于5.1节传染病的SIR 模型，证明：（1）若σ/10>s ，则()t i 先增加，在σ/1=s 处最大，然后减少并趋于零；()t s 单调减少至∞s 。
（2）若σ/10>s ，则()t i 单调减少并趋于零，()t s 单调减少至∞s 。
9. 在5.6节人口的预测和控制模型中，总和生育率()t β和生育模式()t r h ,是两种控制人口增长的手段，试说明我国目前的人口政策，如提倡一对夫妇只生一个孩子、晚婚晚育，及生育第2胎的一些规定，可以怎样通过这两种手段加以实施。
*16. 建立铅球掷远模型，不考虑阻力，设铅球初速度为v ，出手高度为h 出手角度为∂（与地面夹角），建立投掷距离与∂,,h v 的关系式，并在h v ,一定的条件下求最佳出手角度。
参考答案1. SIR 模型（14）式可写作().,1si dt di s i dt di λσμ-=-=由后一方程知()t s dtds ,0<单调减少。
1) 若σ10>s ，当01s s <<σ时，()t i dt di ,0>增加；当σ1=s 时，()t i dt di ,0=达到最大值m i ；当σ1<s 时，()t i dt di ,0<减少且()()式180=∞i 2) 若σ10<s ，()t i dt di ,0<单调减少至零 9. 一对夫妻只生一个孩子，即总和生育率()1=t β；晚婚晚育相当于生育模式()r h 中（5。
6节（13）式）使1r 和c r 增大；生育第2胎一些规定可相当于()t β略高于1，且()r h 曲线（5。
6节图19）扁平一些（规定生2胎要间隔多少年）*16. 在图中坐标下铅球运动方程为()()()().sin 0,cos 0,0,00,,0ααv y v x h y x g yx ====-== 解出()t x ，()t y 后，可以求得铅球掷远为,cos 2sin cos sin 2/12222ααααv g h g v g v R ⎪⎪⎭⎫ ⎝⎛++=这个关系还可表为()ααtan cos 2222R h v g R +=由此计算0*=ααd dR，得最佳出手角度()gh v v +=-21*2sin α，和最佳成绩gh v g v R 22*+=设m h 5.1=，s m v /10=，则0*4.41≈α，m R 4.11*=。
数学建模作业5数学规划模型----供应与选址的问题
三、模型假设
1、假设料场和建筑工地之间都可以由直线到达；
2、运输费用由“吨千米数”来衡量；
3、两料场的日存储量够向各建筑工地供应；
f1=0;
fori=1:6
s(i)=sqrt((x(13)-a(i))^2+(x(14)-b(i))^2);
f1=s(i)*x(i)+f1;
end
f2=0;
fori=7:12
s(i)=sqrt((x(15)-a(i-6))^2+(x(16)-b(i-6))^2);
f2=s(i)*x(i)+f2;
end
一、问题提出
某公司有6个建筑工地要开工，每个工地的位置（用平面坐标系(a，b)表示，距离单位：km）及水泥日用量d（吨）由下表给出。目前有两个料场位于A(5,1)，B(2,7)，日储量各有20吨。
（1）试制定每天的供应计划，即从A，B两料场分别向各工地运送多少水泥，可使运输费用（总的吨千米数）最小，并求出吨千米数。
d=[3 5 4 7 6 11];
x=[5 2];
y=[1 7];
e=[20 20];
fori=1:6
forj=1:2
aa(i,j)=sqrt((x(j)-a(i))^2+(y(j)-b(i))^2);
end
end
CC=[aa(:,1); aa(:,2)]'
A=[1 1 1 1 1 1 0 0 0 0 0 0
(注：先画图，在坐标上标出各工地位置（用蓝色*标示）和料场位置（用红色o标示）)
数学建模的五次作业
图1中是大学校园一角。
图中标示出道路和两点之间的大致距离（单位：百英尺）。
你的同舍同学说服（convince）你在周末时候在某个道路交叉点（intersections）摆个热狗摊。
你希望小摊尽可能方便同学们。
哪里是最合适的地点呢？表1：校园一角从问题开始问题叙述:假如宿舍位于A，C，D，E和F点，A舍楼有200生，C和D各有300生，E 和F楼各有100生。
(1)如果我们知道A和C是女生楼，D，E和F是男生楼，并且只有30%的女生喜欢在你的小摊上吃热狗，而有80%的男生喜欢吃，那么你的选点会有怎样的改变？(2) 如果B和C点以及E和D点之间的路是上坡路，而上坡路比下坡路难走一倍。
你会怎样选点？问题分析:问题(1)分析由于学生主要从宿舍到小摊，所以一个方法是算出从每个舍楼到每个可能的小摊地点的距离。
如表1的数据。
列表示所有可能的小摊位置，行表示从宿舍楼到各摊点位置的距离。
同时，在表格中包括了，从舍楼到小摊位置的最大距离和从小摊到舍楼的平均距离。
表1基于表中数据，如果将热狗摊安在B点，那么没有哪个学生从舍楼到摊点需要走超过500英尺的距离，放在A点则有学生要走800英尺。
如果以最小化最远距离就应该选择B点。
而此时从各舍楼到摊点的平均距离是420英尺。
如果放在E点，则平均距离只有400英尺。
所以如果以最小化平均距离为目标应该设在E点。
接着把宿舍楼所住学生人数乘以所到所设摊点的位置,即算出所有人所到摊位的路程之和.即可得出下表.表2基于表中数据，然后再将男女各自喜欢吃热狗的比率乘以所有人所到摊位的总路程.表3我们就选最大值最小,平均值也相对小的E点.问题(2)分析:如果B和C点以及E和D点之间的路是上坡路，而上坡路比下坡路难走一倍。
设平破路的的困难系数为1,上坡路的为2,下坡路的困难系数为0.5.则B到C和E 到D为上坡,再在每段路的路程乘以各自的困难系数.基于表3中数据的出下表.表4同样,我们就选最大值最小,平均值也相对小的E点。
数学建模习题5
数学建模（I ）习题习 题 51． 某工厂生产两种产品，A 产品每件可获利0.3元，B 产品每件可获利0.15元。
如该厂只选择一种产品生产，每天最多可生产A 产品800个或B 产品1200个，但A 产品还需要某种特殊处理，每天最多处理600个，此外，工厂每天最多可包装A 、B 产品共1000个。
问该厂应该如何安排生产计划，才能获利最大？2． （饮食问题）一位家庭主妇正在菜场里买菜，该菜场共有n 种食品可卖，单价分别为j C ，1=j ，…,n ；为了保证家里人的身体健康，购买的食品中必须包含m 种营养成份，且第i 种营养成份的含量不能少于m i b i ,......,2,1,=；该妇女了解各种食品的营养含量，即她知道每单位重量的第j 种食品中含有第i 种营养成份ij c （n j m i ,......,1;,......,1==）。
假定该妇女近期经济较为紧张，她希望在满足营养要求的前提下能做到花钱最少，试建立本问题的数学模型。
3． .求解运输问题：4． 在本章森林救火模型中，如果考虑消防队员的灭火速度与开始救火时的火势b 有关，试假设一个合理的函数关系，重新求解模型。
5． 要在雨中从一处沿直线跑到另一处，假设雨速为`常数且方向不变，试建立数学模型讨论是否跑得越快，雨淋得越少。
6． 报童每天要向报社定购报纸，已知每卖出一份报纸可赢利a 分，多出来未买完，每份将亏本b 分。
每天买报人数不确定，报童定购报纸如果超出实际需要，就要受到供过于求的损失；反之，要受到供不应求的损失。
设)(m p 是售出m 份报纸的概率（可采用统计方法求其近似值），试为报童确定一个合理的订报份数，使其期望损失最小。
7． 建立一个煤矿开采模型。
假设开采对周围环境无破坏，t 时刻已经开采煤矿的数量为)(t y ，生产率为)(t g ，开采单位数量的煤矿可获利)()(2t cg t by a P --=，其中c b a ,,为正常数，若煤矿资源有限，且不考虑折扣因素，试确定煤矿的最佳产量)(t y ，使开采获利最大。
数学建模实习作业
碎纸片的拼接复原摘要图像碎片自动拼接复原是需要借助计算机把大量碎片重新拼接复原成初始图像的完整模型，这一研究在考古、刑侦犯罪、古生物学、医学图像分析、遥感图像处理以及壁画保存复原等方面具有广泛、实际的应用。
本文主要解决碎纸机破碎文档的自动拼接复原问题。
我们利用图像数字化技术，借助Matlab软件将图像转化为矩阵。
通过建立数学模型，运用矩阵论、自定义相似度方法、遗传算法等方法，对数据进行处理，实现对图像碎片自动拼接，从而将所给碎片拼接复原为完整图像。
我们首先把碎片图形进行二值化处理，根据所给纵切黑白碎片边缘的像素关系(相邻两张碎片，一张碎片矩阵右边的像素与另一张碎片左边的像素相同 )，我们采和自定义相似度算法，利用附件求出碎片间的相似度，然后根据所需要满足的条件即相似度最大原则，建立了纵切碎片拼接模型一及其算法，运用Matlab编程实现该模型，并得到碎片复原结果（见附录1）。
关键词：碎片拼接矩阵论图形二值化相似度模型一、问题重述1.1背景：破碎文件的拼接和复原对于司法物证复原、历史文献再现和军事情报获取等方面都有极其重要的作用。
于是碎纸片的拼接复原技术便成为图像处理与模式识别领域中的一个崭新典型的应用。
图像配准是图像拼接复原的基础，而且图像配准算法的计算量一般非常大，因此图像拼接复原技术的发展很大程度上取决于图像配准技术的创新。
本文将通过图像提取技术获取一组碎纸片的形状、颜色、文字等信息，然后利用计算机进行相应的处理从而实现对这些碎纸片的自动拼接复原。
1.2重述：该题研究的是如何对碎纸片进行拼接复原。
传统上，拼接复原工作需由人工完成，准确率较高，但是效率低。
随着计算机技术的发展，当碎纸片数量巨大的时候，人们试图开发碎纸片的自动拼接技术，以提高拼接复原的效率。
对于给定的来自同一页印刷文字文件的碎纸机破碎纸片（仅纵切），建立碎纸片拼接复原模型和算法，并针对附件给出的中文文件的碎片数据进行拼接复原。
如果复原过程需要人工干预，写出干预方式及干预的时间节点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
改建两个新料场，要同时确定料场的位置(xj,yj)和运送量 Xij，在同样条件下使总吨千米数
最小．这是非线性规划问题．非线性规划模型为：
26
min f
X ij (x j ai )2 ( y j bi )2
j1 i1
2
s.t. Xij di , i 1, 2,, 6 j 1
五、模型求解
（显示模型的求解方法、步骤及运算程序、结果）
(1)先画图，在坐标上标出各工地位置（用蓝色*标示）和料场位置（用红色 o 标示）
程序代码： x=[1.25 8.75 0.5 5.75 3 7.25]; y=[1.25 0.75 4.75 5 6.5 7.25]; x0=[5,2]; y0=[1,7]; plot(x,y,'*b'); hold on; plot(x0,y0,'or'); text(1.25,1.25,'¹¤µØ1'); text(8.75,0.75,'¹¤µØ2'); text(0.5,4.75,'¹¤µØ3'); text(5.75,5,'¹¤µØ4'); text(3.6,5,'¹¤µØ5'); text(7.25,7.25,'¹¤µØ6'); text(5,1,'Áϳ¡A'); text(2,7,'Áϳ¡B');
四、模型建立
（显示模型函数的构造过程）
记工地的位置为(ai，bi)，水泥日用量为 di，i=1,…,6;料场位置为(xj，yj)，日储量为 ej，j=1,2； 料场 j 向工地 i 的运送量为 Xij．
26
目标函数为： min f
X ij (x j ai )2 ( y j bi )2
j1 i1
26
min f aa(i, j) X ij j1 i1 2
s.t. X ij di , i 1,2,,6 j 1 6 X ij e j , j 1,2 i 1
其中 aa(i, j) (x j ai )2 ( y j bi )2 ，i=1,2,…,6,j=1,2,为常数.
设 X11=X1, X21= X 2,, X31= X 3, X41= X 4, X51= X 5,, X61= X 6 X12= X 7, X22= X 8,, X32= X 9, X42= X 10, X52= X 11,, X62= X 12
（2）目前公司准备建立两个新的料场，日储量各为 20 吨，为使运输费用最省，问新的料场 应建在何处，并算出两料场分别向工地运输多少吨水泥和费用。
（注：初始值取 x0=[3 5 4 7 1 0 0 0 0 0 5 11 5 4 7 7]’）
二、问题分析
本问题主要讨论并解决了某公司每天给工地的供应计划与临时料场选址的相关问题。工地的水 泥全部由水泥料场来提供，各个工地的水泥日用量与每个水泥料场的日储量是一定的。各个工 地所需水泥量可以有两个料场同时提供，也可以由一个料场全部提供。这就需要我们最优规划 来解决。为使总吨千米数达到最小，在考虑有直线道路连通的情况下建立相应的数学模型，给 出相关算法，并运用 Matlab 软件编程和处理相关数据，得到最优决策方案。 符号说明：
(2)使用两个临时料场的情形：
程序代码：
clear a=[1.25 8.75 0.5 5.75 3 7.25]; b=[1.25 0.75 4.75 5 6.5 7.75]; d=[3 5 4 7 6 11]; x=[5 2]; y=[1 7]; e=[20 20]; for i=1:6
for j=1:2 aa(i,j)=sqrt((x(j)-a(i))^2+(y(j)-b(i))^2);
i ：第 i 个建筑工地； j ：第 j 个临时料场；
di ：工地 i 的水泥日用量；
c ：料场 j 到工地 i 的水泥运输量； ij
aa(i, j) ：料场 j 到工地 i 的距离；
e ：料场 j 的日储量； j
三、模型假设
（1）假设料场和建筑工地之间都可以由直线到达； （2）运输费用由“吨千米数”来衡量； （3）两料场的日存储量够向各建筑工地供应； （4）运输途中不发生意外，从料场运出的水泥总量不会超过各个料场的日存储量；
2
X ij di ,
约束条件为： j1 6 X ij e j , i 1
i 1,2,,6 j 1,2
当用临时料场时决策变量为：Xij， 当不用临时料场时决策变量为：Xij，xj，yj．
使用两个临时料场的情形：
使用两个临时料场 A(5,1)，B(2,7)．求从料场 j 向工地 i 的运送量 Xij . 在各工地用量必须满足和 各料场运送量不超过日储量的条件下，使总的吨千米数最小，这是线性规划问题． 线性规划 模型为：
1
2
3
4
5
6
a
1.25
8.75
0.5
5.75
3
7.25
b
1.25
0.75
4.75
5
6.5
7.75
d
3
5
4
7
6
11
（1）试制定每天的供应计划，即从 A，B 两料场分别向各工地运送多少水泥，可使运输费用（总 的吨千米数）最小，并求出吨千米数。 ( 注：先画图，在坐标上标出各工地位置（用蓝色*标示）和料场位置（用红色 o 标示）)
课程名称 上机项目 专业班级
佛山科学技术学院
上机报告
数学建模 料场问题
一、 问题提出
某公司有 6 个建筑工地要开工，每个工地的位置（用平面坐标系(a，b)表示，距离单位： km）及水泥日用量 d（吨）由下表给出。目前有两个料场位于 A(5,1)，B(2,7)，日储量各有 20 吨。
工地位置（a，b）及水泥日用量 d
end end CC=[aa(:,1);aa(:,2)]'; A=[1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1]; B=[20;20]; Aeq=[1 0 0 0 0 0 1 0 0 0 0 0
6
Xij ej , j 1, 2
i 1
设 X11=X1, X21= X 2, X31= X 3, X41= X 4, X51= X 5,, X61= X 6
X12= X 7, X22= X 8, X32= X 9, X42= X 10, X52= X 11, X62= X 12
x1=X13, y1=X14, x2=X15, y2=X16