相似多边形的性质同步练习(含答案)
九年级数学相似多边形的性质同步练习

24.4相似多边形的性质同步练习第1题. 如果一个矩形和它的一半矩形相似,那么大矩形与小矩形的相似比是( )A .2:1B .2:2C .2:1D .1:2 答案:A第2题. 如图中,有三个矩形,其中相似的是( )A .甲和乙B .甲和丙C .乙和丙D .没有相似的矩形 答案:B第3题. 下列各组图形中,肯定是相似形的是( ) A .两个腰长不相等的等腰三角形 B .两个半径不等的圆C .两个面积不相等的平行四边形D .两个面积不相等的菱形 答案:B第4题. 在四边形ABCD 与D C B A ''''中,∠A =∠A ',∠B =∠B ',∠C =∠C ',∠D =∠D ',且A D DA D C CD C B BC B A AB ''=''=''=''=32,则四边形 ∽四边形 ,且四边形ABCD 与D C B A ''''的相似比是 , 四边形ABCD 与D C B A ''''的面积比是 . 答案:ABCD ,D C B A '''',23,49第5题. 已知两个多边形相似,它们的面积的比为2516,若其中一个周长为28,则另一个多边形的周长为 . 答案:35或22.4第6题. 顶角都是20°的两个等腰三角形是否相似?各有一个20°角的两个直角三角形是否相似? 答案:相似,相似第7题. 图中的两个多边形相似吗?说说你判断的理由. 答案:不相似,∠D =360°-135°-95°-72°=58°,而∠E =360°-135°-95°-59°=71°,不可能有"对应角相等".A 72°135°95°CBD 72°135° 59° GFH E第8题. 已知下图中的两个四边形相似,找出图中的成比例线段,并用比例式表示.答案:AB BC CD DAEF FG GH HE ===第9题. 用一个放大镜看一个四边形ABCD ,该四边形的边长放大10倍后,下列结论正确的是( )A .∠A 是原来的10倍B .周长是原来的10倍C .面积是原来的10倍D .四边形的形状发生了改变 答案:B第10题. 两个多边形相似,面积的比是1∶4,一个多边形的周长为16,则另一个多边形的周长为 . 答案:8或3280° 75°DCBA80°75°HGFE第11题. 两个多边形相似,相似比是3:5,则其周长之比是 ,面积之比是 . 答案:3∶5,9∶25第12题. 请将下图中的相似图形的序号写出来 .答案:(1)和(3);(2)和(5);(4)和(7);(8)和(9);(6)和(10)第13题. 等腰三角形ABC 的腰长是等腰三角形DEF 的腰长的2倍,讨论这两个三角形什么时候相似.答案:顶角相等或有一个底角相等时都相似,△ABC 的底边是△DEF 底边的2倍时也相似.(1)(3)(2)(6)(10)(9)(8)(5)(4)(7)。
浙教版九年级数学同步训练(39)第四章相似三角形相似多边形(word版附答案)

浙教版九年级数学同步训练(39)第四章相似三角形相似多边形(word版附答案)4.6 相似多边形1.以下多边形中,一定相似的是〔 D 〕A.两个平行四边形B.两个菱形C.两个矩形D.两个正方形2.两个相似多边形的一组对应边区分是3cm 和 4.5cm ,假设它们的面积之和是78cm2,那么较大的多边形的面积是〔 D 〕A.44.8cm2B.42cm2C.52cm2D.54cm23.如下图的三个矩形中,相似的是〔 B 〕A.甲与乙B.乙与丙C.甲与丙D.甲、乙、丙都相似4.如下图的两个四边形相似,那么∠α等于〔 A 〕A.87°B.60°C.75°D.120°5.如下图,矩形ABCD∽矩形ADFE,AE=1,AB=4,那么AD 等于〔 A 〕A.2B.2.4C.2.5D.36.以下说法中,正确的选项是(C)A.一切的等腰三角形都相似B.一切的矩形都相似C.一切的正六边形都相似D.一切的等腰梯形都相似111,那么边长增加为原来的(B)7.把一个多边形改成和它相似的多边形,假设面积增加为原来的31 3A.3B. 3C. 3D.38.四边形ABCD 与四边形A1B1C1D1 相似,且点A 与A1,B 与B1,C 与C1 是对应点,AB=12,BC=18,CD=18,AD=9,A1B1=8,那么四边形A1B1C1D1 的周长为38.9.两个相似多边形的一组对应边区分为3 cm 和4.5 cm,假设它们的面积之和为130 cm2,那么较小的那个多边形的面积是40cm2.10.如图,在一个长8 cm,宽4 cm 的矩形中截去一个矩形(阴影局部),使留下的矩形与原矩形相似,那么留下的矩形面积为8cm2.11.假定两个相似多边形的面积比是16∶25,那么它们的相似比等于4∶5 .12.一个四边形的各边之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为5cm,那么它的最大边长为20 cm.13.如下图,将一根铁丝分红两段,区分围成两个相似的五边形,已知它们的面积比是1∶4,其中小五边形的边长为〔x2-4〕cm,大五边形的边长为〔x2+2x〕cm〔其中x>0〕.求这根铁丝的总长.【解析】∵两个五边形相似,面积比是1∶4,∴相似比为1∶2.由题意得2〔x2-4〕=x2+2x,整理得x2-2x-8=0,解得x1=4,x2=-2〔舍去〕.∴铁丝长为12×5+24×5=180〔cm〕.14.如下图,矩形ABCD 能分红三个全等的小矩形,且每个小矩形都与矩形ABCD 相似,AD=1,求AB 的长.【解析】∵三个小矩形全等,∴DE=DC.∵每个小矩形都与矩形ABCD 相似,∴= ,即AB2=1,解得AB= .∴AB 的长为.15.如下图,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的外部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是〔 B 〕A. B. C. D.16.一个矩形ABCD 的较短边长为2.〔1〕如图1 所示,假设沿较长边对折后失掉的矩形与原矩形相似,那么矩形ABCD 的另一边长为2 .〔2〕如图2 所示,矩形ABCD 的另一边长为4,剪去一个矩形ABEF 后,余下的矩形EFDC与原矩形相似,那么余下的矩形EFDC 的面积为 2 .图1 图2【解析】〔1〕设它的另一边长为 2x ,那么 AM=DM=x.∵矩形 ABNM 与矩形 ADCB 相似, ∴= ,即=,解得 x=. ∴矩形 ABCD 的另一边长为 2. 〔2〕设 DF=a.∵余下的矩形 EFDC 与矩形 ADCB 相似, ∴= ,即=,解得 DF=1.∴矩形 EFDC 的面积为 2×1=2.17.如下图,在△ABC 中,∠C=90°,AC=BC=2,取 BC 边中点 E ,作 ED ∥AB ,EF ∥AC ,失掉四边形 EDAF ,它的面积记做 S1.取 BE 中点 E1,作 E 1D 1∥FB ,E1F1∥EF ,失掉四边形 E1D1FF1,它的面积记做 S2,照此规律作下去,那么 S 2021= 〔 〕2021 .【解析】∵∠C=90°,AC=BC=2,∴S =1×2×2=2. ∵点 E 为 BC 的点,ED ∥AB ,∴=〔 〕2= 1 1,∴S =1.∴S △CDE =2.同理可得 S △BEF =21 ∵E 1D 1∥FB ,E 1F 1∥EF ,E 1 为 BE 中点,1 ∴四边形 E 1D 1FF 1 与四边形 EDAF 相似,相似比为 .∴=〔 〕2= .∴S 2= .. 同理可得 S 3=〔〕2. 由此规律可得 S 2021=〔〕2021.18.如下图,矩形 ABCD 的长 AB=30,宽 BC=20.〔1〕如图 1 所示,假定矩形 ABCD 内周围有宽为 1 的方形区域,图中所构成的两个矩形 ABCD 与 A ′B ′C ′D ′ 相似吗?请说明理由.〔2〕如图 2 所示,当 x 为多少时,图中的两个矩形 ABCD 与 A ′B ′C ′D ′相似?图1 图2【解析】〔1〕不相似.理由:∵AB=30,A′B′=28,BC=20,B′C′=18,而≠,∴矩形ABCD 与矩形A′B′C′D′不相似.〔2〕假定矩形ABCD 与A′B′C′D′相似,那么=,∴①= 或②=,解①得x=1.5,解②得x=9.∴当x=1.5 或9 时,图中的两个矩形ABCD 与A′B′C′D′相似.19.如下图,矩形AGFE∽矩形ABCD,AE,AD 区分为它们的最短边,点F 在AB 上,且3AE=2AD.〔1〕矩形ABCD 的面积为450cm2,求矩形AEFG 的面积.〔2〕求证:∠1=∠2.【解析】〔1〕∵3AE=2AD,∴= .∵矩形AGFE∽矩形ABCD∴相似比为= .∴面积的比为..∵矩形ABCD 的面积为450cm2,∴四边形AEFG 的面积为200cm2.〔2〕∵矩形AGFE∽矩形ABCD,∴∠DAB=∠EAG=90°,AE∶AD=AG∶AB.∴∠DAE+∠EAF=∠GAB+∠EAF.∴∠DAE=∠GAB.∵AE∶AD=AG∶AB,∴△ADE∽△ABG.∴∠1=∠2.20.菱形A1B1C1D1 的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1 相交于点O,以点O 为坐标原点,区分以OA1,OB1 所在直线为x 轴,y 轴,树立如下图的直角坐标系,以B1D1 为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2 为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2 为对角线作菱形B2C3D2A3∽菱形A2B2C2D2……按此规律继续作下去,在x 轴的正半轴上失掉点A1,A2,A3,…,A n,那么点A n 的坐标为(3n-1,0).【解】∵菱形A1B1C1D1 的边长为2,∠A1B1C1=60°,∴∠A1B1O=30°,∴OA1=1,OB1=3,∴点A1(1,0).∵菱形B1C2D1A2∽菱形A1B1C1D1,∴∠B1C2D1=∠A1B1C1=60°,∴∠B1A2O=30°,∴OA2=3OB1=3,∴点A2(3,0).同理可得点A3(9,0),A4(27,0)……∴点A n(3n-1,0).21.过去有甲、乙两个庄主,甲庄主的土空中积大约是乙庄主的4 倍,土地的外形都接近正方形.有一天两个庄主打赌,乙庄主说:〝我骑马绕自己的土地跑一周要1.5 h,绕你的土地跑一周3.5 h 足够.〞甲庄主不信,说:〝假设你3.5 h 能跑回来,我这个庄园给你;假设你3.5 h 跑不回来,那么你的庄园归我.〞乙庄主说:〝一言为定.〞然后就催马而去.你以为谁是成功者?【解】把两个庄园看做是相似多边形,面积之比约为4∶1,所以其相似比为2∶1,所以周长之比为2∶1,即甲庄主的庄园周长大约是乙庄主的庄园周长的2 倍,绕甲庄主的庄园的土地跑一周只需1.5×2=3(h)就差不多了.而3 h<3.5 h,所以乙庄主是成功者.22.在长为3、宽为1 的大矩形内不堆叠地放两个与大矩形相似的小矩形,且每个小矩形的每条边与大矩形的一条边平行.〔1〕按如图1 所示放置时,两个小矩形的周长和〔两个小矩形堆叠的边要重复计算〕为163〔2〕怎样放置才干使两个小矩形的周长和最大?在图2 中画出图形,其最大值为88/9. 图1 图2【解析】〔1〕设小矩形的宽为x.∵小矩形与大矩形相似,∴= ,解得x= .∴两个小矩形周长和为2×2〔1+ 〕= .〔2〕两个矩形的放置方式有如下几种:①如答图1 所示,两个小矩形都〝竖放〞,在这种放法下,周长和最大的两个小矩形边长区分为1 和,周长和的最大值为.图1②两个小矩形都〝横放〞,有如下两种状况,如答图2,图3 所示.图2图3这时两个小矩形的周长和的最大值为: 2〔a+3a〕+2[1-a+3〔1-a〕]=8.③两个小矩形一个〝横放〞,一个〝竖放〞,如答图4 所示.这时两个小矩形的周长和的最大值为: 2×(1+ )+2×图4〔第16 题答图〕∴如答图4 所示为所求,此时最大值为。
22.1 第1课时 相似多边形同步练习沪科版九年级数学上册(含答案)

22.1 第1课时相似多边形同步练习沪科版九年级数学上册(含答案)22.1 第1课时相似多边形一、选择题1.下列说法中,错误的是()A.等边三角形都相似B.等腰直角三角形都相似C.矩形都相似D.正方形都相似2.观察下列每组图形,其中相似图形是()图13.下列说法中正确的是()A.矩形都是相似图形B.各角对应相等的两个五边形相似C.等边三角形都是相似三角形D.各边对应成比例的两个六边形相似二、填空题4.请将图中的相似图形的序号写出来:.5.在如图所示的方格纸中(每个小正方形的边长都相等),已知△ABC和△DEF是相似三角形,AB与DE 是对应边,则△ABC和△DEF的相似比为.6如图,把一张矩形纸片沿图中的虚线裁成三张大小相同的小矩形纸片.若得到的小矩形纸片与原来的大矩形纸片相似,则大矩形纸片的长与宽的比值为.7.如图2,△ABC与△DEF相似,且AC,BC的对应边分别是DF,EF,则△ABC与△DEF的相似比是.图28.五边形ABCDE与五边形A'B'C'D'E'相似,且点A,B,C,D,E 的对应点分别是点A',B',C',D',E',它们的相似比为1∶3.(1)若∠D=135°,则∠D'= °;(2)若A'B'=15cm,则AB= cm.三、解答题9.如图,正方形的边长a=10,菱形的边长b=5,它们相似吗?请说明理由.10.在如图3所示的两个相似的五边形中,试求出未知的边x,y的长度及角α,β的度数.图311.如图4,四边形ABCD的对角线相交于点O,A',B',C',D'分别是OA,OB,OC,OD的中点,试判断四边形ABCD与四边形A'B'C'D'是否相似,并说明理由.图412.如图5,在一矩形花坛ABCD的四周修筑小路,使得相对的两条小路的宽均相等,如果花坛的宽AB=20,长AD=30.小路的宽x和y的比值为多少时,能使得小路四周所围成的矩形A'B'C'D'与矩形ABCD 相似,且A'B'与AB是对应边,A'D'与AD是对应边?请说明理由.图5答案1.C2.D3.C4.(1)和(8),(2)和(3),(4)和(6),(5)和(7)5..126..3 [解析]设原矩形的长与宽分别为x,y,则剪裁后小矩形的长与宽分别为y,x3.根据相似多边形的性质,得xy=yx3,则x2y2=3,故xy=3(负值舍去).4.[答案][解析]由题意,得AB与DE是对应边,则△ABC与△DEF的相似比为ABDE=46=23.8..(1)135(2)59.解:不相似.理由:因为正方形和菱形的角不相等.10.解:因为两个五边形相似,所以它们的对应边长度的比相等,对应角相等.观察两个图形的形状及边的长度,有 3.21.6=1.25x=1.2y,解得x=0.625,y=0.6.β=58°,α=540°-(72°+58°+165°+100°)=145°.11.解:相似.理由如下:∵A',B'分别是OA,OB的中点,∴A'B'是△AOB的中位线,∴A'B'∥AB,A'B'=12AB,∴∠OA'B'=∠OAB,A'B'AB=12.同理,∠OA'D'=∠OAD,A'D'AD=12,∴∠B'A'D'=∠BAD,A'B'AB=A'D'AD.同理,∠A'D'C'=∠ADC,∠D'C'B'=∠DCB,∠C'B'A'=∠CBA,A'D'AD=D'C'DC=B'C'BC,∴四边形ABCD与四边形A'B'C'D'相似.12.解:当小路的宽x 和y的比值为32时,能使得小路四周所围成的矩形A'B'C'D'与矩形ABCD相似,且A'B'与AB是对应边,A'D'与AD是对应边.理由:因为矩形A'B'C'D'与矩形ABCD相似,且A'B'与AB是对应边,A'D'与AD是对应边,所以A'D'AD=A'B'AB,即30+2x30=20+2y20.整理,得4x=6y,所以xy=32.。
2022年北师大版数学《相似多边形》配套精品练习(附答案)
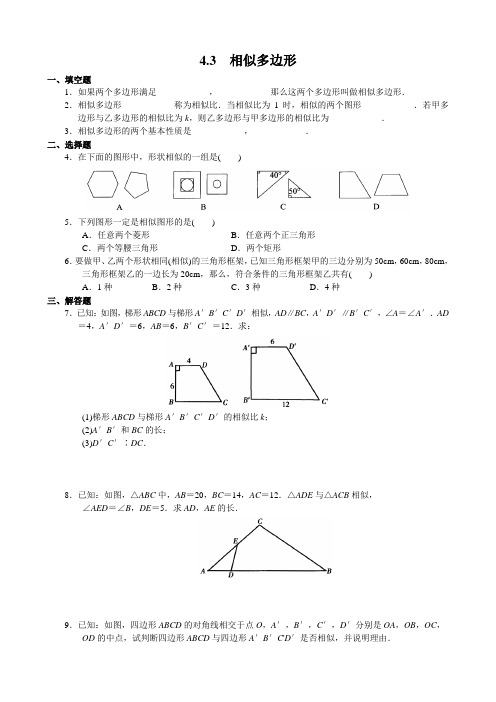
4.3 相似多边形一、填空题1.如果两个多边形满足____________,____________那么这两个多边形叫做相似多边形.2.相似多边形____________称为相似比.当相似比为1时,相似的两个图形____________.若甲多边形与乙多边形的相似比为k,则乙多边形与甲多边形的相似比为____________.3.相似多边形的两个基本性质是____________,____________.二、选择题4.在下面的图形中,形状相似的一组是( )5.下列图形一定是相似图形的是( )A.任意两个菱形B.任意两个正三角形C.两个等腰三角形D.两个矩形6.要做甲、乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么,符合条件的三角形框架乙共有( )A.1种B.2种C.3种D.4种三、解答题7.已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD =4,A′D′=6,AB=6,B′C′=12.求:(1)梯形ABCD与梯形A′B′C′D′的相似比k;(2)A′B′和BC的长;(3)D′C′∶DC.8.已知:如图,△ABC中,AB=20,BC=14,AC=12.△ADE与△ACB相似,∠AED=∠B,DE=5.求AD,AE的长.9.已知:如图,四边形ABCD的对角线相交于点O,A′,B′,C′,D′分别是OA,OB,OC,OD的中点,试判断四边形ABCD与四边形A′B′C'D′是否相似,并说明理由.10.如下图甲所示,在矩形ABCD 中,AB =2AD .如图乙所示,线段EF =10,在EF 上取一点M ,分别以EM ,MF 为一边作矩形EMNH 、矩形MFGN ,使矩形MFGN ∽矩形ABCD ,设MN =x ,当x 为何值时,矩形EMNH 的面积S 有最大值?最大值是多少?答案:1.对应角相等,对应边的比相等. 2.对应边的比,全等,⋅k1 3.对应角相等,对应边的比相等. 4.C 5.B 6.C7.(1)k =2∶3;(2)A 'B '=9,BC =8;(3)3∶2. 8.⋅==750,730AE AD 9.相似. 10.25=x 时,S 的最大值为⋅225《第1章 特殊的平行四边形》单元测试卷一、选择题:(每小题3分,共36分) 1.下列判定正确的是( )A .对角线互相垂直的四边形是菱形B .两条对角线相等且互相垂直的四边形是正方形C .四边相等且有一个角是直角的四边形是正方形D .一组对边平行,一组对边相等的四边形是平行四边形2.下列说法中,错误的是( )A.平行四边形的对角线互相平分B.对角线互相平分的四边形是平行四边形C.菱形的对角线互相垂直D.对角线互相垂直的四边形是菱形3.下列命题原命题与逆命题都是真命题的是( )A.矩形的对角线相等B.对角线互相平分且相等的四边形是矩形C.矩形有一个内角是直角D.对角线互相垂直且平分的四边形是矩形4.既是中心对称图形又是轴对称图形,且只有两条对称轴的四边形是( )A.正方形B.矩形 C.菱形 D.矩形或菱形5.两条对角线相等的平行四边形一定是( )A.矩形 B.菱形 C.矩形或正方形 D.正方形6.如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于( )A.3.5 B.4 C.7 D.147.顺次连接矩形四条边的中点,所得到的四边形一定是( )A.矩形 B.菱形 C.正方形D.平行四边形8.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=( )A.30°B.45°C.22.5° D.135°9.如图,已知点E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE的度数为( )A.30°B.22.5° C.15°D.45°10.如图:长方形纸片ABCD中,AD=4cm,AB=10cm,按如图的方式折叠,使点B与点D重合.折痕为EF,则DE长为( )A.4.8 B.5 C.5.8 D.611.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )A.16 B.17 C.18 D.1912.如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )A.2 B.3 C. D.二、填空题(每小题3分,共12分)13.已知菱形的周长为40cm,两个相邻角度数比为1:2,则较短的对角线长为__________,面积为__________.14.如图,矩形ABCD中,E是AD的中点,将△ABE折叠后得到△GBE,延长BG交CD于点F,若CF=1,FD=2,则BC的长为__________.15.在矩形ABCD中,AB=5,AD=12,P是AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF=__________.16.如图,菱形ABCD的周长为24cm,∠A=120°,E是BC边的中点,P是BD上的动点,则PE﹢PC的最小值是__________.三、解答题:17.如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.18.已知,如图,AD是△ABC的角平分线,DE∥AC,ED=AF.求证:四边形AEDF是菱形.19.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.20.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.21.已知:如图,在△ABC中,AB=AC,D是的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E、F.(1)求证:DE=DF;(2)只添加一个条件,使四边形EDFA是正方形,并给出证明.22.如图,矩形ABCD的对角线AC、BD交于点O,∠AOD=60°,AB=,AE⊥BD于点E,求OE 的长.23.已知,如图1,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.(1)求证:△BCE≌△DCF;(2)求CF的长;(3)如图2,在AB上取一点H,且BH=CF,若以BC为x轴,AB为y轴建立直角坐标系,问在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的P点坐标;若不存在,说明理由.北师大新版九年级上册《第1章特殊的平行四边形》单元测试卷一、选择题:(每小题3分,共36分)1.下列判定正确的是( )A.对角线互相垂直的四边形是菱形B.两条对角线相等且互相垂直的四边形是正方形C.四边相等且有一个角是直角的四边形是正方形D.一组对边平行,一组对边相等的四边形是平行四边形【考点】多边形.【分析】根据平行四边形的判定,菱形的判定,正方形的判定,可得答案.【解答】解:A、对角线互相平分且互相垂直的四边形是菱形,故A错误;B、两条对角线相等且平分且互相垂直的四边形是正方形,故B正确;C、四边相等且有一个角是直角的四边形是正方形,故C正确;D、一组对边平行,一组对边相等的四边形可能是平行四边形、可能是等腰梯形,故D错误;故选:B.【点评】本题考查了多边形,熟记平行四边形的判定与性质、特殊平行四边形的判定与性质是解题关键.2.下列说法中,错误的是( )A.平行四边形的对角线互相平分B.对角线互相平分的四边形是平行四边形C.菱形的对角线互相垂直D.对角线互相垂直的四边形是菱形【考点】菱形的判定与性质;平行四边形的判定与性质.【分析】根据平行四边形和菱形的性质对各个选项进行分析从而得到最后答案.【解答】解:根据平行四边形和菱形的性质得到ABC均正确,而D不正确,因为对角线互相垂直的四边形也可能是梯形,故选:D.【点评】主要考查了平行四边形和特殊平行四边形的特性,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.菱形的特性是:四边相等,对角线互相垂直平分.3.下列命题原命题与逆命题都是真命题的是( )A.矩形的对角线相等B.对角线互相平分且相等的四边形是矩形C.矩形有一个内角是直角D.对角线互相垂直且平分的四边形是矩形【考点】命题与定理.【分析】分别写出四个命题的逆命题,再判断是否是真命题即可.【解答】解:A、矩形的对角线相等,逆命题是对角线相等的四边形是矩形,错误;B、对角线互相平分且相等的四边形是矩形,逆命题是矩形的对角线互相平分且相等,正确;C、矩形有一个内角是直角,逆命题是有一个内角是直角的四边形是矩形,错误;D、对角线互相垂直且平分的四边形是矩形,错误.故选B.【点评】本题考查了命题与定理:判断事物的语句叫命题;题设与结论互换的两个命题互为逆命题;正确的命题叫真命题,错误的命题叫假命题;经过推论论证得到的真命题称为定理.4.既是中心对称图形又是轴对称图形,且只有两条对称轴的四边形是( )A.正方形B.矩形 C.菱形 D.矩形或菱形【考点】中心对称图形;轴对称图形.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:正方形是轴对称图形,也是中心对称图形,有4条对称轴;矩形是轴对称图形,也是中心对称图形,有2条对称轴;菱形是轴对称图形,也是中心对称图形,有2条对称轴.故选D.【点评】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.5.两条对角线相等的平行四边形一定是( )A.矩形 B.菱形 C.矩形或正方形 D.正方形【考点】矩形的判定.【分析】根据对角线相等的平行四边形是矩形,直接得出答案即可.【解答】解:因为对角线相等的平行四边形是矩形.故选:A.【点评】此题考查了特殊平行四边形的判定,需熟练掌握各特殊平行四边形的特点是解题关键.6.如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于( )A.3.5 B.4 C.7 D.14【考点】菱形的性质;直角三角形斜边上的中线;三角形中位线定理.【分析】根据菱形的四条边都相等求出AB,菱形的对角线互相平分可得OB=OD,然后判断出OH是△ABD 的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得OH=AB.【解答】解:∵菱形ABCD的周长为28,∴AB=28÷4=7,OB=OD,∵H为AD边中点,∴OH是△ABD的中位线,∴OH=AB=×7=3.5.故选:A.【点评】本题考查了菱形的对角线互相平分的性质,三角形的中位线平行于第三边并且等于第三边的一半,熟记性质与定理是解题的关键.7.顺次连接矩形四条边的中点,所得到的四边形一定是( )A.矩形 B.菱形 C.正方形D.平行四边形【考点】中点四边形.【分析】因为题中给出的条件是中点,所以可利用三角形中位线性质,以及矩形对角线相等去证明四条边都相等,从而说明是一个菱形.【解答】解:连接AC、BD,在△ABD中,∵AH=HD,AE=EB∴EH=BD,同理FG=BD,HG=AC,EF=AC,又∵在矩形ABCD中,AC=BD,∴EH=HG=GF=FE,∴四边形EFGH为菱形.故选B.【点评】本题考查了菱形的判定,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.8.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=( )A.30°B.45°C.22.5° D.135°【考点】菱形的性质;正方形的性质.【分析】由正方形的性质得对角线AC平分直角,因为菱形的对角线平分所在的角,所以∠FAB为直角的.【解答】解:因为AC为正方形ABCD的对角线,则∠CAE=45°,又因为菱形的每一条对角线平分一组对角,则∠FAB=22.5°,故选:C.【点评】此题主要考查了正方形、菱形的对角线的性质.9.如图,已知点E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE的度数为( )A.30°B.22.5° C.15°D.45°【考点】正方形的性质;等腰三角形的性质.【分析】由正方形的性质得到BC=CD,∠DBC=∠BDC=45°,根据BE=BC,根据三角形的内角和定理求出∠BEC=∠BCE=67.5°,根据∠DCE=∠BCD﹣∠BCE即可求出答案.【解答】解:∵正方形ABCD,∴BC=CD,∠DBC=∠BDC=45°,∵BE=BC,∴∠BEC=∠BCE=67.5°,∴∠DCE=∠BCD﹣∠BCE=90°﹣67.5°=22.5°,故选B.【点评】本题主要考查对正方形的性质,三角形的内角和定理,等腰三角形的性质等知识点的理解和掌握,能根据这些性质求出∠DCE的度数是解此题的关键,题型较好,难度适中.10.如图:长方形纸片ABCD中,AD=4cm,AB=10cm,按如图的方式折叠,使点B与点D重合.折痕为EF,则DE长为( )A.4.8 B.5 C.5.8 D.6【考点】翻折变换(折叠问题).【专题】数形结合.【分析】注意发现:在折叠的过程中,BE=DE,从而设BE即可表示AE,在直角三角形ADE中,根据勾股定理列方程即可求解.【解答】解:设DE=xcm,则BE=DE=x,AE=AB﹣BE=10﹣x,在RT△ADE中,DE2=AE2+AD2,即x2=(10﹣x)2+16.解得:x==5.8(cm).故选C.【点评】此题考查了翻折变换的知识,解答本题的关键是掌握翻折前后对应线段相等,另外要熟练运用勾股定理解直角三角形.11.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )A.16 B.17 C.18 D.19【考点】勾股定理.【分析】由图可得,S2的边长为3,由AC=BC,BC=CE=CD,可得AC=2CD,CD=2,EC=2;然后,分别算出S1、S2的面积,即可解答.【解答】解:如图,设正方形S1的边长为x,∵△ABC和△CDE都为等腰直角三角形,∴AB=BC,DE=DC,∠ABC=∠D=90°,∴sin∠CAB=sin45°==,即AC=BC,同理可得:BC=CE=CD,∴AC=BC=2CD,又∵AD=AC+CD=6,∴CD==2,∴EC2=22+22,即EC=2;∴S1的面积为EC2=2×2=8;∵∠MAO=∠MOA=45°,∴AM=MO,∵MO=MN,∴AM=MN,∴M为AN的中点,∴S2的边长为3,∴S2的面积为3×3=9,∴S1+S2=8+9=17.故选B.【点评】本题考查了勾股定理,要充分利用正方形的性质,找到相等的量,再结合三角函数进行解答.12.如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )A.2 B.3 C. D.【考点】轴对称-最短路线问题;正方形的性质.【专题】几何图形问题.【分析】由于点B与D关于AC对称,所以连接BE,与AC的交点即为P点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为4,可求出AB的长,从而得出结果.【解答】解:连接BD,与AC交于点F.∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE最小.∵正方形ABCD的面积为4,∴AB=2.又∵△ABE是等边三角形,∴BE=AB=2.∴所求最小值为2.故选:A.【点评】此题主要考查轴对称﹣﹣最短路线问题,要灵活运用对称性解决此类问题.二、填空题(每小题3分,共12分)13.已知菱形的周长为40cm,两个相邻角度数比为1:2,则较短的对角线长为10cm,面积为50cm2.【考点】菱形的性质.【专题】计算题.【分析】根据已知可求得菱形的边长及其两内角的度数,根据勾股定理可求得其对角线的长,根据菱形的面积等于两对角线乘积的一半求得其面积.【解答】解:根据已知可得,菱形的边长AB=BC=CD=AD=10cm,∠ABC=60°,∠BAD=120°,∴△ABC为等边三角形,∴AC=AB=10cm,AO=CO=5cm,在Rt△AOB中,根据勾股定理得:BO==5,∴BD=2BO=10(cm),=×AC×BD=×10×10 =50(cm2);则S菱形ABCD故答案为:10cm,50cm2.【点评】本题考查的是菱形的面积求法及菱形性质的综合.菱形的面积有两种求法(1)利用底乘以相应底上的高(2)利用菱形的特殊性,菱形面积=×两条对角线的乘积.14.如图,矩形ABCD中,E是AD的中点,将△ABE折叠后得到△GBE,延长BG交CD于点F,若CF=1,FD=2,则BC的长为.【考点】翻折变换(折叠问题);矩形的性质.【专题】压轴题.【分析】首先过点E作EM⊥BC于M,交BF于N,易证得△ENG≌△BNM(AAS),MN是△BCF的中位线,根据全等三角形的性质,即可求得GN=MN,由折叠的性质,可得BG=3,继而求得BF的值,又由勾股定理,即可求得BC的长.【解答】解:过点E作EM⊥BC于M,交BF于N,∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME是矩形,∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM,在△ENG和△BNM中∵,∴△ENG≌△BNM(AAS),∴NG=NM,∴CM=DE,∵E是AD的中点,∴AE=ED=BM=CM,∵EM∥CD,∴BN:NF=BM:CM,∴BN=NF,∴NM=CF=,∴NG=,∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣=,∴BF=2BN=5,∴BC===2.故答案为:2.【点评】此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.15.在矩形ABCD中,AB=5,AD=12,P是AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF=.【考点】矩形的性质.【分析】连接PO,过D作DM⊥AC于M,求出AC、DM,根据三角形面积公式得出PE+PF=DM,即可得出答案.【解答】解:连接PO,过D作DM⊥AC于M,∵四边形ABCD是矩形,∴∠ADC=90°,AB=CD=5,AD=12,OA=OC,OB=OD,AC=BD,∴OA=OD,由勾股定理得:AC=13,∴OA=OD=6.5,∵S△ADC=×12×5=×13×DM,∴DM=,∵S AOD=S△APO+S△DPO,∴AO×PE+OD×PF=×AO×DM,∴PE+PF=DM=,故答案为:.【点评】本题考查了矩形的性质,勾股定理,三角形的面积的应用,关键是求出DM长和得出PE+PF=DM.16.如图,菱形ABCD的周长为24cm,∠A=120°,E是BC边的中点,P是BD上的动点,则PE﹢PC的最小值是3.【考点】轴对称-最短路线问题;菱形的性质.【专题】探究型.【分析】先求出菱形各边的长度,作点E关于直线BD的对称点E′,连接CE′交BD于点P,则CE′的长即为PE﹢PC的最小值,由菱形的性质可知E′为AB的中点,由直角三角形的判定定理可得出△BCE′是直角三角形,利用勾股定理即可求出CE′的长.【解答】解:∵菱形ABCD的周长为24cm,∴AB=BC==6cm,作点E关于直线BD的对称点E′,连接CE′交BD于点P,则CE′的长即为PE﹢PC的最小值,∵四边形ABCD是菱形,∴BD是∠ABC的平分线,∴E′在AB上,由图形对称的性质可知,BE=BE′=BC=×6=3,∵BE′=BE=BC,∴△BCE′是直角三角形,∴CE′===3,故PE﹢PC的最小值是3.【点评】本题考查的是轴对称﹣最短路线问题及菱形的性质、直角三角形的判定定理,根据轴对称的性质作出图形是解答此题的关键.三、解答题:17.如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.【考点】矩形的判定;菱形的性质.【分析】根据平行四边形的判定推出四边形OBEC是平行四边形,根据菱形性质求出∠AOB=90°,根据矩形的判定推出即可.【解答】证明:∵BE∥AC,CE∥DB,∴四边形OBEC是平行四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOB=90°,∴平行四边形OBEC是矩形.【点评】本题考查了菱形性质,平行四边形的判定,矩形的判定的应用,主要考查学生的推理能力.18.已知,如图,AD是△ABC的角平分线,DE∥AC,ED=AF.求证:四边形AEDF是菱形.【考点】菱形的判定;角平分线的定义;平行线的性质.【专题】证明题.【分析】由已知易得四边形AEDF是平行四边形,由角平分线和平行线的定义可得∠FAD=∠FDA,则可求得AF=DF,故可证明四边形AEDF是菱形.【解答】证明:∵AD是△ABC的角平分线∴∠EAD=∠FAD∵DE∥AC,ED=AF∴四边形AEDF是平行四边形∴∠EAD=∠ADF∴∠FAD=∠FDA∴AF=DF∴四边形AEDF是菱形.【点评】此题主要考查菱形的判定、角平分线的定义和平行线的性质.此题运用了菱形的判定方法“一组邻边相等的平行四边形是菱形”.19.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.【考点】菱形的性质;全等三角形的判定与性质.【专题】证明题.【分析】在菱形中,由SAS求得△ABE≌△ADF,再由等边对等角得到∠AEF=∠AFE.【解答】证明:∵ABCD是菱形,∴AB=AD,∠B=∠D.又∵EB=DF,∴△ABE≌△ADF,∴AE=AF,∴∠AEF=∠AFE.【点评】本题利用了菱形的性质和全等三角形的判定和性质,等边对等角求解.20.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.【考点】矩形的判定;角平分线的性质;等腰三角形的性质;正方形的判定.【专题】证明题;开放型.【分析】(1)根据矩形的有三个角是直角的四边形是矩形,已知CE⊥AN,AD⊥BC,所以求证∠DAE=90°,可以证明四边形ADCE为矩形.(2)根据正方形的判定,我们可以假设当AD=BC,由已知可得,DC=BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.【解答】(1)证明:在△ABC中,AB=AC,AD⊥BC,∴∠BAD=∠DAC,∵AN是△ABC外角∠CAM的平分线,∴∠MAE=∠CAE,∴∠DAE=∠DAC+∠CAE=180°=90°,又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.理由:∵AB=AC,∴∠ACB=∠B=45°,∵AD⊥BC,∴∠CAD=∠ACD=45°,∴DC=AD,∵四边形ADCE为矩形,∴矩形ADCE是正方形.∴当∠BAC=90°时,四边形ADCE是一个正方形.【点评】本题是以开放型试题,主要考查了对矩形的判定,正方形的判定,等腰三角形的性质,及角平分线的性质等知识点的综合运用.21.已知:如图,在△ABC中,AB=AC,D是的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E、F.(1)求证:DE=DF;(2)只添加一个条件,使四边形EDFA是正方形,并给出证明.【考点】正方形的判定.【分析】(1)连接AD,根据等腰三角形的性质可得AD是∠BAC的角平分线,再根据角平分线的性质可得DE=DF;(2)添加∠BAC=90°,根据三角形是直角的四边形是矩形可得四边形AFDE是矩形,再由条件DF=DE可得四边形EDFA是正方形.【解答】解:(1)连接AD,∵AB=AC,D是的BC边的中点,∴AD是∠BAC的角平分线,∵DE⊥AC,DF⊥AB,∴DF=DE;(2)添加∠BAC=90°,∵DE⊥AC,DF⊥AB,∴∠AFD=∠AED=90°,∴四边形AFDE是矩形,∵DF=DE,∴四边形EDFA是正方形.【点评】此题主要考查了等腰三角形的性质,以及正方形的判定,关键是掌握等腰三角形三线合一的性质.22.如图,矩形ABCD的对角线AC、BD交于点O,∠AOD=60°,AB=,AE⊥BD于点E,求OE的长.【考点】矩形的性质;等边三角形的判定与性质.【专题】计算题.【分析】矩形对角线相等且互相平分,即OA=OD,根据∠AOD=60°可得△AOD为等边三角形,即OA=AD,∵AE⊥BD,∴E为OD的中点,即可求OE的值.【解答】解:∵对角线相等且互相平分,∴OA=OD∵∠AOD=60°∴△AOD为等边三角形,则OA=AD,BD=2DO,AB=AD,∴AD=2,∵AE⊥BD,∴E为OD的中点∴OE=OD=AD=1,答:OE的长度为1.【点评】本题考查了勾股定理在直角三角形中的运用,考查了等边三角形的判定和等腰三角形三线合一的性质,本题中求得E为OD的中点是解题的关键.23.已知,如图1,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.(1)求证:△BCE≌△DCF;(2)求CF的长;(3)如图2,在AB上取一点H,且BH=CF,若以BC为x轴,AB为y轴建立直角坐标系,问在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的P点坐标;若不存在,说明理由.【考点】四边形综合题.【分析】(1)利用正方形的性质,由全等三角形的判定定理SAS即可证得△BCE≌△DCF;(2)通过△DBG≌△FBG的对应边相等知BD=BF=;然后由CF=BF﹣BC=即可求得;(3)分三种情况分别讨论即可求得.【解答】(1)证明:如图1,在△BCE和△DCF中,,∴△BCE≌△DCF(SAS);(2)证明:如图1,∵BE平分∠DBC,OD是正方形ABCD的对角线,∴∠EBC=∠DBC=22.5°,由(1)知△BCE≌△DCF,∴∠EBC=∠FDC=22.5°(全等三角形的对应角相等);∴∠BGD=90°(三角形内角和定理),∴∠BGF=90°;在△DBG和△FBG中,,∴△DBG≌△FBG(ASA),∴BD=BF,DG=FG(全等三角形的对应边相等),∵BD==,∴BF=,∴CF=BF﹣BC=﹣1;(3)解:如图2,∵CF=﹣1,BH=CF∴BH=﹣1,①当BH=BP时,则BP=﹣1,∵∠PBC=45°,设P(x,x),∴2x2=(﹣1)2,解得x=2﹣或﹣2+,∴P(2﹣,2﹣)或(﹣2+,﹣2+);②当BH=HP时,则HP=PB=﹣1,∵∠ABD=45°,∴△PBH是等腰直角三角形,∴P(﹣1,﹣1);③当PH=PB时,∵∠ABD=45°,∴△PBH是等腰直角三角形,∴P(,),综上,在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形,所有符合条件的P点坐标为(2﹣,2﹣)、(﹣2+,﹣2+)、(﹣1,﹣1)、(,).【点评】本题是四边形的综合题,考查了正方形的性质,三角形全等的判定和性质,等腰三角形的判定,熟练掌握性质定理是解题的关键.。
青岛版九年级数学上册1.1相似多边形同步训练题含答案
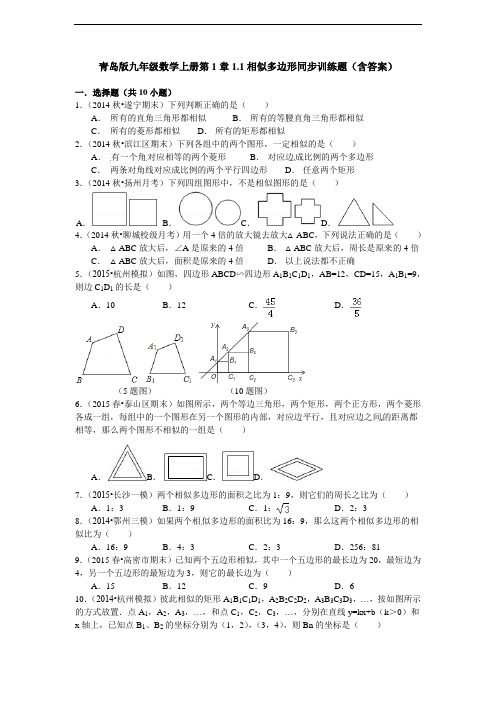
青岛版九年级数学上册第1章1.1相似多边形同步训练题(含答案)一.选择题(共10小题)1.(2014秋•遂宁期末)下列判断正确的是()A.所有的直角三角形都相似B.所有的等腰直角三角形都相似C.所有的菱形都相似D.所有的矩形都相似2.(2014秋•滨江区期末)下列各组中的两个图形,一定相似的是()A.有一个角对应相等的两个菱形B.对应边成比例的两个多边形C.两条对角线对应成比例的两个平行四边形D.任意两个矩形3.(2014秋•扬州月考)下列四组图形中,不是相似图形的是()A.B.C.D.4.(2014秋•聊城校级月考)用一个4倍的放大镜去放大△ABC,下列说法正确的是()A.△ABC放大后,∠A是原来的4倍B.△ABC放大后,周长是原来的4倍C.△ABC放大后,面积是原来的4倍D.以上说法都不正确5.(2015•杭州模拟)如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是()A.10 B.12 C.D.(5题图)(10题图)6.(2015春•泰山区期末)如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是()A.B.C.D.7.(2015•长沙一模)两个相似多边形的面积之比为1:9,则它们的周长之比为()A.1:3 B.1:9 C.1:D.2:3 8.(2014•鄂州三模)如果两个相似多边形的面积比为16:9,那么这两个相似多边形的相似比为()A.16:9 B.4:3 C.2:3 D.256:81 9.(2015春•高密市期末)已知两个五边形相似,其中一个五边形的最长边为20,最短边为4,另一个五边形的最短边为3,则它的最长边为()A.15 B.12 C.9D.6 10.(2014•杭州模拟)彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是()A.(2n﹣1,2n)B.(2n﹣,2n)C.(2n﹣1﹣,2n﹣1)D.(2n﹣1﹣1,2n﹣1)二.填空题(共10小题)11.(2015•江西校级模拟)在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是cm2.12.(2015春•庆阳校级月考)图中的两个四边形相似,则x+y=,a=.(12题图)(18题图)(20题图)13.下列图形中是与相似的.(1)(2)(3)(4)14.(2014秋•高密市期中)两个相似的五边形,一个各边长分别为1,2,3,4,5,另一个五边形的最长边为8,则后一个五边形的周长为.15.(2015春•靖远县校级月考)两个相似五边形,一组对应边的长分别为3cm和4.5cm,如果它们的面积之和是78cm2,则较大的五边形面积是cm2.16.(2015•武威校级模拟)一个四边形的四边长分别是3、4、5、6,另一个和它相似的四边形的最小边长为6,那么后一个四边形的周长为.17.(2015•武威校级模拟)已知两个相似的菱形的相似比为2:3,面积之差为5cm2,则这两个菱形的面积分别是.18.(2015•金堂县一模)如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为s2,s3,…,s n(n为正整数),那么第9个正方形的面积S9=.19.(2015•厦门模拟)在比例尺为1:500的图纸上,一个三角形的面积为120c m2,那么该三角形的实际面积是m2.20.(2015春•桐城市校级期中)如图,一块长3m、宽1.5m的矩形黑板,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗?答:.三.解答题(共4小题)21.(2014秋•海口期中)如图,四边形ABCD和四边形EFGH相似,求∠α、∠β 的大小和EH的长度.22.(2012春•新浦区校级期中)如图:矩形草坪的长为a米,宽为b米(a>b),沿草坪四周外围有宽为x米的环形小路.(1)草坪的长与宽的比值m=,外围矩形的长与宽的比值n=.(用含有a、b、x的代数式表示);(2)请比较m与n的大小;(3)图中的两个矩形相似吗?为什么?23.(2007•宁波)如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.(1)求AD的长;(2)求矩形DMNC与矩形ABCD的相似比.24.如图,已知△AEO∽△ABC,△AOF∽△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明你的理由.青岛版九年级数学上册第1章1.1相似多边形同步训练题参考答案一.选择题(共10小题)1.B 2.A 3.D 4.B 5.C 6.B 7.A 8.B 9.A 10.A二.填空题(共10小题)11.18 12.6385°13.(1)(4)14.24 15.54 16.3617.4cm2,9cm218.256 19.3000 20.不相似三.解答题(共4小题)21.解:∵四边形ABCD和四边形EFGH相似,∴∠α=∠B=83°,∠D=∠H=118°,∠β=360°﹣(83°+78°+118°)=81°,EH:AD=HG:DC,∴=,∴EH=28(cm).答:∠α=83°,∠β=81°,EH=28cm.22.解:(1)∵矩形草坪的长为a米,宽为b米(a>b),∴草坪的长与宽的比值m=a:b,外围矩形的长与宽的比值n=(a+2x):(b+2x);(2)m﹣n=﹣==,∵a>b>0,∴m﹣n=>0,∴m>n;(3)若图中的两个矩形相似,则需m=n,∵m>n,∴图中的两个矩形不相似.故答案为:(1)a:b,(a+2x):(b+2x).23.解:(1)由已知得MN=AB,MD=AD=BC,∵矩形DMNC与矩形ABCD相似,,∵MN=AB,DM=AD,BC=AD,∴AD2=AB2,∴由AB=4得,AD=4;(2)矩形DMNC与矩形ABCD的相似比为=.24.解:四边形ABCD与四边形AEOF相似,理由如下:∵△AEO∽△ABC,∴∠2=∠1,∠4=∠3,==,∵△AOF∽△ACD,∴∠6=∠5,∠8=∠7,==,∴∠2+∠6=∠1+∠5,即∠EOF=∠BCD,===.在四边形AEOF与四边形ABCD中,∵∠EAF=∠BAD,∠4=∠3,∠EOF=∠BCD,∠8=∠7,===,∴四边形AEOF∽四边形ABCD,即四边形ABCD与四边形AEOF相似.。
北师大版九年级数学上册《4.3相似多边形》同步练习题带答案

北师大版九年级数学上册《4.3相似多边形》同步练习题带答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.如图是杭州第19届亚运会的吉祥物“琮琮”,代表的是世界遗产良渚古城遗址,名字来源于文物玉琮.琮琮全身以黄色调为主,头部刻有“饕餮纹”,展示给人们一种不屈不挠、坚强刚毅的精神.文旅部门将选定的“琮琮”形象图通过放大或缩小放置于不同的宣传版面上,这体现了数学中的( )A .图形的平移B .图形的轴对称C .图形的相似D .图形的旋转2.下列图形中不一定是相似图形的是( ) A .两个正方形 B .两个等边三角形 C .两个等腰直角三角形 D .两个矩形3.下列判断正确的是( ) A .所有的等腰三角形都相似 B .所有的等腰直角三角形都相似 C .所有的矩形都相似D .所有的菱形都相似 4.若四边形ABCD ∽四边形A B C D '''',且:3:5AB A B ''=,已知15B C ''=,则BC 的长是( ) A .25B .9C .20D .155.将一张矩形纸片ABCD 沿一组对边AD 和BC 的中点连线EF 对折,对折后所得矩形恰好与原矩形相似,若原矩形纸片的边1AB =,则BC 的长为( )A .12B 2C 2D .26.下列命题错误的是 ( ) A .四边形内角和等于外角和 B .相似多边形的面积比等于相似比C .点P (1,2)关于原点对称的点的坐标为(-1,-2)D .三角形的中位线平行于第三边,且等于第三边的一半二、填空题7.如图是两个形状相同的飞机图案,则x 的值是 .8.已知ABC A B C '''∽△△,AD 与A D ''是它们的对应中线,如果ABC 与A B C '''的面积比是1∶9,那么:AD A D ''为 .9.下列五组图形中,∶两个等腰三角形;∶两个等边三形;∶两个菱形;∶两个矩形;∶两个正方形.一定相似的有 (填序号)10.如图,在梯形ABCD 中,AD//BC 12AD cm = 27BC cm = E 、F 分别在两腰AB 、CD 上,且//EF AD ,如果梯形AEFD ∽梯形EBCF ,则EF = .11.如图,正方形ABCD 的边长为1,以AC 为边作第2个正方形ACEF ,再以CF 为边作第3个正方形,...FCGH 按照这样的规律作下去,第2024个正方形的边长为 .12.如图,某校给初一年级划了一块大的矩形菜地,年级又将它分为大小形状完全相同的三块分给三个班,同学们测量后惊奇的发现,每块小菜地都与原大矩形菜地相似,则原矩形菜地的宽与长之比为 .三、解答题13.正方形ABCD 中,E 是AC 上一点,EF ∶AB ,EG ∶AD ,AB =6,AE :EC =2:1.求四边形AFEG 的面积.14.(1)用配方法解方程:21290x x --=;(2)如图,已知四边形ABCD ∽四边形1111D C B A ,求x ,y 和α的值.15.如图是两个相似的平行四边形,根据给出的条件,求α∠,及边长m .16.已知矩形ABCD 中,AB=2,在BC 中取一点E ,沿AE 将ABE 向上折叠,使B 点落在AD 上的F 点,若四边形EFDC 与矩形ABCD 相似,求AD 的长.题号 1 2 3 4 5 6 答案CDBBC B7.1438.13/1:39.∶∶ 10.18cm11.2023212.解:设原矩形ABCD 的长为x ,宽为y ∶小矩形的长为y ,宽为3x∶小矩形与原矩形相似∶3xy y x= ∶:1:3y x =故答案为:313.解:∶四边形ABCD 为中正方形 ∶90DAB ∠=︒ 45DAC ∠=︒ 又EF ∶AB ,EG ∶AD ∶90AFE AGE ∠=∠=︒∴四边形AFEG 是矩形9045AEG DAC ∠=︒-∠=︒45GAE AEG ∴∠=∠=︒ GE AG ∴=∴矩形AFEG 是正方形四边形ABCD 是正方形 ∴正方形AFEG ∽正方形ABCD∶AE :EC =2:1 ∶AE :AC =2:3 ∴2224()()39AFEG ABCDS AE S AC ===正方形正方形 24461699AFEG ABCD S S ∴==⨯=正方形正方形∶正方形AFEG 的面积为16. 14.解:(1)21290x x --=2129x x -= 21236936x x -+=+()2645x -=635x -=±解得:12635,635x x =+=- (2)四边形ABCD ∽四边形1111D C B A ∴111111AB AD CDA B A D C D == 11111120,5,7,6AB A B A D C D ====1111207285AB A D AD A B ⋅⨯∴===,即28y = 1111206245AB C D CD A B ⋅⨯∴===,即24x = 111,130,70,85C B B A A D D α∠=∠∠=∠=︒∠=∠=︒∠=∠=︒ 11136075C A B D α∴∠=∠=︒-∠-∠-∠=︒.15.∶两个平行四边形相似,∶869a ma = 18055125α∠=︒-︒=︒解得12m =. 16.解:根据已知得四边形ABEF 是正方形. 设AD x =,则2FD x =- 2FE = ∶四边形EFDC 与矩形ABCD 相似 ∶EF AD FD AB=,∶222xx =- 解得115x =215x =. 经检验:15x 是分式方程的解,且符合题意.∶15x即15AD =。
北师大版数学九年级上册第四章第三节4.3 相似多边形 同步练习(包含答案)
第四章图形的相似第三节同步练习一、选择题1. 下图中,各组图形相似的是()A. ①③B. ③④C. ①②D. ①④2. 把一个图形按一定比例放大或缩小时,下列说法中正确的是()A. 图形中线段的长度与角的大小都保持不变B. 图形中线段的长度和角的大小都会改变C. 图形中线段的长度保持不变,角的大小可以改变D. 图形中线段的长度可以改变,角的大小保持不变3. 关于相似多边形的叙述不正确的是()A. 相似多边形对应边的比叫做相似比B. 边数不相同的多边形肯定不相似C. 相似多边形的对应角肯定相等D. 两个多边形不相似,它们肯定没有相等的角4. 一个多边形的边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为()A. 6B. 8C. 9D. 105. 若五边形ABCDE与五边形A1B1C1D1E1相似,且相似比为k1=5,则五边形A1B1C1D1E1与五边形ABCDE的相似比k2为()A. 2B. 15 C. 1.2 D. 16. 将一张矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形的长与宽的比是()A. 2∶1B. 2∶1C. 3∶1D. 2∶27. 已知五边形ABCDE∽五边形A1B1C1D1E1,且AB=2,BC=3,A1B1=4,则B1C1等于()A. 6B. 15C. 5D. 8 38. 在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3,4,5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是()A. 两人都对B. 两人都不对C. 甲对,乙不对D. 甲不对,乙对9. 以下五个命题:①所有的正方形都相似;②所有的矩形都相似;③所有的三角形都相似;④所有的等腰直角三角形都相似;⑤所有的正五边形都相似.其中正确的有.(填序号)10. 如图,四边形ABCD与四边形A′B′C′D′相似,则∠α=,∠β=,AD=.11. 两个正方形的相似比为4∶1,其中较大的正方形的边长为12,则较小正方形的周长为多少?12. 甲同学手中有四根木棒,长度分别为18cm,21cm,12cm,9cm,乙同学手中有四根木棒,长度分别为6cm,7cm,4cm,3cm,甲同学说:以我手中的四根木棒组成的四边形一定与你手中四根棒组成的四边形相似,因为它们的对应边的比是3∶1.乙同学不同意他的看法,为什么?13. 如图,四边形ABCD与四边形EFGH相似吗?请说明理由.14. 如图所示,一个矩形长为a,宽为b(a≠b),若在矩形外侧增加宽度为c的边框,那么所得的矩形和原来的矩形相似吗?为什么?15. 两个正六边形,小正六边形的边长为3cm,大正六边形的周长为24cm.(1)这两个正六边形是否相似?为什么?(2)这两个正六边形中最长对角线的比是多少?16. 如图,已知梯形ABCD,AD∥BC,若EF∥BC,且所分成的梯形AEFD相似于梯形EBCF,AD=12,BC=18,求EF的长.17. 如图,将一张长、宽之比为2的矩形纸ABCD循环多次对折,可以得到矩形纸BCFE,AEML,GMFH,LGPN.(1)矩形ABCD,BCFE,AEML,GMFH,LGPN的长与宽的比改变了吗?(2)在这些矩形中,有成比例的线段吗?(3)你认为这些大小不同的矩形相似吗?1. C2. D3. D4. B5. B6. A7. A8. A9. ①④⑤10. 70° 120° 2811. 解:12 12. 解:因为两个四边形相似除了对应边成比例外,还要求对应角相等,所以虽然它们的对应边之比为3∶1,也不能保证它们相似.13. 解:不一定相似.理由:在四边形ABCD 中,由∠A =80°,∠B =90°,∠C =120°,得∠D =70°.在四边形EFGH 中,由∠F =90°,∠G =120°,∠H =70°,得∠E =80°,∴∠A =∠E ,∠B =∠F ,∠C =∠G ,∠D =∠H .∵根据已知条件无法判定对应边是否对应成比例.∴四边形ABCD 与四边形EFGH 不一定相似.14. 解:不相似.根据题意,外面矩形的长为a +2c ,宽为b +2c ,∵两个矩形的宽之比为b b +2c =1+b 2c ,长之比为a a +2c =1+a 2c ,又∵a ≠b ,∴a 2c ≠b 2c ,1+a 2c ≠1+b 2c ,即a a +2c ≠b b +2c ,∴两个矩形不相似.15. 解:(1)相似,对应角相等,对应边成比例.(2)大正六边形的边长是24÷6=4(cm).因两个正六边形相似,故两个正六边形最长对角线之比为3∶4.16. 解:∵梯形AEFD ∽梯形EBCF .∴EF AD =BC EF ,即EF 2=AD ·BC =12×18=216,∴EF =6(EF =-6不符题意,舍去).17. 解:(1)矩形ABCD ,BCFE ,AEML ,GMFH ,LGPN 的长与宽的比不改变.设纸的宽为a ,长为a ,则BC =a ,BE =22a ;AE =22a ,ME =2a ,MF =2a ,HF =42a ;LG =42a ,LN =4a ;∴BE BC =a ∶22a =;ME AE =22a ∶2a =;HF MF =2a ∶42a =;LN LG =42a ∶4a =;所以这五个矩形的长与宽的比不改变.(2)这些矩形中有成比例的线段.(3)这些大小不同的矩形都相似.。
48相似多边形的性质同步练习及答案
BC=5, AC=6, △ A' B ' C'的最大边长为15,那B' C' 的周长是E⑵如图4 —8—3,在厶ABC中,D、E分别是边AB、AC的中点,△ ADE和四边形BCED的4.8相似多边形的性质(2)同步练习相似多边形的周长比和面积比」、请你填一填(1 )若厶ABCA' B' C', AB=4,么它们的相似比是_________ , △A'(2)两个相似三角形的相似比为 2 : 3,图4—8 —2它们周长的差是25,那么较大三角形的周长是1(3)女口图4—8—1 ,在…ABCD中,延长AB至U E,使BE= —AB,延长CD至U F,使DF=DC,2EF交BC于G,交AD于H,则△ BEG与厶CFG的面积之比是 ____________ .1(4)把一个三角形改做成和它相似的三角形,如果面积缩小到原来的丄倍,那么边长应缩2小到原来的________ 倍.二、认真选一选⑴如图4 —8—2,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )A.2 : 1B. -3 : 1C. . 2 : 1D.4 : 1面积分别记为环彩那么S的值为()1112A. B. C. D.-2 43 3⑶如图4 —8—4,在Rt△ ABC中,AD为斜边BC上的高,若CAD=3S^ABD,贝V AB : AC等于()A.1 : 3B.1 : 4C.1 : 3D.1 : 2(4)顺次连结三角形三边的中点,所成的三角形与原三角形对应高的比是()A.1 : 4B.1 : 3C.1 : , 2D.1 : 2三、灵机一动!哇...某生活小区开辟了一块矩形绿草地,并画了甲、乙两张规划图,其比例尺分别为1 : 200和1 : 500,求这块矩形草地在甲、乙两张图纸上的面积比四、用数学眼光看世界如图4—8—5,^ ABC是一块锐角三角形余料,其中BC=12 cm,高AD=8 cm,现在要把它裁剪成一个正方形材料备用,使正方形的一边在BC上,其余两个顶点分别在AB、AC 上,问这个正方形材料的边长是多少?Q D M图4—8—5参考答案;2 (1) 2 : 5 37.5 (2)75 (3)1 : 16 (4)12二、(1) C(2)C(〕)C (4)D三、解:设这块矩形绿地的面积为S,在甲、乙两张规划图上的面积分别为S1> S2则卷=(1) 2, S2=( 1) 2S200S 500S S• S| =,S2=40000250000c S S 11• ◎: S2= :=25 : 440000250000 425即:这块草地在甲、乙两张图上的面积比为25 : 4四、解:设这个正方形材料的边长为x cm则厶PAN的边PN上的高为(8 —x)cm•••由已知得:△ APN ABCPN 8 —x 口口 x 8 —x 后R/白.•••= ,即一= 解得:x=4.8BC AD 12 8答:这个正方形材料的边长为 4.8 cm.。
相似多边形的性质同步练习(含答案)
相似多边形的性质(典型题汇总)一、选择题1.如图1所示,在△ABC中,DE∥BC,AD:DB=1:2,则下列结论中,正确的是()A.DE BC=12B.DEBC=13C.ADEABC∆∆周长周长=12D.ADEABCSS∆∆=13图1 图2 图32.△ABC三边长分别为2,6,6,△A′B′C′的两边长分别为13 ABC•∽△A′B′C′,那么△A′B′C′的第三边长应为()A2 B.22C633.两相似四边形的面积比为4:9,周长和是20cm,则这两个四边形周长分别是( •)A.8cm和12cm B.9cm和11cm C.7cm和13cm D.4cm和16cm4.如图2所示,已知∠1=∠B,则下列各式正确的是()A.AD:BC=AE:EB B.DE:BC=AD:AC C.AD·AC=AE·AB D.AC·AE=AD·AB 5.如图3,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离为3m,则点P到AB的距离是()A.56m B.67m C.65m D.103m二、填空题6.在△ABC中,D,E分别是AB,AC的中点,则S△ADE:S四边形DEBC=_____.7.用一个3倍的放大镜照一个多边形,则放大后的面积是原来的______倍.8.如图4所示,在△ABC与△DBE中,AB BC ACBD BE DE===53,且△ABC和△BDE周长之差为10cm,•则△ABC的周长为______.图4 图5 9.如图5,已知△ABC∽△DBE,AB=6,DB=8,则S△ABC:S△DBE=______.三、解答题10.如图所示,AD,BE是△ABC的高,A′D′,B′E′是△A′B′C的高,且```` AB A B AD A D=,∠C=∠C′,求证:AD·B′E′=A′D′·BE.11.如图所示,设AB BC CAAD DE EA==,求证:∠1=∠2.12.在△ABC中,如图所示,AB=AC,BD为腰上的高,求证:CD·CA=12BC2.参考答案一、1.B 点拨:因为DE ∥BC ,所以△ADE ∽△ABC ,又因为AD DB =12,所以可知AD AB =13,所以DE BC =13. 2.A 点拨:因为△ABC ∽△A ′B ′C′,所以可知三条边对应成比例,又通过观察知1=所以可知6与另一条边的比也是:1,. 3.A 点拨;根据相似三角形面积比等于相似比的平方,•周长比等于相似比可求得,此题也可采用排除法,因为题中告诉两个三角形面积比为4:9,所以周长比为2:3,可看备选答案中,哪一个符合2:3.4.C 点拨:因为∠1=∠B ,∠A 为公共角,所以△ADE ∽△ABC ,所以有AD AEAB AC=,即AD ·AC=AE ·AB .5.C 点拨:因为AB ∥CD ,所以△PAB ∽△PCD .设点P 到AB 的距离为x ,•根据相似三角形对应高的比等于相似比,得3x =25,所以x=65(m ),故选C .二、6.1:3 点拨:因为△ADE 与△ABC 的相似比为1:2,面积比为1:4,•所以在△ABC 中减去△ADE ,余下的四边形面积是△ADE 面积的3倍. 7.9 点拨:因为放大比例是3:1,所以面积比就应该是9:1.8.25cm 点拨:因为这两个三角形的三边对应成比例,所以这两个三角形相似,•所以周长比等于相似比等于5:3,又因为周长相差10cm ,所以可以求得△ABC 的周长. 9.9:16 点拨:2269()()816ABC DBE S AB S DB ∆∆===. 三、10.证明:因为∠ADB=∠A ′D ′B ′=90°,````AB A B AD A D =, 所以△ABD ∽△A ′B ′D ′,所以∠ABD=∠A ′B ′D ′. 又因为∠C=∠C ′,所以△ABC ∽△A ′B ′C ′.所以``AB A B =````AD BEA DB E =,即AD ·B ′E ′=A ′D ′·BE . 点拨:AD ·B ′E ′=A ′D ′·BE 化成比例式为````AD BEA DB E =,因为AD ,A ′D ′,BE ,B ′E•′是△ABC 与△A ′B ′C ′的高.根据相似三角形对应高的比等于相似比,•所以可以想办法证得△ABC ∽△A ′B ′C ′.11.错解:因为AB BC CAAD DE EA==,所以△ABC ∽△ADE . 所以∠BAC=∠DAE .又因为AB CAAD EA=,•所以△ABD•∽△ACE .所以∠1=∠2. 正确解法:因为AB BC CAAD DE EA==,所以△ABC ∽△ADE ,所以∠α+∠3=∠β+∠3,所以∠α=∠β.又因为AB CAAD EA=,•所以△ABD ∽△ACE .所以∠1=∠2. 点拨:在证△ABD ∽△ACE 时,漏掉条件∠α=∠β,事实上,已证∠BAC=∠DAE ,•只需等式两边都减去∠3即可,但由于存在潜在假设∠BAC=∠DAE 必然得∠α=∠β,•致使判定△ABD ∽△ACE 的理由不充分.12.证明:如图所示,过点A 作AE ⊥BC ,垂足为E ,因为AB=AC ,所以EC=12BC ,∠AEC=90°. 又因为BD 是腰上的高,所以∠BDA=90°,所以∠AEC=∠BDA . 又因为∠C=∠C ,所以△AEC ∽△BDC . 所以EC AC CD BC =,所以CA ·CD=CE ·CB=12BC ·BC=12BC 2.点拨:从结论CD ·CA=12BC 2有CD ·CA=12BC ·BC ,由此想到作底边上的高AE ,有EC=12BC ,则结论化为CD ·CA=CE ·CB ,进而只需证△AEC ∽△BDC 即可.相似多边形的性质一、七彩题1.(一题多解)如图,D,E,F分别是AB,BC,CA的中点,求S△EFD:S△ABC.2.(巧题妙解题)如图所示,把△ABC平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC的一半,若AB=2,则此三角形移动的距离AA′等于______.二、知识交叉题3.(科内交叉题)如图所示,在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,AC=63,求BC和BD的长.4.(当堂交叉题)如图,Y ABCD中,AE:EB=1:2,求△AEF与△CDF的周长的比,如果S△AEF=6cm2,求S△CDF.三、实际应用题5.△ABC是一块锐角三角形的余料,如图所示,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是多少?四、经典中考题6.(2007,青岛,3分)如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为_____cm.(第6题) (第7题) (第8题) 7.(2007,常州,3分)如图,已知DE∥BC,AD=6,DB=3,BC=9.9,∠B=50°,•则∠ADE=_____°,DE=____,ADEABCSS∆∆=_____.8.(2008,河南,3分)如图,在矩形ABCD中,E,F分别是边AD,BC的中点,点G,H 在DC边上,且GH=12DC.若AB=10,BC=12,则图中阴影部分的面积为______.五、课标新型题9.(规律探究题)如图所示,点E是四边形ABCD•的对角线BD•上一点,•且∠ABC=∠BDC=∠DAE.(1)求证:BE·AD=CD·AE;(2)根据图形的特点,猜想BCDE可能等于哪两条线段的比?并证明你的猜想.10.(阅读理解题)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.(1)如图①,四边形DEFG为△ABC的内接正方形,求正方形的边长;(2)如图②,正方形DKHG,EKHF组成的矩形内接于△ABC,求正方形的边长;(3)如图③,三个正方形组成的矩形内接于△ABC,求正方形的边长;(4)如图④,n个正方形组成的矩形内接于△ABC,求正方形的边长.11.如图,E,F分别为Y ABCD的对角线DB上的三等分点,连接AE并延长交DC于P,•连接PF并延长交AB于Q.通过观察,猜测AQ,BQ之间的关系,并说明为什么?参考答案一、1.解法一:因为D ,E ,F 分别是AB ,BC ,AC 的中点,所以DE EF DF AC BA BC ===12,所以△EFD ∽△ABC ,所以S △EFD :S △ABC =1:4.解法二:因为D ,E 分别是AB 和BC 的中点,所以DE ∥AC , 所以∠BDE=∠A ,∠BED=∠C ,所以△BDE ∽△BAC . 所以2()BDE ABC S BD S AB ∆∆==(12)2=14. 同理,2()ADF ABC S AD S AB ∆∆==(12)2=14,2()CEF ABC S CE S BC ∆∆==(12)2=14, 即S △BDE =S △ADF =S △CEF =14S △ABC . 所以S △EFD =S △ABC -(S △BDE +S △ADF +S △CEF )=14S △ABC ,即S △EFD :S △ABC =1:4. 2-1 点拨:因为△A ′B ′C ′是△ABC 沿AB 边平移得到的, 所以A ′C ′∥AC ,•△ABC 与阴影三角形相似, 所以(`A B AB )2=12,因为, 所以A ′B=1,故AA ′-1,•本题的巧妙之处在运用平移的性质得到两个三角形相似.二、3.解:因为CD 是Rt △ABC 中斜边上的高,所以△ACD ∽△CBD ∽△ABC ,•因为∠A=30°,所以∠DCB=30°.又因为CD=12设BD=x ,则BC=2x ,在Rt △BCD 中,BC 2-BD 2=CD 2, 所以4x 2-x 2=27,x=3,所以BC=6,BD=3. 4.解:因为AE :EB=1:2,所以AE AB =13,即AE CD =13. 又因为AB ∥DC ,所以△AEF ∽△CDF . 故C △AEF :C △CDF =1:3,S △AEF :S △CDF =1:9. 故当S △AEF =6cm 2时,S △CDF =6×9=54(cm 2).三、5.解:设正方形PQMN 为加工成的正方形零件,边QM 在BC 上,顶点P ,N 分别在AB ,AC上,△ABC的高AD与PN相交于点E.设正方形的边长为xmm.因为PN∥BC,所以△APN∽△ABC,所以AE PN AD BC=.因此有8080120x x-=,解之得x=48.答:加工成的正方形零件的边长为48mm.四、6.16 点拨:由题意可知,AB∥CD,△OAB∽△OCD,根据相似三角形对应高的比等于相似比,得453620CD=,解得CD=16(cm).7.50;6.6;49点拨:相似三角形对应角相等,对应边成比例,相似三角形面积的比等于相似比的平方.8.35 点拨:连EF,则GH//12EF,S矩形EFCD=6×10=60.设EH交FG于O,则△EFO∽△HGO•相似比为2:1,两三角形EF与GH边上的高h1:h2=2:1,h1+h2=6,故h1=4,h2=2,S△EFO=12EH·h1=12×10×4=20,S△GOH=12GH·h=12×5×2=5,故S阴影=S矩形EFCD-S△EFO -S△GOH =60-25=36.此题综合考查矩形性质,•相似三角形相似比,求阴影部分面积.五、9.(1)证明:因为∠BAC=∠DAE.所以∠BAC+∠1=∠DAE+∠1,即∠EAB=∠DAC.又因为∠AEB=∠2+∠DAE,∠ADC=∠2+∠BDC,∠DAE=∠BDC,所以∠AEB=∠ADC,•所以△AEB∽△ADC,所以BE AEDC AD=,即BE·AD=CD·AE.(2)解:BCDE等于ACAD.因为△AEB∽△ADC,所以AD AEAC AB=.又因为∠DAE=∠CAB,所以△ADE∽△ACB.所以BCDE=ACAD.点拨:学会仔细观察图形,从图形中提取解读思路.10.解:(1)在题图①中作CN⊥AB于点N,交GF于点M.因为∠C=90°,AC=4,BC=3,所以AB=5.因为12×5CN=12×3×4,所以CN=125.因为GF∥AB,所以∠CGF=∠A,∠CFG=∠B.所以△CGF∽△CAB,所以CM GF CN AB=.设正方形的边长为x,则125125x-=5x,解得x=6037.所以正方形的边长为60 37.(2)同(1),125125x-=25x,解得x=6049.(3)同(1),125125x-=35x,解得x=6061.(4)同(1),125125x-=5nx,解得x=602512n+.点拨:根据相似三角形的性质(相等关系)列方程求解,是解答此类问题的一般方法.11.解:猜测:AQ=3BQ.Y ABCD中,DC∥AB,所以△PDF∽△QBF,DP DFBQ BF=,因为E,F分别为BD的三等分点,所以DPBQ=2,•同理ABPD=2,所以ABBQ=4,所以AQBQ=3,即AQ=3BQ.11。
最新2019-2020年度北师大版九年级数学上册《相似多边形》同步练习及答案解析-精品试题
北师大版九年级数学上册3.3相似多边形同步练习一、选择题1.用一个2倍放大镜照一个△ABC,下面说法中错误的是()A.△ABC放大后,是原来的2倍B.△ABC放大后,各边长是原来的2倍C.△ABC放大后,周长是原来的2倍D.△ABC放大后,面积是原来的4倍答案:A解析:解答:∵放大前后的三角形相似,∴放大后三角形的内角度数不变,面积为原来的4倍,周长和边长均为原来的2倍.故本题选A.分析:用2倍的放大镜放大一个△ABC,得到一个与原三角形相似的三角形;根据相似三角形的性质:相似三角形的面积比等于相似比的平方,周长比等于相似比.可知:放大后三角形的面积是原来的4倍,边长和周长是原来的2倍,而内角的度数不会改变.2.我国国土面积约为960万平方千米,画在比例尺为1:1000万的地图上的面积约是()A.960平方千米B.960平方米C.960平方分米D.960平方厘米答案:D解析:解答:16万平方千米平方厘米,=⨯9609.610设画在地图上的面积约为x平方厘米,则162x⨯=:(:万),9.61011000解得x=960.则画在地图上的面积约为960平方厘米.故选D.分析:相似多边形的面积比等于相似比的平方,据此求解,注意统一单位.3.如图,一张矩形纸片ABCD 的长AB=a ,宽BC=b .将纸片对折,折痕为EF ,所得矩形AFED 与矩形ABCD 相似,则a :b=( )A .2:1B .2:1C .3:3D .3:2答案:B解析:解答:∵矩形纸片对折,折痕为EF , ∴1122AF AB a ==, ∵矩形AFED 与矩形ABCD 相似, ∴AB AD AD AF =,即12a b b a =, ∴22a b=(), ∴2a b=. 故选B . 分析:根据折叠性质得到1122AF AB a ==,再根据相似多边形的性质得到AB AD AD AF =,即12a b b a =,然后利用比例的性质计算即可. 4.两个相似多边形的一组对分别是3cm 和4.5cm ,如果它们的面积之和是278cm ,那么较大的多边形的面积是( )A .44.8B .42C .52D .54答案:D解析:解答:设较大多边形与较小多边形的面积分别是m ,n .则2344.59n m ==(). 因而49n m =. 根据面积之和是78cm2.得到4789m m +=. 解得:254m cm =.故选D .分析:根据相似多边形相似比即对应边的比,面积的比等于相似比的平方,即可解决.5.两个相似多边形的面积之比为1:9,则它们的周长之比为( )A .1:3B .1:9C .1:3D .2:3答案:A解析:解答:∵两个相似多边形的面积之比为1:9,∴两个相似多边形的边长之比是1:3,∴它们的周长之比为1:3.故选A .分析:根据相似多边形的面积之比等于相似比的平方和相似多边形的周长之比等于相似比得出即可.6.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )A .B .C .D .解析:解答:由题意得,A 中三角形对应角相等,对应边成比例,两三角形相似;C ,D 中正方形,菱形四条边均相等,所以对应边成比例,又角也相等,所以正方形,菱形相似;而B 中矩形四个角相等,但对应边不一定成比例,所以B 中矩形不是相似多边形 故选B .分析:此题考查相似多边形的判定问题,其对应角相等,对应边成比例.7.某块面积为24000m 的多边形草坪,在嘉兴市政建设规划设计图纸上的面积为2250cm ,这块草坪某条边的长度是40m ,则它在设计图纸上的长度是( )A .4cmB .5cmC .10cmD .40cm答案:C解析:解答:设这块草坪在设计图纸上的长度是xcm ,224000m 40000000m =,40m=4000cm , 根据题意得:2400000004000250x=(), 解得:x=10,即这块草坪在设计图纸上的长度是10cm .故选C .分析:首先设这块草坪在设计图纸上的长度是xcm ,根据题意可得这两个图形相似,根据相似图形的面积比等于相似比的平方,可列方程2400000004000250x=(),解此方程即可求得答案,注意统一单位.8.一个多边形的边长分别为2,3,4,5,6,另一个多边形和这个多边形相似,且最短边长为6,则最长边长为( )A .18B .12C .24答案:A解析:解答:设这个多边形的最长边是x,则26=,6x解得x=18.故选A.分析:根据题意找出最短边与最长边,然后根据相似多边形对应边成比例列式计算即可.9.若两个相似多边形的面积之比为1:4,则它们的周长之比为()A.1:4B.1:2C.2:1D.4:1答案:B解析:解答:∵两个相似多边形面积比为1:4,∴周长之比为112=:.4故选:B.分析:根据相似多边形的面积之比等于相似比的平方,周长之比等于相似比,就可求解.10.如果两个相似多边形面积的比为1:5,则它们的相似比为()A.1:25B.1:5C.1:2.5D.15:答案:D解析:解答:∵两个相似多边形面积的比为1:5,:.∴它们的相似比为15故选:D.分析:根据相似多边形的面积的比等于相似比的平方解答.11.对一个图形进行放缩时,下列说法中正确的是()A.图形中线段的长度与角的大小都保持不变B.图形中线段的长度与角的大小都会改变C.图形中线段的长度保持不变、角的大小可以改变D.图形中线段的长度可以改变、角的大小保持不变答案:D解析:解答:根据相似多边形的性质:相似多边形的对应边成比例,对应角相等,∴对一个图形进行收缩时,图形中线段的长度改变,角的大小不变,故选D.分析:根据相似图形的性质得出相似图形的对应边成比例,对应角相等,即可得出答案.12.下面给出了一些关于相似的命题,其中真命题有()(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.A.1个B.2个C.3个D.4个答案:C解析:解答:(1)所有菱形的对应角不一定相等,故菱形不一定都相似;(2)等腰直角三角形都相似,正确;(3)正方形都相似,正确;(4)矩形对应边比值不一定相等,不矩形不一定都相似;(5)正六边形都相似,正确,故符合题意的有3个.故选:C.分析:利用相似图形的性质分别判断得出即可.13.如果两个相似多边形的面积比为16:9,那么这两个相似多边形的相似比为()A.16:9B.4:3C.2:3D.256:81解析:解答:根据题意得:164.93故选:B.分析:根据两个相似多边形的面积比为16:9,面积之比等于相似比的平方.14.下列判断正确的是()A.所有的直角三角形都相似B.所有的等腰直角三角形都相似C.所有的菱形都相似D.所有的矩形都相似答案:B解析:解答:A、所有的直角三角形只有直角相等,所以不一定都相似,故本选项错误;B、所有的等腰直角三角形都相似正确,故本选项正确;C、所有的菱形只有对应边成比例,对应角不一定相等,所以,不一定相似,故本选项错误;D、所有的矩形对应角相等,对应边不一定成比例,所以不一定相似,故本选项错误.故选B.分析:根据对应边成比例,对应角相等的图形叫做相似图形对各选项分析判断后利用排除法求解.15.如图,用放大镜将图形放大,这种图形的改变是()A.相似B.平移C.轴对称D.旋转答案:A解析:解答:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.分析:根据轴对称变换、平移变换、旋转变换、相似变换的特点,结合图形即可得出答案.二、填空题16.若两个相似多边形的对应边之比为5:2,则它们的周长比是_____.答案:5:2解析:解答:∵两个相似多边形的对应边的比是5:2,∴这两个多边形的周长比是5:2.故答案为:5:2.分析:根据相似多边形的周长的比等于相似比解答即可.17.图中的两个四边形相似,则x y +=______,a=______.答案:63|85°解析:解答:由于两个四边形相似,它们的对应边成比例,对应角相等,所以18486x y ==:::,解得x=36,y=27,则362763x y +=+=. 360778311585a =︒-︒+︒+︒=︒().故答案为63;85°.分析:根据相似多边形的性质:对应角相等,对应边成比例即可求解.18.若两个相似多边形的面积比是16:25,则它们的周长比等于______.答案:4:5解析:解答:∵两个相似多边形面积的比为16:25,∴两个相似多边形周长的比等于4:5,∴这两个相似多边形周长的比是4:5.故答案为:4:5.分析:直接根据相似多边形周长的比等于相似比,面积的比等于相似比的平方进行解答即可.19.如图,在长8cm ,宽4cm 的矩形中截去一个矩形(阴影部分)使留下的矩形与原矩形相似,那么留下的矩形的面积为______2cm .答案:8解析:解答:设留下的矩形的宽为x ,∵留下的矩形与原矩形相似, ∴ 4 48x =, x=2,∴留下的矩形的面积为:2248cm ⨯=()故答案为:8.分析:本题需先设留下的矩形的宽为x ,再根据留下的矩形与矩形相似,列出方程即可求出留下的矩形的面积.20.如图,E 、F 分别是平行四边形ABCD 的边AD 、BC 的中点,若四边形AEFB 与四边形ABCD 相似,AB=4,则AD 的长度为______.答案:42解析:解答:设AE=x ,则AD=2x ,∵四边形ABCD 与矩四边形ABFE 是相似的, ∴AE AB AB AD=, ∴222AB x =, ∴24AB x ==, ∴22x =, ∴42AD =, 故答案为:42.分析:首先设AE=x ,则AD=2x ,进而利用四边形ABCD 与四边形ABFE 是相似的,则AE AB AB AD=,进而求出即可三、解答题21.如图,四边形ABCD 和四边形EFGH 相似,求∠α、∠β的大小和EH 的长度.答案:解答:∵四边形ABCD 和四边形EFGH 相似,∴∠α=∠B=83°,∠D=∠H=118°,360837811881β∠=︒-︒+︒+︒=︒(),EH AD HG DC =::, ∴242118EH =, ∴EH=28(cm ).答:∠α=83°,∠β=81°,EH=28cm .解析:分析:观察图形,根据相似多边形的对应角相等可得出∠α=∠B=83°,∠D=∠H=118°,再根据四边形的内角和等于360°可计算求出β的大小,然后根据相似多边形的对应边成比例即可求出EH 的长度.22.两个相似五边形,一组对应边的长分别为3cm 和4.5cm ,如果它们的面积之和是278cm ,则这两个五边形面积各是多少2cm ?答案:解答:设较小五边形与较大五边形的面积分别是2cm x ,2cm y . 则2344.59x y ==(),因而49x y =. 根据面积之和是278cm ,得到4789y y +=, 解得:54y =, 则454249x =⨯=.即较小五边形与较大五边形的面积分别是224cm ,254cm .解析:分析:根据相似多边形相似比即对应边的比,面积的比等于相似比的平方,即可解决.23.把一个长方形(如图)划分成两个全等的长方形.若要使每一个小长方形与原长方形相似,问原长方形应满足什么条件?答案:解答:设AE=ED=a ,AB=b ,∵每一个小长方形与原长方形相似, ∴2a b b a=, ∴222b a =,∵a,b 均为正数,∴2b a =, ∴2222AD a a AB b a===, ∴原长方形的长与宽之比为21:.解析:分析:设AE=ED=a ,AB=b ,根据每一个小长方形与原长方形相似,可知2a b b a =,再由a ,b 均为正数可知2b a =,故2222AD a a AB b a===,由此即可得出结论. 24.如图,把矩形ABCD 对折,折痕为MN ,矩形DMNC 与矩形ABCD 相似,已知2AD = ,求AB 的长.答案:解答:∵2AD =, ∴22MD NC ==,∵矩形DMNC 与矩形ABCD 相似, ∴NC MN AB AD =,即222AB AB =, ∴AB=1. 解析:分析:先根据2AD =求出MD 的长,再根据矩形DMNC 与矩形ABCD 相似得出矩形对应边的比例式,求出AB 的长即可.25.我们通常用到的一种复印纸,整张称为1A 纸,对折一分为二裁开成为2A 纸,再一分为二成为3A 纸,…,它们都是相似的矩形.求这种纸的长与宽的比值(精确到千分位). 答案:1.414解析:解答:设1A 纸的长为a ,宽为b ,2A 纸的长为b ,宽为2a , 由1A 、2A 纸的长与宽对应比成比例,得 12a b b a =, 故2 1.4141a b =≈. 故答案为:1.414.分析:分别设1A 纸的长为a ,宽为b ,2A 纸的长为b ,宽为2a ,再由相似多边形的对应边成比例列出比例式,求出a b 的值即可.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似多边形的性质(典型题汇总)一、选择题1.如图1所示,在△ABC中,DE∥BC,AD:DB=1:2,则下列结论中,正确的是()A.DE BC=12B.DEBC=13C.ADEABC∆∆周长周长=12D.ADEABCSS∆∆=13图1 图2 图32.△ABC三边长分别为2,6,6,△A′B′C′的两边长分别为13 ABC•∽△A′B′C′,那么△A′B′C′的第三边长应为()A2 B.22C633.两相似四边形的面积比为4:9,周长和是20cm,则这两个四边形周长分别是( •)A.8cm和12cm B.9cm和11cm C.7cm和13cm D.4cm和16cm4.如图2所示,已知∠1=∠B,则下列各式正确的是()A.AD:BC=AE:EB B.DE:BC=AD:AC C.AD·AC=AE·AB D.AC·AE=AD·AB 5.如图3,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离为3m,则点P到AB的距离是()A.56m B.67m C.65m D.103m二、填空题6.在△ABC中,D,E分别是AB,AC的中点,则S△ADE:S四边形DEBC=_____.7.用一个3倍的放大镜照一个多边形,则放大后的面积是原来的______倍.8.如图4所示,在△ABC与△DBE中,AB BC ACBD BE DE===53,且△ABC和△BDE周长之差为10cm,•则△ABC的周长为______.图4 图5 9.如图5,已知△ABC∽△DBE,AB=6,DB=8,则S△ABC:S△DBE=______.三、解答题10.如图所示,AD,BE是△ABC的高,A′D′,B′E′是△A′B′C的高,且```` AB A B AD A D=,∠C=∠C′,求证:AD·B′E′=A′D′·BE.11.如图所示,设AB BC CAAD DE EA==,求证:∠1=∠2.12.在△ABC中,如图所示,AB=AC,BD为腰上的高,求证:CD·CA=12BC2.参考答案一、1.B 点拨:因为DE ∥BC ,所以△ADE ∽△ABC ,又因为AD DB =12,所以可知AD AB =13,所以DE BC =13. 2.A 点拨:因为△ABC ∽△A ′B ′C′,所以可知三条边对应成比例,又通过观察知1=所以可知6与另一条边的比也是:1,. 3.A 点拨;根据相似三角形面积比等于相似比的平方,•周长比等于相似比可求得,此题也可采用排除法,因为题中告诉两个三角形面积比为4:9,所以周长比为2:3,可看备选答案中,哪一个符合2:3.4.C 点拨:因为∠1=∠B ,∠A 为公共角,所以△ADE ∽△ABC ,所以有AD AEAB AC=,即AD ·AC=AE ·AB .5.C 点拨:因为AB ∥CD ,所以△PAB ∽△PCD .设点P 到AB 的距离为x ,•根据相似三角形对应高的比等于相似比,得3x =25,所以x=65(m ),故选C .二、6.1:3 点拨:因为△ADE 与△ABC 的相似比为1:2,面积比为1:4,•所以在△ABC 中减去△ADE ,余下的四边形面积是△ADE 面积的3倍. 7.9 点拨:因为放大比例是3:1,所以面积比就应该是9:1.8.25cm 点拨:因为这两个三角形的三边对应成比例,所以这两个三角形相似,•所以周长比等于相似比等于5:3,又因为周长相差10cm ,所以可以求得△ABC 的周长. 9.9:16 点拨:2269()()816ABC DBE S AB S DB ∆∆===. 三、10.证明:因为∠ADB=∠A ′D ′B ′=90°,````AB A B AD A D =, 所以△ABD ∽△A ′B ′D ′,所以∠ABD=∠A ′B ′D ′. 又因为∠C=∠C ′,所以△ABC ∽△A ′B ′C ′.所以``AB A B =````AD BEA DB E =,即AD ·B ′E ′=A ′D ′·BE . 点拨:AD ·B ′E ′=A ′D ′·BE 化成比例式为````AD BEA DB E =,因为AD ,A ′D ′,BE ,B ′E•′是△ABC 与△A ′B ′C ′的高.根据相似三角形对应高的比等于相似比,•所以可以想办法证得△ABC ∽△A ′B ′C ′.11.错解:因为AB BC CAAD DE EA==,所以△ABC ∽△ADE . 所以∠BAC=∠DAE .又因为AB CAAD EA=,•所以△ABD•∽△ACE .所以∠1=∠2. 正确解法:因为AB BC CAAD DE EA==,所以△ABC ∽△ADE ,所以∠α+∠3=∠β+∠3,所以∠α=∠β.又因为AB CAAD EA=,•所以△ABD ∽△ACE .所以∠1=∠2. 点拨:在证△ABD ∽△ACE 时,漏掉条件∠α=∠β,事实上,已证∠BAC=∠DAE ,•只需等式两边都减去∠3即可,但由于存在潜在假设∠BAC=∠DAE 必然得∠α=∠β,•致使判定△ABD ∽△ACE 的理由不充分.12.证明:如图所示,过点A 作AE ⊥BC ,垂足为E ,因为AB=AC ,所以EC=12BC ,∠AEC=90°. 又因为BD 是腰上的高,所以∠BDA=90°,所以∠AEC=∠BDA . 又因为∠C=∠C ,所以△AEC ∽△BDC . 所以EC AC CD BC =,所以CA ·CD=CE ·CB=12BC ·BC=12BC 2.点拨:从结论CD ·CA=12BC 2有CD ·CA=12BC ·BC ,由此想到作底边上的高AE ,有EC=12BC ,则结论化为CD ·CA=CE ·CB ,进而只需证△AEC ∽△BDC 即可.相似多边形的性质一、七彩题1.(一题多解)如图,D,E,F分别是AB,BC,CA的中点,求S△EFD:S△ABC.2.(巧题妙解题)如图所示,把△ABC平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC的一半,若AB=2,则此三角形移动的距离AA′等于______.二、知识交叉题3.(科内交叉题)如图所示,在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,AC=63,求BC和BD的长.4.(当堂交叉题)如图,Y ABCD中,AE:EB=1:2,求△AEF与△CDF的周长的比,如果S△AEF=6cm2,求S△CDF.三、实际应用题5.△ABC是一块锐角三角形的余料,如图所示,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是多少?四、经典中考题6.(2007,青岛,3分)如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为_____cm.(第6题) (第7题) (第8题) 7.(2007,常州,3分)如图,已知DE∥BC,AD=6,DB=3,BC=9.9,∠B=50°,•则∠ADE=_____°,DE=____,ADEABCSS∆∆=_____.8.(2008,河南,3分)如图,在矩形ABCD中,E,F分别是边AD,BC的中点,点G,H 在DC边上,且GH=12DC.若AB=10,BC=12,则图中阴影部分的面积为______.五、课标新型题9.(规律探究题)如图所示,点E是四边形ABCD•的对角线BD•上一点,•且∠ABC=∠BDC=∠DAE.(1)求证:BE·AD=CD·AE;(2)根据图形的特点,猜想BCDE可能等于哪两条线段的比?并证明你的猜想.10.(阅读理解题)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.(1)如图①,四边形DEFG为△ABC的内接正方形,求正方形的边长;(2)如图②,正方形DKHG,EKHF组成的矩形内接于△ABC,求正方形的边长;(3)如图③,三个正方形组成的矩形内接于△ABC,求正方形的边长;(4)如图④,n个正方形组成的矩形内接于△ABC,求正方形的边长.11.如图,E,F分别为Y ABCD的对角线DB上的三等分点,连接AE并延长交DC于P,•连接PF并延长交AB于Q.通过观察,猜测AQ,BQ之间的关系,并说明为什么?参考答案一、1.解法一:因为D ,E ,F 分别是AB ,BC ,AC 的中点,所以DE EF DF AC BA BC ===12,所以△EFD ∽△ABC ,所以S △EFD :S △ABC =1:4.解法二:因为D ,E 分别是AB 和BC 的中点,所以DE ∥AC , 所以∠BDE=∠A ,∠BED=∠C ,所以△BDE ∽△BAC . 所以2()BDE ABC S BD S AB ∆∆==(12)2=14. 同理,2()ADF ABC S AD S AB ∆∆==(12)2=14,2()CEF ABC S CE S BC ∆∆==(12)2=14, 即S △BDE =S △ADF =S △CEF =14S △ABC . 所以S △EFD =S △ABC -(S △BDE +S △ADF +S △CEF )=14S △ABC ,即S △EFD :S △ABC =1:4. 2-1 点拨:因为△A ′B ′C ′是△ABC 沿AB 边平移得到的, 所以A ′C ′∥AC ,•△ABC 与阴影三角形相似, 所以(`A B AB )2=12,因为, 所以A ′B=1,故AA ′-1,•本题的巧妙之处在运用平移的性质得到两个三角形相似.二、3.解:因为CD 是Rt △ABC 中斜边上的高,所以△ACD ∽△CBD ∽△ABC ,•因为∠A=30°,所以∠DCB=30°.又因为CD=12设BD=x ,则BC=2x ,在Rt △BCD 中,BC 2-BD 2=CD 2, 所以4x 2-x 2=27,x=3,所以BC=6,BD=3. 4.解:因为AE :EB=1:2,所以AE AB =13,即AE CD =13. 又因为AB ∥DC ,所以△AEF ∽△CDF . 故C △AEF :C △CDF =1:3,S △AEF :S △CDF =1:9. 故当S △AEF =6cm 2时,S △CDF =6×9=54(cm 2).三、5.解:设正方形PQMN 为加工成的正方形零件,边QM 在BC 上,顶点P ,N 分别在AB ,AC上,△ABC的高AD与PN相交于点E.设正方形的边长为xmm.因为PN∥BC,所以△APN∽△ABC,所以AE PN AD BC=.因此有8080120x x-=,解之得x=48.答:加工成的正方形零件的边长为48mm.四、6.16 点拨:由题意可知,AB∥CD,△OAB∽△OCD,根据相似三角形对应高的比等于相似比,得453620CD=,解得CD=16(cm).7.50;6.6;49点拨:相似三角形对应角相等,对应边成比例,相似三角形面积的比等于相似比的平方.8.35 点拨:连EF,则GH//12EF,S矩形EFCD=6×10=60.设EH交FG于O,则△EFO∽△HGO•相似比为2:1,两三角形EF与GH边上的高h1:h2=2:1,h1+h2=6,故h1=4,h2=2,S△EFO=12EH·h1=12×10×4=20,S△GOH=12GH·h=12×5×2=5,故S阴影=S矩形EFCD-S△EFO -S△GOH =60-25=36.此题综合考查矩形性质,•相似三角形相似比,求阴影部分面积.五、9.(1)证明:因为∠BAC=∠DAE.所以∠BAC+∠1=∠DAE+∠1,即∠EAB=∠DAC.又因为∠AEB=∠2+∠DAE,∠ADC=∠2+∠BDC,∠DAE=∠BDC,所以∠AEB=∠ADC,•所以△AEB∽△ADC,所以BE AEDC AD=,即BE·AD=CD·AE.(2)解:BCDE等于ACAD.因为△AEB∽△ADC,所以AD AEAC AB=.又因为∠DAE=∠CAB,所以△ADE∽△ACB.所以BCDE=ACAD.点拨:学会仔细观察图形,从图形中提取解读思路.10.解:(1)在题图①中作CN⊥AB于点N,交GF于点M.因为∠C=90°,AC=4,BC=3,所以AB=5.因为12×5CN=12×3×4,所以CN=125.因为GF∥AB,所以∠CGF=∠A,∠CFG=∠B.所以△CGF∽△CAB,所以CM GF CN AB=.设正方形的边长为x,则125125x-=5x,解得x=6037.所以正方形的边长为60 37.(2)同(1),125125x-=25x,解得x=6049.(3)同(1),125125x-=35x,解得x=6061.(4)同(1),125125x-=5nx,解得x=602512n+.点拨:根据相似三角形的性质(相等关系)列方程求解,是解答此类问题的一般方法.11.解:猜测:AQ=3BQ.Y ABCD中,DC∥AB,所以△PDF∽△QBF,DP DFBQ BF=,因为E,F分别为BD的三等分点,所以DPBQ=2,•同理ABPD=2,所以ABBQ=4,所以AQBQ=3,即AQ=3BQ.11。
