材料的应力和应变的关系
应力和应变之间的关系
即为平面应力状态,有
1
1 E
s 1 s 3
3
1 E
s 3 s 1
联立两式可解得:
s1
E 1
2
1 3
210 10 1 0 .3
2
9
240
0 . 3 160 10
6
s3
44 . 3 M Pa 9 E 210 10 3 1 160 0 . 3 240 10 2 2 1 1 0 .3
利用空间应力状态下最大切应力的计算式可得:
t max s1 s3
2 7.25MPa
§7-5 平面应力状态下的电测法
对各向同性材料图示平面应力状态,在线弹性、 小变形条件下,sx、sy与切应变无关,即有:
sy sx
x y
1 E 1 E
s s
E
x
s s s
y
y F a
sy sx sz
x
a
(a)
z
(b)
解:铜块应力状态如图b所示,横截面上的压应力为:
s
y
F A
30 MPa
受钢槽的限制,铜块在另两个方向的应变为零, 并产生压应力,即有:
x z
1 E 1 E
s s
x
s s
y
s s
z
0 0
所以,应变能密度为: v
d V dxdydz
1tx 2 G
而对纯剪应力状态,其主应力为:
s 1 tx
s2tx
s1 t
x
s
2
应力与应变间的关系

22
例题7-7 边长 a = 0.1m 的铜立方块, 无间隙地放入体积较
大, 变形可略去不计的钢凹槽中, 如图 所示。 已知铜的弹 性模量 E=100GPa, 泊松比 =0.34, 当受到P=300kN 的均布 压力作用时, 求该铜块的主应力. 体积应变以及最大剪应力。
P a
y
z
x
23
y
解:铜块上截面上的压应力为
9
3、 特例
(1)平面应力状态下(假设 Z = 0 )
x
1 E
(
x
y)
y
1 E
(
y
x)
z E ( x y)
xy
xy
G
10
(2) 广义胡克定律用主应力和主应变表示时 三向应力状态下:
1
1
E [ 1
(
2
3)]
2
1 E
[
2
(
3
1)]
3
1 E
[
3
( 1
2)]
(7-7-6)
11
平面应力状态下 设 3 = 0, 则
x y z x y y z z x
y
σy
上面
x y z x y y z z x
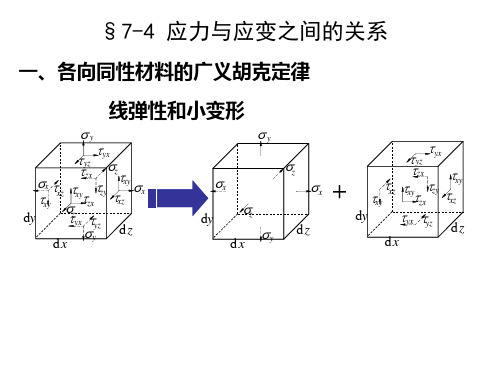
1、各向同性材料的广义胡克定律 (1)符号规定
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量:拉应力为正
σz
x
o
压应力为负。 z
前面
3
(b)三个剪应力分量: 若正面(外法线与坐标轴
dxdydz
dxdydz(1 1 2 3) dxdydz
dxdydz
应变和应力的概念

应变和应力的概念应变和应力的概念引言应变和应力是材料力学学科中的基本概念,它们是研究材料在受外部作用下的变形和破坏行为的重要参数。
本文将深入探讨应变和应力的概念、种类、计算及其在工程实践中的应用。
一、应变的概念1.1 定义应变是指物体在受外部作用下发生形状或大小上的改变程度。
通俗地说,就是物体发生了多少形变。
1.2 种类根据物体发生形变时,不同方向上长度或角度的改变情况,可分为以下几种类型:(1) 线性应变:也称伸长率,是指物体沿着外力作用方向上单位长度发生的相对伸长量。
(2) 非线性应变:也称剪切应变,是指物体内部各层之间因受到外部剪切力而产生相对滑动而引起角度改变。
(3) 体积应变:是指物体在三个互相垂直方向上同时发生尺寸改变所引起的相对体积改变量。
二、应力的概念2.1 定义应力是指物体在外部作用下,单位面积内所受的力。
通俗地说,就是物体受到了多大的力。
2.2 种类根据作用力的不同方向和大小,可分为以下几种类型:(1) 正应力:是指作用在物体上的力与该面积垂直的分量。
(2) 剪应力:是指作用在物体上的力与该面积平行的分量。
(3) 组合应力:是指同时存在正应力和剪应力时,在该面积上所受到的合成作用。
三、应变和应力之间的关系3.1 胡克定律胡克定律是描述弹性材料之间应变和应力之间关系的基本定律。
它表明,当材料受到外部载荷时,其产生的弹性形变量与所施加载荷成正比。
即:σ=Eε其中,σ为材料所受内部单位面积上产生的正应力;E为杨氏模量,表示单位长度内所需施加的正应力;ε为材料所发生线性形变(伸长率)。
3.2 应变-位移关系式对于线弹性材料,在外部载荷不超过其屈服极限时,它的应变与位移之间的关系可以用以下式子表示:ε=δ/L其中,ε为物体的线性应变(伸长率);δ为物体所受外力引起的位移;L为物体的原始长度。
四、应变和应力在工程实践中的应用4.1 应变计应变计是一种用于测量材料应变量的仪器。
它可以通过测量材料在受外部载荷时发生形变的程度来推算出其所受到的应力大小。
应变和应力关系

新能源技术:利用应变和应力原理,优化风力发电机叶片设计,提高风能 利用率和发电效率。
机器人技术:通过研究应变和应力与机器人关节运动的关系,提高机器人 的灵活性和稳定性,拓展机器人的应用领域。
应变和应力对未来科技发展的影响
增强材料性能:通过深入研究应变和应力,可以开发出性能更强的新型材 料,为未来的科技发展提供物质基础。
智能制造:利用应变和应力的知识,可以优化制造过程中的材料性能,提 高生产效率和产品质量,推动智能制造的发展。
生物医学应用:在生物医学领域,应变和应力的研究有助于更好地理解和 控制人体生理机制,为未来的生物医学应用提供支持。
压痕法:利用压痕仪在物体表面压出一定形状的压痕,通过测量压痕的尺寸来计算应力
应变和应力的相互影响
应变和应力之间的关系:应变是应力作用下的物体形状变化,应力是抵抗变形的力。
应变和应力的测量方法:通过应变计和应力计进行测量,应变计测量物体变形,应力计测量物 体受到的力。
应变和应力的相互影响:应变和应力之间存在相互影响,例如在材料屈服点附近,应变和应力 之间会发生突变。
应力的概念
分类:正应力、剪应力、弯 曲应力等
定义:物体受到外力作用时, 内部产生的反作用力
单位:帕斯卡(Pa) 作用效果:使物体产生形变
应变和应力的关系
应变是物体形状 的改变,应力是 物体内部抵抗变
形的力
应变和应力之间 存在线性关系, 即应变正比于应
力
应变和应力之间 的关系可以用胡 克定律表示,即 应力=弹性模量
应变和应力关系
汇报人:XX
应变和应力的定义 应变和应力的测量方法 应变和应力的应用领域 应变和应力的研究进展 应变和应力的未来展望
第四章应力与应变关系

(4-3a)
广义虎克定律
在小变形条件下,应变分量都是微量,(a)式在应变 为零附近做Taylor展开后,忽略2阶以上的微量,例如
对 , 可x 得:
x (f1)0(f1x)0x (f1y)0y (f1z)0z
( f1
yz
)0yz
(f1zx)0zx
(f1xy)0xy
广义虎克定律 展开系数表示函数在其对应变分量一阶导数在应变分 量等于零时的值,而 实( f 1 际) 0 上代表初应力,由于无初应 力假设 等于( f 1零) 0 。 其它分量类推,那么在小变形情况下应力与应变关系 式简化为:
3 t 2 3
和 称 为拉梅(Lame)弹性常数,简称拉梅常数
各向同性体的广义虎克定律
(三)最后通过坐标变换,进一步建立任意正交坐标系应 力与应变关系
在各向同性弹性体中,设 o为x y任z 意正交坐标系,它
的三个轴与坐标系 应O力12主3 轴的方向余弦分别为 、 (l1 ',m1和',n1 ') (l2,',m因2 ',n为2 ')1,(2l3,',m33 ',轴n3是') 主轴,主轴方向的 剪应变和剪应力等于零。 根据转轴时应力分量变换公式得
系O123各轴的方向余弦,知:
l1 n3 cos180 1 m2 cos0 1 l2 l3 m1 m3 n1 n2 cos90 0
各向同性体的广义虎克定律
因此新坐标轴也指向应变主轴方向,剪应变也应该等
于零,且因各向同性时,弹性系数C41,C42和C43应
该不随方向面改变,故取 x, y分, z别为1′,2′和3′轴,同
上式作为虎克定律在复杂受力情况下的一个推广, 因此称为广义虎克定律。式中系数Cm n(m ,n1,是2, ,6) 物质弹性性质的表征,由均匀性假设可知这些弹性性 质与点的位置无关,称为弹性常数。上式也可以写成 矩阵形式
应力与应变间的关系

τ xy
右侧面
σx τ xz
x
γ xy
γ yz
γ zx
O
∠ xOy ∠ yOz
∠zox 。
z
σz
前面
2、各向同性材料的广义胡克定 、 律
(1)线应变的推导 线应变的推导 分别单独存在时, 在σx σy σz 分别单独存在时 x 方 依次为: 向的线应变 εx 依次为
x σ
z
x
x σ
εx ' =
σx
τ = Gγ
或
γ=
τ
G
τ γ γ τ
为剪切弹性模量,单位为N/m G 为剪切弹性模量,单位为N/m2.
三、复杂应力状态下应力与应变的关系 σx σy σz τ x y τ y z τ z x εx ε y ε z γ x y γ y z γ z x
1、各向同性材料的广义胡克定律 (1)符号规定 ) (a)三个正应力分量 拉应力为正 (a)三个正应力分量 三个正应力分量:拉应力为正
因此, 该圆筒变形后的厚度并无变化, 因此 该圆筒变形后的厚度并无变化 仍然为 t =10mm .
G G G
在线弹性范围内, 小变形条件下, 在线弹性范围内 小变形条件下 各向同性材料。 各向同性材料。
1 εx = σx ν (σ y +σz ) E 1 E
[
]
公式的适用范围 : 在线弹性范围内,小 在线弹性范围内 小 变形条件下, 变形条件下 各向同性材 料。
ε y = [σ y ν (σz +σx )]
ν ν ε z = (σ x + σ y ) = (τmax + τmax ) = 0 E E
同理可得,圆筒中任一点 该点到圆筒横截面中心的距离为 该点到圆筒横截面中心的距离为ρ 同理可得 圆筒中任一点 (该点到圆筒横截面中心的距离为ρ) 处 的径向应变为
第四章应力应变关系

4 应力应变关系4.1弹性变形时应力和应变的关系当材料所受应力小于其线弹性极限时,材料应力应变间的关系服从广义Hooke 定律,即1()1()1()111222x x y z y yx zz z x yxy xy yz yz zx zxE E E G G G εσνσνσεσνσνσεσνσνσετετετ⎧=--⎪⎪⎪=--⎪⎨⎪=--⎪⎪⎪===⎩,, (4.1) 式中,E 为拉压弹性模量,G 为剪切模量,ν为泊松比,对于各向同性材料,三个常数之间满足()21E G ν=+关系。
由上式可得11212()()33m x y z x y z m E E ννεεεεσσσσ--=++=++= (4.2) 于是11()'2x m x m x E G νεεσσσ+-=-= 或1112''22x m x x m G G Eνεεσσσ-=+=+ 类似地可以得到1112''22y m y y m G G E νεεσσσ-=+=+ 1112''22z m z z m G G Eνεεσσσ-=+=+于是,方程(4.1)可写成如下形式1212'00'0000'x xy xz x xy xz m v yx y yz yx y yz m G E m zx zy z zx zy z εγγσττσγεγτστσσγγεττσ-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭即'1122ij ij m ij ij m G Eνεεεσδσ-'=+=+ (4.3)显然,弹性变形包括体积改变的变形和形状改变的变形。
前者与球应力分量成正比,即12m m E νεσ-= (4.4)后者与偏差应力分量成正比,即''12''12''12111222x x m x G y y m y G z z m z G xy xy yz yz zx zxG G G εεεσεεεσεεεσετετετ⎧=-=⎪=-=⎪⎨=-=⎪⎪===⎩,,或简写为2ij ij G σε''= (4.5)此即为广义Hooke 定律。
应力与应变之间的关系

2
2
1
1
3
1
1
E
2
E
1
1 E
1
2
3
3
3
E
11
2
1
1 E
1
2
3
1
2
1 E
2
3
1
3
3
1 E
3
1
2
12
3、广义胡克定律的一般形式
x
1 E
[ x
(
y
z )]
x
z
zx zy
xz yz
xy
yx
y
y
1 E
[
y
(
z
x
)]
z
1 E
[
z
(
x
y )]
xy
xy
G
yz
yz
G
zx
zx
G
13
4.单元体体积变化:
V abc
V1 a(1 1) b(1 2 ) c(1 3 ) 2 a b c (1 1 2 3 )
单位体积的体积改变为:
V1 V
V
1 2 3
b 1
3
c
a
也称为体积应变。 14
1
2
3
1
2
E
(
1
2
3)
3(1 2) 1 2 3
E
3
m
K
式中:
K
E
体积弹性模量
3(1 2)
m
1
2
3
3
1
1 E
1
(
2
)
3
2
1 E
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料的应力和应变的关系
臂牵引可能转移的很小的几英寸不削弱其效用。
真实应变,就像真实应力,在此基础上计算的实际长度测试样本在测试和主要用于研究的基本性能的材料。
之间的差异名义应力和应变计算,从最初的规模的标本,和真应力一应变是微不足道的压力通常遇到的工程结构,但有时差别较大的应力和应变成为重要的。
延性材料。
经过大量的塑料拉伸或剪切变形破裂之前。
当柔软材料的最后力量达成,横截面面积的试样开始减少或颈部,和由此产生的负荷,可以进行标本减退。
因此,应根据原始的区域减少超越极限强度的材料,虽然压力继续增加,直至破裂。
渗透和吸收渗透是指容易与水可以缓慢穿过混凝土。
这不应该混淆混凝土的吸水性,两者没有必然联系。
吸收可能被定义为有能力的混凝土吸水到其空隙。
低渗透是一个重要的要求,水力结构和在某些情况下,透水性混凝土可以被认为是更重要的比强度虽然,其他条件相等,低渗透性混凝土也将坚固耐用。
混凝土这很容易吸收水容易恶化。
与混凝土相比,钢是一种高强度材料。
有用的普通钢筋抗拉强度以及压缩,也就是屈服强度,大约是15倍的普通结构混凝土抗压强度,和超过100倍的拉伸强度。
另一方面,钢铁成本高是一个比较具体的材料。
因此,2种材料的最佳组合使用,如果具体是无法抵御压应力和拉伸应力。
弹性模量作为一般规则,混凝土的弹性模量块可以被假定为与他们的实力,增加强度的增加。
然而,对于集料混凝土砌块有很大影响
的类型骨料,在案件的蒸压加气混凝土,由透气度、弹性模量通常是不引用时,这个信息是必需的,制造商应要求提供。
数百年来,地图提供分层图形形式的信息和已被用来作为法律文件和工具、辅助决策等应用城市规划。
最近,地理信息系统(地理信息系统)扩大了所发挥的作用类型的地图,包括整个系统的硬件,软件,和程序设计的捕捉,管理,操纵,和生产信息在空间范围。
地理信息系统应用的确广泛;它们包括基础测绘,地籍管理,基础设施,管理设施,以及许多其他的。
许多的负载可以被认为是由一个固定和非固定部分。
它往往是必要的单独的负载为固定部分和其他部分的随机方式作用在结构上。
非固定荷载分析意味着需要考虑不同加载条件,其中每一个被定义时的程度和位置的所有非固定荷载是有。
结构安全要求结构的强度是足够的负荷,可能会对它采取行动。
如果强度可以准确预测如果负载同样确切地知道,然后就能保证安全提供强度只要稍微超过荷载的要求。
但有许多来源的不确定性的估计负荷以及分析,设计,施工。
这些不确定性需要安全边际。
在开始计算负载和他们的“行动”或应力和挠度设计者必须选择要使用的材料,并有一个明确的概念的方式,转让纵向和横向负载点应用到地面将发生。
稳健的概念实际上这种结构决定了成功或失败的设计,关于它不仅安全,而且其经济。
在任何实际的设计情况的可行性,各种制度和在何种程度上减少或增加的费用,其他元素的结构首先必须建立。
智能选择最佳的概念,他只能在标准的一个具体问题已经彻底的调查和确定。
