材料力学应力和应变之间的关系
如何理解工程力学中的应力与应变?

如何理解工程力学中的应力与应变?在工程力学的广袤领域中,应力与应变是两个至关重要的概念。
它们不仅是理解材料力学性能的基石,也是解决众多工程实际问题的关键。
对于初学者来说,这两个概念可能显得有些抽象和难以捉摸,但只要我们耐心剖析,就能发现其中的奥秘。
让我们先来谈谈应力。
应力,简单来说,就是单位面积上所承受的内力。
想象一下,你手里拿着一根橡皮筋,当你用力拉伸它时,橡皮筋内部就会产生抵抗拉伸的力。
如果我们把橡皮筋的横截面积考虑进去,计算出单位面积上的内力,这就是应力。
应力的单位是帕斯卡(Pa),它表示每平方米所承受的力的大小。
在实际的工程应用中,我们常常会遇到不同类型的应力,比如拉伸应力、压缩应力和剪切应力。
拉伸应力出现在材料被拉长的时候,就像刚刚提到的拉伸橡皮筋;压缩应力则相反,发生在材料被压缩的情况下,比如把一根柱子压短;而剪切应力则常见于材料受到平行于其表面的力的作用,例如用剪刀剪断一张纸。
为了更深入地理解应力,我们来考虑一个具体的例子。
假设我们有一根横截面面积为 1 平方厘米的金属杆,我们对它施加一个 100 牛顿的拉力。
那么,这根金属杆所承受的应力就是 100 牛顿除以 00001 平方米(1 平方厘米= 00001 平方米),即 1000000 帕斯卡。
接下来,我们再看看应变。
应变是用来描述物体形状或尺寸变化程度的量。
它是一个无量纲的量,也就是说,它没有单位。
应变可以分为线应变和角应变。
线应变表示物体在某一方向上长度的相对变化。
如果一根原来长度为 L 的杆子,在受到外力作用后长度变成了 L',那么线应变就等于(L' L)/L 。
还是以刚才的金属杆为例,如果它原来的长度是1 米,被拉伸后变成了 101 米,那么线应变就是(101 1)/ 1 = 001 。
角应变则用于描述物体角度的变化。
比如说,一个原本是直角的物体,在受到外力作用后角度发生了改变,这个角度的变化量就是角应变。
《材料力学》课件7-4应力与应变间的关系

胡克定律
胡克定律是一个简单而重要的材料力学公式,它描述了应力与应变之间的线性关系。
弹性模量与切变模量
弹性模量是一个常用的材料力学参数,它用于衡量材料在受力时的弹性性质。 切变模量是另一个衡量材料性能的参数,它描述了材料抵抗剪切形变的能力。
《材料力学》课件7-4应 力与应变间的关系
本节课将讨论应力与应变之间的关系,以及胡克定律、弹性模量、切变模量、 杨氏模量和泊松比等概念。
应力与应变的定义
应力是单位面积上的力,用于描述物体内部的分子之间的相互作用力。 应变是物体单位长度的发生变化,用于描述物体在受力时的形变程度。
应力与应变之间的关系
杨氏模量
杨氏模量是一个衡量材料刚度的参数,它描于描述材料性质的参数,它衡量了材料在拉伸时的侧向收缩 程度。
剪切模量
剪切模量是一个衡量材料剪切属性的参数,它描述了材料抵抗剪切形变的能力。
应力-应变循环曲线

应力-应变循环曲线应力-应变循环曲线是材料力学中的重要概念,用来描述材料在循环载荷下的变形行为。
循环载荷是指反复施加在材料上的载荷,应力-应变循环曲线则可用来描述材料在这种交替循环载荷下的应力和应变之间的关系。
本文将详细介绍应力-应变循环曲线的概念、特征和应用。
应力-应变循环曲线通常由两个主要的部分组成:弹性阶段和塑性阶段。
在材料的弹性阶段,应变与应力成正比,即应力和应变满足胡克定律。
材料在这个阶段内,完全恢复了外部加载引起的应变,没有残余应变。
应力-应变曲线在这个阶段呈现出一条直线,斜率代表了材料的弹性模量。
当材料超过了弹性极限,进入了塑性阶段,应力-应变曲线就变成了一个回弹曲线。
在每个循环中,材料会出现一个塑性变形区域,在这个区域内,应变与应力的关系是非线性的。
一般来说,塑性变形区域是由初始的弹性后塑性应变(yield strain)和持续的塑性应变组成。
应力-应变循环曲线的特征还包括屈服点和饱和点。
屈服点是指应力-应变曲线上的一个特殊点,表示了材料的屈服强度。
在屈服点之后,材料会出现明显的应力软化效应,即应力下降。
而饱和点则表示了材料在循环载荷下的最大应变能力。
应力-应变循环曲线的形状和特征会受到多种因素的影响,包括加载速率、温度和材料的微观结构等。
这些因素都会对材料的塑性变形机理和位错运动产生影响。
例如,加载速率的增加会导致材料的强化效应,使得应力-应变曲线呈现出更陡峭的斜率和更高的屈服强度。
而温度的增加则会导致材料的软化效应,使得应力-应变曲线呈现出更平缓的斜率和较低的屈服强度。
应力-应变循环曲线的研究在材料科学和工程领域具有重要的意义。
它不仅可以用来评估材料的力学性能和可靠性,还可以用来设计和优化结构的工作寿命和耐久性。
通过分析应力-应变循环曲线,可以获得材料的弹塑性性质、疲劳特性和损伤行为等信息,有助于提高材料的使用寿命和安全性。
总之,应力-应变循环曲线是描述材料在循环载荷下的力学响应的重要工具。
弹性力学弹性材料的应力应变关系与力学行为

弹性力学弹性材料的应力应变关系与力学行为弹性力学是研究物体在受力作用下产生的形变,并研究这种形变与施加力之间的关系的力学学科。
弹性材料是指在受到外力作用时,可以恢复其原有形状和大小的材料。
在弹性力学中,应力应变关系是研究弹性材料变形的重要理论基础,同时也是理解弹性材料力学行为的关键。
一、应力应变关系弹性材料的应力应变关系是指在弹性变形过程中,材料受到的应力与应变之间的关系。
根据前人的研究,线弹性模型是描述弹性材料应力应变关系较为简单的模型。
在线弹性模型中,应力与应变之间满足线性的关系,即应力与应变成正比。
线弹性模型的数学表达为:应力=弹性模量×应变其中,弹性模量是描述材料抵抗形变的能力,常用符号为E,单位为帕斯卡(Pa);应变是材料在受力作用下发生的形变,通常用ε表示。
二、力学行为在实际工程中,弹性材料的力学行为可以通过拉伸试验来研究。
拉伸试验是将材料在两端加以拉伸,观察材料的变形与受力之间的关系。
通过拉伸试验可以得到材料的应力-应变曲线,从而了解其力学行为。
应力-应变曲线通常可分为三个阶段:线弹性阶段、屈服阶段和塑性阶段。
1. 线弹性阶段材料在小应变下,应力与应变之间呈线性关系,即遵循线弹性模型。
在这个阶段,材料受力后会发生弹性形变,一旦撤去外力,材料便会恢复到初始状态。
2. 屈服阶段当应力超过材料的屈服强度时,材料开始发生塑性变形。
此时,材料的应变与外力不再成线性关系,应力-应变曲线开始变得非线性。
3. 塑性阶段在超过屈服阶段后,材料会出现塑性变形,即使撤去外力,材料也不能完全恢复到初始状态。
材料在这个阶段会发生永久性变形。
除了拉伸试验,弹性材料的力学行为还可以通过其他实验方法进行研究,如压缩试验和剪切试验等。
通过这些实验,可以探究材料在不同受力情况下的变形特性。
总结:弹性力学中,弹性材料的应力应变关系是研究弹性材料变形的重要理论基础。
应力应变关系可以通过线弹性模型进行描述,其中应力与应变成正比。
材料力学应力与应变分析

在复杂应力状态下,物体内部某一点处的主应力表示该点处最主要 的应力,次应力则表示其他较小的应力。
应力表示方法
应力矢量
应力矢量表示应力的方向和大小,通常用箭头表示。
应力张量
在三维空间中,应力可以用一个二阶对称张量表示,包括三个主应力和三个剪切 应力分量。
主应力和剪切应力
主应力
在任意一点处,三个主应力通常是不相等的,其中最大和最小的主应力决定了材料在该点的安全程度 。
采用有限元分析方法,建立高 层建筑的三维模型,模拟不同 工况下的应力与应变分布。
结果
通过分析发现高层建筑的关键 部位存在较高的应力集中,需
要进行优化设计。
结论
优化后的高层建筑结构能够更 好地承受各种载荷,提高了安
全性和稳定性。
THANKS FOR WATCHING
感谢您的观看
不同受力状态下的变形行为。
06 实际应用与案例分析
实际应用场景
航空航天
飞机和航天器的结构需要承受高速、高海拔和极端温度下 的应力与应变,材料力学分析是确保安全的关键。
汽车工业
汽车的结构和零部件在行驶过程中会受到各种应力和应变 ,材料力学分析有助于优化设计,提高安全性和耐久性。
土木工程
桥梁、大坝、高层建筑等大型基础设施的建设需要精确的 应力与应变分析,以确保结构的稳定性和安全性。
剪切应力
剪切应力是使物体产生剪切变形的力,其大小和方向与剪切面的法线方向有关。剪切应力的作用可以 导致材料产生剪切破坏。
04 应变分析
应变定义
定义
应变是描述材料形状和尺寸变化的物理量, 表示材料在外力作用下发生的形变程度。
单位
应变的单位是1,没有量纲,常用的单位还有微应变 (με)和工程应变(%)。
应变和应力关系

新能源技术:利用应变和应力原理,优化风力发电机叶片设计,提高风能 利用率和发电效率。
机器人技术:通过研究应变和应力与机器人关节运动的关系,提高机器人 的灵活性和稳定性,拓展机器人的应用领域。
应变和应力对未来科技发展的影响
增强材料性能:通过深入研究应变和应力,可以开发出性能更强的新型材 料,为未来的科技发展提供物质基础。
智能制造:利用应变和应力的知识,可以优化制造过程中的材料性能,提 高生产效率和产品质量,推动智能制造的发展。
生物医学应用:在生物医学领域,应变和应力的研究有助于更好地理解和 控制人体生理机制,为未来的生物医学应用提供支持。
压痕法:利用压痕仪在物体表面压出一定形状的压痕,通过测量压痕的尺寸来计算应力
应变和应力的相互影响
应变和应力之间的关系:应变是应力作用下的物体形状变化,应力是抵抗变形的力。
应变和应力的测量方法:通过应变计和应力计进行测量,应变计测量物体变形,应力计测量物 体受到的力。
应变和应力的相互影响:应变和应力之间存在相互影响,例如在材料屈服点附近,应变和应力 之间会发生突变。
应力的概念
分类:正应力、剪应力、弯 曲应力等
定义:物体受到外力作用时, 内部产生的反作用力
单位:帕斯卡(Pa) 作用效果:使物体产生形变
应变和应力的关系
应变是物体形状 的改变,应力是 物体内部抵抗变
形的力
应变和应力之间 存在线性关系, 即应变正比于应
力
应变和应力之间 的关系可以用胡 克定律表示,即 应力=弹性模量
应变和应力关系
汇报人:XX
应变和应力的定义 应变和应力的测量方法 应变和应力的应用领域 应变和应力的研究进展 应变和应力的未来展望
材料力学应力与应变之间的关系
2
=-34.6MPa
第13页/共20页
例 图示纯弯梁,已知外力为M,横截面对中性轴的惯
惯性矩为Iz,材料弹性常数为E、ν,试求线段AB
的长度改变量ΔlAB。
M
dl
Aa
45°
y
B
M
解: My
Iz
45
45
2
σ σ45° τ σ-45°
45
1 E
( 45
45 )
1
2E
dlAB
45
dl
1
2E
68.85MPa
3)求线应变
τ
0
E
50.86 210103
2.42104
σ
242με
σy≠0!!!
第7页/共20页
90 0 0.3 2.42104 7.26105 σy≠0!!!
y
45
1 E
( 45
45 )
x
45°
x
y
45
x
y
2
x
45
x
y
2
x
第8页/共20页
τ σ
2
45
2
非45°角时!!!
45
1 E
( 45
45 )
1 1
2E 2E
第12页/共20页
计算τ的解法二:
已知:ε0°=500με, ε 45°=400με
90 0 0.3500 150με
E
1
( 0
90
2
45 )
200 103 (500 150 400 ) 106
1 0.3
σ3
1 2E
[
2
1
材料力学的基本假设

材料力学的基本假设
1.应力-应变的线性关系假设:在小变形范围内,材料的应力与应变
之间存在线性关系,即应力是应变的线性函数。
2.同性与各向同性假设:材料在各个方向上具有相同的物理性质,即
同性;在任意方向上的物理性质相同,即各向同性。
3.材料的连续性假设:材料在微观层面上具有连续性,即认为材料是
由无数微小的质点组成的,而且质点之间的距离可以被忽略。
4.材料的弹性本质假设:材料在受力后会发生形变,但当去除作用力时,材料会恢复原始形态,即弹性本质。
5.应力状态的平衡假设:材料在受力时,应力状态必须处于平衡状态,即所受的所有内部力的合力必须为零。
6.多轴应力状态的等效假设:将多轴应力状态转化为等效单轴应力状态,使得应力状态的分析变得简单。
7.破坏准则的假设:材料在受到超过一定程度的应力时会发生破坏,
该程度可以通过破坏准则进行描述。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
σ45°
τ
45°
50 .86 s s 45 t 68.85 94.28MPa 2 2 50 .86 s s 45 t 68.85 43.42MPa 2 2 1 45 (s 45 s 45 ) 非45°角时!!! E 1 [94.28 0.3 (43.42)] 5.11 10 4 210 10 3
a
二、各向同性材料的体积应变
σ2
σ3
t t t t
V 1 2 3 V 1 2 σ1 (s 1 s 2 s 3 ) E 要使一点的体积应变为 零,必须使该点处的三个主 应力之和为零。
s 1 s 3 t
s2 0
1 2 s 1 s 2 s 3 0 E
σ-45°
计算τ的解法二:
已知:ε0°=500με, ε 45°=400με
90 0 0.3 500 150με
E 0 90 t ( 45 ) 1 2
200 10 3 500 150 ( 400 ) 10 6 1 0.3 2
二、形状改变比能
σ2
1 2 (s 1 s 2 s 3 ) E
σ1
1 s m (s 1 s 2 s 3 ) 3
' s 2 s m s 2
σ3
形状改变 体积改变
σm σm (1)
+
' s 3 s m s 3
s 1 s m s 1'
1 2 1 2 1 (s 11 s 21 s 31 ) 3s m E E
AB
s 45 s 45
s
M A
45°
M a B
y
My s Iz
l AB 1 s dl 2E l AB
l AB
2 ( l) a My a M 1 1 2 dl dl 2 E 0 I z 2 E 0 Iz
2 (1 ) M 4 EI z 2 (1 ) Ma 2 0 ldl 8EI z
平面应力状态
ty tx sx sy
tx
sy
sx
ty
1 x (s x s y ) E 1 y (s y s x ) E z (s x s y ) E
xy
1 t xy G
E sx [(1 ) x ( y z )] (1 )(1 2 ) E sy [(1 ) y ( x z )] (1 )(1 2 )
500mm
F
500mm
b t d h
C
h/4 250mm
z
t
2)取C点的应力状态
τ σ
My 18.75 10 6 45 s 16.59 10 6 Iz
50.86MPa
注意σ 和τ 的方向!!!
500mm
F
500mm
b t d h
C
h/4 250mm
z t
S z 94 10.7 (90 10.7 / 2) 6.5 (45 10.7) (45
例 一钢制圆杆受拉扭组合作用,如图所示,已知直径 d=200mm,E=200GPa,ν=0.30。已测得圆轴表面 上a点处的线应变为ε0°=500με, ε 45°=400με。 试求F和T之值。 T F
τ
ε45° a ε0° T
F
解:1)取a点的应力状态
σ
4F F s 2 A d 2)求F 4F 0 E Ed 2
σ-45°
测得ε0°(εx)、ε45°(ε45°)和ε90°(εy)
σy
σx
45°
τx
E sx ( x y ) 2 1 E sy ( y x ) 2 1 E x y tx ( 45 ) 1 2 x y E tx ( 45 ) 1 2
v vV vd
§7-6 空间应力状态下的应变能密度
一、应变能密度 单位体积的应变能
σ
dV v dV
σ2
1 v s 2 1 v (s 11 s 2 2 s 3 3 ) 2
σ1 σ3
1 2 [s 12 s 2 s 32 2 (s 1s 2 s 2s 3 s 3s 1 )] 2E
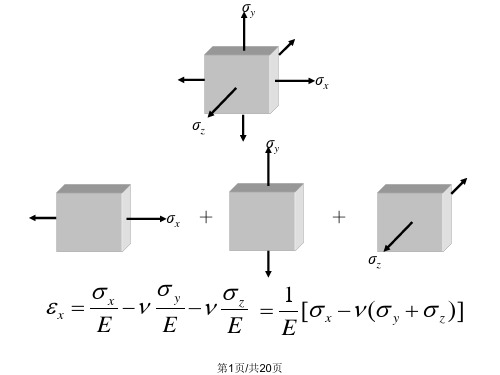
§7-4 应力与应变之间的关系
一、各向同性材料的广义胡克定律 线弹性和小变形
tyx tyz s z tzx sx t t tzy txy sx xz xy tzx txz txy sz dy tyx tyz dz sy
dx
sy
sy sx
dy
sz
sz
dx
sy
dz
txy txz txy tzy sx + tzx txz txy dy tyx tyz
2. 形状改变比能
' s 2 s m s 2
形状改变
s 1 s m s 1'
' s 3 s m s 3
1 1 1 vd s 11 s 2 2 s 3 3 2 2 2 1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 6E
sz 0
说明: 1)x 和 y 必须是两个互相垂直的方向; 2)括号中的第一项必须是与 x 同方位的正应力, 而第二项中的应力必须是与x 垂直的方位上的 正应力; 3)上述公式同样适用于其它方位的应力状态。
ty
tx sx ty tx sy
1 x (s x s y ) E
sy
sx
45 10.7 ) =98997mm3 2
FS S z 75 10 3 98997 68.85MPa t bI z 6.5 16.59 10 6 3)求线应变 s 50.86 0 2.42 10 4 τ E 210 10 3 σ σy≠0!!! 242 με
tyz tzx tyx
xy yz
zx
txy txz txy tzy tzx txz txy dy tyx tyz
dx
dz
1 t xy G 1 t yz G 1 t zx G
E sx [(1 ) x ( y z )] (1 )(1 2 ) E sy [(1 ) y ( x z )] (1 )(1 2 ) E sz [(1 ) z ( x y )] (1 )(1 2 )
T 16T t 3 WP d
σy≠0!!!
注意σ 和τ 的方向!!!
s
F
4 314 .1kN
τ
E 0 d
2
4
200 10 500 10 200
3
6
2
3)求T
s 45
σ σ45° τ
s
2
t t
非45°角时!!!
s 45
s
45
45°
2 1 (s 45 s 45 ) E 1 1 s t 2E 2E
90 0 0.3 2.42 10 4 7.26 10 5
t t sx
45°
σy≠0!!!
sy
45
t sx
1 (s 45 s 45 ) E
sy
t
s 45
s x s y
2
s x s y
2
t x
t x
s ቤተ መጻሕፍቲ ባይዱ 45
τ
σ
=-34.6MPa
例 图示纯弯梁,已知外力为M,横截面对中性轴的惯 惯性矩为Iz,材料弹性常数为E、ν,试求线段AB 的长度改变量ΔlAB。 My dl M M 解: s
A
45°
a
B
Iz
y
σ
σ45° τ σ-45°
2 1 1 s 45 (s 45 s 45 ) 2E E 1 dl AB 45 dl s dl 2E 1 l AB dl AB s dl 2E l AB l
1 2 2 (s 12 s 22 s 32 ) E
=0
(2)
1 2 (s 1 s 2 s 3 ) E
1. 体积改变比能
σm
s m (s 1 s 2 s 3 )
1 3
体积改变
σm
31 2 2 1 3 sm vV (s 11 s 2 2 s 3 3 ) s m m 2E 2 2 1 2 2 s 1 s 2 s 3 6E
例 工字钢梁的截面尺寸如图所示,已知h=180mm, b=94mm,t=10.7mm,d=6.5mm。F=150kN,E=210GPa, ν=0.3,Iz=16.59×106mm4。试求C点处的线应变ε0° 、 ε 45°和ε90°。
500mm
F
500mm
b t d h
C
h/4 250mm
z t
解:1)求C点所在截面上的内力 F F FS 75kN M 0.25 18.75kNm 2 2
dx
tyz tzx
tyx
dz
σy
σx σz
σy
σx
+
+ σz
1 x [s x (s y s z )] E E E E
sx
sy
sz
广义胡克定律
1 x [s x (s y s z )] E 1 y [s y (s x s z )] E 1 z [s z (s x s y )] E
