历年高考数学真题精选31 立体几何中的垂直关系
高中数学立体几何正交与垂直关系分析

高中数学立体几何正交与垂直关系分析在高中数学的立体几何中,正交与垂直是两个非常重要的概念。
它们在几何图形的性质、计算问题中起着至关重要的作用。
本文将通过具体的题目举例,分析正交与垂直的概念、性质以及应用,帮助高中学生和他们的父母更好地理解和掌握这些知识点。
一、正交的概念和性质正交是指两条直线、两个平面或者一条直线和一个平面相互垂直的关系。
在几何图形中,正交的性质十分重要,常常用于求解问题。
例如,考虑以下题目:已知直线l1:x-2y+z=0和直线l2:2x+y-3z=0,求证直线l1与直线l2正交。
解析:要证明直线l1与直线l2正交,需要证明直线l1的法向量与直线l2的方向向量的点积为零。
首先,求出直线l1的法向量和直线l2的方向向量:直线l1的法向量为(1,-2,1);直线l2的方向向量为(2,1,-3)。
然后,计算两个向量的点积:(1,-2,1)·(2,1,-3) = 2-2-3 = -3由于点积结果为-3,不等于零,所以直线l1与直线l2不正交。
通过这个例子可以看出,正交的性质可以通过向量的点积来判断。
如果两个向量的点积为零,则它们正交;如果不为零,则它们不正交。
二、垂直的概念和性质垂直是指两条直线、两个平面或者一条直线和一个平面相互成直角的关系。
垂直在立体几何中也是一个非常重要的概念,常常用于计算问题。
例如,考虑以下题目:已知平面α:2x-y+z=1和平面β:x+2y-3z=4,求证平面α与平面β垂直。
解析:要证明平面α与平面β垂直,需要证明平面α的法向量与平面β的法向量的点积为零。
首先,求出平面α和平面β的法向量:平面α的法向量为(2,-1,1);平面β的法向量为(1,2,-3)。
然后,计算两个向量的点积:(2,-1,1)·(1,2,-3) = 2-2-3 = -3由于点积结果为-3,不等于零,所以平面α与平面β不垂直。
通过这个例子可以看出,垂直的性质也可以通过向量的点积来判断。
立体几何中的平行与垂直问题

立体几何中的平行与垂直问题在立体几何中,点、线、面之间的位置关系,特别是线面、面面的平行和垂直关系,例题如图,四棱锥PABCD的底面为矩形,且AB=2BC,E,F分别为棱AB,PC 的中点.(1)求证:EF∥平面PAD;(2)若点P在平面ABCD内的射影O在直线AC上,求证:平面PAC⊥平面PDE.变式1(2018·苏州一模)如图,在正方体ABCDA1B1C1D1中,已知E,F,G,H分别是A1D1,B1C1,D1D,C1C的中点.(1)求证:EF∥平面ABHG;(2)求证:平面ABHG⊥平面CFED.变式2(2018·苏锡常镇一模)如图,正三棱柱ABCA 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ; (2)AD ⊥平面A 1BN.串讲1如图,在三棱锥PABC 中,BC ⊥平面PAB.已知PA =AB ,D ,E 分别为PB ,BC 的中点.(1)求证:AD ⊥平面PBC ;(2)若点F 在线段AC 上,且满足AD ∥平面PEF ,求AFFC 的值.串讲2如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.(2018·南京、盐城二模)如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE的中点.(1)求证:MN∥平面BEC;(2)求证:AH⊥CE.(2018·江苏卷)如图,在平行六面体ABCDA1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.证明:(1)在平行六面体ABCD-A 1B1C1D1中,AB∥A1B1.因为AB平面A1B1C,A1B1平面A 1B1C,4分所以AB∥平面A1B1C.6分(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1=AB,所以四边形ABB1A1为菱形,因此AB1⊥A1B.8分又因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC.10分又因为A 1B∩BC=B,A1B平面A1BC,BC平面A1BC,所以AB1⊥平面A1BC.12分因为AB 1平面ABB1A1,所以平面ABB1A1⊥平面A1BC.14分例题1证法1如图1,在四棱锥PABCD 中,取线段PD 的中点M ,连接FM ,AM.因为F 为PC 的中点,所以FM ∥CD ,且FM =12CD.因为四边形ABCD 为矩形,E 为AB 的中点,所以EA ∥CD ,且EA =12CD.所以FM ∥EA ,且FM =EA.所以四边形AEFM 为平行四边形.所以EF ∥AM. 又AM 平面PAD ,EF 平面PAD ,所以EF ∥平面PAD. 证法2如图2,在四棱锥PABCD 中,连接CE 并延长交DA 的延长线于点N ,连接PN.因为四边形ABCD 为矩形,所以AD ∥BC.所以∠BCE =∠ANE ,∠CBE =∠NAE.又AE =EB ,所以△CEB ≌△NEA.所以CE =NE. 又F 为PC 的中点,所以EF ∥NP.又NP 平面PAD ,EF 平面PAD ,所以EF ∥平面PAD.证法3如图3,在四棱锥PABCD 中,取CD 的中点Q ,连接FQ ,EQ.在矩形ABCD 中,E 为AB 的中点,所以AE =DQ ,且AE ∥DQ.所以四边形AEQD 为平行四边形,所以EQ ∥AD. 又AD 平面PAD ,EQ 平面PAD,所以EQ ∥平面PAD.因为Q ,F 分别为CD ,CP 的中点, 所以FQ ∥PD.又PD 平面PAD ,FQ平面PAD ,所以FQ ∥平面PAD.又FQ ,EQ 平面EQF ,FQ ∩EQ =Q ,所以平面EQF ∥平面PAD.因为EF 平面EQF ,所以EF ∥平面PAD.(2)在四棱锥PABCD 中,设AC ,DE 相交于点G(如图4).在矩形ABCD 中,因为AB =2BC ,E 为AB 的中点. 所以DA AE =CDDA=2,又∠DAE =∠CDA ,所以△DAE ∽△CDA , 所以∠ADE =∠DCA.又∠ADE +∠CDE =∠ADC =90°,所以∠DCA +∠CDE =90°.由△DGC 的内角和为180°,得∠DGC =90°. 即DE ⊥AC.因为点P 在平面ABCD 内的正投影O 在直线AC 上, 所以PO ⊥平面ABCD.因为DE 平面ABCD ,所以PO ⊥DE. 因为PO ∩AC =O ,PO ,AC 平面PAC , 所以DE ⊥平面PAC ,又DE 平面PDE ,所以平面PAC ⊥平面PDE.变式联想变式1证明:(1)因为E ,F 分别是A 1D 1,B 1C 1的中点,所以EF ∥A 1B 1, 在正方体ABCDA 1B 1C 1D 1中,A 1B 1∥AB , 所以EF ∥AB.又EF 平面ABHG ,AB平面ABHG ,所以EF ∥平面ABHG.(2)在正方体ABCDA 1B 1C 1D 1中,CD ⊥平面BB 1C 1C , 又BH 平面BB 1C 1C ,所以BH ⊥CD.①设BH ∩CF =P ,△BCH ≌△CC 1F ,所以∠HBC =∠FCC 1,因为∠HBC +∠PHC =90°,所以∠FCC 1+∠PHC =90°.所以∠HPC =90°,即BH ⊥CF.②由①②,又DC ∩CF =C ,DC ,CF 平面CFED ,所以BH ⊥平面CFED. 又BH 平面ABHG ,所以平面ABHG ⊥平面CFED.变式2证明:(1)如图,连接MN ,正三棱柱ABCA 1B 1C 1中,AA 1∥CC 1且AA 1=CC 1,则四边形AA 1C 1C 是平行四边形,因为点M ,N 分别是棱A1C1,AC的中点,所以MN∥AA1且MN=AA1,又正三棱柱ABCA1B1C1中AA1∥BB1且AA1=BB1,所以MN∥BB1且MN=BB1,所以四边形MNBB1是平行四边形,所以B 1M∥BN,又B1M平面A1BN,BN平面A1BN,所以B1M∥平面A1BN.(2)正三棱柱ABCA1B1C1中,AA1⊥平面ABC,BN平面ABC,所以BN⊥AA 1,在正△ABC中,N是AB的中点,所以BN⊥AC,又AA 1,AC平面AA1C1C,AA1∩AC=A,所以BN⊥平面AA 1C1C,又AD平面AA1C1C,所以AD⊥BN,由题意得,AA1=6,AC=2,AN=1,CD=63,所以AA1AC=ANCD=32,又∠A1AN=∠ACD=π2,所以△A1AN与△ACD相似,则∠AA1N=∠CAD,所以∠ANA1+∠CAD=∠ANA1+∠AA1N=π2,则AD⊥A1N,又BN∩A1N=N,BN,A 1N平面A1BN,所以AD⊥平面A1BN.说明:变式1和2都通过“计算”来证明垂直,复习时应注意长度,角度等量的“计算”的运用来实现位置关系的求证.串讲激活串讲1解析:(1)因为BC⊥平面PAB,AD平面PAB,所以BC⊥AD.因为PA=AB,D为PB的中点,所以AD⊥PB.因为PB∩BC=B,所以AD⊥平面PBC.(2)连接DC,交PE于点G,连接FG.因为AD∥平面PEF,AD平面ADC,平面ADC∩平面PEF=FG,所以AD∥FG.因为D为PB的中点,E为BC的中点,连接DE,则DE为△BPC的中位线,△DEG∽△CPG.所以DGGC=DEPC=12.所以AFFC=DGGC=12.串讲2解析:(1)在三棱台ABCDEF中,AC∥DF,又AC平面ACE,DF平面ACE,所以DF∥平面ACE,又DF平面DEF,平面ACE∩平面DEF=a,所以DF∥a.(2)线段BE上存在点G,且BG =13BE ,使得平面DFG ⊥平面CDE.证明如下:如图所示,取CE 的中点O ,连接FO 并延长交BE 于点G ,连接GD ,因为CF =EF ,所以GF ⊥CE.在三棱台ABCDEF 中,因为AB ⊥BC ,所以DE ⊥EF ,因为CF ⊥平面DEF ,DE平面DEF ,所以CF ⊥DE ,又CF ∩EF =F ,所以DE ⊥平面CBEF ,GF 平面CBEF ,所以DE ⊥GF.因为GF ⊥CE ,DE ⊥GF ,CE ∩DE =E ,CE 平面CDE ,DE 平面CDE ,所以GF ⊥平面CDE ,又GF 平面DFG ,所以平面DFG ⊥平面CDE ,此时,侧面BCFE 的平面图如图所示,延长FG ,交CB 的延长线于点H ,因为O 是CE 的中点,EF =CF =2BC ,由平面几何知识可证得△HOC ≌△FOE ,所以HB =BC =12EF ,由△HGB ∽△FGE ,可知BG GE =12,即BG =13BE.新题在线(1)证法1取CE 中点F ,连接FB ,MF.因为M 为DE 的中点,F 为CE 的中点, 所以MF ∥CD 且MF =12CD.又因为在矩形ABCD 中,N 为AB 的中点, 所以BN ∥CD 且BN =12CD ,所以MF ∥BN 且MF =BN ,所以四边形BNMF 为平行四边形,所以MN ∥BF. 又MN 平面BEC ,BF 平面BEC ,所以MN ∥平面BEC.证法2取AE 中点G ,连接MG ,GN.因为G 为AE 的中点,M 为DE 的中点,所以MG ∥AD. 又因为在矩形ABCD 中,BC ∥AD ,所以MG ∥BC. 又因为MG 平面BEC ,BC 平面BEC ,所以MG∥平面BEC.因为G为AE的中点,N为AB的中点,所以GN∥BE.又因为GN平面BEC,BE平面BEC,所以GN∥平面BEC.又因为MG∩GN=G,MG,GN平面GMN,所以平面GMN∥平面BEC.又因为MN平面GMN,所以MN∥平面BEC.(2)因为四边形ABCD为矩形,所以BC⊥AB.因为平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,BC平面ABCD,且BC⊥AB,所以BC⊥平面ABE.因为AH平面ABE,所以BC⊥AH.因为AB=AE,H为BE的中点,所以BE⊥AH.因为BC∩BE=B,BC平面BEC,BE平面BEC,所以AH⊥平面BEC.又因为CE平面BEC,所以AH⊥CE.。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)
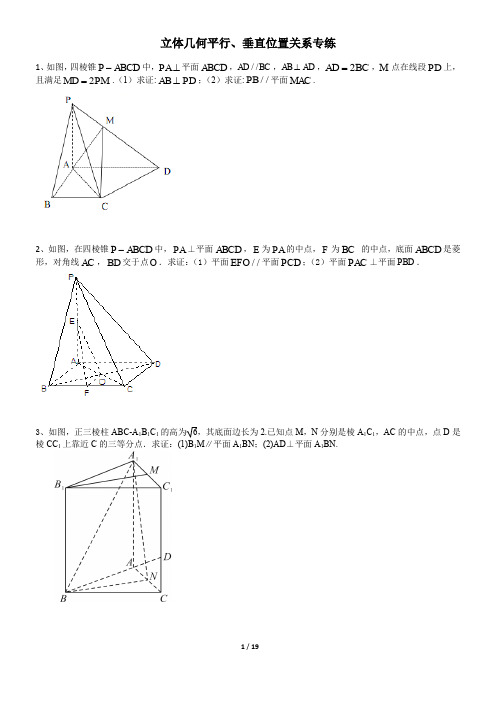
立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
高考数学复习—立体几何:(二)空间直线平面关系判断与证明—平行与垂直关系证明(试题版)
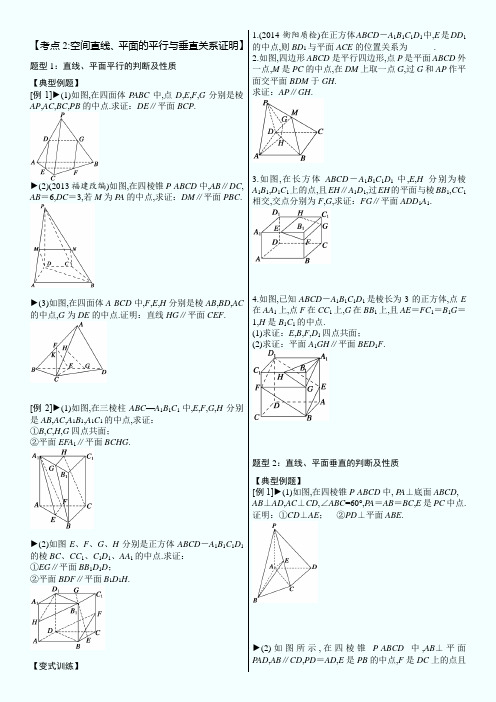
【考点2:空间直线、平面的平行与垂直关系证明】题型1:直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证:DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB=6,DC=3,若M为P A的中点,求证:DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明:直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:①B,C,H,G四点共面;②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:①EG∥平面BB1D1D;②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH .3.如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.4.如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E,B,F,D1四点共面;(2)求证:平面A1GH∥平面BED1F .题型2:直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC中点. 证明:①CD⊥AE;②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=12AB,PH为△P AD中AD边上的高.①证明:PH⊥平面ABCD;②证明:EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(I)求证:EF⊥平面BCG;(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA1,D是棱AA1的中点.(I)证明:平面BDC1⊥平面BDC;(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.①求证:PC⊥BC;②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证:CE⊥平面P AD;(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证:CD⊥平面ABD;(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A=PB=AB =BC,∠PBC=90°,D为AC的中点,AB⊥PD.(1)求证:平面P AB⊥平面ABC;(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-A1B1C1的高.☆题型3:直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;②若l⊂α,l∥β,α∩β=m,则l∥m;③若α∥β,l∥α,则l∥β;④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.(I)求证:平面ABE⊥平面B1BCC1;(II)求证:C1F∥平面ABE;(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A=6,BC=8,DF=5. 求证:(I)直线P A∥平面DEF;(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积;(II)证明:四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证:DE∥平面A1CB;(II)求证:A1F⊥BE;(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β=c.给出下列命题:①若a与b是异面直线,则c至少与a,b中的一条相交;②若a不垂直于c,则a与b一定不垂直;③若a∥b,则必有a∥c;④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证: (1)P A ⊥底面ABCD ; (2)BE ∥平面P AD ;(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB =BC=12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证:AP ∥平面BEF ; (2)求证:BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明:BC 1∥平面A 1CD ;(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证:BC ⊥平面P AC ; (2)设Q 为P A 的中点,G 为△AOC 的重心,求证:QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明:PB ∥平面AEC ;(2)设AP =1,AD =3,三棱锥P - ABD 的体积V =34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1.设AB 1的中点为D ,B 1C ∩BC 1=E . 求证:(1)DE ∥平面AA 1C 1C ; (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3. (1)证明:BC ∥平面PDA ; (2)证明:BC ⊥PD ;(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由); (2)求平面α把该长方体分成的两部分体积的比值.16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE . (Ⅰ)证明:CD ⊥平面A 1OC ;(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值.17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE =CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置. (1)证明:AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′ABCFE 的体积.18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点. (1)证明MN ∥平面P AB ;(2)求四面体N -BCM 的体积.19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ; (2)若PA =PD =AB =DC ,∠ADP =90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明:直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。
2024届高考数学复习:精选历年真题、好题专项(直线、平面的平行与垂直关系)练习(附答案)

2024届高考数学复习:精选历年真题、好题专项(直线、平面的平行与垂直关系)练习一. 基础小题练透篇1.给出以下命题(其中a ,b 表示不同的直线,α表示平面): ①若a ∥α,b ∥α,则a ∥b ; ②若a ∥b ,b ∥α,则a ∥α; ③若a ∥α,b ⊂α,则a ∥b ;④若α的同侧有两点A ,B 到平面α的距离相等,则AB ∥α. 其中正确命题的个数是( )A .0B .1C .2D .3 2.[2023ꞏ湖北省襄阳市部分学校期中试题]某正方体的平面展开图如图所示,在这个正方体中,下列结论正确的是( )A .AF ∥平面BCEB .AD ⊥平面BCEC .AE ∥BCD .BF ⊥CE3.如图,在四棱柱ABCD -A 1B 1C 1D 1中,E ,F 分别是AB 1,BC 1的中点,则下列结论中正确的是( )A.EF ⊥BB 1B .EF ⊥平面BCC 1B 1 C .EF ∥平面D 1BC D .EF ∥平面ACC 1A 1 4.[2023ꞏ陕西省质量检测]如图,在正三棱柱ABC -A 1B 1C 1中,AB =1,AA 1=3 ,点D 是侧棱BB 1的中点,则直线C 1D 与平面ABC 所成角的正弦值为( )A .32B .217C .77 D .277 5.[2023ꞏ邯郸市摸底]如图,在正方体ABCD -A 1B 1C 1D 1中,E 是棱AB 的中点,F 是四边形AA 1D 1D 内一点(包含边界).EF ∥平面BB 1D 1D ,当线段EF 长度最大时,EF 与平面ABCD 所成角的余弦值为( )A .24B .33C .34D .366.在正四面体ABCD 中,E ,F 分别为△BCD ,△ACD 的中心,则下列说法中不正确的是( )A .EF ∥ABB .CD ⊥平面ABEFC .异面直线AB ,CD 所成的角为90°D .AE =13 EF7.如图,在正方体ABCD -A 1B 1C 1D 1中,AB =2,E 为AD 的中点,点F 在CD 上,若EF ∥平面AB 1C ,则EF =________.二. 能力小题提升篇1.[2023ꞏ陕西省西安市模拟]已知直线l ⊥平面α,直线m ⊂平面β,给出下列命题中正确的是( )①α∥β⇒l ⊥m ;②α⊥β⇒l ∥m ;③l ∥m ⇒α⊥β;④l ⊥m ⇒α∥β. A .①②③ B .②③④ C .②④ D .①③2.[2023ꞏ辽宁省实验中学期中]已知m ,n 为两条不同的直线,α,β,γ为三个不同的平面,则下列命题正确的是( )A .若m ∥α,n ∥α,则m ∥nB .若α⊥β,γ⊥β,且α∩γ=m ,则m ⊥βC .若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βD .若m ⊥α,n ∥β,α⊥β,则m ⊥n3.[2023ꞏ四川省成都市月考]如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,N是AB1的中点,则()A.A1N∥C1AB.A1N∥平面BAMC.AB1⊥平面ABMD.BM⊥AB14.[2023ꞏ山西省临汾市联考]如图,在直三棱柱ABC - A1B1C1中,∠BAC=90°,AC=AB=12 AA1=1,设D,E分别是棱CC1上的两个动点,且满足DE=1,则下列结论错误的是()A.平面ABC⊥平面B1DEB.A1A∥平面B1DEC.AB1⊥平面ADED.三棱锥A - B1DE体积为定值5.如图所示,在四棱锥P - ABCD中,P A⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)6.[2023ꞏ聊城模拟]如图,矩形ABCD中,AB=2AD,E为AB的中点,将△ADE沿DE翻折至△A1DE(A1∉平面ABCD),若M为线段A1C的中点,则在△ADE翻折的过程中,下列结论正确的是________.(写出所有正确结论的序号)①VA- A1DE∶VA1- BCDE=1∶3;②存在某个位置,使DE⊥A1C;③总有BM∥平面A1DE;④线段BM的长为定值.三. 高考小题重现篇1.[2019ꞏ全国卷Ⅱ]设α,β为两个平面,则α∥β的充要条件是()A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面2.[全国卷Ⅰ]如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()ABCD3.[全国卷Ⅲ]在正方体ABCD - A1B1C1D1中,E为棱CD的中点,则()A.A1E⊥DC1B.A1E⊥BDC.A1E⊥BC1D.A1E⊥AC4.[2022ꞏ新高考Ⅰ卷](多选)已知正方体ABCD - A1B1C1D1,则()A.直线BC1与DA1所成的角为90°B.直线BC1与CA1所成的角为90°C.直线BC1与平面BB1D1D所成的角为45°D.直线BC1与平面ABCD所成的角为45°5.[全国卷]α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有______.(填写所有正确命题的编号)6.[2019·全国卷Ⅰ]已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB 两边AC,BC的距离均为3,那么P到平面ABC的距离为________.四. 经典大题强化篇1.在如图所示的空间几何体中,AC⊥BC,四边形DCBE为矩形,点F,M分别为AB,CD的中点.求证:(1)FM∥平面ADE;(2)平面ACD⊥平面ADE.2.如图,四棱锥P - ABCD中,P A⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.(1)求证:CE⊥平面P AD;(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P - ABCD的体积.3.如图1,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AED折起到△A1ED的位置,连接A1B,A1C,M,N分别为A1C,BE的中点,如图2.(1)求证:DE⊥A1B;(2)求证:MN∥平面A1ED;(3)在棱A1B上是否存在一点G,使得EG⊥平面A1BC?若存在,求出A1GGB的值;若不存在,说明理由.参考答案一 基础小题练透篇1.答案:B答案解析:如图,在长方体ABCD A′B′C′D′中,A′B′∥平面ABCD,B′C′∥平面ABCD,但A′B′与B′C′相交,故①错误;AB∥A′B′,A′B′∥平面ABCD,但AB⊂平面ABCD,故②错误;A′B′∥平面ABCD,BC⊂平面ABCD,但A′B′与BC异面,故③错误;④显然正确.2.答案:B答案解析:由题意可知,如图所示,对于A,由图可知,AF与平面BCE不平行,故A错误;对于B,易知BC⊥平面AFDE,AD⊂平面AFDE,所以BC⊥AD,同理EC⊥AD,BC∩EC=C,BC,EC⊂平面BCE,所以AD⊥平面BCE,故B正确.对于C,在正方形BDCF中,FD⊥BC,易知四边形AFDE为平行四边形,所以AE∥FD,所以AE⊥BC,故C错误.对于D,在正方形BDCF中,BF∥DC,所以∠DCE为异面直线BF与CE所成角,易知∠DCE =45°,所以BF与CE不垂直,故D错误.故选B.3.答案:D答案解析:题中未涉及垂直条件,故排除A,B;连接BA1,CD1,则BA1与AB1交于点E,所以直线EF与平面CBA1D1相交,即直线EF与平面D1BC相交,故排除C;连接B1C交BC1于点F,由于平行四边形BCC1B1的对角线互相平分,故F是B1C的中点.因为E是AB1的中点,所以EF是三角形B1AC的中位线,故EF∥AC.又AC⊂平面ACC1A1,所以EF∥平面ACC1A1.故选D.4.答案:B答案解析:∵BB1⊥平面A1B1C1,∴C1D与平面A1B1C1所成的角为∠DC1B1.又B1C1=1,B1D=32,可得C1D=72,而平面A1B1C1∥平面ABC,∴C1D与平面ABC所成角的正弦值为B1DC1D=217. 5.答案:B答案解析:设正方体的棱长为a ,如图,取AD 的中点G ,连接EG ,过G 作GH ∥DD 1,与A 1D 1交于点H ,则点F ∈GH ,且HG ⊥平面ABCD ,则∠FEG 即为EF 与平面ABCD 所成角,当EF长度最大时,点F 与点H 重合,EG =22 a ,EH =a 2+12a 2 =62 a ,得cos ∠HEG =22a 62a=33. 6.答案:D答案解析:取CD 的中点O ,连接AO 、BO ,如图所示:对于A ,点A 、F 、O 和点B 、E 、O 分别共线, 因为点E 、F 分别为△BCD 和△ACD 的中心,所以AF FO =BEEO=2, 所以EF ∥AB ,所以选项A 正确;对于B ,因为AO ⊥CD ,BO ⊥CD ,AO ,BO ⊂平面ABO ,且AO ∩BO =O ,所以CD ⊥平面ABO ,即CD ⊥平面ABEF ,选项B 正确;对于C ,因为AB ⊂平面ABO ,所以CD ⊥AB ,选项C 正确;对于D ,因为EF ∥AB ,设AB =1,所以EF =13 ,易知BO =32,在Rt△AEB 中,BE =23 BO =23 ×32 =33 ,所以AE =AB 2-BE 2=1-(33)2 =63 ,AE ≠13EF ,选项D 错误. 7.答案:2答案解析:根据题意,因为EF ∥平面AB 1C ,所以EF ∥AC .又E 是AD 的中点,所以F 是CD 的中点.因为在Rt△DEF 中,DE =DF =1,故EF =2 .二 能力小题提升篇1.答案:D答案解析:①,由直线l ⊥平面α,直线m ⊂平面β,若α∥β⇒l ⊥β⇒l ⊥m ,故①正确;②,若α⊥β⇒l∥m或l、m异面或l、m相交,故②错误;③,利用面面垂直的判定,若l∥m⇒α⊥β,故③正确;④,若l⊥m⇒α∥β或α、β相交或α、β垂直,故④错误.所以①③正确.2.答案:B答案解析:对于选项A,若m∥α,n∥α,则m与n可以平行,相交,或为异面直线,因此不正确;对于选项B,若α⊥β,γ⊥β且α∩γ=m,则m⊥β,因此正确;对于选项C,若m⊂α,n⊂α,m∥β,n∥β,则α与β不一定平行,因此不正确;对于选项D,若m⊥α,n∥β,α⊥β,则m与n不一定垂直,因此不正确.综上,正确的命题是B.故选B.3.答案:D答案解析:因为A1N与C1A异面,所以A项错误;因为A1N的延长线必过点B,则直线A1N与平面BAM相交,所以B项错误;因为AB1与AB不垂直,所以AB1不垂直于平面ABM,所以C项错误;取BC的中点P,连接PB1,在正方形BCC1B1中,△B1BP与△BCM全等,可得BM⊥B1P,连接AP,则AP⊥BC,又平面BCC1B1⊥底面ABC,平面BCC1B1∩底面ABC=BC,所以AP⊥平面BCC1B1,因为BM⊂平面BCC1B1,所以BM⊥AP,又AP∩B1P=P,AP,B1P⊂平面B1AP,所以BM⊥平面B1AP,因为B1A⊂平面B1AP,所以BM⊥AB1.故选D.4.答案:C答案解析:A选项,过A作AF⊥BC,垂足为F,根据直三棱柱的性质可知BB1⊥平面ABC,由于AF⊂平面ABC,所以BB1⊥AF,由于BC∩BB1=B,BC,BB1⊂平面BCC1B1,所以AF⊥平面BCC1B1,即AF⊥平面B1DE,由于AF⊂平面ABC,所以平面ABC⊥平面B1DE,A选项正确.B选项,根据三棱柱的性质可知A1A∥CC1,即A1A∥DE,由于A1A⊄平面B1DE,DE⊂平面B1DE,所以A1A∥平面B1DE,B选项正确.C选项,若AB1⊥平面ADE,即AB1⊥平面AA1C1C,由于A1A⊂平面AA1C1C,所以AB1⊥A1A,这与已知AB1,A1A不垂直矛盾,C选项错误.D选项,VA B1DE=VB1 ADE,由于三角形ADE的面积为定值、B1到平面AA1C1C的距离为定值,所以VA B1DE=VB1 ADE为定值,所以D选项正确.故选C.5.答案:DM⊥PC(或BM⊥PC)答案解析:连接AC ,BD ,则AC ⊥BD ,∵PA ⊥底面ABCD ,BD ⊂底面ABCD ,∴PA ⊥BD . 又PA ∩AC =A ,PA ,AC ⊂平面PAC , ∴BD ⊥平面PAC , ∴BD ⊥PC .∴当DM ⊥PC (或BM ⊥PC )时,即有PC ⊥平面MBD . 而PC ⊂平面PCD ,∴平面MBD ⊥平面PCD . 6.答案:①③④答案解析:①设A 1到平面EBCD 的距离为h ,D 到AB 的距离为h ′,则VA -A 1DE ∶VA 1-BCDE =⎝ ⎛⎭⎪⎫13×S △ADE ×h ∶⎝ ⎛⎭⎪⎫13×S 梯形EBCD ×h =S △ADE ∶S 梯形EBCD =(12 ×AE ×h ′)∶⎝ ⎛⎭⎪⎫CD +BE 2×h ′ =1∶3,故①正确;②A 1C 在平面ABCD 中的射影在AC 上,AC 与DE 不垂直,∴DE 与A 1C 不垂直,故②错误;③取CD 的中点F ,连接MF ,BF ,则MF ∥A 1D 且MF =12A 1D ,FB ∥ED 且FB=ED ,可得平面MBF ∥平面A 1DE ,∴总有BM ∥平面A 1DE ,故③正确;易知∠MFB =∠A 1DE ,由余弦定理可得MB 2=MF 2+FB 2-2MF ·FB ·cos ∠MFB 是定值,故④正确.三 高考小题重现篇1.答案:B答案解析:对于A ,α内有无数条直线与β平行,当这无数条直线互相平行时,α与β可能相交,所以A 不正确;对于B ,根据两平面平行的判定定理与性质知,B 正确;对于C ,平行于同一条直线的两个平面可能相交,也可能平行,所以C 不正确;对于D ,垂直于同一平面的两个平面可能相交,也可能平行,如长方体的相邻两个侧面都垂直于底面,但它们是相交的,所以D 不正确.综上可知选B.2.答案:A答案解析:A 项,作如图①所示的辅助线,其中D 为BC 的中点,则QD ∥AB . ∵QD ∩平面MNQ =Q ,∴QD 与平面MNQ 相交,∴直线AB 与平面MNQ 相交.B 项,作如图②所示的辅助线,则AB ∥CD ,CD ∥MQ ,∴AB ∥MQ .又AB ⊄平面MNQ ,MQ ⊂平面MNQ ,∴AB ∥平面MNQ .①②③④C项,作如图③所示的辅助线,则AB∥CD,CD∥MQ,∴ AB∥MQ,又AB⊄平面MNQ,MQ⊂平面MNQ,∴ AB∥平面MNQ.D项,作如图④所示的辅助线,则AB∥CD,CD∥NQ,∴ AB∥NQ.又AB⊄平面MNQ,NQ⊂平面MNQ,∴ AB∥平面MNQ.3.答案:C答案解析:如图,∵ A1E在平面ABCD上的射影为AE,而AE不与AC,BD垂直,∴ B,D错;∵ A1E在平面BCC1B1上的射影为B1C,且B1C⊥BC1,∴ A1E⊥BC1(证明:由条件易知,BC1⊥B1C,BC1⊥CE,又CE∩B1C=C,∴ BC1⊥平面CEA1B1.又A1E⊂平面CEA1B1,∴ A1E⊥BC1),故C正确;∵ A1E在平面DCC1D1上的射影为D1E,而D1E不与DC1垂直,故A错.4.答案:ABD答案解析:如图(1),连接B1C.因为DA1∥CB1,BC1⊥CB1,所以直线BC1与DA1所成的角为90°,所以A正确.如图(2),连接B1C.因为BC1⊥B1C,BC1⊥A1B1,B1C∩A1B1=B1,B1C,A1B1⊂平面A1B1C,所以BC1⊥平面A1B1C,所以BC1⊥CA1,所以B正确,如图(3),连接A1C1,交B1D1于点O,连接BO,A1B.易证A1C1⊥平面BDD1B1,所以∠C1BO为直线C1B与平面BDD1B1所成的角,∠C1BO=30°,所以C错误.如图(4),因为C1C⊥平面ABCD,所以∠C1BC为直线BC1与平面ABCD所成的角,且∠C1BC =45°,所以D正确.故选ABD.5.答案:②③④答案解析:若m⊥n,m⊥α,则n∥α或n⊂α,又n∥β,则α,β可能相交或平行,所以①错误;若m⊥α,n∥α,则m⊥n,所以②正确;若α∥β,m⊂α,由面面平行的性质可得m∥β,③正确;由线面所成角的定义可得④正确.故正确命题是②③④.6.答案:2答案解析:设PO⊥平面ABC于O,PE⊥AC于E,PF⊥BC于F,连接OE、OF、OC,∵PO⊥平面ABC,∴PO⊥AC,又PO∩PE=P,PO,PE⊂平面POE,∴AC⊥平面POE,OE⊂平面POE,∴AC⊥OE,同理有BC⊥OF,∴四边形OECF为矩形,∵PC=PC且PE=PF,∴Rt△PEC≌Rt△PFC,∴EC=FC=PC2-PE2=1,∴四边形OECF是边长为1的正方形,∴OC=2,在Rt△POC中,PO=PC2-OC2=2.四 经典大题强化篇1.证明:(1)取BE的中点N,连接MN,FN,因为F,M,N分别为AB,CD,BE的中点,所以MN∥DE,FN∥AE.又因为AE,DE⊂平面ADE,FN,MN⊄平面ADE,所以MN∥平面ADE,FN∥平面ADE.又MN∩FN=N,所以平面ADE∥平面FMN.又FM⊂平面FMN,所以FM∥平面ADE.(2)因为四边形DCBE为矩形,所以BC⊥DC.又AC⊥BC,AC∩DC=C,所以BC⊥平面ACD.又因为BC∥DE,所以DE⊥平面ACD.因为DE⊂平面ADE,所以平面ACD⊥平面ADE.2.答案解析:(1)证明:因为PA⊥底面ABCD,CE⊂平面ABCD,所以PA⊥CE. 因为AB⊥AD,CE∥AB,所以CE⊥AD.又PA∩AD=A,所以CE⊥平面PAD.(2)由(1)可知CE⊥AD.在Rt△ECD中,CE=CD·sin 45°=1,DE=CD·cos 45°=1,又因为AB=1,则AB=CE.又CE∥AB,AB⊥AD,所以四边形ABCE为矩形,四边形ABCD为梯形.因为AD=3,所以BC=AE=AD-DE=2,S ABCD=12(BC+AD)·AB=12(2+3)×1=52,V P ABCD=13 S ABCD·PA=13×52×1=56.于是四棱锥P ABCD的体积为56.3.答案解析:(1)证明:∵在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AED折起到△A1ED的位置,∴DE⊥A1E,DE⊥BE,∵A1E∩BE=E,∴DE⊥平面A1BE,∵A1B⊂平面A1BE,∴DE⊥A1B.(2)证明:取CD中点F,连接NF,MF,∵M,N分别为A1C,BE的中点,∴MF∥A1D,NF∥DE,又DE∩A1D=D,NF∩MF=F,DE⊂平面A1DE,A1D⊂平面A1DE,NF⊂平面MNF,MF⊂平面MNF. ∴平面A1DE∥平面MNF,∴MN∥平面A1ED.(3)取A1B的中点G,连接EG,∵A1E=BE,∴EG⊥A1B,由(1)知DE⊥平面A1BE,∵DE∥BC,∴BC⊥平面A1BE,∴EG⊥BC,又A1B∩BC=B,A1B,BC⊂平面A1BC,∴EG⊥平面A1BC.故棱A1B上存在中点G,使得EG⊥平面A1BC,此时A1GGB=1.。
历年高考数学真题精选31 立体几何中的垂直关系

历年高考数学真题精选(按考点分类)专题31 垂直关系(学生版)1.(2019•北京)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 为菱形,E 为CD 的中点.(Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)若60ABC ∠=︒,求证:平面PAB ⊥平面PAE ;(Ⅲ)棱PB 上是否存在点F ,使得//CF 平面PAE ?说明理由.2.(2015•重庆)如图,三棱锥P ABC -中,平面PAC ⊥平面ABC ,2ABC π∠=,点D 、E在线段AC 上,且2AD DE EC ===,4PD PC ==,点F 在线段AB 上,且//EF BC . (Ⅰ)证明:AB ⊥平面PFE .(Ⅱ)若四棱锥P DFBC -的体积为7,求线段BC 的长.3.(2015•福建)如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,PO 垂直于圆O 所在的平面,且1PO OB ==,(Ⅰ)若D 为线段AC 的中点,求证;AC ⊥平面PDO ; (Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若2BC =,点E 在线段PB 上,求CE OE +的最小值.4.(2014•四川)在如图所示的多面体中,四边形11ABB A 和11ACC A 都为矩形 (Ⅰ)若AC BC ⊥,证明:直线BC ⊥平面11ACC A ;(Ⅱ)设D 、E 分别是线段BC 、1CC 的中点,在线段AB 上是否存在一点M ,使直线//DE 平面1A MC ?请证明你的结论.5.(2014•福建)如图,三棱锥A BCD -中,AB ⊥平面BCD ,CD BD ⊥. (Ⅰ)求证:CD ⊥平面ABD ;(Ⅱ)若1AB BD CD ===,M 为AD 中点,求三棱锥A MBC -的体积.6.(2014•广东)如图1,四边形ABCD 为矩形,PD ⊥平面ABCD ,1AB =,2BC PC ==作如图2折叠;折痕//EF DC ,其中点E ,F 分别在线段PD ,PC 上,沿EF 折叠后点P 叠在线段AD 上的点记为M ,并且MF CF ⊥.(1)证明:CF ⊥平面MDF ; (2)求三棱锥M CDE -的体积.7.(2014•新课标Ⅰ)如图,三棱柱111ABC A B C -中,侧面11BB C C 为菱形,1B C 的中点为O ,且AO ⊥平面11BB C C . (1)证明:1B C AB ⊥;(2)若1AC AB ⊥,160CBB ∠=︒,1BC =,求三棱柱111ABC A B C -的高.8.(2014•山东)如图,四棱锥P ABCD -中,AP ⊥平面PCD ,//AD BC ,12AB BC AD ==,E ,F 分别为线段AD ,PC 的中点.(Ⅰ)求证://AP 平面BEF ; (Ⅱ)求证:BE ⊥平面PAC .9.(2013•安徽)如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=︒.已知2PB PD ==,6PA = (Ⅰ)证明:BD ⊥面PAC(Ⅱ)若E 为PA 的中点,求三菱锥P BCE -的体积.10.(2013•重庆)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,23PA =,2BC CD ==,3ACB ACD π∠=∠=.(Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)若侧棱PC 上的点F 满足7PF FC =,求三棱锥P BDF -的体积.11.(2013•新课标Ⅰ)如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=︒ (Ⅰ)证明:1AB AC ⊥; (Ⅱ)若2AB CB ==,16A C =,求三棱柱111ABC A B C -的体积.12.(2019•新课标Ⅲ)图1是由矩形ADEB ,Rt ABC ∆和菱形BFGC 组成的一个平面图形,其中1AB =,2BE BF ==,60FBC ∠=︒.将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的四边形ACGD 的面积.13.(2018•江苏)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥. 求证:(1)//AB 平面11A B C ; (2)平面11ABB A ⊥平面1A BC .14.(2018•新课标Ⅲ)如图,矩形ABCD 所在平面与半圆弧¶CD所在平面垂直,M 是¶CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得//MC 平面PBD ?说明理由.15.(2018•新课标Ⅰ)如图,在平行四边形ABCM 中,3AB AC ==,90ACM ∠=︒,以AC 为折痕将ACM ∆折起,使点M 到达点D 的位置,且AB DA ⊥. (1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.16.(2017•新课标Ⅰ)如图,在四棱锥P ABCD -中,//AB CD ,且90BAP CDP ∠=∠=︒. (1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.历年高考数学真题精选(按考点分类)专题31 垂直关系(教师版)1.(2019•北京)如图,在四棱锥P ABCD-中,PA⊥平面ABCD,底面ABCD为菱形,E 为CD的中点.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若60∠=︒,求证:平面PAB⊥平面PAE;ABC(Ⅲ)棱PB上是否存在点F,使得//CF平面PAE?说明理由.证明:(Ⅰ)Q四棱锥P ABCD-中,PA⊥平面ABCD,底面ABCD为菱形,∴⊥,BD ACBD PA⊥,∴⊥平面PAC.Q I,BD=PA AC A(Ⅱ)Q在四棱锥P ABCD-中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点,60∠=︒,ABCAB AE∴⊥,PA AE⊥,∴⊥平面PAB,Q I,AE=PA AB AQ平面PAE,∴平面PAB⊥平面PAE.AE⊂解:(Ⅲ)棱PB上是存在中点F,使得//CF平面PAE.理由如下:取AB中点G,连结GF,CG,Q在四棱锥P ABCD-中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点,∴,//FG PA,CG AE//I,Q I,AE PA A==CG FG GCFG平面PAE,∴平面//CF ⊂Q 平面CFG ,//CF ∴平面PAE .2.(2015•重庆)如图,三棱锥P ABC -中,平面PAC ⊥平面ABC ,2ABC π∠=,点D 、E在线段AC 上,且2AD DE EC ===,4PD PC ==,点F 在线段AB 上,且//EF BC . (Ⅰ)证明:AB ⊥平面PFE .(Ⅱ)若四棱锥P DFBC -的体积为7,求线段BC 的长.解:(Ⅰ)如图,由DE EC =,PD PC =知,E 为等腰PDC ∆中DC 边的中点,故PE AC ⊥, 又平面PAC ⊥平面ABC ,平面PAC ⋂平面ABC AC =,PE ⊂平面PAC ,PE AC ⊥, 所以PE ⊥平面ABC ,从而PE AB ⊥. 因为2ABC π∠=,//EF BC ,故AB EF ⊥,从而AB 与平面PEF 内两条相交直线PE ,EF 都垂直, 所以AB ⊥平面PEF .(Ⅱ)设BC x =,则在直角ABC ∆中,22236AB AC BC x -=-, 从而2113622ABC S AB BC x x ∆==-g 由//EF BC 知23AF AE AB AC ==,得AFE ABC ∆∆∽, 故224()39AFEABCS S ∆∆==,即49AFE ABC S S ∆∆=,由12AD AE =,2114213622999AFD AFE ABC ABC S S S S x x ∆∆∆∆====-g , 从而四边形DFBC 的面积为:2221173636362918DFBC ABC AFD S S S x x x x x x ∆=-=---=-.由(Ⅰ)知,PE ⊥平面ABC ,所以PE 为四棱锥P DFBC -的高. 在直角PEC ∆中,22224223PE PC EC =-=-=, 故体积2117362373318P DFBC DFBC V S PE x x -==-=g g g g ,故得42362430x x -+=,解得29x =或227x =,由于0x >,可得3x =或33x =. 所以:3BC =或33BC =.3.(2015•福建)如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,PO 垂直于圆O 所在的平面,且1PO OB ==,(Ⅰ)若D 为线段AC 的中点,求证;AC ⊥平面PDO ; (Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若2BC =,点E 在线段PB 上,求CE OE +的最小值.解:(Ⅰ)在AOC ∆中,因为OA OC =,D 为AC 的中点, 所以AC DO ⊥,又PO 垂直于圆O 所在的平面, 所以PO AC ⊥, 因为DO PO O =I , 所以AC ⊥平面PDO .(Ⅱ)因为点C 在圆O 上,所以当CO AB ⊥时,C 到AB 的距离最大,且最大值为1, 又2AB =,所以ABC ∆面积的最大值为12112⨯⨯=,又因为三棱锥P ABC -的高1PO =,故三棱锥P ABC -体积的最大值为:111133⨯⨯=.(Ⅲ)在POB ∆中,1PO OB ==,90POB ∠=︒, 所以22112PB =+=,同理2PC =,所以PB PC BC ==,在三棱锥P ABC -中,将侧面BCP 绕PB 旋转至平面BC P ',使之与平面ABP 共面,如图所示,当O ,E ,C '共线时,CE OE +取得最小值, 又因为OP OB =,C P C B '=',所以OC '垂直平分PB ,即E 为PB 中点. 从而2626OC OE EC +'=+'=+=. 亦即CE OE +的最小值为:26+.4.(2014•四川)在如图所示的多面体中,四边形11ABB A 和11ACC A 都为矩形 (Ⅰ)若AC BC ⊥,证明:直线BC ⊥平面11ACC A ;(Ⅱ)设D 、E 分别是线段BC 、1CC 的中点,在线段AB 上是否存在一点M ,使直线//DE平面1A MC ?请证明你的结论.(Ⅰ)证明:Q 四边形11ABB A 和11ACC A 都为矩形, 1AA AB ∴⊥,1AA AC ⊥, AB AC A =Q I ,1AA ∴⊥平面ABC ,BC ⊂Q 平面ABC , 1AA BC ∴⊥,AC BC ⊥Q ,1AA AC A =I ,∴直线BC ⊥平面11ACC A ;(Ⅱ)解:取AB 的中点M ,连接1A M ,MC ,1A C ,1AC ,设O 为1A C ,1AC 的交点,则O 为1AC 的中点.连接MD ,OE ,则//MD AC ,12MD AC =,//OE AC ,12OE AC =, //MD OE ∴,MD OE =,连接OM ,则四边形MDEO 为平行四边形, //DE MO ∴,DE ⊂/Q 平面1A MC ,MO ⊂平面1A MC ,//DE ∴平面1A MC ,∴线段AB 上存在一点M (线段AB 的中点),使直线//DE 平面1A MC .5.(2014•福建)如图,三棱锥A BCD -中,AB ⊥平面BCD ,CD BD ⊥. (Ⅰ)求证:CD ⊥平面ABD ;(Ⅱ)若1AB BD CD ===,M 为AD 中点,求三棱锥A MBC -的体积.(Ⅰ)证明:AB ⊥Q 平面BCD ,CD ⊂平面BCD , AB CD ∴⊥,CD BD ⊥Q ,AB BD B =I ,CD ∴⊥平面ABD ;(Ⅱ)解:AB ⊥Q 平面BCD ,BD ⊂平面BCD ,AB BD ∴⊥. 1AB BD ==Q ,12ABD S ∆∴=, M Q 为AD 中点,1124ABM ABD S S ∆∆∴==,CD ⊥Q 平面ABD ,11312A MBC C ABM ABM V V S CD --∆∴===g .6.(2014•广东)如图1,四边形ABCD 为矩形,PD ⊥平面ABCD ,1AB =,2BC PC ==作如图2折叠;折痕//EF DC ,其中点E ,F 分别在线段PD ,PC 上,沿EF 折叠后点P 叠在线段AD 上的点记为M ,并且MF CF ⊥.(1)证明:CF ⊥平面MDF ; (2)求三棱锥M CDE -的体积.解:(1)证明:PD ⊥Q 平面ABCD ,PD ⊂平面PCD ,∴平面PCD ⊥平面ABCD ;又平面PCD ⋂平面ABCD CD =,MD ⊂平面ABCD ,MD CD ⊥,MD ∴⊥平面PCD ,CF ⊂平面PCD ,CF MD ∴⊥;又CF MF ⊥,MD 、MF ⊂平面MDF ,MD M F M =I , CF ∴⊥平面MDF ;(2)CF ⊥Q 平面MDF ,CF DF ∴⊥, 又Rt PCD ∆Q 中,1DC =,2PC =, 30P ∴∠=︒,60PCD ∠=︒, 30CDF ∴∠=︒,1122CF CD ==;//EF DC Q ,∴DE CFDP CP =1223=, 3DE ∴=33PE ∴=132CDE S CD DE ∆∴=g ; 22223336()()44MD ME DE =--=, 1136233M CDE CDE V S MD -∆∴==g 7.(2014•新课标Ⅰ)如图,三棱柱111ABC A B C -中,侧面11BB C C 为菱形,1B C 的中点为O ,且AO ⊥平面11BB C C .(1)证明:1B C AB ⊥;(2)若1AC AB ⊥,160CBB ∠=︒,1BC =,求三棱柱111ABC A B C -的高.(1)证明:连接1BC ,则O 为1B C 与1BC 的交点, Q 侧面11BB C C 为菱形, 11BC B C ∴⊥,AO ⊥Q 平面11BB C C , 1AO B C ∴⊥, 1AO BC O =Q I ,1B C ∴⊥平面ABO ,AB ⊂Q 平面ABO ,1B C AB ∴⊥;(2)解:作OD BC ⊥,垂足为D ,连接AD ,作OH AD ⊥,垂足为H , BC AO ⊥Q ,BC OD ⊥,AO OD O =I ,BC ∴⊥平面AOD , OH BC ∴⊥,OH AD ⊥Q ,BC AD D =I ,OH ∴⊥平面ABC , 160CBB ∠=︒Q , 1CBB ∴∆为等边三角形,1BC =Q ,3OD ∴=1AC AB ⊥Q ,11122OA B C ∴==,由OH AD OD OA =g g ,可得2274AD OD OA =+=,2114OH ∴=, O Q 为1B C 的中点, 1B ∴到平面ABC 的距离为217, ∴三棱柱111ABC A B C -的高217.8.(2014•山东)如图,四棱锥P ABCD -中,AP ⊥平面PCD ,//AD BC ,12AB BC AD ==,E ,F 分别为线段AD ,PC 的中点.(Ⅰ)求证://AP 平面BEF ; (Ⅱ)求证:BE ⊥平面PAC .证明:(Ⅰ)连接CE ,则 //AD BC Q ,12BC AD =,E 为线段AD 的中点, ∴四边形ABCE 是平行四边形,BCDE 是平行四边形,设AC BE O =I ,连接OF ,则O 是AC 的中点,F Q 为线段PC 的中点,//PA OF ∴,PA ⊂/Q 平面BEF ,OF ⊂平面BEF ,//AP ∴平面BEF ;(Ⅱ)BCDE Q 是平行四边形, //BE CD ∴,AP ⊥Q 平面PCD ,CD ⊂平面PCD ,AP CD ∴⊥,BE AP ∴⊥,AB BC =Q ,四边形ABCE 是平行四边形,∴四边形ABCE 是菱形,BE AC ∴⊥, AP AC A =Q I ,BE ∴⊥平面PAC .9.(2013•安徽)如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=︒.已知2PB PD ==,6PA =. (Ⅰ)证明:BD ⊥面PAC(Ⅱ)若E 为PA 的中点,求三菱锥P BCE -的体积.(Ⅰ)证明:连接BD ,AC 交于O 点,PB PD =Q ,PO BD ∴⊥,又ABCD 是菱形, BD AC ∴⊥,PO ⊂Q 平面PAC ,AC ⊂平面PAC ,AC PO O =I ,BD ∴⊥平面PAC .(Ⅱ)则23AC =,ABD ∆Q 和PBD ∆的三边长均为2, ABD PBD ∴∆≅∆,3AO PO ∴==,222AO PO PA ∴+=, AC PO ∴⊥, 132PAC S AC PO ∆==g g ,11111131223232P BCE B PEC B PAC PAC V V V S BO ---∆====⨯⨯⨯=g g g .10.(2013•重庆)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,23PA =,2BC CD ==,3ACB ACD π∠=∠=.(Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)若侧棱PC 上的点F 满足7PF FC =,求三棱锥P BDF -的体积.解:(Ⅰ)2BC CD ==Q ,BCD ∴∆为等腰三角形,再由3ACB ACD π∠=∠=,BD AC ∴⊥.再由PA ⊥底面ABCD ,可得PA BD ⊥. 而PA AC A =I ,故BD ⊥平面PAC .(Ⅱ)Q 侧棱PC 上的点F 满足7PF FC =,∴三棱锥F BCD -的高是三棱锥P BCD -的高的18.BCD ∆的面积112sin 22sin 3223BCD S BC CD BCD π∆=∠=⨯⨯⨯=g g .∴三棱锥P BDF -的体积1117133883P BCD F BCD BCD BCD BCD V V V S PA S PA S PA --∆∆∆=-=-=⨯g g g g g g g 77323244=⨯⨯=. 11.(2013•新课标Ⅰ)如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=︒ (Ⅰ)证明:1AB AC ⊥; (Ⅱ)若2AB CB ==,16A C =,求三棱柱111ABC A B C -的体积.(Ⅰ)证明:如图,取AB 的中点O ,连结OC ,1OA ,1A B . 因为CA CB =,所以OC AB ⊥.由于1AB AA =,160BAA ∠=︒,故△1AA B 为等边三角形, 所以1OA AB ⊥.因为1OC OA O =I ,所以AB ⊥平面1OAC . 又1A C ⊂平面1OAC ,故1AB AC ⊥; (Ⅱ)解:由题设知ABC ∆与△1AA B 都是边长为2的等边三角形, 所以13OC OA ==又16A C =22211AC OC OA =+,故1OA OC ⊥. 因为OC AB O =I ,所以1OA ⊥平面ABC ,1OA 为三棱柱111ABC A B C -的高.又ABC ∆的面积3ABC S ∆=,故三棱柱111ABC A B C -的体积1333ABC V S OA ∆=⨯=⨯=.12.(2019•新课标Ⅲ)图1是由矩形ADEB ,Rt ABC ∆和菱形BFGC 组成的一个平面图形,其中1AB =,2BE BF ==,60FBC ∠=︒.将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的四边形ACGD 的面积.解:(1)证明:由已知可得//AD BE ,//CG BE ,即有//AD CG , 则AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面; 由四边形ABED 为矩形,可得AB BE ⊥, 由ABC ∆为直角三角形,可得AB BC ⊥, 又BC BE B =I ,可得AB ⊥平面BCGE ,AB ⊂平面ABC ,可得平面ABC ⊥平面BCGE ;(2)连接BG ,AG ,由AB ⊥平面BCGE ,可得AB BG ⊥,在BCG ∆中,2BC CG ==,120BCG ∠=︒,可得2sin 6023BG BC =︒= 可得2213AG AB BG =+在ACG ∆中,5AC 2CG =,13AG ,可得cos 2255ACG ∠==-⨯⨯,即有sin 5ACG ∠=,则平行四边形ACGD 的面积为2545⨯⨯=.13.(2018•江苏)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥. 求证:(1)//AB 平面11A B C ; (2)平面11ABB A ⊥平面1A BC .证明:(1)平行六面体1111ABCD A B C D -中,11//AB A B ,11//AB A B ,AB ⊂/平面11A B C ,11//A B ⊂平面11//A B C AB ⇒平面11A B C ;(2)在平行六面体1111ABCD A B C D -中,1AA AB =,⇒四边形11ABB A 是菱形,11AB A B ⊥⊥.在平行六面体1111ABCD A B C D -中,1AA AB =,1111AB B C AB BC ⊥⇒⊥. ∴1111111,,AB A B AB BC A B BC B A B A BC BC A BC⊥⊥⎧⎪=⎨⎪⊂⊂⎩n 面面 1AB ⇒⊥面1A BC ,且1AB ⊂平面11ABB A ⇒平面11ABB A ⊥平面1A BC .14.(2018•新课标Ⅲ)如图,矩形ABCD 所在平面与半圆弧¶CD所在平面垂直,M 是¶CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得//MC 平面PBD ?说明理由.(1)证明:矩形ABCD 所在平面与半圆弦¶CD所在平面垂直,所以AD ⊥半圆弦¶CD 所在平面,CM ⊂半圆弦¶CD所在平面, CM AD ∴⊥,M 是¶CD 上异于C ,D 的点.CM DM ∴⊥,DM AD D =I,CM ∴⊥平面AMD ,CM ⊂平面CMB ,∴平面AMD ⊥平面BMC ;(2)解:存在P 是AM 的中点,理由:连接BD 交AC 于O ,取AM 的中点P ,连接OP ,可得//MC OP ,MC ⊂/平面BDP ,OP ⊂平面BDP ,所以//MC 平面PBD .15.(2018•新课标Ⅰ)如图,在平行四边形ABCM 中,3AB AC ==,90ACM ∠=︒,以AC 为折痕将ACM ∆折起,使点M 到达点D 的位置,且AB DA ⊥.(1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.解:(1)证明:Q 在平行四边形ABCM 中,90ACM ∠=︒,AB AC ∴⊥, 又AB DA ⊥.且AD AC A =I ,AB ∴⊥面ADC ,AB ⊂Q 面ABC ,∴平面ACD ⊥平面ABC ;(2)3AB AC ==Q ,90ACM ∠=︒,32AD AM ∴==, 2223BP DQ DA ∴===, 由(1)得DC AB ⊥,又DC CA ⊥,DC ∴⊥面ABC , ∴三棱锥Q ABP -的体积1133ABP V S DC ∆=⨯ 121121133313333323ABC S DC ∆=⨯⨯=⨯⨯⨯⨯⨯⨯=. 16.(2017•新课标Ⅰ)如图,在四棱锥P ABCD -中,//AB CD ,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.证明:(1)Q 在四棱锥P ABCD -中,90BAP CDP ∠=∠=︒, AB PA ∴⊥,CD PD ⊥,又//AB CD ,AB PD ∴⊥,PA PD P =Q I ,AB ∴⊥平面PAD ,AB ⊂Q 平面PAB ,∴平面PAB ⊥平面PAD .解:(2)设PA PD AB DC a ====,取AD 中点O ,连结PO , PA PD AB DC ===Q ,90APD ∠=︒,平面PAB ⊥平面PAD , PO ∴⊥底面ABCD ,且222AD a a a =+=,2PO a =, Q 四棱锥P ABCD -的体积为83, 由AB ⊥平面PAD ,得AB AD ⊥,13P ABCD ABCD V S PO -∴=⨯⨯四边形 31121823333AB AD PO a a a a =⨯⨯⨯=⨯⨯⨯==, 解得2a =,2PA PD AB DC ∴====,22AD BC ==,2PO =, 4422PB PC ∴==+=,∴该四棱锥的侧面积:PAD PAB PDC PBC S S S S S ∆∆∆∆=+++侧221111()22222BC PA PD PA AB PD DC BC PB =⨯⨯+⨯⨯+⨯⨯+⨯⨯- 111122222222822222=⨯⨯+⨯⨯+⨯⨯+⨯⨯- 623=+.。
高中数学-立体几何-空间中的平行和垂直关系
高中数学总复习-第七章立体几何-空间中的平行和垂直关系【知识结构图】第3课空间中的平行关系【考点导读】1.掌握直线和平面平行、两个平面平行的判定定理和性质定理。
2.明确定义与定理的不同,定义是可逆的,既是判定也是性质,而判定定理与性质定理多是不可逆的。
3.要能灵活的对“线线平行”、“线面平行”和“面面平行”进行转化。
【基础练习】1.若ba、为异面直线,直线c∥a,则c与b的位置关系是异面或相交2.给出下列四个命题:①垂直于同一直线的两条直线互相平行. ②垂直于同一平面的两个平面互相平行.③若直线12,l l 与同一平面所成的角相等,则12,l l 互相平行. ④若直线12,l l 是异面直线,则与12,l l 都相交的两条直线是异面直线. 其中假.命题的个数是 4 个。
3.对于任意的直线l 与平面a ,在平面a 内必有直线m ,使m 与l 垂直 。
4. 已知a 、b 、c 是三条不重合的直线,α、β、r 是三个不重合的平面,下面六个命题:①a ∥c ,b ∥c ⇒a ∥b ;②a ∥r ,b ∥r ⇒a ∥b ;③α∥c ,β∥c ⇒α∥β; ④α∥r ,β∥r ⇒α∥β;⑤a ∥c ,α∥c ⇒a ∥α;⑥a ∥r ,α∥r ⇒a ∥α. 其中正确的命题是 ①④ 。
【范例导析】例1.如图,在四面体ABCD 中,截面EFGH 是平行四边形. 求证:AB ∥平面EFG . 证明 :∵面EFGH 是截面.∴点E ,F ,G ,H 分别在BC ,BD ,DA ,AC 上. ∴EH面ABC ,GF面ABD ,由已知,EH ∥GF .∴EH ∥面ABD . 又 ∵EH 面BAC ,面ABC ∩面ABD=AB∴EH ∥AB . ∴AB ∥面EFG .例2. 如图,在正方体ABCD —A 1B 1C 1D 1中,点N 在BD 上,点M 在B 1C 上,并且CM=DN.求证:MN ∥平面AA 1B 1B.分析:“线线平行”、“线面平行”、“面面平行”是可以互相转化的。
立体几何中的垂直关系
立体几何中的垂直关系环节1 明晰高考要求垂直关系是立体几何中元素间关系考查的核心,主要从线线垂直、线面垂直、面面垂直三个方面进行考查,而且以线面垂直为聚焦!线面位置关系的考查强调从平面和空间两个方向研究线线垂直!在 “线线垂直”中要特别重视常规平面几何图形中存在的线线垂直性质与以及从空间角度出发,研究线线垂直的性质的定理。
真题示例① 平面几何角度研究垂直关系题1. (2018全国卷Ⅱ)如图,在三棱锥-P ABC中,==AB BC PA PB PC ===4AC =,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角--M PA C 为30︒,求PC 与平面PAM 所成角的正弦值.题2.(2017新课标Ⅲ)如图,四面体ABCD 中,ABC ∆是正三角形,ACD ∆是直角三角形,ABD CBD ∠=∠,AB BD =.(1) 证明:平面ACD ⊥平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角D AE C --的余弦值.O MPCBAABCDE② 平面几何角度和空间几何角度研究垂直关系题3 .(2018北京)如图,在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11A C ,1BB的中点,AB BC ==12AC AA ==.(1)求证:AC ⊥平面BEF ; (2)求二面角1B CD C --的余弦值;题4.(2018全国卷Ⅲ)如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M ABC -体积最大时,求面MAB 与面MCD 所成二面角的正弦值.环节2 问题自主解决 1回归教材题5 [必修二 P 67 练习第 1 题] 三棱锥V - ABC 中,VA = VC , BA = BC .求证:VB ^ AC .题6.必修二P 79 复习参考题第1 题] 边长为2 的正方形 ABCD 中,点 E 是 AB 的中点,点 F 是 BC 的中点,将△C 1B 1A 1G FE DC BAMD CBAAED 、△ DCF 分别沿 DE 、 DF 折起,使 A 、C 两点重合于点 A ,连接 EF ,求证: A D EF .题7. [必修二 P 74 习题 2.3B 组第 4 题]如图, AB 为圆O 的直径,点C 是圆O 上的动点,过动点C 的直线垂直于圆O 所在的平面, D , E 分别是VA ,VC 的中点,试判断直线 DE 与平面VBC 的位置关系,并说明理由.题8.[必修二 P 66 探究题]直四棱柱 AB C D ABCD (侧棱与底面垂直的棱柱称为直棱柱)中,底面四边形ABCD 满足什么条件时, A C B D ?问题自主探索:①证明线线垂直用到了平面图形的哪些性质? ②请归纳证明线线垂直、线面垂直和面面垂直的方法. 环节3 经典考题选讲题9.(2019浙江19)如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A AC AC E F ∠=︒==分别是AC ,A 1B 1的中点. (1)证明:EF BC ⊥;(2)求直线EF 与平面A 1BC 所成角的余弦值.题10.(2013新课标Ⅰ)如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,1BAA ∠=60°.(Ⅰ)证明1AB A C ⊥;(Ⅱ)若平面ABC ⊥平面11AA B B ,AB CB =,求直线1A C 与平面11BB C C 所成角的正弦值.题11.(2018浙江)如图,已知多面体111ABCA B C ,1A A ,1B B ,1C C 均垂直于平面ABC ,120ABC ∠=,14A A =,11C C =,12AB BC B B ===.(1)证明:1AB ⊥平面111A B C ;(2)求直线1AC 与平面1ABB 所成的角的正弦值.题12.(2017江苏)如图,在三棱锥A BCD -中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E 、F (E 与A 、D 不重合)分别在棱AD ,BD 上,且EF ⊥AD .C 1B 1A 1CBA求证: AD ⊥AC .环节4 规律总结 1. 2. 3. 4.环节5 考题精选精做题13.(2019全国Ⅰ理18)如图,直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ;(2)求二面角A -MA 1-N 的正弦值.题14.(2019北京理16)如图,在四棱锥P ABCD -中,PA ABCD ⊥平面,AD CD ⊥,ADBC ,2PA AD CD BC ====,.E 为PD 的中点,点F 在PC 上,且13PF PC =.FABCDE(Ⅰ)求证:CD PAD ⊥平面; (Ⅱ)求二面角F AE P --的余弦值; (Ⅲ)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF 内,说明理由. 题15.(2019全国Ⅲ理19)图1是由矩形ADEB 、R t △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°,将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2. (1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的二面角B-CG-A 的大小.题16.(2019全国Ⅱ理17)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,求二面角B –EC –C 1的正弦值. 题17.(2019天津理17)如图,AE ⊥平面ABCD ,,CF AE AD BC∥∥,,1,2AD AB AB AD AE BC ⊥====.(Ⅰ)求证:BF ∥平面ADE ;(Ⅱ)求直线CE 与平面BDE 所成角的正弦值; (Ⅲ)若二面角E BD F --的余弦值为13,求线段CF 的长.题18. (2018全国卷Ⅰ)如图,四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把DFC△折起,使点C 到达点P 的位置,且PF BF ⊥. (1)证明:平面PEF ⊥平面ABFD ; (2)求DP 与平面ABFD 所成角的正弦值.题19.(2018江苏)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥.求证:平面11ABB A ⊥平面1A BC .题20.(2017新课标Ⅰ)如图,在四棱锥P ABCD -中,AB ∥CD ,且90BAP CDP ∠=∠=.PF E D C BAD 11B 1A 1DCBA(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠= ,求二面角A PB C --的余弦值.题21.(2016全国I )如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,2AF FD =,90AFD ∠=,且二面角D AF E --与二面角C BE F --都是60.(I )证明:平面ABEF⊥平面EFDC ;(II )求二面角E BC A --的余弦值.题22.(2016全国II )如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将ΔDEF 沿EF折到ΔD EF '的位置,OD ' (I )证明:D H '⊥平面ABCD ; (II )求二面角B D A C '--的正弦值.1.(2019全国Ⅲ理8)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则DCBAPA .BM =EN ,且直线BM 、EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM 、EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线2.(2018全国卷Ⅱ)在长方体1111-ABCD A B C D 中,1==AB BC ,1=AA 1AD 与1DB 所成角的余弦值为A .15B D 4.(2018浙江)已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则 A .123θθθ≤≤ B .321θθθ≤≤ C .132θθθ≤≤ D .231θθθ≤≤5.(2017新课标Ⅱ)已知直三棱柱111ABC A B C -中,120ABC ∠=,2AB =,11BC CC ==,则异面直线1AB 与1BC 所成角的余弦值为A B D 6.(2017浙江)如图,已知正四面体D ABC -(所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP PB =,2BQ CRQC RA==,分别记二面角D PR Q --,D PQ R --,D QR P --的平面角为α,β,γ,则RQ PAB CDA.γ<α<βB.α<γ<βC.α<β<γD.β<γ<α。
第3章3.2 立体几何中的向量方法(二)垂直关系
高考调研 ·新课标 ·数学选修2-1
授人以渔
第6页
高考调研 ·新课标 ·数学选修2-1
题型一 利用空间向量证明线线垂直 例 1 已知正三棱柱 ABC-A1B1C1 的各棱 长都为 1,M 是底面上 BC 边的中点,N 是侧棱 CC1 上的点,且 CN=14CC1.求证:AB1⊥MN.
第7页
第15页
高考调研 ·新课标 ·数学选修2-1
探究 2 如何利用向量法证明线面垂直? 用向量法证明线面垂直的方法步骤: (1)坐标法: ①建立空间直角坐标系,将直线的方向向量用坐标表示. ②求平面内任意两条相交直线的方向向量或平面的法向量. ③证明直线的方向向量与平面内两相交直线的方向向量垂 直或与平面的法向量平行.
高考调研 ·新课标 ·数学选修2-1
1.若两个不同平面 α,β 的法向量分别为 u=(2,1,-1),
v=(3,2,8),则( )
A.α ∥β
B.α ⊥β
C.α ,β 相交不垂直 答案 B
D.以上均不正确
解析 ∵v·u=6+2-8=0.
∴v⊥u,∴α⊥β.
第32页
高考调研 ·新课标 ·数学选修2-1
高考调研 ·新课标 ·数学选修2-1
【解析】 方法一:(基向量法) 设A→B=a,A→C=b,A→A1=c,则由已知条件和正三棱柱的性 质,得|a|=|b|=|c|=1,a·c=b·c=0. A→B1=a+c,A→M=12(a+b),A→N=b+14c, M→N=A→N-A→M=-12a+12b+14c, ∴A→B1·M→N=(a+c)·(-12a+12b+14c) =-12+12cos60°+14=0. ∴A→B1⊥M→N,∴AB1⊥MN.
a,0).
第23页
2024全国高考真题数学汇编:空间中的垂直关系
2024全国高考真题数学汇编空间中的垂直关系一、单选题1.(2024天津高考真题)若,m n 为两条不同的直线, 为一个平面,则下列结论中正确的是()A .若//m ,//n ,则m nB .若//,//m n ,则//m nC .若//, m n ,则m nD .若//, m n ,则m 与n 相交2.(2024全国高考真题)已知正三棱台111ABC A B C -的体积为523,6AB ,112A B ,则1A A 与平面ABC 所成角的正切值为()A .12B .1C .2D .33.(2024全国高考真题)设 、为两个平面,m n 、为两条直线,且m .下述四个命题:①若//m n ,则//n 或//n②若m n ,则n 或n③若//n 且//n ,则//m n④若n 与 , 所成的角相等,则m n 其中所有真命题的编号是()A .①③B .②④C .①②③D .①③④4.(2024北京高考真题)如图,在四棱锥P ABCD 中,底面ABCD 是边长为4的正方形,4PA PB ,PC PD ).A .1B .2CD二、解答题5.(2024全国高考真题)如图,四棱锥P ABCD 中,PA 底面ABCD ,2PA AC ,1,BC AB .(1)若AD PB ,证明://AD 平面PBC ;(2)若AD DC ,且二面角A CP D 的正弦值为7,求AD .6.(2024全国高考真题)如图,//,//AB CD CD EF ,2AB DE EF CF ,4,CD AD BCAE M 为CD 的中点.(1)证明://EM 平面BCF ;(2)求点M 到ADE 的距离.7.(2024上海高考真题)如图为正四棱锥,P ABCD O 为底面ABCD 的中心.(1)若5,AP AD ,求POA 绕PO 旋转一周形成的几何体的体积;(2)若,AP AD E 为PB 的中点,求直线BD 与平面AEC 所成角的大小.参考答案1.C【分析】根据线面平行的性质可判断AB 的正误,根据线面垂直的性质可判断CD 的正误.【详解】对于A ,若//m ,//n ,则,m n 平行或异面或相交,故A 错误.对于B ,若//,//m n ,则,m n 平行或异面或相交,故B 错误.对于C ,//, m n ,过m 作平面 ,使得s ,因为m ,故//m s ,而s ,故n s ,故m n ,故C 正确.对于D ,若//, m n ,则m 与n 相交或异面,故D 错误.故选:C.2.B【分析】解法一:根据台体的体积公式可得三棱台的高h3AM ,进而根据线面夹角的定义分析求解;解法二:将正三棱台111ABC A B C -补成正三棱锥 P ABC ,1A A 与平面ABC 所成角即为PA 与平面ABC 所成角,根据比例关系可得18P ABC V ,进而可求正三棱锥 P ABC 的高,即可得结果.【详解】解法一:分别取11,BC B C 的中点1,D D ,则11AD A D ==可知11111662222ABC A B C S S 设正三棱台111ABC A B C -的为h ,则 11115233ABC A B C V h ,解得3h ,如图,分别过11,A D 作底面垂线,垂足为,M N ,设AM x ,则1AA DN AD AM MN x =--=-,可得1DD 结合等腰梯形11BCC B 可得22211622BB DD ,即 221616433x x ,解得x所以1A A 与平面ABC 所成角的正切值为11tan 1A M A AD AMÐ==;解法二:将正三棱台111ABC A B C -补成正三棱锥 P ABC,则1A A 与平面ABC 所成角即为PA 与平面ABC 所成角,因为11113PA A B PA AB ,则111127P A B C P ABC V V ,可知1112652273ABC A B C P ABC V V ,则18P ABC V ,设正三棱锥 P ABC 的高为d,则11661832P ABC V d,解得d ,取底面ABC 的中心为O ,则PO 底面ABC,且AO 所以PA 与平面ABC 所成角的正切值tan 1PO PAO AO.故选:B.3.A【分析】根据线面平行的判定定理即可判断①;举反例即可判断②④;根据线面平行的性质即可判断③.【详解】对①,当n ,因为//m n ,m ,则//n ,当n ,因为//m n ,m ,则//n ,当n 既不在 也不在 内,因为//m n ,,m m ,则//n 且//n ,故①正确;对②,若m n ,则n 与, 不一定垂直,故②错误;对③,过直线n 分别作两平面与, 分别相交于直线s 和直线t ,因为//n ,过直线n 的平面与平面 的交线为直线s ,则根据线面平行的性质定理知//n s ,同理可得//n t ,则//s t ,因为s 平面 ,t 平面 ,则//s 平面 ,因为s 平面 ,m ,则//s m ,又因为//n s ,则//m n ,故③正确;对④,若,m n 与 和 所成的角相等,如果//,// n n ,则//m n ,故④错误;综上只有①③正确,故选:A.4.D【分析】取点作辅助线,根据题意分析可知平面PEF 平面ABCD ,可知PO 平面ABCD ,利用等体积法求点到面的距离.【详解】如图,底面ABCD 为正方形,当相邻的棱长相等时,不妨设4,PA PB AB PC PD ,分别取,AB CD 的中点,E F ,连接,,PE PF EF ,则,PE AB EF AB ,且PE EF E ,,PE EF 平面PEF ,可知AB 平面PEF ,且AB 平面ABCD ,所以平面PEF 平面ABCD ,过P 作EF 的垂线,垂足为O ,即PO EF ,由平面PEF 平面ABCD EF ,PO 平面PEF ,所以PO 平面ABCD ,由题意可得:2,4PE PF EF ,则222PE PF EF ,即PE PF ,则1122PE PF PO EF ,可得PE PF PO EF,当相对的棱长相等时,不妨设4PA PC ,PB PD因为BD PB PD ,此时不能形成三角形PBD ,与题意不符,这样情况不存在.故选:D.5.(1)证明见解析【分析】(1)先证出AD 平面PAB ,即可得AD AB ,由勾股定理逆定理可得BC AB ,从而//AD BC ,再根据线面平行的判定定理即可证出;(2)过点D 作DE AC 于E ,再过点E 作EF CP 于F ,连接DF ,根据三垂线法可知,DFE 即为二面角A CP D 的平面角,即可求得tan DFE AD 的长度表示出,DE EF ,即可解方程求出AD .【详解】(1)(1)因为PA 平面ABCD ,而AD 平面ABCD ,所以PA AD ,又AD PB ,PB PA P ,,PB PA 平面PAB ,所以AD 平面PAB ,而AB 平面PAB ,所以AD AB .因为222BC AB AC ,所以BC AB ,根据平面知识可知//AD BC ,又AD 平面PBC ,BC 平面PBC ,所以//AD 平面PBC .(2)如图所示,过点D 作DE AC 于E ,再过点E 作EF CP 于F ,连接DF ,因为PA 平面ABCD ,所以平面PAC 平面ABCD ,而平面PAC 平面ABCD AC ,所以DE 平面PAC ,又EF CP ,所以 CP 平面DEF ,根据二面角的定义可知,DFE 即为二面角A CP D 的平面角,即sin DFEtan DFE 因为AD DC ,设AD x,则CD 42x x DE ,又242xCE,而EFC 为等腰直角三角形,所以2EF故22tan 4DFE xxAD6.(1)证明见详解;【分析】(1)结合已知易证四边形EFCM 为平行四边形,可证//EM FC ,进而得证;(2)先证明OA 平面EDM ,结合等体积法M ADE A EDM V V 即可求解.【详解】(1)由题意得,//EF MC ,且EF MC ,所以四边形EFCM 是平行四边形,所以//EM FC ,又CF 平面,BCF EM 平面BCF ,所以//EM 平面BCF ;(2)取DM 的中点O ,连接OA ,OE ,因为//AB MC ,且ABMC ,所以四边形AMCB 是平行四边形,所以AMBC 又AD ,故ADM △是等腰三角形,同理EDM △是等腰三角形,可得,,3,OA DM OE DM OA OE又AE 222OA OE AE ,故OA OE .又,,,OA DM OE DM O OE DM 平面EDM ,所以OA 平面EDM ,易知122EDM S在ADE V 中,cosDEA所以1sin ,24242DEA DEA S .设点M 到平面ADE 的距离为d ,由M ADE A EDM V V ,得1133ADE EDM S d S OA ,得13d ,故点M 到平面ADE 的距离为13.7.(1)12π(2)π4【分析】(1)根据正四棱锥的数据,先算出直角三角形POA 的边长,然后求圆锥的体积;(2)连接,,EA EO EC ,可先证BE 平面ACE ,根据线面角的定义得出所求角为 BOE ,然后结合题目数量关系求解.【详解】(1)正四棱锥满足且PO 平面ABCD ,由AO 平面ABCD ,则PO AO ,又正四棱锥底面ABCD 是正方形,由 AD 3AO ,故4PO ,根据圆锥的定义,POA 绕PO 旋转一周形成的几何体是以PO 为轴,AO 为底面半径的圆锥,即圆锥的高为4PO ,底面半径为3AO ,根据圆锥的体积公式,所得圆锥的体积是21π3412π3(2)连接,,EA EO EC ,由题意结合正四棱锥的性质可知,每个侧面都是等边三角形,由E 是PB 中点,则,AE PB CE PB ,又,,AE CE E AE CE 平面ACE ,故PB 平面ACE ,即BE 平面ACE ,又BD 平面ACE O ,于是直线BD 与平面AEC 所成角的大小即为 BOE ,不妨设6AP AD ,则3BO BE ,sinBOE,又线面角的范围是π0,2 ,故π4BOE .即为所求.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
历年高考数学真题精选(按考点分类)专题31 垂直关系(学生版)1.(2019•北京)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 为菱形,E 为CD 的中点.(Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)若60ABC ∠=︒,求证:平面PAB ⊥平面PAE ;(Ⅲ)棱PB 上是否存在点F ,使得//CF 平面PAE ?说明理由.2.(2015•重庆)如图,三棱锥P ABC -中,平面PAC ⊥平面ABC ,2ABC π∠=,点D 、E在线段AC 上,且2AD DE EC ===,4PD PC ==,点F 在线段AB 上,且//EF BC . (Ⅰ)证明:AB ⊥平面PFE .(Ⅱ)若四棱锥P DFBC -的体积为7,求线段BC 的长.3.(2015•福建)如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,PO 垂直于圆O 所在的平面,且1PO OB ==,(Ⅰ)若D 为线段AC 的中点,求证;AC ⊥平面PDO ; (Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若2BC =,点E 在线段PB 上,求CE OE +的最小值.4.(2014•四川)在如图所示的多面体中,四边形11ABB A 和11ACC A 都为矩形 (Ⅰ)若AC BC ⊥,证明:直线BC ⊥平面11ACC A ;(Ⅱ)设D 、E 分别是线段BC 、1CC 的中点,在线段AB 上是否存在一点M ,使直线//DE 平面1A MC ?请证明你的结论.5.(2014•福建)如图,三棱锥A BCD -中,AB ⊥平面BCD ,CD BD ⊥. (Ⅰ)求证:CD ⊥平面ABD ;(Ⅱ)若1AB BD CD ===,M 为AD 中点,求三棱锥A MBC -的体积.6.(2014•广东)如图1,四边形ABCD 为矩形,PD ⊥平面ABCD ,1AB =,2BC PC ==作如图2折叠;折痕//EF DC ,其中点E ,F 分别在线段PD ,PC 上,沿EF 折叠后点P 叠在线段AD 上的点记为M ,并且MF CF ⊥.(1)证明:CF ⊥平面MDF ; (2)求三棱锥M CDE -的体积.7.(2014•新课标Ⅰ)如图,三棱柱111ABC A B C -中,侧面11BB C C 为菱形,1B C 的中点为O ,且AO ⊥平面11BB C C . (1)证明:1B C AB ⊥;(2)若1AC AB ⊥,160CBB ∠=︒,1BC =,求三棱柱111ABC A B C -的高.8.(2014•山东)如图,四棱锥P ABCD -中,AP ⊥平面PCD ,//AD BC ,12AB BC AD ==,E ,F 分别为线段AD ,PC 的中点.(Ⅰ)求证://AP 平面BEF ; (Ⅱ)求证:BE ⊥平面PAC .9.(2013•安徽)如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=︒.已知2PB PD ==,6PA = (Ⅰ)证明:BD ⊥面PAC(Ⅱ)若E 为PA 的中点,求三菱锥P BCE -的体积.10.(2013•重庆)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,23PA =,2BC CD ==,3ACB ACD π∠=∠=.(Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)若侧棱PC 上的点F 满足7PF FC =,求三棱锥P BDF -的体积.11.(2013•新课标Ⅰ)如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=︒ (Ⅰ)证明:1AB AC ⊥; (Ⅱ)若2AB CB ==,16A C =,求三棱柱111ABC A B C -的体积.12.(2019•新课标Ⅲ)图1是由矩形ADEB ,Rt ABC ∆和菱形BFGC 组成的一个平面图形,其中1AB =,2BE BF ==,60FBC ∠=︒.将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的四边形ACGD 的面积.13.(2018•江苏)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥. 求证:(1)//AB 平面11A B C ; (2)平面11ABB A ⊥平面1A BC .14.(2018•新课标Ⅲ)如图,矩形ABCD 所在平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得//MC 平面PBD ?说明理由.15.(2018•新课标Ⅰ)如图,在平行四边形ABCM 中,3AB AC ==,90ACM ∠=︒,以AC 为折痕将ACM ∆折起,使点M 到达点D 的位置,且AB DA ⊥. (1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.16.(2017•新课标Ⅰ)如图,在四棱锥P ABCD -中,//AB CD ,且90BAP CDP ∠=∠=︒. (1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.历年高考数学真题精选(按考点分类)专题31 垂直关系(教师版)1.(2019•北京)如图,在四棱锥P ABCD-中,PA⊥平面ABCD,底面ABCD为菱形,E 为CD的中点.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若60∠=︒,求证:平面PAB⊥平面PAE;ABC(Ⅲ)棱PB上是否存在点F,使得//CF平面PAE?说明理由.证明:(Ⅰ)四棱锥P ABCD-中,PA⊥平面ABCD,底面ABCD为菱形,∴⊥,BD ACBD PA⊥,∴⊥平面PAC.=,BDPA AC A(Ⅱ)在四棱锥P ABCD-中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点,60ABC∠=︒,∴⊥,PA AEAB AE⊥,∴⊥平面PAB,PA AB A=,AEAE⊂平面PAE,∴平面PAB⊥平面PAE.解:(Ⅲ)棱PB上是存在中点F,使得//CF平面PAE.理由如下:取AB中点G,连结GF,CG,在四棱锥P ABCD-中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点,∴,//FG PA,//CG AE=,AE PA ACG FG G=,CFG平面PAE,∴平面//CF ⊂平面CFG ,//CF ∴平面PAE .2.(2015•重庆)如图,三棱锥P ABC -中,平面PAC ⊥平面ABC ,2ABC π∠=,点D 、E在线段AC 上,且2AD DE EC ===,4PD PC ==,点F 在线段AB 上,且//EF BC . (Ⅰ)证明:AB ⊥平面PFE .(Ⅱ)若四棱锥P DFBC -的体积为7,求线段BC 的长.解:(Ⅰ)如图,由DE EC =,PD PC =知,E 为等腰PDC ∆中DC 边的中点,故PE AC ⊥, 又平面PAC ⊥平面ABC ,平面PAC ⋂平面ABC AC =,PE ⊂平面PAC ,PE AC ⊥, 所以PE ⊥平面ABC ,从而PE AB ⊥. 因为2ABC π∠=,//EF BC ,故AB EF ⊥,从而AB 与平面PEF 内两条相交直线PE ,EF 都垂直, 所以AB ⊥平面PEF .(Ⅱ)设BC x =,则在直角ABC ∆中,22236AB AC BC x -=-, 从而2113622ABC S AB BC x x ∆==- 由//EF BC 知23AF AE AB AC ==,得AFE ABC ∆∆∽, 故224()39AFEABCS S ∆∆==,即49AFE ABC S S ∆∆=,由12AD AE =,2114213622999AFD AFE ABC ABC S S S S x x ∆∆∆∆====-, 从而四边形DFBC 的面积为:2221173636362918DFBC ABC AFD S S S x x x x x x ∆=-=---=-.由(Ⅰ)知,PE ⊥平面ABC ,所以PE 为四棱锥P DFBC -的高. 在直角PEC ∆中,22224223PE PC EC =-=-=, 故体积2117362373318P DFBC DFBC V S PE x x -==-=, 故得42362430x x -+=,解得29x =或227x =,由于0x >,可得3x =或33x =. 所以:3BC =或33BC =.3.(2015•福建)如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,PO 垂直于圆O 所在的平面,且1PO OB ==,(Ⅰ)若D 为线段AC 的中点,求证;AC ⊥平面PDO ; (Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若2BC =,点E 在线段PB 上,求CE OE +的最小值.解:(Ⅰ)在AOC ∆中,因为OA OC =,D 为AC 的中点, 所以AC DO ⊥,又PO 垂直于圆O 所在的平面, 所以PO AC ⊥, 因为DOPO O =,所以AC ⊥平面PDO .(Ⅱ)因为点C 在圆O 上,所以当CO AB ⊥时,C 到AB 的距离最大,且最大值为1, 又2AB =,所以ABC ∆面积的最大值为12112⨯⨯=,又因为三棱锥P ABC -的高1PO =,故三棱锥P ABC -体积的最大值为:111133⨯⨯=.(Ⅲ)在POB ∆中,1PO OB ==,90POB ∠=︒, 所以22112PB =+=,同理2PC =,所以PB PC BC ==,在三棱锥P ABC -中,将侧面BCP 绕PB 旋转至平面BC P ',使之与平面ABP 共面,如图所示,当O ,E ,C '共线时,CE OE +取得最小值, 又因为OP OB =,C P C B '=',所以OC '垂直平分PB ,即E 为PB 中点. 从而2626OC OE EC +'=+'=+=. 亦即CE OE +的最小值为:26+.4.(2014•四川)在如图所示的多面体中,四边形11ABB A 和11ACC A 都为矩形 (Ⅰ)若AC BC ⊥,证明:直线BC ⊥平面11ACC A ;(Ⅱ)设D 、E 分别是线段BC 、1CC 的中点,在线段AB 上是否存在一点M ,使直线//DE平面1A MC ?请证明你的结论.(Ⅰ)证明:四边形11ABB A 和11ACC A 都为矩形, 1AA AB ∴⊥,1AA AC ⊥, ABAC A =,1AA ∴⊥平面ABC ,BC ⊂平面ABC , 1AA BC ∴⊥,AC BC ⊥,1AA AC A =,∴直线BC ⊥平面11ACC A ;(Ⅱ)解:取AB 的中点M ,连接1A M ,MC ,1A C ,1AC ,设O 为1A C ,1AC 的交点,则O 为1AC 的中点.连接MD ,OE ,则//MD AC ,12MD AC =,//OE AC ,12OE AC =, //MD OE ∴,MD OE =,连接OM ,则四边形MDEO 为平行四边形, //DE MO ∴,DE ⊂/平面1A MC ,MO ⊂平面1A MC ,//DE ∴平面1A MC ,∴线段AB 上存在一点M (线段AB 的中点),使直线//DE 平面1A MC .5.(2014•福建)如图,三棱锥A BCD -中,AB ⊥平面BCD ,CD BD ⊥. (Ⅰ)求证:CD ⊥平面ABD ;(Ⅱ)若1AB BD CD ===,M 为AD 中点,求三棱锥A MBC -的体积.(Ⅰ)证明:AB ⊥平面BCD ,CD ⊂平面BCD ,AB CD ∴⊥, CD BD ⊥,ABBD B =,CD ∴⊥平面ABD ;(Ⅱ)解:AB ⊥平面BCD ,BD ⊂平面BCD ,AB BD ∴⊥. 1AB BD ==,12ABD S ∆∴=, M 为AD 中点,1124ABM ABD S S ∆∆∴==,CD ⊥平面ABD ,11312A MBC C ABM ABM V V S CD --∆∴===.6.(2014•广东)如图1,四边形ABCD 为矩形,PD ⊥平面ABCD ,1AB =,2BC PC ==作如图2折叠;折痕//EF DC ,其中点E ,F 分别在线段PD ,PC 上,沿EF 折叠后点P 叠在线段AD 上的点记为M ,并且MF CF ⊥.(1)证明:CF ⊥平面MDF ; (2)求三棱锥M CDE -的体积.解:(1)证明:PD ⊥平面ABCD ,PD ⊂平面PCD ,∴平面PCD ⊥平面ABCD ;又平面PCD ⋂平面ABCD CD =,MD ⊂平面ABCD ,MD CD ⊥,MD ∴⊥平面PCD ,CF ⊂平面PCD ,CF MD ∴⊥;又CF MF ⊥,MD 、MF ⊂平面MDF ,MD M F M =,CF ∴⊥平面MDF ;(2)CF ⊥平面MDF ,CF DF ∴⊥, 又Rt PCD ∆中,1DC =,2PC =, 30P ∴∠=︒,60PCD ∠=︒, 30CDF ∴∠=︒,1122CF CD ==;//EF DC ,∴DE CFDP CP =1223=, 3DE ∴=33PE ∴=132CDE S CD DE ∆∴==; 22223336()()44MD ME DE =--=, 1136233M CDE CDE V S MD -∆∴==⨯ 7.(2014•新课标Ⅰ)如图,三棱柱111ABC A B C -中,侧面11BB C C 为菱形,1B C 的中点为O ,且AO ⊥平面11BB C C .(1)证明:1B C AB ⊥;(2)若1AC AB ⊥,160CBB ∠=︒,1BC =,求三棱柱111ABC A B C -的高.(1)证明:连接1BC ,则O 为1B C 与1BC 的交点, 侧面11BB C C 为菱形, 11BC B C ∴⊥,AO ⊥平面11BB C C , 1AO B C ∴⊥, 1AOBC O =,1B C ∴⊥平面ABO ,AB ⊂平面ABO ,1B C AB ∴⊥;(2)解:作OD BC ⊥,垂足为D ,连接AD ,作OH AD ⊥,垂足为H , BC AO ⊥,BC OD ⊥,AOOD O =,BC ∴⊥平面AOD , OH BC ∴⊥, OH AD ⊥,BCAD D =,OH ∴⊥平面ABC , 160CBB ∠=︒, 1CBB ∴∆为等边三角形,1BC =,3OD ∴=1AC AB ⊥,11122OA B C ∴==,由OH AD OD OA =,可得2274AD OD OA =+=,2114OH ∴=, O 为1B C 的中点, 1B ∴到平面ABC 的距离为217, ∴三棱柱111ABC A B C -的高217.8.(2014•山东)如图,四棱锥P ABCD -中,AP ⊥平面PCD ,//AD BC ,12AB BC AD ==,E ,F 分别为线段AD ,PC 的中点.(Ⅰ)求证://AP 平面BEF ; (Ⅱ)求证:BE ⊥平面PAC .证明:(Ⅰ)连接CE ,则 //AD BC ,12BC AD =,E 为线段AD 的中点, ∴四边形ABCE 是平行四边形,BCDE 是平行四边形,设AC BE O =,连接OF ,则O 是AC 的中点,F 为线段PC 的中点,//PA OF ∴,PA ⊂/平面BEF ,OF ⊂平面BEF ,//AP ∴平面BEF ;(Ⅱ)BCDE 是平行四边形, //BE CD ∴,AP ⊥平面PCD ,CD ⊂平面PCD ,∴⊥,AP CD∴⊥,BE AP=,四边形ABCE是平行四边形,AB BC∴四边形ABCE是菱形,∴⊥,BE AC=,AP AC A∴⊥平面PAC.BE9.(2013•安徽)如图,四棱锥P ABCD∠=︒.已BAD-的底面ABCD是边长为2的菱形,60知2PB PD==,6PA=.(Ⅰ)证明:BD⊥面PAC(Ⅱ)若E为PA的中点,求三菱锥P BCE-的体积.(Ⅰ)证明:连接BD,AC交于O点,=,PB PD∴⊥,PO BD又ABCD是菱形,∴⊥,BD AC=,PO⊂平面PAC,AC⊂平面PAC,AC PO O∴⊥平面PAC.BD(Ⅱ)则23AC =,ABD ∆和PBD ∆的三边长均为2, ABD PBD ∴∆≅∆,3AO PO ∴==,222AO PO PA ∴+=, AC PO ∴⊥, 132PAC S AC PO ∆==, 11111131223232P BCE B PEC B PAC PAC V V V S BO ---∆====⨯⨯⨯=.10.(2013•重庆)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,23PA =,2BC CD ==,3ACB ACD π∠=∠=.(Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)若侧棱PC 上的点F 满足7PF FC =,求三棱锥P BDF -的体积.解:(Ⅰ)2BC CD ==,BCD ∴∆为等腰三角形,再由3ACB ACD π∠=∠=,BD AC ∴⊥.再由PA ⊥底面ABCD ,可得PA BD ⊥. 而PAAC A =,故BD ⊥平面PAC .(Ⅱ)侧棱PC 上的点F 满足7PF FC =,∴三棱锥F BCD -的高是三棱锥P BCD -的高的18.BCD ∆的面积112sin 22sin 3223BCD S BC CD BCD π∆=∠=⨯⨯⨯=.∴三棱锥P BDF -的体积1117133883P BCD F BCD BCD BCD BCD V V V S PA S PA S PA --∆∆∆=-=-=⨯ 77323244=⨯⨯=. 11.(2013•新课标Ⅰ)如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=︒ (Ⅰ)证明:1AB AC ⊥; (Ⅱ)若2AB CB ==,16A C =,求三棱柱111ABC A B C -的体积.(Ⅰ)证明:如图,取AB 的中点O ,连结OC ,1OA ,1A B . 因为CA CB =,所以OC AB ⊥.由于1AB AA =,160BAA ∠=︒,故△1AA B 为等边三角形, 所以1OA AB ⊥. 因为1OCOA O =,所以AB ⊥平面1OAC . 又1A C ⊂平面1OAC ,故1AB AC ⊥; (Ⅱ)解:由题设知ABC ∆与△1AA B 都是边长为2的等边三角形, 所以13OC OA ==又16A C =22211AC OC OA =+,故1OA OC ⊥. 因为OCAB O =,所以1OA ⊥平面ABC ,1OA 为三棱柱111ABC A B C -的高.又ABC ∆的面积3ABC S ∆=,故三棱柱111ABC A B C -的体积1333ABC V S OA ∆=⨯=⨯=.12.(2019•新课标Ⅲ)图1是由矩形ADEB ,Rt ABC ∆和菱形BFGC 组成的一个平面图形,其中1AB =,2BE BF ==,60FBC ∠=︒.将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的四边形ACGD 的面积.解:(1)证明:由已知可得//AD BE ,//CG BE ,即有//AD CG , 则AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面; 由四边形ABED 为矩形,可得AB BE ⊥, 由ABC ∆为直角三角形,可得AB BC ⊥, 又BCBE B =,可得AB ⊥平面BCGE ,AB ⊂平面ABC ,可得平面ABC ⊥平面BCGE ;(2)连接BG ,AG ,由AB ⊥平面BCGE ,可得AB BG ⊥,在BCG ∆中,2BC CG ==,120BCG ∠=︒,可得2sin 6023BG BC =︒= 可得2213AG AB BG =+在ACG ∆中,5AC 2CG =,13AG ,可得cos 2255ACG ∠==-⨯⨯,即有sin 5ACG ∠=,则平行四边形ACGD 的面积为2545⨯⨯=.13.(2018•江苏)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥. 求证:(1)//AB 平面11A B C ; (2)平面11ABB A ⊥平面1A BC .证明:(1)平行六面体1111ABCD A B C D -中,11//AB A B ,11//AB A B ,AB ⊂/平面11A B C ,11//A B ⊂平面11//A B C AB ⇒平面11A B C ;(2)在平行六面体1111ABCD A B C D -中,1AA AB =,⇒四边形11ABB A 是菱形,11AB A B ⊥⊥.在平行六面体1111ABCD A B C D -中,1AA AB =,1111AB B C AB BC ⊥⇒⊥. ∴1111111,,AB A B AB BC A B BC B A B A BC BC A BC⊥⊥⎧⎪=⎨⎪⊂⊂⎩面面 1AB ⇒⊥面1A BC ,且1AB ⊂平面11ABB A ⇒平面11ABB A ⊥平面1A BC .14.(2018•新课标Ⅲ)如图,矩形ABCD 所在平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得//MC 平面PBD ?说明理由.(1)证明:矩形ABCD 所在平面与半圆弦CD 所在平面垂直,所以AD ⊥半圆弦CD 所在平面,CM ⊂半圆弦CD 所在平面,CM AD ∴⊥,M 是CD 上异于C ,D 的点.CM DM ∴⊥,DMAD D =,CM ∴⊥平面AMD ,CM ⊂平面CMB ,∴平面AMD ⊥平面BMC ; (2)解:存在P 是AM 的中点,理由:连接BD 交AC 于O ,取AM 的中点P ,连接OP ,可得//MC OP ,MC ⊂/平面BDP ,OP ⊂平面BDP ,所以//MC 平面PBD .15.(2018•新课标Ⅰ)如图,在平行四边形ABCM 中,3AB AC ==,90ACM ∠=︒,以AC 为折痕将ACM ∆折起,使点M 到达点D 的位置,且AB DA ⊥.(1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.解:(1)证明:在平行四边形ABCM 中,90ACM ∠=︒,AB AC ∴⊥, 又AB DA ⊥.且AD AC A =,AB ∴⊥面ADC ,AB ⊂面ABC ,∴平面ACD ⊥平面ABC ;(2)3AB AC ==,90ACM ∠=︒,32AD AM ∴==, 2223BP DQ DA ∴===, 由(1)得DC AB ⊥,又DC CA ⊥,DC ∴⊥面ABC , ∴三棱锥Q ABP -的体积1133ABP V S DC ∆=⨯ 121121133313333323ABC S DC ∆=⨯⨯=⨯⨯⨯⨯⨯⨯=. 16.(2017•新课标Ⅰ)如图,在四棱锥P ABCD -中,//AB CD ,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.证明:(1)在四棱锥P ABCD -中,90BAP CDP ∠=∠=︒, AB PA ∴⊥,CD PD ⊥,又//AB CD ,AB PD ∴⊥,PA PD P =,AB ∴⊥平面PAD ,AB ⊂平面PAB ,∴平面PAB ⊥平面PAD .解:(2)设PA PD AB DC a ====,取AD 中点O ,连结PO , PA PD AB DC ===,90APD ∠=︒,平面PAB ⊥平面PAD , PO ∴⊥底面ABCD ,且222AD a a a =+=,2PO a =, 四棱锥P ABCD -的体积为83, 由AB ⊥平面PAD ,得AB AD ⊥,13P ABCD ABCD V S PO -∴=⨯⨯四边形 31121823333AB AD PO a a a a =⨯⨯⨯=⨯⨯⨯==, 解得2a =,2PA PD AB DC ∴====,22AD BC ==,2PO =, 4422PB PC ∴==+=,∴该四棱锥的侧面积:PAD PAB PDC PBC S S S S S ∆∆∆∆=+++侧221111()22222BC PA PD PA AB PD DC BC PB =⨯⨯+⨯⨯+⨯⨯+⨯⨯- 111122222222822222=⨯⨯+⨯⨯+⨯⨯+⨯⨯- 623=+.。
