运筹学与最优化方法-第2章
第二章——运筹学建模方法

1第二章、运筹学建模方法综述2定义问题和收集数据 数学建模模型求解 检验模型 准备应用模型 实施3运筹学研究小组首先要做的是研究相关系统,并使被研究的问题得到明确的说明。
包括确定合适的目标、实际的限制条件、研究领域和组织的其他领域间的相互关系、可选择的行动路线、制定决策的时间限制等。
2.1定义问题和收集数据4针对美国企业的大量调查发现,管理层趋向于采取满意利润目标和其他目标相结合的方式代替长期收益最大化。
典型地,其他目标包括维持稳定收益、增加市场份额、实现产品多样化、维持稳定价格、提高员工士气、维持企业的家族控制以及提高企业声望。
另外,存在包含与盈利动机不相吻合的社会责任的其他考虑。
2.1定义问题和收集数据5商业企业一般涉及以下五个方面所用者(股东等),追求盈利员工,期望合理工资水平上的稳定雇佣 客户,期望以合理的价格获得可靠的产品 供应商,期望声誉以及产品的合理出售价格政府以及国家,期望公正的税收和考虑国家利益6例:在为旧金山警察局所开展的运筹学研究中,建立了一个优化调度和配置巡警的计算机系统。
这个新系统每年为警察局节约1100万美元,同时增加了300万美元的交通管理收入,并且将反映时间减少了20%。
在评估该项研究的合适目标时,确定了三个基本目标:(1). 维持高水平的居民安全(2). 维持高水平的警员士气(3). 最小化运作成本7收集数据通常,研究小组会花费大量的时间收集问题的数据。
大部分数据既用于获得对问题的充分理解,又为下一阶段研究建立的数学模型提供所需的输入。
82.2 数学建模商业问题的数学模型,是描述问题实质的方程和相关数学表达式的系统。
n 个相关的可量化的决策,称为决策变量(decision variables)(x 1, x 2, …x n )绩效(如收益)的合理度量被表示成这些决策变量的数学函数(例如,P =3x 1+2x 2+…+5x n ),这个函数称为目标函数(objective function)9 任何对决策变量值的约束也能够被数学表示,通常是通过等式或不等式(例如:x 1+3x 1x 2+2x 2≤10),这些用于限制的数学表达式称为约束(constraints)。
最优化方法PPT

共117页第8页
同时太阳系这个"整体"又是它所属的"更大整 体"--银河系的一个组成部分。世界上的具体系统是 纷繁复杂的,必须按照一定的标准,将千差万别的 系统分门别类,以便分析、研究和管理,如:教育 系统、医疗卫生系统、宇航系统、通讯系统等等。 如果系统与外界或它所处的外部环境有物质、能量 和信息的交流,那么这个系统就是一个开放系统, 否则就是一个封闭系统。开放系统具有很强的生命 力,它可能促进经济实力的迅速增长,使落后地区 尽早走上现代化。如改革开放以来已大大增强了我 们的综合国力。而我国的许多边远山区农村,由于 交通不便,相对封闭,还处于比较落后的状态。
会科学和思维科学的相互渗透与交融汇流,产生了 具有高度抽象性和广泛综合性的系统论、控制论和 信息论。
系统论是研究系统的模式、性能、行为和规律 的一门科学。它为人们认识各种系统的组成、结构、 性能、行为和发展规律提供了一般方法论的指导。 系统论的创始人是美籍奥地利理论生物学家和哲学 家路德维格·贝塔朗菲。系统是由若干相互联系的 基本要素构成的,它是具有确定的特性和功能的有 机整体。如太阳系是由太阳及其围绕它运转的行星 (金星、地球、火星、木星等等)和卫星构成的。
从数学上比较一般的观点来看,所谓最优化问题可 以概括为这样一种数学模型:给定一个“函数”,F(X), 以及“自变量”X应满足的一定条件,求X为怎样的值时, F(X)取得其最大值或最小值。这里在函数和自变量两个 词上之所以打上引号,是想强调它们的含意比中学数学 和大学微积分中函数的定义要广泛得多。通常,称F(X) 为“目标函数”,X应满足的条件为“约束条件”。约 束条件一般用一个集合D表示为:X∈D。求目标函数 F(X)在约束条件X∈D下的最小值或最大值问题,就是一 般最优问题的数学模型,它还可以利用数学符号更简洁 地表示成:Min F(X)或Max F(X)。
运筹学知识点总结

运筹学:应用分析、试验、量化的方法,对经济管理系统中人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。
第一章、线性规划的图解法1.基本概念线性规划:是一种解决在线性约束条件下追求最大或最小的线性目标函数的方法。
线性规划的三要素:变量或决策变量、目标函数、约束条件。
目标函数:是变量的线性函数。
约束条件:变量的线性等式或不等式。
可行解:满足所有约束条件的解称为该线性规划的可行解。
可行域:可行解的集合称为可行域。
最优解:使得目标函数值最大的可行解称为该线性规划的最优解。
唯一最优解、无穷最优解、无界解(可行域无界)或无可行解(可行域为空域)。
凸集:要求集合中任意两点的连线段落在这个集合中。
等值线:目标函数z,对于z的某一取值所得的直线上的每一点都具有相同的目标函数值,故称之为等值线。
松弛变量:对于“≤”约束条件,可增加一些代表没使用的资源或能力的变量,称之为松弛变量。
剩余变量:对于“≥”约束条件,可增加一些代表最低限约束的超过量的变量,称之为剩余变量。
2.线性规划的标准形式约束条件为等式(=)约束条件的常数项非负(b j≥0)决策变量非负(x j≥0)3.灵敏度分析:是在建立数学模型和求得最优解之后,研究线性规划的一些系数的变化对最优解产生什么影响。
4.目标函数中的系数c i的灵敏度分析目标函数的斜率在形成最优解顶点的两条直线的斜率之间变化时,最优解不变。
5.约束条件中常数项b i的灵敏度分析对偶价格:约束条件常数项中增加一个单位而使最优目标函数值得到改进的数量。
当某约束条件中的松弛变量(或剩余变量)不为零时,这个约束条件的对偶价格为零。
第二章、线性规划问题在工商管理中的应用1.人力资源分配问题(P41)设x i为第i班次开始上班的人数。
2.生产计划问题(P44)3.套材下料问题(P48)下料方案表(P48)设x i为按各下料方式下料的原材料数量。
4.配料问题(P49)设x ij为第i种产品需要第j种原料的量。
运筹学与最优化方法习题集

一.单纯性法一.单纯性法1.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 122121212max 25156224..5,0z x x x x x s t x x x x =+£ìï+£ïí+£ïï³î 2.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 12121212max 2322..2210,0z x x x x s t x x x x =+-³-ìï+£íï³î 3.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 1234123412341234max 24564282..2341,,,z x x x x x x x x s t x x x x x x x x =-+-+-+£ìï-+++£íï³î4.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 123123123123123max 2360210..20,,0z x x x x x x x x x s t x x x x x x =-+++£ìï-+£ïí+-£ïï³î 5.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 12312312123max 224..26,,0z x x x x x x s t x x x x x =-++++£ìï+£íï³î6.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 12121212max 105349..528,0z x x x x s t x x x x =++£ìï+£íï³î7.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 16 分)分) 12121212max 254212..3218,0z x x x x s t x x x x =+£ìï£ïí+£ïï³î二.对偶单纯性法二.对偶单纯性法1.灵活运用单纯形法和对偶单纯形法解下列问题(共灵活运用单纯形法和对偶单纯形法解下列问题(共 15 分)分)12121212max 62..33,0z x x x x s t x x x x =++³ìï+£íï³î 2.灵活利用单纯形法和对偶单纯形法求解下列线性规划问题(共灵活利用单纯形法和对偶单纯形法求解下列线性规划问题(共 15 分)分) 121212212max 3510501..4,0z x x x x x x s t x x x =++£ìï+³ïí£ïï³î 3.用对偶单纯形法求解下列线性规划问题(共用对偶单纯形法求解下列线性规划问题(共 15 分)分) 1212121212min 232330210..050z x x x x x x s t x x x x =++£ìï+³ïï-³íï³ïï³î4.灵活运用单纯形法和对偶单纯形法求解下列线性规划问题(共灵活运用单纯形法和对偶单纯形法求解下列线性规划问题(共 15 分)分) 124123412341234min 262335,,,0z x x x x x x x s t x x x x x x x x =+-+++£ìï-+-³íï³î5.运用对偶单纯形法解下列问题(共运用对偶单纯形法解下列问题(共 16 分)分) 12121212max 24..77,0z x x x x s t x x x x =++³ìï+³íï³î6.灵活运用单纯形法和对偶单纯形法解下列问题(共灵活运用单纯形法和对偶单纯形法解下列问题(共 15 分)分) 12121212max 62..33,0z x x x x s t x x x x =++³ìï+£íï³î三.0-1整数规划整数规划1.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共10 分) 12345123451234512345123345max 567893223220..32,,,,,01z x x x x x x x x x x x x x x x s t x x x x x x x x x x x or =++++-++-³ìï+--+³ïí--+++³ï=î 2.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共 10 分) 12312312323123min 4322534433..1,,01z x x x x x x x x x s t x x x x x or =++-+£ì++³ïí+³ïï=î 3.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共 10 分) 1234512345123451234512345max 20402015305437825794625..81021025,,,,01z x x x x x x x x x x x x x x x s t x x x x x x x x x x =++++++++£ìï++++£ïí++++£ïï=î或 4.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共10 分) 12345123451234512345max 2534327546..2420,,,,01z x x x x x x x x x x s t x x x x x x x x x x =-+-+-+-+£ìï-+-+£íï=î或 5.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共10 分) 12341234123412341234min 25344024244..1,,,01z x x x x x x x x x x x x s t x x x x x x x x =+++-+++³ì-+++³ïí+-+³ïï=î或6.7.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共10 分) 123451234513451245max 325232473438..116333z x x x x x x x x x x x x x x s t x x x x =+--+++++£ìï+-+£ïí-+-³ï 1231231231223max 3252244..346z x x x x x x x x x s t x x x x =-++-£ìï++£ïï+£íï+£ïï=四.K-T 条件条件1.利用库恩-塔克(K-T )条件求解以下问题(共)条件求解以下问题(共 15 分)分)22121122121212max ()104446..418,0f X x x x x x x x x s t x x x x =+-+-+£ìï+£íï³î2.利用库恩-塔克(K-T )条件求解以下非线性规划问题。
(运筹学与控制论专业优秀论文)一类最优化问题的算法设计

知识水坝为您提供优质论文
承诺书
本人郑重声明:所呈交的学位论文,是本人在导师指导下,独立 进行研究工作所取得的成果。尽我所知,除文中已经注明引用的内容 外,本学位论文的研究成果不包含任何他人享有著作权的内容。对本 论文所涉及的研究工作做出贡献的其他个人和集体,均已在文中以明 确方式标明。
本人授权南京航空航天大学可以有权保留送交论文的复印件,允 许论文被查阅和借阅,可以将学位论文的全部或部分内容编入有关数 据库进行检索,可以采用影印、缩印或其他复制手段保存论文。
1.3 本文的主要内容
本文主要研究一类具有特殊形式的最优化问题,求解这一类最优化问题的全 局最优解,并应用到求解互补问题上。虽然目前已经有很多算法,但是我们考虑 到本最优化问题的约束条件是特殊的,因此可以利用约束条件的特殊性构造更为 简单有效的算法。
本文提出了一类新的函数,将它定义为半正定函数。利用这类函数将原问题; 分别转化为无约束最优化和含等式约束的最优化问,并分别设计了算法,进行了 数值实验,验证了算法的有效性。为了给出问题的全局最优解,我们又研究了算 法子问题的全局最优化算法,利用填充函数法来求解子问题。这样就保证了前面 设计的算法可以求得问题的全局最优解。最后,针对约束最优化问题(P),提出 了拟填充函数的概念,构造了一类拟填充函数并设计了算法。具体内容如下:
In this article we propose a new type of function, which is called a semi-positive function. We use this function to make another function, then we can turn the original problem into another one. We give algorithms and numerical results. Then we investigate the sub-problem. Also we propose the definition of quasi-filled function. We propose a quasi-filled function and design algorithm. It mainly contains the following six chapters:
运筹与优化第1-2章

◆锥、凸锥 定义2 . 1 . 2 设有集合C ⊂ E n,若对C 中每 一点x,当λ取任何非负数时,都有 λx∈C ,则称C 为锥,又若C 为凸集,则 称C为凸锥。
lim x
k→∞
(k )
=x
序列若存在极限,则任何子序列有相 同的极限,极限唯一
四、聚点
定义1.3.5设{x(k)}是Rn中的一个向量序 (k j ) 列,如存在一个子序列{x } ,使
k j →∞
lim x
(k j )
ˆ = x
ˆ 则称 x 是序列{x(k)}的一个聚点 • 如无穷序列有界,即存在正数M,使得 对所有k均有|| x(k) ||≤ M,则该序列必 有聚点
八、梯度
• 函数f在x处的梯度为n维列向量:
⎡ ∂ f ( x ) ∂f ( x ) ∇f ( x ) = ⎢ , , ∂x 2 ⎣ ∂x1
∂f ( x ) ⎤ , ⎥ ∂x n ⎦
T
九、Hesse矩阵
∂ f ( x) [∇ f ( x )]ij = ,1 ≤ i , j ≤ n ∂x i ∂x j
n×k
第2章 凸集与凸函数
§2.1凸集(Convex Set)
一、凸集的概念
◆
实空间上定义了+、数乘、内积
x(1)和 x(2)的凸组合(convex combination x(1) x(2) x(1) x(2)
●例2.1.1 集合H = { x | pTx = α}为凸集, 其中,p为n维列向量, α为实数。
• 设每人每天需要各种食品的数量分别为x1、 x2、…、xn • Min c1x1+ c2x2+ …+ cnxn a11x1 +a12x2+ …+ a1nxn≥b1 a21x1 +a22x2+ …+ a2nxn≥b2 s.t. … am1x1 +am2x2+ …+ amnxn≥bm x1 、x2、 … 、 xn≥ 0
运筹学答案_刁在筠等(2-4章)
4
44
1
15
ቤተ መጻሕፍቲ ባይዱ
x2 2 1 0 2
2
x3
−1 4
0
1
−1 4
7 4
根据最优化准则知,问题(P)的最优解为 x* = (0, 5 , 7)T , 最优值为 7 .
24
4
(2) 将问题(P)化为一般形式
8
运筹学 (第三版) 刁在筠等
⎧min z = x1 + x3
⎪⎪⎪s.t. − x1 − 2x2
≥ −5
⎪⎪s.t. ⎨ ⎪
x1 + 4x2 − 2x3 + 8x4 = 2 − x1 + 2x2 + 3x3 + 4x4 = 1
⎪⎩
x1 , x2 , x3, x4 ≥ 0
添加人工变量 x5 , x6 得到辅助问题
⎧min g = x5 + x6
⎪⎪s.t. ⎨ ⎪
x1 + 4x2 − 2x3 + 8x4 + x5 = 2 − x1 + 2x2 + 3x3 + 4x4 + x6 = 1
⎪⎩ x2 ≥ 2
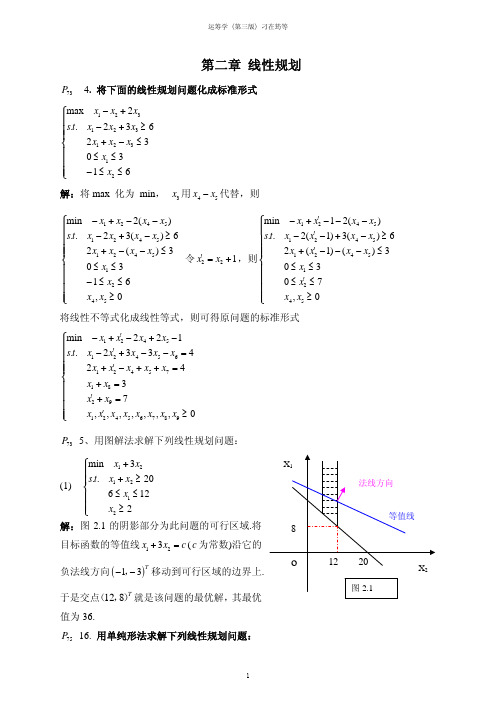
解:图 2.1 的阴影部分为此问题的可行区域.将
8
目标函数的等值线 x1 + 3x2 = c ( c 为常数)沿它的
负法线方向 (−1,− 3)T 移动到可行区域的边界上.
o
于是交点(12,8)T 就是该问题的最优解,其最优 值为 36. P75 16. 用单纯形法求解下列线性规划问题:
进基变量代替离基变量
以 x2 为进基变量, x6 为离基变量旋转得
2
运筹学 (第三版) 刁在筠等
x1 x2 x3 x4 x5 x6 x7 RHS z -1 1 -1 0 -1 1 0 0 x5 0 0 3 0 1 1 0 6 x2 0 1 2 -1 0 0 0 10 x1 1 0 0 0 0 -1 0 0 x7 0 0 1 0 0 1 1 6
北交大交通运输学院《管理运筹学》知识点总结与例题讲解第2章 线性规划

第二章线性规划教学目的:了解线性规划的基本概念,理解线性规划最优化原理、单纯形法原理,掌握单纯形法及其矩阵描述、人工变量法、,能够对简单的问题建模。
教学重点:线性规划的含义、性质;线性规划问题的求解方法——图解法、单纯形法。
线性规划模型的建立非标准型线性规划问题转化为标准线性规划问题;线性规划问题的图解法;解的存在情况判断;大M法;两阶段法;单纯形法的矩阵表示;教学难点:单纯形法的求解思想、矩阵表示、对偶理论、对偶单纯形法以及灵敏度分析。
学时: 8学时2.1 线性规划(Linear Programming,LP)问题及其数学模型(1学时)我们应用数学规划模型求解实际问题中,将实际问题抽象成数学模型,然后再对其求解。
2.1.1线性规划问题提出我们用一个简单例子来说明如何建立数学规划问题的数学模型。
例2.1 某家具厂生产桌子和椅子两种家具,有关资料见表2-1。
解:用数学语言来描述生产计划安排问题,这个过程称为建立其数学模型,简称建模。
设:①桌子、椅子生产的数量分别为x1,x2,称为决策变量。
因为产量一般是一个非负数,所以有x1,x2≥0,称非负约束。
②限制条件为木工和油漆工的加工时间约束了产品的生产量x1,x2。
约束如下:4x1+3x2≤1202x1+x2≤50③生产桌子、椅子x 1,x 2所得总收入为Z ,显然Z =50x 1+30x 2。
我们希望总收入值能达到最大,这个关系用公式表达为max Z =50x 1+30x 2 把上述所有数学公式归纳如下12121212max .0z 50x 30x 4x 3x 120s t 2x x 50x x =++≤⎧⎪+≤⎨⎪≥⎩,这就是一个最大化的线性规划模型。
例 2.2(运输工具的配载问题)有一辆运输卡车,载重2.5t ,容积183m ,用来装载如下的两种货物:箱装件125kg/个、0.43m /个;包装件20kg/个、1.53m /个。
问:如何装配,卡车所装物件个数最多?解 根据题意,设箱装件1x 个,包装件2x 个,那么需要满足条件:体积约束 120.4 1.518x x +≤重量约束 12125202500x x +≤非负约束12,0x x ≥目标要求 max z=12x x +我们对上面的式子稍作整理,便得到下面的形式:max z=12x x +1212120.4 1.518125202500,0x x x x x x +≤⎧⎪+≤⎨⎪≥⎩ 上述两例中所提出的问题,最终都归结为在变量满足线性约束条件的前提下,求使线性目标函数最大或最小的问题,这种问题称为线性规划问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定理1 S是凸集S中任意有限点的凸组合属于S。 (1) (2) (m ) (1) (2) 多胞形 H(x , x , … , x ):由 x , x , … , (m ) x 的所有凸组合构成。 (1) (2) (m) 单纯形:若多胞形 H(x , x , … , x )满足, (2) (1) (3) (1) (m ) (1) x - x , x - x , … , x - x 线性无关。
注: f 在 S 上不一定连续。 例如 : f(x)=2(当x=1); f(x)=x2 (当x<1) 。
n
3)设f 凸,则对任意方向的方向导数存在(前提首 先要是“可行方向”)。 4)设 S 是开集,f 在 S 上可微,则f凸 x*S,有
f (x) ≥ f (x*)+ f T(x*)(x-x*) , x S。
2.2 凸集、凸函数和凸规划
定义4 设集合 S R ,函数 f :SR, R ,
称 S = { x S∣f (x) ≤ } 为 f (x) 在 S 上 的 水平集。 n 定理3 设集合 S R 是凸集,函数 f :SR是 凸函数,则对 R ,S 是凸集。
n
2.2凸集、凸函数和凸规划
凸集
非凸集
非凸集
2.2凸集、凸函数和凸规划
例1 证明集合 S = { x∣Ax = b } 是凸集。 其中,A为 mn矩阵,b为m维向量。 (1) (2) (m) n 凸组合:设 x , x , … , x R , j≥ 0
m m (j) (1) (2) (m)
例
题
类似可得到极点 x(2) = (5, 25, 0, 5, 0 )T (对应B2) x(7) = (20, 0, 5, 0, 75 )T (对应B5) x(8) = (0, 25, 15, 15, 0 )T (对应B7) x(9) = (0, 0, 65, 40, 75 )T (对应B10) 而 x(3)= (0, 32.5, 0, 7.5, - 22.5 )T(对应B9) x(4)= (65/3, 0, 0, - 10/3, 75 )T (对应B6) x(5 )= (7.5, 25, - 7.5, 0, 0 )T (对应B1) x(6) = (0, 40, - 15, 0, - 45 )T (对应B8) 不是极点。
S中必存在有限多个极方向 ( ≤
m (n-m)Cn
)。
例2 考虑多面体S = 中 3 2 1 A = 2 1 0 0 3 0
{ xR Ax = b , x≥0 },其
0 0 1 0 0 1 65 b = 40 75
例
n
题
即
3 x1 + 2 x2 + x3 = 65 2 x1 + x2 + x4 = 40 3 x2 + x5 = 75 x1 , x2 , x3 , x4 , x5 ≥ 0
n
则称 f (x) 为在点x*沿方向d的方向导数存在,记 f ′ (x*;d) = lim [ f (x*+ d ) - f (x*) ] /
•
若 f (x) 在 x* 可导,则 f ′ (x*;d) = [f (x*) ] d 。
T
2.2 凸集、凸函数和凸规划
以下设 S R 为非空凸集,函数 f :SR 2)若f 凸,则 f 在 S 的内点集上连续。
5) 设 S 是开集,f 在 S 上二次可微,则
①f 凸 xS,2f (x) 半正定; ②若 xS,2f (x) 正定,则f严格凸。
2.2 凸集、凸函数和凸规划
1) 2) 3)
例: f (x)=x12+2x1x2+2x22+10x1 - 4 f (x)= - 3x12+x1x2 - x22 - 2x32 -2x2x3+26 f (x)=3x12+ax1x2+2x22-4x1+6 ( a=5, 4.5 )
2.3 多面体、极点、极方向
定理5(极点特征)设 A 满秩,x 是 S 极 点的充分必要条件是: 存在分解 A = (B , N ),其中B为 m阶非奇异矩阵,使 xT = ( xBT, xNT ), 这里 xB = B-1b≥0, xN =0。
S中必存在有限多个极点
( ≤ Cn ) 。
m
2.3 多面体、极点、极方向
严格凹函数 严格凸函数 凸函数
2.2 凸集、凸函数和凸规划
定理2 f (x) 为凸集 S 上的凸函数 S 上任 意有限点的凸组合的函数值不大于各点函 数值的凸组合。 思考:设f1, f2是凸函数。 1) 设1, 2 > 0, 1f1+2f2 , 1f1 -2f2是否凸函 数?(都是) 2)f (x)= max{ f1(x) , f2 (x) } , g(x)= min{ f1(x) , f2 (x) }是否凸函数? (不一定)
,
= 1 , 那么称 x 为 x , x , … , x 的 j j j =1 j=1 凸组合。 • 比较: z = j x j =1
m (j)
jR ——构成线性组合 —— 线性子空间 j≥0 , j >0 —— 构成半正组合 —— 凸锥 j≥0 , j =1 —— 构成凸组合 —— 凸集
2.2 凸集、凸函数和凸规划
2.凸函数 (1)凸函数及水平集 n 定义3 设集合 S R 为凸集,函数 f :SR。若 x(1), x(2) S, ( 0 , 1 ) ,均有 f(x(1)+(1-) x(2) ) ≤f(x(1))+(1 - )f(x(2)) , 则称 f (x) 为凸集 S 上的凸函数。 若进一步有上面不等式以严格不等式成立,则 称 f(x) 为凸集 S 上的严格凸函数。(几何意义见P27) 当- f (x) 为凸函数(严格凸函数)时,则称 f (x) 为凹函数(严格凹函数)。
2.2 凸集、凸函数和凸规划
3.凸规划 当(f S)中,S为凸集,f是S上的凸函数 (求min)时,称(f S)为凸规划。 对于(fgh), 当f ,gi为凸函数,hj为线性函 数时,(fgh)为凸规划。 n 定理4 设集合 S R 为凸集,函数 f :SR 。 f(x) 为凸集 S 上的凸函数。x*为问题(fs)的 l.opt.,则x*为g.opt.;又如果f是严格凸函数, 那么x*是(fs)的唯一g.opt.。
严格l .opt .
严格g .opt .
l .opt .
2.1数学规划模型的一般形式
函数形式: f (x), gi(x) , hj(x) : RnR Min f (x) (fgh) s.t. gi(x) ≤ 0 , i = 1,2,…,m hj(x) = 0 , j = 1,2,…,l 矩阵形式: Min f (x) , f (x) : RnR (fgh) s.t. g(x) ≤ 0 , g(x) : RnRm h(x) = 0 , h(x) : RnRl
最优值:
2.1数学规划模型的一般形式
局部最优解: x*S, x* 的邻域 N(x*) ,使满足 f (x*)≤ f (x), x S N(x*) ,则称 x*为(f S)的局部 最优解,记 为l .opt.(local optimum) 。 在上述定义中,当x x* 时有严格不等式成立,则 分别称 x* 为(f S)的严格全局最优解和严格局部最 优解。
2.2凸集、凸函数和凸规划
多胞形
单纯形
单纯形
2.2凸集、凸函数和凸规划
(2)凸集的性质
1)
2)
3) 4)
凸集的交集是凸集;(并?) 凸集的内点集是凸集;(逆命题是否成立?) 凸集的闭包是凸集。 (逆命题是否成立?) 分离与支撑:凸集边界上任意点存在支 撑超平面;两个互相不交的凸集之间存基础
第2章 基本概念和理论基础
Min ( f S) s.t. 其中,S 最优解:
1.1数学规划模型的一般形式 f(x) ——目标函数 xS ——约束集合,可行集 n R ,f :S R,xS称(f S )的可行解 x*S,满足f (x*)≤ f (x), xS,则称 x*为(f S)的全局最优解(最优解),记为 g.opt.(global optimum),简记 为opt. 。 x*为(f S)的最优解, 则称 f * = f (x*) 为 (f S)的最优值(最优目标函数值) 。
例
题
其中B4= 0,因而B4不能构成极点和极方向。其余 均为非奇异方阵,因此该问题共有9个可构成极点、 极方向的子矩阵,我们称之为基。 对于基 B3=(p1 ,p2 ,p5),令x3 = 0, x4 = 0,在等 式约束中令x3 = 0,x4 = 0,解线性方程组 3 x1 + 2 x2 + 0 x5 = 65 2 x1 + x2 + 0 x5 = 40 0 x1 + 3 x2 + x5 = 75 得到x1 =15,x2 = 10,x5 = 45,对应的极点 x = (x1,x2,x3,x4,x5 )T = (15,10,0,0,45 )T
支撑
强分离
分离
非正常 分离
2.2 凸集、凸函数和凸规划
(3)凸锥
定义2 C R , 若 x C, > 0 ,有 x C, 则 称 C 是以 0 为顶点的锥。如果 C 还是凸集,则 称为凸锥。 n 集合 { 0 }、R 是凸锥。
n
0
命题:C是凸锥C中任意有限点的半正组合属于S 。
例
题
3 2 1 0 0 A = ( p1 , p2 , p 3 , p 4 , p 5 ) = 2 1 0 1 0 0 3 0 0 1 A矩阵包含以下10个3×3的子矩阵: B1=(p1,p2 ,p3) B2=(p1 ,p2 ,p4) B3=(p1 ,p2 ,p5) B4=(p1 ,p3 ,p4) B5=(p1 ,p3 ,p5 ) B6=(p1 ,p4 ,p5 ) B7=(p2 ,p3 ,p4) B8=(p2 ,p3 ,p5) B9=(p2 ,p4 ,p5) B10=(p3 ,p4 ,p5)
