微分方程的应用举例
微分方程在医学中的应用

微分方程在医学中的应用引言:微分方程是数学中的一种重要工具,广泛应用于各个领域。
在医学领域,微分方程的应用也非常广泛。
本文将探讨微分方程在医学中的应用,并介绍一些具体的例子。
主体:1. 生物医学工程:生物医学工程是将工程学的原理和方法应用于医学领域的学科。
微分方程在生物医学工程中发挥了重要作用。
例如,在心脏起搏器的设计中,可以使用微分方程来描述心脏的电活动和脉冲发放的机制。
这些微分方程可以帮助工程师设计出更加精确和可靠的起搏器,从而提高心脏病患者的生活质量。
2. 癌症治疗:微分方程在癌症治疗中也有重要的应用。
例如,在放射治疗中,可以使用微分方程来描述肿瘤细胞的生长和死亡过程,从而帮助医生确定合适的放射剂量和治疗方案。
此外,微分方程还可以用于预测肿瘤的生长速度和扩散范围,从而帮助医生制定更有效的治疗策略。
3. 心血管疾病:微分方程在研究心血管疾病方面也发挥了重要作用。
例如,在研究血流动力学过程中,可以使用微分方程来描述血液在心血管系统中的流动和压力变化。
这些微分方程可以帮助医生了解心血管疾病的发展机制,并指导治疗和预防措施的制定。
4. 神经科学:微分方程在神经科学中也有广泛的应用。
例如,在研究神经元的电活动和突触传递过程中,可以使用微分方程来描述神经元的动力学行为。
这些微分方程可以帮助科学家理解神经系统的工作原理,从而为治疗神经系统疾病提供理论基础。
结论:微分方程在医学中的应用广泛而重要。
它不仅可以帮助医生和工程师设计更好的医疗设备和治疗方案,还可以为科学家提供理论基础,深入研究人体的生理和病理过程。
通过对微分方程在医学中的应用的探索,我们可以更好地理解和治疗各种疾病,提高人类的健康水平。
参考文献:1. L. Perko, Differential Equations and Dynamical Systems, Springer, 2001.2. F. Verhulst, Nonlinear Differential Equations andDynamical Systems, Springer, 1996.3. H.W. Hethcote, "The Mathematics of Infectious Diseases," SIAM Review, vol. 42, no. 4, pp. 599-653, 2000.4. S. Busenberg and C. Castillo-Chávez, "A General Solution of the Problem of Mixing of Substances by Several Methods," SIAM J. Appl. Math., vol. 58, no. 5, pp. 1650-1688, 1998.5. E. Beretta and Y. Kuang, "Geometric Stability Switch Criteria in Delayed Differential Systems with Applications to Chemostat Models," SIAM J. Math. Anal., vol. 33, no. 6, pp. 1144-1165, 2002.。
例谈微分方程在实际问题中的简单应用

例谈微分方程在实际问题中的简单应用微分方程是数学领域中一个重要的分支,它研究的是包含未知函数及其导数的方程。
微分方程在物理学、工程学、经济学等实际问题中有着广泛的应用。
本文将以实际问题为例,说明微分方程在实际中的应用。
一、弹簧振子的运动弹簧振子是物理学中的一个经典问题,可以通过微分方程来描述其运动。
假设弹簧的质量为m,弹簧常数为k,弹簧的形变量(位移)为x(t),则弹簧振子的运动可以描述为二阶线性微分方程:m*x''(t)+k*x(t)=0二、放射性衰变放射性元素的衰变过程可以用微分方程进行建模。
设放射性物质的衰变速率与物质的量成正比,即衰变速率为a(a>0)与物质的量x(t)成正比,可得微分方程:x'(t)=-a*x(t)三、生物种群增长生物种群增长问题也可以通过微分方程进行描述。
设种群数量为N(t),种群增长速率与种群数量成正比,即增长速率为k(k>0)与种群数量N(t)成正比,可得微分方程:N'(t)=k*N(t)四、空气中的弥散空气中的弥散问题可以用微分方程进行建模。
设空气中其中一种气体的浓度为C(x,t),C满足浓度的扩散方程:C_t = D*C_xx其中,C_xx表示浓度在x方向上的二阶导数,D为气体的扩散系数。
五、电路中的RLC振荡电路中的RLC振荡是电子学中的一个重要问题,可以通过微分方程进行描述。
设电路的电感L、电阻R和电容C分别为常数,电路的电压为V(t),则振荡电路的微分方程为:L*V''(t)+R*V'(t)+1/C*V(t)=0以上是几个常见实际问题的微分方程应用,说明了微分方程在实际问题中的简单应用。
通过建立微分方程模型,可以定量地描述和分析复杂的实际问题,从而为问题的解决提供了理论依据。
微分方程在实际问题中的应用不仅帮助人们更好地理解和解决问题,而且还推动了数学理论和方法的发展。
随着科学技术的进步,微分方程将在更多领域中发挥重要作用。
微分方程应用

微分方程应用微分方程是数学中的重要分支,它有着广泛的应用。
本文将介绍微分方程在不同领域的应用,包括物理学、生物学和经济学等。
通过这些应用实例,我们将看到微分方程在解决实际问题中的重要性和价值。
一、物理学中的物理学是微分方程的一个主要应用领域。
许多自然现象可以通过微分方程来描述和解释。
例如,牛顿第二定律将物体的运动与其所受的力联系在一起,可以用微分方程表示为:$$m\frac{{d^2x}}{{dt^2}} = F(x)$$其中,$m$代表物体的质量,$x$代表物体的位置,$t$代表时间,$F(x)$代表作用在物体上的力。
通过解这个微分方程,我们可以预测物体随时间的变化和轨迹。
二、生物学中的微分方程在生物学中也有广泛的应用。
许多生物过程可以用微分方程建模,如人口增长、药物动力学和神经元的激活等。
以人口增长为例,我们可以用以下微分方程描述:$$\frac{{dN}}{{dt}} = rN(1-\frac{{N}}{{K}})$$其中,$N$代表人口数量,$t$代表时间,$r$代表人口的增长率,$K$代表环境的承载能力。
通过解这个微分方程,我们可以了解人口随时间的变化趋势,从而制定相应的政策措施。
三、经济学中的微分方程在经济学中也有重要的应用。
例如,经济增长模型可以用以下微分方程表示:$$\frac{{dY}}{{dt}} = sY - c$$其中,$Y$代表经济产出,$t$代表时间,$s$代表储蓄率,$c$代表消费。
通过解这个微分方程,我们可以预测经济增长的速度和趋势,为经济政策的制定提供依据。
总结:微分方程是数学中的重要工具,具有广泛的应用领域。
无论是在物理学、生物学还是经济学中,微分方程都能用来描述和解释自然现象,并从中得出有用的结论。
通过研究微分方程的应用,我们可以更好地理解和预测现实世界中的各种问题,为解决这些问题提供有效的方法和方案。
在实际应用中,需要根据具体问题选择合适的微分方程模型,并结合相关领域的知识和数据进行求解和验证。
数学与微分方程解析微分方程在科学与工程领域中的应用案例

数学与微分方程解析微分方程在科学与工程领域中的应用案例在科学与工程领域中,微分方程是一种重要的数学工具,用于描述物理、化学、生物等领域中的各种现象和问题。
微分方程解析的应用案例有很多,下面将介绍其中一些典型的案例。
案例一:电路中的RLC电路在电路中,RLC电路是一种常见的电路类型,由电阻(R)、电感(L)和电容(C)组成。
我们可以利用微分方程来描述电路中电压和电流的变化情况。
设电容的电压为Vc(t),电感的电流为I(t),电阻上的电压为VR(t)。
根据基尔霍夫电压定律和欧姆定律,可以得到如下微分方程:L(dI/dt) + RI + 1/C∫I(t)dt = V(t)通过解这个微分方程,我们可以得到电路中电流和电压随时间的变化规律,从而对电路的稳定性和响应进行分析和预测。
案例二:化学反应动力学在化学反应中,微分方程可以用来描述反应物的浓度随时间的变化规律。
例如,一级反应的速率可以用下面的微分方程来表示:d[A]/dt = -k[A]其中,[A]表示反应物A的浓度,k为反应速率常数。
通过求解这个微分方程,我们可以得到反应物浓度随时间的变化曲线,从而研究反应的速率和影响因素。
案例三:机械振动系统在工程领域中,微分方程可以用来描述机械振动系统的运动规律。
例如,单自由度弹簧振子的运动可以由下面的微分方程表示:m(d2x/dt2) + kx = 0其中,m为质量,k为弹簧的弹性系数,x为位移。
通过求解这个微分方程,我们可以得到振子的运动规律,包括振幅、频率和相位等信息。
案例四:人口增长模型微分方程还可以用来描述人口增长模型。
例如,常见的Logistic增长模型可以用下面的微分方程表示:dP/dt = rP(1-P/K)其中,P表示人口数量,r为人口增长率,K为环境容量。
通过解这个微分方程,我们可以研究人口的增长趋势和极限状态。
总结:微分方程在科学与工程领域中有着广泛的应用,上述案例只是其中的一部分。
数学与微分方程解析的应用可以帮助科学家和工程师更好地理解和预测自然和人工系统的行为,优化设计和控制方案。
高考数学中的微分方程应用及实例题解析

高考数学中的微分方程应用及实例题解析一、微分方程的应用微分方程在数学中有着广泛的应用,而在高考数学中尤为重要。
微分方程可以用来描述各种物理和工程问题中的连续变化。
在高考数学中,微分方程的应用主要包括解决物理和工程问题,并用微分方程模型求解。
下面,我们将以几个实例来解释微分方程的应用。
二、实例题解析1. 一个水箱有一个进水口和一个排水口,进水口的水速是10升/分钟,排水口排水的速度是6升/分钟。
在水箱的初态下,水箱的水量是7升。
求15分钟之后水箱的水量是多少?解答:由于水箱的进水口和排水口都是连续变化的,因此可以用微分方程来模拟。
不妨设水箱的初始状态下的水量为y,当t时间后,进水和排水的水量都为10-6=4升/分钟,因此有:y'(t)=4根据微分方程得:y(t)=4t+C由于初态下,水量为7升,因此C=7。
当t=15时,有:y(15)=4*15+7=67因此,15分钟后水箱的水量是67升。
2. 某商品的回报率为r,市场容量有限,其市场占有率y变化满足dy/dt=ry(1-y),y初始为0.2,求当市场占有率达到60%时所需的时间。
解答:由于市场占有率随时间的变化是连续变化的,因此可以用微分方程来模拟。
设市场占有率为y,时间为t,有:dy/dt=ry(1-y)将该微分方程分离变量得:1/(y(1-y))dy=rdt两边积分得:ln|y/(1-y)|=rt+C由于当y=0.2时,t=0,因此C=ln(1/4)。
当y=0.6时,有:ln|0.6/(1-0.6)|=0.4r+C代入C得:ln(3/2)=0.4r+ln(1/4)解得r=ln3/16,因此所需的时间为:t=[ln(3/2)-ln(1/4)]/0.4ln3/16≈8.25因此,市场占有率达到60%时所需的时间为8.25。
三、总结微分方程在高考数学中的应用极为广泛,需要考生有扎实的微积分和数学建模的基础。
通过多做微分方程的实例题目,可以帮助考生更好地掌握微分方程的应用方法和技巧。
高中数学中的微分方程应用题

高中数学中的微分方程应用题微分方程是数学中的一个重要分支,也是高中数学的一部分。
它能够描述许多实际问题,并提供解决问题的方法。
本文将聚焦于高中数学中微分方程的应用题,通过一些具体的例子来展示微分方程在实际问题中的应用。
第一节:人口增长模型假设一个城市的人口增长速度与当前人口成正比,可以建立以下微分方程:$\frac{{dp}}{{dt}}=k \cdot p$其中,$p$代表城市的人口数量,$t$代表时间,$k$代表增长率。
以某城市的人口增长为例,已知该城市当前的人口数量为100万,增长率为10%。
我们可以利用上述微分方程来求解未来几年该城市的人口数量。
解微分方程可得:$\frac{{dp}}{{p}}=0.1 \cdot dt$对上式两边同时积分,可得:$\ln|p|=0.1t+C$其中,$C$为常数。
由已知条件可知,当$t=0$,$p=100$。
代入上式得:$\ln|100|=C$解得$C=\ln 100$。
因此,原微分方程的通解为:$\ln|p|=0.1t+\ln 100$化简得:$\ln|p|=0.1t+\ln 100=0.1t+\ln e^{4.60517}$再次化简得:$\ln|p|=0.1t+\ln(e^{4.60517})$$\ln|p|=0.1t+4.60517$取指数得:$p=e^{0.1t+4.60517}$经过计算可得,当$t=10$时,$p\approx22026$。
即在10年之后,该城市的人口数量约为22万。
第二节:放射性衰变模型放射性衰变是非常常见的物理现象,可以使用微分方程来描述。
某放射性元素的衰变速率与其当前的数量成正比,可以建立以下微分方程:$\frac{{dN}}{{dt}}=k \cdot N$其中,$N$代表放射性元素的数量,$t$代表时间,$k$代表衰变常数。
以某放射性元素的衰变为例,已知初始时刻$t=0$时,放射性元素的数量为1000克,衰变常数为0.1年$^{-1}$。
微分方程应用举例
L23 )C2
Um C
(
2L
C
L23 )C1
(R C
RL 2 )C2
0
解得
C1
1
Um C
(R C
RL2 )
C2
1
Um C
( L2 3
2L )
C
( R RL 2 )2 2 ( 2L L2 2 )2
C
C
变形 i2 Asin(t )
A C12 C22
arctan C2
C1
负载R上的电流 i2 Asin(t )
di2 dt
R C
i2
Um C
sin t
三阶常系数线性非齐次常微分方程。
需要消去i1,只保留i2
解
L2
d 3i2 dt 3
RL
d 2i2 dt 2
2L C
di2 dt
R C
i2
Um C
sin t
所对应其次方程的特征方程为
L2r3 RLr2 2L r R 0 CC
由于特征方程的三个特征根的实部均为负值,因此其次方程的通解是指数 衰减的,所对应的那部分电流将很快消失掉(即瞬态电流)。
Umax R Um C
1
2 (L22 )2
R
CL3
输出电压的最大值比输入电压最大值要小得多, 表明高频电压基本上不能通过这一电路。
因此,如果输入信号中有多种频率时,仅仅低频信号可以通过,而 高频信号被电路耗散掉。 这说明该电路具有滤波作用,故称为滤波电路。
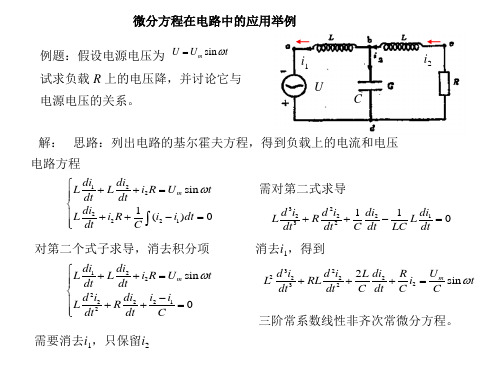
微分方程在电路中的应用举例
例题:假设电源电压为 U Um sin t
i1
i2
试求负载 R 上的电压降,并讨论它与 U
电源电压的关系。
微分方程应用举例

ln M t ln c , 即M ce t ,
代入M
t 0
M 0 , 得 M 0 ce C
0
M M 0e
t
衰变规律
案例3【 物体冷却问题】 将某高温物体置于空气中冷却,假定空气 温度恒为 24o C ,在时刻 t 0时,测得其温度 为 150o C , 10分钟后测得温度为 100o C .已知 牛顿冷却定律:物体冷却速率与物体和介质的 温差成正比.求物体的温度与时间的函数关系, 并计算 分钟后该物体的温度. 20
解 设 T T (t ),
则T (t ) 0. 由牛顿冷却定律,有
dT k ( t 24), k 0 dt T (0) 150.
用通解公式法解得 24 126e T
将T (10) 100代入,解得
k t
1 126 k ln 0.051 10 76
R sin t L cos t
代入上式,得
E0 R sin t L cos t Ce i 2 2 2 R L
R t L
又i (0) 0,代入上式,求得
E0 L C 2 , 2 2 R L
所以
R t E0 R sin t L cos t L e L i (t ) 2 2 2 R L
所以 T 24 126e
0.051t
将t 20代入,解得
T ( 20) 24 126e
0.05120
64(C )
案例4【电路电流问题】 设有一电路如图所示,R 是电阻,L是电感,它们 都是常数,电源的电动 势为 E E0 sin t
R
L E
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dS SI dt
其中 S I N , I (0) 1 代入上式,得
dS S ( N S ) dt
分离变量后积分,得
dS S ( N S ) dt
1 S 即 ln t C N N S
再由初始条件 I (0) 1,可得
1 C ln( N 1) N
例如,牛顿冷却定律、化学中的一 级反应、早期肿瘤的生长、药物的分解 等自然现象,都按指数规律变化。
指数生 长模型
例2.(细菌增殖模型) 理想环境:
(1)除系统本身的繁殖外,没有由系统外向 系统内的迁入和由系统内向外迁出等情况; (2)系统本身的繁殖不受空间和营养供应的 限制; (3)温度、湿度等各项环境因素均对系统适 宜。
dx k0 kx dt
dx k0 kx dt
此方程是一个可分离变量的一阶微分方程,
易求得其在初始条件t=0时x=0下的特解为
k0 kt x (1 e ) k
k0 静脉滴注的速率越大,最后体 lim x(t ) t k 内药量的稳定水平越高。
例4.(流行病数学模型)
dM kM dt
(常数k 0)
分离变量、两边积分,得
ln M kt ln C 或
M Ce
kt
将初始条件 t 0时M M 0 代入,得 C M 0 因此镭的质量M关于时间t 的变化规律为:
M (t ) M 0e .
kt
当变量关于时间的变化率与变量的量成 正比时,这个变量总是按指数规律变化。
因此,有
1 S 1 ln t ln( N 1) N N S N
整理后得:
N ( N 1) S Nt ( N 1) e
当t 时,S 0, 从而有I N.
结论:对于无移除的流行病,最终将导 致团体内全部成员被感染。
x x0 . 假设初次取样即t=0时,
代入上式,有
x0 C r kx0
于是有
x0 x rt e r kx r kx0
自然生长方程
或
r x r kx0 rt k e x0
r 当t 时,x . k r 即 是该蓄水池中大肠杆菌密度的极限值。 k
例3.(药物动力学一室模型)
药物动力学是一门研究药物、毒物
及其代谢物在机体内的吸收、分布、代
谢和排泄过程定量规律的科学。
假定药物以恒定的速率 k 0 进行静脉滴 注,试求体内药量随时间的变化规律。
假定药物在体内 解:
k0 按一级速率过程 消除,消除速率
v, x
k
常数为k . 设静脉滴注t时刻体内药量为x(t),则有
微分方程的应用
数学模型
根据研究对象的内在规律运用适当
的数学工具建立起来的一种数学结构。
微分方程是建立数学模型时应用
得最为广泛的工具之一。
一、微分方程建模的基本步骤:
1、根据已知规律建立微分方程; 2、根据已知条件找出初始条件; 3、解微分方程(求通解、特解); 4、用所得结果解释实际问题。
二、生物医药模型举例
检验人员对某蓄水池定期抽取单位容积水样
观察,测得该水池中大肠杆菌的相对增殖率为
单位时间内单位数 量的生物的增长。
1 dx r kx x dt
(k、r为正常数)
试分析该水池中大肠杆菌的繁殖规律。
解: 将关于相对增殖率的关系式进行变量
分离,得
dx dt x(r kx)
x rt 两边积分,得: Ce r kx
无移除的流行病模型:
(1)感染通过一个团体成员之间的接触而传播,
感染者不因死亡、痊愈或隔离而被移除;
(2)团体是封闭的,总人数为N,最初假设只 有一个感染者; (3)团体种各成员之间接触机会均等,因此易 感者转化为感染者的变化率与当时的易感人数 和感染人数的乘积成正比。
解:记时刻t的未感染人数为S,已感染人 数为I,根据以上假设即可建立下面 的微分方程:
例.(放射性元素的衰变)
放射性元素因不断放射出各种射线 而逐渐减少其质量的现象,称为衰变。
由原子物理学知道,放射性元素镭的衰变
速度与存量成正比,比例系数为k(k>0)。如 果当时间t=0时,镭的质量为M 0 ,求镭的质量
M关于时间t的变化规律M (t ) 。
解:设镭在时刻t的留存量为M(t),则镭从时 刻0到时刻t的消耗量为 M 0 M (t ) 。 根据导数的定义,镭的衰变速度就是镭 的消耗量关于时间的导数,即 d dM [ M 0 M (t )] dt dt 将“镭的衰变速度与存量成正比”表达成 数学语言,即写成微分方程,得
