光电子技术(第一章电磁波与光波)
光电子教学大纲

《光电子技术》教学大纲课程编码:课程英文名称: Optoelectronics Technology学时数:60学时学分:3.5学分适用专业:电子科学技术专业教学大纲说明一、课程的性质、教学目的与任务课程性质:光电子技术是由电子技术和光子技术互相渗透、优势结合而产生的,是一门新兴的综合性交叉学科,已经成为现代信息科学的一个极为重要的组成部分,以光电子学为基础的光电信息技术是当前最为活跃的高新技术之一。
光电子技术课程是电子科学与技术专业学生的必修专业课程,它的开设为培养合格的专业技术人才提供了必备的理论和实践基础,本门课程不仅是本专业学生在校学习的重要环节,而且对学生毕业后的工作和进一步学习新理论、新技术都将发生深远的影响。
教学目的:该课程介绍光电子技术的理论和应用基础,内容可以分为四大主要部分:(1) 激光原理基础及典型激光器;(2) 光的耦合与调制技术;(3) 光电探测器及其应用;(4) 光电子集成器件及光电子器件在光通信中的应用。
主要介绍了光电子系统中关键器件的原理、结构、应用技术和新的发展。
该课程在阐明基本原理的同时,突出应用技术,使学生能够把握光电子技术的总体框架,有兴趣、有信心投入实践和创新活动。
教学任务:通过本课程的学习,使学生熟悉光电子技术的基础知识以及实际应用,为今后从事光电子技术方面的研究和开发工作打下一定的基础。
并通过实验教学环节使学生加深光电子技术课程的理论知识的掌握,通过一定的实验,培养学生应用所学知识解决实际问题的能力,获得相应技术、实验方法和技能锻炼。
二、课程教学的基本要求本课程以课堂讲授为主,课下自学为辅。
对自学的内容布置讨论及思考题,提高学生独立思考及解决问题的能力。
适当增加flash动画、视频材料,同时安排一些课外科技学术报告,使学生了解到本学科的最新前沿进展。
通过本课程的学习,应使学生掌握光电子技术的基本原理、基本概念,了解光电子技术的应用实例,了解光电子领域的新成果和新进展,对光电子技术有比较全面、系统的认识和理解。
光电子技术电子课件-光电子技术电子课件-电磁波谱

电磁波谱
一、波长、频率和波速
1.描述波动的物理量:波长、频率和波速
2.波峰、波谷:凸起的最高处叫做波峰;凹下
的最低处叫波谷。
3.波长:邻近的两个波峰(或波谷)间的距离叫
做波长
4、频率:1S内通过的波峰或波谷的次数叫频率。
5、波速公式:波速=波长×频率C=λ×f
6、电磁波在真空中的速度:C=3.00×108m/s
二、电磁波谱
1、电磁波谱:按电磁波的波长或频率大小的顺序把它们排列成谱,叫做电磁波谱
2、波长从大到小的顺序:无线电波、光波(红外线、可见光、紫外线)、X射线、γ射线
三、电磁波的能量
电磁波有能量。
电磁波是一种物质。
四、太阳辐射
太阳辐射的能量集中在可见光、红外线和紫外线三个区域。
黄绿光附近,辐射的能量最强。
关于电磁波谱的几点强调:
频率(波长)不同的电磁波表现出作用不同.
红外线主要作用是热作用,可以利用红外线来加热物体和进行红外线遥感;
紫外线主要作用是化学作用,可用来杀菌和消毒;
伦琴射线有较强的穿透本领,利用其穿透本领与物质的密度有关,进行对人体的透视和检查部件的缺陷;
γ射线的穿透本领更大,在工业和医学等领域有广泛的应用,如探伤,测厚或用γ刀进行手术.。
光电子技术(第5版)第一章 光辐射与发光光源

同的黑体的温度;
➢ 色温度并非热辐射光源本身的温度;
➢ 色温度相同的热辐射光源的连续谱也可能不相似,若规定的
波长不同,色温度往往也不相同;
➢ 非热辐射光源,色温度只能给出这个光源光色的大概情况,
一般来说,色温高代表蓝、绿光成分多些,色温低则表示橙
光电子技术(第5版)
第一章
本章内容
1.1 电磁波谱与光辐射
1.2 辐度学与光度学基本知识
1.3 热辐射基本定律
1.4 激光基本原理
1.5 典型激光器
1.6 光频电磁波的基本理论和定律
1.1.1 电磁波的性质与电磁波谱
EH k
横波特性
电场、磁场、传播方向构成右手螺旋系
偏振特性
电场、磁场分别在各自平面内振动
T 2698μm K
➢
时,
维恩公式与普朗克公式的误差小于1%。
M v (T )
0 得到
➢ 单色辐射出射度最大值对应的波长λm,由
mT 2897.9(μm K)
1.3.7 斯忒藩-玻尔兹曼定律
➢ 黑体的辐射出射度
0
0
M eb (T ) M eb (T )d
黑体:物体在任何温度下,对任何波长
的辐射能的吸收比都等于1,即αλ (T)
恒等于1。
1.3.2 基尔霍夫辐射定律
• 在同样的温度下,各种不同物体对相同波长的单色辐射
出射度与单色吸收比之比值都相等,并等于该温度下黑
体对同一波长的单色辐射出射度。
M e1 (T ) M e 2 (T )
e1 (T ) e 2 (T )
光电子技术(前言)

20
光传感器
15
30
激光加工设备
10
5 20
0
10
显示元件 发光元件 光纤 光敏元件 复合光元件 光传输网络 太阳能电池 0
前言——全球光电产业发展趋势(日本)
▪
按美国光电子工业发展协会的看法,日本在显示器、光
存储、光通讯及硬拷贝组成的光电子产业中已超过了美国和
欧洲,在世界上占主导地位。日本在光电子领域之所以能创
4500亿美元
2010年
前言——全球光电产业发展趋势(美国)
▪
美国政府将光电子技术列入“美国国家关键技术”、
“商务部新兴技术”和“国防部关键技术”的研究计划。
1995年,美国光电子工业发展协会(OIDA)在考察和对
比了美国和日本的光电子技术发展情况后,认为美国在
光通信产业要注意市场开发,在光电显示领域要加强制
其领先地位一直没有被动摇,特别是在
▪ 消费光电子领域,如激光音响、影碟机、激光打
印机、传真机、数码相机、平面显示器、光驱、光纤
组件系统等。
▪ 据日本光产业技术振兴协会(OITDA)发表 的光学产业日本市场产值统计与预测,2003年度 (2003/4~2004/3)总产值达7.8万亿日元,年 增率19.8%;2004年度(2004/4~2005/3)产值 可望达8.4万亿日元,年增率13.8%;而2005年 度预计增长10.4%,总产值突破9万亿日元。对
最终成绩结构
▪ 平时成绩50%+期末考试成绩50%
平时成绩
▪ 1、出勤:缺3次以上课,平时成绩为零, 直接重修;
▪ 2、作业:缺3次以上,平时成绩为零,直 接重修;
前言
全球光电产业背景 全球光电产业发展趋势 我国光电产业的诞生 我国光电产业概况 光电子学科发展史
光电子技术---清华大学

边界条件表示界面两侧的场以及界面上电荷电流的 制约关系,它实质上是边界上的场方程。由于实际问题往 往含有几种介质以及导体在内,因此,边界条件的具体 应用对于解决实际问题十分重要。
平面电磁波的性质
电磁波是横波,电矢量E、磁矢量H和传播方 向K(K为传播方向的单位矢量)两两垂直。
E和H幅度成比例、复角相等
激光的基本原理、特性和应用 ——粒子数正常分布
按这个正则分布规律:
N2 exp(E2 / kT) N1 exp(E1 / kT) exp[(E2 E1) / kT] 1
在热平衡状态中,高能级上的粒子数N2一定小于低能 级上的粒子数N1,两者的比例由体系的温度决定。
三种跃迁过程(自发辐射)
电场与磁场的激发
B
D
t
t
不符合右手法则(为负)
符合右手法则
电磁波的传播
电场
电场
电场
磁场
电场
磁场
磁场
波源
磁场
磁场
边界条件
n
E2 E1
0
n
H 2 H 1
n •
D 2 D 1
n • B2 B1 0
▪ 界面两侧电场的切向分量连续 ▪ 界面两侧磁场的切向分量发生了跃变 ▪ 界面两侧电场的法向分量发生了跃变 ▪ 界面两侧磁场的法向分量连续
(1)当(N2/N1)<1时,粒子数按波尔兹曼正则分布。 此时有dN12>dN21,宏观效果表现为光被吸收。
(2)当(N2/N1)>1时,高能级E2上的粒子数N2大于低能 级E1上的粒子数N1,出现所谓的“粒子数反转分布”情况。 形成激光的必要条件。此时有dN21>dN12,宏观效果表现 为光被放大,或称光增益。
激光的基本原理、特性和应用 ——玻尔假说
光电子技术复习要点

第一章 绪论1. 光电子技术(optoelectronic technology )准确地应该称为信息光电子技术,是电子技术与光子技术相结合而形成的一门新兴的综合性的交叉学科,主要研究光与物质中的电子相互作用及其能量相互转换的相关技术,涉及光显示、光存储、激光等领域,是未来信息产业的核心技术。
2. 本课程主要讲了四大部分分别是:激光光源、光波的传输、光波的调制与控制、光波的探测。
第二章 激光原理与半导体光源1. 世界上第一台激光器是1960年梅曼制作的红宝石激光器。
2. 原子从高能级向低能级跃迁时,相当于光的发射过程;而从低能级向高能级跃迁时,相当于光的吸收过程;两个相反的过程都满足玻尔条件:n m n m E E h E E hνν-=-=或。
3. 处于热平衡状态的原子体系,设其热平衡绝对温度为T ,则原子体系的各能级上粒子数目的分布将服从波尔兹曼分布律:exp(/)n n N E kT ∝-,其中N n 为在能级E n 上的粒子数,k 为波尔兹曼常数, k=1.3807×10-23 J·K -1。
即,随着能级增高,能级上的粒子数N n 按指数规律减少。
4. 爱因斯坦在玻尔工作的基础上于1916年发表《关于辐射的量子理论》。
该文提出的受激光辐射理论是激光理论的核心基础。
在这篇论文中,爱因斯坦将光与物质的作用分为三种过程:受激吸收、自发辐射、受激辐射。
5. 在二能级系统中,粒子在高能级E 2 能级上停留的平均时间称为粒子在该能级上的平均寿命,简称寿命6. 下面三个图分别描述了二能级系统中光与物质的作用的三种过程:它们可以由下面三个方程描述:对于受激辐射过程(E2→E1 ):21212()dN B u v N dt= 对于受激吸收过程(E1→E2):12121()dN B u v N dt= 对于自发辐射过程(E2→E1 ):21212dN A N dt = 其中u(v)为辐射场中单色辐射能量密度:()()30348(),exp 1h u v T c c hv kT πνγν==-7. 二能级系统中,当(N 2/N 1)>1时,高能级E 2上的粒子数N 2大于低能级E 1上的粒子数N 1,出现所谓的“粒子数反转分布”情况,它是形成激光的必要条件之一。
光电子技术复习
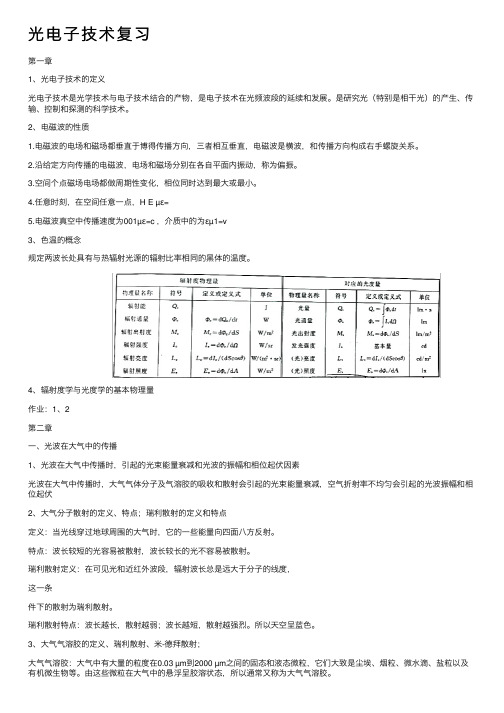
光电⼦技术复习第⼀章1、光电⼦技术的定义光电⼦技术是光学技术与电⼦技术结合的产物,是电⼦技术在光频波段的延续和发展。
是研究光(特别是相⼲光)的产⽣、传输、控制和探测的科学技术。
2、电磁波的性质1.电磁波的电场和磁场都垂直于博得传播⽅向,三者相互垂直,电磁波是横波,和传播⽅向构成右⼿螺旋关系。
2.沿给定⽅向传播的电磁波,电场和磁场分别在各⾃平⾯内振动,称为偏振。
3.空间个点磁场电场都做周期性变化,相位同时达到最⼤或最⼩。
4.任意时刻,在空间任意⼀点,H E µε=5.电磁波真空中传播速度为001µε=c ,介质中的为εµ1=v3、⾊温的概念规定两波长处具有与热辐射光源的辐射⽐率相同的⿊体的温度。
4、辐射度学与光度学的基本物理量作业:1、2第⼆章⼀、光波在⼤⽓中的传播1、光波在⼤⽓中传播时,引起的光束能量衰减和光波的振幅和相位起伏因素光波在⼤⽓中传播时,⼤⽓⽓体分⼦及⽓溶胶的吸收和散射会引起的光束能量衰减,空⽓折射率不均匀会引起的光波振幅和相位起伏2、⼤⽓分⼦散射的定义、特点;瑞利散射的定义和特点定义:当光线穿过地球周围的⼤⽓时,它的⼀些能量向四⾯⼋⽅反射。
特点:波长较短的光容易被散射,波长较长的光不容易被散射。
瑞利散射定义:在可见光和近红外波段,辐射波长总是远⼤于分⼦的线度,这⼀条件下的散射为瑞利散射。
瑞利散射特点:波长越长,散射越弱;波长越短,散射越强烈。
所以天空呈蓝⾊。
3、⼤⽓⽓溶胶的定义、瑞利散射、⽶-德拜散射;⼤⽓⽓溶胶:⼤⽓中有⼤量的粒度在0.03 µm到2000 µm之间的固态和液态微粒,它们⼤致是尘埃、烟粒、微⽔滴、盐粒以及有机微⽣物等。
由这些微粒在⼤⽓中的悬浮呈胶溶状态,所以通常⼜称为⼤⽓⽓溶胶。
瑞利散射:散射粒⼦的尺⼨远⼩于光波长时,散射光强。
⽶德拜散射:散射粒⼦的尺⼨⼤于等于光波长时,散射光强对波长的依赖性不强。
⼆、光波在电光晶体中的传播1、电光效应的定义及分类电光效应:在外电场作⽤下,晶体的折射率发⽣变化的现象。
光电子学完整PPT课件

.
未来是光通信的世界。
第一章 光波与电磁波
➢麦克斯韦方程组的积分形式 ➢高斯定理 斯托克斯定律 ➢麦克斯韦方程组的微分形式 ➢边界条件 ➢电磁波的性质 ➢电磁波谱
.
麦克斯韦方程组及其物理意义
E和H幅度成比例、复角相等
0E0 0H0
E H
电磁波的传播速度
v 1 k 00
C
1
00
3108.m/ s
介质中 真空中
为什么说光波是电磁波?
1) 根据麦氏方程推导, 电磁波在真空中的速度为
c 1 3.107 140 8ms
00
当时通过实验测得的真空中的光速也为 3108 m s
2) 根据麦氏方程: 电磁波在介质中的速度为
玻尔频率条件: h En Em 或 En Em
h
式中h为普郎克常数:
h 6 .6 2 1 3 0 J 4s
.
激光的基本原理、特性和应用 ——玻尔假说
原子能级
原子从高能级向低能 级跃迁时,相当于光 的发射过程;而从低 能级向高能级跃迁时, 相当于光的吸收过程; 两个相反的过程都满 足玻尔条件。
(对于非铁磁质)
v c
根据光学中折射率的定义,则
.
v c
nc vc vn
为什么说光波是电磁波?
如果光波是电磁波,比较上面两式:
v c 和v c
n
n
麦克斯韦 关系式
➢而当时测得的无极分子物质,按上式计算的折射率与测量的折射率 能很好的符合。 ➢当时测得的为有极分子物质,上式中的ε用光波频率时的值,则上式 就成立了。平时ε在低频电场下测量。 ➢所以麦克斯韦判定,光波是电磁波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高斯(Gauss)定理
高斯定理是关于空间区域上的三重积分与其边界 上的曲面积分之间关系的一个定理,表示为: A A dS
V S
高斯定理描述了矢量场中矢量函数沿封闭曲面S的 面积分,等于该矢量函数的散度对该曲面包围体积的体 积分。 散度是描述矢量场中一个点上的特性,而高斯定理 表达式左端描述的是矢量场A在一个范围上的特性。
介质方程
对于各项异性的介质:
D1 11 E1 12 E2 13 E3 D2 21 E1 22 E2 23 E3 D3 31 E1 32 E2 33 E3
1.19
角标1,2,3代表x,y,z分量,上式可简写为:
在解麦克斯韦方程组的时候,只有电磁波 在介质分界面上的边界条件已知的情况下,才 能惟一地确定方程组的解。如电磁波(光波) 在介质分界面上的反射和折射等,都得利用边 界条件才能得到解决。麦克斯韦方程组可以用 于任何连续介质内部。在两介质分界面上,由 于一般出现面电荷电流分布,使物理量发生跃 变,可由麦克斯韦方程组的积分形式进行分析。
边界条件:法向分量的跃变
B2或D2
S
n
分界面
D dS D dS
底面1
D dS D dS q
底面 2 侧面
0
B1或D1
因侧面面积趋于零,对底面1来说, n是内法线方向所以:
法向分量
D dS D2 D1 nS q0
界面两侧磁场的法向分量连续
2 1 0
由于△L为界面上任一矢量
H 2 H1
||
n
边界条件:切向分量的跃变
式中||表示投影到界面上的矢量。因此
n H 2 H1
同理,由(1.12)式中的Ⅱ式,可得电场 切向分量的边界条件:
n E2 E1 0
B d s 0
D H d l I 0 t d s
Ⅰ Ⅱ Ⅲ Ⅳ
去
去
去
D d s q
库仑定律
0
的推导
QQ' F r 3 4 0 r
F Q' E
q E dS D dS q0
0
1.4 1.5
(1.5)式中的q0为高斯面内的自由电荷,而(1.4)式中的q则是包括 束缚电荷在内的总电荷。
回
B E d l t d s
的获得
表示变化的磁场可感应出涡旋电场
(S ) (V )
根据高斯定理,得:
D dS DdV
(S ) (V )
DdV 0 dV
V V
D 0
安培环路定理的微分形式推导
假定传导电流是体分布的,其密度为 j0 ,则
D HdS j0 t dS S s
D dS 0 t
H 2t H1t
边界条件:切向分量的跃变
流过△L的自由电流为:
I 0 n l n l
对于狭长回路用麦氏方程(1.12)式中 的Ⅳ式得 : H dl H H l I n l
边界条件:切向分量的跃变
把麦氏方程(1.12)式中的 Ⅳ式应用于狭长回路上。回路 短边的长度趋于零,因而有:
介质2 分解面 介质 1
B C
l
A D
H 2或E2 H1或E1
H dl H 2t H1t l
其中t表示沿△l的切向分量。 通过回路的总自由电流为:
D t
D H dl j0 t dS l s
H dl HdS
S
根据斯托克斯定律
l
D H j0 t
麦克斯韦方程组的微分形式
D 0 B E t B 0 D H j0 t
1.23
边界条件:切向分量的跃变
在高频情况下,由于趋肤效应,电流、电 场和磁场都将分布在导体表面附近的一薄层内。 若导体的电阻可忽略,薄层的厚度趋于零,则 可以把传导电流看成沿导体表面分布。定义电 流线密度α,其大小等于垂直通过单位横切线 的电流。由于存在面电流,在界面两侧的磁场 强度将发生跃变。
数量场的梯度
梯度的倒三角符号表示方法(哈密顿算符), 定义为:
ex ey ez x y z
因此可得某个标量场的表示为:
gradf f f f f ex e y e z x y z
矢量场的散度
散度的概念
场中某点单位体积矢量场发散的净通量。一个矢量 场A的散度(divergence)可缩写为divA。
磁学中的高斯定理:通过任一封闭曲面S 的磁通量恒等于零。
B d s 0
1.8
回
D H d l I 0 t d s
的获得
表示了电场随时间变化,将产生变化磁场,同 时传导电流也将产生磁场。
安培环路定律:磁感应强度沿任何闭合环路l的线积分等于穿
——麦克斯韦方程组的微分形式
高斯定理:
AdV A dS
V S
斯托克斯定律:
l
A dl A dS
S
高斯定理的微分形式推导
设自由电荷 q0是体分布的,0 为电荷的体密度,则 (1.12)式的(I)式为: D dS 0 dV
静电场中的环路定理:静电场中的场强沿任意
E dl 0 非稳定条件下的环路定理:
B E d l t d s
闭合环路的线积分恒等于零,即“静电场力作功与路 径无关”。
1.6
1.7
回
B d s 0 的获得
表示磁力线是闭合的,无头无的。
边界条件:法向分量的跃变
令 q0 S 为导体分界面上的自由电荷面密度,于是得到:
n ( D2 n D1n ) 或D2 n D1n
1.21
对于磁场B,把(1.12)式中的Ⅲ式应用得到:
n ( B2n B1n ) 0或B2n B1n
散度的倒三角符号表示式
矢量场A 的散度用倒三角符号表示为 div A A
矢量场的旋度
旋度的概念 矢量场旋度的大小是指场中某点单位面积上的最大
涡旋量;其方向是具有最大涡旋时面积元的方向。 旋度(rotation)可缩写为rotA。
旋度的三角符号表示式
rot A A
边界条件
n n n n
E2 E1 0 H 2 H1 D2 D1 B2 B1 0
界面两侧电场的切向分量连续
界面两侧磁场的切向分量发生了跃变
界面两侧电场的法向分量发生了跃变
Ⅰ Ⅱ Ⅲ Ⅳ
1.15
麦克斯韦方程组的物理意义
(Ⅰ)式:电位移矢量或电感应强度D的散度 0,即电 场为有源场。 等于电荷密度 (Ⅲ)式:磁感强度B的散度为零,即磁场为 无源场。 (Ⅱ)式:随时间变化的磁场激发涡旋电场。 (Ⅳ)式:随时间变化的电场激发涡旋磁场。
3 Di ij E j , i 1,2,3 j 1
1.19a
小结
麦克斯韦方程组(1.15)式加上描述介 质性质的方程(1.16)~(1.18)式,全面总结 了电磁场中的规律,是宏观电动力学的基 本方程组,利用它们原则上可以解决各种 宏观电动力学的问题。
边界条件
光电子技术 电磁波与光波
电磁波与光波
麦克斯韦方程组及其物理意义
麦克斯韦方程组的积分形式 麦克斯韦方程组的微分形式 介质方程与边界条件
平面电磁波的性质 光的电磁理论与电磁波谱
麦克斯韦方程组及其物理意义
——麦克斯韦方程组的积分形式
D d s q0
B E d l t d s
斯托克斯(Stokes)定理
斯托克斯(Stokes)定理是关于曲面积分与其边 界曲线积分之间关系的定理,即:
A dl A dS
l S
斯托克斯公式描述矢量场中,矢量A沿闭合周界l 的线积分,它等 于这个矢量的旋度沿场中以l为周界的曲面的面积分。
麦克斯韦方程组及其物理意义
场的概念
所谓场,就是指物理量在空间或一部分空间中的分布。 如电位场、温度场等。
数量场 矢量场
数量场,分布在空间的物理量是数量(又称标量场), 例如电位场。 矢量场,分布在空间的物理量是矢量(又称向量场), 例如,力场、速度场、电场强度场、磁场强度场等。
数量场的梯度
梯度的概念
在一个数量场中(例如一个描述电位分布的 场),场中某点的梯度,是指在该点沿某个方向 上具有最大的变化率(变化最陡),那么这个最 大变化率就是该点梯度的值;这个具有最大变化 率的方向就是梯度的方向。 梯度是一个矢量,gradent (grad u)。
(1.16) (1.17) (1.18)
, 和 分别是相对界电常数、相对磁导率和电导率。
