数列的函数特征

合集下载

数列的函数特征(主要内容)

青苗辅导1
7
二是作商比较法，若数列的通项公式为根式形式,用作商法
比作差法更简便一些.
an＞0
an1 ＞1 an
递增数列
0＜an1 ＜1 an
递减数列
a n1 1 an
常数列
an＜0 递减数列递增数列常数列青苗辅导1
8
在利用作商比较法时，要确保数列的每一项都不是零，再确认相邻两项的正负，然后进行比较.
青苗辅导1
14
【例2】设函数f(x)＝log2x－logx2(0<x<1)，数列{an}满足 f( 2an )=2n(n∈N+). (1)求数列{an}的通项公式； (2)判断数列的单调性. 【审题指导】解决本题的关键是把函数的解析式通过关系式转化求解得到数列的通项公式，然后再根据通项公式进行作差，判断与零的大小或者作商判断与1的大小，从而判断数列的单调性.
可知：对称轴是x=8，所以当0<n<8时数列是递减数列；
当n≥8时，数列是递增数列.
青苗辅导1
11
数列的函数性质的应用数列的函数性质的应用数列是特殊的函数，由数列的项与项数之间构成特殊的函数关系可知：数列的通项an与n的关系公式就是函数f(x)的解析式,所以根据函数解析式得出数列的通项公式是重要途径.
青苗辅导1
26
青苗辅导1
28
青苗辅导1
22
【规范解答】(1)令30＋n－n2＝－60，
即n2－n－90＝0，
∴n＝10或n＝－9(舍)，…………………………………2分
∴－60是这个数列的第10项，即a10＝－60. …………4分 (2)令30＋n－n2＝0，即n2－n－30＝0.
∴n＝6或n＝－5(舍)，即当n＝6时，an＝0. …………6分

高一数学必修5：数列(知识点梳理)

第二章：数列一、数列的概念1、数列的概念：一般地，按一定次序排列成一列数叫做数列，数列中的每一个数叫做这个数列的项，数列的一般形式可以写成a a a a n ,,,,,123，简记为数列a n {}，其中第一项a 1也成为首项；a n 是数列的第n 项，也叫做数列的通项.数列可看作是定义域为正整数集*N （或它的子集）的函数，当自变量从小到大取值时，该函数对应的一列函数值就是这个数列.2、数列的分类：按数列中项的多数分为：（1）有穷数列：数列中的项为有限个，即项数有限；（2）无穷数列：数列中的项为无限个，即项数无限.3、通项公式：如果数列a n {}的第n 项a n 与项数n 之间的函数关系可以用一个式子表示成=a f n n ()，那么这个式子就叫做这个数列的通项公式，数列的通项公式就是相应函数的解析式.4、数列的函数特征：一般地，一个数列a n {}，如果从第二项起，每一项都大于它前面的一项，即>+a a n n 1，那么这个数列叫做递增数列;高一数学必修5：数列（知识点梳理）如果从第二项起，每一项都小于它前面的一项，即1n n a a +<，那么这个数列叫做递减数列; 如果数列的各项都相等，那么这个数列叫做常数列.5、递推公式：某些数列相邻的两项（或几项）有关系，这个关系用一个公式来表示，叫做递推公式．二、等差数列1、等差数列的概念：如果一个数列从第二项起，每一项与前一项的差是同一个常数，那么这个数列久叫做等差数列，这个常数叫做等差数列的公差.即1n n a a d +-=（常数），这也是证明或判断一个数列是否为等差数列的依据.2、等差数列的通项公式：设等差数列的首项为1a ，公差为d ，则通项公式为：()()()11,n m a a n d a n m d n m N +=+-=+-∈、.3、等差中项：（1）若a A b 、、成等差数列，则A 叫做a 与b 的等差中项，且=2a bA +; （2）若数列为等差数列，则12,,n n n a a a ++成等差数列，即1n a +是与2n a +的等差中项，且21=2n n n a a a +++；反之若数列满足21=2n n n a a a +++，则数列是等差数列.4、等差数列的性质：（1）等差数列中，若(),m n p q m n p q N ++=+∈、、、则m n p q a a a a +=+，若2m n p +=，则2m n p a a a +=；（2）若数列和{}n b 均为等差数列，则数列{}n n a b ±也为等差数列；（3）等差数列{}n a 的公差为d ，则{}0n d a >⇔为递增数列，{}0n d a <⇔为递减数列，{}0n d a =⇔为常数列.5、等差数列的前n 项和n S ：（1）数列{}n a 的前n 项和n S =()1231,n n a a a a a n N -++++++∈；（2）数列{}n a 的通项与前n 项和n S 的关系：11,1.,2n n n S n a S S n -=⎧=⎨-≥⎩（3）设等差数列{}n a 的首项为1,a 公差为d ，则前n 项和()()111=.22n n n a a n n S na d +-=+6、等差数列前n 和的性质：（1）等差数列{}n a 中，连续m 项的和仍组成等差数列，即12122,,m m m m a a a a a a ++++++++21223m m m a a a +++++,仍为等差数列（即232,,,m m m m m S S S S S --成等差数列）；（2）等差数列{}n a 的前n 项和()2111==,222n n n d d S na d n a n -⎛⎫++- ⎪⎝⎭当0d ≠时，n S 可看作关于n 的二次函数，且不含常数项；（3）若等差数列{}n a 共有2n+1（奇数）项，则()11==,n S n S S a S n++-奇奇偶偶中间项且若等差数列{}n a 共有2n （偶数）项，则1==.n nS a S S nd S a +-偶奇偶奇且7、等差数列前n 项和n S 的最值问题：设等差数列{}n a 的首项为1,a 公差为d ，则（1）100a d ><且（即首正递减）时，n S 有最大值且n S 的最大值为所有非负数项之和；（2）100a d <>且（即首负递增）时，n S 有最小值且n S 的最小值为所有非正数项之和.三、等比数列1、等比数列的概念：如果一个数列从第二项起，每一项与前一项的比是同一个不为零的常数，那么这个数列就叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母q 表示（0q ≠）.即()1n na q q a +=为非零常数，这也是证明或判断一个数列是否为等比数列的依据.2、等比数列的通项公式：设等比数列{}n a 的首项为1a ，公比为q ，则通项公式为：()11,,n n m n m a a qa q n m n m N --+==≥∈、.3、等比中项：（1）若a A b 、、成等比数列，则A 叫做a 与b 的等比中项，且2=A ab ; （2）若数列{}n a 为等比数列，则12,,n n n a a a ++成等比数列，即1n a +是与2n a +的等比中项，且212=n n n a a a ++⋅；反之若数列{}n a 满足212=n n n a a a ++⋅，则数列{}n a 是等比数列.4、等比数列的性质：（1）等比数列{}n a 中，若(),m n p q m n p q N ++=+∈、、、则m n p q a a a a ⋅=⋅，若2m n p +=，则2m n p a a a ⋅=；（2）若数列{}n a 和{}n b 均为等比数列，则数列{}n n a b ⋅也为等比数列；（3）等比数列{}n a 的首项为1a ，公比为q ，则{}1100101na a a q q ><⎧⎧⇔⎨⎨><<⎩⎩或为递增数列，{}1100011n a a a q q ><⎧⎧⇔⎨⎨<<>⎩⎩或为递减数列， {}1n q a =⇔为常数列.5、等比数列的前n 项和：（1）数列{}n a 的前n 项和n S =()1231,n n a a a a a n N -++++++∈；（2）数列{}n a 的通项与前n 项和n S 的关系：11,1.,2n n n S n a S S n -=⎧=⎨-≥⎩ （3）设等比数列{}n a 的首项为1a ，公比为()0q q ≠，则()11,1.1,11n n na q S a q q q=⎧⎪=-⎨≠⎪-⎩由等比数列的通项公式及前n 项和公式可知，已知1,,,,n n a q n a S 中任意三个，便可建立方程组求出另外两个.6、等比数列的前n 项和性质：设等比数列{}n a 中，首项为1a ，公比为()0q q ≠，则（1）连续m 项的和仍组成等比数列，即12122,,m m m m a a a a a a ++++++++21223m m m a a a +++++,仍为等比数列（即232,,,m m m m m S S S S S --成等差数列）；（2）当1q ≠时，()()11111111111111n n n n n a q a a a a aS q q q qq q q q q -==⋅-=-⋅=⋅-------，设11a t q =-，则n n S tq t =-.四、递推数列求通项的方法总结1、递推数列的概念：一般地，把数列的若干连续项之间的关系叫做递推关系，把表达递推关系的式子叫做递推公式，而把由递推公式和初始条件给出的数列叫做递推数列.2、两个恒等式：对于任意的数列{}n a 恒有：（1）()()()()12132431n n n a a a a a a a a a a -=+-+-+-++-（2）()23411231,0,nn n n a a a a a a a n N a a a a +-=⨯⨯⨯⨯⨯≠∈3、递推数列的类型以及求通项方法总结：类型一（公式法）：已知n S （即12()n a a a f n +++=）求n a ，用作差法：{11,(1),(2)n n n S n a S S n -==-≥类型二（累加法）：已知：数列的首项,且()()1,n n a a f n n N ++-=∈，求n a 通项.给递推公式()()1,n n a a f n n N ++-=∈中的n 依次取1,2,3，……，n-1,可得到下面n-1个式子：()()()()21324311,2,3,,1.n n a a f a a f a a f a a f n --=-=-=-=-利用公式()()()()12132431n n n a a a a a a a a a a -=+-+-+-++-可得：()()()()11231.n a a f f f f n =+++++-类型三（累乘法）：已知：数列的首项,且()()1,n na f n n N a ++=∈，求n a 通项. 给递推公式()()1,n na f n n N a ++=∈中的n 一次取1,2,3，……，n-1,可得到下面n-1个式子： ()()()()23412311,2,3,,1.nn a a aa f f f f n a a a a -====- 利用公式()23411231,0,nn n n a a a a a a a n N a a a a +-=⨯⨯⨯⨯⨯≠∈可得： ()()()()11231.n a a f f f f n =⨯⨯⨯⨯⨯-类型四（构造法）：形如q pa a n n +=+1、n n n q pa a +=+1（q p b k ,,,为常数）的递推数列都可以用待定系数法转化为公比为k 的等比数列后，再求n a 。

浅谈数列的函数特征

例２已知等比数列｛，３２求此数列的前５．ｊ口＝・～，项，
判断该数列从第几项开始小于００１．０７
时是等比数列，ａ＝１时＝０，数列为等差数列。三、巧妙利用数列的递推公式的结构特征。
解：通公得主：析由项式，ａ
ｉ素壹且，，，
（２，．）
（）求数列｛ｎ的通项公式；１ａ｝
（）证明：对于一切正整数ｎ，２Ｏ１－＋２特点，）
例３已知数列ａ｝．的通项公式＝２。９＋，求数列一ｎ＋ｎ３
｛｝的最大项。
解析：由通项公式ａ＝－ｎ２＋９＋３ａ是ｎ的二次函ｎ知ｎ
Ａ一定是等差数列Ｂ或是等差数列，或是等比数列Ｃ一定是等比数列Ｄ既不是等差数列，也不是等比数列解析：由等比数列等比数列的前ｎ项和公式特点得：ａ≠１
此数列是减数列（或增数列），该数列项的变化具有指数函数
的变化趋势。当ｑ０，此数列是摆动数列。时
１
ｎ－
— —
１
＝
，
：
（１）由
＝＋ —
等
差
数
列
的
求
和
公
式
ａｎ１
的指数型函数，所以等比数列项的变化具有指数函数的特征。暑．巍．当ｇ＞１，此数列是增数列（－时或减数列），当０ｑ－１，４时
例６已知数列ｊｎ项和Ｓ＝ｌ ≠０，．的前ａ一（）那么数ａ列｛（）｝
浅谈数列的函数特征

新教材2023版高中数学第一章数列1数列的概念及其函数特性1

故选ACD.
方法归纳
正确理解数列及相关概念，注意以下几点： (1)数列与数集不同，数集具有互异性和无序性，而数列中各项可以相同，但与顺序有关； (2)数列a1，a2，…，an，…可以记为{an}，但不能记作{a1，a2，…， an，…}.
跟踪训练1 (多选题)下列说法正确的是( )
A．数列{2n＋1}的第5项是10
2．在数列－1，0，19 ， 18，…，nn−22，…中0.08是它的(
)
A．第100项 B．第12项
C．第1nn−22. 令an＝0.08，即nn−22＝1080，所以n＝10或n＝52(舍去)，故选C.
3 ．已知数列 {an} 的通项公式为 an ＝ n2 － n ，则下列结论正确的是
例2 写出数列的一个通项公式，使它的前4项是下列各数：
(1)－1，12，－13
，
1；
4
(2) 3，3， 15， 21；
(3)0.9，0.99，0.999，0.999 9；
(4)3，5，3，5.
方法归纳
(1)据所给数列的前几项求其通项公式时，需仔细观察分析，抓住以下几方面的特征：
①分式中分子、分母的特征； ②相邻项的变化特征； ③拆项后的特征； ④各项符号特征等，并对此进行归纳、联想． (2)观察、分析数列中各项的特点是最重要的，观察出项与序号之间的关系、规律，利用我们熟知的一些基本数列(如自然数列、奇偶数列等)转换而使问题得到解决，对于正负符号变化，可用(－1)n或(－ 1)n＋1来调整．
变式探究本例中，数列{an}中有多少个负数项？
解析：an＝3n2－28n＝n(3n－28)，令an<0，则0<n<238，又n∈N＋，所以n＝1，2，3，4，5，6，7，8，9. 即数列{an}中共有9个负数项．

抓住函数特征探究数列本质

ｂｅｍｏｒｅｉｎｎｏｖａｔｉｖｅａｎｄｃｏｍｐｒｅｈｅｎｓｉｖｅ．Ｔｈｅｓｔｕｄｅｎｔｓｃｏｕｌｄａｃ — ｃｏｒｄｉｎｇｌｙｄｅｖｅｌｏｐｔｈｅｉｒａｂｉｌｉｔｉｅｓｏｆｈｉｔｎｋｉｎｇａｎｄｂｅｃｏｍｅｃｒｅａｔｉｖｅ．Ｋｅｙｗｏｒｄｓｐｏｐｒｅｒｔｙ；ｉｍａｇｅ；ｓｐｅｃｉｉｆｃｆｕｎｃｔｉｏｎｓ；ｂｓａｔｒａｃｔｆｕｎｃｔｉｏｎｓ；
摘要
数列是一种特殊的函数，在教学中，利用函数的特
上单调递增，在（
，＋ａ。）单调递减，而１２＜
：１
，＝
＜１３故
１３
：
征，去处理数列的问题，会具有更强的新意和综合性，能更有效地培养学生的思维品质和创新意识。关键词性质图像具体函数抽象函数特殊函数
１．２构造抽象函数，成功突围难点
例２：已知数列ｆａｒＩ｝满足ａ，￣ａ＝ａｎ＋２一ａｎ，ａ１＝１，则ｓ２００５＝
—
。
—
ｔｈｅｓｅｑｕｅｎｃｅｐｒｏｂｌｅｍｓｗｉｔｈｈｅｔｃｈａｒａｃｔｅｒｉｓｉｔｃｓｏｆｆｕｎｃｔｉｏｎｓｗｏｕｌｄ
：ａｌ＝１．

等差数列与等比数列的函数特征

等差数列与等比数列的函数特征作者：赵国栋来源：《神州·中旬刊》2013年第04期数列是高中数学中重要的知识章节，每年高考对这一章节均进行重点考查。

数列是定义在正整数集合上的离散函数。

若能把一些数列问题转化为函数知识解决，可以起到事半功倍的效果。

一. 等差数列的函数特征数列{an}是一个等差数列，公差为d，则通项公式■，从式子结构看，■是关于n的广义的一次函数，当d=0时，■为常数。

当d>0时，■是一个增函数，d例1，数列{an}是等差数列，■，■是其前n项之和，若■且■，试问n取何值时■最大？分析：■，则■又■，则■■ ■又■ ，■■是一个减函数，当■时，■最大。

例2，数列{an}是一个等差数列，■表示其前n项之和，若■，并且■，求■.分析：■，■∵■是一个二次函数，且由■可知，直线■是其图像的一条对称轴。

设■，该抛物线与x轴有一个交点为P（0，0），则P关于■的对称点为■，■例3，数列{an}是一个等差数列，■，当n取何值时■最小，并求出最小值。

解：■，■当n≤5时，an0当n=5时，■最小，此时s5=-25.二. 等比数列的函数特征{an}是一个等比数列，公比为q，则■，令■，则■.上式体现出an是一个类似指函数的形式，而它的前n项和■ ，当q≠1时，）■，以下举例说明。

例4，数列{an}是一个等比数列，它的前n项和■，求a的值。

分析：■，由上面讨论可知，a与3互为相反数，■.例5，设{an}是一个等比数列，■，求最小的自然数n，使■.分析：■■使得■成立的最小自然数为7.点评：数列是高中代数的重要内容，也是与大学衔接的内容，由于其在测试学生逻辑思维能力与推理能力方面的不可替代的作用，数列在历年高考中占据重要地位。

数列的认识和特征

数列的认识和特征数列是数学中的一个重要概念，广泛应用于各个领域。

本文将介绍数列的基本定义、分类以及一些常见的数列特征。

1. 数列的定义数列是按照一定规律排列的一组数，通常用{ }表示。

数列中的每一个数称为该数列的项，用a₁,a₂,a₃,...表示，其中a₁为第一项，a₂为第二项，以此类推。

2. 数列的分类根据数列的规律性质，数列可以分为等差数列、等比数列、递推数列等多种类型。

2.1 等差数列在等差数列中，任意两个相邻的项之间的差值是相等的。

设首项为a₁，公差为d，则等差数列可以表示为：a₁，a₁+d，a₁+2d，...2.2 等比数列在等比数列中，任意两个相邻的项之间的比值是相等的。

设首项为a₁，公比为r（r≠0），则等比数列可以表示为：a₁，a₁r，a₁r²，...2.3 递推数列递推数列是通过前一项或多项来确定后一项的数列。

递推数列没有明确的公式，但可以通过给定的初始项和递推关系来求解。

常见的递推数列有斐波那契数列、汉诺塔数列等。

3. 数列的特征通过对数列的观察和分析，我们可以得到数列的一些重要特征。

3.1 首项和公差（公比）对于等差数列，首项a₁和公差d是唯一确定数列的两个重要特征。

3.2 通项公式通项公式是一个能够表达数列第n项与n的关系的式子。

对于等差数列而言，通项公式可以表示为：aₙ = a₁ + (n-1)d。

对于等比数列而言，通项公式可以表示为：aₙ = a₁r^(n-1)。

3.3 求和公式求和公式是指数列的前n项和的公式。

对于等差数列而言，求和公式可以表示为：Sₙ = (n/2)(a₁+aₙ)。

对于等比数列而言，求和公式可以表示为：Sₙ = a₁(r^n-1)/(r-1)。

4. 应用举例数列的概念和特征在数学和实际问题中有很多应用。

例如，在数学中，数列可以用来描述函数的性质和行为；在物理中，数列可以用来描述粒子的运动轨迹；在经济学中，数列可以用来预测市场趋势等。

综上所述，数列是按照一定规律排列的一组数，并根据规律性质可以分为等差数列、等比数列和递推数列等不同类型。

北师大版高中数学选择性必修第二册第一章 1.2 数列的函数特性、递推公式

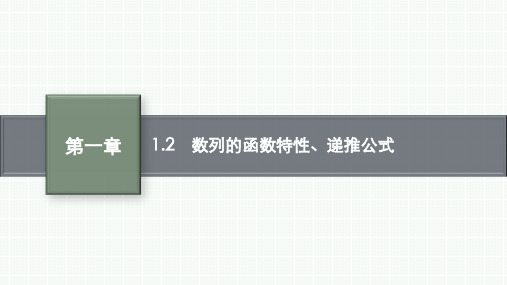
n
}是递增数列
n+1
答案 D
解析由数列的通项 an=
n
n+1
递增数列,故选 D.
知,an+1-an=
n+1
n+2
−
n
n+1
=
1
>0,即数列{
(n+2)(n+1)
n
n+1
}是
二、数列的递推公式
不是所有的数列
都能写出递推公式
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么
这个式子叫作这个数列的递推公式.
(2)作图如下:
由图知数列{bn}是递减数列.
反思感悟数列的单调性除了画出散点图进行判断外,还可以根据数列单调
性的定义,利用an+1与an的大小进行判断.
Байду номын сангаас
变式训练1已知数列{an}的通项公式为an=-n2+2n-2.画出数列{an}的图象,
并判断其单调性.
解作图如下:
由图知数列{an}为递减数列.
2 3

a1· · ·…· =an(n≥2,n∈N+)成立.试
1
2
-1

根据这一结论,完成问题:已知数列{an}满足:a1=1,
-1
数列{an}的通项公式.
=
-1
(n≥2,n∈N
+),求

解 (1)当 n≥2 时,
an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+2 + 2 + … + 2=2(n-1)+1=2n-1.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一是作差比较法.
(1)an+1-an>0⇔an+1>an⇔数列{an}是递增数列. (2)an+1-an<0⇔an+1<an⇔数列{an}是递减数列. (3)an+1-an=0⇔an+1=an⇔数列{an}是常数列.
二是作商比较法，若数列的通项公式为根式形式,用作商法
比作差法更简便一些.
a n 1 ＞1 an a 0＜ n 1 ＜ 1 an a n 1 1 an
断数列的单调性.
【规范解答】(1)f( 2 a )＝log2 2 a n -log
n
2
1 2=a －，所以 an n an
1 a n－＝2n⇒ an
－2nan－1＝0， a2 n
所以an＝ n n 2 1 . 因为x∈(0,1)，所以 2 a n ∈(0,1)，所以an<0.
所以an＝n－ n 2 1 .
径.
【例2】设函数f(x)＝log2x－logx2(0<x<1)，数列{an}).
n
(1)求数列{an}的通项公式； (2)判断数列的单调性.
【审题指导】解决本题的关键是把函数的解析式通过关系
式转化求解得到数列的通项公式，然后再根据通项公式进
行作差，判断与零的大小或者作商判断与 1的大小，从而判
方法二：由于本题数列的通项公式为an= 数是f(x)=
1 2
1 2 n -8n对应的函 2
x2-8x，定义域为正整数集，根据函数的单调性
可知：对称轴是x=8，所以当0<n<8时数列是递减数列；当 n≥8时，数列是递增数列.
数列的函数性质的应用数列的函数性质的应用数列是特殊的函数，由数列的项与项数之间构成特殊的函数关系可知：数列的通项an与n的关系公式就是函数f(x)的解析式,所以根据函数解析式得出数列的通项公式是重要途
a n＞0 a n＜0
递增数列递减数列
递减数列递增数列
常数列常数列
在利用作商比较法时，要确保数列的每一项都不是零，再确认相邻两项的正负，然后进行比较 .
【例1】已知数列{an}的通项公式为an= 1 n 2 -8n，判断数列
2
{an}的单调性.
【审题指导】解决本题的关键是正确采取比较的方式，比
n=-5
在利用二次函数的性质进行配方求解数列的第三问最值时，忽略了n只能取正整数这一问题，导致错误，一般地借助函数解决数列问题时，都需要认真考虑定义域.
n= 1 2
(3)an＝30＋n－n2＝－(n－ 1 ) 2＋121，
2 4
又∵n∈N+，故当n＝1时，an有最大值，其最大值为30. ………… 12分
【误区警示】对解答本题时易犯的错误具体分析如下：
常见
错误第二问
错误原因解出了n的值后，没有考虑n的定义域，直接下结论导致错误，事实上，解决这类问题需要特别注意n的取值范围.
较an+1与an的大小，也可用函数的观点判断.
【规范解答】方法一：根据题意可知 a n 1 n 2 8n，则 an+1-an= 1 (n+1)2-8(n+1)-( 1 n2-8n)
2 2
n 2
15 由数列的定义域为正整数集可知，当0<n<8时，， 2
an+1-an<0，数列是递减数列；当n≥8时，an+1-an>0，数列是递增数列.
(2)方法一：an＋1－an
＝(n＋1)－ n 12 1 (n n 2 1) ＝1－ ( n 12 1 n 2 1)
＝1－
2n 1
n 1
2
1 n2 1
1 －
2n 1 ＝0. n 1 n
所以 a n＋1 a n ，即数列{an}是递增数列. 方法二：∵ a n 1
丰城九中高一数学组
从数列表示的角度理解数列的函数特性
数列是一种特殊函数,其定义域是正整数集N+(或它的有限子集{ 1, 2, 3，…, n}) ,值域是当自变量顺次从小到大依次取值时的对应值.
0000
0000
确定数列的增减性确定数列的增减性的方法判断数列是递增数列还是递减数列,关键是比较相邻两项an+1 与an的大小,常见的比较方法有两种：
an n 1
n 1 1
2
n n2 1

n n2 1 n 1
n 1
2
1
1 ，
又∵an<0，∴an＋1>an， ∴数列{an}是递增数列.
【典例】(12分)一个数列的通项公式为an＝30＋n－n2.
(1)问－60是否为这个数列中的项？ (2)当n分别为何值时，an＝0，an>0，an<0； (3)当n为何值时，an有最大值，并求出最大值. 【审题指导】本题的解决关键是用函数的观点思考解决数列问题，三问逐步深入递进，首先第一问判断是否是数列的项，代入验证判断求出的n是否为正整数即可，第二问和第三问，结合二次函数进行判断求解.
【规范解答】(1)令30＋n－n2＝－60，
即n2－n－90＝0，
∴n＝10或n＝－9(舍)，…………………………………2分 ∴－60是这个数列的第10项，即a10＝－60. …………4分 (2)令30＋n－n2＝0，即n2－n－30＝0. ∴n＝6或n＝－5(舍)，即当n＝6时，an＝0. …………6分结合数列{an}的图像可知当n等于1,2,3,4,5时，an>0. 当n>6且n∈N+时，an<0. …………………………………8分

数列的函数特征