eviews时间序列分析实验
EVIEWS时间序列实验指导(上机操作说明)

⒉在工作文件窗口中选取所要删除或更名的变量,点击工作文件窗口菜单栏中的Objects/Delete selected…(Rename selected…),即可删除(更名)变量
进行预测:打开对应的方程窗口,点forecast按纽,将出现对话框,修改对话框 sample range for forecast中的时间期限的截止日期为预测期.
相对误差的计算公式为:(实际值-预测值)/实际值
二、单参数和双参数指数平滑法进行预测的操作练习
2、某地区1996~2003年的人口数据如表1.2,运用二次指数平滑法预测该镇2004年底的人口数(单位:人)。
掌握确定性时间序列建立模型的几种常用方法。
【实验内容】
一、多项式模型和加权最小二乘法的建立;
二、单参数和双参数指数平滑法进行预测的操作练习;
三、二次曲线和对数曲线趋势模型建立及预测;
【实验步骤】
一、多项式模型和加权最小二乘法的建立;
1、我国1974—1994年的发电量资料列于表中,已知1995年的发电量为10077.26亿千瓦小时,试以表1.1中的资料为样本:
建立系列方程:smpl 1974 1994
ls y c t
ls y c t t^2
ls y c t t^2 t^3
通过拟合优度和外推检验的结果发现一元三次多项式模型效果最好。
首先生成权数序列:genr m=sqr(0.6^(21-t))
加权最小二乘法的命令方式:ls(w=m) y c t
普通最小二乘法命令方式:ls y c t
步骤:(1)打开该文件。
时间序列分析应用实例(使用Eviews软件实现)

时间序列分析应⽤实例(使⽤Eviews软件实现)引⾔某公司的苹果来货量数据是以时间先后为顺序记录的⼀组数据,从计量经济学的⾓度来分类就是⼀组时间序列数据。
为了提⾼苹果来货量预测的准确度以及预测结果的可信度,下⾯运⽤Eviews软件包(即Econometrics Views 计量经济学软件包)并结合计量经济学的理论知识,选取2017年1⽉⾄2019年4⽉的苹果来货量⽉度数据(事前对原始数据进⾏处理,把数值单位从吨转换为万吨)为样本数据,⽤⼀个时间序列模型来拟合上述样本数据,然后利⽤建⽴好的模型预测苹果未来⼏个⽉的来货量情况,并对预测结果进⾏分析。
1 平稳性检验1.1 初步检验设来货量时间序列为Qt,⾸先观察Qt的折线图,如图1所⽰:图1 Qt的折线图从图1可知,苹果来货量的⽉度数据总体呈下降趋势,并存在季节性因素,进⽽通过序列原⽔平的⾃相关系数图进⼀步探讨序列的平稳性,结果如图2所⽰:图2 Qt的⾃相关系数图从图2可以看到,所有的⾃相关系数(Autocorrelation)均落在2倍标准差之内(垂⽴的两道虚线表⽰2倍标准差),初步判定序列Qt是平稳的。
下⾯运⽤ADF单位根检验法证明序列的平稳性。
1.2 ADF单位根检验假设序列Qt的特征⽅程存在多个特征根,那么序列平稳的条件为所有特征根λi的绝对值均⼩于1,即所有特征根都在单位圆内。
构造该ADF 检验的原假设H0:存在i,使得λi>1,备择假设H1:λ1, λ2, … , λp<1,运⽤Eviews软件对序列Qt的原⽔平进⾏带常数项(Intercept)的ADF检验,采⽤SC准则⾃动选择滞后阶数,检验结果如图3所⽰:图3 ADF检验根据图3的检验结果可知,t统计量(t-Statistic)的伴随概率p为0.00,在显著性⽔平α=0.05下,因此我们有理由拒绝原假设(p<α),说明序列Qt是平稳的。
2 模型识别从图2可知,序列Qt的⾃相关系数(Autocorrelation)和偏⾃相关系数(Partial correlation)均在阶数1处突然衰减为在零附近⼩值波动,因此我们初步选择AR(1)、ARMA(1,1)这两个模型拟合样本数据3 模型参数估计3.1 AR(1)模型的拟合与参数估计设AR(1)模型为:Qt=C + Φ*Qt-1 +εt,其中C为常数项,Φ为待估计的Qt滞后⼀阶的系数,εt为服从均值为零、⽅差为常数正态分布的正态分布(即⽩噪声序列),下⾯运⽤Eviews软件对AR(1)模型的参数采⽤最⼩⼆乘估计法(⽆偏估计)进⾏参数估计,模型估计结果如图4所⽰:图4 AR(1)模型拟合结果根据图4的参数估计结果来看,在显著性⽔平α=0.05下,常数项显著不为零,⽽参数Φ的显著性估计结果并不是太好,另外AR(1)模型的特征⽅程的根(Inverted AR Roots)为-0.16,印证了序列Qt是平稳的。
Eviews时间序列分析报告实例

Eviews时间序列分析实例时间序列是市场中经常涉与的一类数据形式,本书第七章对它进展了比拟详细的介绍。
通过第七章的学习,读者了解了是时间序列,并接触到有关时间序列分析方法的原理和一些分析实例。
本节的主要内容是说明如何使用Eviews软件进展分析。
一、指数平滑法实例所谓指数平滑实际就是对历史数据的加权平均。
它可以用于任何一种没有明显函数规律,但确实存在某种前后关联的时间序列的短期。
由于其他很多分析方法都不具有这种特点,指数平滑法在时间序列中仍然占据着相当重要的位置。
〔-〕一次指数平滑一次指数平滑又称单指数平滑。
它最突出的优点是方法非常简单,甚至只要样本末期的平滑值,就可以得到结果。
一次指数平滑的特点是:能够跟踪数据变化。
这一特点所有指数都具有。
过程中添加最新的样本数据后,新数据应取代老数据的地位,老数据会逐渐居于次要的地位,直至被淘汰。
这样,值总是反映最新的数据结构。
一次指数平滑有局限性。
第一,值不能反映趋势变动、季节波动等有规律的变动;第二,这种方法多适用于短期,而不适合作中长期的;第三,由于值是历史数据的均值,因此与实际序列的变化相比有滞后现象。
指数平滑是否理想,很大程度上取决于平滑系数。
Eviews提供两种确定指数平滑系数的方法:自动给定和人工确定。
选择自动给定,系统将按照误差平方和最小原如此自动确定系数。
如果系数接近1,说明该序列近似纯随机序列,这时最新的观测值就是最理想的值。
出于的考虑,有时系统给定的系数不是很理想,用户需要自己指定平滑系数值。
平滑系数取值比拟适宜呢?一般来说,如果序列变化比拟平缓,平滑系数值应该比拟小,比如小于0.l;如果序列变化比拟剧烈,平滑系数值可以取得大一些,如0.3~0.5。
假如平滑系数值大于0.5才能跟上序列的变化,明确序列有很强的趋势,不能采用一次指数平滑进展。
[例1]某企业食盐销售量。
现在拥有最近连续30个月份的历史资料〔见表l〕,试下一月份销售量。
表1 某企业食盐销售量单位:吨解:使用Eviews对数据进展分析,第一步是建立工作文件和录入数据。
时序分析实验报告
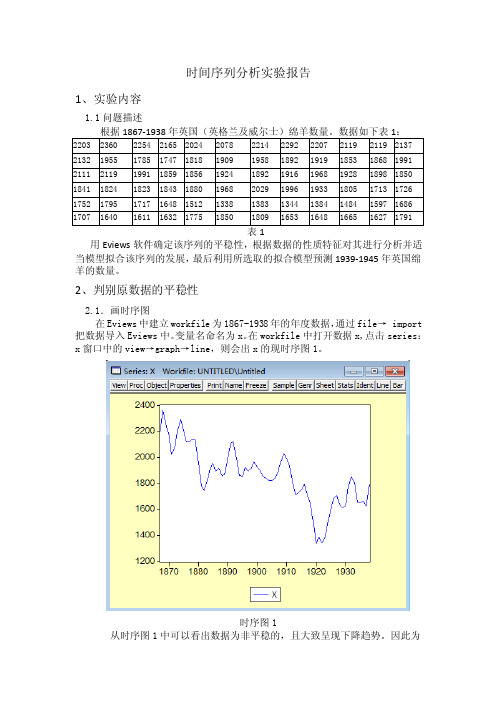
时间序列分析实验报告1、实验内容1.1问题描述用Eviews软件确定该序列的平稳性,根据数据的性质特征对其进行分析并适当模型拟合该序列的发展,最后利用所选取的拟合模型预测1939-1945年英国绵羊的数量。
2、判别原数据的平稳性2.1.画时序图在Eviews中建立workfile为1867-1938年的年度数据,通过file→ import 把数据导入Eviews中。
变量名命名为x。
在workfile中打开数据x,点击series:x窗口中的view→graph→line,则会出x的现时序图1。
时序图1从时序图1中可以看出数据为非平稳的,且大致呈现下降趋势。
因此为经一步说明该数据的平稳性,做相关分析。
2.2.自相关分析继续在该时序图窗口中点击view→correlogram,在弹出的correlogram Specification 的对话框中的lags to include中输入12,点击OK。
则x的自相关图2如下。
自相关图2从自相关图的autocorrelation的一栏可以看出自相大部分都关超出了(至少第三个自相关值要落入两倍的标准差中则为平稳的)两倍的标准差。
则可以进一步认为该数据为非平稳的。
为作出最终的判断,对数进行单位根检验。
2.3.单位根检验同样在自相关图2的窗口中点击view→unit root test在弹出的unit root test 的对话空中的automatic selection的下拉框中选择Schwarz Info,并在Include in test equation中选择intercept点击ok则有如下结果输出单位根表3。
单位根表3从表3中以看所有的ADF值没有都小于值临界值,因此结合时序图和自相关图可以判断出该数据为非平稳的。
3、对数据进行平稳化3.1.对数据做一阶差分在代码窗口中输入genr dx=d(x)并按回车键则在workfile窗体中新生成变量为dx的数据该数据即为x的一阶差分。
eviews时间序列分析实验Word版

实验一ARMA 模型建模一、实验目的学会检验序列平稳性、随机性。
学会分析时序图与自相关图。
学会利用最小二乘法等方法对ARMA 模型进行估计,以及掌握利用ARMA 模型进行预测的方法。
学会运用Eviews 软件进行ARMA 模型的识别、诊断、估计和预测和相关具体操作。
二、基本概念 1 平稳时间序列:定义:时间序列{zt}是平稳的。
如果{zt}有有穷的二阶中心矩,而且满足:(a )ut= Ezt =c;(b )r(t,s) = E[(zt-c)(zs-c)] = r(t-s,0) 则称{zt}是平稳的。
2 AR 模型:AR 模型也称为自回归模型。
它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测。
具有如下结构的模型称为P 阶自回归模型,简记为AR(P)。
⎪⎪⎪⎪⎨⎧<∀=≠===≠+++++=---ts Ex t s E Var E x x x x t s s t t t p t p t p t t t ,0,0)(,)(,0)(0222110εεεσεεφεφφφφε3 MA 模型:MA 模型也称为滑动平均模型。
它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。
具有如下结构的模型称为Q 阶移动平均回归模型,简记为MA(q)。
4 ARMA 模型:ARMA 模型:自回归模型和滑动平均模型的组合, 便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA 。
具有如下结构的模型称为自回归移动平均回归模型,简记为ARMA(p,q)。
112220()0(),()0,t t t t q t q q t t t s x E Var E s t εμεθεθεθεθεεσεε---⎧=+----⎪≠⎨⎪===≠⎩,⎪⎪⎪⎪⎨⎧<∀=≠===≠≠---++++=----ts Ex t s E Var E x x x t s s t t t q p q t q t t p t p t t ,0,0)(,)(,0)(0,0211110εεεσεεθφεθεθεφφφε三、实验内容及要求 1 实验内容:(1)根据时序图判断序列的平稳性;(2)观察相关图,初步确定移动平均阶数q 和自回归阶数p ;2 实验要求:(1)深刻理解平稳性的要求以及ARMA 模型的建模思想;(2)如何通过观察自相关,偏自相关系数及其图形,利用最小二乘法,以及信息准则建立合适的ARMA 模型;如何利用ARMA 模型进行预测;(3)熟练掌握相关Eviews 操作,读懂模型参数估计结果。
时间序列计量经济学模型实证分析(EVIEWS篇)

时间序列计量经济学模型实证分析(EVIEWS篇)时间序列计量经济学模型实证分析(EVIEWS篇)0、预备知识:建立工作文件:打开Eviews,,Workfile,确定数据类型,起止时间,ok。
输入数据:在Workfile工作框中,objects,New object,Series,输入变量名,ok,出现数据编辑框,,Edit+/-,即可开始输入数据。
OLS估计参数:(1)在Workfile工作框中,选中相关变量,点右键,Open,as Equation,注意估计对话框中的变量顺序,变量间空一格,估计方法的选择。
或(2)在主菜单中Quick,Estimate Equation。
什么?这些你都不知道,那算了。
出门左拐去百度视频看T om和Jerry吧,少年。
1、平稳性的单位根检验:选中需要进行检验的数据(单个变量),双击,view,URT(unit root test),ADF;(水平数据)Level;trend and intercept,automatic selection,AIC,maximum (10啊5啊都可以);看结果AIC,然后试试intercept或者none,选AIC最小的,为最终结果;拷出来,看ADF的t值是不是都小于1%5%10%的临界值(主要5%),不是就接受零假设,认为存在单位根,是非平稳的,需要进行一阶差分。
(然后一阶差分)1st difference;trend and intercept,automatic selection,AIC,maximum (10啊5啊都可以);看结果AIC,然后试试intercept或者none,选AIC最小的,为最终结果;拷出来,看ADF的t值是不是都小于1%5%10%的临界值(主要5%),是就拒绝零假设,认为不存在单位根,是平稳的,没有必要进行二阶差分。
如果是一阶平稳的,在eviews命令栏中输入“genr d什么=d (什么)”,引入一阶差分变量,进行下步检验。
时间序列_实验报告

一、实验目的1. 了解时间序列分析的基本原理和方法;2. 掌握时间序列数据的平稳性检验、模型识别和参数估计等基本操作;3. 通过实例,学习使用ARIMA模型进行时间序列预测。
二、实验环境1. 操作系统:Windows 102. 软件环境:EViews 9.0、R3.6.1三、实验数据1. 数据来源:某城市1980年1月至2020年12月每月的GDP数据;2. 数据格式:Excel表格。
四、实验步骤1. 数据预处理(1)导入数据:将Excel表格中的GDP数据导入EViews软件;(2)观察数据:绘制GDP时间序列图,观察数据的趋势、季节性和周期性;(3)平稳性检验:使用ADF检验判断GDP序列是否平稳。
2. 模型识别(1)自相关函数(ACF)和偏自相关函数(PACF)图:观察ACF和PACF图,初步确定ARIMA模型的阶数;(2)模型选择:根据ACF和PACF图,选择合适的ARIMA模型。
3. 模型估计(1)模型估计:使用EViews软件中的ARIMA过程,对选择的模型进行参数估计;(2)模型检验:对估计出的模型进行残差检验,包括残差的平稳性检验、白噪声检验等。
4. 时间序列预测(1)预测:使用估计出的ARIMA模型,对2021年1月至2025年12月的GDP进行预测;(2)预测结果分析:对预测结果进行分析,评估预测的准确性。
五、实验结果与分析1. 数据预处理(1)导入数据:将Excel表格中的GDP数据导入EViews软件;(2)观察数据:绘制GDP时间序列图,发现GDP序列存在明显的上升趋势和季节性;(3)平稳性检验:使用ADF检验,发现GDP序列在5%的显著性水平下拒绝原假设,序列是平稳的。
2. 模型识别(1)自相关函数(ACF)和偏自相关函数(PACF)图:根据ACF和PACF图,初步确定ARIMA模型的阶数为(1,1,1);(2)模型选择:根据ACF和PACF图,选择ARIMA(1,1,1)模型。
实验二 EVIEWS中时间序列相关函数操作

实验二 EVIEWS中时间序列相关函数操作【实验目的】熟悉Eviews的操作:菜单方式,命令方式;练习并掌握与时间序列分析相关的函数操作。
【实验内容】一、EViews软件的常用菜单方式和命令方式;二、各种常用差分函数表达式;三、时间序列的自相关和偏自相关图与函数;【实验步骤】一、EViews软件的常用菜单方式和命令方式;㈠创建工作文件⒈菜单方式启动EViews软件之后,进入EViews主窗口在主菜单上依次点击File/New/Workfile,即选择新建对象的类型为工作文件,将弹出一个对话框,由用户选择数据的时间频率(frequency)、起始期和终止期。
选择时间频率为Annual(年度),再分别点击起始期栏(Start date)和终止期栏(End date),输入相应的日期,然后点击OK按钮,将在EViews软件的主显示窗口显示相应的工作文件窗口。
工作文件窗口是EViews的子窗口,工作文件一开始其中就包含了两个对象,一个是系数向量C(保存估计系数用),另一个是残差序列RESID(实际值与拟合值之差)。
⒉命令方式在EViews软件的命令窗口中直接键入CREATE命令,也可以建立工作文件。
命令格式为:CREATE 时间频率类型起始期终止期则菜单方式过程可写为:CREATE A 1985 1998㈡输入Y、X的数据⒈DATA命令方式在EViews软件的命令窗口键入DATA命令,命令格式为:DATA <序列名1> <序列名2>…<序列名n>本例中可在命令窗口键入如下命令:DATA Y X⒉鼠标图形界面方式在EViews软件主窗口或工作文件窗口点击Objects/New Object,对象类型选择Series,并给定序列名,一次只能创建一个新序列。
再从工作文件目录中选取并双击所创建的新序列就可以展示该对象,选择Edit+/-,进入编辑状态,输入数据。
㈢生成log(Y)、log(X)、X^2、1/X、时间变量T等序列在命令窗口中依次键入以下命令即可:GENR LOGY=LOG(Y)GENR LOGX=LOG(X)GENR X1=X^2GENR X2=1/XGENR T=@TREND(84)㈣选择若干变量构成数组,在数组中增加变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一ARMA 模型建模
一、实验目的
学会检验序列平稳性、随机性。
学会分析时序图与自相关图。
学会利用最小二乘法等方法对ARMA 模型进行估计,以及掌握利用ARMA 模型进行预测的方法。
学会运用Eviews 软件进行ARMA 模型的识别、诊断、估计和预测和相关具体操作。
二、基本概念 1 平稳时间序列:
定义:时间序列{zt}是平稳的。
如果{zt}有有穷的二阶中心矩,而且满足: (a )ut= Ezt =c;
(b )r(t,s) = E[(zt-c)(zs-c)] = r(t-s,0) 则称{zt}是平稳的。
2 AR 模型:
AR 模型也称为自回归模型。
它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测。
具有如下结构的模型称为P 阶自回归模型,简记为AR(P)。
⎪
⎪⎩⎪⎪
⎨⎧<∀=≠===≠+++++=---t s Ex t s E Var E x x x x t s s t t t p t
p t p t t t ,0,0)(,)(,0)(02
22110εεεσεεφεφφφφε
3 MA 模型:
MA 模型也称为滑动平均模型。
它的预测方式是通过过去的干扰值和现
在的干扰值的线性组合预测。
具有如下结构的模型称为Q 阶移动平均回归模型,简记为
MA(q)。
11222
0()0(),()0,t t t t q t q q t t t s x E Var E s t εμεθεθεθεθεεσεε---⎧=+----⎪
≠⎨⎪===≠⎩,
4 ARMA 模型:
ARMA 模型:自回归模型和滑动平均模型的组合, 便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA 。
具有如下结构的模型称为自回归移动平均回归模型,简记为ARMA(p,q)。
⎪
⎪⎩⎪⎪
⎨⎧<∀=≠===≠≠---++++=----t s Ex t s E Var E x x x t s s t t t q p q
t q t t p t p t t ,0,0)(,)(,0)(0,02
11110εεεσεεθφεθεθεφφφε
三、实验内容及要求 1 实验内容:
(1)根据时序图判断序列的平稳性;
(2)观察相关图,初步确定移动平均阶数q 和自回归阶数p ;
2 实验要求:
(1)深刻理解平稳性的要求以及ARMA 模型的建模思想;
(2)如何通过观察自相关,偏自相关系数及其图形,利用最小二乘法,以及信息准则建立合适的ARMA 模型;如何利用ARMA 模型进行预测; (3)熟练掌握相关Eviews 操作,读懂模型参数估计结果。
四、实验指导 1 数据录入
首先用命令series x = nrnd 生成一个500个白噪声序列。
然后利用excel 生成一个平稳序列如图1所示,其中设定方程为X(t) = *X(t-1)+*X(t-2)+ε(t)。
图1
2 绘制序列时序图
双击打开series y 。
选择View—Graph—Line & Symbol。
得到的时序图如下所示:
图2
从图2中可以看出序列为平稳序列,但是仍需进一步验证。
3 模型定阶及参数估计:
对于ARMA(p,q) 模型,可以利用其样本的自相关函数和样本的偏自相关函数的截尾性判定模型的阶数。
若平稳时间序列的偏相关函数是截尾的,而自相关函数是拖尾的,则可断定此序列适合AR 模型; 若平稳时间序列的偏相关函数是拖尾的,而自相关函数是截尾的,则可断定此序列适合MA 模型;若平稳时间序列的偏相关函数和自相关函数均是拖尾的,则此序列适合ARMA 模型。
(1)绘制时序相关图
首先绘制y的相关图如图3所示。
从图3中可以看出,自相关明显拖尾,偏自相关明显截尾,故考虑使用AR模型。
图3
(2)ADF检验序列的平稳性
图4
由图4表明拒绝存在一个单位根的原假设,序列平稳。
(3)模型定阶:
在序列工作文件窗口点击View/Descriptive Statistics/Histogram and States对原序列做描述统计分析见图5。
图5
(3)模型参数估计:
根据偏自相关的截尾性,首先尝试AR模型。
在主菜单选择Quick/Estimate Equation,出现图2-10的方程定义对话框,在方程定义空白区键入x ar(1) ar(2) ar(3) 。
模型估计结果和相关诊断统计量见图6。
图6
根据图6中的模型估计结果和相关诊断统计量,可以明显的看出AR(1),AR(2)高度显著,AR(3)不显著。
切AIC,SC,DW等指标均表明模型拟合度很好。
所以得到的自相关回归模型如下:X(t) = *X(t-1)+*X(t-2)+ε(t)。
