生存分析及COX回归
cox回归分析

生存分析之COX回归分析1、生存分析,就是将终点事件出现与否与对应时间结合起来分析得一种统计方法;2、生存时间,就是从规定得观察起点到某一特定终点事件出现得时间,如膀胱癌术后5年存活率研究,及膀胱癌手术为观测起点,死亡为事件终点,两点为生存时间;3、完全数据,观测起点到终点事件所经历得时间,上述例子即膀胱癌手术到因膀胱癌死亡得时间;4、删失数据,因失访、研究结束终点事件未发生或患者死于规定得终点事件以外得原因而终止观察,不能确定具体生存时间得一类数据;5、生存概率,表示某时段开始存活得个体到该时段结束仍存活得概率,p=活满某时段得人数/该时段期初有效人口数;6、生存率,为观察起点起到研究时间点内各个时段得生存概率得累积概率,S(tk)=p1、p2、pk=S(tk-1)、pk;7、生存曲线,以生存时间为横轴,将各个时间点得生存率连在一起得曲线图;8、中位生存期,又称半数生存期,表示50%得个体存活得时间;9、PH假定(等比例风险假定),某研究因素对生存得影响不随时间得改变而改变,就是COX回归模型建立得前提条件。
Cox回归分析及其SPSS操作方法概述前面我们已经讲过生存分析及KM法得内容,详细可以回复数字26-28查瞧。
但有对统计不太熟悉得“微粉”还不太明白生存分析与一般统计得区别,不知道如何区别Cox回归与Logistic回归。
在我们做研究时,有时我们不仅关心某种结局就是否出现,还会关心结局出现得时间,例如肺部手术后观察五年生存率,一个有在1年之后死亡,另外一个人在在4、5后死亡,如果只瞧第5年时得结局,两者就是一样得(均死亡),但就是实际我们认为后者得治疗效果可能优于前者,即生存分析同时考虑结局与结局出现得时间,而一般分析只考虑结局。
另外在队列随访时,可能有人在没有到5年时就失访了,如迁徙或者电话更改,我们不了解其结局如何,在一般得分析中这种病例无法使用,而中间失访得病例结局可能更差,如果直接扔掉,可能会产生偏倚;而用生存分析,这种病例可以给我们提供部分资料,即我们记录最后一次随访时病例得状态,失访前得资料可以用于分析。
生存分析与Cox回归解析

流行病与卫生统计学教研室 曹 明 芹
生存分析与Cox回归
生存资料概述
生存分析的基本概念 生存资料的统计描述 生存曲线的比较 Cox回归
2018/10/24
生存分析与Cox回归
2
一、生存资料概述
举例 某医师分别用中药、西药各治疗急性肝炎病人 40例,结果如下表,试问:哪种药物的治疗效果好?
2018/10/24
生存分析与Cox回归
4
一、生存资料概述
医学随访研究一般有两种
所有研究对象同时进入研究(观察起始时间相同)
例如,队列研究、动物的随访观察
被研究对象逐个进入研究(观察起始时间不同)
例如,临床随访研究
由于受经费和时间的限制,最终观察时间不能无限延长
2018/10/24
生存分析与Cox回归
2018/10/24
生存分析与Cox回归
19
3. 生存资料的数据形式
10年间346例大肠癌患者手术后的生存时间 患者编号 性别 年龄(岁) dtime 结局 生存时间(月) 1 1 32 10 1 11 2 2 48 12 0 10 3 2 26 6 1 37 4 1 55 3 0 25 5 2 58 8 0 9 … … … … … …
② 可用于时间未分组的资料,也可用于时间分组资料
③ 各组间生存时间的比较根据各组生存曲线的高低及中位生存时 间判断 ④ 需满足生存资料的基本要求,且各样本生存曲线不能交叉 ⑤ 生存曲线若出现交叉,则提示可能存在混杂因素,应采用分层
对数秩检验或Cox比例风险回归模型进行分析
2018/10/24
生存分析与Cox回归
1. 基本概念
完全数据提供了观察对象确切的生存时间,是生存分
Cox回归模型【生存分析】

Cox回归模型【⽣存分析】参考:《复杂数据统计⽅法——基于R的应⽤》吴喜之在⽣存分析中,研究的主要对象是寿命超过某⼀时间的概率。
还可以描述其他⼀些事情发⽣的概率,例如产品的失效、出狱犯⼈第⼀次犯罪、失业⼈员第⼀次找到⼯作、青少年第⼀次吸毒等等。
⽣存函数S(t):S(t)=P(T>t)=1-P(T<=t),t>0T:表⽰寿命的随机变量t:特定时间综合⽣存函数图:⽤到包survival案例:⼝腔癌数据实验分成两组:TX=1:仅放疗TX=2:放疗+化疗#读取数据u=read.csv("pharynx1.csv")#因⼦化定性变量x=1:11(x=x[-c(5,11)]) #去掉第五个和第11个(定性变量的下标)for(i in x) u[,i]=factor(u[,i]) #把定性变量从数值型转换成因⼦型#回归分析a=lm(TIME~.,data=u)summary(a)R2和调整R2不⾼,结果不理想。
同时正态性条件不满⾜,所以检验得到的p-值也没有多⼤意义。
对TIME做指数变换,Box-Cox变换是统计建模中常⽤的⼀种数据变换,⽤于连续的响应变量不满⾜正态分布的情况。
MASS包中的boxcox()函数可以寻找λ。
#BOX-COX变换library(MASS)b=boxcox(TIME~.,data=u)I=which(b$y==max(b$y)) #which⽤于找到值在数组中的位置使对数似然最⼤的λ位置b$x[I]尝试⽤TIME的0.4次⽅作为因变量来拟合数据a=lm(TIME^0.4~INST+SEX+TX+AGE+COND+T.STAGE+N.STAGE+STATYS,data=u)b=step(a)summary(b)anova(b)shapiro.test(b$res)拟合并不好。
cox回归分析

生存分析之COX回归分析1.生存分析,是将终点事件出现与否与对应时间结合起来分析的一种统计方法;2.生存时间,是从规定的观察起点到某一特定终点事件出现的时间,如膀胱癌术后5年存活率研究,及膀胱癌手术为观测起点,死亡为事件终点,两点为生存时间;3.完全数据,观测起点到终点事件所经历的时间,上述例子即膀胱癌手术到因膀胱癌死亡的时间;4.删失数据,因失访、研究结束终点事件未发生或患者死于规定的终点事件以外的原因而终止观察,不能确定具体生存时间的一类数据;5.生存概率,表示某时段开始存活的个体到该时段结束仍存活的概率,p=活满某时段的人数/该时段期初有效人口数;6.生存率,为观察起点起到研究时间点内各个时段的生存概率的累积概率,S(tk)=p1.p2.pk=S(tk-1).pk;7.生存曲线,以生存时间为横轴,将各个时间点的生存率连在一起的曲线图;8.中位生存期,又称半数生存期,表示50%的个体存活的时间;9.PH假定(等比例风险假定),某研究因素对生存的影响不随时间的改变而改变,是COX回归模型建立的前提条件。
1.Cox回归分析及其SPSS操作方法概述前面我们已经讲过生存分析及KM法的内容,详细可以回复数字26-28查看。
但有对统计不太熟悉的“微粉”还不太明白生存分析与一般统计的区别,不知道如何区别Cox回归与Logistic回归。
在我们做研究时,有时我们不仅关心某种结局是否出现,还会关心结局出现的时间,例如肺部手术后观察五年生存率,一个有在1年之后死亡,另外一个人在在4.5后死亡,如果只看第5年时的结局,两者是一样的(均死亡),但是实际我们认为后者的治疗效果可能优于前者,即生存分析同时考虑结局和结局出现的时间,而一般分析只考虑结局。
另外在队列随访时,可能有人在没有到5年时就失访了,如迁徙或者电话更改,我们不了解其结局如何,在一般的分析中这种病例无法使用,而中间失访的病例结局可能更差,如果直接扔掉,可能会产生偏倚;而用生存分析,这种病例可以给我们提供部分资料,即我们记录最后一次随访时病例的状态,失访前的资料可以用于分析。
【统计学】生存分析和COX回归

小样本资料的乘积极限法 (Kaplan-Meier法 )
例14-4 某医师对11例脑瘤患者用甲法治疗,另9例脑瘤患者用 乙法治疗试估计两法的生存率,并比较两种疗法的生存率有无 差别。
甲法组:5 7* 13 13 23 30 30* 38 42 42 45*
乙法组:1 3 3 7 10 15 15 23 30
2020/11/19 Thursday
10
data ex14_1; do group='A','B'; input n; do i=1 to n; input t ; if t<0 then censor=0; else censor=1; t=abs(t); output; end; end; cards;
Stratum 1: group = A
Product-Limit Survival Estimates
t Survival 生存时间 生存率
数据为删失数据、截尾数据、终检数据(censored data)
2020/11/19 Thursday
。
1
❖生存率(survival rate) 又称累积生存概率,即个体活过时点t 的概率,用S(t)表示。
❖
如果没有删失数据,生存率可以直接估计。
S (t )
t时刻存活的观察例数 期初总观察例数
如果有删失数据,则要分时段估计每个时段的生存概率pi(i=1,2,…,t),然后 根据概率乘法原理估计累积生存概率。
[ freq <变量名>;] /*指定频数变量名 */
PROC过程[选项]
1.method=方法 /*指定估计生存率所用的方法:*/
生存分析-cox回归与sas应用总结x

生存分析的应用场景
01
02
03
医学研究
在临床试验和流行病学研 究中,生存分析用于评估 患者的生存时间,探究疾 病进展和治疗效果。
生物学研究
在生物学和生物医学研究 中,生存分析用于研究生 物体的寿命、疾病发生和 种群动态。
经济学研究
在经济学领域,生存分析 用于研究企业的寿命、市 场退出和产业动态等。
比例风险假设
Cox回归模型要求满足比例风险假设,即风险函数 的比例不随时间变化。
数据完整性
数据需要完整,包括每个观察对象的结局和生存 时间。
独立性
自变量之间需要满足独立性条件,避免多重共线 性问题。
Cox回归模型在生存分析中的重要性
广泛应用
Cox回归模型是生存分析 中最常用的方法之一,适 用于多种生物医学和工程 领域。
• 多模态数据融合:未来的研究可以探索如何将不同来源和类型的数据进行融合 ,以提高生存分析的精度和预测能力。例如,可以将基因组学、影像学等多模 态数据与临床数据相结合,以更全面地了解疾病进展和预后。
• 个性化治疗:随着精准医学的发展,未来的研究可以关注如何利用生存分析的 方法来评估个性化治疗的效果,为患者提供更精准的治疗方案。
PHREG过程用于执行 Cox比例风险回归模型, 用于分析生存时间数据 并评估协变量的影响。
LIFETEST过程可用于估 计生存函数、计算生存 时间的中位数和进行生
存比较等。
使用SAS进行Cox回归的步骤与示例
导入数据
01 使用SAS的数据导入功能将数
据加载到适当的SAS数据集中 。
数据清理和预处理
未来研究方向与展望
• 改进模型:针对Cox回归的限制,未来研究可以探索改进的模型和方法,以提 高生存分析的准确性和适用性。例如,可以考虑使用半参数模型、混合效应模 型等其他方法来处理生存数据。
cox回归生存分析在stata中实现
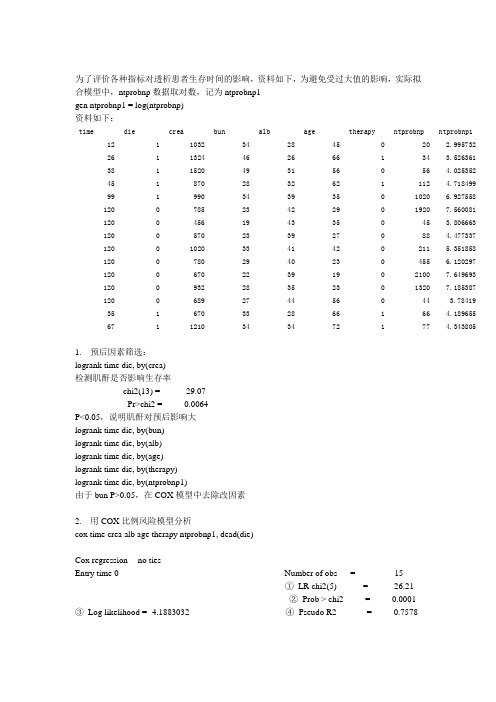
为了评价各种指标对透析患者生存时间的影响,资料如下,为避免受过大值的影响,实际拟合模型中,ntprobnp数据取对数,记为ntprobnp1gen ntprobnp1 = log(ntprobnp)资料如下:time die crea bun alb age therapy ntprobnp ntprobnp112 1 1032 34 28 45 0 20 2.99573226 1 1324 46 26 66 1 34 3.52636138 1 1520 49 31 56 0 56 4.02535245 1 870 28 32 62 1 112 4.71849999 1 990 34 39 35 0 1020 6.927558120 0 785 23 42 29 0 1920 7.560081 120 0 456 19 43 35 0 45 3.806663 120 0 570 23 39 27 0 88 4.477337 120 0 1020 33 41 42 0 211 5.351858 120 0 780 29 40 23 0 455 6.120297 120 0 670 22 39 19 0 2100 7.649693 120 0 932 28 35 23 0 1320 7.185387 120 0 689 27 44 56 0 44 3.7841935 1 670 33 28 66 1 66 4.18965567 1 1210 34 34 72 1 77 4.3438051.预后因素筛选:logrank time die, by(crea)检测肌酐是否影响生存率chi2(13) = 29.07Pr>chi2 = 0.0064P<0.05,说明肌酐对预后影响大logrank time die, by(bun)logrank time die, by(alb)logrank time die, by(age)logrank time die, by(therapy)logrank time die, by(ntprobnp1)由于bun P>0.05,在COX模型中去除改因素2.用COX比例风险模型分析cox time crea alb age therapy ntprobnp1, dead(die)Cox regression -- no tiesEntry time 0 Number of obs = 15①LR chi2(5) = 26.21②Prob > chi2 = 0.0001③Log likelihood = -4.1883032 ④Pseudo R2 = 0.7578------------------------------------------------------------------------------time | ⑤Coef. ⑥Std. Err. ⑦z ⑧P>|z| ⑨[95% Conf. Interval]-------------+----------------------------------------------------------------crea | -.0032338 .0031113 -1.04 0.299 -.0093319 .0028643alb | -1.260323 .8536905 -1.48 0.140 -2.933525 .4128797age | .2428877 .2597176 0.94 0.350 -.2661495 .7519248 therapy | -7.685876 7.077233 -1.09 0.277 -21.557 6.185245ntprobnp1 | -.2293586 1.013952 -0.23 0.821 -2.216669 1.757952①为模型无效假设(即:所有协变量的回归系数为0) 所对应的似然比检验( 自由度为协变量个数的卡方); ②模型无效假设检验对应的p值;③对数似然比;④伪决定系数;⑤回归系数;⑥回归系数的标准误;⑦单个回归系数检验(Ho:该回归系数为0)的Z统计量;⑧单个回归系数验的p值;⑨回归系数的95% 可信限。
生存资料的Cox回归分析(3)-结果解读及结论撰写

生存资料的Cox回归分析(3)-结果解读及结论撰写读前提示:本篇文章是“Cox回归分析”的第三部分,如需前情回顾,请返回医咖会主界面,查看 9 月 5 日推送的前两条内容。
结果解读( 1 )CaseProcessingSummary 表格给出了分析数据的基本情况,其中包括事件发生数(Event )、删失数(Censored )和总数(Total )等信息。
(2 )Categorical Variable Codings 表格给出了 Categorical Covariates 选项中设置的变量(本例中为group )所对应的赋值情况和频率(Frequency )。
最后一列给出了变量编码的情况。
脚注b. Indicator Parameter Coding 说明了本研究中group 变量以First 为参照组(Categorical Covariates 选项中的设置)。
(3 )OmnibusTests of Model Coefficients 表格给出了模型中所有变量的回归系数全为0 的检验结果。
对于本例,①Score统计量为5.065, P=0.024 ;②对数似然比检验χ2 =5.399, P=0.020。
说明模型中至少有一个自变量的 HR 值不为1 ,模型整体检验有统计学意义。
( 4 )Variables in the Equation 表格给出了参数估计的结果。
结果显示最后筛选后的模型仅包含group 变量,①P =Sig.=0.029 说明治疗方式为影响肺癌患者预后的独立因素。
②相对危险度 HR=Exp(B)=0.410 ,说明使用新药的患者死亡风险为使用常规药物患者的 0.410 倍,③H R 的 95% 可信区间( 95% CI )为 0.184-0.914。
( 5 )生存曲线。
前述Plots 选项的设置要求输出按照不同药物分组的生存曲线。
新药组(赋值为 1 ,绿色线条)比常规药物组(赋值为0 ,蓝色线条)的生存率高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章生存分析及COX回归在临床医学中, 对病人治疗效果的考查. 一方面可以看治疗结局的好坏,另一方面还可以通过治疗时间的长短来衡量。
例如某种疾病治愈的时间, 某癌症病人手术后的存活时间等, 把这类与时间有关的资料统称为生存资料。
生存资料一般通过随访收集,从某标准时刻(发病、手术或出院等)开始,按某种相等或不等时间间隔,对观察对象定期观察预定项目所得的资料,它的结局是死亡,治愈、复发、阳性等。
但在临床上,往往由于各种原因:(1)因迁移原因失去联系;(2)死于其他原因而造成失访;(3)预定终止结果迟迟不发生,致使在一定时期内,一部分病例得不到确切的生存期,但它们提供了其生存期长于观察期的信息,这种数据称为删失数据,也称截尾数据或终检值(censored data),包含终检值的数据即为不完全数据。
处理这类数据的统计分析方法称为生存分析。
它包括三个方面的内容1)生存过程的描述,主要是生存率的估计;2)生存过程的比较;3)影响因素的分析。
§12.1 生存率的估计生存率估计常用的有两种方法乘积极限法和寿命表法。
1乘积极限法又称Kaplan-Meier 法适用于小样本资料。
基本思想:将生存时间由小到大依次排列,在每个死亡点上,计算其期初人数、死亡人数、死亡概率、生存概率和生存率。
CHISS实现:点击重复测量→生存分析→乘积极限法应用举例:例12-1某疗法治疗白血病后的存活月数为: 2+,13,7+,11+,6,1,11,3,17,7。
试估计其生存率。
带“+”为存活终检值。
解步骤:1 进入数据模块此数据库已建立在CHISS\data文件夹中,文件名为:a9_0生存分析.DBF。
打开数据库点击数据→文件→打开数据库表找到文件名为:a9_0生存分析.DBF →确认2 进入统计模块进行统计计算点击重复测量→生存分析→乘积极限法时间变量: time 终检值指标:censor→确认3 进入结果模块查看结果点击结果乘积限估计法生存分析, 数据来自文件: C:\CHISS\Data\a9_0生存分析.DBF数据过滤条件:━━━━━━━━━━━━━━━━━━━秩观察死亡观察生存率次时间序号数生存率标准误(i) t(i) (j) n(i) S(j) Ss(j)───────────────────0 0 0 10 1.0000 ...1, 1 1 10 0.9000 0.09492, 2+ ... 9 ... ...3, 3 2 8 0.7875 0.13404, 6 3 7 0.6750 0.15515, 7 4 6 0.5625 0.16516, 7+ ... 5 ... ...7, 11 5 4 0.4219 0.17378, 11+ ... 3 ... ...9, 13 6 2 0.2109 0.172610, 17 7 1 0.0000 ...━━━━━━━━━━━━━━━━━━━注:删失数据为1。
平均生存期= 9.7750 标准差= 2.2664§12.2 时序检验(log rank test)用于比较两个或多个样本生存期,即对各样本不同时点生存率的综合分析。
其原理是计算出不同时期两种疗法的观察人数和死亡人数,并由此根据两种疗法疗效相同的假设计算出两种疗法在该日期的理论死亡数,若无效假设是对的,则实际值和理论值不会相差很大,如相差过大,则不象仅仅由于机遇所产生的差异,对此可作 2检验以推断。
CHISS实现:点击重复测量→生存分析→时序检验例12-2两种疗法治疗白血病后的存活月数如下:对照组: 2+,13,7+,11+,6,1,11,3,17,7中药组: 10,2+,12+,13,18,6+,19+,26,9+,8+,6+,43+,9,4,31,24带“+”为终检值试分析两种疗法治疗的生存期有无差别解步骤:1 进入数据模块此数据库已建立在CHISS\data文件夹中,文件名为:a9_1生存分析(小样本).DBF。
打开数据库点击数据→文件→打开数据库表找到文件名为:a9_1生存分析(小样本).DBF →确认2 进入统计模块进行统计计算点击重复测量→生存分析→时序检验时间变量: time 终检值指标:censor分组因素:g →确认3 进入结果模块查看结果点击结果小样本时序检验(生存期比较, 处理分组为g数据来自文件: "C:\CHISS\Data\a9_1生存分析(小样本).DBF"),━━━━━━━━━━━━━━━━━━━━━━━观察时间期初观察数发理论发生数──────────生──────1 2 1 2 小计数 1 2───────────────────────1 ... 10 16 26 1 0.385 0.6152+ 2+ 9 16 25 03 ... 8 15 23 1 0.348 0.652... 4 7 15 22 1 0.318 0.6826 ...7 14 21 1 0.333 0.667... 6+ 6 14 20 07 ... 6 12 18 1 0.333 0.6677+ ... 5 12 17 0... 8+ 4 12 16 0... 9 4 11 15 1 0.267 0.733... 9+ 4 10 14 0... 10 4 9 13 1 0.308 0.69211 ... 4 8 12 1 0.333 0.66711+ ... 3 8 11 0... 12+ 2 8 10 013 13 2 7 9 2 0.444 1.55617 ... 1 6 7 1 0.143 0.857... 18 0 6 6 1 0.000 1.000... 19+ 0 5 5 0... 24 0 4 4 1 0.000 1.000... 26 0 3 3 1 0.000 1.000... 31 0 2 2 1 0.000 1.000... 43+ 0 1 1 0━━━━━━━━━━━━━━━━━━━━━━━注:删失数据为1。
实际发生数与期望发生数━━━━━━━━━━━━━━━━━━━━组别总例数删失数实际发生理论发生────────────────────g.1 10 3 7 3.21g.2 16 8 8 11.79━━━━━━━━━━━━━━━━━━━━Log-Rank检验,QPH = 5.683 自由度 =1 P =0.0171 说明两种疗法治疗的生存期差别有显著性。
§12.3 COX 比例风险模型生存时间的长短不仅与治疗措施有关, 还可能与病人的体质, 年龄, 病情的轻重等多种因素有关, 把这类因素称为伴随变量或协变量。
由于失访、试验终止、意外事故、改变治疗方案等原因造成某些数据观察不完全,这些数据称为删失数据。
这种数据显然不服从正态分布和方差齐性, 不能用多元线性回归分析。
1972年英国统计学家Cox DR. 提出了一种能处理多因素生存分析数据的比例危险模型 ( Cox's proportional harzard model)。
Cox 回归模型: 在p 个危险因素同时影响生存过程的情况下, 在时点t 的危险率模型为:H(t)=h0(t)exp(b1x1+b2x2+….b pxp)其中h(t)-- 表示在时点t 的死亡率;h 0(t)--表示在时点t 的基本死亡率; 即不存在p x x ~1因素影响时的死亡率;1β--回归系数, 其意义是: 当因素x 1每改变一个测量单位时所引起的相对危险度的自然对数改变量即)exp(11β=RR 。
若x 1对生存无影响, 则理论上1β=0。
例12-3 现有50例急性淋巴细胞性白血病病人的随访记录. 在入院治疗时, 测得外周血中白细胞数x 1和浸润淋巴结等级x 2,经过治疗达到完全缓解后, 有的病人有巩固治疗有的没有x 3, 并随访取得每例病人的生存时间的资料如下。
50例急性淋巴细胞性白血病病人的随访记录病例号 X 1 X 2 X 3 T (月) 病例号 X 1 X 2 X 3 T (月)1 2.5 0 0 3.40 26 4.7 0 0 11.002 1.2 2 0 3.73 27 6.0 0 0 11.77 3 173.0 2 0 3.73 28 128.0 2 1 11.834 3.5 0 0 3.83 29 3.5 0 1 11.83 5 119.0 2 0 4.00 30 35.0 0 0 11.976 39.7 0 0 4.03 31 62.2 0 0 13.16 7 10.0 2 0 4.17 32 2.0 0 0 14.838 62.4 0 0 4.20 33 10.8 0 1 15.179 502.2 2 0 4.20 34 8.5 0 1 18.23 10 2.4 0 0 5.00 35 21.6 0 1 18.23 11 4.0 0 0 5.27 36 2.0 2 1 19.16+ 12 34.7 0 0 5.67 37 2.0 0 1 20.17+ 13 14.4 0 1 7.07 38 2.0 0 1 20.17+ 14 28.4 2 0 7.26 39 3.4 2 1 20.17+ 15 2.0 2 0 7.33 40 4.3 0 1 20.57 16 0.9 0 1 7.53 41 5.1 0 1 21.00 17 40.0 2 0 7.53 42 244.8 2 1 21.87 18 30.6 2 0 7.60 43 2.4 0 0 23.77 19 6.6 0 0 7.67 44 4.0 0 1 26.00 20 5.8 0 1 7.67 45 1.7 0 1 28.33 21 21.4 2 1 8.30 46 5.1 0 1 31.3322 6.1 0 1 8.33 47 1.1 0 1 37.7723 2.8 0 0 8.33 48 32.0 0 1 66.8324 2.7 2 1 8.80 49 12.8 0 1 73.5725 2.5 0 0 9.23 50 1.4 0 1 124.17+表中“+”代表仍存活, X1代表白细胞数(千个/mm3), X2代表浸润淋巴结程度,分为0、1、2三级, X3代表是否有巩固治疗,1为有, 0为无。
试进行COX回归分析。
解步骤:1 进入数据模块此数据库已建立在CHISS\data文件夹中,文件名为:a9_3cox模型.DBF。
打开数据库点击数据→文件→打开数据库表找到文件名为:a9_3cox模型.DBF →确认2 进入统计模块进行统计计算点击模型→数学模型→COX模型解释变量x1,x2,x3反应变量:time删失标记变量:CENSOR→确认3 进入结果模块查看结果点击结果Cox 模型的估计参数(生存时间=TIME, 删失标记=CENSOR, 数据来自:C:\CHISS\Data\a9_3cox模型.DBF)━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━参数名估计值标准误 u值 p值 RR 95%CI────────────────────────────────X1 0.001 0.002 0.591 0.5543 1.00 0.997~1.005X2 0.456 0.206 2.211 0.0270 1.58 1.053~2.364X3 -1.885 0.376 5.008 0.0000 0.15 0.073~0.317━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━G(卡方)= 244.7115 自由度=3 p值=0.0000。
