立体几何中的角度会这样考查
2018届高三理科数学答题模板 立体几何中角度问题

高考立体几何中角度问题【直线与平面所成的角】直线与平面所成的角的定义:①直线和平面所成的角有三种:a.斜线和平面所成的角:一条直线与平面α相交,但不和α垂直,这条直线叫做平面α的斜线.斜线与α的交点叫做斜足,过斜线上斜足以外的点向平面引垂线,过垂足与斜足的直线叫做斜线在平面α内的射影,平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.b.垂线与平面所成的角:一条直线垂直于平面,则它们所成的角是直角。
c.一条直线和平面平行,或在平面内,则它们所成的角为00.②取值范围:00≤θ≤900.求斜线与平面所成角的思路类似于求异面直线所成角:“一作,二证,三计算”。
最小角定理:斜线和它在平面内的射影所成的角(即线面角),是斜线和这个平面内的所有直线所成角中最小的角。
【求直线与平面所成的角的方法】(1)找角:求直线与平面所成角的一般过程:①通过射影转化法,作出直线与平面所成的角;②在三角形中求角的大小.(2)向量法:设PA是平面α的斜线,,向量n为平面α的法向量,设PA与平面α所成的角为θ,则【异面直线所成的角】异面直线所成角的定义:直线a、b是异面直线,经过空间任意一点O,分别引直线a′∥a,b′∥b,则把直线a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角。
两条异面直线所成角的范围是(0°,90°],若两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直。
在异面直线所成角定义中,空间一点O是任取的,而和点O的位置无关。
【求异面直线所成角的步骤】A、利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选在特殊的位置上。
B、证明作出的角即为所求角;C、利用三角形来求角。
【二面角】半平面的定义:一条直线把平面分成两个部分,每一部分都叫做半平面.二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
探讨立体几何中的角

探讨立体几何中的角在立体几何学中,角是我们经常遇到的一个重要概念。
通过研究角的性质和特点,我们可以更好地理解立体图形的结构和性质。
本文将探讨立体几何中的角,从不同角度分析其定义、分类、性质以及应用。
一、角的定义角是由两条射线或线段的端点组成的,可以看作是平面上两条向量的夹角。
通常以大写字母表示,如∠ABC,其中A、B为角的两个端点,C为角的顶点。
二、角的分类根据角的大小和性质,可以将角分为以下几类:1. 零角:两条重合的射线或线段构成的角,角的度数为0°。
2. 直角:两条相交的射线或线段构成的角,角的度数为90°。
3. 钝角:大于90°但小于180°的角。
4. 锐角:小于90°的角。
5. 平角:两条射线或线段在平面上所成的角,角的度数为180°。
三、角的性质1. 余角性质:两个互为余角的角的和为平角,即∠A和∠B是互为余角,则∠A+∠B=180°。
2. 角的大小性质:角度的大小可以通过度数来衡量,一圆周角的度数为360°。
3. 角的对立角性质:两个互为对立角的角的度数相等,即∠A和∠B是互为对立角,则m∠A=m∠B。
4. 角的补角性质:两个互为补角的角的和为直角,即∠A和∠B是互为补角,则∠A+∠B=90°。
四、角的应用角的概念在几何学以及其他科学领域中有广泛的应用。
下面列举了一些重要的应用场景:1. 几何图形的构造:通过合理利用角的性质和大小,我们可以进行几何图形的构造和计算,例如三角形、四边形等的计算和作图。
2. 地理导航:在地理导航系统中,我们可以利用角的概念来计算方位和航向,帮助人们找到目的地。
3. 建筑设计:在建筑设计中,角的概念可以为建筑师提供指导,帮助设计出美观且结构稳定的建筑物。
4. 机械设计:在机械设计中,角的概念可以用于设计传动机构和运动装置,确保机械设备的正常运转。
总结:通过对立体几何中角的探讨,我们了解了角的定义、分类、性质以及应用。
立体几何中二面角和线面角

立体几何中的角度问题一、 异面直线所成的角1、如图,在四棱锥ABCD P -中,底面ABCD 是矩形,⊥PA 底面ABCD ,E 是PC 的中点,已知2=AB ,22=AD ,2=PA ,求: (1)三角形PCD 的面积;(2)异面直线BC 与AE 所成的角的大小。
2、如图6,已知正方体1111ABCD A B C D -的棱长为2,点E是正方形11BCC B 的中心,点F、G分别是棱111,C D AA 的中点.设点11,E G 分别是点E,G在平面11DCC D 内的正投影. (1)求以E为顶点,以四边形FGAE 在平面11DCC D 内的正投影为底面边界的棱锥的体积; (2)证明:直线11FG FEE ⊥平面; (3)求异面直线11E G EA 与所成角的正弦值二、直线与平面所成夹角1、如图,在四棱锥P ABCD -中,底面为直角梯形,//AD BC ,90BAD ∠=,PA ⊥ 底面ABCD ,且2PA AD AB BC ===,M N 、分别为PC 、PB 的中点。
求CD 与平面ADMN 所成的角的正弦值。
2、长方体ABCD-A 1B 1C 1D 1 , AB=3 ,BC=2, A 1A= 4 ,求AB 与面 AB 1C 1D 所成的角的正弦值。
三、二面角与二面角的平面角问题1、如图5.在椎体P-ABCD 中,ABCD 是边长为1的棱形, 且∠DAB=60︒,2PA PD ==,PB=2,E,F 分别是BC,PC 的中点. (1) 证明:AD ⊥平面DEF; (2) 求二面角P-AD-B 的余弦值.2、如图5,AEC 是半径为a 的半圆,AC 为直径,点E 为AC 的中点,点B 和点C 为线段AD 的三等分点,平面AEC 外一点F 满足5FB FD a ==,6EF a =。
(1)证明:EB FD ⊥;(2已知点,Q R 为线段,FE FB 上的点,23FQ FE =,23FR FB =,求平面BED 与平面RQD 所成二面角的正弦值。
高考数学立体几何中与角有关的四大定理及其证明
则 cosθ = cos2β + cos2γ - 2cosαcosβcosγ sinα
证明:设 ∠HAC = θ1,∠HAB = θ2 ⇒ α = θ1 + θ2,
由三余弦定理得:
cos β cosγ
= =
cosθ cosθ
cosθ1 cosθ2
① ②
由①和②得 cosθ = cosβ = cosγ ③ cosθ1 cosθ2
α
Aβ
γ
P α : 线面角 β : 斜线角 γ : 射影角 则 cosβ = cosαcosγ ⇒ β > α,β > γ
Q
B
证明:cosβ =
AB PA
,cosα =
QA PA
,cosγ =
AB QA
⇒ cosβ = cosαcosγ
·1·
3. 三夹角公式
P
θ
Aβ
γ
α
C H
B
若 θ 为 PA 与平面 ABC 的夹角
⋅
HO BO
AH AO
⋅
BH BO
= cosθ - cosθ1cosθ2 sinθ1sinθ2
注:若 φ =
π 2
,
则该定理退化为三余弦定理
·3·
立体几何中与角有关的四大定理及其证明
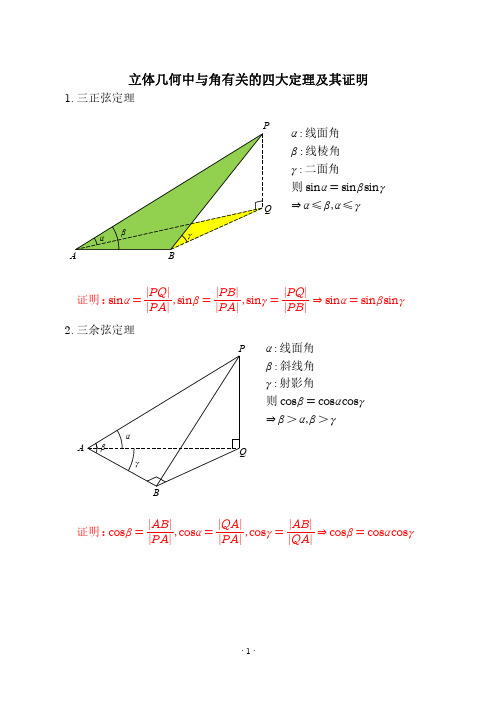
1. 三正弦定理
β α
A
γ
B
P
α : 线面角 β : 线棱角 γ : 二面角 则 sinα = sinβsinγ Q ⇒ α ≤ β,α ≤ γ
证明:sinα =
PQ PA
,sinβ =
PB PA
,sinγ =
PQ PB
⇒ sinα = sinβsinγ
高中数学立体几何角度计算技巧

高中数学立体几何角度计算技巧在高中数学中,立体几何是一个重要的考点,其中涉及到角度的计算。
正确计算角度是解决立体几何问题的关键,因此我们需要掌握一些角度计算的技巧。
本文将通过具体的题目来说明这些技巧,并给出一些解题思路和方法。
一、角度计算的基本概念在立体几何中,角度是指由两条射线或线段构成的图形,常用度(°)作为单位来表示。
我们首先需要了解一些基本概念:1. 直角:两条相互垂直的线段所形成的角度称为直角,常用符号“∠”表示。
例如,直角的度数为90°。
2. 锐角:两条相互交叉且夹角小于90°的线段所形成的角度称为锐角。
例如,30°、60°都是锐角。
3. 钝角:两条相互交叉且夹角大于90°的线段所形成的角度称为钝角。
例如,120°、150°都是钝角。
二、角度计算的常见题型1. 直角三角形的角度计算直角三角形是立体几何中常见的一种形式。
在计算直角三角形的角度时,我们可以运用三角函数的知识。
例如,已知直角三角形的两条边的长度,我们可以通过正弦、余弦、正切等函数来计算角度。
举个例子,已知直角三角形的斜边长为5,一条直角边长为3,我们需要计算另一条直角边与斜边的夹角。
首先,我们可以利用正弦函数来计算这个夹角的正弦值:sinθ = 对边/斜边 = 3/5。
然后,通过反正弦函数,我们可以求得这个夹角的度数:θ = arcsin(3/5) ≈ 36.87°。
2. 平行线与横截线的角度计算在立体几何中,平行线与横截线的角度计算也是一个常见的考点。
当两条平行线被一条横截线所截断时,我们需要计算出相应的角度。
例如,已知两条平行线AB和CD,横截线EF与这两条平行线相交于点G,我们需要计算出∠GEF的度数。
根据平行线的性质,我们知道∠ABG和∠DCE是对应角,它们的度数相等。
因此,我们可以通过计算∠DCE的度数来得到∠GEF的度数。
立体几何中的角度、体积、距离问题

第02讲 玩转立体几何中的角度、体积、距离问题【学习目标】1.掌握各种角的定义,弄清异面直线所成的角与两直线所成的角,二面角与二面角的平面角,直线与平面所成的角和斜线与平面所成的角,二面角与两平面所成的角的联系与区别,弄清他们各自的取值范围。
2.细心体会求空间角的转化和数形结合思想。
3.掌握各种距离和距离的求解方法.【基础知识】知识点1.求点线、点面、线面距离的方法(1)若P 是平面α外一点,a 是平面α内的一条直线,过P 作平面α的垂线PO ,O 为垂足,过O 作OA ⊥a ,连接P A ,则以P A ⊥a .则线段P A 的长即为P 点到直线a 的距离(如图所示).(2)一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离叫直线与平面的距离.(3)求点面距离的常用方法:①直接过点作面的垂线,求垂线段的长,通常要借助于某个直角三角形来求解.②转移法:借助线面平行将点转移到直线上某一特殊点到平面的距离来求解.③体积法:利用三棱锥的特征转换位置来求解.知识点2.异面直线所成角的常用方法求异面直线所成角的一般步骤:(1)找(或作出)异面直线所成的角——用平移法,若题设中有中点,常考虑中位线.(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的角.(3)结论——设(2)所求角大小为θ.若090θ︒<≤︒,则θ即为所求;若90180θ︒<<︒,则180θ︒-即为所求.知识点3.直线与平面所成角的常用方法求平面的斜线与平面所成的角的一般步骤(1)确定斜线与平面的交点(斜足);(2)通过斜线上除斜足以外的某一点作平面的垂线,连接垂足和斜足即为斜线在平面上的射影,则斜线和射影所成的锐角即为所求的角;(3)求解由斜线、垂线、射影构成的直角三角形.知识点4.作二面角的三种常用方法(1)定义法:在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.如图①,则∠AOB 为二面角α-l -β的平面角.(2)垂直法:过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角.如图②,∠AOB 为二面角α-l -β的平面角.(3)垂线法:过二面角的一个面内异于棱上的一点A 向另一个平面作垂线,垂足为B ,由点B 向二面角的棱作垂线,垂足为O ,连接AO ,则AOB ∠为二面角的平面角或其补角.如图③,AOB ∠为二面角l αβ--的平面角.知识点5.求体积的常用方法选择合适的底面,再利用体积公式求解.【考点剖析】考点一:异面直线所成的角例1.在空间四边形ABCD 中,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,若2==AC BD ,且AC 与BD 所成的角为60°,则EG 的长为()A .1或2B .2或3C .1或3D .12或32考点二:线面角例2.如图,在三棱柱ABC A B C '''-中,底面ABC 是正三角形,AA '⊥底面ABC ,且1AB =,2AA '=,则直线BC '与平面ABB A ''所成角的正弦值为______.考点三:二面角例3.在四棱锥P ABCD -中,底面ABCD 是菱形,60ABC ∠=︒,PA ⊥平面ABCD ,2PA AB ==.(1)求证:PC BD ⊥;(2)求二面角P CD A --的正弦值.考点四:距离问题例4.如图,在直三棱柱111ABC A B C -中,1,,22AB BC AA AC AB BC ⊥===,E ,F 分别是11,AC AB 的中点.(1)证明:AE ∥平面11B C F .(2)求点C 到平面11B C F 的距离.考点五:体积问题例5.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,四边形ABCD 为正方形,点F 为线段PC 上的点,过A ,D ,F 三点的平面与PB 交于点E .(1)证明://EF 平面ABCD ;(2)若E 为PB 中点,且2AB PA ==,求四棱锥P AEFD -的体积.【真题演练】1.在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为()A .π2B .π3C .π4D .π62.如图,四棱锥S -ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确的是( ) A .AC ⊥SBB .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角D .AB 与SC 所成的角等于DC 与SA 所成的角1.线面平行垂直的判定;2.线面角,异面直线所成角3.已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则A .123θθθ≤≤B .321θθθ≤≤C .132θθθ≤≤D .231θθθ≤≤4.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为A 235D 7 5.已知正方体1111ABCD ABCD -中,E 、F 分别为11、BB CC 的中点,那么异面直线AE 与1D F 所成角的余弦值为____________.6.如下图,在四棱锥S ABCD -中,底面ABCD 是正方形,平面SAD ⊥平面ABCD ,2SA SD ==,3AB =. (1)求SA 与BC 所成角的余弦值;(2)求证:AB SD ⊥.7.如图,三角形DC P 所在的平面与长方形CD AB 所在的平面垂直,D C 4P =P =,6AB =,C 3B =. (1)证明:C//B 平面D P A ;(2)证明:C D B ⊥P ;(3)求点C 到平面D P A 的距离.8.如图,在圆锥PO 中,已知2PO O 的直径2AB =,点C 在AB 上,且30CAB ∠=,D 为AC 的中点.(I )证明:AC ⊥平面POD ;(II )求直线OC 和平面PAC 所成角的正弦值.9.如图,P 是边长为1的正六边形ABCDEF 所在平面外一点,1PA =,P 在平面ABC 内的射影为BF 的中点O .(Ⅰ)证明PA ⊥BF ;(Ⅰ)求面APB 与面DPB 所成二面角的大小的余弦值.10.在四棱锥P ABCD -中,底面ABCD 为正方形,平面PAD ⊥平面ABCD ,点M 在线段PB 上,PD ∥平面MAC ,PA PD =.(1)判断M 点在PB 的位置并说明理由;(2)记直线DM 与平面P AC 的交点为K ,求DK KM的值;(3)若异面直线CM 与AP M CD A --的平面角的正切值. 11.如图,在长方体1111ABCD A B C D -中,AD =1,12AB AA ==,H ,F 分别是棱11C D ,1BB 的中点.(1)判断直线HF 与平面11A BCD 的位置关系,并证明你的结论;(2)求直线HF 与平面ABCD 所成角的正弦值;(3)在线段HF 上是否存在一点Q ,使得点Q 到平面11A BCD ,若存在,求出HQ HF的值;若不存在,说明理由. 【过关检测】1.在长方体1111ABCD A B C D -中,12AB AA ==,3AD =,点E 、F 分别是棱AB 、1AA 的中点,E 、F 、1C ∈平面α,直线11A D 平面P α=,则直线BP 与直线1CD 所成角的余弦值为()A C 2.在正方体1111ABCD ABCD -中,E ,F 分别为棱AD ,11A B 的中点,则异面直线EF 与1CD 夹角的余弦值为()A D3.如图所示,三棱锥P ABC -的底面ABC 是等腰直角三角形,90ACB ∠=,且2PA PB AB ===,=PC 则PC 与平面P AB 所成角的余弦值等于()A B 4.在空间四边形ABCD 中,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,若2==AC BD ,且AC 与BD 所成的角为60°,则EG 的长为()A.1.1.125.在棱长为1的正方体1111ABCD A B C D -中,O 为正方形1111D C B A 的中心,则下列结论错误的是() A .BO AC ⊥B .BO ∥平面1ACDC .点B 到平面1ACD D .直线BO 与直线1AD 的夹角为3π 6.在正方体1111ABCD A B C D -中,,,E F G 分别为11,,BC CC BB 的中点,则下列结论中正确的是() A .1D D AF ⊥B .二面角F AEC --的正切值为2C .异面直线1A G 与EFD .点G 到平面AEF 的距离是点C 到平面AEF 的距离的2倍7.如图,AB 是半球的直径,O 为球心,4,,AB M N =依次是半圆AB 上的两个三等分点,P 是半球面上一点,且PN MB ⊥,(1)证明:平面PBM ⊥平面PON ;(2)若点P 在底面圆内的射影恰在BM 上,求二面角--A PB N 的余弦值.8.已知平面四边形ABCD ,2AB AD ==,60BAD ∠=︒,30BCD ∠=︒,现将ABD △沿BD 边折起,使得平面ABD ⊥平面BCD ,此时AD CD ⊥,点P 为线段AD 的中点.(1)求证:BP ⊥平面ACD ;(2)若M 为CD 的中点,求MP 与平面BPC 所成角的正弦值;(3)在(2)的条件下,求二面角P BM D --的平面角的余弦值.9.已知四棱锥P ABCD -的底面是边长为2的菱形,PD ⊥底面ABCD .(1)求证:AC ⊥平面PBD ;(2)当1PD =,BD =PB 与AD 所成角的余弦值;10.已知四棱锥P ABCD -的底面是边长为2的菱形,PD ⊥底面ABCD .(1)求证:AC ⊥平面PBD ;(2)已知1PD =,(Ⅰ)当BD PB 与AD 所成角的余弦值;(Ⅰ)当直线PB 与平面ABCD 所成的角为45︒时,求四棱锥P ABCD -的体积.11.在直三棱柱111ABC A B C -中,90ABC ∠=︒,1AB BC ==,12BB =.(1)求异面直线11B C 与1A C 所成角正切值的大小;(2)求点1B 与平面1A BC 的距离.第02讲 玩转立体几何中的角度、体积、距离问题【学习目标】1.掌握各种角的定义,弄清异面直线所成的角与两直线所成的角,二面角与二面角的平面角,直线与平面所成的角和斜线与平面所成的角,二面角与两平面所成的角的联系与区别,弄清他们各自的取值范围。
高中数学必修二立体几何角的问题-教师版(含几何法和向量法)
立体几何线线、线面、面面所成角的问题几何法1、两异面直线及所成的角:不在同一个平面的两条直线,叫做异面直线,已知异面直线a,b,经过空间任一点O 作直线a '∥a ,b '∥b ,我们把a '与b '所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).如果两条异面直线所成的角是直角,我们就说这两条直线互相垂直.2、直线和平面所成的角:一条直线PA 和一个平面α相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A 叫做斜足。
过斜线上斜足以外的一点向平面引垂线PO ,过垂足O 和斜足A 的直线 AO 叫做斜线在这个平面上的射影。
平面的一条斜线和它在平面内的摄影所成的锐角,叫做这条直线和这个平面所成的角。
一条直线垂直于平面,我们就说它们所成的角是直角。
一条直线和平面平行,或在平面内,我们说它们所成的角是00.3、二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
在二面角βα--l 的棱l 上任取一点O ,以点O 为垂足,在半平面α和β内分别作垂直于棱l 的射线OA 和OB ,则射线OA 和OB 构成的∠AOB 叫做二面角的平面角。
二面角的大小可以可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度。
常见角的取值范围:① 异面直线所成的角⎥⎦⎤ ⎝⎛20π,,直线与平面所成的角⎥⎦⎤⎢⎣⎡20π,,二面角的取值范围依次[]π,0② 直线的倾斜角[)π,0、到的角[)π,0、与的夹角的取值范围依次是⎥⎦⎤⎢⎣⎡20π,4、点到平面距离:求点到平面的距离就是求点到平面的垂线段的长度,其关键在于确定点在平面内的垂足,当然别忘了转化法与等体积法的应用. 向量法1、两异面直线及所成的角:设异面直线a ,b 的夹角为θ,方向向量为a ,b ,其夹角为ϕ,则有cos cos a b a bθϕ⋅==.2、直线和平面所成的角:设直线l 的方向向量为l ,平面α的法向量为n ,l 与α所成的角为θ,l 与n 的夹角为ϕ,则有sin cos l n l nθϕ⋅==.3、二面角:设1n ,2n 是二面角l αβ--的两个面α,β的法向量,则向量1n ,2n 的夹角(或其补角)就是二面角的平面角的大小.若二面角l αβ--的平面角为θ,则1212cos n n n n θ⋅=.4、点到平面距离:点P 是平面α外一点,A 是平面α内的一定点,n 为平面α的一个法向量,则点P 到平面α的距离为cos ,n d n nPA⋅=PA 〈PA 〉=.例题例1.长方体ABCD -A 1B 1C 1D 1中,AB =AA 1=2,AD =1,E 为CC 1的中点,则异面直线BC 1与AE 所成角的余弦值为( )A.1010B.3010C.21510D.31010 解析:建立空间直角坐标系如图.则A (1,0,0),E (0,2,1),B (1,2,0),C 1(0,2,2).BC 1→=(-1,0,2),AE →=(-1,2,1),cos 〈BC 1→,AE →〉=BC 1→·AE →|BC 1→|·|AE →|=3010.所以异面直线BC 1与AE 所成角的余弦值为3010.答案:B例 2.已知ABCD 是矩形,PA ⊥平面ABCD ,2AB =,4PA AD ==,E 为BC 的中点.(1)求证:DE ⊥平面PAE ;(2)求直线DP 与平面PAE 所成的角. 证明:在ADE ∆中,222AD AE DE =+,∴AE DE ⊥ ∵PA ⊥平面ABCD ,DE ⊂平面ABCD ,∴PA DE ⊥又PA AE A ⋂=,∴DE ⊥平面PAE (2)DPE ∠为DP 与平面PAE 所成的角在Rt PAD ∆,PD =Rt DCE ∆中,DE =在Rt DEP ∆中,2PD DE =,∴030DPE ∠=例3.如图,在四棱锥P ABCD -中,底面ABCD 是060DAB ∠=且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD . (1)若G 为AD 的中点,求证:BG ⊥平面PAD ; (2)求证:AD PB ⊥;(3)求二面角A BC P --的大小.证明:(1)ABD ∆为等边三角形且G 为AD 的中点,∴BG AD ⊥ 又平面PAD ⊥平面ABCD ,∴BG ⊥平面PAD(2)PAD 是等边三角形且G 为AD 的中点,∴AD PG ⊥ 且AD BG ⊥,PG BG G ⋂=,∴AD ⊥平面PBG ,PB ⊂平面PBG ,∴AD PB ⊥(3)由AD PB ⊥,AD ∥BC ,∴BC PB ⊥ 又BG AD ⊥,AD ∥BC ,∴BG BC ⊥∴PBG ∠为二面角A BC P --的平面角在Rt PBG ∆中,PG BG =,∴045PBG ∠=例4.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱AA 1、BB 1的中点,G 为棱A 1B 1上的一点,且A 1G =λ(0≤λ≤1),则点G 到平面D 1EF 的距离为( D ) A.3 B.22C.32λ D.55练习:1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点,(1)求证:EFGH 是平行四边形;(2)若BD=AC=2,EG=2。
第三讲立体几何中的角度
第三讲立体几何中的角度 1、异面直线所成的角(1)定义:a 、b 是两条异面直线,经过空间任意一点O ,分别引直线a ′∥a,b ′∥b,则a ′和b ′所成的锐角(或直角)叫做异面直线a 和b 所成的角.(2)取值范围:0°<θ≤90°. (3)求解方法①根据定义,通过平移,找到异面直线所成的角θ; ②解含有θ的三角形,求出角θ的大小.例1.如图,在四面体ABCD 中,已知所有棱长都为a ,点E 、F 、G 分别是AB 、CD 、BC 的中点. (1)、求证:EG ∥平面ACD ; (2)、求线段EF 的长; (3)、求异面直线BC 、AD 所成角的大小.22a1.正四面体ABC S -中,E ,F 为中点,求异面直线BE ,SF 所称角度SEA CFB32323247343cos =⨯⨯-+=QEB arcos 32异面直线角的求法只需记住平移和向量即可,但是有些小题考查可能不好建系,所以需要大家对平移好好掌握,而平移其实就是构建辅助线,辅助线的构造基本和证明线面平行时的构造相同,即平行四边形构造和中位线构造,相对而言中位线可能够难想一点,中位线构造常常出现在三棱锥中。
如图,ABCD —A 1B 1C 1D 1是正四棱柱.(Ⅰ)求证:BD ⊥平面ACC 1A 1;(Ⅱ)若二面角C 1—BD —C 的大小为60o, 求异面直线BC 1与AC 所成角的大小.2、直线和平面所成的角——斜线和射影所成的锐角(1)取值范围0°≤θ≤90° (2)求解方法①作出斜线在平面上的射影,找到斜线与平面所成的角θ. ②解含θ的三角形,求出其大小.例2. 如图,在四棱锥P-ABCD 中,PA 、AB 、AD 两两互相垂直,BC ∥AD ,且AB=AD=2BC ,E ,F 分别是PB 、PD 的中点。
(Ⅰ)证明:EF ∥平面ABCD ;(Ⅱ)若PA=AB ,求PC 与平面PAD 所成的角的正弦值.arcsin 322.如图,在Rt AOB △中,π6OAB ∠=,斜边4AB =.Rt AOC △可以通过Rt AOB △以直线AO 为轴旋转得到,且二面角B AO C --是直二面角.动点D 的斜边AB 上.(I )求证:平面COD ⊥平面AOB ; (II )当D 为AB 的中点时,求异面直线AO 与CD 所成角的大小; (III )求CD 与平面AOB 所成角的最大值..∴异面直线AO 与CD 所成角的大小为15arctan 3.CD ∴与平面AOB 所成角的最大值为23arctan 3.3.正方体1111D C B A ABCD -,E 是1BC 中点,求DE 与ABCD 所成角。
几何体角度常用结论及方法(如何计算几何体的角度)
几何体角度常用结论及方法(如何计算几
何体的角度)
几何体角度常用结论及方法
介绍
本文档将介绍几何体角度的常用结论及计算方法。
了解几何体的角度可以帮助我们解决一些与角度相关的几何问题。
直线和平面角度
1. 直线与平面的角度:直线与平面的交角是直线与平面所成的最小正角度。
2. 直线的倾斜角度:直线与某参考方向之间的夹角被称为倾斜角度。
多边形角度
1. 三角形:三角形的内角和为180度。
任意两边之和大于第三边。
2. 四边形:四边形的内角和为360度。
3. 正多边形:正n边形的内角和为180 * (n - 2) 度。
圆的角度
1. 圆心角:圆心角是以圆心为顶点的角。
圆心角的度数等于其所对应的弧度数。
(1弧度等于57.3度)
2. 弧度:圆的一部分被度量出来被称为弧度。
弧度角的度数等于其所对应的圆心角度数的弧度数。
计算方法
1. 角度计算:通过已知的几何形状和角度结论,我们可以利用几何定理和性质来计算未知角度的大小。
2. 三角函数:三角函数(如正弦、余弦和正切等)可以帮助我们计算角度的值。
- 正弦:已知一个角的某边与斜边的比值,可以使用正弦函数求解角度。
- 余弦:已知一个角的邻边与斜边的比值,可以使用余弦函数求解角度。
- 正切:已知一个角的对边与邻边的比值,可以使用正切函数求解角度。
希望本文档对您理解和计算几何体的角度有所帮助。
如有任何问题,请随时向我咨询。
立体几何角度的求法
3)角的边都要垂直于二面角的棱
l
B
A
此 图
×正
O
确 ?
B
10
二面角的平面角的作法:
1、定义法
A
根据定义作出来
O
l
B
2、垂面法 作与棱垂直的平面与
l
O
两半平面的交线得到
γ
A
B
3、三垂线定理法 借助三垂线定理或
其逆定理作出来
A
D
l
O
12
二面角的计算步骤:
1、找到或作出二面角的平面角 2、证明 (指出)1中的角就是所求的 角 3、计算出此角的大小
斜线和平面所成的角(或斜线和平面的夹角) • 直线和平面垂直<=>直线和平面所成的角是直角 • 直线和平面平行或在平面内<=>直线和平面所成的
角是0°
思考
• 直线与平面所成的角θ的取值范围
是: 0≤θ≤π/2
。
• 斜线与平面所成的角θ的取值范围
是: 0<θ<π/2
。
斜线和平面所成的角的求法
(1)射影法:在线上取一点作面的垂线,斜 足与垂足的连线与斜线所成的角即为所求。 问题2.正方体ABCD-A1B1C1D1中,E、F分别为BB1 、
问题3.在正四棱柱AC1中,底面的边长AB=2,E 为线段AB的中点,F为线段AD上的点,点C在 平面C1EF上的射影H为△ C1EF的重心. (1)求证:AF=FD; (2)求BF与平面C1EF所成角的大小D1 正弦值. C1
A1
B1
DF AE来自C B3.二面角的概念
B
A
O
B
A
从一条直线出发的两个半平面所组成的图 形叫做二面角。 这条直线叫做二面角的棱。
