C弯曲-04
本章主要内容1.环烷烃、环烯烃的命名.2.环烷烃的化学性质.

例2: 顺-4-叔丁基环己醇的两种构象
• 叔丁基在 e 键上的构象比在 a 键上的另一种构象 要稳定的多.
分子式为C4H6的甲、乙、丙三个化合物高 温催化加氢都得到正己烷。甲与浓KMnO4作用 生成CH3CH2COOH;乙生成 CH2COOH ;丙生成
CH2COOH COOH COOH
.请推测甲、乙、丙三个化合物的结构.
5.2 脂环烃的性质 (一) 物理性质 • 环烷烃的熔点和沸点都比同碳数的烷烃要高一些. • 相对密度也比相应的烷烃高,但比水轻. (二) 化学性质 • 脂环烃的化学性质与相应的脂肪烃类似. • 环烷烃的化学特性: 三、四元环结构不稳定,易开环;
五、六元环结构较稳定,一般不会开环.
5.2.1 环烷烃的反应 (1) 取代反应--在光或热的引发下发生卤代反应, (自由基反应). Cl
每个 CH2高38.5 kJ/mol.这个差值就是环丙烷分子中 每个 CH2的张力能. 总张力能 --环丙烷的总张力能38.53=115.5 kJ/mol
张力能 --环丙烷的 Hc/n 为697.1 kJ/mol,比烷烃的
环丙烷的总张力能38.5 3 = 115.5 kJ/mol
环丁烷的总张力能27.6 4 = 110.4 kJ/mol 环戊烷的总张力能5.4 5 = 27.0 kJ/mol 环己烷的总张力能为 0 环庚烷的总张力能3.7 7 = 25.9 kJ/mol
环辛烷的总张力能5.0 8 = 40.0 kJ/mol
...................
•环烷烃的张力能越大,能量越高,分子越不稳定.
∴环丙烷,环丁烷不稳定,容易开环;环己烷和以 上的大环化合物的张力能很小或等于零,它们都 是稳定的化合物.
材料力学第5章弯曲变形ppt课件
qL
4.22kNm
4.22kNm
M
max
32 M
max
76.4MPa
WZ
d 3
例题
20kN m
A
4m
FA
20kN m
A
MA
4m
试求图示梁的支反力
40kN
B
D
2m
2m
B
B1 FB
FB 40kN
B
D
B2
2m
2m
在小变形条件下,B点轴向力较小可忽略不
计,所以为一次超静定.
C
B1 B2
FBBBMF12AA2383qFEqELBqqLI84LI2LLZZ32F35BFF4FEFB83PBPLIEL7Z3L12IZ.218352.k75N5kFkN2PNmEL2IZ2
x
边界条件
A
L2
B
L2
C
y
连续条件
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
全梁仅一个挠曲线方程
C
q
EA
共有两个积分常数 边界条件
L1
A
x
B
EI Z
L
y
例题 5.5
用积分法求图示各梁挠曲线方程时,试问在列各梁 的挠曲线近似微分方程时应分几段;将分别出现几个 积分常数,并写出其确定积分常数的边界条件
q
a
B C LBC
B
2a
FN
B
q2a4
8EIZ
FN 2a3
3EIZ
C
FN
a
D
表面安装零件编带规格(适用JISC0806-3标准)
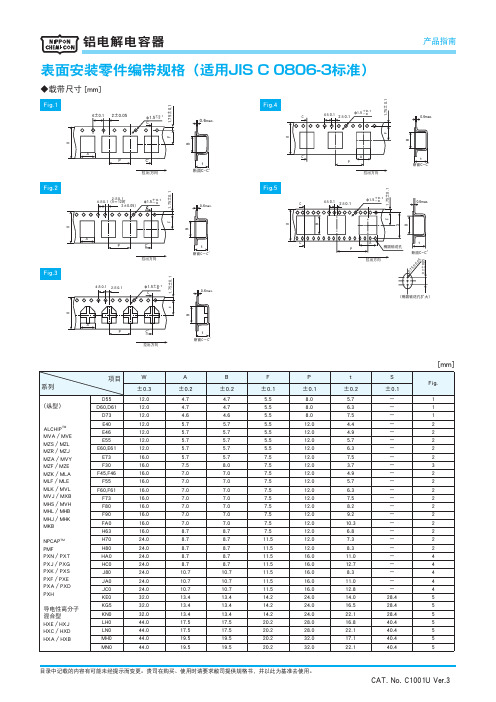
Fig.3
4±0.1 2±0.1
φ1.5+ -00.1 C
1.75±0.1
0.6max.
F
W
B
A
P
C′
拉出方向
t 断面C-C′
系列
(纵型)
ALCHIPTM MVA/MVE MZS/MZL MZR/MZJ MZA/MVY MZF/MZE MZK/MLA MLF/MLE MLK/MVL MVJ/MXB MHS/MVH MHL/MHB MHJ/MHK MKB
A
±0.2
4.7 4.7 4.6 5.7 5.7 5.7 5.7 5.7 7.5 7.0 7.0 7.0 7.0 7.0 7.0 7.0 8.7 8.7 8.7 8.7 8.7 10.7 10.7 10.7 13.4 13.4 13.4 17.5 17.5 19.5 19.5
B
±0.2
4.7 4.7 4.6 5.7 5.7 5.7 5.7 5.7 8.0 7.0 7.0 7.0 7.0 7.0 7.0 7.0 8.7 8.7 8.7 8.7 8.7 10.7 10.7 10.7 13.4 13.4 13.4 17.5 17.5 19.5 19.5
公差 - - - ±0.05 ±1.0 ±0.2 ±0.7 ±1.0
梁的弯曲(工程力学课件)

02 弯曲的内力—弯矩与剪力
3-3截面
M 3 q 2a a 2qa 2
4-4截面
qa 2
5qa 2
2
M 4 FB 2a M C
3qa
2
2
5-5截面
qa 2
M 5 FB 2a
2
02 弯曲的内力—弯矩与剪力
由以上计算结果可以看出:
(1)集中力作用处的两侧临近截面的弯矩相同,剪力不同,说明剪力在
后逐段画出梁的剪力图和弯矩图。
04 弯矩、剪力与载荷集度之间的关系
例8 悬臂梁AB只在自由端受集中力F作用,如图(a)所示,
试作梁的剪力图和弯矩图。
解:
1-1截面: Q1=-F M1=0
2-2截面: Q1=-F M1=-Fl
04 弯矩、剪力与载荷集度之间的关系
例9 简支梁AB在C点处受集中力F作用,如图(a)所示,作此梁的剪力
(2)建立剪力方程和弯矩方程;
(3)应用函数作图法画出剪力Q(x),弯矩M(x)的图线,即为剪力
图和弯矩图
03 弯矩图和剪力图
例9.3 悬臂梁AB在自由端B处受集中载荷F作用,如图(a)所示,试作
其剪力图和弯矩图。
解 :(1)建立剪力方程和弯矩方程
() = ( < < )
() = −( − ) ( ≤ ≤ )
方程和弯矩方程,并作剪力图和弯矩图。
解:(1)求支反力
(2)建立剪力方程和弯矩方程
03 弯矩图和剪力图
(3)绘制剪力图、弯矩图
计算下列5个截面的弯矩值:
03 弯矩图和剪力图
二、用简便方法画剪力图、弯矩图 (从梁的左端做起)
1.无载荷作用的梁段上 剪力图为水平线。 弯矩图为斜直线(两点式画图)。
大写字母c的四种写法 -回复

大写字母c的四种写法-回复大写字母C的四种写法是:C、ㄡ、ꐃ、千。
C是拉丁字母表中C的大写形式。
它是许多现代字母表中的第三个字母,也是英语、法语、德语、西班牙语等其他许多语言中的重要字母之一。
作为一个大写字母,C具有许多用途和意义。
下面将详细介绍大写字母C的不同写法。
首先,C是最常见的大写形式。
它由一个较小的侧弯线向右上方弯曲而成。
这种写法被广泛用于字母表、标识、商标、标题和其他许多场合。
C也经常作为代表儿童、团队、公司和个人的首字母。
其次,ㄡ是中文拼音字母表中C的一种特殊写法。
ㄡ的发音与C的发音相似,因此被用来表示C音。
它是由一个凹型弯曲线和一个斜线组成。
ㄡ通常出现在拼音发音注释、学术论文、语言学研究和其他与拼音相关的场合中。
第三种写法是ꐃ,它是尼日尔语言符号中C的一种写法。
ꐃ由一个直线和向左下方弯曲的垂直线形成。
尼日尔回音符号的音节延音,以及尼日尔地区一些民族文化的象征,例如土地、家庭和身份。
ꐃ经常出现在吉支纳语、霍萨语等语言的书写中。
最后,千在汉字表中通常作为数字1000的意义出现,但它也可以表示字母C的大写形式。
千由一个旁边有弧线的横线和两个弯曲的直线组成。
这种写法常常在标识、标题、节目、竞赛和其他宣传活动中使用。
在这篇文章中,我们详细介绍了大写字母C的四种写法,并解释了它们在不同语言和文化中的用途和意义。
每种写法都有自己独特的特点和背后的文化背景。
无论是C、ㄡ、ꐃ还是千,它们都是人类交流和文字表达不可或缺的组成部分,对于构建我们的语言、文化和认同感都起着重要的作用。
我们应该尊重和珍视不同文化中的文字符号,并将它们作为了解和欣赏多元世界的桥梁。
工程力学c材料力学部分第六章 弯曲变形

A l/2
C l
B
解:此梁上的荷载可视为 正对称和反对称荷载的叠加, 正对称和反对称荷载的叠加, 如图所示。 如图所示。 正对称荷载作用下:
q/2
5(q / 2)l 4 5ql 4 wC1 = − =− 384 EI 768 EI
B
(q / 2)l 3 ql 3 θ A1 = −θ B1 = =− 24 EI 48EI
w P A a D
a
A C a H a B
EI
Pl 3 wB = − 3 EI
P
B
l
Pl 2 θB = − 2 EI
P A a 2a 2a C B
P/2
P/2 B
P/2
=
A
+
P/2
力分解为关于中截面的对称和反对称力( )之和的形式。 解:将P力分解为关于中截面的对称和反对称力(P/2)之和的形式。 力分解为关于中截面的对称和反对称力 显然,在反对称力( / )作用下, 显然,在反对称力(P/2)作用下,wc=0 对称力作用的简支梁, 对称力作用的简支梁,可以等效为悬臂梁受到两个力的作用 的问题。 的问题。
wA=0 θA=0
B
②、变形连续条件 变形连续条件: 连续条件
P A C θC左 wC左= wC右, =θ C右 B
的悬臂梁, 例1:图示一弯曲刚度为 的悬臂梁,在自由端受一集中力 作 :图示一弯曲刚度为EI的悬臂梁 在自由端受一集中力F 试求梁的挠曲线方程,并求最大挠度及最大转角。 用,试求梁的挠曲线方程,并求最大挠度及最大转角。 解:① 建立坐标系并写出弯矩方程 ①
在小变形情况下, 曲线弯曲平缓, 在小变形情况下,挠曲线弯曲平缓,
∴ w′ ≪ 1
2
材料力学-弯曲应力
对于宽为b高为h的矩形截面:
W
bh3 12
bh2
h
6
2
对于直径为d的圆形截面:
W d 4 64 d 3
d
32
2
限定最大弯曲正应力不得超过许用应力,于是强度条件为:
max
M max W
设σt 表示拉应力,σc 表示压应力,则:
t max t
cmax c
塑性材料, [σt]= [σc]= [σ];
所以由(1)式:
A
d
A
A E
y
d
A
E
A y d
A
E
Sz
0
由(2)式:
说明中性轴过形心
A z
d
A
A zE
y
d
A
E
A
yz d
A
E
I yz
0
由于y轴是对称轴,此 式自然满足。
由(3)式:
A
y
d
A
A
yE
y
d
A
E
A
y2
d
A
E
Iz
M
1 M
EI z
1 为梁轴线变形后的曲率 ;
由变形几何关系得到 y
由物理关系得到
bh2 2b3 W
63
故: b 121.6 mm
h 2b 243.2 mm
选取截面为: 125 250 mm 2
e.g.3 已知:l=1.2m,[σ]=170MPa, 18号工字钢,不计自重。
求:P 的最大许可值。
P A
解:作弯矩图, 由图可得:
M
| M |max Pl 1.2P N m
螺纹基本尺寸及公差
螺纹基本尺寸及公差浙江苏强格液压有限公司质量作业文件产品代号规则Q/SQ-G8.4-031 过渡接头编号规则1.1 直通过渡接头编号规则直通过渡接头型号左端标号右端标号直通过渡接头型号中的第一位为数字,表示两端内外螺纹的组合情况;第二、三位为字母,分别表示左右端的结构型式,当左右端结构型式相同时,则使用一位字母,当左右端标号相同时,也使用一组标号。
1.1.1 型号中的第一位数字的含义如下表1 外螺纹/外螺纹 6 过板接头(右端过板)1 法兰/对接式焊接头 7 固定内螺纹/固定内螺纹(无螺母或插入焊)2 外螺纹/活动内螺纹(活动螺母) 8 锁母3 活动内螺纹/活动内螺纹 9 内螺纹堵头4 外螺纹堵头.堵板5 外螺纹/固定内螺纹5 外螺纹/较短焊接管1.1.2 型号中第二、三位字母的含义如下表A 英管螺纹球面 M 公制60?锥面或六角端面组合垫密封B 英管螺纹60?锥面或六角端面组合垫密封 N 美制布锥管C 公制24?轻系列 O 美制SAE O-Ring BOSSD 公制24?重系列 P 美制SAE 90?E 公制平面带O形圈 Q 公制74?F 美制ORFS平面 S 日式英管螺纹60?外锥G 英管螺纹平面、O-Ring密封 T 英锥管螺纹H 公制六角端面O-Ring密封 U NPSMI 710xx系列国标公制铰接体 W 焊接管J 美制JIC 74? X 表示与软管相连用卡环固定K 公制螺纹60?外锥(小松) Y 矿用接头(SAE标准)L 公制组合垫圈密封 Z BSP平面用组合垫密封1Q/SQ-G8.4-031.1.3 左右端标号根据左右端头部的螺纹或尺寸大小定,如下表:英管G1/8” G1/4” G3/8” G1/2” G5/8” G3/4” G1.1/4” G1.1/2” --G1”x11 G2”x11 螺纹 x28 x19 x19 x14 x14 x14 x11 x11 英锥管R1/8”R1/4” R3/8” R1/2” R3/4” R1.1/4” R1.1/2” -- -- R1”x11 R2”x11 螺纹x28 x19 x19 x14 x14 x11 x11 布锥管Z1/8” Z1/4” Z3/8” Z1/2” Z3/4”Z1.1/4” Z1.1/2” Z2” -- Z1”x11.5 螺纹 x27 x18 x18 x14 x14 x11.5 x11.5 x11.5 美制JIC 7/16” 1/2” 9/16” 3/4” 7/8” 1.1/16” 1.5/16” 1.5/8”1.7/8”2.1/2” -- 螺纹 x20 x20 x18 x16 x14 x12 x12 x12 x12 x12 美制ORFS9/16” 11/16” 13/16” 1” 1.3/16” 1.7/16” 1.11/16” 2” -- -- -- 螺纹 x18 x16 x16 x14 x12 x12 x12 x12 美制SAE5/8” 1.1/16” 螺纹 x18 x14 法兰1/2“ 5/8“ 3/4“ 1“ 1.1/4“ 1.1/2“ 2“ 插装式 04 06 08 12 16 20 24 32 标号 02 04 05 06 08 10 12 16 20 24 32 注:公制螺纹的标号按螺纹外径,卡套式直管的标号按直管外径。
板坯连铸机板坯连铸机液压系统系统..
M B4
T
P
20× 3
a
ab
P1 T1 L1
马达离合器动作 (带压啮合)
大包液压马达事故驱动 0.05M Pa
L
A1
B1
制动盘 (带 压制动)
释放
制动
12 ×2
制动
12 ×2
释放
大包 回转 台 机上 配 管
16×2 16×2
1 6×2
20X 3 20X 3
1 6×2
车 间配 管
阀台区
MA1 A1 B1 MB1
弧形扇形段由固定辊子的上下框架、辊子,连接上下 框架的液压缸,扇形段定位固定装置,气水自动连通 装置等组成。辊缝调节由分布在四个角的液压缸实现, 四个液压缸将上下框架连接起来,并使扇形段夹紧, 传动辊布置在中间并由液压缸压下;所有扇形段均采 用径向更换方式。
压下缸压力: 3-18MPa 扇形段1∼6 压下缸: Φ125/Φ90-140 (XJS06BBE125/720-80HD-B10) 压
为保持钢水温度,回转台设有钢包加盖装置。钢包加盖 装置设置在钢包回转台升降臂上,由两个可独立旋转和升降 的悬臂组成,旋转可由液压马达或液压缸驱动,升降由液压 缸驱动。
L2d1a Pbd1a T2d1a φ 18X3 φ 28X3
φ18x3 φ18x3 φ18x3 φ18x3
钢包升降(臂1)
L A DL E TU RR ET LI FT IN G / A RM 1
油 口连接尺 寸:G1/4
阀台 中间配管 结晶器上配管
φ16x2
最小报警压力 10MPa
SPAHM:
4 .1
SPALM:
-F001
6
5
4.2 Am 1
材料力学第八章-弯曲变形
L
A
L
解:建立静定基 确定超静定次数 用反力代替多余约束 得新结构 —— 静定基
或
q0
A
B L RB
32
q0 A L B RB
几何方程——变形协调方程
f B f Bq f BRB 0
物理方程
=
A B RB q0 A B
qL RB L f Bq ; f BRB 8EI 3EI
A A 铰连接
P
C D
C
D
B
A点:f A 0, A 0
B点: f B左 f B右
C点: f C左 f C右 C左 C右
D点:f D 0
21
边界条件、连续条件应用举例
P
弯矩图分二段,
共积分常数 需4个边界条件 和连续条件
A B
C
(+)
A点: A 0 B点: f B左 f B右 , C点:f C 0
解:载荷分解如图
=
P A B
查梁的简单载荷变形表,
得到变形
Pa PA 4 EI
q B
2
Pa f PC 6 EI
3
+
A
qa qA 3EI
3
5qL f qC 24 EI24
4
P
A
C a a
q B
Pa PA 4 EI
qa 3 qA 3EI
2
Pa 3 f PC 6 EI
Differential Equation of beam deformation 1 M ( x) 已知曲率为 EI z x
M>0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梁截面上的正应力
当梁上有横向外力作用时,一般情况下,梁的横截面上 既又弯矩 M , 又有剪力 FS 。
m M
FS m
m
m
M
FS
m
m
只有与切应力有关的切向内力元素 dFS = dA 才能合成剪力 只有与正应力有关的法向内力元素 dFN = dA 才能合成弯矩 所以,在梁的横截面上一般既有 正应力,又有 切应力
y (d ) dx
O1
dx
y
O2
d
y B B1
A
dx
y (d ) AB1 B1 B dx AB1 O1 O 2
中性层的曲率为
d
d dx 1
y
y
O1
dx y
O2
d
A
dx
B1
B
y
d
该式说明 , 和 y 坐标成正比 , 因而, 横截面上到中性轴等 远的各点,其线应变相等。
d
O1O2 的长度为 dx 。
O1
dx
O2
中性层与横截面的交线称
为 中性轴 。 中性轴与横截面的 对称轴成正交 。
d
O1
dx
O2
d
横截面的 对称轴
横截面
O1
dx
O2
中性层
中性轴
d Z
x
y
将梁的轴线取为 x 轴 。
O1
dx
O2
横截面的对称轴取为 y 轴 。 中性轴取为 z 轴 。
为中性层上的纵向线段 O1O2
M Z A y (dA)
E
A y dA
2
E
Iz M
1 M EI z
EIz 称为截面的抗弯刚度
y E E
My Iz
该式为等直梁 纯弯曲 时横截面上任一点处正应力的计算公式 式中 : M Iz y 横截面上的弯矩。 横截面对中性轴的惯性矩。 求应力点的 y 坐标 。
y
F N A dA 0
M y A z (dA) 0
M
Z
M Z A y (dA) M
y
O
x
dA
dA Z
该梁段各横截面上 FN 和 My 均 等于零, 而 Mz 就是横截面上 的弯矩 M 。
y
E E
E
y
E
Sz
F N A dA
A
ydA
横力弯曲时横截面上有切应力(翘曲) 平面假设 不再成立
此外, 横力弯曲时纵向纤维无挤压假设也不成立. 由弹性力学的理论,有结论: 当梁的长度l与横截面的高度h的比值:
l 5 h
则用纯弯曲的正应力公式计算横力弯曲时的正应 力有足够的精度。 l / h > 5 的梁称为细长梁。
4,讨论
My Iz
(1)应用公式时,一般将 M ,y 以绝对值代入。根据梁变形
的实际情况直接判断 的正,负号。
以中性轴为界
梁变形后凸出边的应力为拉应力( 为正号)
梁变形后凹入边的应力为压应力( 为负号)
My Iz
(2)横截面 中性轴上 各点的正应力最小。且 min = 0
M M C C Z
Z
b
c
dx
z 切应力互等定理:
单元体两个相互垂直平面上,沿垂直于两面交线作用的切应力必 定成对出现,且大小相等,都指相(或背离)该两平面的交线。
§9-5 弯曲切应力
一、矩形截面梁
图示一矩形截面梁受任意横向荷载作用。
P1
P2
q(x)
横力弯曲时, 横截面上既有正应力, 又有切应力。 推导切应力公式的方法: 假设切应力的分布规律,然后根据平衡条件求出 切应力。 按截面形状,分别讨论。 矩形截面梁的切应力分布假设: (1) 各点切应力方向平行于剪力FS;
几何 物理 静力学
实验: 取 一 纯弯曲 梁来研究 。
1,几何方面
m a n a
b m n
b
梁在加力前先在其侧面上画上一系列的横向线(如 mm ,nn 等) 以及横向线相垂直的一系列的纵向线 (如 aa ,bb 等) 。
m
a
n
a
m
m
b m n
b
梁变形后观察到的现象 (1)变形前相互平行的纵向直线(aa ,bb 等),变形后均为 圆弧线(a’a’ ,b’b’等 ),且靠上部的缩短靠下部的伸长。
o
I xy A xydA
x
x
一,纯弯曲梁横截面上的正应力
RA P P RB
C a P
D a
+
+
P
Pa
+
P
P
C a D a
横力弯曲
梁的横截面上同时有弯 矩和剪力的弯曲。
P
纯弯曲
+ +
P
梁的横截面上只有弯矩 没有剪力的弯曲。
横截面上只有正应 力而无切应力。
Pa
+
推导 纯弯曲 梁横截面上正应力的计算公式。
(2) 切应力沿宽度均匀分布。
(1)推导公式的思路
1
F1
F2
m n
q(x)
假想地用横截面 m—m , n—n
从梁中截取 dx 一段 。
两横截面上均有剪力和弯矩。 弯矩 剪力 正应力, 切应力。
M
m x dx
n
m FS
n FS M+dM
m
n
m M FS
n
m
FS
M+dM
n
y
m n
m
n
正应力()分布图
y
O1
dx
O2
d
y
A dx dx
B1
B
d
y
Z
O
O1
x
dx
O2
d
y y
y
y
A dx dx
B
B1
2,物理方面 假设: 纯弯曲时横截面上各点处的处于单轴应力状态 。 材料在线弹性范围内工作,且拉,压弹性模量相等 。 由单轴应力状态下的 胡克定律 可得物理关系
=E
y
E
截面的几何性质
静矩和形心
惯性矩和惯性积
惯性矩和惯性积的平行移轴公式,主轴和主惯性矩
组合截面惯性矩的计算
截面对 y , x 轴的静矩为:
S y A xdA
I x A y dA
2
y
S x A ydA
dA
y
2 I y A x dA
截面对 x , y 轴的惯性矩
截面对 x , y 轴的惯性积
M C 2.5KN .m
M B 3KN .m
最大负弯矩在截面B上
80
RA
P1=8KN
RB
P2=3KN
35
20
A
1m
z c
1m
3
B
1m
D
80
65
20
C
B
+
2.5
B 截面
{
MB t max
0.035
Iz M B 0.065 67.1MPa c max Iz
36.1MPa
C
Z
C
Z
中性轴 中性轴
y y
M
压
M C Z
拉
C
Z
中性轴
中性轴 拉
y
y
压
中性轴将横截面分为 受拉 和 受压 两部分。
My
A z (dA)
E
A z
y dA
E
I yz 0
I yz 0
因为 y 轴是横截面的对称轴,所以 Iyz 一定为零。 该式自动满足
中性轴是横截面的形心主惯性轴
中性轴 中性轴
y
y
My Iz
(3)最大正应力发生在横截面上离中性轴最远的点处
中性轴为对称轴
My Iz
tmax
拉 M
yt max
Z
C
压
yc max
Cmax
y
tmax
拉
M
yt max
Z
C
压
yc max
Cmax
y
My Iz
用 ymax 表示最大 拉(压)应力点到中性轴的距离。
对于中性轴不是对称轴的横截面
Cmax
yc max
M
z
yt max
y
tmax
Cmax
yc max
M
z
yt max
y
tmax
应分别以横截面上受拉和受压部分距中性轴最远的距离 ytmax 和 yCmax 直接代入公式。求得相应的最大拉应力和最大压应力。
Cmax
σ c max
yc max
A z
0
E I yz 0
My
A z (dA)
E
y dA
M Z A y (dA)
E
A y dA
2
E
Iz M
F N A dA
E
A ydA
E
Sz
0
SZ 0
中性轴必通过横截面的形心
中性轴过截面形心且与横截面的对称轴 y 垂直
IZ WZ y max
