17.2.2函数的图象(2)
新华东师大版八年级数学下册《17章 函数及其图象 17.2 函数的图象 阅读材料 笛卡尔的故事》教案_2

《阅读材料:笛卡尔的故事》教学设计教学目标:1.知识与技能:笛卡尔的生平,以及他对各领域的贡献。
2.过程与方法:通过自主查阅资料,小组介绍的方式让大家了解笛卡尔,以及笛卡尔坐标系的产生和发展,从而锻炼学生的自学总结和合作交流的能力。
3.情感态度价值观:在学习的过程中,培养学生独立思考精神,和对数学史的探索精神。
教学重难点:1.重点:笛卡尔在数学领域的贡献,主要体现在解析几何方面,为微积分奠定了基础。
2.难点:解析几何的理解和笛卡尔斜角坐标系的理解。
教学过程:一、背景介绍,先入为主著名的法国哲学家、科学家和数学家,西方现代哲学思想的奠基人,是近代唯物论的开拓者。
提出了“普遍怀疑”的主张。
最重要的贡献是创立了解析几何。
他的这一成就为微积分的创立奠定了基础。
创立了坐标系,成功地将当时完全分开的代数学和几何学联系到了一起。
二、小组展示,解读探究各小组展示他们对笛卡尔在哲学、天文学、物理学和数学领域的主要成就。
笛卡尔的方法论笛卡尔研究问题的四个出发点“我思故我在”关于上帝存在的证明物质实体和身心二元论(二)天文学1.发展了宇宙演化论,提出了天体演化说,形成了他关于宇宙发生与构造的学说。
2.创立了漩涡说。
(三)物理学1. 运用坐标几何学从事光学研究,在《屈光学》中第一次对折射定律提出了理论上的推证。
2. 对人眼进行光学分析,解释了视力失常的原因是晶状体变形,设计了矫正视力的透镜。
3. 在《哲学原理》第二章中以第一和第二自然定律的形式比较完整地第一次表述了惯性定律。
4. 在《哲学原理》第二章中他还第一次明确地提出了动量守恒定律。
5. 在力学上,笛卡尔发展了伽利略的运动相对性的思想,提出了运动与静止需要选择参照物的道理。
6. 他还发展了宇宙演化论、漩涡说等理论学说,虽然具体理论有许多缺陷,但依然对以后的自然科学家产生了影响。
7. 对碰撞和离心力等问题曾作过初步研究,给后来惠更斯的成功创造了条件。
笛卡尔最杰出的数学成就是在创立了坐标系后成功地创立了解析几何学,并为微积分的创立奠定了基础。
平面直角坐标系

17.2.1平面直角坐标系导学案班级____班级_____学习目标:1、认识平面直角坐标系,了解点的坐标的意义,正确画坐标和找对应点。
2、理解平面内的点与有序数对的一一对应关系。
学习重难点:平面直角坐标系和点的坐标.一、独立看书34——35页(8分钟)二、学习导航:1、平面直角坐标系在平面内画两条互相__、原点重合的数轴,组成____________.水平的数轴称为______,习惯上取______为正方向;竖直的数轴称为__________,取______为正方向;两坐标轴的交点为平面直角坐标系的_____. 请你动手,在页面空白处画一个平面直角坐标系。
2、点的坐标(1)已知点的位置写坐标:有了平面直角坐标系,平面内的点就可以用一个坐标来表示了.图中点A的坐标是(3,4),请写出点B、C、D的坐标:B(___,___)、C(___,___)、D(___,___).原点的坐标是(___,___).(2)已知点坐标确定点的位置:如给你一个坐标G(-2,3),则先在x轴上找到表示-2的点,过这个点做x轴的垂线;再在y 轴上找到表示3的点,过这个点做y轴的垂线,两条垂线的交点为G(-2,3)。
你能画出已知点E(-5,0),F(5,-2)吗?,请在图中画出点E、F.平面内点的坐标是有序数对,其顺序是_____在前,____在后,中间用“,”分开.当a b≠时,(),a b和(),b a表示相同的点吗?3、象限的概念(1)建立了平面直角坐标系的平面是坐标平面,坐标平面被两条坐标轴分成四个部分,分别叫做第一、二、三、四象限. 如上图中的点A在第___象限,点B在第___象限.坐标轴上的点不属于_____.(2)坐标平面内的点的坐标有如下特征:点(),P x y在第一象限:0,0.>>x y点(),P x y在第二象限:_________.点(),P x y在第三象限:_________.点(),P x y在第四象限:_________.点(),P x y在x轴上:点(),P x y在y轴上:点(),P x y在原点上:三、练习案:【第一关】1. . 写出图中点A、B、C、D、E、F的坐标.2. 在上图中描出下列各点:L(-2, 3),M(-4,-1),N(4,5),P(2.5,-2).,Q(0,-4)3. 在平面直角坐标系中,点P的坐标为(-4,6),则点P在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限★4.已知有一点P(m-1,m+2)在直角坐标系中的x轴上,则点P的坐标为(,)。
2022年华师大版八年级数学下册第十七章《函数的图形(第1课时-平面直角坐标系)》优课件 (2)

-1,-4,2.5,0,-1.5,-3,0.5
–4–3 –2 –1 0 1 2 3 4 5 6
Байду номын сангаас
讲台
第一排 第二排 第三排 第四排 第五排 第六排 第七排 第八排
第一组
黄平 田静 阿米 郭璐 王璐 权智威 陈学良 朱凯
第二组
李鑫 李科 虞苗苗 张泽 郑怡 崔珊珊 陈巍 张天
C
-1
-2
-3
1 23 4x D
课堂练习<2>
4.在坐标系中描出下列各点: A(4,3)、B(-4,1)、C(-3,-3)、
D(3,-2)、E(-2,0)、F(0,2)
课堂练习<3>
y
黄平 李鑫 卢璐 杨 杨 宫珊 王涛
田 静 李 科 木妮热 漆佳莹 韩丽娟 艾能达
阿米 郭璐 王璐
虞苗苗 张泽 郑怡
1N A
-3 -2 -1 O
M 1 2 3x
-1
-2
-3
想一想:
我为们什么规不定是(:1,2) 横坐标在前,纵坐标在后
例 1 写出图中A、B、C、D、各点的坐标。
y
3
D
2A
1
B
-4 -3 -2 -1 O -1
C
-2
-3
1 23 4x
例 2 写出图中A、B、O各点的坐标。
y
3
2
1
-4 -3 -2 -1 O -1
c. A点在数轴上的坐标是2。
d. B点在数轴上的坐标是-3。
课堂练习<1>
1.写出A、B、C、D、E各点在数轴上的坐标。
17.2实际问题与反比例函数2

例1 小伟欲用雪撬棍撬动一块大石头,已知阻力和阻力
臂不变,分别为1200牛顿和0.5米.
(1)动力F与动力臂L有怎样的函数关系?当动力臂为
1.5米时,撬动石头至少需要多大的力?
解:
(1)根据“杠杆定律”有 FL=1200×0.5
得函数关系式 当L=1.5时,
600 F (l 0) l
600 F 400 1.5
D
SAOB SONB SONA 4 2 6.
分析:根据动力×动力臂=阻力×阻力臂 解:(1)由已知得F×L=1200×0.5 变形得: F 600 L
问题与情景
(2)小刚、小强、小健、小明分别选取了动力臂 为1米、1.5米、2米、3米的撬棍,你能得出 600 他们各自撬动石头至少需要多大的力吗? F 从上述的运算中我们观察出什么规律? 解:(2)
1.2 1032 F L
当F=500时,L=2.4×1029米
阻力×阻力臂=动力×动力臂
阻力
阻力臂 动力臂
动力
例1
小伟欲用雪撬棍撬动一块大石头,已知阻力和阻力 臂不变,分别为1200牛顿和0.5米. (1)动力F与动力臂L有怎样的函数关系?当动力臂为 1.5米时,撬动石头至少需要多大的力? (2)若想使动力F不超过题(1)中所用力的一半,则 动力臂至少要加长多少?
解:(1)U=IR=2×5=10V (2)把I=0.5代入
10 I R
10 I R
,得:R=20
古希腊科学家阿基米德曾 说过:“给我一个支点, 我可以把地球撬动。”
你认为这可能吗?为什么?
阻力
阻力臂 动力臂
动力
阻力×阻力臂=动力×动力臂
问题与情景
问题1:几位同学玩撬石头的游戏,已知阻力和 阻力臂不变,分别是1200牛顿和0.5米, 设动力为F,动力臂为L.回答下列问题: (1)动力F与动力臂L有怎样的函数关系? (2)小刚、小强、小健、小明分别选取了动力臂 为1米、1.5米、2米、3米的撬棍,你能得出 他们各自撬动石头至少需要多大的力吗? 从上述的运算中我们观察出什么规律?
17.2.2 函数的图象-2020-2021学年八年级数学下课堂专练(华师大版)(解析版)
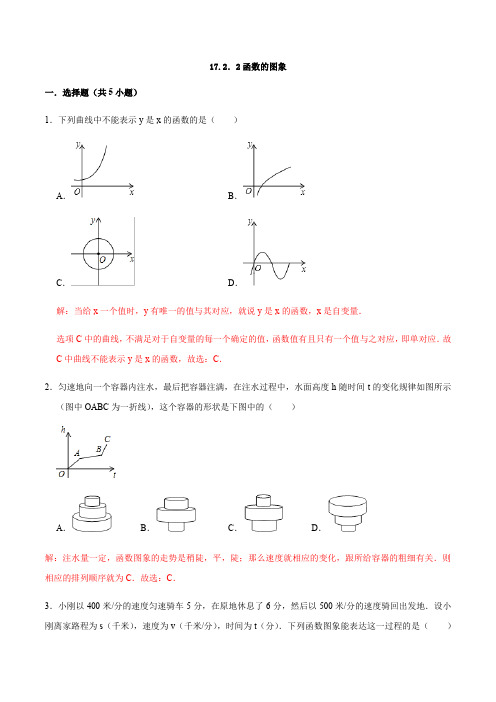
17.2.2函数的图象一.选择题(共5小题)1.下列曲线中不能表示y是x的函数的是()A.B.C.D.解:当给x一个值时,y有唯一的值与其对应,就说y是x的函数,x是自变量.选项C中的曲线,不满足对于自变量的每一个确定的值,函数值有且只有一个值与之对应,即单对应.故C中曲线不能表示y是x的函数,故选:C.2.匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的()A.B.C.D.解:注水量一定,函数图象的走势是稍陡,平,陡;那么速度就相应的变化,跟所给容器的粗细有关.则相应的排列顺序就为C.故选:C.3.小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地.设小刚离家路程为s(千米),速度为v(千米/分),时间为t(分).下列函数图象能表达这一过程的是()A.B.C.D.解:由题意,得以400米/分的速度匀速骑车5分,路程随时间匀速增加;在原地休息了6分,路程不变;以500米/分的速度骑回出发地,路程逐渐减少,故选:C.4.图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是()A.体育场离张强家2.5千米B.张强在体育场锻炼了15分钟C.体育场离早餐店4千米D.张强从早餐店回家的平均速度是3千米/小时解:A、由函数图象可知,体育场离张强家2.5千米,故A选项正确;B、由图象可得出张强在体育场锻炼30﹣15=15(分钟),故B选项正确;C、体育场离张强家2.5千米,体育场离早餐店距离无法确定,因为题目没说体育馆,早餐店和家三者在同一直线上,故C选项错误;D、∵张强从早餐店回家所用时间为95﹣65=30(分钟),距离为1.5km,∴张强从早餐店回家的平均速度1.5÷0.5=3(千米/时),故D 选项正确.故选:C .5.一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程随时间变化的图象如图所示,下列结论错误的是( )A .轮船的速度为20千米/小时B .快艇的速度为803千米/小时C .轮船比快艇先出发2小时D .快艇比轮船早到2小时解:轮船的速度为:160÷8=20千米/小时,快艇的速度为:160÷(6﹣2)=40千米/小时,故A 正确,B 错误;由函数图象可知,C 、D 正确.故选:B .二.填空题(共3小题)6.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y (米)与时间t (分)的函数图象,则小明回家的速度是每分钟步行 80 米.解:通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),所以小明回家的速度是每分钟步行800÷10=80(米).故答案为:80.7.如图,这是一个数据转换器的示意图,三个滚珠可以在槽内左右滚动.输入x的值,当滚珠发生撞击,就输出相撞滚珠上的代数式所表示数的和y.已知当三个滚珠同时相撞时,不论输入x的值为多大,输出y的值总不变.(1)a=﹣2;(2)若输入一个整数x,某些滚珠相撞,输出y值恰好为﹣1,则x=2.解:(1)(2x﹣1)+3+ax=2x﹣1+3+ax=(2+a)x+2,∵当三个滚珠同时相撞时,不论输入x的值为多大,输出y的值总不变,∴2+a=0,得a=﹣2,故答案为:﹣2;(2)当y=2x﹣1+3=2x+2时,令y=﹣1,则﹣1=2x+2,得x=﹣1.5(舍去),当y=3+(﹣2x)=﹣2x+3时,令y=﹣1,则﹣1=﹣2x+3,得x=2,故答案为:2.8.如图(1)是两圆柱形联通容器(联通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲容器的底面半径为1cm,则乙容器的底面半径为2cm.解:观察函数图象可知:乙容器底面积为甲容器底面积的4倍,∴乙容器底面半径为2cm.故答案为:2三.解答题(共2小题)9.在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:情境a:小芳离开家不久,发现把作业本忘在家里,于是返回了家里找到了作业本再去学校;情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.(1)情境a,b所对应的函数图象分别是③、①(填写序号);(2)请你为剩下的函数图象写出一个适合的情境.解:(1)∵情境a:小芳离开家不久,即离家一段路程,此时①②③都符合,发现把作业本忘在家里,于是返回了家里找到了作业本,即又返回家,离家的距离是0,此时②③都符合,又去学校,即离家越来越远,此时只有③返回,∴只有③符合情境a;∵情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进,即离家越来越远,且没有停留,∴只有①符合,故答案为:③,①.(2)情境是小芳离开家不久,休息了一会儿,又走回了家.10.李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)李大爷自带的零钱是多少?(2)降价前他每千克黄瓜出售的价格是多少?(3)卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,问他一共批发了多少千克的黄瓜?(4)请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?解:(1)由图可得农民自带的零钱为50元.(2)(410﹣50)÷100=360÷100=3.6(元).答:降价前他每千克黄瓜出售的价格是3.6元;(3)(530﹣410)÷(3.6﹣1.6)=120÷2=60(千克),100+60=160(千克).答:他一共批发了160千克的黄瓜;(4)530﹣160×2.1﹣50=144(元).答:李大爷一共赚了144元钱.。
华东师大版八年级下册17.2 函数的图形(第1课时 平面直角坐标系)

徐源 罗杰元 周婉婷 胡国平 徐颖婷 宋博熙 朱子迅 王婷婷 程虹杰 邓芹苛
赵紫鹏 易国庆 刘安然
O
聂睿 4
周权红 简桢宸 何亚舟 何明星
x
杜文骏 李品龙
1 2
颜果
3
罗明聪 黄彬伦 魏嘉浚 曹秘丸
5 讲台 6 7
龙飞
8
前门
以宋搏熙为原点建立直角坐标系。
探索
• • • • 1.在各个象限内点的坐标的特点 2.在x轴,y轴上的点的坐标的特点 3.原点o的坐标 4.关于x轴与y轴对称的两点的特 点 • 关于原点对称的两点的特点 • 5.平面直角坐标系内的点P(a,b)到 x轴和y轴的距离.
2.用A、B、C、D、E、F、G在数轴上 标出如下各点的位置:
-1,-4,2.5,0,-1.5,-3,0.5
–4 – 3 –2 –1 0 1 2 3 4 5 6
7
桂宾 唐雨锋 欧阳雪 邓杨 朱军 赵紫鹏 杜文骏 1
周俊佑
范佳伟
余卓
陈飞宇
张忍吉
周睿哲
罗梓阳
6
马可
黄璐瑞 江成灏 胡国平 易国庆 李品龙 2
平面直角坐标系
(对称点坐标)
ⅱ、如图,以矩形ABCD的中心为原点建立平面 直角坐标系: (1)点A与点B有什么位 y 置关系?点C与点D呢? A D (3, 5) 点A与点B关于x (–3, 5) 轴对称,点C与点D 关于x轴对称; (2)关于x轴对称的点的 O x 坐标有什么特征? 关于x轴对称的点 B C 横坐标相同,纵坐标 (3, –5) (–3, –5) 互为相反数。
华东师大版八年级(下册)
第17章 函数及其图象
17.2 函数的图象(第1课时)
复习引入
第17章 函数及其图象
知识点 函数的表示方法
棱长为a的小正方体,按照如图所示的方法一直
摆放下去,自上而下分别叫第1层,第2层,…,第n(n>0)层,第n层的小正方体 的个数记为S,则第n个图中第n层小正方体的个数S可用下表来表示:
知识点 函数的表示方法
第1个图有1层,共1个小正方体; 第2个图有2层,第2层共有小正方体的个数为1+2=3; 第3个图有3层,第3层小正方体的个数为1+2+3=6,…, 以此类推,第n个图有n层,第n层小正方体的个数为S=1+2+3+4+…+n=
知识点 一次函数的性质
(1)当k>0时,y随x的增大而增大,这时函数的图象从左向右呈现上升趋势.
知识点 一次函数的性质
(2)当k<0时,y随x的增大而减小,这时函数的图象从左向右呈现下降趋势.
知识点 一次函数的性质
由k,b的符号可以确定一次函数y=kx+b(k≠0)图象所经过的象限;反过来, 由一次函数y=kx+b(k≠0)图象所经过的象限也可以确定k,b的符号.
k
知识点 反比例函数y= x (k≠0)的图象和性质
双曲线教堂 伦敦著名的建筑事务所steynstudio,最近在南非,美丽的乡村庄园中完成 了一个惊艳世界的作品——双曲线建筑的教堂,建筑师通过双曲线的设 计元素赋予了这座教堂轻盈、极简和雕塑般的气质.
k
知识点 反比例函数y= x (k≠0)的图象和性质
知识点 平面直角坐标系内点的坐标特征
(2)平面直角坐标系中对称点的坐标特征:
知识点 函数的图象及其画法
“龟兔赛跑”讲述了这样的故事:兔子和乌龟同时起跑后,领先的兔子看着慢慢 爬行的乌龟骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙 追赶,但为时已晚,乌龟还是先到达了终点……下面表示的是乌龟和兔子所行 的路程s与时间t的函数图象,你觉得这个图象与故事情节相吻合关概念
三角、反三角函数图像
六个三角函数值在每个象限的符号:
sinα·cscα cosα·secα tanα·cotα
三角函数的图像和性质:
函数
y=sinx
y=cosx
y=tanx
y=cotx
定义域
R
R
{x|x∈R且x≠kπ+ ,k∈Z}
{x|x∈R且x≠kπ,k∈Z}
值域
[-1,1]x=2kπ+ 时ymax=1
奇偶性
arcsin(-x)=-arcsinx
arccos(-x)=π-arccosx
arctan(-x)=-arctanx
arccotห้องสมุดไป่ตู้-x)=π-arccotx
周期性
都不是同期函数
恒等式
sin(arcsinx)=x(x∈[-1,1])arcsin(sinx)=x(x∈[- , ])
cos(arccosx)=x(x∈[-1,1]) arccos(cosx)=x(x∈[0,π])
y=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosy
y=tanx(x∈(- , )的反函数,叫做反正切函数,记作x=arctany
y=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty
理解
arcsinx表示属于[- , ]
且正弦值等于x的角
arccosx表示属于[0,π],且余弦值等于x的角
在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)
在(kπ- ,kπ+ )内都是增函数(k∈Z)
在(kπ,kπ+π)内都是减函数(k∈Z)
.反三角函数:
17.2.2函数的图象 2
3.小明家距学校m 千米,一天他从 家上学先以a千米 /时的匀速跑步 锻炼前进,后以 匀速b千米/时步 行到达学校,共 用n小时。右图中 能够反映小明同 学距学校的距离s (千米)与上学 的时间t(小时)之 间的大致图象是 (C )
4.某装水的水池按一定的速度放掉水池的一 半后,停止放水并立即按一定的速度注水,水 池注满后,停止注水,又立即按一定的速度放 完水池的水。若水池的存水量为v(立方米), 放水或注水的时间为t(分钟),则v与t的关 系的大致图象只能是( A )
(2)作出函数图象,并结合图象指出重叠部分面积的 最大值.
1 2 y x (0≦x≦10) 2
1 2 y x 0 x 10 2
x 1 y 0.5 2 y
50 40 30 20 10 -2 -1
3
4
5
6
7
8
9
10
2 4.5
8 12.5 18 24.5 32 40.5 50
o
-1 -2
3 4 5 … -2 -1.5 -1.2 …
解:(1)列表 取自变量 的一些值,并求出对 应的函数值,填入表 中. (2)描点 分别以表中 对应的x、y为横纵 坐标,在坐标系中描 出对应的点. (3)连线 用光滑的曲 线把这些点依次连 接起来.
为什么没有 “0”?
y
x
(1,-6)
3 0.5 1.若点(a,6),在函数y= 的图象上,则a=___. x
-7 2.若函数y=kx+5的图象经过(1,-2),则k=_______. 10 3、已知点Q(-8,6),它到原点的距离是_____
4、在平面直角坐标系内,已知点(1-2a,a-2) 在第三象限的角平分线上,求a的值及点的坐标?
华师大版数学八年级下册17.2《函数的图象》(第1课时)教学设计
华师大版数学八年级下册17.2《函数的图象》(第1课时)教学设计一. 教材分析《函数的图象》是华师大版数学八年级下册17.2章节的第1课时,本节课的主要内容是让学生了解函数的图象,掌握一些基本的函数图象,如正比例函数、一次函数和二次函数的图象,并能够通过图象来分析函数的性质。
教材通过具体的例子引导学生从数形结合的角度去理解函数,培养学生的数形结合思想。
二. 学情分析学生在八年级上学期已经学习了函数的概念和性质,对函数有一定的理解。
但是,对于函数的图象,学生可能还比较陌生,需要通过具体的例子和实践活动来加深理解。
此外,学生可能对如何绘制函数图象还不够熟练,需要在本节课中进行操练和巩固。
三. 教学目标1.了解函数的图象,能够通过图象来分析函数的性质。
2.掌握正比例函数、一次函数和二次函数的图象的绘制方法。
3.培养学生的数形结合思想,提高学生的数学思维能力。
四. 教学重难点1.重难点:函数的图象,如何通过图象来分析函数的性质。
2.难点:正比例函数、一次函数和二次函数的图象的绘制方法。
五. 教学方法1.采用问题驱动的教学方法,引导学生从实际问题中抽象出函数的图象。
2.采用数形结合的教学方法,让学生通过绘制图象来理解函数的性质。
3.采用分组合作的学习方法,让学生在小组内共同探讨和学习函数的图象。
六. 教学准备1.准备一些实际的例子,让学生能够从实际问题中抽象出函数的图象。
2.准备函数图象的绘制工具,如纸张、直尺、圆规等。
3.准备一些函数图象的图片,让学生能够直观地看到函数的图象。
七. 教学过程1.导入(5分钟)通过一些实际的例子,让学生感受函数的图象,引导学生从实际问题中抽象出函数的图象。
2.呈现(10分钟)展示一些正比例函数、一次函数和二次函数的图象,让学生直观地看到函数的图象,并引导学生分析函数的性质。
3.操练(10分钟)让学生分组合作,自己动手绘制一些正比例函数、一次函数和二次函数的图象,并分析图象的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5题p41: 等腰三角形的周长为12 (2) 3<x<6 (1) y=12-2x y 12
11 10 9 8 7 6 5 4 3
x
x
A(3,6)
y
2 1
-1 o 1 2 3 4
B(6,0)
5 6
x
第 6题 s(千米)
30 25 20
10
o
……
8
9
10
11
12 13t(时)
3.小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了 一段时间,然后回家.下面的图描述了小明在散步过程中离家的距离s(米)与散 步所用时间t(分)之间的函数关系 .请你由图具体说明小明散步的情况. s(米)
450 400 350 300 250 200 150 100
50
解 小明先走了约3分钟,到达离家250 米处的一个阅报栏前看了5分钟报,又 向前走了2分钟,到达离家450米处返 回,走了6分钟到家.
17.2.2函数的图象
函数的图象(二)
复习回忆
1、描点法画函数图象有哪些步骤?
2、如何判断一个点是否在函数图像上?
问题1
300
y(米)
(1)小强让爷爷先上多少米?60米 (2)山顶高多少米?谁先爬上山顶?
山顶离山脚的距离有300米,小强先爬上山顶.
240
180
爷爷
120
60
小强
o
1
2
3
4
5
6
7
8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
o
t(分)
试一试(3)如图,等腰直角△ABC的直角边长与正
方形MNPQ的边长均为10 cm,AC与MN在同一直线 上,开始时 A 点与 M 点重合,让△ ABC 向右运动, 最后A点与N点重合.试写出重叠部分面积 y cm2与 MA长度x cm之间的函数关系式.
作出函数图象,并结合图象指出重叠部分面积的最大值.
1 2 y x 2
1 2 y x 0 x 10 2
x 1 y 0.5 2 y
50 40 30 20 10 -2 -1
3
4
5
6
7
8
9
10
2 4.5
8 12.5 18 24.5 32 40.5 50
o
-1
1
2
3
4
5
6
7
8
9
10
x
-2
9
10
11
x(分)
练习 1.下图为世界总人口数的变化图.根据该图回答: (1)从1830年到1998年,世界总人口数呈怎样的变化趋势? (2)在图中,显示哪一段时间中世界总人口数变化最快?
y
60 50
40
30 20 10
o
1830
1930
1960
1987 1976 1998
x
2.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中 能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的 函数关系的是( ).
