第3章 线性控制系统的时域分析
合集下载
自动控制原理(3-1)

动态性能指标定义1
hh((tt))
AA
超超调调量量σσ%% ==
AA BB
110000%%
峰峰值值时时间间ttpp BB
上上 升升 时时间间ttrr
调调节节时时间间ttss
tt
动态性能指标定义2 h(t)
调节时间 ts
上升时间tr
t
动态性能指标定义3
h(t)
A
σ%=
A B
100%
B tr tp
一阶系统对典型输入的输出响应
输入信号
输出响应
1(t) 1-e-t/T t≥0
δ(t)
1 et T t 0
T
t
t-T(1-e-t/T) t≥0
1 t2
1 t 2 Tt T 2 (1 et T ) t 0
2
2
由表可见,单位脉冲 响应与单位阶跃响应 的一阶导数、单位斜 坡响应的二阶导数、 单位加速度响应的三 阶导数相等。
自动控制原理
朱亚萍 zhuyp@ 杭州电子科技大学自动化学院
第三章 线性系统的时域分析法
3.1 系统时间响应的性能指标 3.2 一阶系统的暂态响应 3.3 二阶系统的暂态响应 3.4 高阶系统的暂态响应 3.5 线性系统的稳定性分析 3.6 控制系统的稳态误差 3.7 利用MATLAB对控制系统进行时域分析
超调量σ%:指响应的最大偏离量h(tp)与终值 h(∞)的差与终值h(∞)比的百分数,即
% h(tp ) h() 100%
h()
在实际应用中,常用的动态性能指标多为上升 时间tr、调整时间ts和超调量σ%。 用上升时间tr或峰值时间tp评价系统的响应速度; 用超调量σ%评价系统的阻尼程度;
第三章 线性系统时域分析法 第2讲

1
[
e
( 2 1 )n t
e
( 2 1 )n t
2 1
]
1时,二阶系统的单位阶跃响应含有两个衰减指 从上式看出,
数项。当阻尼比
远大于1时,闭环极点 s ( 2 1) 1 n
n 3 n 2 1 n
一定时,随n 的增大,系统的响应速度变快。
4、无阻尼情况 0
0 时 ,特征根为一对纯共轭虚数,将欠阻尼二阶系统的单 位阶跃响应中的 用零代替,可得到无阻尼二阶系统的单位阶
跃响应为:
C(t ) 1 sin(nt 900 ) 1 cos(nt )
同时反映响应速度和阻尼程度的综合性指标。
% 评价系统的阻尼程度。
1.等价关系——线性定常系统的重要特性: 系统对输入信号导数的响应,就等于系统对该输入信号响 应的导数; 系统对输入信号积分的响应,就等于系统对该输入信号响 应的积分; 注意:积分常数由零初始条件确定。该结论可推广至高阶系统。 2.动态特性: 由时间常数T决定。T响应速度,即响应时间,反之亦 然 3.跟踪能力: 阶跃输入无稳态误差,能跟踪阶跃信号,跟踪速度取决于T; 斜坡输入有位置误差,且稳态误差等于时间常数T; 加速度输入稳态误差无穷大,一阶系统不能跟踪加速度信号。 4. 一阶系统只有一个特征参数T,即时间常数。在一定的输入 信号作用下,其时间响应c(t)由其时间常数惟一确定。
越大,超调量越小,响应速度越慢;决定了系统振荡特性
2) 0 1时,系统输出有超调,且
n 越大,响应速度越快。
3) 1时,系统输出无超调,系统的响应速度随
的
增大而变慢,随 n 的增大而变快。
二阶系统极点分布同单位阶跃响应之间的对应关系
[
e
( 2 1 )n t
e
( 2 1 )n t
2 1
]
1时,二阶系统的单位阶跃响应含有两个衰减指 从上式看出,
数项。当阻尼比
远大于1时,闭环极点 s ( 2 1) 1 n
n 3 n 2 1 n
一定时,随n 的增大,系统的响应速度变快。
4、无阻尼情况 0
0 时 ,特征根为一对纯共轭虚数,将欠阻尼二阶系统的单 位阶跃响应中的 用零代替,可得到无阻尼二阶系统的单位阶
跃响应为:
C(t ) 1 sin(nt 900 ) 1 cos(nt )
同时反映响应速度和阻尼程度的综合性指标。
% 评价系统的阻尼程度。
1.等价关系——线性定常系统的重要特性: 系统对输入信号导数的响应,就等于系统对该输入信号响 应的导数; 系统对输入信号积分的响应,就等于系统对该输入信号响 应的积分; 注意:积分常数由零初始条件确定。该结论可推广至高阶系统。 2.动态特性: 由时间常数T决定。T响应速度,即响应时间,反之亦 然 3.跟踪能力: 阶跃输入无稳态误差,能跟踪阶跃信号,跟踪速度取决于T; 斜坡输入有位置误差,且稳态误差等于时间常数T; 加速度输入稳态误差无穷大,一阶系统不能跟踪加速度信号。 4. 一阶系统只有一个特征参数T,即时间常数。在一定的输入 信号作用下,其时间响应c(t)由其时间常数惟一确定。
越大,超调量越小,响应速度越慢;决定了系统振荡特性
2) 0 1时,系统输出有超调,且
n 越大,响应速度越快。
3) 1时,系统输出无超调,系统的响应速度随
的
增大而变慢,随 n 的增大而变快。
二阶系统极点分布同单位阶跃响应之间的对应关系
第三章 线性系统的时域分析法(第三四五讲)
若变号系统不稳定!
变号的次数为特征根在s右半平面的个数!
劳斯表出现零行
设系统特征方程为:
s4+5s3+7s2+5s+6=0 劳 斯 表
s4 1 s3 5 1 s2 6 1 s1 0 2 s0 1 7 6 1 5 6 1 这是零行
① 有大小相等符号相反的 特征根时会出现零行 ② 由零行的上一行构成 辅助方程:
或 %
100%
tg
e
100%
欠阻尼二阶系统动态性能计算
tr d
tr 特征根的虚部
弧度
tp d
tp 特征根的虚部
cos
5%
3.5 ts n
% e
1 2
100%
tg
3.5 ts 特征根的实部
n=[0.05 10]; d=[0.0025 0.5125 2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析
3.4 高阶系统的时域分析
3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
1
t T 2 2
0<ξ<1 s1, 2 n jjn 1 2 ξ=0 0<ξ<1
0
h( t ) 1 ξ=0 e n t 1
2
j 0 0 j
sin(,d jn 欠阻尼t ) s1 2
0 零阻尼 h(t ) 1 cos n t
欠阻尼二阶系统动态性能分析
它们的阶跃响应曲线如图所示,试在同一平面画出3个系统闭环 极点的相对位置,并说明理由。
变号的次数为特征根在s右半平面的个数!
劳斯表出现零行
设系统特征方程为:
s4+5s3+7s2+5s+6=0 劳 斯 表
s4 1 s3 5 1 s2 6 1 s1 0 2 s0 1 7 6 1 5 6 1 这是零行
① 有大小相等符号相反的 特征根时会出现零行 ② 由零行的上一行构成 辅助方程:
或 %
100%
tg
e
100%
欠阻尼二阶系统动态性能计算
tr d
tr 特征根的虚部
弧度
tp d
tp 特征根的虚部
cos
5%
3.5 ts n
% e
1 2
100%
tg
3.5 ts 特征根的实部
n=[0.05 10]; d=[0.0025 0.5125 2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析
3.4 高阶系统的时域分析
3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
1
t T 2 2
0<ξ<1 s1, 2 n jjn 1 2 ξ=0 0<ξ<1
0
h( t ) 1 ξ=0 e n t 1
2
j 0 0 j
sin(,d jn 欠阻尼t ) s1 2
0 零阻尼 h(t ) 1 cos n t
欠阻尼二阶系统动态性能分析
它们的阶跃响应曲线如图所示,试在同一平面画出3个系统闭环 极点的相对位置,并说明理由。
第3章 线性系统的时域分析第九节_3

(3)根轨迹起始于开环极点,终止于开环零点
说明 当根轨迹增益K1从0变化到∞时,在s平面就会画 出一条一条的根轨迹,每条根轨迹都有起点和终 点,对应于K1 =0的s点叫根轨迹的起点,对应于 K1 →∞的s点叫根轨迹的终点。 由幅值条件
可见 当s=pj时, K1 =0 ;根轨迹起始于开环极点; 当s=zi时, K1 →∞ ;终止于开环零点; 当|s|→∞且n≥m时, K1 →∞。如果开环零点个 数m少于开环极点个数n,则有(n-m)条根轨迹终 止于无穷远处。
(5)两条根轨迹的交点方程为
其中sd为交点。
说明: 交点sd是指两支根轨迹会合后分离的点, 该点为闭环特征方程的重根
假设闭环特征方程有2个重根,则可将其 改写为
例3-6 单位负反馈系统开环传递函数为
试画出系统实轴上的根轨迹并求出系统根轨迹 的交点。
解: 由规则1),系统有3条根轨迹; 由规则3),3条根轨迹的起点为
(4)实轴上的根轨迹 实轴上的某一区域,若其右边开环实数零、 极点个数之和为奇数,则该区域必是根轨迹。 (如红线所示)
红色部分 为根轨迹
说明:以实轴上的s0点为例,根据相角条 件,分三个方面说明这个法则。
G ( s ) H ( s )
m n
(s z ) (s p )
解 系统有3条根轨迹分支,且3条根轨迹都趋 于无穷远处。 实轴上的根轨迹: ,2 1,0 渐近线:
根轨迹的交点满足以下方程
交点必须在根轨迹上,所以交点取
根轨迹与虚轴的交点及临界增益。
令s=iω
令实部及虚部分别为0
解得
第一组解为根迹的起点,第二组得根迹和虚轴的 交点 ,临界根轨迹增益为6
K s ( s 1)( s 2) K 1 s ( s 1)( s 2)
自动控制原理第3章

arctan 9 3
1.25rad
则响应为 y(t) 1 2 e 3t 0.95e j1.25e (1 j)t 0.95e j1.25e (1 j)t 5
1 2 e 3t 0.95e t e j(t1.25) e j(t1.25) 5 1 2 e 3t 1.9e t cos(t 1.25)
平衡位置:力学系统中,当系统外的作 D
用力为零时,位移保持不变的位置。
此时位移对时间的各阶导数为零。 A点和D点是平衡位置, B点和C点不是平衡位置。
O
B
C
A
稳定的平衡位置:若在外力作用下,系统偏离了平衡位置,但 当外力去掉后,系统仍能回到原来的平衡位置,则称这一个平 衡位置是稳定的平衡位置。
所以A点是稳定的平衡位置,而D点不是稳定的平衡位置。
注意:输入信号为非单位阶跃信号时,依齐次性,响应 只是沿纵轴拉伸或压缩,基本形状不变。所以ts 、 tr、 tp 、 σ并不发生变化。
当t < ts时,称系统处于动态;当t > ts时,称系统处于稳态。
3.2 一阶系统的单位阶跃响应
一阶系统(惯性环节)
G(s) 1 Ts 1
单位阶跃响应为
t
y(t) 1 e T
设零初始状态,y(0)=0 r (t)=1(t)时,y(t)的响应曲线为
y(t)
1.05 y(∞)
ym
y(∞)
0.95 y(∞)
tr tp
ts
ym:单位阶跃响应的最大偏离量。 y(∞):单位阶跃响应的稳态值。并非期望值。 ts:调节时间。y(t)进入0.5*y(∞)或0.2* y(∞)构成的误差带 后不再超出的时间。 tr:上升时间。 y(t) 第一次达到 y(∞)的时间。
自动控制原理-第3章

响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
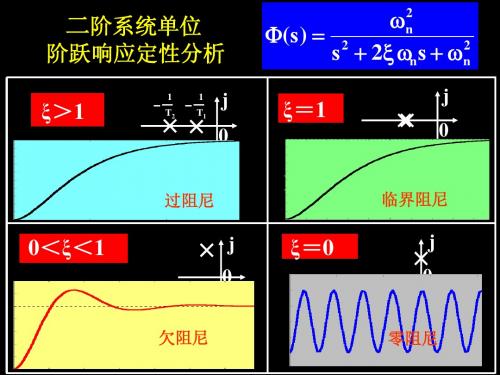
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4<ζ<0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法
自控(第六版 胡寿松)第三章

3.1
时间响应性能指标
3.2
3.3
一阶系统的时域响应
二阶系统的时域响应
3.4
3.5
系统的稳定性分析
系统稳态性能分析
2
3.1
时间响应性能指标
工程实际中,有些系统的输入信号是已知的(如恒值系 统),但对有些控制系统来说,常常不能准确地知道其输 入量是如何变化的(如随动系统)。
因此,为了方便系统的分析和设计,使各种控制系统有一 个进行比较的统一的基础,需要选择一些典型试验信号作 为系统的输入,然后比较各种系统对这些输入信号的响应。
11
y(t) p
1 0.5 0
稳态误差
td tr t p
ts
t
峰值时间tp:响应超过其稳态值到达第一个峰值所需时间。 调节时间ts:响应到达并保持在稳态值内所需时间。 超调量%:响应的最大偏离量h(tp)与稳态值h(∞)之差的百 分比,即 h( t p ) h() % 100% h() 稳态性能:由稳态误差ess描述。
17
3.2.2 单位斜坡响应
设系统的输入为单位斜坡函数r(t)=t,其拉氏变换为 R( s ) 1 / s 2 则输出的拉氏变换为
C ( s) 1 1 1 T T 2 2 Ts 1 s s s s 1
t T
T
t T
r(t)=t
C ( t ) t T Te
R( s ) L[ r ( t )] A ( t )e st dt
0
A ( t )e dt A ( t )e st dt A
st 0 0
0
单位脉冲函数的拉氏变换为R(s)=1。
《自动控制原理》第三章-3-5-稳态误差计算

伺服电动机
R(s)
E(s)
1
C(s)
-
s(s 1)
K 1, 1
r(t) 1(t),k p , ess 0
r(t) t, kv 1, ess 1
r(t)
1 2
t2, ka
0, ess
位置随动系统
能源与动力学院 第三章 线性系统的时域分析法
14
4.扰动作用下稳态误差
R(s)
-
E(s)
R(s) E(s) 20
s4
N (s)
+
2
C(s)
s(s 2)
能源与动力学院 第三章 线性系统的时域分析法
28
3-20
R
-
K1
U
K2 S(T1S 1)
C
G(s)
K1K 2
B
s(T1s 1)(T2s 1)
1 T2S 1
(s)
C(s) R(s)
T1T2 s 3
K1K2 (T2s 1) (T1 T2 )s2 s
1
能源与动力学院 第三章 线性系统的时域分析法
7
3.输入作用下稳态误差计算
(1)阶跃作用下的稳态误差
r(t) R 1(t), R(s) R s
ess
Lim sR(s) s0 1 G(s)H (s)
Lim s1R(s)
s0
K Lim s
s0
1
R LimG(s)H (s)
Lim s R
s0
K Lim s
27
参考答案: Kp= ,kv=5,ka=0,essr=0.4,essn=-0.2
四、控制系统如图, r(t) 1 2t, n(t) 1(t), 试计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当H=1时,称为单位脉冲信号,记为 (t)。如果令 0,则称为单位理
想脉冲函数,如图所示,并用 (t) 表示。
2020/2/6
第三章 线性控制系统的时域分析
4
自动控制原理
典型输入信号
• 5.正弦信号
r(t) Asin t
实际工作中,如:电源的波动、机械振动、元件的噪声干扰、海浪对 舰艇的扰动力等均可视为正弦作用。另外,还可以用不同频率的正弦 输入,得到系统的频率特性,据此判断系统的性能。 在分析控制系统时,究竟采用哪一种输入信号,取决于系统正常工作 时,最常见、最不利的输入情况。但是无论选用哪一种输入信号,系 统表现的性能是一样的。
是由 R(s) 的极点形成; e T 为暂态分量,当 t 时, e T 0 ,暂态分量是由传递函
数的极点形成。一阶系统的单位阶跃响应是一单调上升的指数曲线,如图 3.6 所示。
2020/2/6
第三章 线性控制系统的时域分析
12
自动控制原理
一阶系统的时域分析
图3.6 一阶系统的单位阶跃响应
自动控制原理
第3章 线性控制系统的时域分析
2020/2/6
第三章 线性控制系统的时域分析
1
自动控制原理Biblioteka 3.1 系统时间响应的性能指标
一个控制系统的时域响应 不仅取决于系统本身的结构和 参数,即系统的传递函数 ,而且和系统的初始状态以及系统 的输入信号有关。为便于研究,规定系统在外加输入信号之 前是相对静止的,即为零初始状态。
一阶系统的数学模型
T dc(t) c(t) r(t) dt
式中,c(t) 为电路的输出电压;r(t) 为电路的输入电压,T RC ,T为时间 常数。
零初始条件下,其传递函数为
C(s) G(s) 1
R(s)
Ts 1
2020/2/6
第三章 线性控制系统的时域分析
10
自动控制原理
一阶系统的时域分析
2020/2/6
第三章 线性控制系统的时域分析
6
自动控制原理
动态性能与稳态性能
图3.3 系统的单位阶跃响应
2020/2/6
第三章 线性控制系统的时域分析
7
自动控制原理
动态性能与稳态性能
• (1)延迟时间 阶跃响应曲线从零第一次到达稳态值的10% 所需的 时间。
• (2)上升时间 阶跃响应曲线从零第一次上升到稳态值所需的时间。 若阶跃响应曲线为过阻尼的单调变化状态,其响应不超过稳态值,则 定义阶跃响应曲线从稳态值的10%上升到90%所需的时间为上升时间。
(a)RC电路
(b)一阶系统框图
(c)等效框图 图:一阶系统及结构框图
2020/2/6
第三章 线性控制系统的时域分析
11
自动控制原理
一阶系统的时域分析
• 一阶系统的时域响应
1)单位阶跃响应
设 r(t) 为单位阶跃输入,即 r(t) 1(t) , R(s) 1 s ,零初始条件下一阶系统单位阶跃
控制系统的实际输入信号往往是未知的,为了便于对系 统进行分析和设计,常需要一些输入函数作为测试信号。根 据其响应情况,对系统的性能作出评价。选取的测试信号应 具有下列特点:
• (1)能反映系统工作时的实际情况;
• (2)易于在实验室中获得;
• (3)数学表达形式简单,以便数学上的分析和处理。
2020/2/6
2020/2/6
第三章 线性控制系统的时域分析
5
自动控制原理
动态性能与稳态性能
• 1)稳定性
• 稳定性是控制系统分析和设计中最为重要的概念,也是对控制系统性 能的最基本要求,是控制系统在各种非理想条件下能够可靠工作,对 外部扰动有自调节能力的前提条件。
• 2)稳态性能
• 稳态误差 :指稳态响应的期望值与实际值的差值。若系统输入为单位 阶跃信号,则
2020/2/6
第三章 线性控制系统的时域分析
13
自动控制原理
一阶系统的时域分析
一阶系统的单位阶跃响应具有两个特征: • 时间常数 为表征响应特性的唯一参数 • 响应曲线的初始上升斜率为 1/T
响应的拉氏变换为
C(s) 1 R(s) 1 1 T
Ts 1
s(Ts 1) s Ts 1
(3.9)
对上式取拉氏反变换,得
1t
c(t) 1 e T
(3.10)
由式(3.10)可见,一阶系统的单位阶跃响应包含两个分量:“1”为稳态分量,c(t) 的终值,
1t
1t
第三章 线性控制系统的时域分析
2
自动控制原理
典型输入信号
• 1.阶跃信号
r
(t)
0,
t0
R0 , t 0
(a)阶跃信号
当阶跃信号的幅值为1,即 时,称为单位阶跃信号。
• 2.斜坡信号
r(t)
0,
t0
v0t, t 0
当v0 1 时,称为单位斜坡信号。
(b)斜坡信号
• (3)峰值时间 阶跃响应曲线超过稳态值到达第1个峰值所需的时 间。
• (4)调节时间 阶跃响应曲线到达并保持在其稳态值允许的误差范 围(即误差带)内所需的时间,通常误差范围定义为5%c() 或2%c()。
• (5)超调量 阶跃响应曲线的最大值 cmax 与其稳态值c() 之差与稳态 值的百分比,即
M
p
%
c(tp ) c() c()
100%
2020/2/6
第三章 线性控制系统的时域分析
8
自动控制原理
抗扰动性能
系统突加扰动的动态过程
2020/2/6
第三章 线性控制系统的时域分析
9
自动控制原理
3.2 控制系统的时域分析
• 一阶系统时域分析
用一阶微分方程式描述的控制系统称为一阶系统。它是工程中最基 本、最简单的系统,如:RC电路、热处理器、体温计等,均为一阶系统 的实例。
• 稳态误差是系统控制精度的一种度量,若稳态误差 ,则称系统是无静 差的,反之称系统是有静差的。
• 3)动态性能
• 稳定是控制系统能够运行的首要条件,因此只有当动态过程收敛时, 研究系统的动态性能才有意义。系统的输出能准确地跟踪或复现阶跃 输入时,认为是较为严格的工作条件,所以评价系统时域性能指标, 通常是根据系统的单位阶跃响应确定。
2020/2/6
第三章 线性控制系统的时域分析
3
自动控制原理
典型输入信号
• 3.等加速度信号
0, t 0
r
(t
)
1 2
a0t
2
,
t0
当a0 1时,称为单位等加速度信号。
• 4.脉冲信号
(c)等加速度信号
0, t 0, t
r (t )
H
,
0t
