清华大学材料力学习题详解(范钦珊)第6章
清华大学材料力学范钦珊主讲---第六章--弹性杆件位移分析

约束对位移的影响
连续光滑曲线;铰支座对位移的限念
约束对位移的影响
连续光滑曲线;固定端对位移的限制
第6 章
弹性杆件位移分析
确定梁位移 的积分方法
第6章
弹性杆件位移分析
确定梁位移的积分方法
对于拉伸(压缩)、扭转位移定积分 对于梁的位移不定积分
弹性曲线的小挠度微分方程 弯矩方程的两种写法及其利弊
第6 章
弹性杆件位移分析
奇异函数的应用
梁挠度方程的 奇异函数形式 (2)挠度微分方程
w M ( x) 3 F x F x l EI d P 4 4 P dx
2 2
1
(3)微分方程的积分
2 F 3 d w EI dx EI 8 FP x P 2 3 F 3 l P EIw 1 F x x 6 4 8 P
F P1
M1
q1
F P2
q2
M2
F P3
第6章
弹性杆件位移分析
奇异函数的应用
集 中 力 偶 作 用 的 情 形
弯矩方程的奇异函数表示
M ( M i ) M i x ai
0
第6章
弹性杆件位移分析
奇异函数的应用
弯矩方程的奇异函数表示
集 中 力 作 用 的 情 形
j
M ( FP j ) FP j x b j
xa
n
0
( x a)
( x a)
n
( x a)
第6章
弹性杆件位移分析
奇异函数的应用
奇 异 函 数 图 形
第6章
弹性杆件位移分析
奇异函数的应用
清华出版社工程力学答案-第6章 拉压杆件的应力变形分析与强度设计

∑ Fx = 0 , FNAC cos 45D + FNAD = 0
解得 AD 杆轴力大小为: FNAD = 15kN(拉)
2. 强度条件
拉杆:
AAD
=
FNAD [σ ]+
=
15 ×103 120 ×10−6
= 125mm2
压杆:
AAC
=
2. 钢杆的伸长量:
ΔlBC
=
FPlBC Es As
=
60×103 × 2.1 200×109 × π ×152 ×10−6
= 3.565mm
4
3. 钢杆 C 端向下移动的距离: uC = ΔlAB + ΔlBC = 0.935 + 3.565 = 4.50 mm
6-3 螺旋压紧装置如图所示。现已知工件所受的压紧力为 F=4 kN。装置中旋紧螺栓
10
习题 6-10 图
解:1.活塞杆 受到的轴力为:
FN
=
pA
=
p
⎡π ⎢ ⎣
(
D
2− 4
d2)⎤ ⎥ ⎦
=
⎡π 2.5⎢
⎣
(5602 − 4
1002
)
⎤ ⎥ ⎦
=
596.12kN
活塞杆的正应力: σ = FN = 596.12 ×103 = 75.9MPa A杆 π ×1002 / 4
工作安全系数: n = σ s = 300 = 3.95 σ 75.9
弹性模量E和泊松比ν 。
l0
b
解:1.计算弹性模量E
h 习题 6-11 图
11
εx
=
材料力学_范钦珊_习题参考解答
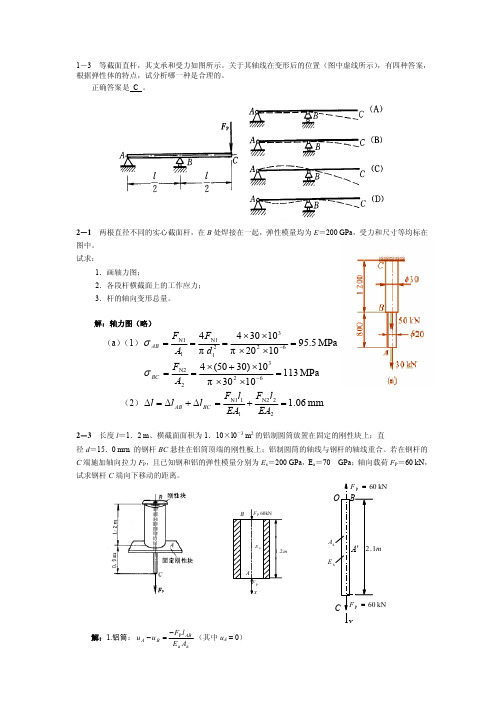
2-11 图示组合柱由钢和铸铁制成,组合柱横截面为边长为 2b 的正方形,钢和铸铁各占横截面的一 半(b×2b)。载荷 FP,通过刚性板沿铅垂方向加在组合柱上。已知钢和铸铁的弹性模量分别为 Es=196 GPa, Ei=98.0 GPa。今欲使刚性板保持水平位置,试求加力点的位置 x=?
解: ∑ M 0
( ) ( ) τmax
AB
= M xAB WPAB
= M xAB πd13
= π×
2936 70 ×10-3
3
= 43.6 MPa
16
16
BC 段:
M xBC = M e1 = 1171 N ⋅ m
( ) ( ) τmax
BC
=
M xBC WP 2
= M xBC
πd
3 2
= π×
1171 50 ×10−3
解:1. τ1max
=
Mx WP
=T WP
=T πd 3
= 3 ×103 ×16 = 70.7 MPa π× 0.063
16
∫ ∫ 2.
Mr =
ρ ⋅τdA =
A1
r
ρ
⋅
M
x
ρ ⋅ 2πρdρ
=
2πM x
⋅
r4
0 Ip
Ip
4
M r = 2πr 4 = 2πr 4 = 16r 4 = 16 × (15 )4 = 1 = 6.25%
Mx
4Ip
4 ⋅ πd 4
d4
60 16
32
3.
τ 2 max
=
Mx Wp
=
T
=75.4MPa
πd 3 ⎜⎛1 − ( 1 )4 ⎟⎞
高教范钦珊材料力学习题集_【有答案】

习题1-1图 习题1-2图习题1-3图习题1-4图习题1-5图习题1-6图 材料力学习题集第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图ABABC)(ql 2lM QF QF 454141第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A ))(d d Q x q x F =;Q d d F x M=; (B ))(d d Q x q x F -=,Q d d F x M-=; (C ))(d d Q x q x F -=,Q d d F x M=; (D ))(d d Q x q x F =,Q d d F xM-=。
理论力学课后问题详解(范钦珊)
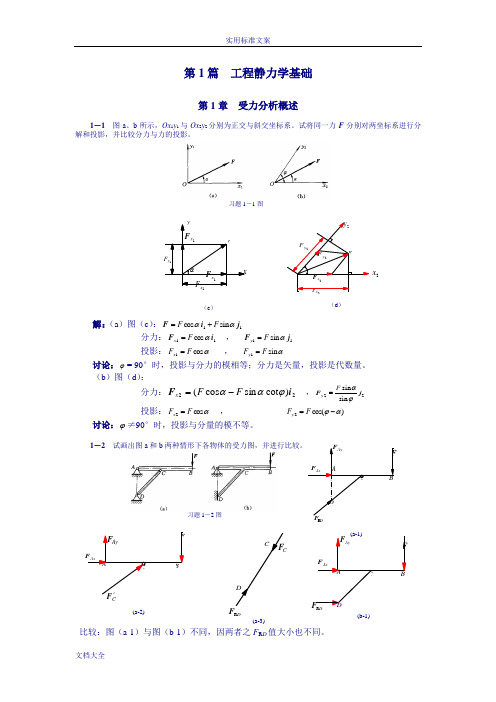
C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 s i n c o s j i F ααF F +=分力:11 cos i F αF x = , 11 s i n j F αF y =投影:αcos 1F F x = , αs i n 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
(c )2x(d )1-3 试画出图示各物体的受力图。
习题1-3图B或(a-2)(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D ,则A 端受力改变,因为HG 与ABC 为不同的刚体。
1(f-1)'A(f-2)1(f-3)F F'F 1(d-2)AF yB 21(c-1)F A B1FDx y(b-2)1(b-3)F yB 2 F A B1B F习题1-5图AxF'(b-3)E D(a-3)B(b-2)(b-1)F 'CDDF EFBC(c)AxF1-6 试画出图示连续梁中的AC 和CD 梁的受力图。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第6章 圆轴扭转

习题 6-6 图
τ 套 max =
Mx Wp 2
T2 ≤ 60 × 10 6 ×
∴
Tmax ≤ T2 = 2883 N·m = 2.88 ×10 3 N·m
4
6-7 由同一材料制成的实心和空心圆轴,二者长度和质量均相等。设实心轴半径为 R0,空心圆轴的内、外半径分别为 R1 和 R2,且 R1/R2 =n;二者所承受的外加扭转力偶矩分 别为 Mes 和 Meh。若二者横截面上的最大剪应力相等,试证明:
该轴的扭转强度是安全的。
上一章
返回总目录
下一章
8
3
习题 6-5 图
解:1. τ 1 max =
Mx T T 3 × 10 3 × 16 = = = = 70.7 MPa WP WP π π× 0.06 3 d3 16
A1
2. M r =
∫
ρ ⋅ τdA =
∫
r
0
ρ⋅
2πM x r 4 Mx ρ ⋅ 2πρ d ρ = ⋅ 4 Ip Ip
Mr r4 r4 1 2π 2π 16r 4 15 = = = = 16 × ( ) 4 = = 6.25% 4 4 Mx 16 4I p 60 d d π 4⋅ 32 Mx T = 3. τ 2 max = =75.4MPa Wp 1 4⎞ π d3 ⎛ ⎜1 − ( ) ⎟ 16 ⎝ 2 ⎠
eBook
工程力学
(静力学与材料力学)
习题详细解答
(教师用书) (第 6 章) 范钦珊 唐静静
2006-12-18
1
第 6 章 圆轴扭转
材料力学课后答案范钦珊

材料力学课后答案范钦珊第一篇:材料力学课后答案范钦珊材料力学课后答案范钦珊普通高等院校基础力学系列教材包括“理论力学”、“材料力学”、“结构力学”、“工程力学静力学材料力学”以及“工程流体力学”。
目前出版的是前面的3种“工程力学静力学材料力学”将在以后出版。
这套教材是根据我国高等教育改革的形势和教学第一线的实际需求由清华大学出版社组织编写的。
从2002年秋季学期开始全国普通高等学校新一轮培养计划进入实施阶段新一轮培养计划的特点是加强素质教育、培养创新精神。
根据新一轮培养计划课程的教学总学时数大幅度减少为学生自主学习留出了较大的空间。
相应地课程的教学时数都要压缩基础力学课程也不例外。
怎样在有限的教学时数内使学生既能掌握力学的基本知识又能了解一些力学的最新进展既能培养学生的力学素质又能加强工程概念。
这是很多力学教育工作者所共同关心的问题。
现有的基础教材大部分都是根据在比较多的学时内进行教学而编写的因而篇幅都比较大。
教学第一线迫切需要适用于学时压缩后教学要求的小篇幅的教材。
根据“有所为、有所不为”的原则这套教材更注重基本概念而不追求冗长的理论推导与繁琐的数字运算。
这样做不仅可以满足一些专业对于力学基础知识的要求而且可以切实保证教育部颁布的基础力学课程教学基本要求的教学质量。
为了让学生更快地掌握最基本的知识本套教材在概念、原理的叙述方面作了一些改进。
一方面从提出问题、分析问题和解决问题等方面作了比较详尽的论述与讨论另一方面通过较多的例题分析特别是新增加了关于一些重要概念的例题分析著者相信这将有助于读者加深对于基本内容的了解和掌握。
此外为了帮助学生学习和加深理解以及方便教师备课和授课与每门课材料力学教师用书lⅣ程主教材配套出版了学习指导、教师用书习题详细解答和供课堂教学使用的电子教案。
本套教材内容的选取以教育部颁布的相关课程的“教学基本要求”为依据同时根据各院校的具体情况作了灵活的安排绝大部分为必修内容少部分为选修内容。
材料力学高教第二版范钦珊第6章习题答案要点

材料力学_高教第二版_范钦珊_第6章习题答案第6章杆件横截面的位移分析6-1 直径d = 36mm的钢杆ABC与铜杆CD在C处连接,杆受力如图所示。
若不考虑杆的自重,试: 1.求C、D二截面的铅垂位移;Fl2.令FP1 = 0,设AC段长度为l1,杆全长为l,杆的总伸长,写出E的表达式。
EA习题6-1图(a) (F)l(F)l解:(1)πdπdEsEs2332(FN)CDlCDπdEc4(2)EAEsAEcAEEsEclEcEs令FP6-2 承受自重和集中载荷作用的柱如图所示,其横截面积沿高度方向按材料的比重。
试作下列量的变化曲线: 1.轴力FNx(x); 2.应力; 3.位移u(x)。
解:(1),(FN变化,其中为FPFN(x)-FPx习题6-2图(a)FPFPA0FP(2)A(x)A0eFPFP— 89 —(3)A0,当。
∴,则EA0EA0EA06-3 图示连接件由两片宽20mm、厚6mm的铜片与一片同样宽厚的钢片在B处连接而成。
已知钢与铜的弹性模量分别为Es = 200GPa,Ec =105GPa,钢片与铜片之间的摩擦忽略不计。
试求E和B处的位移。
F习题6-3图解:6-4 长为1.2m、横截面面积为的铝制筒放置在固定刚块上,直径为15.0mm的钢杆BC悬挂在铝筒顶端的刚性板上,若二者轴线重合、载荷作用线与轴线一致,且已知钢和铝的弹性模量分别为kNEs = 200Gpa,Ea = 70GPa,FP = 60kN。
试求钢杆上C处位移。
Am EkN(a) 习题6-4图 (b)解:(其中uA = 0) EaAa ∴钢杆6-5 变截面圆锥杆下端B处固定,上端A处承受外力偶矩T作用,如图所示,试证明A端扭转角表达式为解:Mx = T习题6-5图6-6 试比较图示二梁的受力、内力(弯矩)、变形和位移,总结从中所得到的结论。
(a) 解:(b) wmaxFPl3 48EIFlEI— 90 —两者弯矩相同,挠曲线曲率相同,但(b)梁的最大挠度比(a)梁要大,即不相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I y + Iz
−
= ( 9.422 − 8.223) ×106 = 1.199 × 106 mm 4 = 1.199 × 10−6 m 4 Iz0 = I y + Iz 2 I y + Iz + 1 2 −
(I
y
− I z ) + 4 ( I yz )
2
2
I y0 =
= ( 9.422 + 8.223) × 106 = 1.765 × 107 mm 4 = 1.765 × 10−5 m 4
组合图形对于 z 轴的惯性矩:
Iz =
其中
⎛ 100 × 803 π642 ⎞ − 2 ⎜1.15 × 105 + a 2 × ⎟ 12 8 ⎠ ⎝
a = 40 −
代入上式后,算得
2 × 64 = 26.4 mm 3π
Iz =
⎛ 100 × 803 π642 ⎞ 6 4 − 2 ⎜1.15 ×105 + 26.42 × ⎟ = 1.792 × 10 mm 12 8 ⎠ ⎝
解:若用右手系,z 轴坐标朝上为正,则由 h1 = b1 得
—7—
习题 6-7 图
3 S y (I) = b1h12 > 0 , S y (II) = −2b1h12 < 0 2
若考虑正负号,正确答案是 A;若考虑静矩的绝对值,则正确答案为 B。
6-8 图示矩形中 y1、z1 与 y2、z2 为两对互相平行的 坐标轴。试判断下列关系式中,哪一个是正确的。
2、计算 Iz 取微面积如图 b 所示:
⎛ y⎞ dA = −h( y )dy = −h ⎜ 1 − ⎟ dy ⎝ b⎠
I z = −∫
3、计算 Iyz 由图 b,
−b
0
hb3 ⎛ y⎞ y h ⎜ 1 − ⎟ dy = 12 ⎝ b⎠
2
I yz = ∫ yzdA = ∫ yzb( z )dz
A A
(A) ( B) ( C) ( D)
正确答案是 C
I y 2 z 2 = I y1z1 > 0; I y 2 z 2 < I y1z1 = 0; I y 2 z 2 > I y1z1 = 0; I y 2 z 2 = I y1z1 < 0.
。
习题 6-10 图
6-11 半圆形截面如图所示,其 C 为形心。关于截 面对 y、z 轴的惯性矩,有下列结论,试判断哪一个是正确的。
b( z ) =
b z h b( z ) b y=− =− z 2 2h
—3—
b2 h2 ⎛ b ⎞ ⎛b ⎞ I yz = ∫ yzb( z )dz = ∫ ⎜ − z ⎟ z ⎜ z ⎟ dz = − A 2h ⎠ ⎝ h ⎠ 8 0⎝
h
6-2 试确定图中所示图形的形心主轴和形心主惯性矩。 解: (a)题:
(b)题: 先求图形心位置:z 轴为对称轴,所以形心必在 z 轴上。 yC = 0
—4—
100 × 60 × ( −20 ) − 0 = 25.3 mm π × 402 100 × 60 − 4 3 100 × 60 π × 404 Iz = − = 1.674 × 106 mm 4 12 64 3 ⎛ 60 ×100 ⎞ ⎛ π × 404 π × 402 ⎞ Iy = ⎜ + 5.32 × 100 × 60 ⎟ − ⎜ + 25.32 × ⎟ 4 ⎠ ⎝ 12 ⎠ ⎝ 64 zC = = ( 5.0 + 0.1674 ) ×106 − ( 0.1256 + 0.8044 )×106 = 4.239 × 106 mm 4
(A) ( B) ( C) ( D)
S z 1 = − S z 2 , S y1 = − S y 2 , I y1 z 1 = I y 2 z 2 ; S z 1 = − S z 2 , S y1 = − S y 2 , I y1 z 1 = − I y 2 z 2 ; S z 1 = − S z 2 , S y1 = S y 2 , I y1 z 1 = I y 2 z 2 ; S z 1 = S z 2 , S y1 = S y 2 , I y1 z 1 = − I y 2 z 2 .
I yz = I yz (1) + I yz ( 2 ) + I yz ( 3) = 0 + 2 I yz ( 2 ) = 0+ 2⎡ ⎣0 − ( 20 × 70 × 70 × 30 ) ⎤ ⎦ = 2 × −49.6 ×104 = −5.88 × 106 mm 4
3、确定形心主轴与 z 轴的夹角
6-3 几何图形尺寸如图所示(单位为 mm) 。试: 1、 确定形心主轴与水平方向的夹角; 2、 确定形心主惯性矩。
(a) 习题 6-3 图
(b)
解:1、确定形心位置 将组合图形分解为 1、2、3 三个矩形。根据反对称性,矩形 1 的形心 C1 即为组合图形 的形心。 2、建立初始坐标系,确定组合图形对于初始坐标系的惯性矩与惯性积 以 C1 为坐标原点,奖励 C1zy 坐标系,利用叠加的方法,求组合图形对于 z、y 轴的惯 性矩与惯性积
b ⎡ ⎤ I z = 2 ⎢ I z 1 + ( y0 + ) 2 A ⎥ 2 ⎣ ⎦
习题 6-4 图
—6—
若 Iy = Iz,则
b I y 1 = I z 1 + ( y0 + ) 2 A 2 ⎛ I −I ⎞ ⎛ 1780.4 − 128 ⎞ 2.01 b = 2 ⎜ y1 z1 − y0 ⎟ = 2 ⎜ − ⎟ ⎜ ⎟ = 11.11 cm=111.1mm ⎜ ⎟ 28.83 A ⎝ ⎠ ⎝ ⎠
2 2 1 I y − I z ) + 4 ( I yz ) ( 2 2 2 2⎤ ⎡ 3.674 + 15.17 1 × 106 =⎢ + ( 3.674 − 15.17 ) + 4 ( −5.88) ⎥ 2 2 ⎣ ⎦
6-4 图中所示组合截面为两根 No.20a 的普通热轧槽 形钢所组成的截面,今欲使 Ix = Iy,试求 b =?(提示:计算 所需要数据均可由型钢表中查得。 ) 解:由型钢表查到 No.20a 普通热轧槽钢 Iy1 = 1780.4 cm4,Iz1 = 128 cm4 yO = 2.01cm,A = 28.83cm2 Iy= 2Iy1
(a) 习题 6-2 图
(b)
图中 y、z 即为形心主轴
Iy =
80 ×1003 π 644 − = 5.84 ×106 mm 4 12 64
2
半圆对于自身形心轴的惯性矩:
I z′ =
π 644 ⎛ 2 × 64 ⎞
π642 −⎜ × = 1.15 × 105 mm 4 ⎟ 128 ⎝ 3π ⎠ 8
—8—
(A)
πd 4 πd 4 ⎛ 2d ⎞ πd 2 I y = Iz = , I y1 = ; +⎜ ⎟ 64 64 ⎝ 3π ⎠ 8 πd 4 πd 4 ⎛ 2d ⎞ πd 2 , I y1 = ; +⎜ ⎟ 128 128 ⎝ 3π ⎠ 8
2 ⎛ 2d ⎞ πd ; −⎜ ⎟ ⎝ 3π ⎠ 8 2 2 2
D 。
习题 6-5 图
解:正确答案是
6-6 图示 T 字截面中 z 轴通过组合图形的形心 C,两个矩形分别用 I 和 II 表示。试判 断下列关系式中哪一个是正确的。
(A) ( B) ( C) ( D)
S y ( I ) > S y ( II ) ; S y ( I ) = S y ( II ) ; S y ( I ) = − S y ( II ) ; S y ( I ) < S y ( II )。
2
( B) I y = I z = ( C) (A)
解:正 = I y = Iz = 128 128 I y = Iz =
C 。
πd 4 πd 4 ⎛ 2d ⎞ πd 2 , I y1 = −⎜ 。 ⎟ 64 64 ⎝ 3π ⎠ 8
习题 6-11 图
上一章
返回总目录
下一章
—9—
I y = I y (1) + I y ( 2 ) + I y ( 3) = ⎡ 70 × 203 ⎤ 120 × 103 + 2⎢ + 20 × 70 × 302 ⎥ 12 ⎣ 12 ⎦
(
)
= 1× 104 + 2 57.2 × 104 + 126 × 104 = 3.674 × 106 mm 4
—5—
(
)
I z = I z (1) + I z ( 2 ) + I z ( 3) ⎡ 20 × 703 ⎤ 10 × 1203 = + 2⎢ + 702 × 20 × 30 ⎥ 12 ⎣ 12 ⎦
(
)
= 1.44 ×106 + 2 4.667 × 104 + 6.86 × 106 = 15.17 × 106 mm 4
范钦珊教育教学工作室
FAN Qin-Shan’s Education & Teaching Studio
eBook
材料力学习题详细解答
教师用书
(第 6 章)
2006-01-18
—1—
习题 6-1 习题 6-3 习题 6-5 习题 6-7 习题 6-9
习题 6-2 习题 6-4 习题 6-6 习题 6-8 习题 6-10
习题 6-11
—2—
第 6 章 梁的弯曲问题(2)截面的几何性质
6-1 图示的三角形中 b、h。试用积分法求 Iz、Iy、Iyz 。 解:1、计算 Iy 取微面积如图 b 所示:
(a)
(b) 习题 6-1 图
(c)
dA = b ( z ) dz , b ( z ) =
